New tuning rules for PID controllers based on IMC with minimum IAE for inverse response processes

In this paper new tuning rules for Proportional Integral Derivative (PID) are presented, which are based on Internal Model Control (IMC). This set of equations minimizes the performance index, in this case, the Integral Absolute Error (IAE). Furthermore, a correlation is proposed in order to calculate the tuning parameter of the method, where a holding oscillation response is obtained regarding changes in the set point. This value represents a stability limit for the IMC method. The overall development is then applied to an Inverse Response System of second order and with dead time.

DOI: https://doi.org/10.15446/dyna.v82n194.46744

Nuevas reglas de sintonía basadas en IMC para un controlador PID con IAE mínimo en procesos con respuesta inversa

Duby Castellanos-Cárdenas ^a & Fabio Castrillón-Hernández ^b

^a Facultad de Ingeniería, Universidad de Medellín, Medellín, Colombia. dcastellanos@udem.edu.co
^b Escuela de Ingeniería, Universidad Pontificia Bolivariana, Medellín, Colombia. fabio.castrillon@upb.edu.co

Received: October 23^th, 2014. Received in revised form: March 13^th, 2015. Accepted: October 10^th, 2015.

This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.

---

Abstract
In this paper new tuning rules for Proportional Integral Derivative (PID) are presented, which are based on Internal Model Control (IMC). This set of equations minimizes the performance index, in this case, the Integral Absolute Error (IAE). Furthermore, a correlation is proposed in order to calculate the tuning parameter of the method, where a holding oscillation response is obtained regarding changes in the set point. This value represents a stability limit for the IMC method. The overall development is then applied to an Inverse Response System of second order and with dead time.

Keywords: Inverse Response, PID Controller, Internal Model Control, IAE, Experimental Design.

Resumen
En este artículo se presentan nuevas reglas de sintonía para un controlador PID (Proporcional Integral Derivativo) basado en IMC (por sus siglas en inglés Internal Model Control). Este conjunto de ecuaciones minimiza un índice de desempeño óptimo, para este caso la Integral del Error Absoluto (IAE por sus siglas en inglés, Integral Absolute Error). Adicionalmente se presenta una correlación para calcular el valor crítico del parámetro de sintonía del método, 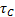, donde se obtiene una respuesta de oscilación sostenida frente a cambios en el punto de control. Este valor representa un límite de estabilidad para el método IMC. Todo este desarrollo es aplicado a un Sistema con Respuesta Inversa (SRI) de segundo orden y con tiempo muerto.

Palabras clave: Respuesta Inversa, controlador PID, Control por Modelo Interno, Integral del Error Absoluto, Diseño de Experimentos.

---

1. Introducción

El comportamiento de los sistemas con respuesta inversa (SRI) ha sido de interés en muchos trabajos académicos ya que a nivel industrial se pueden encontrar sistemas que exhiben este tipo de dinámica [1]. Algunos ejemplos de procesos con respuesta inversa son: el nivel en una caldera de vapor y en la sección del rehervidor de una columna de destilación, la temperatura tanto en reactores catalíticos exotérmicos como en reactores tubulares adiabáticos [1-3], el caudal de silicio en reactores para la producción de silicio de metal [4] y el caudal de vapor en plantas de incineración de residuos [5].

En este tipo de procesos aparecen problemas asociados con el comportamiento dinámico que dificultan su control y que generan limitaciones importantes en el rendimiento y robustez del sistema. Por este motivo las técnicas de control tradicional presentan un bajo desempeño cuando son aplicadas a este tipo de plantas. Estos inconvenientes se hacen más notorios cuando el proceso también presenta tiempo muerto [2,6].

Aunque son varios los métodos de control de SRI que se reportan en la literatura, estos pueden agruparse básicamente en dos tipos de estructuras de control: compensadores de respuesta inversa, que generalmente utilizan el concepto del predictor de Smith para sus diseños; y controladores PID en los que se han utilizado muchas técnicas de sintonía [7].

En general, los compensadores basados en el predictor de Smith eliminan el tiempo muerto de la ecuación característica del sistema, colocan los ceros de fase no mínima fuera del lazo de realimentación, arrojan controladores con una alta sensibilidad a errores en los parámetros del modelo y se consideran útiles en procesos que presentan un tiempo muerto significativo [7,8].

Con relación a los controladores PID aplicados a procesos con respuesta inversa y tiempo muerto, se han obtenido muy buenos resultados, inclusive en uno de los primeros trabajos realizados sobre el tema se compararon las ventajas poco significativas de las estructuras de control para compensar la presencia de polos y ceros complejos frente al control PID convencional propuesto por Ziegler y Nichols [9]. Una de las razones del éxito del controlador PID reside en la acción derivativa que logra anticipar la dirección errónea en la respuesta inicial del sistema [7]. Además, gracias al desarrollo de los componentes de hardware y software necesarios para su implementación, el control PID es el más utilizado a nivel industrial [10,11].

En este trabajo se introduce un conjunto de reglas de sintonía para un controlador PID sintonizado ante cambios tipo escalón en la perturbación para SRI de segundo orden más tiempo muerto, ya que son sistemas que no se analizan comúnmente en la literatura por su complejidad, debido al orden del sistema y la inclusión del tiempo muerto. Las correlaciones obtenidas minimizan el índice de desempeño IAE lo que se traduce en un beneficio para los usuarios de este tipo de sistemas.

En la primera parte del artículo se explican las características de los SRI, luego se presenta tanto la técnica de sintonía como la metodología utilizada para el desarrollo de las reglas propuestas. A continuación se introducen las correlaciones halladas y, con el fin de verificar la validez de estas, se compara un controlador sintonizado con el método propuesto con otros controladores sintonizados con algunas reglas reportadas por la literatura. Finalmente se presentan las conclusiones del trabajo realizado.

2. Sistemas con respuesta inversa

Un SRI se caracteriza por tener uno o más ceros de fase no mínima. Cuando este tipo de proceso es excitado con una entrada tipo escalón, la respuesta inicial del sistema es opuesta al valor final de estado estable. Este efecto se debe a que en el proceso se ponen en marcha dos fenómenos físicos con dinámicas opuestas. Un primer fenómeno al que se le asocia una función de transferencia con ganancia pequeña y de respuesta rápida, responsable de que el sistema responda en forma inversa inicialmente; y un fenómeno más lento, con una ganancia mayor que la anterior y cuyo efecto finalmente predomina sobre el inicial [3,12,13].

La función de transferencia de un sistema con respuesta inversa de segundo orden con un retardo 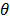, que es el sistema que se analiza en este trabajo, puede considerarse como:

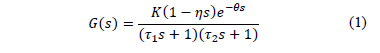
Donde 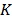es la ganancia del proceso, 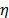determina el cero de fase no mínima, 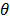corresponde al tiempo muerto y , son las constantes de tiempo.

En este tipo de procesos la pendiente de la respuesta en el origen es de signo opuesto a la ganancia y a medida que la magnitud del parámetro 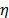se incrementa el comportamiento de inversión que aparece en la respuesta transitoria es mucho más pronunciado y las dificultades asociadas al control de este proceso aumentan. El valor de estado estable de un sistema con respuesta inversa es igual su ganancia [3,14,15].

En este tipo de procesos es común tener problemas de estabilidad y, cuando el SRI posee tiempo muerto, se puede presentar una salida no acotada para una excitación tipo escalón en la perturbación; adicionalmente aparecen limitaciones en el ajuste del controlador a bajas frecuencias [6,16].

3. Método de sintonía

En la literatura se han presentado algunos trabajos que estudian el problema del control de sistemas de primer o segundo orden con respuesta inversa, pero pocos autores han analizado SRI que además incluyan tiempo muerto. Como el fenómeno de la respuesta inversa presenta algunas similitudes con la respuesta de sistemas con tiempo muerto, es común encontrar técnicas de sintonía que utilizan la estructura del predictor de Smith [17]. Otras técnicas modelan el efecto del cero de fase no mínima como un tiempo muerto, con el fin de utilizar alguna técnica de sintonía tradicional para este tipo de procesos, aunque esto origina controladores mucho más conservativos [7,16,18]. Adicionalmente, estas aproximaciones introducen un error adicional en el modelo, el cual se ve reflejado en una disminución del ancho de banda del sistema [19]. Otra forma de abordar el problema de la respuesta inversa consiste en reducir el orden del sistema, aproximándolo a uno de primer orden, lo que permite hallar un controlador PI. La respuesta de este último controlador es mucho más lenta cuando se compara con la respuesta que generan las técnicas descritas anteriormente [6].

En cuanto al diseño de controladores PID utilizando las técnicas de análisis de la respuesta en frecuencia para sistemas con respuesta inversa, este fue abordado por Luyben [20] pero las expresiones que obtuvo fueron muy complejas. Por otra parte, el método de síntesis directa ante cambios en la perturbación fue estudiado por Chen y Seborg [21] aunque no abordaron el tratamiento de los sistemas con respuesta inversa así que para hacer uso de sus ecuaciones se tendría que utilizar la aproximación de Padé o de Taylor con el fin de reemplazar el cero de fase no mínima, generando los problemas antes mencionados.

Otro de los métodos más utilizados para la sintonía de controladores PID es el IMC. Este método ha resultado de interés a nivel industrial porque, al igual que el método de síntesis directa, utiliza un único parámetro de sintonía (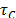). Las ecuaciones del controlador IMC son función de los parámetros de la función de transferencia del sistema y de 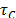. Este último parámetro está relacionado con la velocidad de la respuesta de lazo cerrado del sistema y a medida que se incrementa su magnitud también lo hace la robustez del lazo de control. Por otra parte, a nivel experimental, se ha encontrado que este controlador mejora el comportamiento del sistema ante perturbaciones y minimiza las interacciones del controlador. Además, la correcta selección del filtro pasa bajo que utiliza el método, evita que la respuesta de lazo cerrado sea oscilatoria y con sobreimpulso; estas características reducen los efectos de la perturbación [22]. Por estos motivos, en este trabajo se utilizó el IMC ya que es una técnica que le brinda al diseñador del controlador la posibilidad de especificar el comportamiento del sistema en lazo cerrado y de obtener un controlador con un único parámetro de sintonía. En el trabajo presentado por Chien y Fruehauf (1990) se proponen un conjunto de reglas de sintonía para sistemas de segundo orden con respuesta inversa que tienen la ventaja de no contener términos negativos, por lo que no se hace necesario resolver inecuaciones que finalmente se traducen en limitaciones en el rango útil del parámetro 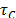[23].

El IMC factoriza la función de transferencia de la planta como:

Tal que 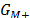es una función que contiene todos los ceros de fase no mínima y el tiempo muerto, mientras que 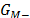contiene los polos de la función de transferencia. El controlador IMC se define en términos del inverso de la función 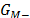y un filtro pasabajo en serie. La ecuación para el controlador es:

Donde 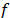es la función del filtro pasa bajo especificado por el usuario. La estructura del controlador IMC puede ser reducida a la clásica estructura de control al definir la función del controlador como:

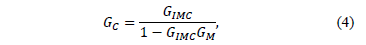
De manera que se puede utilizar la estructura del controlador IMC para obtener los parámetros de un controlador PID clásico [24]. Los autores utilizan la aproximación de Padé, o la de Taylor, para reemplazar la expresión del tiempo muerto en la función de transferencia y sugieren definir la función del filtro para sistemas de primer y segundo orden, sin integrador, de la siguiente forma:

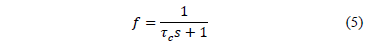
A continuación se utilizan las ecuaciones (2) y (4) para hallar la función de transferencia del controlador 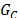y el resultado se compara con la estructura de un controlador PID, serie o paralelo, con el fin de obtener la relación para los parámetros del controlador. Para un sistema con respuesta inversa de segundo orden más tiempo muerto la estructura del controlador PID ideal y las ecuaciones de sus parámetros son:

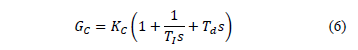
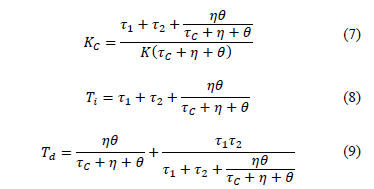
Como se observa, los parámetros PID del controlador dependen del valor de los parámetros de la función de transferencia del SRI y de 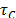, que es el parámetro de sintonía del método.

4. Metodología para generar las reglas de sintonía

El primer paso consistió en elaborar con la herramienta Simulink de Matlab^®, un programa para simular la respuesta del lazo cerrado del sistema con un controlador IMC. A continuación se utilizaron técnicas de análisis dimensional, tanto en la ecuación que describe la función de transferencia del sistema (6) como en las del controlador (7)-(9); lo que hizo posible la reducción de la cantidad de parámetros involucrados. Las ecuaciones adimensionalizadas para el sistema de interés son:

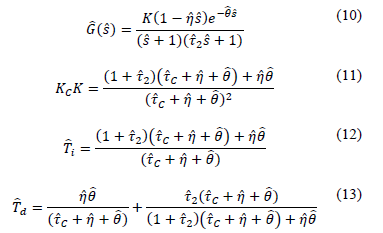
Donde , , 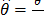y , lo que puede interpretarse como un escalamiento en el tiempo o en la frecuencia. Los rangos típicos de los valores de cada uno de los parámetros de la planta reportados en la literatura [16, 25], son:

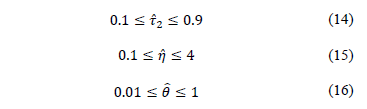
Se diseñó un experimento factorial de tipo central compuesto circunscrito y uniforme que suministró los conjuntos de valores más apropiados para cada corrida de simulación. Posteriormente se elaboró una regresión para evaluar diferentes modelos de ajuste y, para definir la forma exacta de la correlación de interés, se desarrolló un análisis de varianza (ANOVA) utilizando el software Statgraphics. Adicionalmente, esta aplicación suministró diferentes estadísticos que con el fin de medir la calidad del ajuste. Finalmente, se procedió a evaluar el comportamiento del sistema con un controlador sintonizado con las correlaciones obtenidas.

5. Correlación para el límite de estabilidad

El parámetro de sintonía del IMC es denominado 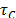y, como se mencionó anteriormente, este se encuentra asociado con la velocidad de respuesta de lazo cerrado. A medida que 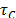toma valores más pequeños el sistema responde más rápidamente, característica deseable para un lazo de control; sin embargo tendrá como consecuencia una respuesta cada vez más oscilatoria, al punto que la estabilidad del sistema puede afectarse drásticamente.

Ninguno de los artículos revisados han usado el IMC o la técnica de síntesis directa, que también utiliza este parámetro para la sintonía del controlador, entregan un límite o al menos una sugerencia, para el valor mínimo que puede tomar sin que se lleve el sistema a la inestabilidad. Por este motivo, la primera tarea a desarrollar en este trabajo consistió en encontrar una expresión que entregara el valor crítico de 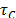, para un proceso de segundo orden con respuesta inversa y tiempo muerto, en el cual la respuesta del sistema fuera una oscilación sostenida. Esta expresión resulta de mucha utilidad para cualquier usuario del método de sintonía, pues le permite conocer una aproximación del valor que le garantizará la respuesta de lazo cerrado más rápida sin llevar el sistema a la inestabilidad.

La forma de la correlación para el parámetro de sintonía, considerando que se realizó un proceso de adimensionalización de la función de transferencia y de las ecuaciones del controlador (10)-(13), es:

De esta expresión se observa que 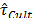es función de tres variables, por lo que se diseñó un diseño central compuesto de tres factores y se realizó una regresión no lineal. La correlación que se halló fue:

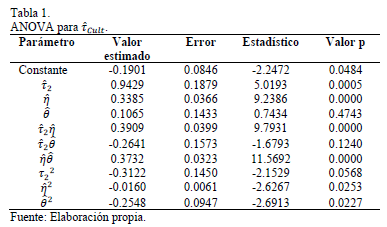
Para analizar la influencia de un factor en la variable de salida se hace uso de diferentes estadísticos para medir el grado de influencia de un factor en la correlación, en el caso de la ANOVA se utiliza el estadístico p [26]. Se acepta que una variable tiene influencia sobre la respuesta si el estadístico p es inferior a 0.05. Este valor está asociado con el nivel de significancia prefijado de la prueba que típicamente es del 95% y entre más pequeña sea su magnitud mayor será la influencia del factor asociado [27]. Después de optimizar el modelo en Statgraphics el factor fue eliminado de la correlación final debido a que su influencia no era significativa.

Adicionalmente, se utilizan otros estadísticos, según el tipo de regresión que se realice, con el fin de verificar las suposiciones hechas sobre el polinomio ajustado. Para este caso al tratarse de una regresión no lineal se usaron los estadísticos: R-cuadrado (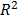), R-cuadrado-ajustado (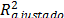) y el Durbin-Watson (DW). 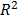Para todas las correlaciones presentadas en este trabajo se consideró que los polinomios ajustados explicaban la variabilidad de los datos si los valores para y 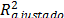eran superiores al 95% y que no existía una correlación serial entre los residuos si el estadístico DW estaba en el rango . En las Tablas 1 y 2 se presentan los resultados de la ANOVA y los estadísticos analizados.

En la Fig. 1. se muestra la respuesta del sistema ante una entrada tipo escalón unitario, con un controlador sintonizado con las ecs. (11)-(13) y (18); para tres conjuntos de parámetros diferentes de la función de transferencia del proceso seleccionados en la Tabla 3.

En la Fig. 2 se observa como la respuesta del sistema es oscilatoria cuando se sintoniza el controlador con un valor del parámetro de sintonía calculado con (18) y para diferentes valores de los parámetros de la planta. En caso de sintonizar el controlador con valores superiores a 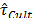el sistema es inestable, mientras que para valores inferiores no; luego la correlación hallada permite encontrar el límite de estabilidad del sistema ante una entrada tipo escalón.

6. Correlación para 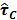que minimiza el IAE

En este caso se encontró una correlación para calcular el valor de que minimiza el índice de desempeño IAE. Para todas las corridas experimentales se utilizó como estímulo una perturbación tipo escalón unitario, es decir, las pruebas realizadas se enfocaron en un control regulatorio.

Ya que es función de los parámetros del modelo, tal como en el caso anterior, se utilizó el mismo diseño de experimentos y la forma de la correlación propuesta también es igual. A continuación se elaboró un algoritmo para variar el valor del parámetro manteniendo fijos los parámetros del proceso, de manera que con cada cambio de se afectaban únicamente los parámetros del controlador. El valor de partida de se obtuvo de (18), por lo tanto, el valor mínimo que se le asignó a este parámetro correspondía con el valor del límite de estabilidad del sistema. El resultado final del procedimiento de simulación fue una tabla de datos que contenía el valor de que hacía mínimo el IAE para cada conjunto de parámetros. Con base en esta información y en el conjunto de valores de parámetros del proceso se llevó a cabo el ajuste de los datos. La correlación hallada se presenta a continuación:

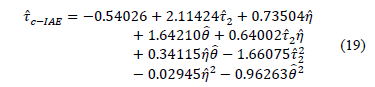
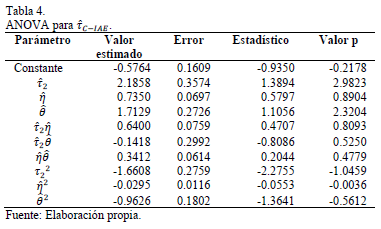
Los estadísticos utilizados para evaluar esta correlación y los resultados de la ANOVA aparecen en las Tablas 4 y 5.

Según los resultados de las tablas anteriores se puede afirmar que la correlación que se encontró explica en alto grado el comportamiento de los datos.

7. Evaluación de desempeño

Para los ejemplos que se presentan a continuación se seleccionaron tres conjuntos de valores para los parámetros del proceso, ver Tabla ; luego se sintonizó un controlador utilizando las correlaciones propuestas en este trabajo (CD-CF), ver ecs. (11)-(13) y (19); y se obtuvo la respuesta del sistema ante una entrada tipo escalón unitario. Las pruebas se realizaron tanto para operación servo como regulatoria. En la operación servo la señal de entrada se ingresa como un cambio en la referencia mientras que en la operación regulatoria la señal de excitación del sistema ingresa como una perturbación. En la Tabla se presenta una comparación entre el valor obtenido para con (19) y el que se calcula con 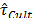, esto con el fin de mostrar que siempre el valor del parámetro de sintonía del método debe ser mayor que 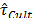para evitar la inestabilidad del lazo de control.

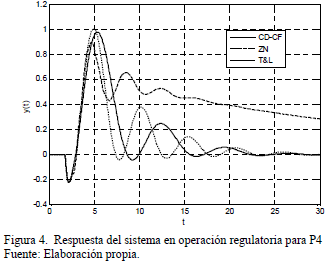
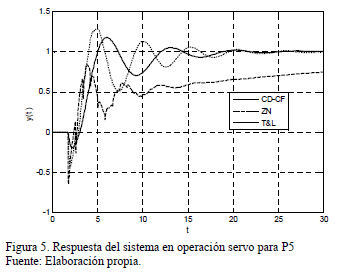
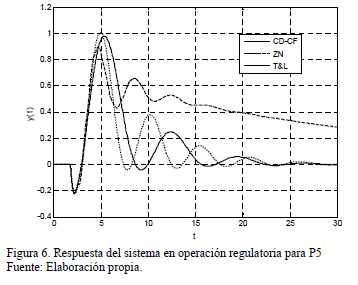
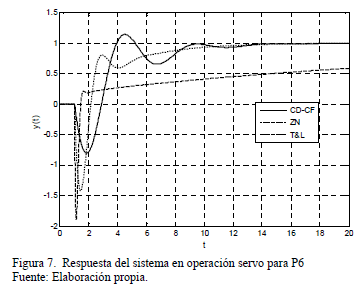
A continuación se comparó el desempeño del sistema tanto con un controlador en el que se utilizó el método de sintonía PID tradicional propuesto por Ziegler y Nichols (ZN) [9], como con un controlador PID sintonizado con las ecuaciones de Tyreus y Luyben (TL) [28]. El método de sintonía de ZN se utiliza como punto de referencia para establecer comparaciones en muchos estudios, por otra parte, la técnica TL es similar a la ZN pero esta ofrece la ventaja de que el coeficiente de amortiguación de lazo cerrado presenta un valor mucho mayor al de ZN, por lo que la respuesta es más suave. En las Figuras 3 - 8 se presentan las respuestas del sistema, tanto en operación servo como regulatoria, para tres conjuntos diferentes de parámetros del proceso y con los tres controladores estudiados.

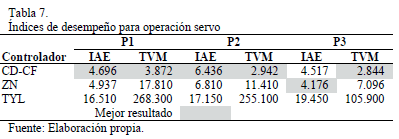
Para cada uno de los ejemplos se calcularon dos indicadores de desempeño: el IAE y el Trabajo de la Variable Manipulada (TVM). Este último se define como la integral del valor absoluto del cambio de la variable manipulada. En las Tablas 7 y 8 se presentan los valores de estos índices tanto para operación servo como regulatoria.

En general, para los diferentes parámetros de la función de transferencia estudiados, el controlador CD-CF presenta los mejores resultados tanto para el índice de desempeño IAE como para TVM. Aunque los valores obtenidos para el IAE con el controlador ZN en algunos casos son cercanos a los del controlador CD-CF, es notorio el esfuerzo que realiza el elemento final de control con ZN. Respecto al controlador TYL, este se caracterizó por presentar un menor sobre impulso en la respuesta transitoria con la desventaja de que generar siempre el mayor tiempo de estabilización.

8. Conclusiones

En este trabajo se propone un método de sintonía para ajustar un controlador PID para un sistema de segundo orden y tiempo muerto con respuesta inversa basado en el método IMC para lo que se presenta una correlación que permite calcular el valor de que minimiza el IAE. La correlación que se obtuvo es de tipo polinómica y es función de los parámetros del proceso.

En este trabajo se presenta una correlación que permite calcular el valor límite que se le puede asignar al parámetro de sintonía del controlador de manera que la respuesta del sistema sea lo más rápida posible, pero sin llegar a la inestabilidad. Esta expresión resulta de interés para cualquier usuario del método. La literatura no reporta hasta el momento una correlación o método para calcular el valor de 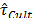a partir de los datos del modelo.

Se resalta el buen desempeño del controlador CD-CF para un rango variado de los parámetros del proceso y tanto para operación servo como regulatoria del lazo de control. Adicionalmente, se observa una disminución del efecto de respuesta inversa en el sistema con este controlador.

Un sistema con un controlador sintonizado con las reglas de sintonía propuestas alarga la vida útil del elemento final de control.

Para la generación de datos se realizó un diseño estadístico de experimentos de tipo central compuesto, uniforme y circunscrito; que permitió una reducción considerable del número de corridas de simulación y un mejor ajuste de los datos al polinomio propuesto.

References

[1] Luyben, W.L., Tuning proportional-Integral controllers for processes with both inverse response and deadtime. Industrial Engineering Chemical Research, 39, pp. 973-976, 2000. DOI: 10.1021/ie9906114

[2] Chien, I., Chung, Y., Chen, B. and Chuang, C., Simple PID controller tuning method for processes with inverse response plus dead time or large overshoot response plus dead time. Industrial Engineering Chemical Research, 42, pp. 4461-4477, 2003. DOI: 10.1021/ie020726z

[3] Ogunnaike, B. and Harmon, W., Process dynamics and modeling and control. USA. Oxford University Press, 1994.

[4] Lund, B.F., Foss, B.A. and Løvåsen, K.R., Analysis and characterization of complex reactor behaviour: A case study. Journal of Process Control, 16, pp. 711-718, 2006. DOI: 10.1016/j.jprocont.2006.01.005

[5] Manca, D., Rovaglio M., Pazzaglia G. and Serafini G., Inverse response compensation and control optimization of incineration plants with energy. Computers & Chemical Engineering. 22(12), pp.1879-1896, 1998. DOI: 10.1016/S0098-1354(98)00239-7

[6] Ocampo, J.E. y Castrillón, F., Control de sistemas con respuesta inversa. Madrid. Ingeniería química, 42(486), pp. 76-85, 2010.

[7] Jeng, J. and Lin, S., PID controller tuning based on smith-type compensator for second-order process with inverse response and time delay. Proceedings of 2011 8th Asian Control Conference (ASCC), 56, pp. 15-18, 2011.

[8] Barberà, E., Predictor de Smith + PI en el control de procesos con tiempo muerto dominante. Revista de Ingeniería Química, 43(491), pp. 46-50, 2011.

[9] Ziegler, J.G. and Nichols, N.B., Optimum setting for automatic controllers. Transactions ASME, 64, pp. 759-768, 1942.

[10] Alfaro, V.M., Ecuaciones para controladores PID universales. San José de Costa Rica. Revista Ingeniería de Costa Rica, 12(1,2), pp. 11-20, 2002.

[11] Yu, C.C., Autotuning of PID Controllers: A relay feedback approach. Springer, 2006.

[12] De Castro, P. y Fernández, E., Control e instrumentación de procesos químicos. Madrid. Editorial Síntesis, 2006.

[13] Stephanopoulos, G., Chemical process control. An introduction to theory and practice. New Jersey, Prentice Hall, 1984.

[14] Alcántara, S., Pedret, C., Vilanova, R. and Zhang, W.D., Analytical H^∞ design for a Smith-type inverse-response compensator. American Control Conference, Hyatt Regency Riverfront, St. Louis, MO, USA; pp. 10-12, 2009. DOI: 10.1109/ACC.2009.5160324

[15] Scali, C. and Rachid, A., Analytical design of proportional-integral-derivative controllers for inverse response process. Industrial Engineering Chemistry, 37(4), pp. 1372-1379, 1998. DOI: 10.1021/ie970558o

[16] Pai, N.S., Changb, S.C. and Huangb, C.T., Tuning PI/PID controllers for integrating processes with deadtime and inverseresponse by simple calculations. Journal of Process Control 20, pp.726-733, 2010. DOI: 10.1016/j.jprocont.2010.04.003

[17] Romagnoli, J. and Palazoglu, A., Introduction to process control. Taylor & Francis Group, 2006.

[18] Castellanos, D. y Castrillón, F., Controladores PI/PID en procesos con respuesta inversa evaluación de la robustez. Ingeniería Química, 502, pp. 48-52, 2012.

[19] Rivera, D., Morari, M. y Skogestad, S., Internal model control: PID controller design. Ind. Eng. Chem. Process, 25(1), pp. 252-265, 1986. DOI: 10.1021/i200032a041

[20] Luyben, W., Identication and tuning of integrating processes with deadtime and inverse response. Industrial Engineering Chemical Research, 42, pp. 3030-3035, 2003. DOI: 10.1021/ie020935j

[21] Chen, D. and Seborg, D.E., PI/PID Controller design based on direct synthesis and disturbance rejection. Industrial Engineering Chemical Research, 41, pp. 4807-4822, 2002. DOI: 10.1021/ie010756m

[22] Chien, I. and Fruehauf ,P., Consider IMC tuning to improve controller performance. Chemical Engineering Progress, 86, pp. 33-41, 1990.

[23] Castellanos, D. y Castrillón, F., Propuesta de nuevas reglas de sintonía para el ajuste de controladores PI/PID para sistemas con respuesta inversa. Tesis MSc., Escuela de Ingenierías, Universidad Pontificia Bolivariana, Medellín, Colombia, 2013.

[24] García, Y. y Lobo, I., Control PID integrado por la estructura de control de modelo interno (IMC) y lógica difusa. Revista Ciencia e Ingeniería, 30, pp. 29-40, 2009.

[25] Balaguer, P., Alfaro, V. y Arrieta, O., Second order inverse response process identification from transient step response. ISA Transactions, 50, pp. 231-238, 2011. DOI: 10.1016/j.isatra.2010.11.005

[26] Morales, H., Claudio, A., Adam, M. and Mina, J., An improved measurement strategy based on statistical design of experiments for a boost Converter. Revista DYNA, 78(166), pp. 7-16, 2011.

[27] Gutiérrez H. y De la Vara, R., Análisis y diseño de experimentos. McGraw Hill, 2008.

[28] Tyreus, B.D. and Luyben, W.L., Tuning PI controllers for integrator/dead time process. Industrial Engineering Chemistry Research. 31(11), pp. 2625-2628, 1992. DOI: 10.1021/ie00011a029

D. Castellanos-Cárdenas, es Ing. Electrónica en 2006, de la Universidad de Antioquia, Colombia, Sp. en Automática en 2010 y MSc. en Ingeniería en 2013 ambos de la Universidad Pontificia Bolivariana, Colombia. Es profesora de tiempo completo de la Universidad de Medellín, Colombia y pertenece al grupo de investigación ARKADIUS. Sus áreas de interés son: control e instrumentación de procesos, sintonía de controladores PID. ORCID: 0000-0003-1496-9958

F. Catrillón-Hernández, es Ing. Químico en 1996, de la Universidad Pontificia Bolivariana, Colombia, Sp. en Automática en 2000 y MSc. en Ingeniería en 2007, de la misma institución. Es profesor titular de la Facultad de Ingeniería Química, de la Universidad Pontificia Bolivariana, Colombia; investigador asociado según Colciencias y pertenece al Grupo de Investigación en Automática y Diseño A+D. Sus áreas de interés son: control de procesos, sintonía de controladores PID y educación en ingeniería. ORCID: 0000-0003-3906-4610