Publicado
Crack growth in pyrographite under the conditions of radiation
DOI:
https://doi.org/10.15446/dyna.v83n195.47532Palabras clave:
Pyrographite, crack, irradiation, HVTEM, stress state. (es)
Descargas
DOI: https://doi.org/10.15446/dyna.v83n195.47532
Crack growth in pyrographite under the conditions of radiation
Crecimiento de grietas en pirografito bajo condiciones de radiación
Pedro Alejandro Tamayo-Meza a, Viacheslav Alexandrovich Yermishkin b, Usiel Sandino Silva-Rivera c, Alejandro Leyva-Díaz d, Josué Osmar Trejo-Escandón e, Juan Manuel Sandoval-Pineda f & Luis Flores-Herrera g
a Escuela Superior de Ingeniería Mecánica y Eléctrica, Instituto
Politécnico Nacional, Ciudad de México, México. ptamayom@ipn.mx
b Institute of Metallurgy, Russian Academy of Science, Moscow,
Russian Federation.
c Escuela Superior de Ingeniería Mecánica y Eléctrica, Instituto
Politécnico Nacional, Ciudad de México, México. usiel31@yahoo.com.mx
d Escuela Superior de Ingeniería Mecánica y Eléctrica, Instituto
Politécnico Nacional, Ciudad de México, México. a.leyvadíaz@gmail.com
e Escuela Superior de Ingeniería Mecánica y Eléctrica, Instituto
Politécnico Nacional, Ciudad de México, México. jtescandon@hotmail.com
f Escuela Superior de Ingeniería Mecánica y Eléctrica, Instituto
Politécnico Nacional, Ciudad de México, México. jsandovalp@ipn.mx
g Escuela Superior de Ingeniería Mecánica y Eléctrica, Instituto
Politécnico Nacional, Ciudad de México, México. lafloresh@ipn.mx
Received: November 27th, 2014. Received in revised form: April 12th, 2015. Accepted: December 10th, 2015.
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.

Abstract
The damage
induced by radiation in the pyrographite is accompanied by significant plastic
deformation. Microcracks arise in the edges of the radiated areas that develop
radially in the direction of the unaffected matrix. The peculiarities in the
formation of the tension state of the radiated area and adjacent unaffected
areas are analyzed in order to explain the reasons behind the growth of cracks.
The analysis is carried out on graphite disks with constant thicknesses that
are exposed to radiation with high-energy electrons in an HVTEM-JEOL 1000. A
differential equation for specific load conditions is obtained from the
analysis of equilibrium conditions of a disc-shaped element.
Keywords: Pyrographite, crack, irradiation, HVTEM, stress state.
Resumen
El daño inducido por radiación en el
pirografito va acompañado por una significativa deformación plástica. En los
bordes de la zona radiada surgen microgrietas que se desarrollan de manera
radial en dirección de la matriz no afectada. Se analizan las particularidades
en la formación del estado de tensión de la zona radiada, y en los campos
adyacentes no afectados por la radiación para explicar las razones que originan
el crecimiento de grietas. El análisis se lleva a cabo sobre discos de grafito
con espesor constante, expuestos a radiación con electrones de altas energías
dentro de un HVTEM-JEOL 1000. Del análisis de las condiciones de equilibrio de
un elemento en forma de disco, se obtiene una ecuación diferencial para
condiciones específicas de carga.
Palabras clave: Pirografito, grieta, irradiación, HVTEM, estado de esfuerzos.
1. Introduction
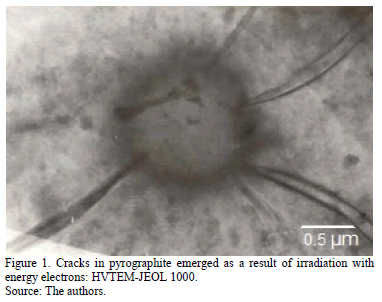
Exposure of pyrographite to radiation with high-energy electrons causes a type K → A phase transition, accompanied by considerable plastic deformation. It was established that microcracks emerge at the edges of the irradiated zone, these microcracks then grow unceasingly in the radial direction within the irradiated matrix, Fig. 1.
To clarify the possible causes of the incubation and growth of cracks, it is necessary to examine the peculiarities in the formation of a stress state in the irradiated zone as well as in the conjugated matrix zone that is not affected by the radiation. This cannot be caused by the change of the temperature field in the irradiated zone, since the heating magnitude in the HVTEM column by means of the electron beam does not exceed 40ºC [1,2]. Besides, prolonged radiation experiments undoubtedly favor the balance of the temperature field gradients in both the sample thickness and the radial direction within the irradiated zone limits.
2. Theoretical approach
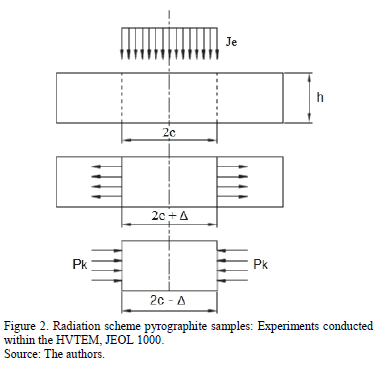
The radiation scheme of pyrographite samples in the form of flat disks performed within the HVTEM is shown in Fig. 2.
As a result of a prolonged high energy electron bombing, the amorphization is developed in the pirografites, which leads to a decrease in the material specific volume in the irradiated zone [3]. Considering that the irradiated zone is surrounded by a matrix that is not affected by radiation, a forced interaction consequently arises between it and the loosened of the irradiated zone's material [4].
From the equilibrium conditions of a circular sheet element of constant thickness analysis, it is possible to obtain a differential equation for a determined loading scheme. Following the plate theory methods [5,6], we obtain the equilibrium equation for the plate and solve it for the initial and boundary conditions that are derived from the supposed scheme of interaction between an irradiated zone wrapped by a sample matrix. The differential equation is obtained as follows:
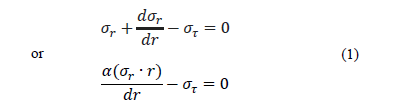
where 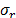 is the radial stress, and
is the radial stress, and 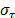 is the tangential stress.
is the tangential stress.
The link between the components of the
stress tensor 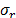 ,
, 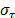 ,
, 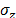 and the deformations
and the deformations  ,
,  can be expressed in terms of
the Generalized Hook's Law:
can be expressed in terms of
the Generalized Hook's Law:
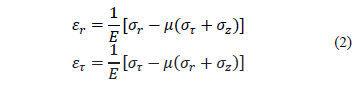
where E is the Young modulus, 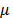 is the Poisson modulus.
is the Poisson modulus.
Supposing that in the conditions of our
problem 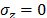 , it is possible to obtain the expressions for
, it is possible to obtain the expressions for 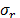 and
and 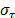 from the eq. (2) as follows:
from the eq. (2) as follows:
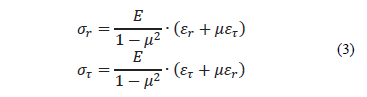
It is not difficult to prove that
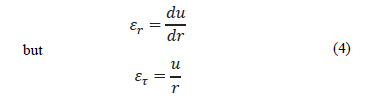
where  is the radial deformation,
is the radial deformation,  is the tangential
deformation, u is the radial
displacement.
is the tangential
deformation, u is the radial
displacement.
After substituting eq. (4) in the eq. (3) we obtain:
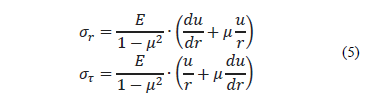
After substituting eq. (5) in the equilibrium differential equation (1), the latter can be expressed as:
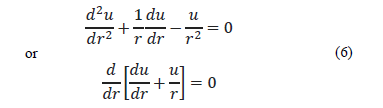
Finally, it can be presented in the following form:
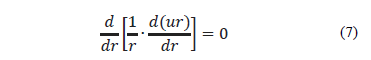
Observations of the zone irradiated by HVTEM show an absolute absence of extinction contours, even in the very moment when microcracks start to form. This circumstance reveals the absence of bending during the interaction of forces in the irradiated zone and the surrounding matrix, i.e., the latter has compression characteristics at the edges of the zone. The integration of eq. (6) provides a general solution for radial displacements in the zone affected by radiation:
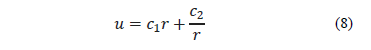
where 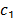 and
and 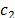 are integration constants,
the values of which come from the contour conditions.
are integration constants,
the values of which come from the contour conditions.
In our problem, these can be expressed as r = c; 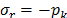 ; r=∞;
; r=∞; 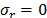 for the matrix outside the
zone of radiation, and r = c;
for the matrix outside the
zone of radiation, and r = c;  ; r = 0; u = 0 for the irradiated zone.
; r = 0; u = 0 for the irradiated zone.
To determine the integration constants in solution (8), we inserted them in eq. (5) and consequently obtain:
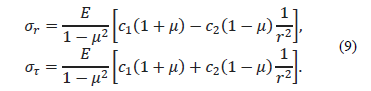
Considering the contour conditions, eq. (9) for the plate placed outside the irradiated zone obtained the following form:

from which the expression for the integration constants c1 y c2 can be presented as
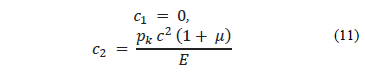
Substituting expression (10) in eq. (8) and (9), we obtain
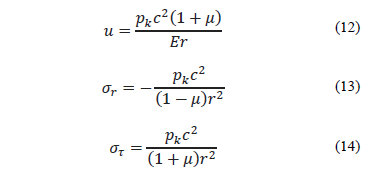
Similarly, for the irradiated zone, the substitution of the corresponding boundary conditions leads to the following expressions:
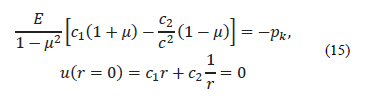
From which we deduce:

After substituting the values of 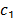 and
and 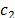 in eq. (8) and (9) we obtain:
in eq. (8) and (9) we obtain:
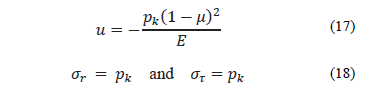
3. Discussion of the results
The
material in the irradiated area has been under the effect of a biaxial stress
state in compression, the magnitude of which can be determined by the degree of
amorphization process development. The surrounding matrix is also in a state of
biaxial stress. However, the compression forces decrease in the radial
direction that is inversely proportional to the square of the radius measured
from the center spot of radiation, but the stress forces, which are equal by
modulus to compression forces, act in the tangential direction,. A physical
approach to the problem is to determine the magnitudes of the contact pressures 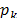 , which act in the limits of the
irradiated area. To find the value of this pressure, we use the solution
proposed by Lame [5], which describes the emergence of a contact pressure when
a cylindrical piece joins a sheet having a central perforation with a certain
tightening Dc:
, which act in the limits of the
irradiated area. To find the value of this pressure, we use the solution
proposed by Lame [5], which describes the emergence of a contact pressure when
a cylindrical piece joins a sheet having a central perforation with a certain
tightening Dc:
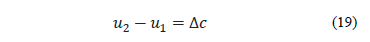
where 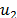 is the sheet displacement in
the borders of the irradiated zone described by eq. (12),
is the sheet displacement in
the borders of the irradiated zone described by eq. (12), 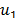 is the zone of displacement
in the boundary described by eq. (17),
is the zone of displacement
in the boundary described by eq. (17), 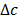 is the tightening intensity.
is the tightening intensity.
In this case the tightening is a result of the swelling of the irradiated zone due to amorphization development stimulated by radiation. We determined its size from the conditions of substance mass conservation in the irradiated zone during the radiation process applied to it:
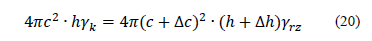
where 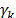 is the initial crystalline pyrographite
density,
is the initial crystalline pyrographite
density, 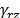 is the present value of the material density
in the irradiated zone, h is the
sample thickness, and c is the
irradiated zone radius.
is the present value of the material density
in the irradiated zone, h is the
sample thickness, and c is the
irradiated zone radius.
After certain transformations, eq. (20) can be represented in the following form:
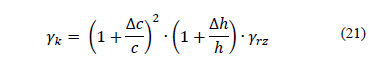
Recognizing that during the pyrographite
amorphization process the deformation develops isotropically, i.e., 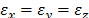 , and
, and 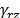 is the density of totally
amorphized pyrographite
is the density of totally
amorphized pyrographite 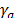 , and the crystalline pyrographite is expressed as
, and the crystalline pyrographite is expressed as 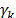 , then according to the mixture law:
, then according to the mixture law:
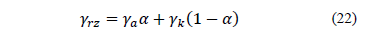
where 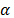 is the amorphization degree.
is the amorphization degree.
Eq. (21) can be expressed in the following form:
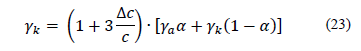
Solving eq. (23) with respect to c and substituting eq. (22) in it we obtain
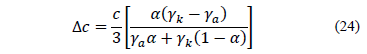
Substituting eq. (24) in eq. (19), we have that for r = c

where eq. (26) is for the contact pressure:

where 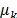 and
and 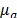 are Poisson coefficients for
the crystalline and amorphous pyrographite, respectively; and
are Poisson coefficients for
the crystalline and amorphous pyrographite, respectively; and 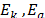 are Young moduli for the
crystalline and amorphous pyrographite, respectively.
are Young moduli for the
crystalline and amorphous pyrographite, respectively.
As there is no
data on the physical properties of pyrographite in the amorphous state, eq.
(26) can only be used to estimate the tendency in the change of the localized
stress state to the degree of amorphization development. From this it is
observed that in the initial state, when 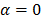 , the tightening
, the tightening 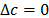 . The maximum value of
. The maximum value of 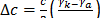 is reached when pyrographite
is amorphized totally in the irradiated zone. At this moment the contact
pressure reaches the value of
is reached when pyrographite
is amorphized totally in the irradiated zone. At this moment the contact
pressure reaches the value of
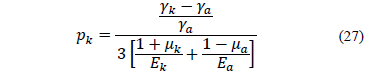
When the character of stress distribution in the matrix zone not exposed to radiation described by formula 11 is analyzed, the reasons for the emergence of cracks at the border of the irradiated area and their propagation in the radial direction become clear.
For r = c, the stress forces in the
tangential direction reach their maximum value. The resistance under these
forces is much weaker in pyrographite compared with the effects of compression
forces [7]. The fact that the cracks propagate along the crystallographic
directions 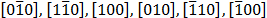 indicates that the fracture anisotropy resulting
from the crystallographic structure of pyrographite expresses itself, and the
characteristics of the deformation and stress state in an anisotropic
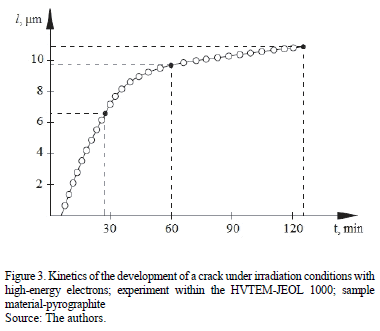
approximation can be considered to be approximations. In Fig. 3, the kinetics
of crack development in a matrix of pyrographite unaffected by the radiation is
observed. It can be seen that the curve consists of two sections:
indicates that the fracture anisotropy resulting
from the crystallographic structure of pyrographite expresses itself, and the
characteristics of the deformation and stress state in an anisotropic
approximation can be considered to be approximations. In Fig. 3, the kinetics
of crack development in a matrix of pyrographite unaffected by the radiation is
observed. It can be seen that the curve consists of two sections:
I. A section in which the crack
grows at a rate of 1.10-5 cm/sec, and
II. A section in which the crack develops at a rate of 1.1 x 10-7 cm/sec.
4. Conclusions
1. We established that when a stream of high-energy electrons impacts pyrographite, amorphization is stimulated in it, which can be described as a transformation of the crystalline phase into the amorphous state. We studied the influence of the radiation parameters on the amorphization kinetics.
2. We proposed a phenomenological model of amorphization by radiation, which considers a possibility of a direct phase transformation of the type K → A, as well as the inverse transformation A → K. Based on this, we obtained a formula that describes the kinetics of amorphization by radiation in the following form:
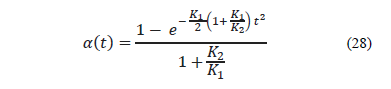
3. We detected the effect of pyrographite amorphization under the influence of a high-energy electron stream inside an HVTEM. We proposed a phenomenological model that describes the kinetics of amorphization in pyrographite due to radiation using reference points put in the material surface. This was performed by means of the implantation of ionized copper atoms.
We studied the deformation and stress state of pyrographite, both in the zone irradiated by electrons as well as in the zones adjacent to the matrix unaffected by radiation.
We proposed a method to determine the energy threshold of radiation damage in pyrographite using data from the kinetics analysis of its amorphization under conditions of radiation by high-energy electrons performed inside the HVTEM column under various stress acceleration values.
Acknowledgment
The authors express their gratitude to all the staff at the Laboratory 20, Baikov Institute of Metallurgy, Russian Academy of Sciences, for their support. We also thank the Secretary of Research of the National Polytechnic Institute of Mexico, SIP, for their support for Project 20131380, 20141031.
References
[1] Snykers, M. and Janssens, C., The use of the JEM-1250 HVTEM of the University of Antwerpen as an instrument for void swelling simulation experiment. BLG.521, 18 P., 1978.
[2] Timofeev, V.N., Izmereniye temperatury nagreva obraztsa puchkom elektronov v prosvechivayushem elektronom mikroskope s pomoshiyu lorentsevoy elektronnoy mikroskopii. Teplofizika kondensirovannyj sred. Selected Papers. M: Nauka, pp. 74-78, 1985.
[3] Abe, H., Naramoto, H. and Kinoshita, C., Amorphization of graphite under ion or electron irradiation. Mater. Res. Soc Proc., pp.373-383, 2011.
[4] Panyukov, S.V., Subbotin, A.V. and Arzhakov, M.V., Irradiation induced dimensional changes in bulk graphite: The theory. Journal of Nuclear Materials, 439, pp. 72-83, 2013. DOI: 10.1016/j.jnucmat.2013.03.070
[5] Ponomariov, S.D., Biderman, V.L. and Lijariov, K.K., Razshety na prochnost v mashinostroyenii. M: MASHGIZ, 974 P., 1958.
[6] Timoschenko, S.P. and Voynovski-Criger, S. Plastin, I., Obolochki, M., FITMAZGIZ, 576 P., 1963.
[7] Birgiliev, Y.S., Makarchenko, V.G. and Chirilov, Y.S., Sootnosheniya mezhdu prochnostnymi jarakteristikami v obluchennom grafite. Problemy Prochnosti, 1. pp. 95-100, 1977.
P.A. Tamayo-Meza, is a Dr. of Technology and Metallurgy. He holds a PhD. in Engineering from the Academy of Sciences of the USSR, Moscow, Russia, and an MSc. in Mechanical Engineering from the Faculty of Engineering, University of Moscow, Russia. His professional experience in research includes the development of fiber reinforced materials, mechanics of materials characterization by quasi-relaxation, transmission electron microscopy, scanning, and atomic force; the study of corrosion phenomena, solid state physics, physics, and fracture mechanics; creep and fatigue, physical mechanics of materials, and theory of heat treatment; and mechanical cryogenic treatment. ORCID: 0000-0001-8026-8928
V.A. Yermishkin, obtained his Dr. in Physical Sciences and Mathematics in Lomonosov State University. He works as chief of Laboratory of High-Voltage Electron Microscopy in the Institute of Metallurgy and Materials Science at the Russian Academy of Sciences. His professional experience in research includes physics, fracture mechanic, creep and fatigue, transmission electron microscopy, scanning and atomic force and development of fiber reinforced materials. He has published more than 132 works. ORCID: 0000-0001-7280-4516
U.S. Silva-Rivera, obtained his Dr. of Science in Mechanical Engineering, specializing in Mechanical Design (2015) and his MSc. degree in Manufacturing Engineering (2011) from the School of Mechanical and Electrical Engineering in the National Polytechnic Institute of Mexico, and his BSc. degree in Military Industrial Engineering, specializing in Chemical Engineering (2003), from Military Engineering School in the University of the Army and Air Force. His research interests are experimental ballistics, computational fluid dynamics, materials and mechanical design; he has a knowledge of production processes and quality control of small arms ammunition, as well as in design, development and production of assault rifles. ORCID: 0000-0001-5597-1638
A. Leyva-Díaz, obtained his BSc. degree from the Technological Institute of Tuxtla Gutierrez in 2011, and his MSc. in Manufacturing Engineering from the School of Mechanical and Electrical Engineering in the National Polytechnic Institute of Mexico in 2014. He has a knowledge of mechanical design, static and dynamic analysis in 3D models through finite element method software. His research interests are Mechanical Design, Finite Element Analysis, and the development and characterization of new materials. ORCID: 0000-0002-7478-9441
J.O. Trejo-Escandón received his BSc. in Mechanical Engineering in 2012, from the Technological Institute of Tuxtla Gutierrez, Mexico and a MSc. in Manufacturing Engineering in 2015, from the National Polytechnic Institute - IPN, Mexico. He currently works at the Development & Innovation Center in Schneider-Electric in Monterrey, Mexico, where he works as a Structural Simulation Specialist. His areas of research interest focus on Mechanical Design, Finite Element analysis and development and characterization of new materials. ORCID: 0000-0002-5076-7045
J.M. Sandoval-Pineda, is a professor in the National Polytechnic Institute of México. He obtained his Dr. of Science in Mechanical Engineering with honors in 2008 and his MSc. in Mechanical Engineering in 2004, from the National Polytechnic Institute, Mexico. His professional experience in research includes physics, fracture mechanic, creep and fatigue, and transmission electron microscopy. ORCID: 0000-0002-6529-7920
L.A. Flores-Herrera, is a professor in the National Polytechnic Institute of México. He obtained his Dr. of Science in Mechanical Engineering with honors in 2007 and his MSc. in Mechanical Engineering in 2003 from the National Polytechnic Institute, Mexico. Hi is a specialist in Finite Element Analysis and his research area focuses on Microelectromechanical systems (MEMS). ORCID: 0000-0003-1081-5193
Cómo citar
IEEE
ACM
ACS
APA
ABNT
Chicago
Harvard
MLA
Turabian
Vancouver
Descargar cita
Licencia
Derechos de autor 2016 DYNA

Esta obra está bajo una licencia internacional Creative Commons Atribución-NoComercial-SinDerivadas 4.0.
El autor o autores de un artículo aceptado para publicación en cualquiera de las revistas editadas por la facultad de Minas cederán la totalidad de los derechos patrimoniales a la Universidad Nacional de Colombia de manera gratuita, dentro de los cuáles se incluyen: el derecho a editar, publicar, reproducir y distribuir tanto en medios impresos como digitales, además de incluir en artículo en índices internacionales y/o bases de datos, de igual manera, se faculta a la editorial para utilizar las imágenes, tablas y/o cualquier material gráfico presentado en el artículo para el diseño de carátulas o posters de la misma revista.