Publicado
Distributed Generation Placement in Radial Distribution Networks using a Bat-inspired Algorithm
DOI:
https://doi.org/10.15446/dyna.v82n192.48573Palabras clave:
bat-inspired algorithm, distributed generation, particle swarm optimization, distribution system. (es)Descargas
Distributed generation (DG) is an important issue for distribution networks due to the improvement in power losses, but the location and size of generators could be a difficult task for exact techniques. The metaheuristic techniques have become a better option to determine good solutions and in this paper the application of a bat-inspired algorithm (BA) to a problem of location and size of distributed generation in radial distribution systems is presented. A comparison between particle swarm optimization (PSO) and BA was made in the 33-node and 69-node test feeders, using as scenarios the change in active and reactive power, and the number of generators. PSO and BA found good results for small number and capacities of generators, but BA obtained better results for difficult problems and converged faster for all scenarios. The maximum active power injections to reduce power losses in the distribution networks were found for the five scenarios.
DOI: https://doi.org/10.15446/dyna.v82n192.48573
Distributed generation placement in radial distribution networks using a bat-inspired algorithm
Ubicación de generación distribuida en redes de distribución radiales usando un algoritmo inspirado en murciélagos
John Edwin Candelo-Becerra a & Helman Enrique Hernández-Riaño b
a Departamento de Ingeniería Eléctrica y Automática, Facultad de
Minas, Universidad Nacional de Colombia - Sede Medellín, Medellín, Colombia, jecandelob@unal.edu.co
b Departamento de Ingeniería Industrial,
Universidad de Córdoba, Montería, Colombia and Universidad
del Norte, Barranquilla, Colombia, hhernandez@correo.unicordoba.edu.co
Received: October 07th, 2014. Received in revised form: February 13th, 2015. Accepted: July 02nd, 2015.
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.

Abstract
Distributed generation (DG) is an important issue for
distribution networks due to the improvement in power losses, but the location
and size of generators could be a difficult task for exact techniques. The
metaheuristic techniques have become a better option to determine good
solutions and in this paper the application of a bat-inspired algorithm (BA) to
a problem of location and size of distributed generation in radial distribution
systems is presented. A comparison between particle swarm optimization (PSO)
and BA was made in the 33-node and 69-node test feeders, using as scenarios the
change in active and reactive power, and the number of generators. PSO and BA
found good results for small number and capacities of generators, but BA
obtained better results for difficult problems and converged faster for all
scenarios. The maximum active power injections to reduce power losses in the
distribution networks were found for the five scenarios.
Keywords: bat-inspired algorithm; distributed generation; particle swarm optimization; distribution system.
Resumen
La generación distribuida (DG) es un tema
importante para las redes de distribución debido a la reducción de las pérdidas
de energía, pero la ubicación y el tamaño de generadores puede ser una tarea
difícil para las técnicas de solución exactas. Las técnicas metaheurísticas se
han convertido en una mejor opción para determinar soluciones válidas y en este
trabajo se presenta la aplicación de un algoritmo inspirado en murciélagos (BA)
a un problema de ubicación y dimensionamiento de generación distribuida en
sistemas de distribución radial. Una comparación entre la técnica de
optimización por enjambre de partículas (PSO) y BA fue hecha en los sistemas de
prueba de 33 nodos y 69 nodos, utilizando como escenarios el cambio en la
potencia activa y reactiva, y el número de generadores. PSO y BA encontraron
buenos resultados para un número pequeño y pocas capacidades de generación,
pero BA obtuvo mejores resultados para problemas difíciles y converge más
rápido para todos los escenarios. Las máximas inyecciones de potencia activa
para reducir las pérdidas de energía en las redes de distribución fueron
encontradas para los cinco escenarios.
Palabras clave: algoritmo inspirado en murciélagos; generación distribuida; optimización con cúmulo de partículas; sistemas de distribución.
1. Introduction
Power losses of distribution networks have always been an important issue due to the energy efficiency and the costs that the problem represents for electricity companies. This problem has usually been solved using feeder restructuring [1], DG placement [1-10], capacitor placement [1,11] and network reconfiguration [12, 13].
Location and size of distributed generation in distribution networks has difficulties due to the combination of the number and capacities of generators, and the selection of the best nodes. Several algorithms have been used to solve the problem such as particle swarm optimization [14-16], ant colony [17], optimal power flow [18], analytical methods [19,20], evolutionary algorithm [21-24], and simulated annealing [25-27], among others [14,28,29].
PSO have been widely used to solve this problem [30], but some convergence problems have been identified [31]. BA has been proposed as a good technique to optimize several functions [32], but more research is needed to determine the performance for power system problems.
In this paper, BA and PSO were used to obtain the solutions to a problem of location and size of generators. A comparison of the two algorithms was conducted changing capacities and the number of generators in two distribution networks.
2. Power losses
The total active power losses in distribution networks can be calculated as the sum of the active power losses of each branch, as shown in (1).

where, PLoss is the total active power losses, b is the branch number, nb is the number of branches, Ib is the series current that circulates through the branch b, and Rb is the resistance of the branch b.
The total reactive power losses can be calculated as the sum of the reactive power losses of each branch, as shown in (2).

where, QLoss is the total reactive power losses, b is the branch number, nb is the number of branches, Ib is the series current that circulates through the branch b, and Xb is the reactance of branch b.
As the demand increases, the current increases and the power losses are higher, due to the long distance from the generators to supply the demand. Centralized generation does not allow a reduction of power losses, to improve voltage levels at critical nodes or to reduce network congestion. Therefore, distributed generation is a better option to supply power to the load.
3. Distributed generation model
Location and size of DG were modeled in this research as a vector representing the active power, the reactive power, and the node at each iteration k, as shown in (3).

where, d is the DG number (d=1, 2…ndg),
and ndg is the maximum number of DG.  is the generator d located at node i with an active and a reactive power at the iteration k.
is the generator d located at node i with an active and a reactive power at the iteration k.  and
and 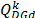 are the active and reactive
power of the generator d, located at node i at the iteration k.
are the active and reactive
power of the generator d, located at node i at the iteration k.  is the node of the DG at the
iteration k.
is the node of the DG at the
iteration k.
 changes between the minimum
active power
changes between the minimum
active power 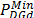 and the maximum active power
and the maximum active power 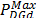 of the generator d.
of the generator d. 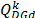 changes between the minimum
reactive power
changes between the minimum
reactive power 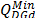 and the maximum reactive power
and the maximum reactive power  of the generator d.
of the generator d.  changes position among
all possible PQ nodes, searching for the best location during the iterations.
changes position among
all possible PQ nodes, searching for the best location during the iterations.
The new active power injection can be calculated as the sum of the real power and the change of active power at each iteration, as shown in (4).

where, 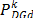 is the new active power at the
iteration k,
is the new active power at the
iteration k,  is the last value of active
power at the iteration k-1, and
is the last value of active
power at the iteration k-1, and  is the changes in active power
at the iteration k.
is the changes in active power
at the iteration k.
The new reactive power generation can be modeled as the sum of the last reactive power calculated and the new power change at the current iteration k, as shown in (5).
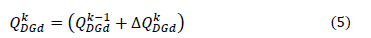
where, 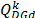 is the new reactive power at the
iteration k,
is the new reactive power at the
iteration k, 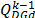 is the last value of the
reactive power at the iteration k-1, and
is the last value of the
reactive power at the iteration k-1, and  is the new change in reactive
power at the iteration k.
is the new change in reactive
power at the iteration k.
The active and reactive power supplied by the generators located at each node i, were limited by the minimum and maximum values as shown in (6) and (7).

where, 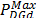 and
and  are the maximum active and
reactive power of the generator d, respectively.
are the maximum active and
reactive power of the generator d, respectively. 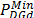 and
and  are the minimum active and
reactive power of the generator d, respectively.
are the minimum active and
reactive power of the generator d, respectively.
In this research, all generators were considered to supply the active power up to the maximum value with a power factor of 0.98. During the search of an active power, the reactive power was adjusted to maintain the operation of each generator at the same power factor.
4. Location and size of distributed generation
This optimization problem was formulated as the minimization of the active power losses, with respect to the change in power of all new DG at nodes i, as shown in (8).
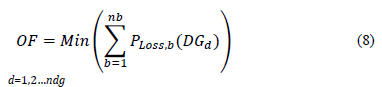
where, OF is the objective function, b is
the branch number and nb is the number of branches. PLoss,b is the active power losses of each branch b.  is the vector of
generators located at different nodes in the distribution network, as defined
in (3). d is the generator number and nd the total number of
generators.
is the vector of
generators located at different nodes in the distribution network, as defined
in (3). d is the generator number and nd the total number of
generators.
This objective function is subject to the following constraints:
Active power balance
Reactive power balance
Active power limits
Reactive power limits
Voltage at node i
Line current from i to j
Line current from j to i
where, i is the node and n is the number of nodes. PGi and QGi are the active and reactive power generation at node i,
respectively. PL and QL are the active and
reactive power of all loads, respectively. PLoss and QLossare the active and reactive power losses, respectively. 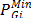 and
and  are the minimum and maximum active power of the
generator located at node i, respectively.
are the minimum and maximum active power of the
generator located at node i, respectively.  and
and  are the minimum and maximum reactive power
generation, respectively. Vi is the voltage at node i, Iij is the current supplied from node i to node j,
and Iji is the current supplied from node j to node i.
are the minimum and maximum reactive power
generation, respectively. Vi is the voltage at node i, Iij is the current supplied from node i to node j,
and Iji is the current supplied from node j to node i. 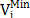 and
and  are
the minimum and maximum voltage at node i, respectively.
are
the minimum and maximum voltage at node i, respectively.  and
and  are
the maximum line currents from buses i to j and j to i,
respectively.
are
the maximum line currents from buses i to j and j to i,
respectively.
5. Optimization techniques
5.1. Particle swarm optimization
PSO is a metaheuristic based on the behavior of birds or fishes. This iterative method moves all particles to the best local and the best global solutions.
The algorithm presented in this paper was based on [30] with the following steps:
Initial velocities are generated between the minimum and maximum values, as shown in (9).

Where vp is the velocity of the particle
and  is the maximum velocity of each
particle p.
is the maximum velocity of each
particle p.
The velocity of each particle is updated at each iteration k, as shown in (10).
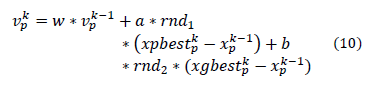
where,  is the velocity updated at the
iteration k. w, a and b are the parameters of PSO,
respectively. p is the number of the particle (p=1,2,3….np)
and np is the number of particles.
is the velocity updated at the
iteration k. w, a and b are the parameters of PSO,
respectively. p is the number of the particle (p=1,2,3….np)
and np is the number of particles. 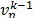 is the previous velocity at the
iteration k-1.
is the previous velocity at the
iteration k-1.  and
and 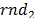 are random numbers generated at
each iteration to multiply the action over the direction of each particle to
the local best or the global best, respectively.
are random numbers generated at
each iteration to multiply the action over the direction of each particle to
the local best or the global best, respectively.  is the position of each particle p at the iteration k,
is the position of each particle p at the iteration k, 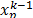 is the previous position of the
particle p at the iteration k-1, and
is the previous position of the
particle p at the iteration k-1, and  is the position of the best
particle.
is the position of the best
particle.
The new position of the particle 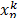 ,
is updated after adding the new velocity
,
is updated after adding the new velocity  to the previous position
to the previous position 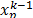 , as shown in (11).
, as shown in (11).

A vector containing the position of the DG, 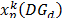 , was considered to locate the
generation at PQ buses. This vector contains all DG installed in the
distribution network, with the active and reactive power and the nodes (12)
, was considered to locate the
generation at PQ buses. This vector contains all DG installed in the
distribution network, with the active and reactive power and the nodes (12)
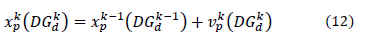
where,  is the position of the particle
containing the power and the nodes of all DG.
is the position of the particle
containing the power and the nodes of all DG.  is the vector of velocities for
each generator at the iteration k.
is the vector of velocities for
each generator at the iteration k.  is the vector of positions of
all DG at the previous iteration k-1.
is the vector of positions of
all DG at the previous iteration k-1.
5.2. Bat-inspired algorithm
BA is a metaheuristic based on the behavior of the bats during the search for their prey. This algorithm was presented by [32] and the steps used in this paper were defined as follows:
The frequency fp, used to update each bat during iterations, is calculated using (13) [32].
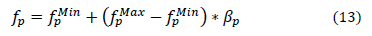
where, p is the number of the bat, fp is the frequency of the bat p, 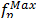 is the maximum frequency,
is the maximum frequency,  is the minimum frequency and bp is a random number to generate different frequencies.
is the minimum frequency and bp is a random number to generate different frequencies.
The velocity of each
bat was updated using the previous velocity k-1, and the difference
between previous position xp and the best  ,
multiplied by the frequency fp, as shown in (14).
,
multiplied by the frequency fp, as shown in (14).

The new position of each bat is
calculated using (11), with  as the new position of the bat,
the new velocity
as the new position of the bat,
the new velocity 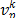 and the previous position
and the previous position 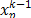 . The vector of position of DG
for this technique was modeled using (12).
. The vector of position of DG
for this technique was modeled using (12).
6. Test systems and simulations
6.1. Test system cases
Most of the loads are supplied using radial distribution networks and this test focused on determining the location and size of distributed generation. Therefore, the 33-node and the 69-node test feeders were selected to test the algorithms. General information about the test feeders can be found in Table 1.
Fig. 1 shows the
diagram of the 33-node test feeder. This distribution network has 32 possible
nodes to locate DG. The total load is 3715 kW and 2300 kVAr distributed in 32
nodes. The centralized generation supplies 3926 kW and 2443 kVAr, and the power
losses are 210 kW and 143 kVAr. The voltage limits were defined as  =0.9
p.u. and
=0.9
p.u. and  =1.1
p.u.
=1.1
p.u.
Fig. 2 shows the diagram of the 69-node test feeder. This
radial distribution network has 68 possible nodes to locate DG. The total load
is 4014 kW and 2845 kVAr, distributed in 49 nodes. The centralized generation
supply 4265 kW and 2957 kVAR and the power losses are 265 kW and 112 kVAr. The
voltage limits considered for this distribution network were defined as 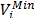 =0.9 p.u. and
=0.9 p.u. and  =1.1 p.u.
=1.1 p.u.
6.2. Scenarios for the simulation
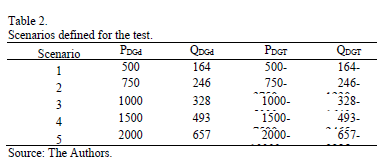
Five scenarios of active and reactive power capacities of DG were tested to determine the best algorithm. Table 2 shows the five scenarios, the maximum active and reactive power per generator, and the total active and reactive power generation.
where, PDGd and QDGd are the active and reactive power of generator d, respectively. PDGT and QDGT are the total active and reactive power of all generators to be installed in the distribution network, respectively.
6.3. General parameter of the algorithms
PSO and BA were compared in this research to determine the best location and size of DG in distribution networks. Comparisons of the minimum objective functions were carried out, considering the following parameters:
- 200 individuals
- 100 iterations
- The same initial population
- The same programming structure.
- Comparable velocities for updating positions.
The test consisted in achieving similar characteristics for the algorithms to obtain the efficiency of each technique. Furthermore, the test was based on determining the best solutions according to the number of generators and capacities.
7. Results and Discussion
7.1. Location and size of DG
Tables 3 and 4 show the results of DG location and size for the five scenarios and the seven generators installed in the 33-node and 69-node test feeders, respectively.
PT is the total power supplied by the new generators located in the network. PLoss is the total power losses of the distribution network obtained for each scenario.
From the results shown in the two tables, the algorithm PSO obtained good results for the location of a small number of generators and small capacities. When the number of generators and the capacity increase, the convergence was affected and the solutions were not what was expected.
BA obtained similar results to PSO for a small number of generators and capacities, but when the problem increased the solutions were improved using BA. BA determined a better reduction in power losses and the results were consistent according to the number, capacity and location of generators.
The two algorithms found compensations according to the maximum power inclusions of each node. The results show the power generation for cases with the maximum power generation, the algorithms found solutions where not all capacity is needed and the power losses increase with more injection from generators.
The algorithms found different solutions around the maximum power inclusion for each node according to the power losses reduction. Some scenarios supply more real power, but the power losses are higher.
7.2. Convergence of the algorithms
Fig. 3 shows the convergence of the algorithms using the scenario of maximum active power and five generators. The test was conducted using 200 individuals and 100 iterations. The average of all solutions were used to evaluate the behavior of the individuals and the evolution of all values.
PSO slowly reduced the average of the solutions and the number of evaluations made to solve the problem was not enough to find better solutions.
BA converged faster than PSO and found better solutions for the same number of iterations. During the first ten iterations, this technique reached good solutions and the search is centered on reducing to the minimum value.
7.3. Power losses reduction
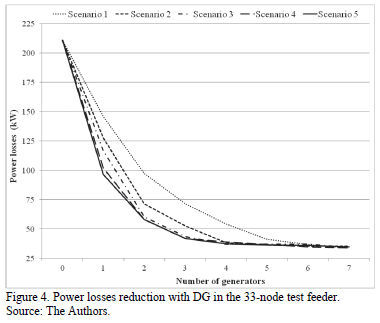
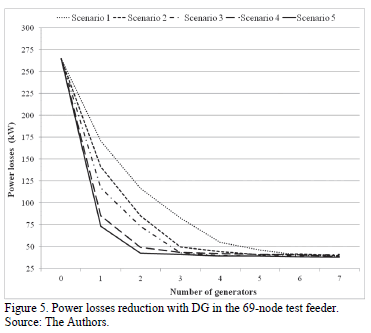
Fig. 4 and 5 show the results of BA to reduce power losses with DG in the 33-node and the 69-node test feeders, respectively.
Fig. 4 shows that the active power losses were reduced according to the number, capacities and locations of generators. The maximum active power injection to reduce power losses was found for all five scenarios in the 33-node test feeder.
Fig. 5 shows similar results for power loss reduction in the 69-node test feeder, but the maximum power injection was found for a smaller number of generators and capacities.
8. Conclusions
PSO and BA were tested to find location and size of DG in two radial distribution networks. PSO found good results with a small number of generators and capacities, but for more difficult problems the search was not successful. BA showed good results for minimizing power losses for the five scenarios, obtaining consistent results when changing capacities, locations, and the number of generators. BA converged faster than PSO and found better solutions for all scenarios. Power losses were reduced according to the number of generators and capacities, but the maximum reduction was found depending on the number of generators and capacities.
Acknowledgments
This research was supported in part by the energy strategic area of the Universidad del Norte. The authors would like to thank the Power Systems Research Group of the Universidad del Norte for the valuable information provided for this research.
References
[1] Ramesh, L., Chowdhury, S.P., Chowdhury, S., Natarajan, A.A. and Gaunt, C.T., Minimization of power loss in distribution networks by different techniques. In Proc. World Academy of Science, Engineering and Technology, 3, pp. 521-527, 2009.
[2] Gopiya-Naik, S., Khatod, D.K. and Sharma, M.P., Optimal allocation of distributed generation in distribution system for loss reduction. In Proc. IACSIT Coimbatore Conferences, 28, pp. 42-46, 2012.
[3] Singh, A.K. and Parida, S.K., Selection of load buses for DG placement based on loss reduction and voltage improvement sensitivity. In Proc. International Conference on Power Engineering, Energy and Electrical Drives, pp. 1-6, 2011. DOI: 10.1109/powereng.2011.6036559
[4] Atwa, Y.M., El-Saadany, E.F., Salama, M.M.A. and Seethapathy, R., Optimal renewable resources mix for distribution system energy loss minimization, IEEE Transactions on Power Systems, 25 (1), pp. 360-370, 2010. DOI: 10.1109/TPWRS.2009.2030276
[5] Hung, D.Q., Mithulananthan, N. and Bansal, R.C., Analytical strategies for renewable distributed generation integration considering energy loss minimization, Applied Energy, 105, pp. 75-85, 2013. DOI: 10.1016/j.apenergy.2012.12.023
[6] Shaaban, M.F. and El-Saadany, E.F., Optimal allocation of renewable DG for reliability improvement and losses reduction. In Proc. IEEE Power and Energy Society General Meeting, pp. 1-8, 2012. DOI: 10.1109/pesgm.2012.6345054
[7] Albadi, M.H., Al-Hinai, A.S., Al-Abri, N.N., Al-Busafi, Y.H. and Al-Sadairi, R S., Optimal allocation of renewable-based DG resources in rural areas using genetic algorithms. In Proc. APPEEC Power and Energy Engineering Conference, pp. 1-4, 2012. DOI: 10.1109/appeec.2012.6307161
[8] Riyami, M.A., Khalasi, F.A., Hinai, A.A., Shuraiqi, M.A. and Bouzguenda, M., Power losses reduction using solar photovoltaic generation in the rural grid of Hij-Oman. In Proc. IEEE International Energy Conference, pp. 553-557, 2010. DOI: 10.1109/energycon.2010.5771743
[9] Chen, X. and Gao, W., Effects of distributed generation on power loss, loadability and stability. In Proc. IEEE SoutheastCon, pp. 468-473, 2008.
[10] Junjie, M.A., Yulong, W. and Yang, L., Size and location of distributed generation in distribution system based on immune algorithm, Syst. Eng. Procedia, 4, pp. 124-132, 2012. DOI: 10.1016/j.sepro.2011.11.057
[11] Zhang, D., Fu, Z. and Zhagn, L., Joint optimization for power loss reduction in distribution system, IEEE Transaction on Power Systems, 23 (1), pp. 161-169, 2008. DOI: 10.1109/TPWRS.2007.913300
[12] Wu, Y.-K., Lee, C.-Y., Liu, L.-C. and Tsai, S.-H., Study of reconfiguration for the distribution system with distributed generators, IEEE Transactions on Power Delivery, 25 (3), pp. 1678-1685, 2010. DOI: 10.1109/TPWRD.2010.2046339
[13] Rao, R.S., Ravindra, K., Satish, K. and Narasimham, S.V.L., Power Loss minimization in distribution system using network reconfiguration in the presence of distributed generation, IEEE Transactions on Power Systems, 28 (1), pp. 317-325, 2013. DOI: 10.1109/TPWRS.2012.2197227
[14] Hajizadeh, A. and Hajizadeh, E., PSO-based planning of distribution systems with distributed generations. In Proc. World Academy of Science, Engineering and Technology, 21, pp. 598-603, 2008.
[15] Lalitha, M.P., Reddy, V.C.V. and Usha, V., Optimal DG placement for minimum real power loss in radial distribution system using PSO, Journal of Theoretical and Applied Information Technology, 13 (2), pp. 107-16, 2010.
[16] Kansal, S., Sai, B.B.R., Tyagi, B. and Kumar, V., Optimal placement of distributed generation in distribution networks, International Journal of Engineering, Science and Technology, 3 (3), pp. 47-55, 2011. DOI: 10.4314/ijest.v3i3.68421
[17] Wang, L. and Singh, C., Reliability-constrained optimum placement of reclosers and distributed generators in distribution networks using an ant colony system algorithm, IEEE Transactions on Systems, Man, and Cybernetics- Part C: Application and Reviews, 38 (6), pp. 757-64, 2008. DOI: 10.1109/TSMCC.2008.2001573
[18] Gautam, D. and Mithulananthan, N., Optimal DG placement in deregulated electricity market, Electric Power Systems Research, 77 (12), pp. 1627-1636, 2007. DOI: 10.1016/j.epsr.2006.11.014
[19] Hung, D.Q., Mithulananthan, N. and Bansal, R.C., Analytical expressions for DG allocation in primary distribution networks, IEEE Transactions on Energy Conversion, 25 (3), pp. 814-820, 2010. DOI: 10.1109/TEC.2010.2044414
[20] Wang, C. and Nehrir, M.H., Analytical approaches for optimal placement of distributed generation sources in power systems, IEEE Transactions on Power Systems, 19 (4), pp. 2068-2076, 2004. DOI: 10.1109/TPWRS.2004.836189
[21] Teng, J-H., Luor, T-S. and Liu, Y-H., Strategic distributed generator placements for service reliability improvements. In Proc. IEEE Power Engineering Society Summer Meeting, 2, pp. 719-724, 2002. DOI: 10.1109/PESS.2002.1043399
[22] Borges, C.L.T. and Falcao, D.M., Optimal distributed generation allocation for reliability, losses, and voltage improvement, International Journal of Electrical Power and Energy Systems, 28 (6), pp. 413-420, 2006. DOI: 10.1016/j.ijepes.2006.02.003
[23] Shaaban, M.F., Atwa, Y.M. and El-Saadany, E.F., DG allocation for benefit maximization in distribution networks, IEEE Transactions on Power Systems, 28 (2), pp. 639-649, 2012. DOI: 10.1109/TPWRS.2012.2213309
[24] Celli, G., Ghiani, E., Mocci, S. and Pilo, F., A multiobjective evolutionary algorithm for the sizing and siting of distributed generation, IEEE Transactions on Power Systems, 20 (2), pp. 750-757, 2005. DOI: 10.1109/TPWRS.2012.2213309
[25] Sutthibun, T. and Bhasaputra, P., Multi-objective optimal distributed generation placement using simulated annealing. In Proc. ECTI-CON International conference on electrical engineering/electronics computer telecommunications and information technology, pp. 810-813, 2010.
[26] Aly, A.I., Hegazy, Y.G. and Alsharkawy, M.A., A simulated annealing algorithm for multi-objective distributed generation planning. In Proc. IEEE Power and Energy Society General Meeting, pp. 1-7, 2010. DOI: 10.1109/PES.2010.5589950
[27] Ghadimi, N. and Ghadimi, R., Optimal allocation of distributed generation and capacitor banks in order to loss reduction in reconfigured system, Research Journal of Applied Sciences, Engineering and Technology, 4 (9), pp. 1099-1104, 2012.
[28] Nara, K., Hayashi, Y., Ikeda, K. and Ashizawa, T., Application of Tabu search to optimal placement of distributed generators. In Proc. IEEE power engineering society winter meeting, 2, pp. 918-923, 2001. DOI: 10.1109/pesw.2001.916995
[29] Mokhtari-Fard, M., Noroozian, R. and Molaei, S., Determining the optimal placement and capacity of DG in intelligent distribution networks under uncertainty demands by COA. In Proc. ICSG 2nd Iranian conference on smart grids, pp. 1-8, 2012.
[30] Tan, W-S., Hassan, M., Majid, M. and Rahman, H., Optimal distributed renewable generation planning: A review of different approaches, Renewable and Sustainable Energy Reviews, 18, pp. 626-645, 2013. DOI: 10.1016/j.rser.2012.10.039
[31] Van den Bergh, F. and Engelbrecht, A.P., A new locally convergent particle swarm optimizer. In Proc. IEEE Conference on Systems, Man, and Cybernetics, pp. 96-101, 2002. DOI: 10.1109/ICSMC.2002.1176018
[32] Yang, X.-S., A new metaheuristic bat-inspired algorithm. In Proc. NISCO Nature Inspired Cooperative Strategies for Optimization, Studies in Computational Intelligence, 284, pp. 65-74, 2010. DOI: 10.1007/978-3-642-12538-6_6
[33] University of Washington. Power systems test case archive. [Online] [date of reference: February 10th of 2014]. Available at: http://www.ee.washington.edu/research/pstca/
[34] Phonrattanasak, P. and Leeprechanon, N., Optimal location of fast charging station on residential distribution grid, Int. J. Innov. Manag. Technol., 3 (6), pp. 675-681, 2012.
J.E. Candelo-Becerra, received his BSc. degree in Electrical Engineering in 2002 and his PhD in Engineering with emphasis in Electrical Engineering in 2009 from Universidad del Valle, Cali, Colombia. His employment experiences include the Empresa de Energía del Pacífico EPSA, Universidad del Norte, and Universidad Nacional de Colombia. He is now an assistant professor of the Universidad Nacional de Colombia, Medellín, Colombia. His research interests include: planning, operation and control of power systems, artificial intelligence and smart grids.
H.E. Hernández-Riaño, received his BSc. degree in Industrial Engineering in 1999 from Universidad Distrital Francisco José de Caldas, Bogotá, Colombia and the MSc. degree in Management of Organizations in 2006 from Universidad EAN, Bogotá, Colombia. He is now an assistant professor of the Department of Industrial Engineering in the Universidad de Córdoba, Montería, Colombia. He is actually studying a PhD in Industrial Engineering in the Universidad del Norte, Barranquilla, Colombia. His research interests include: planning, operation and control of power systems, operations management, supply chain management, total quality management, continual improvement process, artificial intelligence and optimization.
Cómo citar
IEEE
ACM
ACS
APA
ABNT
Chicago
Harvard
MLA
Turabian
Vancouver
Descargar cita
CrossRef Cited-by
1. Olusayo A. Ajeigbe, Josiah L. Munda, Yskandar Hamam. (2020). Towards maximising the integration of renewable energy hybrid distributed generations for small signal stability enhancement: A review. International Journal of Energy Research, 44(4), p.2379. https://doi.org/10.1002/er.4864.
2. Emad Ali Almabsout, Ragab A. El-Sehiemy, Ahmed Saeed Abdelrazek Bayoumi. (2023). Enhanced Real Coded Genetic Algorithm for Optimal DG Placement in a Radial Distribution System. Journal of Electrical Engineering & Technology, 18(4), p.2581. https://doi.org/10.1007/s42835-022-01355-1.
3. Rasheed Abdulkader, Hayder Ghanimi, Pankaj Dadheech, Meshal Alharbi, Walid El-Shafai, Mostafa Fouda, Moustafa Aly, Dhivya Swaminathan, Sudhakar Sengan. (2023). Soft Computing in Smart Grid with Decentralized Generation and Renewable Energy Storage System Planning. Energies, 16(6), p.2655. https://doi.org/10.3390/en16062655.
4. Rana.H.A. Zubo, Geev Mokryani, Haile-Selassie Rajamani, Jamshid Aghaei, Taher Niknam, Prashant Pillai. (2017). Operation and planning of distribution networks with integration of renewable distributed generators considering uncertainties: A review. Renewable and Sustainable Energy Reviews, 72, p.1177. https://doi.org/10.1016/j.rser.2016.10.036.
5. John Edwin Candelo, Gladys Caicedo Delgado. (2019). Voltage stability assessment using fast non-dominated sorting algorithm 1. DYNA, 86(208), p.60. https://doi.org/10.15446/dyna.v86n208.62957.
6. Younes Noorollahi, Amir Shahriar Kalantari, Amirali Saifoddin, Hossein Yousefi. (2021). Distributed wind and solar power for grid sustainability and emission reduction. Environmental Progress & Sustainable Energy, 40(6) https://doi.org/10.1002/ep.13686.
7. Eshan Karunarathne, Jagadeesh Pasupuleti, Janaka Ekanayake, Dilini Almeida. (2020). Optimal Placement and Sizing of DGs in Distribution Networks Using MLPSO Algorithm. Energies, 13(23), p.6185. https://doi.org/10.3390/en13236185.
8. U. Sultana, Azhar B. Khairuddin, M.M. Aman, A.S. Mokhtar, N. Zareen. (2016). A review of optimum DG placement based on minimization of power losses and voltage stability enhancement of distribution system. Renewable and Sustainable Energy Reviews, 63, p.363. https://doi.org/10.1016/j.rser.2016.05.056.
9. Essam A. Al-Ammar, Kiran Farzana, Asad Waqar, Muhammad Aamir, Saifullah, Azhar Ul Haq, Muhammad Zahid, Memoona Batool. (2021). ABC algorithm based optimal sizing and placement of DGs in distribution networks considering multiple objectives. Ain Shams Engineering Journal, 12(1), p.697. https://doi.org/10.1016/j.asej.2020.05.002.
10. Anagha Rajendran K P, Soumyabrata Barik, Sudarshan Swain. (2024). Logic OR Based Modified Forward Backward Load Flow Method for the Siting and Sizing of DGs in Radial Distribution Networks. 2024 International Conference on Recent Innovation in Smart and Sustainable Technology (ICRISST). , p.1. https://doi.org/10.1109/ICRISST59181.2024.10921968.
11. Hossein Ghaemi, Sajjad Tohidi, Mehdi Abapour, Vahid Sohrabi Tabar. (2020). Determining the size and location of variable speed wind turbines for reducing power losses and improving voltage profile. Journal of Renewable and Sustainable Energy, 12(6) https://doi.org/10.1063/5.0020580.
Dimensions
PlumX
Visitas a la página del resumen del artículo
Descargas
Licencia
Derechos de autor 2015 DYNA

Esta obra está bajo una licencia internacional Creative Commons Atribución-NoComercial-SinDerivadas 4.0.
El autor o autores de un artículo aceptado para publicación en cualquiera de las revistas editadas por la facultad de Minas cederán la totalidad de los derechos patrimoniales a la Universidad Nacional de Colombia de manera gratuita, dentro de los cuáles se incluyen: el derecho a editar, publicar, reproducir y distribuir tanto en medios impresos como digitales, además de incluir en artículo en índices internacionales y/o bases de datos, de igual manera, se faculta a la editorial para utilizar las imágenes, tablas y/o cualquier material gráfico presentado en el artículo para el diseño de carátulas o posters de la misma revista.