Nuevo par de engranajes no circulares para reducir las aceleraciones del eje: Comparación con engranajes sinusoidales y elípticos
A new noncircular gear pair to reduce shaft accelerations: A comparison with sinusoidal and elliptical gears
DOI:
https://doi.org/10.15446/dyna.v83n198.49170Palabras clave:
perfiles de engranajes no circulares, aceleraciones del eje, engranajes sinusoidales, engranajes elípticos (es)noncircular gear centrodes, shaft accelerations, sinusoidal gears, elliptical gears (en)
Descargas
DOI: https://doi.org/10.15446/dyna.v83n198.49170
A new noncircular gear pair to reduce shaft accelerations: A comparison with sinusoidal and elliptical gears
Nuevo par de engranajes no circulares para reducir las aceleraciones del eje: Comparación con engranajes sinusoidales y elípticos
Libardo V. Vanegas-Useche a, Magd M. Abdel-Wahab b & Graham A. Parker c
a Facultad de Ingeniería Mecánica, Universidad Tecnológica de
Pereira, Colombia. lvanegas@utp.edu.co
b Faculty of Engineering and
Architecture, Ghent University, Ghent, Belgium. magd.abdelwahab@ugent.be
c Faculty of Engineering and Physical
Sciences, The University of Surrey, Guildford, UK. g.parker@surrey.ac.uk
Received: May 28th, 2015. Received in revised form: January 16th, 2016. Accepted: March 23th, 2016.
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.

Abstract
This article presents a new noncircular
gear pair to obtain small shaft accelerations. The centrode contours may be
controlled depending on the required maximum acceleration and smoothness of the
centrodes. A comparison among elliptical, sinusoidal, and the new gears is
provided. Results show that, for two-lobule gears, the maximum and minimum
polar radii and gear ratios are the same for the new and sinusoidal profiles
but differ for the elliptical ones. Conversely, there are significant
differences in the maximum angular acceleration, tangential acceleration, and
pressure angle. It is concluded that the novel gears provide not only small
shaft accelerations, but also small tangential accelerations and pressure
angles, and it is excepted that the elliptical gears may exhibit lower
tangential accelerations and pressure angles for large values of the angular
speed alternating component. Consequently, shaft and tooth loads and stresses
may be lower for the new gears. This may result in more compact systems.
Keywords: noncircular gear centrodes; shaft accelerations; sinusoidal gears; elliptical gears.
Resumen
Se presenta un
nuevo par de engranajes no circulares para obtener pequeñas aceleraciones del
eje. Las formas de los engranajes pueden ser controladas dependiendo de la
máxima aceleración y suavidad de los contornos requeridos. Se hace una
comparación con engranajes elípticos y sinusoidales. Los resultados muestran
que, para engranajes de dos lóbulos, los valores máximos y mínimos de los
radios polares y de la relación de transmisión son iguales para los perfiles
desarrollados y los sinusoidales, pero difieren para los elípticos. En
contraste, los valores máximos de la aceleración angular, aceleración
tangencial y ángulo de presión difieren. Se concluye que los nuevos perfiles
proporcionan pequeñas aceleraciones angulares y tangenciales y menores ángulos
de presión, excepto que los elípticos pueden exhibir menores aceleraciones
tangenciales y ángulos de presión para grandes variaciones de la velocidad.
Consecuentemente, las cargas y esfuerzos podrían ser menores. Esto podría
resultar en sistemas más compactos.
Palabras clave: perfiles de engranajes no circulares; aceleraciones del eje; engranajes sinusoidales, engranajes elípticos.
1. Introduction
Mechanisms, such as linkages and gears, are used in a huge number of applications: several types of machines [1], devices [2], vehicles, computers, and prosthesis [3], among many others. Noncircular gears (NCGs) are a particular class of gears, the centrodes of which are non-circular; therefore, the speed ratio and the ratio between the angular displacements are not constant. For this reason, they are used for special purposes. For example, they may improve the efficiency, function, or versatility of a mechanical system; they may be used to obtain vibrations, a certain function for the velocity of the driven shaft, or for controlling the force function in a human powered vehicle. Applications of NCGs include bicycles, agricultural mechanisms, textile machines, mechanical presses, and high torque hydraulic engines for bulkhead drives [4]. The most common types of NCGs are elliptical gears, true or high-order, and logarithmic-spiral gears. Two true elliptical gears in mesh are identical geared ellipses rotating about their foci, and they produce one speed cycle per revolution.
This article builds on a previous work [5], which reviews noncircular gears and explains in detail the main variables of NCGs. The reader can, therefore, refer to this or other works to read reviews (e.g., [6]) and descriptions (e.g., [7]) of noncircular gear variables. Despite this, all the relevant information is provided in this paper.
Compared to research on circular gears, the amount of research on NCGs is very small, and it may be the case that articles from the early twentieth century or previous to this are unavailable [8].
Most of the papers on NCGs can be categorized into three research areas: (a) new pitch centrodes that satisfy particular requirements or functions [9-20]. For example, Litvin et al. [18] developed NCGs to obtain various functions: when the derivative of the function changes its sign and pitch profiles that have unclosed curves. Ottaviano et al. [19] developed and experimentally validated a pair of NCGs to attain a prescribed motion for an application related to external blood circulation in cardiac surgery. The NCGs performance is compared with a cam-follower system, and the paper outlines the advantages and disadvantages. (b) Development of novel profiles of NCG teeth [8,21,22]. (c) Development of mathematical models to describe or manufacture NCGs teeth and their cutters [23-30]. For example, Xia et al. [30] developed a method for hobbing noncircular helical gears, which is based on a method with axial shift of the hob. The approach derived from this method includes two schemes: fixed and moving meshing point on hob. The advantages of the methodology are that it can increase machine tool operating range and that gears with large eccentricity and large NCGs may be hobbed by the latter.
Other areas in which research has been conducted include: undercutting analysis [23,24,29,31], pointed teeth [29], computer aided design or engineering [24,32], mechanisms comprising linkages combined with NCGs [33,34]. For example, Mundo et al. [33] propose a five-bar linkage combined with NCGs to move a point of the mechanism along a prescribed trajectory and Modler et al. [34] present a general methodology to design a desired transmission function.
In this article, a new noncircular gear pair that produces small shaft accelerations is proposed. Their characteristics are compared with their elliptical and sinusoidal gears counterparts, which are two common types of NCGs. In the comparison, gears with two lobules are considered. The following sections describe the equations for these three types of gear centrodes. Then, in Section 6, a comparison is presented. Finally, Section 7 concludes this article.
2. Geometric and kinematic equations of NCGs
This section presents the relevant equations for the design and analysis of noncircular gears. A more detailed theory on NCGs is presented in other papers [5-7].
The gear ratio in a NCG pair is not constant and may be expressed as
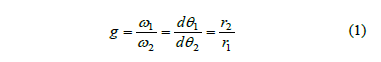
where w1 and w2 are the angular speed of gear 1 and gear 2 respectively (hereafter "1" will refer to the driving gear and "2" to the driven gear), and q and r are the gear polar angle and polar radius (Fig. 1). The gear ratio is normally expressed as a function of q1.
The sum of the polar radii of two external gears is constant and is given by
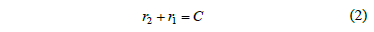
where C is the fixed center distance (O1 and O2 are fixed).
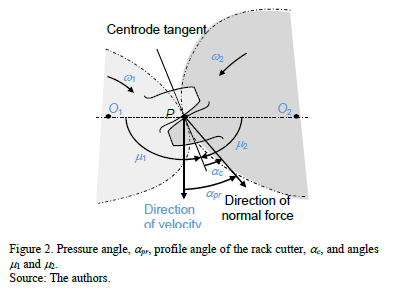
The angles m1 and m2 (Fig. 2) correspond to the direction of the centrode tangent and are given by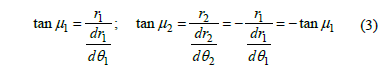
The pressure angle may be expressed as
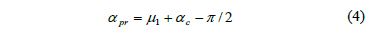
where ac is the profile angle of the rack cutter.
In a NCG pair, gear 1 usually rotates at a constant speed w1, whereas the speed of gear 2, w2, varies (Fig. 3); the latter one is characterized by
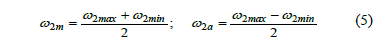
where w2m and w2a are the mean and alternating component of w2; w2max and w2min are the maximum and minimum components, respectively.
The following expression is useful to derive the equations of NCG pair's centrodes. It can be demonstrated that [5]:

where nlob1 is the number of lobules (protuberances) of gear 1, f is the frequency of w2 and t is time.
The shapes of the NCGs can be determined by [5]

The kinematics of NCGs may be determined by the following expressions
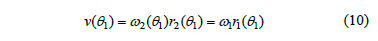
where v is the velocity at the contact point P (Fig. 2).
The angular acceleration is defined by

The tangential component of acceleration at P can be calculated by [5]

Lastly, it has that [5]
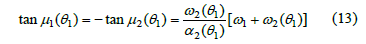
The following sections present the specific equations for the second order elliptical gears, sinusoidal gears, and the novel gear pair developed.
3. Elliptical gears
Two second-order elliptical gears rotating about their geometric centers are identical. The polar radius of gear 1, r1, as a function of its polar angle, q1, is given by [35]
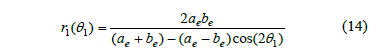
where ae and be, which satisfy ae + be = C and be< ae, are the semi-axes of each centrode. The equations for this pair can be obtained from eq. (14) and some of those in Section 2. Fig. 1 presents an example of a pair of elliptical gears.
Fig. 4, 5 show the shapes of the curves w-t and a-t for the elliptical gears.
4. Sinusoidal gears
For the sinusoidal gears, the angular speed of gear 2 is given by
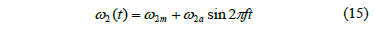
Also, by using eq. (6), it can be given by
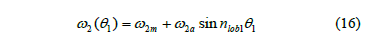
The angular acceleration of gear 2 is calculated by differentiating eq. (15) with respect to time. By using eq. (6), and taking into account that for sinusoidal gears, as well as for the novel gear pair, the following applies [5]
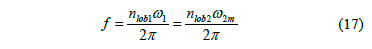
And the following are yielded
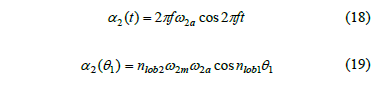
Therefore, the maximum and minimum angular accelerations, a2max and a2min, are respectively
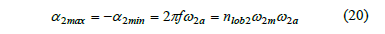
Finally, substitution of eq. (16) into eq. (9) produces

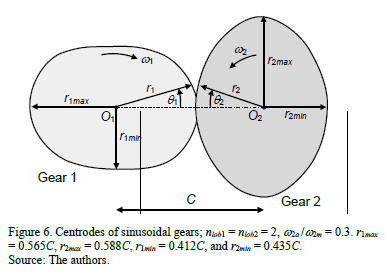
A sinusoidal NCG pair's centrodes can be obtained from eq. (7), (8), (21). Fig. 6 provides an example by showing a sinusoidal NCG pair's centrodes, with two lobules each, when w2a /w2m = 0.3. Also, Fig. 4, 5 show the shapes of the curves w-t and a-t for the sinusoidal gears.
5. A new NCG pair
For a given set of parameters f, w2a, and w2m, the minimum value of the maximum acceleration of the driven shaft is obtained when the velocity increases linearly from its minimum value and then decreases linearly from its maximum value. However, this speed variation will produce pointed centrodes and, subsequently, gears that are not able to produce teeth generation. In view of this, this work presents the mathematical equations for the NCG centrodes of a new pair that has been devised to minimize shaft accelerations, while the centrodes obtained are sufficiently smooth. To the authors' knowledge no other researchers have dealt with NCGs to minimize shaft accelerations.
For the angular speed of gear 2, the following equation has been devised:

which satisfies
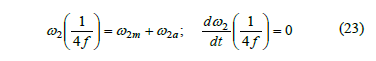
Substitution of eq. (6) into eq. (22) yields
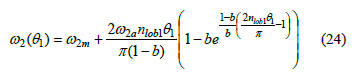
The parameter b is called a "smooth parameter" and may vary from a value close to 0 (when the centrodes become pointed) to 1. As b is increased from 0, the centrodes become smoother; however, in order to achieve small shaft accelerations, b has to be much closer to 0 than to 1.
Eq. (22), (24) are valid for a quarter of an w2 cycle. These are extended as follows:

Where
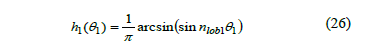
And

It can be demonstrated that
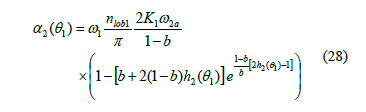
Where

where "int" is a function that rounds the argument down to the closest integer.
The maximum and minimum values of a(t) are given by

It can be demonstrated that the polar angle of gear 2 is given by
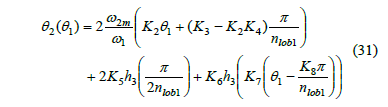
where h3 is a function of an angular variable, say q, given by
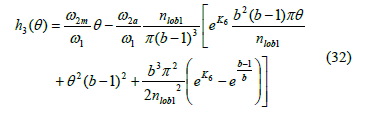
And

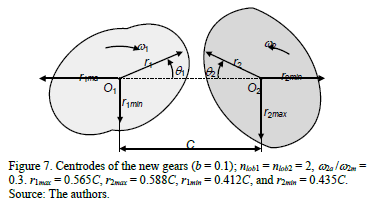
The profiles of the NCGs may be obtained from eq. (7), (8), (31). As an example, Fig. 7 shows the centrodes of a NCG pair with b = 0.1. Also, Fig. 4, 5 show the shapes of the curves w-t and a-t for the new gears with b » 0. It should be noted that these gears produce the smallest angular accelerations.
6. Comparison of geometric and kinematic characteristics of the three profiles
The equations presented in Sections 2 to 5 are applied in order to analyze and compare the three types of gears that this paper addresses. The independent variables for this study are w2a /w2m, w2m, b, ac, nlob1, and nlob2. However, the NCGs analyzed in this article have two lobules (nlob1 = nlob2 = 2). The dependent variables to be studied are the nondimensional polar radii terms r1/C and r2/C, the tangential acceleration term at / C, maximum and minimum apr, and maximum angular acceleration a2. As the profile angle of the rack cutter only affects the pressure angle as an addend (eq. 4), any value, say the standard value of 20°, may be used for the comparison. It should be noted that w2a /w2m has been taken as an independent variable, as r1/C, r2/C, apr, and g are independent of the values of w2a and w2m for a certain ratio w2a /w2m; the rest of the variables and terms are proportional to w2m.
Fig. 8, 9 show the variation of the maximum and minimum values of apr for the elliptical, sinusoidal, and new profiles (indicated by "VAP" in the figures), for ac = 20° and nlob1 = nlob2 = 2. For the last ones, three values of b are taken: ~0, 0.1, and 0.4. Both figures indicate that the differences in the maximum and minimum pressure angle are not so large for the small ratios w2a /w2m. However, they tend to become larger for higher ratios. For small ratios, the new profiles (with b £ 0.4) produce the smallest maximum values of pressure angle, as well as the largest minimum ones, and the sinusoidal ones produce the largest maximum values and the smallest minimum ones. This result indicates that the derived profiles may have an advantage to reduce tooth forces and stresses. In contrast, for example, when w2a /w2m > 0.28 o 0.325 the elliptical gears and the sinusoidal gears, respectively, produce smaller values than the new gears with b » 0. For w2a /w2m = 0.5, aprmax is 49.0°, 53.9°, 60.3°, and 54.9° for the elliptical, sinusoidal, b » 0, and b = 0.1, respectively.
Therefore, the elliptical profiles provide the smallest values and the new gears the larger ones. The largest difference in the interval study is 11.3° (23% of 49.0°), which corresponds to the difference in the maximum or minimum pressure angle between the elliptical and the new function with b » 0.
On the one hand, the developed profiles have been devised to use a value of b greater than 0; therefore, for the new profiles, apr max becomes smaller and apr min becomes larger. On the other hand, it may be more appropriate, as far as the pressure angle is concerned, to use elliptical gears if the ratio w2a /w2m is large. Lastly, from Fig. 8, it can be concluded that the derived gears with b ³ 0.1 outperforms the other profiles for w2a /w2m £ 0.35 in terms of the pressure angle.
Fig. 10, 11, 12 present the results regarding the maximum and minimum values of the polar radii and gear ratio. It can be observed that regardless the value of b, the derived gears, as well as the sinusoidal one, have the same maximum and minimum values of r1, r2, and g. Only the elliptical gears have different values; these gears tend to have larger polar radii for gear 1 and smaller polar radii for gear 2 than their counterparts with other profiles. However, the variation of the polar radii, i.e., the difference between the maximum and minimum values of each gear (driving and driven) is virtually the same. Additionally, the maximum values increase and the minimum ones decrease as the ratio w2a /w2m increases, as expected. In light of this, it may be concluded that the variation of polar radii does not seem to be an important criterion for gear performance.
Regarding gear kinematics, Fig. 13 presents the variation of the maximum angular acceleration of gear 2 for w2m = 100 rpm. As expected, the angular acceleration increases as the ratio w2a /w2m increases. As eq. (20) and (30) show, the relationship between a2max and w2a /w2m is linear; this is not the case for the elliptical gears. Also, as expected, the proposed centrodes produce the minimum angular accelerations for small values of b (when b £~0.5); the elliptical gears are the ones that produce the highest accelerations. However, the important finding is that the differences in the angular acceleration are large. For example, there are differences between the values for the sinusoidal and new gears with b = 0.1 is 29.3%, with respect to a2max of the sinusoidal pair (regardless of the value of w2a /w2m). The difference between the values for the elliptical and new gears with b = 0.1 has a maximum value of 35.5% with respect to a2max of the elliptical profiles. Therefore, the novel gears outperform the other profiles and, thus, will produce significantly smaller shaft accelerations.
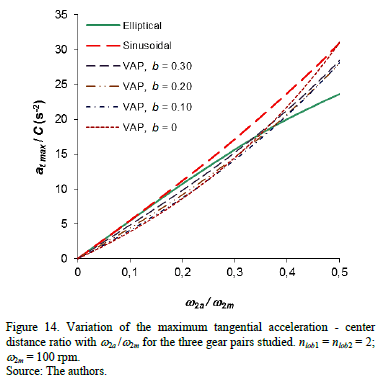
Fig. 14 shows the variation of the ratio maximum tangential acceleration at the contact point - center distance, for w2m = 100 rpm. It can be observed that the teeth of the new profiles withstand lower tangential accelerations than those of the sinusoidal gears. A similar situation occurs when comparing the elliptical and new gears for w2a /w2m <~0.35.
For larger ratios, the elliptical gears provide smaller tangential accelerations. In view of this, as far as the tangential accelerations at the contact points are concerned, the new gears will outperform the other profiles for w2a /w2m <~0.35, and the elliptical gears will outperform the other gears for w2a /w2m >~0.35.
The discussion in this section indicates that, overall, the derived gear profiles tend to outperform the sinusoidal and elliptical gears, as far as the shaft accelerations, the tangential accelerations, and the pressure angle are concerned. The only exception is that the elliptical gears produce smaller values of the maximum tangential accelerations if w2a /w2m >~0.35 and there are smaller maximum values of the pressure angle for w2a /w2m >~0.28. The new gears would only have large positive or negative pressure angles for very small values of b together with very high ratios w2a /w2m, which may increase tooth forces and stresses. However, a suitable value of b might be selected, so that the gears withstand low stresses. The advantage of all this will be reflected in smaller forces, torques, and stresses in the drive system and in the gear teeth. Thus, the gears may be more compact and provide a smoother operation. However, it is necessary to perform additional research so as to ascertain the effect of the smoothness parameter on tooth forces and stresses.
7. Conclusions
In this article, a new noncircular gear pair has been proposed. This has been devised so that the angular velocity of the driven gear increases and decreases virtually linearly from its minimum and maximum values, respectively, with the aim of producing small accelerations for the driven shaft. The profiles of the new gears are aimed at reducing driven gear accelerations and are based on an exponential function that depends on a smoothness parameter that controls the smoothness of the centrodes in order to avoid pointed lobules.
A comparison of the geometric and kinematic characteristics of three NCG pairs, namely elliptical, sinusoidal, and new gears is presented. The results indicate that for two-lobule centrodes the new gears tend to outperform the other two profiles. This is particularly true for the angular acceleration of the driven shaft; therefore, it is expected that the loads and stresses of the driven shaft are smaller than those produced by the other profiles. Additionally, for certain ranges of the ratio between the alternating and mean angular velocities, the new pair also tends to produce smaller maximum values of the pressure angle and of the tangential accelerations at the contact point. Therefore, the developed gears may exhibit lower tooth forces and stresses.
Acknowledgements
The authors would like to acknowledge the support given by the Universidad Tecnológica de Pereira, Colombia, the University of Surrey, UK, and the Programme Alban: the European Union Programme of High Level Scholarships for Latin America, identification number (E03D04976CO).
References
[1] Peña-Bustos, F.M. and Álvarez-Vargas, C.A., Design and construction of a torsional fatigue testing machine operated by inertial loads. DYNA, 79(172), pp. 46-55, 2012.
[2] Marulanda, D. and Olaya, J.J., Unbalanced magnetron sputtering system for producing corrosion resistance multilayer coatings. DYNA, 79(171), pp. 74-79, 2012.
[3] Loaiza, J.L. and Arzola, N., Evolución y tendencias en el desarrollo de prótesis de mano. DYNA, 78(169), pp. 191-200, 2011.
[4] Zarebski, I. and Salacinski, T., Designing of non-circular gears. The Archive of Mechanical Engineering, LV(3), pp. 275-292, 2008.
[5] Vanegas-Useche, L.V., Abdel-Wahab, M.M. and Parker, G.A., Design of noncircular gears to minimise shaft accelerations, Proc. of the 8th ASME Conf. Eng. Sys. Des. Analysis ESDA 2006, pp. ESDA2006-95560-1 - ESDA2006-95560-10, 2006. DOI: 10.1115/ESDA2006-95560
[6] Quintero, H.F., Cardona, S. and Jordi, L., Engranajes no circulares: aplicaciones, diseño y manufactura. Scientia et Technica, 24, pp. 133-138, 2004.
[7] Olsson, U., Non-circular cylindrical gears. Acta Polytechnica, 2(10), pp. 1-216, 1953. DOI: 10.1002/zamm.19540340711
[8] Lozzi, A., Non-circular gears - graphic generation of involutes and base outlines. Proc. Inst. Mech. Engrs., 214(C), pp. 411-422, 2000. DOI: 10.1243/0954406001523074
[9] Dooner, D.B., Function generation utilizing an eight-link mechanism and optimized non-circular gear elements with application to automotive steering. Proc. Instn. Mech. Engrs. (ImechE), Part C: J. Mech. Eng. Sc., 215(7), pp. 847-857, 2001. DOI: 10.1243/0954406011524090
[10] Dooner, D.B., Use of noncircular gears to reduce torque and speed fluctuations in rotating shafts. ASME J. Mech. Des., 119(2), pp. 299-306, 1997. DOI: 10.1115/1.2826251
[11] Dooner, D., Yoon, H-D. and Seireg, A., Kinematic considerations for reducing the circulating power effects in gear-type continuously variable transmissions. Proc. Inst. Mech. Engrs., 212(D), pp. 463-478, 1998. DOI: 10.1243/0954407981526118
[12] Tong, S-H. and Yang, D.C.H., Generation of identical noncircular pitch curves. ASME J. Mech. Des., 120(2), pp. 337-341, 1998. DOI: 10.1115/1.2826978
[13] Doege, E., Meinen, J., Neumaier, T. and Schaprian, M., Numerical design of a new forging press drive incorporating non-circular gears. Proc. Inst. Mech. Engrs. (ImechE), Part B: J. Eng. Man., 215(4), pp. 465-471, 2001. DOI: 10.1243/0954405011518430
[14] Guo, L.S. and Zhang, W.J., Kinematics analysis of a rice transplanting mechanism with eccentric planetary gear trains. Mechanism and Machine Theory, 36(11-12), pp. 1175-1188, 2001. DOI: 10.1016/S0094-114X(01)00052-0
[15] Librovich, B.V., Dynamics of rotary vane engine. ASME J. Mech. Des., 125(3), pp. 498-508, 2003. DOI: 10.1115/1.1582500
[16] Tucker, R.W., Wang, C. and Librovich, B.V., Mathematical modelling of rotary vane engines. Proc. Inst. Mech. Engrs. (ImechE), Part C: J. Mech. Eng. Sc., 217(6), pp. 687-704, 2003. DOI: 10.1243/095440603321919608
[17] Yao, Y-A. and Yan, S-H., A new method for torque balancing of planar linkages using non-circular gears. Proc. Inst. Mech. Engrs. (ImechE), Part C: J. Mech. Eng. Sc., 217(5), pp. 495-503, 2003. DOI: 10.1243/095440603765226786
[18] Litvin, F.L., Gonzalez-Perez, I., Fuentes, A. and Hayaska, K., Design and investigation of gear drives with non-circular gears applied for speed variation and generation of functions. Comput. Methods Appl. Mech. Engrg., 197, pp. 3783-3802, 2008. DOI: 10.1016/j.cma.2008.03.001
[19] Ottaviano, E., Mundo, D., Danieli, G.A. and Ceccarelli, M., Numerical and experimental analysis of non-circular gears and cam-follower systems as function generators. Mechanism and Machine Theory, 43, pp. 996-1008, 2008. DOI: 10.1016/j.mechmachtheory.2007.07.004
[20] Figliolini, G., Stachel, H. and Angeles, J., Synthesis of the base curves of non-circular gears via the return circle, Int. Gear Conf., pp. 540-550, 2014. DOI: 10.1533/9781782421955.540
[21] Yang, D.C.H., Tong, S-H. and Lin, J., Deviation-function based pitch curve modification for conjugate pair design. ASME J. Mech. Des., 121(4), pp. 579-586, 1999. DOI: 10.1115/1.2829502
[22] Danieli, G.A., Analytical description of meshing of constant pressure angle teeth profiles on a variable radius gear and its applications. ASME J. Mech. Des., 122(1), pp. 123-129, 2000. DOI: 10.1115/1.533551
[23] Chang, S-L., Tsay, C-B. and Wu, L-I., Mathematical model and undercutting analysis of elliptical gears generated by rack cutters. Mechanism and Machine Theory, 31(7), pp. 879-890, 1996. DOI: 10.1016/0094-114X(95)00121-E
[24] Chang, S-L. and Tsay, C-B., Computerized tooth profile generation and undercut analysis of noncircular gears manufactured with shaper cutters. ASME J. Mech. Des., 120(1), pp. 92-99, 1998. DOI: 10.1115/1.2826682
[25] Bair, B-W., Computer aided design of elliptical gears. ASME J. Mech. Des., 124(4), pp. 787-793, 2002. DOI: 10.1115/1.1485092
[26] Bair, B-W., Computer aided design of non-standard elliptical gear drives. Proc. Inst. Mech. Engrs. (ImechE), Part C: J. Mech. Eng. Sc., 216(4), pp. 473-483, 2000. DOI: 10.1243/0954406021525250
[27] Bair, B-W., Computerized tooth profile generation of elliptical gears manufactured by shaper cutters. J. Mat. Proc. Tech., 122(2-3), pp. 139-147, 2002. DOI: 10.1016/S0924-0136(01)01242-0
[28] Figliolini, G. and Angeles, J., The synthesis of elliptical gears generated by shaper-cutters. ASME J. Mech. Des., 125(4), pp. 793-801, 2003. DOI: 10.1115/1.1631573
[29] Bair, B-W., Computer aided design of elliptical gears with circular-arc teeth. Mechanism and Machine Theory, 39(2), pp. 153-168, 2004. DOI: 10.1016/S0094-114X (03)00111-3
[30] Xia, L., Liu, Y., Li, D. and Han, J., A linkage model and applications of hobbing non-circular helical gears with axial shift of hob. Mechanism and Machine Theory, 70, pp. 32-44, 2013. DOI: 10.1016/ j. mechmachtheory. 2013.07.002
[31] Bair, B-W., Sung, M-H., Wang, J-S. and Chen, C-F., Tooth profile generation and analysis of oval gears with circular-arc teeth. Mechanism and Machine Theory, 44, pp. 1306-1317, 2009. DOI: 10.1016/ j. mechmachtheory. 2008.07.003
[32] Barkah, D., Shafiq, B. and Dooner, D., 3D mesh generation for static stress determination in spiral noncircular gears used for torque balancing. ASME J. Mech. Des., 124(2), pp. 313-319, 2002. DOI: 10.1115/1.1470492
[33] Mundo, D., Gatti, G. and Dooner, D.B., Optimized five-bar linkages with non-circular gears for exact path generation. Mechanism and Machine Theory, 44, pp. 751-760, 2009. DOI: 10.1016/j.mechmachtheory. 2008.04.011
[34] Modler, K.-H., Lovasz, E.-C., Bär, G.F., Neumann, R., Perju, D., Perner, M. and Mărgineanu, D., General method for the synthesis of geared linkages with non-circular gears. Mechanism and Machine Theory, 44, pp. 726-738, 2009. DOI: 10.1016/j.mechmachtheory.2008.05.006
[35] Bloomfield, B. Design guide when you need noncircular gears, in Chironis - N. P. Gear design and application, New York, McGraw-Hill, Inc., 1967. DOI: 10.1016/0022-2569(68)90361-3
L.V. Vanegas-Useche, PhD., is full professor in the Mechanical Engineering Department, Universidad Tecnológica de Pereira, Colombia. He received his BSc. in Mechanical Engineering from the Universidad Tecnológica de Pereira, Pereira, Colombia, in 1994, his MSc. degree in Advanced Manufacturing Technology and Systems Management from the University of Manchester, Manchester (UK), in 1999, and his PhD. degree in Mechanical Engineering from the University of Surrey, Guildford (UK), in 2008. He has published more than 50 scientific papers. His research interests include: Fracture Mechanics, Fatigue, Mechanical Design, and Finite Element Modeling of Machine Elements and Structures. E-mail: lvanegas@utp.edu.co. ORCID: 0000-0002-5891-8696
M.M. Abdel-Wahab, PhD., is a Professor of Applied Mechanics in the Department of Mechanical Construction and Production at Ghent University, Belgium. He received his BSc., 1988, in Civil Engineering and his MSc., 1991, in Structural Mechanics, both from Cairo University. He completed his PhD. in Fracture Mechanics in 1995 at KU Leuven, Belgium. He was awarded a D.Sc. from the University of Surrey in 2008. He has published more than 200 scientific papers on Solid Mechanics and Dynamics of Structures. His research interests include Finite Element Analysis, Fracture Mechanics, Damage Mechanics, Fatigue of Materials, Durability, and Dynamics and Vibration. ORCID: orcid.org/0000-0002-3610-865X
G.A. Parker, PhD., is emeritus professor of Mechanical Engineering in the Department of Mechanical and Physical Sciences at The University of Surrey. He holds the following qualifications and titles: BSc., PhD., FIMechE, MEM.ASME, CEng, Eur.Ing. He is also member of the EPSRC Mechanical Engineering College. His research interests include virtual and augmented reality, control and systems integration, machine vision, brushing technology, fluid control systems. ORCID: 0000-0003-0677-6451
Referencias
Peña-Bustos, F.M. and Álvarez-Vargas, C.A., Design and construction of a torsional fatigue testing machine operated by inertial loads. DYNA, 79(172), pp. 46-55, 2012.
Marulanda, D. and Olaya, J.J., Unbalanced magnetron sputtering system for producing corrosion resistance multilayer coatings. DYNA, 79(171), pp. 74-79, 2012.
Loaiza, J.L. and Arzola, N., Evolución y tendencias en el desarrollo de prótesis de mano. DYNA, 78(169), pp. 191-200, 2011.
Zarebski, I. and Salacinski, T., Designing of non-circular gears. The Archive of Mechanical Engineering, LV(3), pp. 275-292, 2008.
Vanegas-Useche, L.V., Abdel-Wahab, M.M. and Parker, G.A., Design of noncircular gears to minimise shaft accelerations, Proc. of the 8th ASME Conf. Eng. Sys. Des. Analysis ESDA 2006, pp. ESDA2006-95560-1 - ESDA2006-95560-10, 2006. DOI: 10.1115/ESDA2006-95560
Quintero, H.F., Cardona, S. and Jordi, L., Engranajes no circulares: aplicaciones, diseño y manufactura. Scientia et Technica, 24, pp. 133- 138, 2004.
Olsson, U., Non-circular cylindrical gears. Acta Polytechnica, 2(10), pp. 1-216, 1953. DOI: 10.1002/zamm.19540340711
Lozzi, A., Non-circular gears - graphic generation of involutes and base outlines. Proc. Inst. Mech. Engrs., 214(C), pp. 411-422, 2000. DOI: 10.1243/0954406001523074
Dooner, D.B., Function generation utilizing an eight-link mechanism and optimized non-circular gear elements with application to automotive steering. Proc. Instn. Mech. Engrs. (ImechE), Part C: J. Mech. Eng. Sc., 215(7), pp. 847-857, 2001. DOI: 10.1243/0954406011524090
Dooner, D.B., Use of noncircular gears to reduce torque and speed fluctuations in rotating shafts. ASME J. Mech. Des., 119(2), pp. 299- 306, 1997. DOI: 10.1115/1.2826251
Dooner, D., Yoon, H-D. and Seireg, A., Kinematic considerations for reducing the circulating power effects in gear-type continuously variable transmissions. Proc. Inst. Mech. Engrs., 212(D), pp. 463-478, 1998. DOI: 10.1243/0954407981526118
Tong, S-H. and Yang, D.C.H., Generation of identical noncircular pitch curves. ASME J. Mech. Des., 120(2), pp. 337-341, 1998. DOI: 10.1115/1.2826978
Doege, E., Meinen, J., Neumaier, T. and Schaprian, M., Numerical design of a new forging press drive incorporating non-circular gears. Proc. Inst. Mech. Engrs. (ImechE), Part B: J. Eng. Man., 215(4), pp. 465-471, 2001. DOI: 10.1243/0954405011518430
Guo, L.S. and Zhang, W.J., Kinematics analysis of a rice transplanting mechanism with eccentric planetary gear trains. Mechanism and Machine Theory, 36(11-12), pp. 1175-1188, 2001. DOI: 10.1016/S0094-114X(01)00052-0
Librovich, B.V., Dynamics of rotary vane engine. ASME J. Mech. Des., 125(3), pp. 498-508, 2003. DOI:10.1115/1.1582500
Tucker, R.W., Wang, C. and Librovich, B.V., Mathematical modelling of rotary vane engines. Proc. Inst. Mech. Engrs. (ImechE), Part C: J. Mech. Eng. Sc., 217(6), pp. 687-704, 2003. DOI: 10.1243/095440603321919608
Yao, Y-A. and Yan, S-H., A new method for torque balancing of planar linkages using non-circular gears. Proc. Inst. Mech. Engrs. (ImechE), Part C: J. Mech. Eng. Sc., 217(5), pp. 495-503, 2003. DOI: 10.1243/095440603765226786
Litvin, F.L., Gonzalez-Perez, I., Fuentes, A. and Hayaska, K., Design and investigation of gear drives with non-circular gears applied for speed variation and generation of functions. Comput. Methods Appl. Mech. Engrg., 197, pp. 3783-3802, 2008. DOI: 10.1016/j.cma.2008.03.001
Ottaviano, E., Mundo, D., Danieli, G.A. and Ceccarelli, M., Numerical and experimental analysis of non-circular gears and camfollower systems as function generators. Mechanism and Machine Theory, 43, pp. 996-1008, 2008. DOI: 10.1016/j.mechmachtheory.2007.07.004 Vanegas-Useche et al / DYNA 83 (198), pp. 220-228, Septiembre, 2016. 228
Figliolini, G., Stachel, H. and Angeles, J., Synthesis of the base curves of non-circular gears via the return circle, Int. Gear Conf., pp. 540- 550, 2014. DOI:10.1533/9781782421955.540
Yang, D.C.H., Tong, S-H. and Lin, J., Deviation-function based pitch curve modification for conjugate pair design. ASME J. Mech. Des., 121(4), pp. 579-586, 1999. DOI: 10.1115/1.2829502
Danieli, G.A., Analytical description of meshing of constant pressure angle teeth profiles on a variable radius gear and its applications. ASME J. Mech. Des., 122(1), pp. 123-129, 2000. DOI: 10.1115/1.533551
Chang, S-L., Tsay, C-B. and Wu, L-I., Mathematical model and undercutting analysis of elliptical gears generated by rack cutters. Mechanism and Machine Theory, 31(7), pp. 879-890, 1996. DOI:10.1016/0094-114X(95)00121-E
Chang, S-L. and Tsay, C-B., Computerized tooth profile generation and undercut analysis of noncircular gears manufactured with shaper cutters. ASME J. Mech. Des., 120(1), pp. 92-99, 1998. DOI: 10.1115/1.2826682
Bair, B-W., Computer aided design of elliptical gears. ASME J. Mech. Des., 124(4), pp. 787-793, 2002. DOI: 10.1115/1.1485092
Bair, B-W., Computer aided design of non-standard elliptical gear drives. Proc. Inst. Mech. Engrs. (ImechE), Part C: J. Mech. Eng. Sc., 216(4), pp. 473-483, 2000. DOI: 10.1243/0954406021525250
Bair, B-W., Computerized tooth profile generation of elliptical gears manufactured by shaper cutters. J. Mat. Proc. Tech., 122(2-3), pp. 139-147, 2002. DOI: 10.1016/S0924-0136(01)01242-0
Figliolini, G. and Angeles, J., The synthesis of elliptical gears generated by shaper-cutters. ASME J. Mech. Des., 125(4), pp. 793- 801, 2003. DOI: 10.1115/1.1631573
Bair, B-W., Computer aided design of elliptical gears with circulararc teeth. Mechanism and Machine Theory, 39(2), pp. 153-168, 2004. DOI: 10.1016/S0094-114X (03)00111-3
Xia, L., Liu, Y., Li, D. and Han, J., A linkage model and applications of hobbing non-circular helical gears with axial shift of hob. Mechanism and Machine Theory, 70, pp. 32-44, 2013. DOI: 10.1016/ j. mechmachtheory. 2013.07.002
Bair, B-W., Sung, M-H., Wang, J-S. and Chen, C-F., Tooth profile generation and analysis of oval gears with circular-arc teeth. Mechanism and Machine Theory, 44, pp. 1306-1317, 2009. DOI: 10.1016/ j. mechmachtheory. 2008.07.003
Barkah, D., Shafiq, B. and Dooner, D., 3D mesh generation for static stress determination in spiral noncircular gears used for torque balancing. ASME J. Mech. Des., 124(2), pp. 313-319, 2002. DOI:10.1115/1.1470492
Mundo, D., Gatti, G. and Dooner, D.B., Optimized five-bar linkages with non-circular gears for exact path generation. Mechanism and Machine Theory, 44, pp. 751-760, 2009. DOI: 10.1016/j.mechmachtheory. 2008.04.011
Modler, K.-H., Lovasz, E.-C., Bär, G.F., Neumann, R., Perju, D., Perner, M. and Mărgineanu, D., General method for the synthesis of geared linkages with non-circular gears. Mechanism and Machine Theory, 44, pp. 726-738, 2009. DOI: 10.1016/j.mechmachtheory.2008.05.006
Bloomfield, B. Design guide … when you need noncircular gears, in Chironis - N. P. Gear design and application, New York, McGraw- Hill, Inc., 1967. DOI: 10.1016/0022-2569(68)90361-3
Cómo citar
IEEE
ACM
ACS
APA
ABNT
Chicago
Harvard
MLA
Turabian
Vancouver
Descargar cita
CrossRef Cited-by
1. İbrahim Pazarkaya, Mehmet Yazar, Ahmet Özdemir. (2023). Computational fluid dynamics analysis of flowmeters with elliptical gear pairs and evaluation of calculated flow rate by Taguchi method. Flow Measurement and Instrumentation, 94, p.102476. https://doi.org/10.1016/j.flowmeasinst.2023.102476.
2. Nguyen Hong Thai, Phung Van Thom. (2024). Replacing the involute profile with an improved cycloid profile to improve the bearing capacity for the elliptical gear drives . Vietnam Journal of Science and Technology, 62(3), p.588. https://doi.org/10.15625/2525-2518/18247.
3. İbrahim PAZARKAYA, Mehmet YAZAR, Ahmet ÖZDEMİR. (2022). Eliptik Dişli Tasarımı, İmalatı, Analizi ve Eliptik Dişlilerin Endüstriyel Uygulamaları. Gazi Üniversitesi Fen Bilimleri Dergisi Part C: Tasarım ve Teknoloji, 10(3), p.558. https://doi.org/10.29109/gujsc.1103492.
Dimensions
PlumX
Visitas a la página del resumen del artículo
Descargas
Licencia
Derechos de autor 2016 DYNA

Esta obra está bajo una licencia internacional Creative Commons Atribución-NoComercial-SinDerivadas 4.0.
El autor o autores de un artículo aceptado para publicación en cualquiera de las revistas editadas por la facultad de Minas cederán la totalidad de los derechos patrimoniales a la Universidad Nacional de Colombia de manera gratuita, dentro de los cuáles se incluyen: el derecho a editar, publicar, reproducir y distribuir tanto en medios impresos como digitales, además de incluir en artículo en índices internacionales y/o bases de datos, de igual manera, se faculta a la editorial para utilizar las imágenes, tablas y/o cualquier material gráfico presentado en el artículo para el diseño de carátulas o posters de la misma revista.