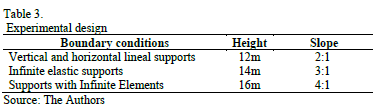Determinación de las dimensiones del dominio en la modelación numérica de terraplenes

Determination of the domain dimensions in embankment numerical modeling

El presente artículo presenta un estudio de la influencia de las dimensiones del subdominio en el estado tenso-deformacional de terraplenes viales. Su objetivo principal es determinar la distancia más aconsejable desde el pie de talud hasta la condición de frontera empleando como herramienta fundamental la modelación numérica y realizando un diseño de experimento 33 para cumplir con el mismo. Este trabajo ofrece recomendaciones para el empleo de diferentes condiciones de contorno al variar las pendientes de los taludes en problemas relacionados con la modelación de terraplenes de obras viales.

This article presents a study of the influence of subdomain dimensions on the stress-strain state of road embankments. Its purpose is to determine the most advisable distance from the base of the slope to the boundary condition using computational numerical modeling as the chief tool, and performing an experimental design 33 in order to achieve the stated goal. Recommendations are given for using different boundary conditions when varying the embankment slopes in problems related to road embankment modeling.

DOI: https://doi.org/10.15446/dyna.v83n198.49211

Milena Mesa-Lavista ^a, José Álvarez-Pérez ^a Eduardo Tejeda-Piusseaut ^a & Carlos A. Recarey-Morfa ^b

^a School of Civil Engineering, Polytechnic University José Antonio Echeverría (CUJAE), Havana, Cuba. milenaml@civil.cujae.edu.cu, joseap@civil.cujae.edu.cu, etejeda@civil.cujae.edu.cu
^b School of Constructions, Center for Mechanical Computational Investigations and Numerical Methods in Engineering. Central University of Las Villas (UCLV), Villa Clara, Cuba. recarey@uclv.edu.cu

Received: February 16th, 2015. Received in revised form: September 11th, 2015. Accepted: January 22th, 2016

This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.

---

Abstract
This article presents a study of the influence of subdomain dimensions on the stress-strain state of road embankments. Its purpose is to determine the most advisable distance from the base of the slope to the boundary condition using computational numerical modeling as the chief tool, and performing an experimental design 3³ in order to achieve the stated goal. Recommendations are given for using different boundary conditions when varying the embankment slopes in problems related to road embankment modeling.

Keywords: Boundary conditions, Road embankment modeling, Numerical Modeling.

Resumen
El presente artículo presenta un estudio de la influencia de las dimensiones del subdominio en el estado tenso-deformacional de terraplenes viales. Su objetivo principal es determinar la distancia más aconsejable desde el pie de talud hasta la condición de frontera empleando como herramienta fundamental la modelación numérica y realizando un diseño de experimento 3³ para cumplir con el mismo. Este trabajo ofrece recomendaciones para el empleo de diferentes condiciones de contorno al variar las pendientes de los taludes en problemas relacionados con la modelación de terraplenes de obras viales.

Palabras claves: Condiciones de frontera; Modelación de terraplenes viales, Modelación numérica.

---

1. Introduction

In order to determine the active depth of the soil foundations, it is necessary to calculate the stress that emerges due to the load imposed by the embankment weight; that is, the ratio result of the stresses produced by the weight of the soil foundation and the load imposed by the embankment, which should be between 0.1 and 0.2 [1,2]. As the depth of the soil foundation is infinite, the smaller the mathematical model of the problem, the smaller the computational resources [3]. Therefore, to optimize the computational cost, we have to decrease the size of the model without affecting the solutions in the working area.

2. Model conceptualization

The modeling of a real problem is described through a physical and mathematical model in which there is an interrelation between the characteristics each of them possesses: geometric model, constitutive model, load model, boundary condition model, governing equations, initial conditions, and definition of the work domain (Fig. 1). It is precisely the latter that is the most essential feature dealt with in this paper. Since soil is considered an infinite area, it is necessary to carry out a study of the adjacent domain of the geometric model that characterizes it as well as of the influence of boundary conditions.

2.1. Construction of the numerical model

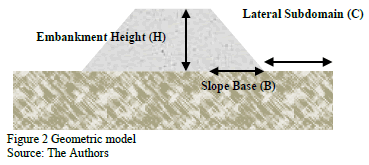
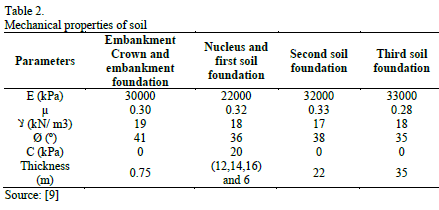
In this study, the numerical model was implemented based on the Finite Element Method (FEM); a plane strain was applied to the numerical model, and the slopes and the height of the embankments varied (Fig. 2). The letter C denotes the distance of the subdomain which is defined according to the relationship B/H, (ratio between the slope base and its height) (Table1). The constitutive model and the load model were used, taking into consideration the specialized literature and standard regulations [1,5-7] (Table 2).

In previous studies, the analysis was carried out [4,8,9] using the physical and mathematical parameters of the road embankment problems calibrated simultaneously after a homogenization process. As a result, the four-node quadrilateral Finite Element Type (FET) and 50cm of the domain fragmentation were chosen as a solution to this problem.

2.2. Boundary condition modeling

In this study, the boundary conditions applied were vertical and horizontal lineal supports, infinite elastic supports (Winkler´s Model), and supports with infinite elements.

• Vertical and horizontal lineal supports are used to inhibit the displacements in the X and Y axes as stated in the literature [10], by restricting the lateral and depth displacements, or imposing the null displacements to the ends of the model of the problem (Fig. 3, a). When these elements are used, the constitutive material model is not restricted.

• Infinite elastic supports (Fig. 3, b) are equivalent to an infinite number of elastic springs whose rigidity is the relationship between the pressure applied to the soil and the resultant displacement. For the numerical representation, the ballast coefficient of Winkler´s theory [11-14] is considered. Winkler´s Model supports are also employed in solving the problems concerning soil-structure interaction. Thus, an elastic constitutive material model is preferable when using this model.
• Supports with infinite elements (Fig. 3, c) are special elements which use a polynomial interpolation in such a way that the interpolation function describes an asymptote. When the working area decreases, the function makes the working space a continuous and infinite soil area. Consequently if it is necessary to design a numerical model of large-scale geometry, the infinite elements will guarantee the continuity of the soil foundation to reduce the geometric model to a smaller size. In this case, the constitutive model has to be lineal and elastic.

3. Determination of the subdomain dimensions

Different methodologies can be followed to determine the dimension of a subdomain in an infinite soil space:

1.1. The displacements in the nodes are analyzed in front of the supports, which should tend to zero. Otherwise, the approximation to the numerical solution of the boundary will affect the answer to the problem in the working area (Fig. 4, a).

1.1.1. If vertical and horizontal lineal supports are used, the null displacements are imposed.

1.1.2. If infinite elastic supports are employed, the solution will be found according to the ballast coefficient.

1.1.3. If the supports are infinite elements, the continuity of the soil foundation area will be guaranteed.

1.2. Stress, strain and displacement can also be analyzed at a point inside a key area, and the order of these values is compared to the order of the corresponding variables values near the supports, to determine the distance where the variables acquired the approximation desired (Fig. 4, b).

1.3. Another criterion to obtain the value of the subdomain dimensions is the analysis of several nodes in front of the supports or in the key area by applying the Standards of Error at several points [3].

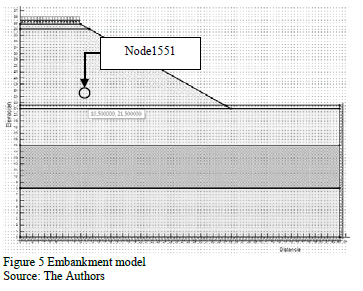
To obtain the subdomain dimensions of the numerical model in a semi-space of soil foundation corresponding to an embankment, an experimental design 3³ was performed. The three following factors: boundary conditions, height, and slope varied by three levels each (Table 3). In the experimental design presented, the dependent variables were obtained in a node located within a chosen key area (Fig. 5).

4. Results and discussion

Twenty-seven models were applied to the embankment design to determine the subdomain dimensions which varied from 4B/H up to 16B/H each (Table 1). Throughout the analysis of the post-process, the results for the horizontal strain values were studied in terms of the influence of the boundaries.

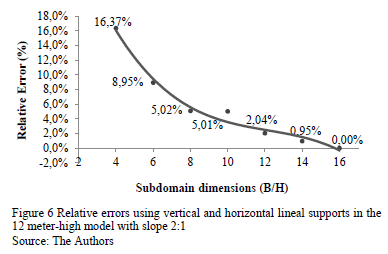
The relative errors (Eq. 1) were obtained taking into account the subdomain maximum values. The maximum value for parameter "C" was 16B/H, which was considered the standard error value. Errors were analyzed when the results were lower than 5%.

Relative errors in the problem solution were calculated for the three specific heights analyzed by using slope 2:1 with vertical and horizontal lineal supports as well as infinite elastic supports. Errors were lower than 5% in the subdomain values ranking between 8B/H and 16B/H whereas relative errors increased for the smallest values of the subdomains 6B/H and 4B/H (Figs. 6-8).

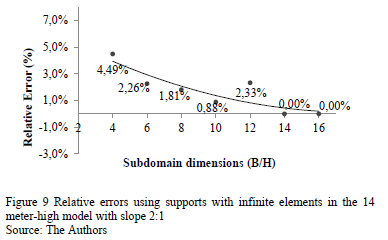
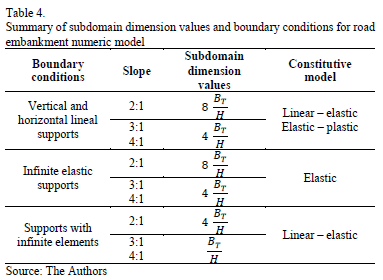
Since the relative error values were in the same numerical order and the results were lower than 5%, the recommended value for the subdomain dimension is 4B/H (Fig. 9) if supports with infinite elements are used. On the other hand, when the results of slopes 3:1 and 4:1 were analyzed with vertical and horizontal lineal supports and infinite elastic supports then, the subdomain values were 4B/H. However, slopes 3:1 and 4:1 with infinite elements provided a relative error of lower than 5% for each value of the sub-domain dimensions including B/H. Hence any value for the subdomain dimension can be used. Each case analyzed is shown in Table 4.

5. Conclusions

1. The C=4B/H value is suggested for the sub-domain dimension when slope 2:1 is employed with infinite elements.
2. The recommended value of the sub-domain dimension is C=4B/H when slopes 3:1 and 4:1 are used.
3. With slope 2:1 and vertical and horizontal lineal supports, the appropriate proportion for the geometrical model is C=8B/H.
4. When using supports with infinite elements the constitutive model should be elastic and lineal, and the sub-domain dimension can vary indistinctly for slopes 3:1 and 4:1.
5. If infinite elastic supports are employed the constitutive model should be elastic according to the ballast coefficient.

Acknowledgments

We would like to thank professor Odalys Morales Chacon for reviewing the English in this text.

References

[1] Jiménez-Salas, J.A., De-Justo, J.L. y Serrano, A., Geotecnia y Cimientos III, 2a ed. vol. 1, Madrid, España, 1981.

[2] Juarez-Badillo, E. and Rico, A., Mecánica de Suelos vol. 1. Ciudad Habana, Cuba: Pueblo y Educación, 1972, pp. 20-443.

[3] Recarey, C.A., Modelación del terreno y las estructuras en el dominio del tiempo, Tesis Dr., Departamento de Ingeniería Civil, Facultad de Construcciones, Universidad Central "Marta Abreu" de las Villas. (UCLV), Villa Clara, Cuba, 1999, 140 P.

[4] Mesa, M., Álvarez, J. y Recarey, C., Proceso de algoritmo para calibración matemática, Memorias de la 16 Convención Científica de Ingeniería y Arquitectura, 2012, 13 P.

[5] Escario, V., Los materiales para terraplenes. Construcción de terraplenes, in Kraemer, C., Uriel, R.S., ed., Explanaciones y drenaje I, E.T.S. de Ingenieros de Caminos, Canales y Puertos, Universidad Politécnica de Madrid, España, 1993, pp. 43-74.

[6] Torres-Vila, J.A., Introducción a la construcción de las explanaciones, in Diseño y construcción de explanaciones. Vol. 1, ed La Habana, Cuba: Avenida del Bosque, 1986, pp. 227-242.

[7] NC-63-153, Empuje de tierra, procedimiento de calculo,"ed: Norma cubana de la construcción, 1985.

[8] Mesa, M. y Álvarez, J., Técnicas de calibración numérica para problemas de ingeniería, Memorias de la XXXIII Convención Panamericana de ingenierías (UPADI), 2012, 12 P.

[9] Mesa, M. y Álvarez, J., Calibración numérica de un problema de ingeniería vial, Revista de la Construcción, vol. 10, pp. 52-63, 2011. DOI: 10.4067/S0718-915X2011000300006

[10] Zienkiewicz, O.C. y Taylor, R.L., El método de los elementos finitos, 5ta ed. vol. 1, 2 y 3, Barcelona, España: CIMNE, 2004.

[11] Muzás, F., Consideraciones sobre la elección de coeficientes de balasto, Revista de Obras Públicas, [En línea]. 3(425), pp. 45-51, 2002. [Fecha de consulta julio de 2011]. Disponible en: http://worldcat.org/issn/00348619

[12] Leoni, A.J., Apunte de coeficiente de balsto, Facultad de Ingenieria U.N.L.P., [En líena]. 2009, 30 P, [fecha de consulta Marzo de 2011]. Disponible en: http://materias.fi.uba.ar/7411/curso/teoria/balasto/leoni.pdf

[13] López-Menchero, J. y Lozano, J., Presión admisible por el terreno para losa., 2009, 11 P.

[14] Aragón, J., El coeficiente de balasto, [En línea]. 2006, [fecha de consulta marzo de 2011]. Dsiponible en: http://radioamericahn.net

M. Mesa-Lavista, has a degree in Civil Engineering from the Polytechnic University José Antonio Echeverría (CUJAE), Cuba. At present, she is researching Mechanical Computational and Numerical Methods in Engineering for her PhD. She has worked as a researcher at the Center for Research and Development of Structures and Materials (CIDEM) and at the National Company for Applied Investigations of Cuba (ENIA). As well as teaching, she currently works as a researcher at the Road Department of the School of Civil Engineering, at the CUJAE. Her research topics include simulation, embankment numeric modeling, mathematical calibration problems and road modeling problems. ORCID:0000-0001-5310-3255

J. Álvarez-Pérez, is graduated from the School of Civil Engineering at the Polytechnic University José Antonio Echeverría (CUJAE), Cuba in 2009. He completed his PhD at the Central University of Las Villas (UCLV), Cuba, in 2014 with a specialization in "Laminar Structures". In 2010, he worked at the National Project Engineering Company (EMPROI). Besides teaching, he also carries out research at the Department of Structures at the School of Civil Engineering, CUJAE. His research interests include simulation, numerical modeling, mathematical calibration problems, laminar structures, and calculus of laminar structures in relative coordinates. ORCID: 0000-0002-6210-8477

E. Tejeda-Piusseaut, is a full professor at the Roads Department at the School of Civil Engineering at the Polytechnic University José Antonio Echeverría (CUJAE), Cuba. He has a PhD from the University of Madrid, Spain, specializing in pavement recycling. He has carried out several studies on recycled materials for pavement construction, flexible and rigid pavements, and embankment modeling. ORCID: 0000-0002-0589-9989

C.A. Recarey-Morfa, completed his PhD at the Central University of Las Villas (UCLV) in 1999, specializing in Simulation of Rheology Modeling. In addition to being the director of the CIMCNI (Research Center on Computational and Numerical Method in Engineering), he is also a professor and researcher at the School of Construction at the UCLV. He is a member of the International Center for Numerical Methods in Engineering (CIMNE), Barcelona, Spain. His research areas comprise particles simulation, numerical simulation, rheological and structural modeling, and geotechnical and foundation modeling. ORCID: 0000-0002-0408-4032