Diseño de un observador de estado para estimación de biomasa y etanol en biorreactores a partir de modelos cibernéticos

State observer design for biomass and ethanol estimation in bioreactors using cybernetic models

En los últimos años, el modelado del crecimiento microbiano en múltiples sustratos ha recibido especial atención. Sin embargo, no hay evidencia en la literatura acerca de la aplicación de observadores de estado en sistemas de crecimiento microbiano descritos por modelos cibernéticos. Este trabajo se enfoca en el diseño de un observador asintótico aplicable a la estimación de biomasa y etanol en una fermentación con dos sustratos y en condiciones anóxicas, bajo una perspectiva cibernética. Los resultados de simulación del observador propuesto muestran un buen desempeño en régimen continuo, semicontinuo y por lotes.

Over recent years, the problem of multi-substrate microbial-growth modeling has received more and more attention. However, there is no evidence in the literature referring to state observer design that is applied to microbial growth described by cybernetic models. This paper focuses on the design of an asymptotic observer applicable to the estimation of biomass and ethanol in a two-substrate anoxic-fermentation process described by cybernetic modeling. Simulation results for the proposed observer show good performance for continuous, fed-batch and batch regimes.

DOI: https://doi.org/10.15446/dyna.v83n198.50549

Pablo De Villeros ^a, Héctor Botero ^b & Hernán Alvarez ^c

^a Escuela de Química, Universidad Nacional de Colombia, Medellín, Colombia. padea@unal.edu.co
^b Facultad de Minas, Universidad Nacional de Colombia, Medellín, Colombia. habotero@unal.edu.co
^c Facultad de Minas, Universidad Nacional de Colombia, Medellín, Colombia. hdalvare@unal.edu.co

Received: May 8^th, 2015. Received in revised form: February 15^th, 2016. Accepted: May 02^nd, 2016

This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.

---

Abstract
Over recent years, the problem of multi-substrate microbial-growth modeling has received more and more attention. However, there is no evidence in the literature referring to state observer design that is applied to microbial growth described by cybernetic models. This paper focuses on the design of an asymptotic observer applicable to the estimation of biomass and ethanol in a two-substrate anoxic-fermentation process described by cybernetic modeling. Simulation results for the proposed observer show good performance for continuous, fed-batch and batch regimes.

Keywords: asymptotic observer; cybernetic modeling; microbial growth; bioreactor.

Resumen
En los últimos años, el modelado del crecimiento microbiano en múltiples sustratos ha recibido especial atención. Sin embargo, no hay evidencia en la literatura acerca de la aplicación de observadores de estado en sistemas de crecimiento microbiano descritos por modelos cibernéticos. Este trabajo se enfoca en el diseño de un observador asintótico aplicable a la estimación de biomasa y etanol en una fermentación con dos sustratos y en condiciones anóxicas, bajo una perspectiva cibernética. Los resultados de simulación del observador propuesto muestran un buen desempeño en régimen continuo, semicontinuo y por lotes.

Palabras clave: observador asintótico; modelado cibernético; crecimiento microbiano; biorreactor.

---

1. Introduction

Measuring of process variables is mandatory in order to implement control loops, perform troubleshooting detection and monitor critical tasks. In many cases, this measurement is difficult to perform owing to the unavailability of sensors, time delays, errors in the measurement system, the high cost of devices or the environmental conditions where the measurement is to be performed [5]. For bioreactors, a precise knowledge of the state variables is vital due to the high sensitivity of microorganisms to slight changes in the culture medium.

Many state variables are difficult to measure (such as biomass), so indirect measurement techniques are needed. One of those techniques is known as state estimation, also known as: state observers, filters, software sensors and more generally, model-based virtual sensors [4]. The purpose is to estimate one or more variables of interest through directly measuring the inputs and outputs of the real system, based on a mathematical model. The extended Kalman Filter [12], Asymptotic Observers [2,7,8] and High Gain Observers [3], are some of the most commonly used in chemical and biotechnological processes.

State estimators/observers have been applied in both continuous and batch processes. The latter is much more complicated since the absence of inflows and outflows could not excite dynamics that may be decisive for the observer performance.

The use of state observers in chemical and biotechnological processes has become a common practice in the last decade because it can be relatively easily implemented and it has an undeniable utility. Examples of successful applications can be found in [4]. However, there is no evidence in the literature referring to state observer design applied to microbial growth described by cybernetic models. These models originated in the 1980s and they have proven to be very accurate in predicting the growth of various microorganisms on two substrates (diauxic growth) and three substrates (triauxic growth) [13-15,19]. In addition, cybernetic models exhibit the following great advantages compared to other multi-substrate models:

• There is no need for a-priori specification of the order in which the substrates are consumed.
• They describe the simultaneous or sequential use of substrates depending on the culture conditions.
• They are applicable to both batch and continuous cultures.
• The inputs are the values of the parameters obtained from experiments on individual substrates.
• They are relatively easy from a mathematical point of view (ordinary differential equations).

This paper has three main objectives. One is to address the problem of the inherent discontinuity present in the cybernetic model. The second is to evaluate local observability using a linear approximation. The last is to design an observer, applicable to biomass and ethanol estimation in a two-substrate anoxic-fermentation process described by cybernetic models. Continuous, fed-batch, and batch regimes will be considered.

The paper is organized as follows: in Section 2, cybernetic modeling for microbial growth is described. Section 3 deals with the nonlinear observability of the cybernetic model and presents a methodology to estimate biomass and ethanol via an asymptotic observer. In Section 4, simulations are performed in order to test the behavior of the proposed observer. Finally, in Section 5 conclusions are presented as well as some final remark.

2. Cybernetic modeling of anoxic

The assumption that the internal mechanics of microorganisms is determined by a single nutrient is valid for very specific cases in which the culture medium is prepared in a laboratory (i.e. defined culture medium). Such a class of culture is undertaken with the purpose of decreasing the degree of uncertainty in the experiment and ensuring growth and / or production of specific metabolites. This nutritional restriction contrasts with natural ecosystems, in which there is a huge range of potential substrates that are available to suit a particular physiological requirement [9,10]. In this case, simplification suggested by one limiting substrate is inadequate and it becomes necessary to take another approach.

The first scientist who explored the problem was Jacques Monod [18]. During an experiment with Bacillus subtilis, he observed two clearly distinguishable growth phases in a batch culture with a mixture of two sugars. This phenomenon was called diauxic growth and led to the systematic study of multi-substrate growth.

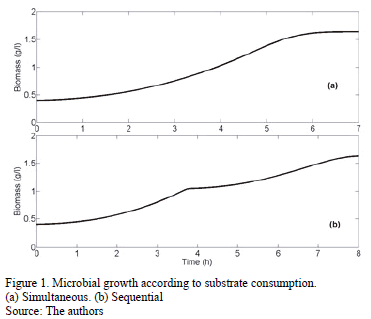
Fig. 1 shows the behavior of a certain microorganism in a two-substrate culture. In (a), a second exponential phase is not observed, indicating that the microorganism has a similar affinity for both substrates and consumes them simultaneously. In (b), a second exponential phase can be observed, which shows the sequential use of substrates, and it has an intermediate phase in which the microorganism changes its enzymatic machinery to degrade the second substrate. The order in which the substrates are consumed depends on the affinity substrate-microorganism. In other words, the first substrate to be degraded will be the one that provides the highest growth rate [15].

As can be seen, microbial growth on multiple substrates exhibits different behaviors from sequential to simultaneous use of all substrates, giving rise to multi-exponential growth phases. This indicates that cells have a high capacity to regulate their metabolism and optimize the consumption of substrates. Kompala et al. [15] addressed this regulatory behavior by introducing two variables: one considers the induction or repression of a key enzyme involved in the degradation of a specific substrate, while the other considers the activation or inhibition of preexisting enzymes. These two variables are described by the following expressions:

When variable ui is close to zero, the i-th enzyme is repressed, thus its corresponding substrate is not degraded, whereas if its value is close to one, the i-th enzyme is induced. This leads to the consumption of the associated substrate.

Variable n_i incorporates the regulatory actions of inhibition and activation of enzymes that are already present in the cell. If n_i is close to zero, then the degradation reaction of the specific substrate does not take place, even if the said substrate and the corresponding enzyme are present. If its value is close to one, the reaction is activated with the subsequent catabolism of the substrate. Note the discontinuity in the definition of this variable due to the presence of a max function. This issue will be considered in Section 3.1.

m_i is the specific growth rate in the i-th substrate that is obtained from a modified version of the well-known Monod equation:

m_max,iis the maximum growth rate for substrate i; S_i is the concentration of substrate i; K_i is the affinity constant; E_R,i is the relative level of enzyme for the i-th substrate and can be calculated from the following relations:

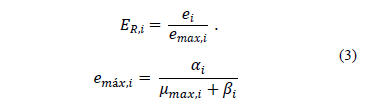
where a_i and b_i represent synthesis and degradation constants, respectively. The state variable e_i is the actual enzyme concentration in grams per gram of biomass, while e_max,i is the maximum concentration of enzyme for the i-th substrate.

Based on typical dynamic balances, without considering cellular death and introducing the previous expressions, a set of six ODEs can be derived as a process model [11, 20]:

X, S, P and C represent the concentration of biomass, substrate, product (ethanol) and dissolved CO₂ in time t, respectively, while V stands for volume. Eq. (5) illustrates the dynamics of the i-th enzyme, limiting the rate of consumption of the corresponding substrate. The first term on the right corresponds to enzyme synthesis. The following term represents the degradation of the enzyme. The third term represents the dilution of the enzyme concentration due to cell growth and, finally, the term a* is included to ensure a low level of enzyme even in the absence of substrate. Parameters and 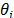are stoichiometric coefficients for ethanol and CO₂ production, respectively. is the biomass yield for substrate i. kla_c is the mass transfer coefficient and C* is the saturation concentration, both for CO₂. F represents the volumetric flow.

Jones and Kompała [13] introduced an additional dynamic of intracellular storage of carbohydrates in their aerobic model. However, for the present work it is not considered since in anoxic cultures the storage rate is significantly low compared to the growth rate. The model uses pressure, temperature and pH as controlled variables. Table 1 shows the complete parameters for the model represented by eq. (4)-(9) and applied to the growth of Saccharomyces cerevisiae on a mixture of glucose (substrate 1) and galactose (substrate 2). Continuous, fed-batch and batch regimes are considered individually.

Within the development of their mathematical model, Kompała et al. presented four basic principles to be followed by any model that addresses the multisubstrate growth [15]:

• Given multiple substrates, on which growth rates are distinctly different, the microbes prefer to grow on the fastest substrate when the growth curve showing multiauxial behavior.
• More generally, the growth behavior ranges from simultaneous utilization of multiple substrates (which occurs when growth rates are very nearly the same) to sequential utilization with intermediate lag periods.
• The growth rate on a mixture of substrates is never greater than the maximum of the growth rates on individual substrates.
• While growing on a slower substrate, if a faster substrate is added, the microbes inhibit the activity of the already available enzymes for the slower substrates.

3. Observer design

Having defined the cybernetic model for an anoxic microbial culture, the next step is to review the concepts of nonlinear observability and state observers. These two concepts are needed to establish a consistent methodology that relates cybernetic modeling and observer designing.

Section three begins with a mathematical approach to the discontinuity of the cybernetic variable n_i, in order to have a continuous system in which observability can be analyzed.

3.1. Max function approximation

This section deals with the discontinuity of the max function found in eq. (1) in order to analyze the nonlinear observability of the cybernetic system. For observability analysis and the designing of Jacobian-based observers, the system has to be differentiable. As shown in the cybernetic model presented in Section 2, variable n_i contains a discontinuous max function that needs to be converted into a continuously differentiable one, without substantially modifying the intrinsic dynamics of the process. The mathematical characteristics of the max function show that it can be considered as a vector norm. This issue suggests that it can be substituted with another vector norm. For instance, p-norm (which is continuous) would be a good candidate:

Applying this approximation, variable n_i takes the following form:

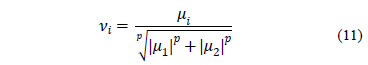
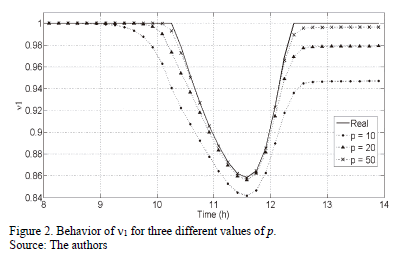
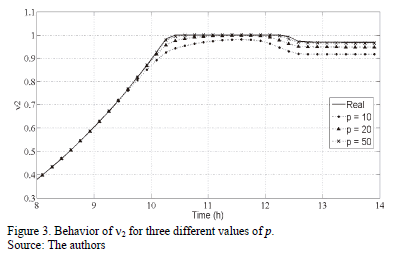
To verify this approximation, n₁ and n₂ were simulated for several values of p based on the parameters previously given in Table 1. The results are shown in Figs. 2, 3:

As can be seen that when p is increased the values of n_i converge to those established by the original cybernetic model, whereby the proposed approach is valid for the case being studied. Therefore, in this work, a value of p = 50 was taken for the simulations.

3.2. Nonlinear observability analysis

Observability is an important property to take into account when designing an observer. This property allows it to be discovered if there are sufficient information channels between the outputs and the states.

A dynamic system can be expressed in the form:

where x(t) ∈; Rⁿ denotes the state variables, u(t) ∈; R^m denotes control inputs, and y(t) ∈; R^p denotes the measured outputs.

In very general terms, a nonlinear system is locally observable if the initial states x₀ and x'₀ are distinguishable for every input u(t) at t ≥ 0:

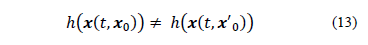
This criterion can be verified with three different perspectives or conditions: a geometric condition, an algebraic condition, and a linear approximation condition [1]. The first two conditions are not suitable for large systems due to, firstly, the enormous computer-time required to obtain Lie derivatives and secondly, due to the degree of variable cross-linking. So, this work will be based on the linear approximation condition.

Consider the following linearized system based on the system in eq. (12). It is evaluated in the stationary state x_ss and u_ss:

From eq. (14), it is possible to generate an observability matrix W of the form:

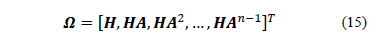
Once W is calculated, the system is considered observable if W is full rank [2], i.e., matrix Whas the same rank of the process (which is seven for the model presented in section 2). For small systems (two or three state variables), matrix W rank analysis can be undertaken by visual inspection, but for the cybernetic model it is not possible due to the extension of the Jacobian. Therefore, we propose rank evaluation over time, by calculating the rank of matrix Win each simulation-time step as an attempt to find out the local observability. It is assumed that in each simulation-time an operational equilibrium state is achieved. This approach is a necessary but not a sufficient condition for observability, and it just provides a means of identifying processes that are normally not observable.

As mentioned in Section 1, some variables in bioreactors are very difficult to measure online. These variables include biomass and sugars (substrates). Common biomass measurement techniques are dry/wet weight measurement, optical density via spectrophotometry and direct cell counting; sugar analysis usually also involves spectrophotometric methods. All of those methods are time consuming and are carried out offline. Conversely, dissolved CO₂ concentration is easily measured online through submerged sensors found in bioreactors that are standard equipment. For this reason, in this work, the dissolved CO₂ is taken as measured, without considering other aqueous species that may occur in equilibrium (H₂CO₃, HCO₃^-).

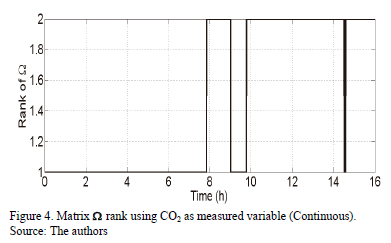
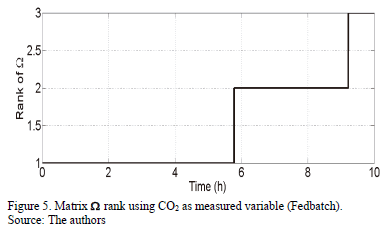
Figs. 4-6 show that the cybernetic system is not locally observable when CO₂ is used as the measured variable. This is because the observability matrix is not full rank at any point or at any regime. The preliminary conclusion is that the CO₂, despite being an easy-to-measure variable, does not offer enough conditions for local observability of the full cybernetic system. However, in this work, some additional considerations will permit the use of CO₂ measurement for observer design.

3.3. Asymptotic observer

The conclusion derived from the analysis in Section 3.2 leads us to think that the best option is to employ an observer that does not require the kinetics of the process so that CO₂ measure can be used directly. The observer that fulfills this condition is the asymptotic observer (AO) [2, 7].

The dynamics of biotechnological processes can be represented by the following general nonlinear state space model, written in matrix form:

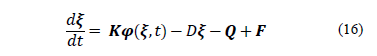
State variables are presented by ∈; Rⁿ. The first term 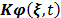describes the kinetics of the biochemical and microbiological reactions that are involved in the process. Matrix K ∈; R^{n x m} represents the yield coefficients while matrix 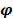∈; R^m denotes the reaction rates.

The remaining terms 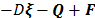describe the transport dynamics of the components through the reactor. D is the dilution factor, calculated as F_in/V. Q ∈;, Rⁿ is the vector of rate of mass outflow from the reactor in gaseous form. F ∈; Rⁿ is the vector of mass feed rate in the reactor.

aking 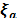∈; R^p to be the vector of measured variables and ∈; R^n-p as the vector of non-measured variables, the system in eq. (16) can be rewritten:

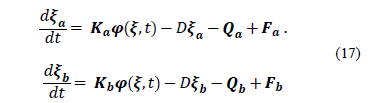
Now, consider vector Z as a linear state transformation:

where is the unique solution of the matrix equation:

So, the state space model is equivalent to:

Vector Z can be rewritten as a linear combination of the form:

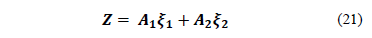
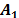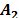with appropriate dimension for matrices and . If 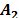has a left inverse, the following asymptotic observer can be derived from eq. (20):

where is a left inverse of 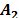. and denote online estimates of and 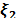, respectively.

3.4. Asymptotic observer design for biomass and ethanol estimation

In order to design an AO, the system must be expressed in the form of state-space representation, based on eq. (16):

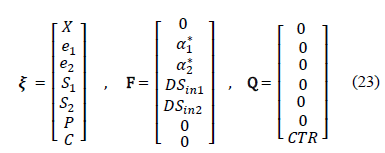
As can be seen in eq. (23)-(25) and in the cybernetic model described in eq. (4)-(9), the dynamics of state variables X, P and C are similar, specifically in the term 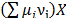. This leads to the proposal for a reduced system of the form:

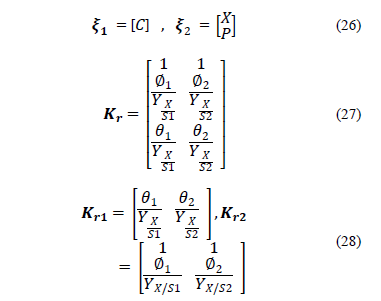
However, asymptotic observers present a restriction referring to the dimension of the coefficient matrix K. As there is just one measured variable (CO₂), the dimension of K_r must be one [7]. In order to overcome this issue, the dimension of K_r is reduced to one using the following coefficient averaging:

The advantage of this averaging is that it is calculated only using the yield coefficients (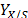) and the stoichiometric production coefficients for CO₂ () and Ethanol ().

Finally, the equations that govern the behavior of the asymptotic observer take the following form:

Therefore, it is possible to estimate X and P without considering the kinetics of the process and using dissolved CO₂ concentration as the only measured variable.

4. Simulation results and analysis

The estimation of Biomass and Ethanol via an asymptotic observer was performed in a continuous regime (F_in = F = 1.1 l/h), a fedbatch regime (F_in = 1.1 l/h, F = 0) and a batch regime (F_in = F = 0) until cryptic growth was achieved (16 hours, 10 hours and 6 hours, respectively). White noise was added to the CO₂ measurement signal, with a power of 2.0E-4 and a sample time of 0.01 h. Fig. 7 illustrates the evolution of the signal with and without noise, for the continuous case:

Figs. 8-10 show the performance of the proposed observer for biomass estimation. In all simulations, the initial condition of the observer was 10% above the real initial condition of the process. F_in and F in continuous and fedbatch regimes had the same fixed value of 1.1 liters per hour.

This value was chosen to be as large as the parameters of the culture permitted (Table 1) whilst avoiding cell wash out. The initial volume of the culture was 6.0 l.

As shown in Figs. 8-10, the asymptotic observer closely follows the actual trajectory of the biomass, but it should be noted that the speed of convergence is given by the value of the dilution rate D. For this reason, in the batch regime (Fig.10), in which the dilution rate is zero, the observer presents a steady-state error and does not converge to the actual value of the biomass while in continuous and fed-batch regimes (Figs. 8 - 9). The observer converges approximately four hours after initiating the process. Taking this into account, the initial state of the observer in a batch regime should be identical to the initial state of the process. Even though the AO is not a filter, it can be seen that the noisy signal was smoothed and the noise did not induce appreciable peaks in the estimation.

For ethanol estimation, the performance is similar to that shown by the estimated biomass in all regimes, as can be seen in Figs. 11 - 13:

5. Conclusions

This work approached the discontinuity of the max function on the cybernetic variable n_i by using a substitution based on p-norm. This approximation did not appreciably affect the dynamics of the original process and allowed the jacobian of the system and the rank of the observability matrix of the linearized system to be calculated. Derived from observability analysis, it has been shown that dissolved CO₂ concentration is not a suitable variable for estimating all states of cybernetic system. However, it can be used to estimate biomass and product through a reduced-order asymptotic observer. In terms of the design of this observer, a mathematical approach was proposed to reduce the rank of the coefficient matrix K_r to one.

The designed observer estimated biomass and ethanol satisfactorily, but in batch regime (where the dilution rate is zero) it had to be initiated close to the initial condition of the original system in order to prevent steady-state deviations due to initial estimation error.

It is possible to improve the convergence of the asymptotic observer to the real value of biomass by increasing the dilution rate. The limit is given by the maximum dilution rate before culture washout is reached.

In the design of asymptotic observers, it is essential to have adjusted values of parameters and yield stoichiometric coefficients since the dynamics of these type of observers is totally dependent on them. This is due to the absence of feedback terms or kinetics.

References

[1] Aguilar, R., Mata, J. and Martínez, R., On the observability for a class of nonlinear (Bio)chemical Systems, International Journal of Chemical Reactor Engineering, 8(1), A3, pp. 1-27, 2010.

[2] Bastin, G. and Dochain, D., On-line estimation and adaptive control of bioreactors. Amsterdam, Elsevier Science Publishing, 1998.

[3] Biagiola, S. and Figueroa, J.L., A high gain nonlinear observer: Application to the control of an unstable nonlinear process, Computers and chemical engineering, Elsevier, ISSN 0098-1354, 2004.

[4] Botero, H. y Álvarez, H., Una revisión de los métodos más frecuentes para la estimación del estado en procesos químicos, DYNA, 76(158), pp. 135-146, 2009.

[5] De Assis, A. and Maciel, R., Soft sensors development for on-line bioreactor state estimation, Computers & Chemical Engineering, 24, pp. 1099-1103, 2000. DOI: 10.1016/S0098-1354(00)00489-0

[6] Di Serio, M., De Alteriis, E., Parascandola, P. and Santacesaria, E., A general kinetic and mass transfer model to simulate baker's yeast growth in bioreactors, Catalysis Today, 66, pp. 437-445, 2001. DOI: 10.1016/S0920-5861(00)00644-1

[7] Dochain, D., State and parameter estimation in chemical and biochemical processes: A Tutorial, Journal of Process Control, 13, pp. 801-818, 2003. DOI: 10.1016/S0959-1524(03)00026-X

[8] Dochain, D., Automatic control of bioprocesses. USA, John Wiley & Sons, 2008. DOI: 10.1002/9780470611128

[9] Egli, T., Lendermann, U. and Snozzi, M., Kinetics of microbial growth with mixtures of carbon sources, Antonie van Leeuwenhoek, 63, pp. 289-298, 1993. DOI: 10.1007/BF00871224

[10] Egli, T. and Zinn, M., The concept of multiple-nutrient-limited growth of microorganisms and its applications in biotechnological process, Biotechnology Advances, 22, pp. 35-43, 2003. DOI: 10.1016/j.biotechadv.2003.08.006

[11] Fogler, H., Elements of chemical reaction engineering 3rd edition. Upper Saddle River, New Jersey, Prentice Hall, 1999.

[12] Grewal, M. and Andrews, A., Kalman Filtering: Theory and practice using Matlab. New York, John Wiley & Sons Inc, 2001.

[13] Jones, K.D. and Kompala, D.S., Cybernetic model of the growth dynamics of Saccharomyces cerevisiae in batch and continuous cultures, Journal of Biotechnology, 71, pp. 105-131, 1999. DOI: 10.1016/S0168-1656(99)00017-6

[14] Kompala, D., Bioprocess engineering: Fundamentals and applications [Online]. University of Colorado, 2013 [date of reference June 16th of 2014], section 7.3, Microbial growth on multiple substrates. Available at: http://www.umich.edu/~elements/07chap/html/kompala.pdf

[15] Kompala, D., Ramkrishna, D. and Tsao, G., Cybernetic modeling of microbial growth on multiple substrates, Biotechnology and Bioengineering, 26, pp. 1272-1281, 1984. DOI: 10.1002/bit.260261103

[16] Lubenova, V., Rocha, I. and Ferreira, E.C., Estimation of multiple biomass growth rates and biomass concentration in a class of bioprocesses, Bioprocess and Biosystem Engineering, 25, pp. 395-406, 2003.

[17] Magaña-Ramírez, L., Rubio-Nuñez, R., Jiménez-Islas, H. and Martínez-García, M., Anaerobic treatment of lactic waste and goat manure, Ingeniería e Investigación, 31(1), pp. 93-98, 2011. DOI: 10.15446/ing.investig

[18] Monod, J., The growth of bacterial cultures, Annual Review of Microbiology, 3, pp. 371-394, 1949. DOI: 10.1146/annurev.mi.03.100149.002103

[19] Narang, A., Konopka, A. and Ramkrishna, D., The dynamics of microbial growth on mixtures of substrates in batch reactors, Journal of Theoretical Biology, 184, pp. 301-317, 1997. DOI: 10.1006/jtbi.1996.0275

[20] Nielsen, J., Villadsen, J. and Lidén, G., Bioreactor engineering principles 2nd ed. New York, Kluwer Academic, 2003. DOI: 10.1007/978-1-4615-0767-3

[21] Rangel-Jara, H. et al., Biorreactores: Modelos matemáticos y su simulación sobre una hoja electrónica, Ingeniería e Investigación, 48, pp. 20-23, 2001. DOI: 10.15446/ing.investig

P. De Villeros, received his BSc. degree in Process Engineering in 2005 from Eafit University and his MSc. degree in Chemical Engineering from Universidad Nacional de Colombia, Medellin, Colombia in 2015. Currently, he is a professor in General Chemistry at the Facultad de Ciencias, Universidad Nacional de Colombia, Sede Medellin and a professor in Physical Chemistry at Eafit University, Medellin. His research interests are State Estimation and Bioprocesses. ORCID: 0000-0002-1053-8213

H. Botero, received his BSc. degree in Electrical Engineering and his Post-Graduate Diploma in Industrial Automation from Universidad de Antioquia, Colombia, his MSc. in Engineering from the Universidad del Valle, Colombia, and his PhD. from the Universidad Nacional de Colombia, Medellín. He is currently a professor in the Departamento de Energía Eléctrica y Automática, Facultad de Minas, Universidad Nacional de Colombia, Medellín. His research interests are state estimation and engineering education. ORCID: 0000-0003-3567-4550

H. Alvarez, received his BSc. degree in Chemical Engineering and his MSc. in Systems Engineering from the National University of Colombia. In 2000 he received his Ph.D. degree in Control Systems Engineering from the Instituto de Automática in National University of San Juan, Argentina. Currently he is a full professor at the Departamento de Procesos y Energía, Facultad de Minas, Universidad Nacional de Colombia, Medellín. His research interests are Chemical Process Modeling and Control. ORCID: 0000-0002-2253-3583