Dual arm compressive spectral imaging in the visible and IR range
Sistema dual para muestreo compresivo de imágenes espectrales en el rango visible e infrarrojo
DOI:
https://doi.org/10.15446/dyna.v83n199.51422Palabras clave:
Spectral Imaging, Compressive Sensing, Dual arm, Infrared, Visible (en)Imágenes Espectrales, Muestreo Compresivo, Sistema Dual, Infrarrojo, Visible (es)
Descargas
DOI: https://doi.org/10.15446/dyna.v83n199.51422
Dual arm compressive spectral imaging in the visible and IR range
Sistema dual para muestreo compresivo de imágenes espectrales en el rango visible e infrarrojo
Yenni Paloma Villa-Acuña a & Henry Arguello-Fuentes b
a Escuela de Ingenierías Eléctrica, Electrónica y de Telecomunicaciones,
Universidad Industrial de Santander, Bucaramanga, Colombia.
yenni.villa@correo.uis.edu.co
b Escuela de Ingeniería de Sistemas e Informática, Universidad
Industrial de Santander, Bucaramanga, Colombia. henarfu@uis.edu.co
Received: June 21th, 2015. Received in revised form: June 03rd, 2016. Accepted: July 21th, 2016.
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.
Abstract
Imaging spectroscopy involves sensing spatial
information in a scene across a range of wavelengths in order to acquire a three-dimensional
data cube. Spectral images play an important role in science and technology.
Some of their applications require image acquisition in both the visible and
the infrared ranges in order to detect characteristics that are not noticeable
to the bare eye. These can be perceived in lower layers of the scene where the
visible radiation does not penetrate. This paper proposes a compressive image
acquisition system that reduces the number of optical elements by jointly and
compressively acquiring the images in the visible and infrared spectra. It also
evaluates whether the quality of the reconstructed images is good enough to
consider the optical implementation of the proposed system. Diverse simulations
are performed to determine the peak signal to noise ratio (PSNR) of the data
cubes as a function of the coded apertures transmittance, the Gaussian noise
applied to the measurements and the number of snapshots. The simulations
provide PSNR values of up to 33 dB in the reconstructed images.
Keywords: Spectral Imaging; Compressive Sensing; Dual arm; Infrared; Visible.
Resumen
La
espectroscopia de imágenes involucra el muestreo de la información espacial de
un objetivo a lo largo de un conjunto de longitudes de onda, en el que se
adquiere un cubo de datos de tres dimensiones, dos de ellas espaciales y una
espectral. Las imágenes espectrales juegan un papel importante en muchos campos
de la ciencia y la tecnología, algunas de sus aplicaciones exigen la
adquisición de la imagen en el espectro visible e infrarrojo, con el fin de
detectar características no distinguibles a simple vista, presentes en capas
inferiores del objetivo donde la luz visible no alcanza a atravesar. Este
trabajo propone un sistema que reduce dichos costos de implementación
adquiriendo simultáneamente y de forma comprimida la imagen en el espectro
visible e infrarrojo. Además evalúa si la calidad de las imágenes reconstruidas
es lo suficientemente buena para considerar su implementación óptica. Se
realizaron diversas simulaciones para determinar la relación señal a ruido pico
(PSNR, por su sigla en inglés) de los cubos de datos reconstruidos, en función
de la transmitancia de los códigos de apertura, el ruido Gaussiano aplicado a
las mediciones y el número de capturas. Los valores de PSNR obtenidos alcanzan
los 33 dB.
Palabras clave: Imágenes Espectrales; Muestreo Compresivo; Sistema Dual; Infrarrojo; Visible.
1. Introduction
Spectrometers are instruments to measure the
intensity or polarization of electromagnetic waves across a wide range of
wavelengths, this is known as their spectral signature. Despite spectrometers
providing precise spectral information for a specific spatial point, some
applications are more interested in scanning the whole scene, thus involving
all spatial points [1]. These instruments are known as spectral imagers as they
acquire a scene's spatial and spectral
and spectral  information in a 3D data
cube. There are two main classes of spectral imagers, which can be either
spectrally or spatially discriminatory. This depends on the dimension of the scan
across the remaining 2D to complete the 3D data cube. An example of a
spectrally discriminatory instrument is a 2D spatial camera based on bandpass
filters [2]. This architecture is used
to scan all spectral channels by sequentially tuning the bandwidth in steps. It
requires the scene to be completely static during each spectral acquisition in
order to acquire the same spatial matrix for every frequency range. The main
drawback of this technique is that the number of zones to be scanned increases
proportionally to the desired spatial or spectral resolution.
information in a 3D data
cube. There are two main classes of spectral imagers, which can be either
spectrally or spatially discriminatory. This depends on the dimension of the scan
across the remaining 2D to complete the 3D data cube. An example of a
spectrally discriminatory instrument is a 2D spatial camera based on bandpass
filters [2]. This architecture is used
to scan all spectral channels by sequentially tuning the bandwidth in steps. It
requires the scene to be completely static during each spectral acquisition in
order to acquire the same spatial matrix for every frequency range. The main
drawback of this technique is that the number of zones to be scanned increases
proportionally to the desired spatial or spectral resolution.
Conversely, in the relatively new compressive spectral imaging (CSI) approach, the detector measures 2D random coded compressed projections. In this, the number of required measurements for the reconstruction is far less than in the linear scanning case. CSI relies on CS principles: sparsity and incoherence [3,4].
The coded aperture snapshot spectral imager (CASSI) is an architecture that effectively applies the CS theory to improve the sensing speed and reduce the large amount of data to far fewer measurements than the ones established by the Nyquist/Shannon theorem. This makes it possible to acquire the entire data cube with just a few focal plane array (FPA) measurements [1-4]. The theoretical background of CASSI is applicable for any region of the electromagnetic spectrum determined by the spectral sensitivity of the optical elements. Therefore, as there is no technology developed in sensitive sensors that applies to such wide frequency ranges to capture images in both visible and infrared spectral bands, it is necessary to use an architecture that separately acquires the information through the appropriate detector. This could be created by using two CASSI systems separately, which results in an expensive system to implement. The dual arm (DA)-CASSI system is an alternative to reduce the implementation costs of the previous solution by jointly catching both ranges' spectral information. This system is proposed in this paper.
Spectral images play a very important
role in various areas of science and technology such as: remote sensing [5],
agriculture [6] and quality control [7]. Near infrared (NIR) spectroscopy
utilizes the spectral information in the range from 780 to 2500  to provide more complex
structural information related to the combination of bonds' vibration. Numerous
NIR studies demonstrate that the previous is a non-destructive and rapid
technique -in the area of food quality assessment- since it reveals information
related to the vibrational behavior of molecular bonds. Therefore, it can give
details of the variety of molecules present in food [8]. For this reason, some
applications require the image acquisition in both the visible (V) and infrared
spectrum (IR) in order to detect characteristics not visible to the bare eye.
These can be perceived in lower layers of the scene where the visible radiation
does not penetrate [9]. Thus, not only visible but also infrared data is of the
utmost interest for these applications. For this reason, the main objective of
this paper is to design an optical architecture that allows multiple random
projections of images to be acquired in the visible and infrared spectrum. It
also includes the theoretical model and the evaluation of the reconstructed
quality of the images in order to consider its optical implementation.
to provide more complex
structural information related to the combination of bonds' vibration. Numerous
NIR studies demonstrate that the previous is a non-destructive and rapid
technique -in the area of food quality assessment- since it reveals information
related to the vibrational behavior of molecular bonds. Therefore, it can give
details of the variety of molecules present in food [8]. For this reason, some
applications require the image acquisition in both the visible (V) and infrared
spectrum (IR) in order to detect characteristics not visible to the bare eye.
These can be perceived in lower layers of the scene where the visible radiation
does not penetrate [9]. Thus, not only visible but also infrared data is of the
utmost interest for these applications. For this reason, the main objective of
this paper is to design an optical architecture that allows multiple random
projections of images to be acquired in the visible and infrared spectrum. It
also includes the theoretical model and the evaluation of the reconstructed
quality of the images in order to consider its optical implementation.
This paper is organized as follows: first, the background about CS theory and the multi-shot CASSI system are presented. There is also a brief explanation about system parallelization in order to separately acquire the image in each spectral range. After, the optical-mathematical model for the dual arm CASSI (DA-CASSI) system is presented. Finally, simulations and results to quantitatively compare the performance of the proposed system against two separate CASSI systems are presented.
2. Compressive sensing background
CS effectively reduces the acquisition time and the number of acquired measurements by simultaneously sensing and compressing the data instead of directly sensing the signal and then compressing it in the post processing stage. In this way, the cost of the system is reduced as well as its storage requirements. In order to do so, CS relies on two principles: sparsity and incoherence.
2.1. Sparsity
CS exploits the fact that many natural
signals have a more compact representation on a convenient basis [3]. More
formally, let  be the signal of interest and,
be the signal of interest and,  be the representation of
be the representation of on the basis
on the basis  We can then say that
We can then say that  is
is  if the orthonormal basis
if the orthonormal basis  sparsifies
sparsifies , when
, when  has only
has only  non-zero entries, where
non-zero entries, where  is the transpose matrix of
is the transpose matrix of . Otherwise, we can say that
. Otherwise, we can say that  compresses
compresses , if the sorted by magnitude entries of
, if the sorted by magnitude entries of  decay according to
decay according to  for any
for any  and
and . Then, it is said that
. Then, it is said that  is
is  -compressible in
-compressible in  by retaining the
by retaining the  largest coefficients by
magnitude and setting the rest to zero [10].
largest coefficients by
magnitude and setting the rest to zero [10].
A sparse representation means that the
number of non-zero coefficients in  is
is  with
with . A compressible representation, on the other hand, means that the
coefficient's magnitudes on a given basis, when sorted, have fast power-law
decay. Strictly speaking, most signals of interest are not exactly sparse but
approximately sparse or compressible on a convenient basis, and the selection
of the basis on which the signal is compressible is crucial in order to obtain
better reconstruction results. Previous work has proven that the Kronecker
product sparsifying basis gives the sparsest spectral images since such
matrices act as sparsifying bases that jointly model the structure present in
every signal dimension for multidimensional signals [10]. Suppose
. A compressible representation, on the other hand, means that the
coefficient's magnitudes on a given basis, when sorted, have fast power-law
decay. Strictly speaking, most signals of interest are not exactly sparse but
approximately sparse or compressible on a convenient basis, and the selection
of the basis on which the signal is compressible is crucial in order to obtain
better reconstruction results. Previous work has proven that the Kronecker
product sparsifying basis gives the sparsest spectral images since such
matrices act as sparsifying bases that jointly model the structure present in
every signal dimension for multidimensional signals [10]. Suppose  is a hyperspectral signal, or
its vector representation
is a hyperspectral signal, or
its vector representation is
is  -sparse on some basis
-sparse on some basis then
then can be expressed as a linear
combination of
can be expressed as a linear
combination of  vectors of
vectors of  as follows:
as follows:

where  and
and  is the Kronecker product of three
basis
is the Kronecker product of three
basis Usually,
Usually,  is set to be the Kronecker
product of the 2D-Wavelet symmlet 8 basis (used for the spatial dimensions) and
the 1D-DCT basis (for the spectral), such that
is set to be the Kronecker
product of the 2D-Wavelet symmlet 8 basis (used for the spatial dimensions) and
the 1D-DCT basis (for the spectral), such that  [11,12].
[11,12].
2.2. Incoherence
The compressibility of
spectral images also depends on how similar the sparsifying and the sensing
basis are, which can be quantified by their mutual coherence. Mathematically,
the mutual coherence of two orthonormal bases  and
and  is defined
as the maximum absolute value for the inner product between elements of two
bases, as follows:
is defined
as the maximum absolute value for the inner product between elements of two
bases, as follows:

In this case,  and
and  are the sparsifying and sensing bases, respectively,
are the sparsifying and sensing bases, respectively,  is the
is the  column of the representation
basis matrix and,
column of the representation
basis matrix and,  is the
is the  row of the sensing matrix.
From eq. (2), if
row of the sensing matrix.
From eq. (2), if  and
and  contain correlated elements,
the coherence is large. Otherwise, it is small. Thus, a lower value of
contain correlated elements,
the coherence is large. Otherwise, it is small. Thus, a lower value of  indicates lower coherence or better
incoherence between the measurement and the sparsifying basis. For CS, smaller
mutual coherence values demand fewer measurements to achieve a certain accuracy
in the reconstructed signals. For this reason, as random matrices are largely
incoherent with any fixed basis
indicates lower coherence or better
incoherence between the measurement and the sparsifying basis. For CS, smaller
mutual coherence values demand fewer measurements to achieve a certain accuracy
in the reconstructed signals. For this reason, as random matrices are largely
incoherent with any fixed basis , the selection of an orthobasis
, the selection of an orthobasis  uniformly at random promotes
CS efficiency [3].
uniformly at random promotes
CS efficiency [3].
2.3. CASSI background
The CASSI system depicted in
Fig. 1 is composed by six optical elements: an objective lens that focuses scene  onto the
fixed coded aperture (CA); a set of coded apertures
onto the
fixed coded aperture (CA); a set of coded apertures to perform
the coding, with
to perform
the coding, with  and K the
total number of shots; a band pass filter that limits the incoming source; a
dispersive element
and K the
total number of shots; a band pass filter that limits the incoming source; a
dispersive element  to shift the
coded field horizontally; and an imaging lens to relay the coded filtered and
spectrally sheared field onto the FPA image plane where it is finally
integrated over the spectral sensitivity
to shift the
coded field horizontally; and an imaging lens to relay the coded filtered and
spectrally sheared field onto the FPA image plane where it is finally
integrated over the spectral sensitivity .
.
Assuming that all optical elements are ideal,
including linear dispersion by the dispersive element, the  FPA
measurement in the
FPA
measurement in the  pixel,
pixel, can be expressed as:
can be expressed as:

where L is the total number of
resolvable bands and  is the noise present in the system. Let
is the noise present in the system. Let  denote the
vector representation of the
denote the
vector representation of the  FPA
measurements
FPA
measurements which is
written in matrix form as
which is
written in matrix form as , where
, where  is the
transfer function that accounts for the effects of the dispersive element and
the
is the
transfer function that accounts for the effects of the dispersive element and
the  CA. The set
of K FPA measurements can then be
assembled as
CA. The set
of K FPA measurements can then be
assembled as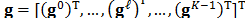 , which, in turn, can be expressed as:
, which, in turn, can be expressed as:

where is the
vertical concatenation of the
is the
vertical concatenation of the  matrices.
matrices.
The CASSI principles that are described above are general and applicable to imaging in any region of the electromagnetic spectrum that is determined by the spectral sensitivity of all the optical elements. To acquire It is possible to create a scene's spectral information in both visible and IR range by using two CASSI systems separately so that each one acquires the image in a different spectral range. However, in order to reduce implementation costs, an architecture that jointly senses the scene in both ranges and also gives the information separated on the correspondent detector is proposed in the following section.
3. Dual-Arm (DA)-CASSI system.
Fig. 2 depicts the DA-CASSI architecture. It is composed of two arms corresponding to the visible and IR paths. When the impinging light source focused by the objective is coded by the DMD, the coded field is divided and addressed by the beam splitter towards each path. Both arms are composed by a band pass filter that band limits the incoming fields; a dispersive element (usually a prism), which horizontally shears the filtered and coded fields; and the appropriate FPA detector, into which the resulting spectral densities are finally integrated.
3.1. DA-CASSI mathematical model
The light
propagation in the optical system begins when the reflected light source is
focused by the objective lens into the CA, where the coding is realized by
applying  to the spatio-spectral density source
to the spatio-spectral density source . This yields
. This yields 
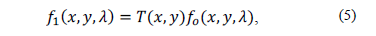
where  are the spatial coordinates
and
are the spatial coordinates
and  is the wavelength of the
impinging light. The spectral density
is the wavelength of the
impinging light. The spectral density  power is equally divided by
the beam splitter and sent to the respective arm's filter. In each path, only
the wavelengths belonging to that spectral range will pass to the corresponding
prism where they will consequently be dispersed. This will result in the following
coded fields:
power is equally divided by
the beam splitter and sent to the respective arm's filter. In each path, only
the wavelengths belonging to that spectral range will pass to the corresponding
prism where they will consequently be dispersed. This will result in the following
coded fields:

where  and
and  are the optical impulse
responses of the system for the visible and infrared systems, respectively,
are the optical impulse
responses of the system for the visible and infrared systems, respectively,  and
and  are the dispersion functions
induced by the prisms and corresponding to each spectral range. Finally,
are the dispersion functions
induced by the prisms and corresponding to each spectral range. Finally, and
and  are the filtered versions of
are the filtered versions of  in the visible and IR respectively.
in the visible and IR respectively.
Every coded and dispersed field is focused by an imaging lens into the respective FPA where they are integrated over the detector's spectral range sensitivity.

where the primed variables refer to the spatial location before the CA and the non-primed in the FPA.
Assuming that (i), the PSF  and
and  are shift invariant; (ii) there is a one-to-one match between coded
aperture features and the detectors' pixels and; (iii) supposing idealities in the
optical elements, including linear dispersion by the dispersive element, the
measurements at the detectors can be expressed as:
are shift invariant; (ii) there is a one-to-one match between coded
aperture features and the detectors' pixels and; (iii) supposing idealities in the
optical elements, including linear dispersion by the dispersive element, the
measurements at the detectors can be expressed as:

For analysis
and computational purposes, the underlying analog phenomenon is discretized
such that the spatio-spectral signal  is defined as
is defined as  , and its vector representation is assembled as
, and its vector representation is assembled as  where
where  indexes the spatial axes
indexes the spatial axes  and
and  the spectral axis
the spectral axis . The discretized coded aperture is represented by
. The discretized coded aperture is represented by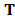 . Assuming that the visible filter limits the spectral components
between
. Assuming that the visible filter limits the spectral components
between and the infrared between
and the infrared between , the total number of resolvable bands
, the total number of resolvable bands  is limited by
is limited by  and
and , where the spectral
resolution is given by
, where the spectral
resolution is given by  and
and . Fig. 3 depicts the discretized model of the light propagation
through the DA-CASSI system.
. Fig. 3 depicts the discretized model of the light propagation
through the DA-CASSI system.
According to Fig. 3, the discretized
output in each detector is modeled as the independent sum of the underlying
spectral voxel slices that are modulated by the same coded aperture  and dispersed by the
corresponding prism.
and dispersed by the
corresponding prism.
More strictly, the two FPA measurements
in  for each detector can be
expressed as:
for each detector can be
expressed as:

In matrix form, eq. (9) can be expressed as eq. (4); however, the structure of the sensing
matrix is represented as a diagonal matrix where the first sub matrix
corresponds to the visible spectrum  and the second to the infrared
and the second to the infrared , as follows:
, as follows:

An example of the sensing matrix  is illustrated in Fig. 4.
This matrix has a diagonal pattern where the circled diagonal vectors repeating
horizontally correspond to the distribution of the coded aperture used for both
the visible (top left) and infrared (bottom right) ranges.
is illustrated in Fig. 4.
This matrix has a diagonal pattern where the circled diagonal vectors repeating
horizontally correspond to the distribution of the coded aperture used for both
the visible (top left) and infrared (bottom right) ranges.
In order to increase the number of compressive measurements when spectrally rich or very detailed spatial scenes are sensed, the multi-shot DA-CASSI allows multiple FPA measurements [11] to be acquired, each using a different CA during the integration time of the detector. This can be accomplished in two different ways: a) by moving a printed thin-film-based CA [13] back and forth using a high precision piezo-electric device to accurately perform the nanoposition realignment procedure (which significantly increases the system costs), or b) by using a DMD-based CA [14] that takes advantage of its tilting capabilities to address or deflect the impinging source light to the objective without requiring realignment. Therefore, the DMD-based CA becomes the best practical implementation since it offers a more robust, accurate and reliable multi-shot modulation system at a reduced cost [12].
The  matrix for the multi-shot
DA-CASSI system can also be expressed as in the conventional CASSI, eq. (4),
since the modification is implicit for every
matrix for the multi-shot
DA-CASSI system can also be expressed as in the conventional CASSI, eq. (4),
since the modification is implicit for every . Fig. 5 shows an example of a multi-shot
. Fig. 5 shows an example of a multi-shot  matrix for M=4, N=8, K=2 and L=5. In this matrix, three bands for the visible and two for the
infrared range are used. The upper half of this matrix corresponds to the first
shot and the lower half matrix accounts for the second.
matrix for M=4, N=8, K=2 and L=5. In this matrix, three bands for the visible and two for the
infrared range are used. The upper half of this matrix corresponds to the first
shot and the lower half matrix accounts for the second.
Finally, the multi-shot vector of measurements is given by the following expression:

It can be noticed that the  matrix in eq. (11) is sparse
and highly structured. Each row contains at most
matrix in eq. (11) is sparse
and highly structured. Each row contains at most  non-zero elements, and each
column contains up to
non-zero elements, and each
column contains up to non-zero elements.
non-zero elements.
The non-linear dispersion curve of the prisms and other elements such as the imaging or objective lenses, the spectral response of the camera and the coded apertures might be considered ideal mathematically as long as a prior calibration process is conducted in order to partially mitigate all the deviations from the ideal characteristics assumed.
As shown in Fig. 2, the source light
splits after the modulation undertaken by the DMD. For this reason, the
DA-CASSI does not require an objective lens and a DMD as two CASSI systems are
used simultaneously in parallel for the same purpose. This significantly
reduces the total costs of the proposed system. Notice that the and
and  images are implicitly aligned
in the DA-CASSI, whereas the separate CASSI systems need to be aligned to acquire
the same spatial matrix.
images are implicitly aligned
in the DA-CASSI, whereas the separate CASSI systems need to be aligned to acquire
the same spatial matrix.
3.2. DA-CASSI Reconstruction Process
As the number of voxels (columns of ) is greater than the number of detector pixels (rows of
) is greater than the number of detector pixels (rows of ) obtained, the system of linear equations represented by
) obtained, the system of linear equations represented by becomes under-determined or ill-conditioned,
hence direct inversion of the transfer function
becomes under-determined or ill-conditioned,
hence direct inversion of the transfer function is unfeasible. However,
several numerical algorithms have been designed to solve these kinds of convex
unconstrained optimization problems. The gradient projection for the sparse
reconstruction (GPSR) is one such example, and it is employed to obtain an
approximation
is unfeasible. However,
several numerical algorithms have been designed to solve these kinds of convex
unconstrained optimization problems. The gradient projection for the sparse
reconstruction (GPSR) is one such example, and it is employed to obtain an
approximation  of the original data cube
of the original data cube . This provides a good trade-off between computational complexity
and reconstruction quality. The complexity per GPSR iteration is better explained
in [15].
. This provides a good trade-off between computational complexity
and reconstruction quality. The complexity per GPSR iteration is better explained
in [15].
The set of measurements acquired by the
FPA  is used as an input to the
GPSR algorithm, and the reconstruction is attained by solving the optimization
problem:
is used as an input to the
GPSR algorithm, and the reconstruction is attained by solving the optimization
problem:

where  is a regularization constant, H is the sensing matrix in eq. (10),
is a regularization constant, H is the sensing matrix in eq. (10),  is a sparse representation of
is a sparse representation of  on basis
on basis and the
and the  minimization norm turns small
components of
minimization norm turns small
components of  to zero and helps to boost sparse solutions. As the GPSR finds a
sparse representation of the original data cube in the given basis Y, to obtain
to zero and helps to boost sparse solutions. As the GPSR finds a
sparse representation of the original data cube in the given basis Y, to obtain from the coefficients given
by the GPSR, they must be returned to their original domain by applying
from the coefficients given
by the GPSR, they must be returned to their original domain by applying .
.
Notice that the DA-CASSI reconstruction
process uses  measurements per iteration to
recover
measurements per iteration to
recover , compared with the parallelized CASSI systems where only
, compared with the parallelized CASSI systems where only  or
or  measurements are employed to
separately obtain
measurements are employed to
separately obtain  and
and  respectively.
respectively.
4. Coded apertures design, compression ratio and Gaussian noise
The design of the coded aperture used to
modulate the source light plays an important role in the reconstructed signal
quality since this sets up the spatial modulation. Traditionally, the coded
apertures employed in the CASSI system include Boolean [11,13], Bernoulli [12]
and gray scaled [16] codes designed randomly [11-13], or they follow a Hadamard
structure [11,16]. However, a recent work developed in order to enrich coding
strategies proposed the use of colored coded apertures. This would replace the
block-unblock photomasks with patterned optical filter arrays as a combination
of low-pass, high-pass and band-pass filters so that every pixel from the coded
aperture only allows a desired set of wavelengths to pass. This permits the
modulation of the scene, not only spatially but also spectrally [12]. When
developing this work, we used Boolean random
coded apertures in order to employ every pixel of the coded aperture,  with
with  representing a transmissive code element and
representing a transmissive code element and  a blocking code element. The transmittance
a blocking code element. The transmittance  of the coded aperture is defined as:
of the coded aperture is defined as:

where  represents the size of the
coded aperture. Fig. 6 represents the transmittance concept. The pattern in Fig. 6a is blocking a greater number of
pixels (a smaller transmittance) than that in Fig. 6c.
represents the size of the
coded aperture. Fig. 6 represents the transmittance concept. The pattern in Fig. 6a is blocking a greater number of
pixels (a smaller transmittance) than that in Fig. 6c.
In addition to the transmittance, another
important variable to analyze is the number of captured snapshots [4, 11-14]. The compression
ratio is the relation between the number of measurements acquired and the size of
the spectral image to recover. As such, the compression ratio
[4, 11-14]. The compression
ratio is the relation between the number of measurements acquired and the size of
the spectral image to recover. As such, the compression ratio can be expressed as a linear
function of the number of shots K in
the following way:
can be expressed as a linear
function of the number of shots K in
the following way:

where  is the average between the
number of visible and infrared bands.
is the average between the
number of visible and infrared bands.
In any real
application, the measurements acquired are corrupted by at least a small amount
of noise as sensing devices do not have infinite precision. In order to analyze
the impact caused by different amounts of sensor noise, zero-mean Gaussian
noise  was added to the set of FPA measurements
was added to the set of FPA measurements  , as in eq. (11). The variance of
the noise is selected so we achieved a desired signal to noise ratio (SNR). The
SNR can be expressed as:
, as in eq. (11). The variance of
the noise is selected so we achieved a desired signal to noise ratio (SNR). The
SNR can be expressed as:
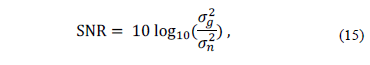
where  is the variance of the FPA measurement set
is the variance of the FPA measurement set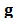 , and
, and  is the variance of the noise.
is the variance of the noise.
5. Computer simulations and results
Diverse simulations were performed using
two hyperspectral data cubes that were acquired with the AVIRIS sensor [17].
The selected scenes were found in AVIRIS' official website: Moffet and Salinas
fields. Both
hyperspectral images were acquired between  to
to , and contained
, and contained  spectral reflectance bands. For each of the scenes' bands, the data was
rescaled so that only 128x128 pixels are used due to the restriction of using
only dyadic numbers that were required for the fast implementation of the 2-D
wavelet transform. Furthermore, once the water absorption bands were removed,
the remaining bands were linearly averaged so that the final data had 8 bands for the visible range and 8 bands for the IR.
spectral reflectance bands. For each of the scenes' bands, the data was
rescaled so that only 128x128 pixels are used due to the restriction of using
only dyadic numbers that were required for the fast implementation of the 2-D
wavelet transform. Furthermore, once the water absorption bands were removed,
the remaining bands were linearly averaged so that the final data had 8 bands for the visible range and 8 bands for the IR.
For the first data set, the Moffet field aerial view, contains 16 classes of agricultural components such as corn, oats, wheat, woods, grass, etc. The original spatial resolution is 1924x753 pixels. The number of bands was reduced to 190 by removing bands covering the water absorption region: {1328.125 hm - 1440.625 hm}, {1487.500 hm - 1515.625 hm} and {1834.375 hm - 1984.375 hm}. An RGB representation of this database is presented in the upper left of Fig. 7. Here, the eight visible spectral bands are represented with their corresponding wavelength by using false color, and the remaining eight bands belonging to the IR spectrum on gray scale.
The second spectral image was acquired over "Salinas Valley", California. The original image size in pixels is 512x217, and, as in the "Moffet Field" data cube, 36 water absorption bands were discarded from the 224 original ones. However, in this case, the removed bands were: {400.000 hm - 428.125 hm}, {1393.750 hm - 1478.125 hm}, {1815.625 hm - 1975 hm} and {2462.500 hm - 2490.625 hm}. This scene includes vegetables, bare soils, and vineyard fields, as shown in Fig. 8.
The following section is divided into two subsections: in the first, the goal is to compare the sparsity of the spectral images when their visible and IR spectral band sets are separately and jointly sparsified. In the second, the analysis pretends to determine the performance of the proposed system in contrast with the parallelized CASSI systems.
5.1. Power analysis of the sparse representations
The
objective of this experiment is to understand if the infrared extra content
provides valuable information that increases sparsity in the images when the
whole data cube  is represented by the sparsifying basis
is represented by the sparsifying basis . The energy contained in the jointly
transformed
. The energy contained in the jointly
transformed  is compared with the sorted vector's energy in
coefficients
is compared with the sorted vector's energy in
coefficients , where
, where  and
and are transformed separately.
are transformed separately.
In order to do this, we compare the percentage
of energy content as a function of the number of coefficients for  and
and . A zoomed version for the first 25 coefficients is shown in Fig. 9.
It can be noticed that in Database 2 (Fig. 9 right)
. A zoomed version for the first 25 coefficients is shown in Fig. 9.
It can be noticed that in Database 2 (Fig. 9 right)  has a sharper growth rate since
more than 80% of the energy is contained in the first 5 coefficients compared
with 60% achieved in the separated approach. Conversely, in the first Database
(Fig. 9 left),
has a sharper growth rate since
more than 80% of the energy is contained in the first 5 coefficients compared
with 60% achieved in the separated approach. Conversely, in the first Database
(Fig. 9 left),  is less sparse compared with
is less sparse compared with  since it has a slower power growth.
It is important to take into account that regardless of the approach used to
obtain the sparse representation, the total energy of each database must add up
to the same value for both cases. The difference lies in the energy
distribution among the coefficients.
since it has a slower power growth.
It is important to take into account that regardless of the approach used to
obtain the sparse representation, the total energy of each database must add up
to the same value for both cases. The difference lies in the energy
distribution among the coefficients.
Under the assumption that the sparsity of the signal is highly related to the correlation between all the bands, a correlation analysis was undertaken, and the resulting 16x16 matrices are presented in Fig. 10. It can be observed that, as expected, Database 2 (right) presents a high correlation between all the visible bands. These, in turn, highly correlate with the latest infrared bands. Thus, the more correlated the bands of the data cube are, the greater the sparsity that is achieved.
5.2. Reconstruction of the spectral images
Diverse simulations were performed in order to determine the best Peak-Signal-to-Noise-Ratio (PSNR) of the reconstructed data cubes as a function of the transmittance, the compression ratio and the Gaussian noise applied to the measurements. In this section, the performance of the proposed DA-CASSI system and the conventional CASSI are compared by reconstructing of both databases.
To compare the performance of the DA-CASSI
model with the traditional CASSI model, two different analyses were proposed.
The first experiment focuses on the impact of two important factors, the coded
aperture transmittance  and the number of snapshots
taken (as a function of
and the number of snapshots
taken (as a function of ); the second refers to the noise analysis for the best results obtained
in the first part. For both analyses, the regularization parameter
); the second refers to the noise analysis for the best results obtained
in the first part. For both analyses, the regularization parameter has been carefully selected
so that optimum results are obtained; each experiment was repeated five times
for every case, and the results were averaged. Finally, all simulations were
conducted and timed using an Intel Core i7 3960x3.3 GHz processor with a 32 GB
RAM memory.
has been carefully selected
so that optimum results are obtained; each experiment was repeated five times
for every case, and the results were averaged. Finally, all simulations were
conducted and timed using an Intel Core i7 3960x3.3 GHz processor with a 32 GB
RAM memory.
5.2.1. Optimal parameters analysis
In order to
analyze the effect of the transmittance, we used several values of  Transmittances above 0.8 are not analyzed
given that they need to be solved by an extremely ill-posed inverse problem.
Additionally, transmittances below 0.3 are also discarded due to their
extremely low light efficiency [12]. In order to analyze the effect of the
number of snapshots, we either varied K from 1 to 4 or we made the compression ratio
Transmittances above 0.8 are not analyzed
given that they need to be solved by an extremely ill-posed inverse problem.
Additionally, transmittances below 0.3 are also discarded due to their
extremely low light efficiency [12]. In order to analyze the effect of the
number of snapshots, we either varied K from 1 to 4 or we made the compression ratio  and 52.73%.
and 52.73%.
Fig. 11 manifests the reconstruction results obtained in the transmittance analysis at a different number of snapshots for both databases using the traditional CASSI and the proposed
DA-CASSI. It can be observed that for a given  , and regardless of the database used, the reconstructed PSNR values
increase as K increases. In addition,
it can be noticed that, on average, the best results were always obtained for
transmittances between 0.4 and 0.7.
, and regardless of the database used, the reconstructed PSNR values
increase as K increases. In addition,
it can be noticed that, on average, the best results were always obtained for
transmittances between 0.4 and 0.7.
A more detailed comparison can be quantitatively undertaken by analyzing Table 1, in which the averaged PSNR of the reconstructed data cubes are presented as a function of the optimal transmittance value for each number of shots.
From Table 1, it can be observed that:
(i) as the two databases are the same size, the compression ratio  is the same for a given K,
and in turn, its optimal transmittance value
is the same for a given K,
and in turn, its optimal transmittance value  opt is inversely related to the number of shots; (ii) for the visible
range, the proposed DA- CASSI model recovers the bands with higher accuracy,
yielding to a gain of up to 2 dB when more than 2 FPA shots are used; (iii) as
a consequence of the low correlation between the infrared bands, the results
obtained for this range are lower than in the visible range. However, for
Database 2, due to the better sparsity boosted by the high correlation
presented between the visible and the last four infrared bands, the proposed
system is able to surpass the traditional CASSI by up to 1 dB when more than 2
snapshots are used. For both databases, the best results are obtained for x=0.4
and
opt is inversely related to the number of shots; (ii) for the visible
range, the proposed DA- CASSI model recovers the bands with higher accuracy,
yielding to a gain of up to 2 dB when more than 2 FPA shots are used; (iii) as
a consequence of the low correlation between the infrared bands, the results
obtained for this range are lower than in the visible range. However, for
Database 2, due to the better sparsity boosted by the high correlation
presented between the visible and the last four infrared bands, the proposed
system is able to surpass the traditional CASSI by up to 1 dB when more than 2
snapshots are used. For both databases, the best results are obtained for x=0.4
and  =52.73%; the reconstructed bands with
their corresponding attained PSNR are shown in Fig. 12. In summary, it is
possible to asseverate that the improvement achieved in the DA-CASSI, is caused
not only by the greater number of measurements used in the reconstruction per
iteration compared with the CASSI system, but also by the correlation between
the visible and infrared bands that boost the sparsity when this is high.
Otherwise, the incoherence does not affect the performance as the sensing and
sparsifying basis are the same for both models.
=52.73%; the reconstructed bands with
their corresponding attained PSNR are shown in Fig. 12. In summary, it is
possible to asseverate that the improvement achieved in the DA-CASSI, is caused
not only by the greater number of measurements used in the reconstruction per
iteration compared with the CASSI system, but also by the correlation between
the visible and infrared bands that boost the sparsity when this is high.
Otherwise, the incoherence does not affect the performance as the sensing and
sparsifying basis are the same for both models.
In order to analyze the spectral performance, two spatial points were randomly chosen from each database (P1 and P2 in Fig. 7 and Fig. 8 respectively), and their spectral signatures are shown in Fig. 13. It can be observed that the signature reconstructed with the DA-CASSI fits better with the original curve.
5.2.2. Noise analysis
We have shown that the proposed system efficiently recovers the spectral images from just a few measurements, but in order to be truly powerful, it is necessary for the DA-CASSI system to be able to deal with noise. For this reason, the best performed measurements obtained in the analysis were corrupted with five different amounts of noise, and the results were then compared.
Table 2 shows the impact in the PSNR of the reconstructed images (with respect to the SNR) when adding noise to the measurements. As has been shown, the PSNR improves as the signal to noise ratio increases, ranging from 10 to 40 dB. It is worthwhile noting how the reconstruction quality increases as the noise decreases. It should also be noted that in most the cases, the DA-CASSI outperforms the traditional CASSI, even when there is noise present.
6. Conclusions
We have presented a variation of the CASSI system for spectral images in the visible and infrared range. The architecture design, as well as the mathematical model for the single-frame and multi-frame DA-CASSI system, have been proposed. The DA-CASSI system is a possible solution to reduce the implementation costs of such a broad spectrum acquisition system. The improvement achieved in the DA-CASSI is caused not only by the greater number of measurements used in the reconstruction compared with the CASSI system, but also by the correlation between the visible and infrared bands that boost the sparsity when this is high. In general, the PSNR of the reconstructed images with the proposed model reaches up to 33 dB and 23.32 dB for the visible and infrared bands, respectively.
References
[1] Arce, G.R., Brady, D.J., Carin, L., Arguello, H. and Kittle, D.S., Compressive coded aperture spectral imaging: an introduction. IEEE Signal Processing, 31(1), pp. 105-115, 2014. DOI: 10.1109/MSP.2013.2278763
[2] Gat, N., Imaging spectroscopy using tunable filters: A review, Proceedings of SPIE, pp. 50-64, 2000. DOI: 10.1117/12.381686
[3] Candès, E.J. and Wakin, M.B., An introduction to compressive sampling. IEEE Signal Processing Magazine, 25(2), pp. 21-30, 2008. DOI: 10.1109/MSP.2007.914731
[4] Ye, P., Arguello, H. and Arce, G.R., Spectral aperture code design for multi-shot compressive spectral imaging, In Digital Holography and Three-Dimensional Imaging (OSA), p. DWA6, 2010. DOI: 10.1364/DH.2010.DWA6
[5] Shaw, G.A. and Burke, H.H.K., Spectral imaging for remote sensing. Lincoln Laboratory Journal, [Online] 14(1), pp. 3-28, 2003. Available at: https://www.ll.mit.edu/publications/journal/journalarchives14-1.html#1
[6] Govender, M., Chetty, K. and Bulcock, H., A review of hyperspectral remote sensing and its application in vegetation and water resource studies. Water Sa, 33(2), 2007. DOI: 10.4314/wsa.v33i2.49049
[7] Gowen, A.A., O'Donnell, C., Cullen, P.J., Downey, G. and Frias, J.M., Hyperspectral imaging-an emerging process analytical tool for food quality and safety control. Trends in Food Science and Technology, 18(12), pp. 590-598, 2007. DOI: 10.1016/j.tifs.2007.06.001
[8] Cen, H. and He, Y., Theory and application of near infrared reflectance spectroscopy in determination of food quality. Trends in Food Science and Technology, 18(2), pp. 72-83, 2007. DOI: 10.1016/j.tifs.2006.09.003
[9] Ding, H.B. and Xu, R.J., Differentiation of beef and kangaroo meat by visible/near-infrared reflectance spectroscopy. Journal of Food Science, 64(5), pp. 814-817, 1999. DOI: 10.1111/j.1365-2621.1999.tb15918.x
[10] Duarte, M.F., and Baraniuk, R.G., Kronecker compressive sensing. IEEE Transactions on Image Processing, 21(2), pp. 494-504, 2012. DOI: 10.1109/TIP.2011.2165289
[11] Arguello, H. and Arce, G.R., Code aperture optimization for spectrally agile compressive imaging. Journal of the Optical Society of America, 28(11), pp. 2400-2413, 2011. DOI: 10.1364/JOSAA.28.002400
[12] Rueda, H., Arguello, H. and Arce, G.R., DMD-based implementation of patterned optical filter arrays for compressive spectral imaging. Journal of the Optical Society of America, 32(1), pp. 80-89, 2015. DOI: 10.1364/JOSAA.32.000080
[13] Kittle, D., Choi, K., Wagadarikar, A. and Brady, D.J., Multiframe image estimation for coded aperture snapshot spectral imagers. Applied Optics, 49(36), pp. 6824-6833, 2010. DOI: 10.1364/AO.49.006824
[14] Wu, Y., Mirza, I.O., Arce, G.R. and Prather, D.W., Development of a digital-micromirror-device-based multishot snapshot spectral imaging system. Optics Letters, 36(14), pp. 2692-2694, 2011. DOI: 10.1364/OL.36.002692
[15] Figueiredo, M., Nowak, R.D. and Wright, S.J., Gradient projection for sparse reconstruction: Application to compressed sensing and other inverse problems. IEEE Journal of Selected Topics in Signal Processing, 1(4), pp. 586-597, 2007. DOI: 10.1109/JSTSP.2007.910281
[16] Rueda, H., Calderon, A.R. and Arguello, H., Spectral selectivity in compressive spectral imaging based on grayscale coded apertures, Image Signal Processing and Artificial Vision (STSIVA), pp. 1-5, 2013. DOI: 10.1109/STSIVA.2013.6644929
[17] Green, R.O., Eastwood, M.L., Sarture, C.M., Chrien, T.G., Aronsson, M., Chippendale, B.J. and Williams, O., Imaging spectroscopy and the airborne visible/infrared imaging spectrometer (AVIRIS). Remote Sensing of Environment, 65(3), pp. 227-248, 1998. DOI: 10.1016/S0034-4257(98)00064-9
Y.P. Villa-Acuña, graduated with a BSc in Electronics Engineering in 2015 from the Universidad Industrial de Santander. Her research interests include digital signal processing, image processing and remote sensing. ORCID: 0000-0001-7046-4984.
H. Arguello-Fuentes, graduated with a BSc in Electrical Engineering in 2000 and an MSc. in Electrical Power in 2003, both from the Universidad Industrial de Santander, Colombia. He was awarded his PhD in Electrical and Computer Engineering from the University of Delaware, United States. He is an associate professor in the Department of Systems Engineering at the Universidad Industrial de Santander, Colombia. His research interests include compressive sensing, high dimensional signal processing and computational imaging. ORCID: 0000-0002-2202-253X.
Referencias
Arce, G.R., Brady, D.J., Carin, L., Arguello, H. and Kittle, D.S., Compressive coded aperture spectral imaging: an introduction. IEEE Signal Processing, 31(1), pp. 105-115, 2014. DOI: 10.1109/MSP.2013.2278763
Gat, N., Imaging spectroscopy using tunable filters: A review, Proceedings of SPIE, pp. 50-64, 2000. DOI: 10.1117/12.381686
Candès, E.J. and Wakin, M.B., An introduction to compressive sampling. IEEE Signal Processing Magazine, 25(2), pp. 21-30, 2008. DOI: 10.1109/MSP.2007.914731
Ye, P., Arguello, H. and Arce, G.R., Spectral aperture code design for multi-shot compressive spectral imaging, In Digital Holography and Three-Dimensional Imaging (OSA), p. DWA6, 2010. DOI: 10.1364/DH.2010.DWA6
Shaw, G.A. and Burke, H.H.K., Spectral imaging for remote sensing. Lincoln Laboratory Journal,
[Online] 14(1), pp. 3-28, 2003. Available at: https://www.ll.mit.edu/publications/journal/journalarchives14- 1.html#1
Govender, M., Chetty, K. and Bulcock, H., A review of hyperspectral remote sensing and its application in vegetation and water resource studies. Water Sa, 33(2), 2007. DOI: 10.4314/wsa.v33i2.49049
Gowen, A.A., O'Donnell, C., Cullen, P.J., Downey, G. and Frias, J.M., Hyperspectral imaging–an emerging process analytical tool for food quality and safety control. Trends in Food Science and Technology, 18(12), pp. 590-598, 2007. DOI: 10.1016/j.tifs.2007.06.001
Cen, H. and He, Y., Theory and application of near infrared reflectance spectroscopy in determination of food quality. Trends in Food Science and Technology, 18(2), pp. 72-83, 2007. DOI: 10.1016/j.tifs.2006.09.003
Ding, H.B. and Xu, R.J., Differentiation of beef and kangaroo meat by visible/near-infrared reflectance spectroscopy. Journal of Food Science, 64(5), pp. 814-817, 1999. DOI: 10.1111/j.1365- 2621.1999.tb15918.x
Duarte, M.F., and Baraniuk, R.G., Kronecker compressive sensing. IEEE Transactions on Image Processing, 21(2), pp. 494-504, 2012. DOI: 10.1109/TIP.2011.2165289
Arguello, H. and Arce, G.R., Code aperture optimization for spectrally agile compressive imaging. Journal of the Optical Society of America, 28(11), pp. 2400-2413, 2011. DOI: 10.1364/JOSAA.28.002400
Rueda, H., Arguello, H. and Arce, G.R., DMD-based implementation of patterned optical filter arrays for compressive spectral imaging. Journal of the Optical Society of America, 32(1), pp. 80-89, 2015. DOI: 10.1364/JOSAA.32.000080
Kittle, D., Choi, K., Wagadarikar, A. and Brady, D.J., Multiframe image estimation for coded aperture snapshot spectral imagers. Applied Optics, 49(36), pp. 6824-6833, 2010. DOI: 10.1364/AO.49.006824
Wu, Y., Mirza, I.O., Arce, G.R. and Prather, D.W., Development of a digital-micromirror-device-based multishot snapshot spectral imaging system. Optics Letters, 36(14), pp. 2692-2694, 2011. DOI: 10.1364/OL.36.002692
Figueiredo, M., Nowak, R.D. and Wright, S.J., Gradient projection for sparse reconstruction: Application to compressed sensing and other inverse problems. IEEE Journal of Selected Topics in Signal Processing, 1(4), pp. 586-597, 2007. DOI: 10.1109/JSTSP.2007.910281
Rueda, H., Calderon, A.R. and Arguello, H., Spectral selectivity in compressive spectral imaging based on grayscale coded apertures, Image Signal Processing and Artificial Vision (STSIVA), pp. 1-5, 2013. DOI: 10.1109/STSIVA.2013.6644929
Green, R.O., Eastwood, M.L., Sarture, C.M., Chrien, T.G., Aronsson, M., Chippendale, B.J. and Williams, O., Imaging spectroscopy and the airborne visible/infrared imaging spectrometer (AVIRIS). Remote Sensing of Environment, 65(3), pp. 227-248, 1998. DOI: 10.1016/S0034-4257(98)00064-9
Cómo citar
IEEE
ACM
ACS
APA
ABNT
Chicago
Harvard
MLA
Turabian
Vancouver
Descargar cita
Licencia
Derechos de autor 2016 DYNA

Esta obra está bajo una licencia internacional Creative Commons Atribución-NoComercial-SinDerivadas 4.0.
El autor o autores de un artículo aceptado para publicación en cualquiera de las revistas editadas por la facultad de Minas cederán la totalidad de los derechos patrimoniales a la Universidad Nacional de Colombia de manera gratuita, dentro de los cuáles se incluyen: el derecho a editar, publicar, reproducir y distribuir tanto en medios impresos como digitales, además de incluir en artículo en índices internacionales y/o bases de datos, de igual manera, se faculta a la editorial para utilizar las imágenes, tablas y/o cualquier material gráfico presentado en el artículo para el diseño de carátulas o posters de la misma revista.































