Uplift force and momenta on a slab subjected to hydraulic jump
Fuerza de levantamiento y momentos en una losa sometida a salto hidráulico
DOI:
https://doi.org/10.15446/dyna.v83n199.52252Palabras clave:
Uplift pressure, hydrodynamics uplift, slabs, physical model, stilling basins, hydraulic jump. (en)Presiones de levantamiento, levantamiento hidrodinámico, losas, modelo físico, tanques de amortiguación, salto hidráulico. (es)
Descargas
DOI: https://doi.org/10.15446/dyna.v83n199.52252
Uplift force and momenta on a slab subjected to hydraulic jump
Fuerza de levantamiento y momentos en una losa sometida a salto hidráulico
Mauricio González-Betancourt
Investigador del convenio COLCIENCIAS- Servicio Nacional de Aprendizaje SENA y miembro del Grupo de investigación del Posgrado en Aprovechamiento de Recursos Hidráulicos, Universidad Nacional de Colombia, Colombia. magonzalezb@sena.edu.co; mao275@yahoo.com
Received: August 03th, 2015. Received in revised form: February 14th, 2016. Accepted: July 18th, 2016.
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.
Abstract
As part of the search for safe and
economic design criterion to line slabs of stilling basins, the present study
is one of the first to calculate the center of pressure, uplift forces, and
momenta from a spatiotemporal analysis of the pressures measured above and
below instrumented slabs in a physical model. Controlled release of the
waterstops, and variation in the dimensions of expansion joints and in the gap
between foundation and the lining slab were carried out in order to consider
their effects on the magnitudes of uplift forces and momenta. An offset of the
center of pressure from the slab's center of gravity was identified. The objective
of this work was to consider the failure mechanism induced by momentum in the
slab's design. Design criterion to make the lining slab's thickness to length
between 6 and 12 times the incident flow depth, is proposed, and this is
compared to other design criteria.
Keywords: Uplift pressure; hydrodynamics uplift; slabs, physical model; stilling basins; hydraulic jump.
Resumen
Buscando un
criterio de diseño seguro y económico para las losas de los tanques de
amortiguación, se calcularon fuerzas de levantamiento, centros de presión y
momentos a partir de un análisis espacio-temporal de las presiones medidas
encima y debajo de losas instrumentadas en un modelo físico. La liberación
controlada de los sellos y la variación en las dimensiones de las juntas y de
la separación entre la cimentación y la losa, fueron realizadas para considerar
sus efectos sobre la fuerza de levantamiento y los momentos. Se identificó
desplazamiento del centro de presión respecto al centro de gravedad de la losa.
Para considerar el mecanismo de falla inducido por el momento en el diseño de
losas, objetivo del trabajo, se propone un criterio de diseño para el espesor
equivalente de las losas con longitudes entre 6 y 12 veces la profundidad del
flujo incidente y se compara con otros criterios.
Palabras clave: Presiones de levantamiento; levantamiento hidrodinámico; losas; modelo físico; tanques de amortiguación; salto hidráulico.
1. Introduction
Outlet works conduit typically requires dissipation of excess kinetic energy to prevent downstream channel erosion as this flow often discharges at a high velocity. An energy dissipator, such as a stilling basin, is used to retard the fast moving water by creating a hydraulic jump [1]. The design of an energy dissipating structure need criteria to avoid cavitation, abrasion, internal erosion, hydrodynamic uplift, etc.
Historical reporting of the failure of slabs in flumes and stilling basins, with an equivalent thickness ranging from 0.3 m to 4 m, has show the hydrodynamic uplift to be a structural design problem [2-5]. Equivalent thickness is the real slab thickness, and anchors are defense against uplift.
Since the early 60s, design criteria for lining slabs to calculate the uplift force and equivalent thickness have been proposed. The most recognized design criteria were based on stochastic analysis of the pressure and force fluctuations at the floor of the hydraulic jump in a physical model [6-10]. A summary of the criteria can be found in references [11-12]. They determine the uplift force taking into account the length (L) and width (W) of the slab. Researchers agree with the criteria that the length of the slab in direction of flow has an inverse relation to the uplift force [6,7,9,10,12]. However, there is no complete agreement as to the slab's width influence on the uplift force. Bellin and Fiorotto [10] suggest building the slab with the minimum width technically possible, and other criteria indicate otherwise [8,9,12].
There are differences between design criteria due to simplifications in the physical and conceptual models that were supported. For the same condition, the slab's equivalent thickness that was calculated using existing criteria shows large differences. Thus, it is difficult to choose criteria that guarantee the stability of the slab with the lowest cost and, generally, the designer chooses the more conservative criteria. According to Khatsuria [11], the vast variation between criteria points to the fact that this science is still in an evolutionary stage. While Bollaert [13] expressed that "despite major advances in measurement technology and data acquisition, a safe and economic design method for any kind of concrete lined stilling basin is still missing today. Especially the dynamic or even transient character of pressure pulsations as a function of their two-dimensional spatial distribution above and underneath the lining is not fully assessed and implemented in existing design methods. [13]".
In addition, the physical models that supported the design criteria were not simulated in their true scale joints, waterstops, slab thickness (s), and gap between soil foundation and the concrete slab (d) since the pressure drop through the joints to the foundation was depreciated. In the prototype, gap d and width joint (e) can change by sources of natural movement, internal erosion, etc. Furthermore, the position and number of sensors reported by the references [6-10] were not sufficient to be able to accurately estimate both the uplift force and its center of pressure.
To date, the evidence suggests that hydrodynamic uplift is also influenced by the interaction of fluid with joint and detachment of the waterstops [13-19]. However, these factors have not been considered in the design criteria of the slab subjected to a hydraulic jump with horizontal aprons.
Previous work was observed in which joints and waterstops act as pressure filter fluctuations generated in the flume [18]. Also, the joints generate a time delay between the entry of the pressure wave at the joint and its arrival below the slab. It leads to the pressure differential between top and bottom of the slab and, therefore, the uplift force emerges. The interactions between the joints and the main stream alter the amplitude of pressure wave below the slab. Joints and waterstops promote generating pressure gradients below the slab and some instants, the pressure gradients will have positive or negative linear correlation. With only one open transversal joint, the pressure below the slab was uniform. With two or more open joints, pressure gradients below the slab were generated.
No uniformity in pressure over a slab leads to the consideration of the failure mechanism induced by momentum of force. If a slab turns a little due to momentum, offset between slabs occurs and the stagnation point increases the uplift pressure and drag force. Failure or loss of intimate contact with the soil is typically the result of a slab overturning its downstream contact point [1]. The forces of interest in a momentum balance are slab weight (Fweight), strength of the anchors, the resultant forces F- and F+ of field pressure acting on the surface above and below the slab, and drag force (FR). The net uplift force (Fnet) is a vector sum of the forces F+ and F-, which could have a center of pressure in a different coordinate to the center of gravity of the slab that changes over time (Fig. 1).
Therefore, in this study the author determined the forces F+, F- and Fnet from a spatial integration of pressure fields and balance forces. The author established the pressure fields from measured pressures with multiple sensors above and below a slab that was subject to hydraulic jump. The center of pressure to be able to calculate the momenta of force F+ and F- was also identified, and the momentum Ma in terms of the downstream contact point of the slab, and the momentum Mc, in terms of the upstream contact point of the slab (Fig. 1) was calculated. The author also contemplated the variation of magnitude of the force F+ and its center of pressure by the joints, the damage of the waterstops, and the variation of gap d and e.
Multiple tests including physical and hydrodynamic variations were evaluated. They were analyzed and helped improve the understanding of the uplift hydrodynamic of the lining slabs. The author present the design criterion that has an equivalent thickness of the slabs with lengths between 6 and 12 times the depth of the incident flow. This paper is based on the author's PhD thesis [18].
2. Materials and methods
Pressures were measured above and below
slabs in a physical model that was made in the Hydraulic Laboratory at the
"University of Valle" in Cali, Colombia (Fig. 2). The physical model contains
slabs fixed under the horizontal flume floor at different distances from the
load tank. The flume was 0.5 m high, 8m long, and 0.35 m wide. The slab and its
details such as expansion joints, slab thickness, gaps d, and e, were
simulated with several acrylic boxes with dimensions from largest ((L+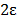 )*(W+
)*(W+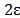 )*(s+d), internal dimensions) to smallest (L*W*s, external dimensions;
Table 1; Figs. 1, 2).
)*(s+d), internal dimensions) to smallest (L*W*s, external dimensions;
Table 1; Figs. 1, 2).
The length (L) of individual slabs ranged from 6 to 12 times the incident flow depth (y1), and the slab's width was approximately half its length. The gap d was possible by interposing aluminum sheet rings 1 mm in diameter and thickness that were required to achieve the desired separation.
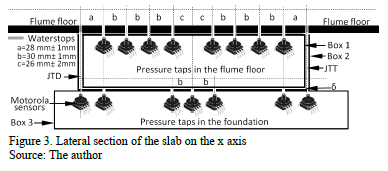
The flume floor was drilled and slotted to provide continuity to pressure taps and joints (Fig. 3). The model slabs were fixed to the basin to prevent motion. The coupling between elements in the system was monitored to avoid stagnation points by the offset between edges, as was recommended and studied in references [19-20]. The offset was estimated to be 10-5m. This could be the case for the prototype due to imperfections in the finishing of the slabs and their rearrangement by natural movement.
The flow entering the hydraulic jump was full and partially developed with a Reynolds number in the boundary layer (Rex) between 300,000 and 17,380,000. The first slab (S1) was located at a distance at which the Rex was between 300,000 and 660,000 (transition), the second slab 2 (S2) was in the area of Rex between 4,150,000 and 9,130,000, and the third slab (S3) was the farthest from the load tank with Rex between 7,900,000 and 17,380,000. The experimental design varied the state of development of the boundary layer since the magnitude of pressure fluctuation depended on whether the flow is fully developed or undeveloped [11]. However, the flow regime was always turbulent with Reynolds numbers between 90,000 and 200,000. Incident flow velocities (V1) ranged from 1.65 and 5.76 m/s.
The pressure was measured with 32 Motorola sensors (MPXV 4006GC7U, range 0-6 kpa and accuracy ±5 %) and with circular pressure taps of 2 mm in diameter above and below the slab with two distributions (Fig. 4). The first sensors distribution (D1) selected 16 pressure taps above and below the slab that had an equal distribution (Fig. 4a, sensor symbol "•" and "■"). The second sensors distribution (D2) selected 8 pressure taps that were located above the slab in the central line (Fig. 4a; sensor symbol "•"). When these sensors failed, the pressure taps next to the longitudinal joint were used (Fig. 4a; sensor symbol "■"). Furthermore, 24 pressure taps below the slab and the bottom of the joints were implemented to achieve a higher resolution of the pressure field (Fig. 4b; sensor symbol "♦").
Every five working hours, in accordance with the methodology proposed in the reference [21], the pressure measurement system was dynamically calibrated, and dynamic uncertainty was, on average, 8.82%. The signs that were acquired with a data acquisition system (DAQ National Instruments, NI SCXI: 1000, 1102B, 1600, 1300) were sent to a laptop. The sampling frequency (fs) was 200 Hz and was limited by the data acquisition system available. In addition, it held the sampling theorem (avoiding aliasing) and improved the resolution in the time of the digitized signal (5 ms). In signal processing, a median digital filter was used to remove frequency components that were not part of the phenomenon since it closely recovers the original signal while removing noise [22]. According to the analysis of the frequency signal and the dynamic characteristics of the pressure measurement system, the cutoff frequency of the digital filter was 10.5 Hz (window median filter equal to nineteen). Thus, the typical overshoot of the pressure measurement system in response to a sudden change of pressure (pressure fluctuation) was minimized. "Overshoot is the amount of output measured beyond the final steady output value in response to a step change in the measurand" [23].
In each test, the slab type (S1A, S1A*, S1B, S2, and S3: Table 1), the open joint(s), and the Fr1, were selected. Hydrodynamic variations included a minimum seven different Fr1 between 2.3 and 10 for each physical variation.
Physical variations include the controlled release of the waterstop(s) in: a) one of the four joints, front transverse joint (FTJ), rear transverse joint (RTJ), or longitudinal joint (LJ); b) two joints simultaneously, longitudinal joints (LJ), or transverse joints (TJ); c) all joints (AJ).
The flow depth was measured on a) FTJ, b) LJ in the middle of the slab, c) RTJ. At each point, the minimum and maximum depth detected in 30 seconds were measured with depth gages that had a 300 mm range and an accuracy of ± 0.2 mm. The discharge was regulated between 8.15 and 14.1 Gallon/min, as was the vertical gate of the load tank (1.8m high, 1m long and 0.35 m wide) between 2.5 and 5.5 cm. The discharge was measured from an Omega flow meter (FMG-901). The flow rate was measured with a Prandtl tube at a point located 0.05 m upstream of the front transverse joint, and the measurement error was 4%.
The test was run over 15 minutes and the data acquisition was performed during in the last five minutes. Data acquisition time was mainly associated with extensive data and the number of tests explored (420). One test had 60,000 discrete samples in which the pressure fields were analyzed.
The hydraulic jump with rectangular weirs of heights ranging from 5 to 20 cm at the end of the flume was induced. Because, in general, the highest pressure fluctuations are reported in the first third of the length of the free hydraulic jump [8,24-30], the slabs were located under 30% of its length. Some tests in the slab "S1" had a submerged hydraulic jump.
3. Data processing and results
This researcher evaluated each sampling instant from the 58 test samples that had an S1A configuration, the forces F+, F-, Fnet, their center of pressure over the slab surfaces, and the momenta Ma and Mc. Using data processing, the pressure fields from the pressure measured above and below the slab in each sampling instant were adjusted. According to the theory of Riemann integration, to obtain the total force vectors F+ and F- (eq. 1 and eq. 2), the area of slab was discretized and the sum of the partial pressures was computed.
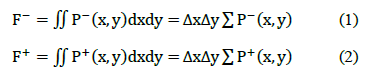
Where, P- and P+ are the pressures above and below the slab's surfaces.  (L/186 x B/115) are area
elements in which the slab area (AL) was
discretized.
(L/186 x B/115) are area
elements in which the slab area (AL) was
discretized.
The x-coordinate of center of pressure (intersection of the resultant force and the surface's line of action) was obtained with eq. 3.

Where xi is x coordinate of the center of the differential element of area.
The forces F+ and F-'s centers of pressure were different to their centers of gravity, which affect momenta that induce rotation of the slab. The offset percentage of the center of pressure from the center of gravity in x-coordinate was calculated using eq. 4 (Fig. 5).

Where xc is x-coordinate of the slab's center of gravity (or centroid).
The author calculated the momenta balances with respect to the slab's extreme contact points. The clockwise momentum was positive. The Fnet and net momenta (Manet and Mcnet) determine the possibility of the slab's uplift or rotation (Fig. 1). Then, the maximum value of Fnet, Manet, Mcnet in each test was selected and expressed in terms of net instability dimensionless coefficients (FNM*, MaNM*, |McNM*|; eq. 5 -7).

Where g is the specific weight of water and g is the gravity.
The coefficients FNM* were lower than the coefficient MaNM* and |McNM*| (Fig. 6), which show that the mechanism of initial failure is the slab's rotation. The dotted boundary was called the enveloping curve of instability net coefficients (Cnet) and it will be used to predict the uplift hydrodynamic in the next subsection. Two values of |McNM*| that fall outside the area of the curve (Fig. 6). These values manifest the combination of a great uplift force with a great center of pressure offset from the center of gravity below the slab (Fig. 6).
To expand upon the above, the author analyzed the impact on uplift force of the variations of Rex, the gap d, the gap e, and the controlled release of the waterstops. It was considered that these physical variables only affect pressure fields below the slab, i.e. the force F+. Thus, in each sampling instant from the 420 tests we calculated the force F+ (eq. 2) and then expressed it in the form of a dimensionless coefficient, according to eq. 8.

Where  was
calculated as the average of three minimum depths measured on FTJ, LJ, RTJ with
a baseline below the slab.
was
calculated as the average of three minimum depths measured on FTJ, LJ, RTJ with
a baseline below the slab.
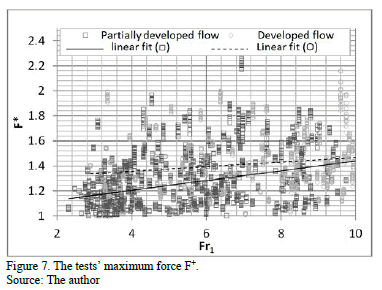
To avoid the mistake of basing the analyses on a spurious value, ten maximum values identified in each test were plotted (Figs. 7-10). For same Froude number, coefficient F* varied as a result of pressure fluctuations of the hydraulic jump and the geometric variations made in each test.
The incidence of the
state of development of flow over force F+ was not clear. The force F+ is proportional to the Froude
number and, generally, it was lower than twice the average hydrostatic force
below the slab ( ; Fig. 7).
; Fig. 7).
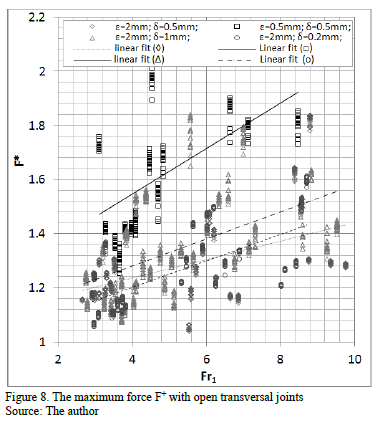
The effect on the force F+ by detachment of the waterstops, the change of the gaps e, and d can be deduced from Figs. 8-10. These showed the maximum F+ found in the different tests with S1 configuration and open transversal joints (Fig. 8), open longitudinal joints (Fig. 9), and all open joints (Fig. 10). Furthermore, a slab configuration with gap e of 0.5 mm and 2 mm; and gap d of 0.2 mm, 0.5 mm, and 1 mm was also considered
As a result of these tests, it is possible to say that the narrowest joint (e=0.5 mm) induced a greater uplift force F+ (Fig. 8-10). Tests with open traversal joints induced major uplift forces under the slabs, and these were followed by tests with all open joints.
The incidence of gap d on uplift force was not clear. For the condition of open transverse joints an inverse relationship between the uplift force and the gap d was observed (Fig. 8).
However, occasionally the author identified a proportional relationship between F+ and gap d in tests with longitudinal joints or all open joints (Figs. 8, 9). The greatest uplift forces obtained from the combination of gap e of 0.5 mm and gap d of 0.5 mm, and the results showed in references [15,16], led to us leaving the hypothesis open (narrower gap d leads to a hydraulic jack).
The study of net uplift force and its point of application showed that it is necessary to consider the equivalent thickness of lining slabs in design criteria as well as the failure mechanism induced by momentum. Also, detachment of the waterstops, the size and the orientation joints that have an effect on the uplift force, and consequently influence its momentum should also be considered.
4. Estimation of hydrodynamic uplift
The author proposes experimental tests
and design criterion to estimate the equivalent thickness of a slab with
lengths between 6 and 12 times the incident flow depth. The design of concrete
slabs for hydrodynamic loading focuses on the determination of the maximum
possible destabilizing force and momentum. In this criterion, uplift force and
momenta are considered by the dimensionless design coefficient  , calculated by eq. 9.
, calculated by eq. 9.

Where, Cnet is the instability net coefficients, which can be obtained from Fig. 6's
envelope curve. " " is an dimensionless experimental coefficient that takes into account the increase of the force F+ and its momentum from the
detachment of the waterstops, and the size and the orientation joints. "
" is an dimensionless experimental coefficient that takes into account the increase of the force F+ and its momentum from the
detachment of the waterstops, and the size and the orientation joints. " " is a dimensionless experimental coefficient that takes into account extreme instabilities.
" is a dimensionless experimental coefficient that takes into account extreme instabilities.
To
obtain the coefficients  and
and  , the force F+ found in
each sampling instant from 420 tests was used to calculate the momenta Ma+ and Mc+. The largest momenta Ma+ and Mc+ in each
test were selected and expressed in form of dimensionless coefficients (eq. 10 and eq. 11).
, the force F+ found in
each sampling instant from 420 tests was used to calculate the momenta Ma+ and Mc+. The largest momenta Ma+ and Mc+ in each
test were selected and expressed in form of dimensionless coefficients (eq. 10 and eq. 11).

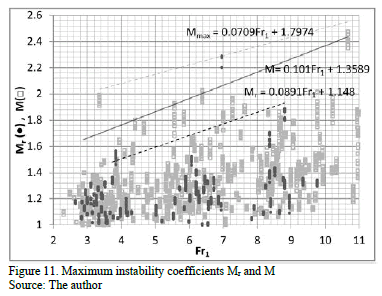
The largest absolute value of the coefficients Ma* and Mc* in each test were identified and called coefficient M (eq. 12).

M coefficients from 58 tests with an S1A configuration were added to the subscript r (Mr). A curves adjustment over the maximum value of Mr and M vs. Fr1 was plotted (Fig. 11). The M curves that were proposed as lines ensured that the slope is always positive as the uplift force F+ is proportional to Fr1. Furthermore, since the positive and negative maximum pressure coefficient increases over time [8,27], the line fits the data conservatively to compensate for the short-time data acquisition (5 min).
The
amplification factor  that depends on Fr1 is calculated
according to equation 13 (Fig. 11).
that depends on Fr1 is calculated
according to equation 13 (Fig. 11).
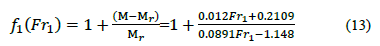
Mmax were associated with the extreme
instabilities and the low probability of occurrence (Fig. 11). To determine the coefficient  the same
methodology used to determine
the same
methodology used to determine was implemented, and the M curve was compared with a curve fit to Mmax (eq. 14, Fig. 11).
was implemented, and the M curve was compared with a curve fit to Mmax (eq. 14, Fig. 11).
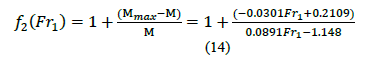
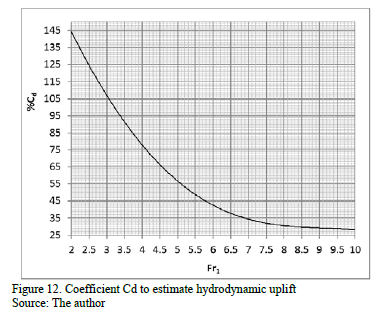
The design coefficient in the Fr1 function is presented in Fig. 12. The buoyancy is considered by the design coefficient if the real thickness used in the prototype is less than the calculated thickness scaling model to prototype (Table 1). If the above are fulfilled, the thickness of the slab can be calculated with equation 15.

Where  is the specific weight of
concrete. In a scenario in which the slab could be immersed in a water-sediment
mixture (for example, during the flushing of sediments from reservoirs), it is
necessary to replace the specific weight of water by mixture (
is the specific weight of
concrete. In a scenario in which the slab could be immersed in a water-sediment
mixture (for example, during the flushing of sediments from reservoirs), it is
necessary to replace the specific weight of water by mixture ( ). The above equation intends to compensate for the increase in the
buoyancy force on the slab by the increased density of the mixture.
). The above equation intends to compensate for the increase in the
buoyancy force on the slab by the increased density of the mixture.
The slab thickness is most often selected empirically as achieving stability to resist uplift force alone with this parameter requires a heavy slab, and this is not always possible. In these cases, the methodology of equivalent thickness through the anchor should be used [31]. Slab thickness and the anchor could be calculated with eq. 16
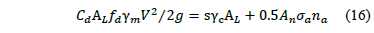
The left side of eq. 16 is considered the
hydrodynamic uplift. " " is the drainage coefficient, and it can be used as a
means to theoretically reduce up to 50% of the pressure uplift (
" is the drainage coefficient, and it can be used as a
means to theoretically reduce up to 50% of the pressure uplift ( = 0.5; [32-33]). The right side of eq. 16 represents the forces that
counteract the uplift force, including the weight of the concrete slab and the
force that provides the anchor. Where, "
= 0.5; [32-33]). The right side of eq. 16 represents the forces that
counteract the uplift force, including the weight of the concrete slab and the
force that provides the anchor. Where, "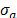 " is the tensile stress between steel-slab,
" is the tensile stress between steel-slab,  is the number of steel bars,
and
is the number of steel bars,
and  is the area of the steel bar. For safety purposes, double the area
of the anchor steel is assumed to design slabs in stilling basins [31].
is the area of the steel bar. For safety purposes, double the area
of the anchor steel is assumed to design slabs in stilling basins [31].
Underdrains, anchors, cutoffs, and slab thickness are all provided to stabilize the slabs [32]. A slab that is about 600 mm thick is the minimum recommended [33], and this shall be determined by analyzing hydrostatic uplift and an elastic foundation analysis [32]. Uplift momenta and misalignment between slabs can be prevented by adding steel in the partial contraction deboned joint located the transversal joint (the joint with slip dowels). Thus, the deboned joint allows the expansion or contraction of the slab while the steel counteracts the shear loads void misalignment between slabs [32,34-35]. Also, safety reinforcement counteracts the momentum of force FR.
5. Analysis
To ensure that the physical model represents the prototype, there must be geometrical, kinematic, and dynamic similarity [36-38]. Therefore, it is necessary to consider the effects of scale before using any lining slabs design criteria.
In hydraulic jump, when the large eddies are well reproduced in a model, the representation of turbulence is nearly achieved since the eddies are the energy carriers [11]. The large eddies in the turbulent flow are proportional to the principal dimension of the flow field, and they ensure correct simulation using a geometrically similar model [11]. The author recommends using a geometric scale more generous than 1:50 [36].
Viscous effects can lead to scale effects, especially in models based on Froude, for which the Reynolds number is always less than the prototype [11]. In tests with an Fr1 between 2.3 and 7.15, viscous effects and scale effects in terms of void fraction, bubble count rate, and bubble chord time distributions were overcome. Their influence was at least minimized since in the model the flow depth was greater than 30 mm, and there was a turbulent flow with Reynolds numbers greater than 100,000 [39,36-41]. When the physical model does not take into account the concentration of air in the evaluation of the pressures, it may require an additional safety factor. Pinheiro [25] found that increased air concentration decreases the mean pressure value and the standard deviation of force.
According to Lopardo et al. [29], the pressure data collected in a physical model with a free vertical gate system and horizontal flume can be extrapolated to sloping channels in hydraulic jump stilling basins. That is as long as the error is on the side of safety. Similarity law of fluctuating pressure spectrum in the strongly rolling area agrees with gravity law [41]. Thus, data from basic research provides pressure values that are useful for stilling basin predesign, despite the limits in scale similarity.
Viscous and inertial forces dominate physical processes involving flow through small cracks or joints along a channel boundary [19]. The dimensions used to simulate the expansion joints (0.5 mm - 2 mm) lead us to suggest the use of a geometric scale more generous than 1:30. To establish similarity between the roughness implemented in the general contour of the model (coated in acrylic: nManning = 0.009) and prototype (coated concrete: nManning = 0.014), the geometric scale should be 1:14. Thus, the Manning roughness scale factor limits the geometric scale [36]. When this parameter has no similarity, the model is rougher than its prototype, and scale effects are generated.
Inside the joints and the d gap, as with the cavities, constrictions, and junctions, the propagation speed of pressure wave (c) becomes a function of the variation of fluid density (compressibility), and area (distensibility) increases in pressure [42]. For a given Fr1, the effects of the Reynolds number on the two-phase flow properties are particularly notable in the developed shear layer [38]. Thus, aeration in a prototype will be higher than in the model, and a similar or smaller "c" can be expected in the prototype. Pressure waves experience diffraction, interference, reflection, and refraction that depend of solid material in the boundary. These can alter the propagation speed, amplitude and the transmitted energy [14,18]. In the prototype, the boundary may be concrete and soil. The boundary was acrylic in the model, in which "c" may decrease and energy losses in the reflection of the pressure wave increase. Nevertheless, in a prototype designed with the criterion and a scale more generous than 1:14, the impact of the last variables are less in the resonance phenomena and persistence time of the net uplift pressure due to the length of the slabs [27], the hydraulic jump's low frequency [27,31,37], and the role of the joints as frequency filters [17,18]. The pressure amplification under the slab for the effects of fluid, joints interaction, and pressure waves at frequencies below 10.5 Hz were considered as part of this criterion.
In these cases that Fr1 is greater than 7.16, and/or the stilling basin demands a greater geometric scale than 1:15 to be able to establish similarity. The criterion proposed can be used for the predesign of lining slabs. "For a joint length of 18 m and c of 100 m/s, one obtains a resonance frequency < 3 Hz [13]". If the resonance is demonstrated, the transient approach needs a quantification of pressure amplification inside the joints, which can be the use of an appropriate pressure amplification coefficient [13]. To verify resonance inside the joints and the gap d, a model scale 1:1, pressure sensors with high natural frequency and with a damping close to 0.6 to prevent overshoot error are required. To check the stability of the slabs in the physical model of the prototype, a scale more generous than 1:14 is recommended. Given the opportunity to try alternatives, analyze different solutions, view operating conditions in extreme situations, and eventually, reduce the risk [43], physical modeling allows details to be refined so to as find a safer and more economical project.
To compare the developed criterion with other traditional criteria to estimate the slab equivalent thickness, some scale effects are ignored and two illustrative examples are shown. The author consider the hydraulic jump stilling basin with the following details. The first example: y1=2.43m, y2=31.45m (major conjugate of the hydraulic jump). Size of panel monolith: W=11.5 m (W=4.4y1) and L= 25 m (L= 9.76y1). V1 = 46.1 m/s and Fr1 = 9.44. Second illustrative example: y1=0.45m, y2=3.54 m, W= 4.5 m (W=4.4y1), L=2 m (L=10y1), V1 = 16.5 m/s and Fr1 = 5.5. In the computation, the submerged specific weight is 1.6 ton/m3, and a safety factor and an operating drainage system are not considered.
Hydrostatic uplift is evaluated using
three conditions: spillway design flood,
stilling basin empty, and sudden drawdown following design flood [11,33].
Usually, the first condition gives the maximum uplift force in the slab close
to the hydraulic jump [11]. The latter is due to the pressure of tail water
level (Tw), which is transmitted by a saturated foundation that has greater
fluid pressure on the slab. The criteria belonging to Hajdin [7] and Toso et al. [8] was used, which are based on
the measurement of fluctuating pressures, and the criteria of Farhoudi et al. [9] and Bellin et al. [10], which are based on direct
measurement of fluctuating force. In all these studies, except Bellin et al. [10], propagation of fluctuating
pressures below the apron was not considered. For the criteria to be applied,
the influence of the length and width of the slab are taken into account by
using the coefficient of spatial correlation (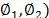 , the force coefficient (
, the force coefficient ( ), or the uplift coefficient (
), or the uplift coefficient ( . This paper also considers the dimensionless pressure coefficient
(Cp), which is based on the maximum positive (Cp+) and negative
pressure (Cp-) deviation from the mean pressure, and the coefficient
based on root-mean-square pressure fluctuations (Cp') that is reported in the
references [7-10, 27, 30].
. This paper also considers the dimensionless pressure coefficient
(Cp), which is based on the maximum positive (Cp+) and negative
pressure (Cp-) deviation from the mean pressure, and the coefficient
based on root-mean-square pressure fluctuations (Cp') that is reported in the
references [7-10, 27, 30].
In each example, two computations to evaluate Bellin et al. [10] and Toso's [8] criteria with two Cp were used as it is important acknowledge the importance of a correct selection pressure coefficient when estimating the equivalent thickness. The slab equivalent thickness computation using various relationships is presented in Table 2.
The first computation of the two illustrative Cp examples was based on Cp+ and Cp- experimental data. In this case, the equivalent thickness estimated by criteria from Bellin et al. [10], Hajdin [7], and Farhoudi et al. [9] were similar. The equivalent thickness that was estimated by the criterion proposed in this paper (last row, table 2) is greater than those mentioned above while Toso et al.'s criterion [8] was most conservative.
In the second computation in the two illustrative examples, Cp was based on the suggestions from each group of researchers. Bellin et al. [10] suggest assuming the pressure coefficients Cp+, Cp- =1 in case of a lack of experimental data while Toso et al. [10] suggest Cp 0.9 for the incident Froude number between 7.7 and 10. In this case, the criteria were very conservative.
The Toso [8] criteria may be safely assumed, but it is conservative for a large slab that presents the compensation of the pressure pulses on its upper face. In the hydraulic jump, the pressure pulses on big slabs are uncorrelated since the slab length is larger than the integral scale of the pressure fluctuations. The integral scale is thereby defined as the distance on which, on average, two pressure pulses become fully uncorrelated. In other words, it defines the maximum possible area in which a pulse may reasonably act [13,17].
Thus, extreme pulses recorded by a single sensor in the large slab are not a representative sample of the pressure fields above and below the slab to accurately calculate the uplift force [13,18]. Above the large slab, a positive or negative pulse is a local effect.
In the first illustrative example, for the first computation and the discarded Toso criterion, hydrostatic uplift was the most critical condition for the slab's stability. This clearly shows that the release of waterstops at two different points in the floor stilling basin leads to critical situations that deserve to be paid more attention from engineers.
In this study, a slab was located in the highest pressure fluctuations zone of the hydraulic jump as the study of Farhoudi et al. [9] and Bellin et al. [10] indicated. Differential heads resulting from the sloping water surface of the jump can cause a circulating flow under the slab if leakage is allowed to enter the joint at the downstream end of the basin and to flow out of the joint at the upstream end [32]. Therefore, it is necessary in future research to mount several slabs along the hydraulic jump and to vary the number of waterstops detached on two different slabs: one at the area of maximum pressure fluctuation in the toe jump and the other at the area of maximum depth.
The criterion proposed contributed to the search for a safe and economic design method for a concrete lined stilling basin because it considers uplift force and momenta. It was computed from a spatiotemporal analysis of the pressure fields that was measured above and below the instrumented slabs in a physical model. Furthermore, the criterion was supported by a large amount of experimental information, for which details that had previously been poorly studied such as joints, waterstops, and gaps between foundations and the concrete slab were considered. The design coefficient that is supplied by a curve in an Fr1function facilitates the designer's application of the criterion.
6. Conclusions
The waterstops, the size, and the orientation joints have an effect on the uplift pressures, and consequently, influence the magnitude of uplift forces and momenta. The narrower joints and open traversal joints generated major uplift forces below the slabs. An offset of the center of pressure from the center of gravity in the flow direction increased the momenta Ma and Mc by up to 30%. Thus, it was necessary to consider the failure mechanism induced by momentum in the design criteria.
Considering the maximum force and momenta in each test, a design coefficient was found that defines the equivalent thickness depending on the incident Froude number between 3 and 10. It considers the effects of the offset on the center of pressure from the slab's center of gravity. This is generated by the influence of waterstops, joints, and hydraulic jump macroturbulence with full and partially developed inflow. According to changes in the hydrodynamic conditions and the physical model's characteristics, the study involves slabs with lengths between 6 and 12 times the incident flow depth.
The author discuss the scale effect that is inherent to the physical model and conclude that the experimental results are useful for: a) Designing the lining slabs in hydraulics structures that are similar to the model using scale more generous than 1:14, and an Fr1 between 2.3 and 7.15; b) Predesigning the lining slabs in stilling basins that require a geometric scale greater than 1:15 in order to establish similarity and/or an Fr1 between 7.16 and 10.
Acknowledgments
This research project was partially funded by COLCIENCIAS. The author would like to give a special thanks to Efraín del Risco and Lilian Posada for their valuable suggestions and insights in this field. The experiments necessary for the development of this research were undertaken in the Hydraulic Laboratory at the University of Valle in Cali, Colombia. The author sincerely appreciate the support.
References
[1] Federal Emergency Management Agency., Outlet works energy dissipators best practices for design, construction, problem identification and evaluation, inspection, maintenance, renovation, and repair. Technical manual, USA, FEMA P-679, pp. 1-66, 2010.
[2] Hepler, T.E. and Johnson, P.L., Analysis of spillway failure by uplift pressure. ASCE National Conference, Colorado Springs, Colorado, august 8-12, pp 857-862, 1988.
[3] VSL International. Soil and rock anchors, Examples from practice. Berne, Switzerland. [Online]. pp 19-20, 1992 [Consulted: 15th of august of 2009]. Available at: www.vsl.net/Portals/0/vsl_techreports/PT_Ground_Anchors.pdf
[4] Bowers, C.E. and Tsai, F.Y., Fluctuating pressures in spillway stilling basins. J. Hydraulic Division, ASCE, 95(6), pp. 2071-2079, 1969.
[5] Bribiescas, S. and Capella, V., Turbulence effects on the linning of stilling basins. Proceedings ICOLD. Congrés des Grands Barrages. Madrid. Q.41. R.83. pp. 1575-1592, 1973.
[6] Bribiescas, S. and Fuentes, O., Tanques amortiguadores. Technical Report, Project 7045. UNAM, México D. F. pp. 1-50, 1978.
[7] Hajdin, G., Contribution to the evaluation of fluctuation pressure on fluid currents limit areas- based on the pressures recorded at several points of the area. VIII Conference of Yugoslav Hydraulics Association, Portoroz. 1982.
[8] Toso, J. and Bowers, C., Extreme pressures in hydraulic-jump stilling basins, J. of Hydraulic Engineering, 114(8), pp. 829-843, 1988. DOI: 10.1061/(ASCE)0733-9429(1988)114:8(829)
[9] Farhoudi, J. and Narayanan, R., Force on slab beneath hydraulic jump. J. of Hydraulic Engineering, 117(1), pp. 64-82, 1991. DOI: 10.1061/(ASCE)0733-9429(1991)117:1(64)
[10] Bellin, A. and Fiorotto, V., Direct dynamic force measurements on slab in spillway stilling basin. J. of Hydraulic Engineering. 121(10), pp. 686-693, 1995. DOI: 10.1061/(ASCE)0733-9429(1995)121:10(686)
[11] Khatsuria R.M., Hydraulics of spillways and energy dissipators. New York: Marcel Dekker, 2005. pp 411-424.
[12] Pinheiro, A., Quintela, A. and Ramos, C., Hydrodynamic forces in hydraulic jump stilling Basins. Proceedings of the symposium on fundamentals and advancements in hydraulic measurements and experimentation. ASCE. New York. USA. pp. 321-330, 1994.
[13] Bollaert, E.F.R., Dynamic uplift of concrete linings: Theory and case studies, USSD Annual Meeting, April 24-26 2009, Nashville, United States. pp. 1-16, 2009.
[14] Bollaert, E.F.R. and Schleiss, A.J., Transient water pressures in joints and formation of rock scour due to high-velocity jet impact. Communication 13, Laboratoire de Constructions Hydrauliques, Ecole Polytechnique Fédérale de Lausanne. 2002.
[15] del Risco, E., Hurtado, E. y González, M., Estudio experimental de las presiones de levantamiento bajo una losa con juntas transversales al flujo. Tecnología y Ciencias del Agua. I(1), pp. 31-42, 2010.
[16] Hurtado, E., del Risco, E. y González, M., Presiones medidas en la base de una losa de fondo con juntas paralelas al flujo en un canal. Revista de la Facultad de Ingeniería de la Universidad de Antioquia, 47, pp. 39-52, 2009.
[17] Melo, J., Pinheiro, A. y Ramos, C., Forces on plunge pool slabs: Influence of joints location and width. J. of Hydraulic Engineering, 132(1), pp. 49-60. 2006. DOI: 10.1061/(ASCE)0733-9429(2006)132:1(49)
[18] González, M., Levantamiento de una losa de piso sometida a un flujo turbulento. PhD Tesis, Facultad de Minas, Universidad Nacional de Colombia, Medellín, Colombia. 2013.
[19] Frizell, W.K., Uplift and crack flow resulting from high velocity discharges over. Report DSO-07-07 U.S. Department of the interior, Bureau of Reclamation. Denver, Colorado, 2007, pp. 2-5.
[20] del Risco, E., Investigación experimental de la falla de losas de revestimiento de tanques amortiguadores. MSc. Tesis, Facultad de Ingeniería. UNAM, México, 1983.
[21] González, M. y Giraldo, S., Caracterización dinámica de sensores de presión utilizando el principio de la botella de mariotte. Rev. Fac. Ing. Univ. Antioquia, 71, pp. 146-156, 2014.
[22] Proakis, J.G. and Manolakis D.G., Tratamiento Digital de Señales. Prentice Hall. España, 2000.
[23] The International Society of Automation (ISA 37.16.01). A guide for the dynamic calibration of pressure transducers. pp. 13-38, 2002.
[24] Vasiliev, O.F. and Bukreyev, V.I., Statistical characteristics of pressure fluctuations in the region of hydraulic jump. Proceedings 12th IAHR Congress, Fort Collins, USA, pp. 1-8, 1967.
[25] Pinheiro, A., Accoes hidrodinámicas em bacias de dissipacao de energia por ressalto. PhD. dissertation, Universidad Técnica de Lisboa, Lisboa, Portugal, 353 P., 1995.
[26] Khader, M. and Elango, K., Turbulent pressure field beneath a hydraulic jump. J. of Hydraulic Research, 12(4), pp. 469-489, 1974. DOI: 10.1080/00221687409499725
[27] Fiorotto, V. and Rinaldo, A., Fluctuating uplift and linnings design in spillway stilling basins. J. Hydraulic Enginnering ASCE. 118(4), pp. 578-596. 1992a. DOI: 10.1061/(ASCE)0733-9429(1992)118:4(578)
[28] Fiorotto, V. and Rinaldo, A., Turbulent pressure fluctuations under hydraulic jumps. J. of Hydraulic Research, 130, pp. 499-520, 1992b. DOI: 10.1080/00221689209498897
[29] Lopardo, R., de Lio, J. and Lopardo, M., Physical modelling and design estimation of instantaneous pressures in stilling basins. Proceedings of the XXVIII IAHR Congress. Graz. 132 P., 1999.
[30] Mees, A., Estudo dos esforços hidrodinâmicos em bacias de dissipação por ressalto hidráulico com baixo número de Froude. MSc. Thesis. Universidade Federal do Rio Grande do Sul, Porto Alegre, Brasil. 2008.
[31] Fiorotto, V. and Salandin, P., Design of anchored slabs in spillway stilling basins. ASCE. J. of Hydraulic Engineering. 126(7), pp. 502-512. 2000. DOI: 10.1061/(ASCE)0733-9429(2000)126:7(502)
[32] Blair, H.K. and Rhone, T.J., Design of small dams. Bureau of Reclamation, 3a ed., Washington, DC, cap. 9, Spillways structural design details. 1987, pp. 429-434.
[33] Bureau of Indian Standards., Structural design of energy dissipators for spillways criteria. Doc. WRD 09(489). Preliminary Indian Standard. July 2007. Available at: www.bis.org.in/sf/wrd/WRD09(489).pdf
[34] Bussell, M. and Cather, R., Design and construction of joints in concrete structures, report 146. Construction industry research and information association. London, UK, pp.12-64, 1995.
[35] British Standard 8007., Code of practice for design of concrete structures for retaining aqueous liquids. UDC 624.953, pp. 11-19. 1987.
[36] Chanson, H., The hydraulics of open channel flow. Edward Arnold, London, UK. 1999.
[37] Murzyn, F., and Chanson, H., Free surface, bubbly flow and turbulence measurements in hydraulic jumps. Report CH63/07, Div. of Civil Engineering, University of Queensland, Brisbane, Australia, August, July. 2007. 116 P.
[38] Chanson, H., Turbulent air-water flows in hydraulic structures: dynamic similarity and scale effects. Environ. Fluid. Mechanics 9(2), pp. 125-142, 2009. DOI: 10.1007/s10652-008-9078-3
[39] Lopardo, R., Discussion: Prototype measurements of pressure fluctuations in The Dalles Dam stilling basin. Journal of Hydraulic Research, 48(6), pp. 822-823. 2010. DOI: 10.1080/00221686.2010.536432
[40] Novak P., Nalluri C. and Narayanan R., Hydraulic Structures. Fourth Edition Taylor & Francis. New York pp: 246-265. 2007
[41] JiJian, L. JiMin, W. and JinDe, G., Similarity law of fluctuating pressure spectrum beneath hydraulic jump. Chinese Science Bulletin. 53(14). pp. 2230-2238, 2008. DOI: 10.1007/s11434-008-0300-y
[42] Lightthill, J., Waves in fluids. Cambridge University Press. pp. 89-202, 1979.
[43] Lopardo, R., Algunos aportes de los modelos físicos en la optimización hidráulica de grandes presas Argentinas. V Congreso argentino de presas y aprovechamientos hidroeléctricos. San Miguel de Tucumán (Tucumán). pp. 1 -19, 2008.
M. Gonzalez-Betancourt, is BSc. in Agricultural Engineering jointly from the Universidad Nacional de Colombia (Palmira campus), and Universidad del Valle, Cali, Colombia, in 2008. He received his PhD in Engineering with an emphasis on Hydraulic Resources in 2014 from the Universidad Nacional de Colombia, Medellin, Colombia. Between 2008 and 2010, he worked at the Hydraulic Laboratory at the Universidad del Valle. Since 2009 he has been associated with the Posgrado en Aprovechamiento de Recursos Hidráulicos research group [Postgraduate program on the use of Hydraulic Resources] at the Universidad Nacional de Colombia. From 2014 to date, he has been a researcher in Colombia subject to the terms of the joint agreement between the Organización de Estados Iberoamericanos [Organization of Iberoamerican States], the Servicio Nacional de Aprendizaje [National Apprenticeship Service] and COLCIENCIAS [Administrative Department of Science, Technology and Innovation]. ORCID: 0000-0001-5485-8043
Referencias
Federal Emergency Management Agency., Outlet works energy dissipators best practices for design, construction, problem identification and evaluation, inspection, maintenance, renovation, and repair. Technical manual, USA, FEMA P-679, pp. 1-66, 2010.
Hepler, T.E. and Johnson, P.L., Analysis of spillway failure by uplift pressure. ASCE National Conference, Colorado Springs, Colorado, august 8–12, pp 857-862, 1988.
VSL International. Soil and rock anchors, Examples from practice. Berne, Switzerland. [Online]. pp 19-20, 1992 [Consulted: 15th of august of 2009]. Available at: www.vsl.net/Portals/0/vsl_techreports/PT_Ground_Anchors.pdf
Bowers, C.E. and Tsai, F.Y., Fluctuating pressures in spillway stilling basins. J. Hydraulic Division, ASCE, 95(6), pp. 2071-2079, 1969.
Bribiescas, S. and Capella, V., Turbulence effects on the linning of stilling basins. Proceedings ICOLD. Congrés des Grands Barrages. Madrid. Q.41. R.83. pp. 1575-1592, 1973.
Bribiescas, S. and Fuentes, O., Tanques amortiguadores. Technical Report, Project 7045. UNAM, México D. F. pp. 1-50, 1978.
Hajdin, G., Contribution to the evaluation of fluctuation pressure on fluid currents limit areas- based on the pressures recorded at several points of the area. VIII Conference of Yugoslav Hydraulics Association, Portoroz. 1982.
Toso, J. and Bowers, C., Extreme pressures in hydraulic-jump stilling basins, J. of Hydraulic Engineering, 114(8), pp. 829-843, 1988. DOI: 10.1061/(ASCE)0733-9429(1988)114:8(829)
Farhoudi, J. and Narayanan, R., Force on slab beneath hydraulic jump. J. of Hydraulic Engineering, 117(1), pp. 64-82, 1991. DOI: 10.1061/(ASCE)0733-9429(1991)117:1(64)
Bellin, A. and Fiorotto, V., Direct dynamic force measurements on slab in spillway stilling basin. J. of Hydraulic Engineering. 121(10), pp. 686-693, 1995. DOI: 10.1061/(ASCE)0733-9429(1995)121:10(686)
Khatsuria R.M., Hydraulics of spillways and energy dissipators. New York: Marcel Dekker, 2005. pp 411-424.
Pinheiro, A., Quintela, A. and Ramos, C., Hydrodynamic forces in hydraulic jump stilling Basins. Proceedings of the symposium on fundamentals and advancements in hydraulic measurements and experimentation. ASCE. New York. USA. pp. 321-330, 1994.
Bollaert, E.F.R., Dynamic uplift of concrete linings: Theory and case studies, USSD Annual Meeting, April 24-26 2009, Nashville, United States. pp. 1-16, 2009.
Bollaert, E.F.R. and Schleiss, A.J., Transient water pressures in joints and formation of rock scour due to high-velocity jet impact. Communication 13, Laboratoire de Constructions Hydrauliques, Ecole Polytechnique Fédérale de Lausanne. 2002.
del Risco, E., Hurtado, E. y González, M., Estudio experimental de las presiones de levantamiento bajo una losa con juntas transversales al flujo. Tecnología y Ciencias del Agua. I(1), pp. 31-42, 2010.
Hurtado, E., del Risco, E. y González, M., Presiones medidas en la base de una losa de fondo con juntas paralelas al flujo en un canal. Revista de la Facultad de Ingeniería de la Universidad de Antioquia, 47, pp. 39-52, 2009.
Melo, J., Pinheiro, A. y Ramos, C., Forces on plunge pool slabs: Influence of joints location and width. J. of Hydraulic Engineering, 132(1), pp. 49-60. 2006. DOI: 10.1061/(ASCE)0733-9429(2006)132:1(49)
González, M., Levantamiento de una losa de piso sometida a un flujo turbulento. PhD Tesis, Facultad de Minas, Universidad Nacional de Colombia, Medellín, Colombia. 2013.
Frizell, W.K., Uplift and crack flow resulting from high velocity discharges over. Report DSO-07-07 U.S. Department of the interior, Bureau of Reclamation. Denver, Colorado, 2007, pp. 2-5.
del Risco, E., Investigación experimental de la falla de losas de revestimiento de tanques amortiguadores. MSc. Tesis, Facultad de Ingeniería. UNAM, México, 1983.
González, M. y Giraldo, S., Caracterización dinámica de sensores de presión utilizando el principio de la botella de mariotte. Rev. Fac. Ing. Univ. Antioquia, 71, pp. 146-156, 2014.
Proakis, J.G. and Manolakis D.G., Tratamiento Digital de Señales. Prentice Hall. España, 2000.
The International Society of Automation (ISA 37.16.01). A guide for the dynamic calibration of pressure transducers. pp. 13-38, 2002.
Vasiliev, O.F. and Bukreyev, V.I., Statistical characteristics of pressure fluctuations in the region of hydraulic jump. Proceedings 12th IAHR Congress, Fort Collins, USA, pp. 1-8, 1967.
Pinheiro, A., Accoes hidrodinámicas em bacias de dissipacao de energia por ressalto. PhD. dissertation, Universidad Técnica de Lisboa, Lisboa, Portugal, 353 P., 1995.
Khader, M. and Elango, K., Turbulent pressure field beneath a hydraulic jump. J. of Hydraulic Research, 12(4), pp. 469-489, 1974. DOI: 10.1080/00221687409499725
Fiorotto, V. and Rinaldo, A., Fluctuating uplift and linnings design in spillway stilling basins. J. Hydraulic Enginnering ASCE. 118(4), pp. 578-596. 1992a. DOI: 10.1061/(ASCE)0733-9429(1992)118:4(578)
Fiorotto, V. and Rinaldo, A., Turbulent pressure fluctuations under hydraulic jumps. J. of Hydraulic Research, 130, pp. 499-520, 1992b. DOI: 10.1080/00221689209498897
Lopardo, R., de Lio, J. and Lopardo, M., Physical modelling and design estimation of instantaneous pressures in stilling basins. Proceedings of the XXVIII IAHR Congress. Graz. 132 P., 1999.
Mees, A., Estudo dos esforços hidrodinâmicos em bacias de dissipação por ressalto hidráulico com baixo número de Froude. MSc. Thesis. Universidade Federal do Rio Grande do Sul, Porto Alegre, Brasil. 2008.
Fiorotto, V. and Salandin, P., Design of anchored slabs in spillway stilling basins. ASCE. J. of Hydraulic Engineering. 126(7), pp. 502-512. 2000. DOI: 10.1061/(ASCE)0733-9429(2000)126:7(502)
Blair, H.K. and Rhone, T.J., Design of small dams. Bureau of Reclamation, 3a ed., Washington, DC, cap. 9, Spillways structural design details. 1987, pp. 429-434.
Bureau of Indian Standards., Structural design of energy dissipators for spillways criteria. Doc. WRD 09(489). Preliminary Indian Standard. July 2007. Available at: www.bis.org.in/sf/wrd/WRD09(489).pdf
Bussell, M. and Cather, R., Design and construction of joints in concrete structures, report 146. Construction industry research and information association. London, UK, pp.12-64, 1995.
British Standard 8007., Code of practice for design of concrete structures for retaining aqueous liquids. UDC 624.953, pp. 11-19. 1987.
Chanson, H., The hydraulics of open channel flow. Edward Arnold, London, UK. 1999.
Murzyn, F., and Chanson, H., Free surface, bubbly flow and turbulence measurements in hydraulic jumps. Report CH63/07, Div. of Civil Engineering, University of Queensland, Brisbane, Australia, August, July. 2007. 116 P.
Chanson, H., Turbulent air-water flows in hydraulic structures: dynamic similarity and scale effects. Environ. Fluid. Mechanics 9(2), pp. 125-142, 2009. DOI: 10.1007/s10652-008-9078-3
Lopardo, R., Discussion: Prototype measurements of pressure fluctuations in The Dalles Dam stilling basin. Journal of Hydraulic Research, 48(6), pp. 822-823. 2010. DOI: 10.1080/00221686.2010.536432
Novak P., Nalluri C. and Narayanan R., Hydraulic Structures. Fourth Edition Taylor & Francis. New York pp: 246-265. 2007
JiJian, L. JiMin, W. and JinDe, G., Similarity law of fluctuating pressure spectrum beneath hydraulic jump. Chinese Science Bulletin. 53(14). pp. 2230-2238, 2008. DOI: 10.1007/s11434-008-0300-y
Lightthill, J., Waves in fluids. Cambridge University Press. pp. 89-202, 1979.
Lopardo, R., Algunos aportes de los modelos físicos en la optimización hidráulica de grandes presas Argentinas. V Congreso argentino de presas y aprovechamientos hidroeléctricos. San Miguel de Tucumán (Tucumán). pp. 1 -19, 2008.
Cómo citar
IEEE
ACM
ACS
APA
ABNT
Chicago
Harvard
MLA
Turabian
Vancouver
Descargar cita
CrossRef Cited-by
1. Rafael André Wiest, Renato Steinke Júnior, Eder Daniel Teixeira, Maurício Dai Prá, Aloysio Portugal Maia Saliba, Marcelo Giulian Marques. (2020). Start position of a sloping hydraulic jump. RBRH, 25 https://doi.org/10.1590/2318-0331.252020190090.
Dimensions
PlumX
Visitas a la página del resumen del artículo
Descargas
Licencia
Derechos de autor 2016 DYNA

Esta obra está bajo una licencia internacional Creative Commons Atribución-NoComercial-SinDerivadas 4.0.
El autor o autores de un artículo aceptado para publicación en cualquiera de las revistas editadas por la facultad de Minas cederán la totalidad de los derechos patrimoniales a la Universidad Nacional de Colombia de manera gratuita, dentro de los cuáles se incluyen: el derecho a editar, publicar, reproducir y distribuir tanto en medios impresos como digitales, además de incluir en artículo en índices internacionales y/o bases de datos, de igual manera, se faculta a la editorial para utilizar las imágenes, tablas y/o cualquier material gráfico presentado en el artículo para el diseño de carátulas o posters de la misma revista.