High performance control of a three-phase PWM rectifier using odd harmonic high order repetitive control
Control de alto desempeño de un rectificador PWM trifásico usando control repetitivo de alto orden
DOI:
https://doi.org/10.15446/dyna.v83n198.53276Palabras clave:
current control, Odd Harmonic High Order Repetitive Controller, Three- Phase PWM rectifier (en)Control de Corriente, Controlador Repetitivo de Alto Orden Impar, Rectificador PWM Trifásico (es)
Descargas
DOI: https://doi.org/10.15446/dyna.v83n198.53276
High performance control of a three-phase PWM rectifier using odd harmonic high order repetitive control
Control de alto desempeño de un rectificador PWM trifásico usando control repetitivo de alto orden
Germán Ramos a, Iván Dario Melo-Lagos b & Jenny Cifuentes c
a Departamento de Ingeniería Eléctrica y Electrónica, Universidad
Nacional de Colombia, Bogotá, Colombia. garamosf@unal.edu.co
b Departamento de Ingeniería Eléctrica y Electrónica, Universidad
Nacional de Colombia, Bogotá, Colombia. idmelol@unal.edu.co
c Programa de Ingeniería Eléctrica, Universidad de La Salle, Bogotá,
Colombia. jacifuentesq@unal.edu.co
Received: September 30th, 2015. Received in revised form: April 8th, 2016. Accepted: April 24th, 2016.
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.

Abstract
The control goal for three-phase pulse
width-modulated rectifiers focuses on generating sinusoidal input currents and
regulating the DC output voltage. Despite the fact that control strategies such
as resonant and repetitive control have been proposed in recent works, with
many notable results on the area, they have significant performance decay when
the frequency changes in the exogenous signal. In this paper, it is shown that
the use of an Odd Harmonic High Order Repetitive Controller can be used to
control the three-phase rectifier current loops with a performance that is
considerably superior to traditional alternatives developed in this field. This
compensator's Odd Harmonic property keeps a computational complexity similar to
that of the conventional repetitive controllers but it has the advantage of
increasing the robustness when the signal frequency varies. Simulation and
experimental results show the high performance that was obtained even in the
case of deviation of network frequency from its nominal value.
Keywords: current control; Odd Harmonic High Order Repetitive Controller; Three- Phase PWM rectifier.
Resumen
El objetivo de
control en rectificadores de potencia trifásicos se basa en generar corrientes
de entrada sinusoidales y regular el voltaje de salida DC. Aunque el Control
Repetitivo y Resonante son enfoques de control que han presentado excelentes
resultados, su principal desventaja se basa en la pérdida considerable de
desempeño cuando la frecuencia de la red se desvía de su valor nominal. En este
artículo, se presenta el uso de un Controlador Repetitivo Impar de Alto Orden
para controlar los lazos de corrientes de un rectificador trifásico con un
desempeño considerablemente superior a otras alternativas tradicionalmente
implementadas en este campo. Este controlador permite el rechazo de los
armónicos impares introducidos en el sistema, lo que mantiene una complejidad
computacional similar a la obtenida con los controladores repetitivos
convencionales con la ventaja de incrementar la robustez cuando la frecuencia
de la señal varíe. Las simulaciones y los resultados experimentales muestran un
alto desempeño aún cuando se presenten desviaciones de la frecuencia de la red
respecto a su valor nominal.
Palabras clave: Control de Corriente; Controlador Repetitivo de Alto Orden Impar; Rectificador PWM Trifásico.
1. Introduction
More recently, reactive power and harmonic currents generated by power converters have become a crucial issue in many electric power systems [1]. In this case, diode bridge and phase controlled bridge rectifiers have been considered as one of the most important causes of electrical pollution [2]. Although these solutions have been widely implemented in industrial applications because of their economic advantages, they begin to look unsustainable due to the impositions of stricter harmonic standards.
Pulse width modulation rectifiers (PWM) have arisen as a solution to overcome these problems, reducing harmonic pollution [3,4] and adapting in accordance to the highest requirements for energy quality [5,6]. Using these devices, it is possible to control the output voltage and to obtain sinusoidal ac currents. In order to assess the performance of a three-phase PWM rectifier, two parameters are taken into account: the Total Harmonic Distortion (THD), which is a measurement of the harmonic content of the current signal; and the Power Factor (PF), which accounts for phase differences between the current and the voltage. With this thread in mind, PWM rectifiers seek a unity PF and a small THD.
Several strategies have been proposed to control three-phase PWM rectifiers. In the reported research, multiple Proportional Integral controllers [7] have been implemented in the current loops, mainly due to the ease of implementing them as well as their satisfactory performance. However, the main limitation of this approach lies in an inherent tracking (amplitude and phase) error [8].
Over the last few years, interesting emerging control techniques such as resonant control [9,10] and repetitive control (RC) [11-13] have been developed to track/reject periodic signals. Good response characteristics are achieved by using these strategies, ensuring near unit power factor and constant output dc voltage under parameter uncertainties, as well as load disturbances. The main disadvantage is related to the lost of performance caused by variations of the network frequency from its nominal value [14].
In this paper, an odd harmonic HORC Controller is proposed for the current loops of a three-phase PWM rectifier. Hence, taking advantage of its inherent properties, only the odd harmonics are removed. By using this strategy, two aims are achieved: 1) Computational complexity is substantially reduced by the odd property of this compensator, which is very similar to that obtained with the conventional repetitive controllers, and 2) Robustness is increased when the signal frequency varies. Experimental results show a high performance at nominal frequency, even when harmonics are present in the voltage source waveforms and have the additional characteristic of preserving low THD and unitary PF, despite network frequency variations.
The paper is organized as follows: section 2 describes the three-phase PWM rectifier model, introduces the control objectives, and presents the controller structure. In Section 3, the structure of an Odd HORC Controller for the current loops is explained in detail; the control implemented for the voltage loop is described in Section 4. Section 5 reports experimental results and demonstrates a comparison to a classical HORC Controller. Finally, in Section 6 we present conclusions and future directions.
2. System description
2.1. Three-phase PWM rectifier
PWM techniques have been widely implemented to control the outputof power converters as they allow shaping voltage and/or current waves based on specific applications [15].
The three-phase PWM rectifier circuit, as shown in Fig. 1, has three-legs with IGBT transistors. It is known as a bi-directional boost rectifier (increasing the voltage) and works using fixed DC voltage polarity. Input inductors are an integral part of the rectifier and are selected based on their design [16]. We achieve harmonic compensation through the input inductors, and we ensure smooth voltage waveforms by using capacitors.
The dynamics of the three-phase PWM rectifier (as shown in Fig. 1) can be described as:

where Ln,, C and Ro are the nominal values of inductances, the capacitor and the load resistance, respectively; iL1, iL2 and iL3 are the phase currents and Vc is the capacitor voltage; Vin1, Vin2 and Vin3 are the known three-phase sinusoidal voltages; Vin1+Vin2+Vin3=0; RLn is the parasitic inductor resistance for each phase; + ; and is the control action used to trigger the IGBTs. Their values range within the interval
2.2. Control system structure
Control objectives for three-phase PWM rectifier systems are quite similar to the objectives for the single-phase case. They are focused on achieving unit power factor, constant output dc voltage and a suitable low harmonics sinusoidal waveform for the input current. The difference is to be found in the fact that the control aim for the current loop should be achieved for every phase, taking into account the shifts associated with a three-phase current flow.
Fig. 2 depicts the general control system structure. It consists of a double-loop structure: two inner current loops that ensure a sinusoidal waveform in the current input, and an outer dc voltage loop designed to regulate the output voltage and proportionate the active power balance in the system. The voltage loop gives the amplitude, Idn(t), of the reference currents that is to be used in the two inner current loops. The reason behind only using two current loops is that, under the assumption of a balanced system (Vin1+Vin2+Vin3=0), the compensation action applied in two phases will generate the action to be applied for the third phase. Thus, control action will be generated form and using , as shown in Fig. 2.
A PLL (Phase Locked Loop) system takes the phase voltages and produces sine waves with appropriate phases. These signals, together with the amplitude Idn(t), create the two current references for the current loops.
In this way, the control system should track sinusoidal signals with suitable magnitudes and phases and reject the system disturbances. Among these disturbances, two are recurrent in these kinds of systems: low-frequency signals and harmonics generated by distortions in the network voltage. Due to the fact that symmetrical waveforms only contain odd harmonics, distortions in the voltage waveform are regularly found between the 3th and 9th harmonic [17].
In addition, in order to keep a constant output dc voltage, the system should react to changes in the network voltage and in the rectifier load. Finally, it is worth drawing the reader's attention to the fact that the voltage control loop uses the average of the measured dc voltage to avoid introducing its ripple into the loops.
In this work, an Odd Harmonic High Order Repetitive Controller is adopted for the current loops in order to compensate the odd harmonics that are introduced to the system by the network voltage and increase system robustness to changes in the network frequency. A PI controller is integrated into the voltage loop for the purpose of achieving an active power balance and keeping the average value of the output voltage constant.
3. Current control loops
This section describes the Odd Harmonic High Order Repetitive Controller that is proposed for the current loops. Identical current control loops are designed for two of the system phases and can be seen in Fig. 2.
Primarily, the structure of conventional repetitive control scheme is explained in order to introduce the high-order controller design.
3.1. The odd harmonic high order repetitive controller
Repetitive control (RC) has proven to be a useful control strategy to track/reject periodic signals [18,19]. Using this control strategy, the sinusoidal signal references in the current loops are tracked and the harmonics generated by the network voltage are rejected. In order to accomplish this, the RC scheme incorporates a generator of periodic signals (also known as internal model) in the control structure [20]:

where W(z)is a time delay function, H(z) is a low-pass filter which provides robustness at high frequencies, and takes the values 1 or -1 and determines if the control is applied to all harmonic components; or only for odd harmonics. The way in which the internal model (eq. 5) is added to the control structure will be described in the next section.
The standard internal model, used in
repetitive control [21], can be determined by using 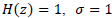 ,
,  , or
with N=Tp/Ts, where Tp is the period of the signal being tracked/rejected and Tsis the sampling period of the control system. This
model provides infinite gain at fundamental
frequency and all its harmonics until the (N/2-1)-th. Having high gains
at selected frequencies guarantees the tracking/rejecting capability in
closed-loops for signals with this frequency content.
, or
with N=Tp/Ts, where Tp is the period of the signal being tracked/rejected and Tsis the sampling period of the control system. This
model provides infinite gain at fundamental
frequency and all its harmonics until the (N/2-1)-th. Having high gains
at selected frequencies guarantees the tracking/rejecting capability in
closed-loops for signals with this frequency content.
However, an internal model which only
generates infinite gain at odd-harmonic components [22] can be obtained using 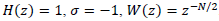 .
.
The magnitude frequency responses of the standard and odd internal models are shown in Fig. 3. The sampling period is selected to be Ts=15 kHz, which yields N=250, and the fundamental frequency is set to 60 Hz. As can be appreciated from the figure, these models generate infinite gain at fundamental and harmonic frequencies. This establishes a very limited frequency band that is centered around each harmonic component. This feature currently represents the main disadvantage of standard and odd internal models. As a result, the standard repetitive control exhibits a considerable loss of performance when the exogenous signal frequency varies from its nominal value, even with very small deviations [14].
In this regard, by modifying the time delay function W(z), an internal model can provide high gain over a broader frequency interval around the fundamental and harmonic modes. This increases the robustness against changes in network frequency. Accordingly, , , and the time delay function is given by [5]:

where M denotes the Harmonic High Order Repetitive Controller (HORC). By using this definition, the internal model (eq. 5) is given by:

Fig. 4 compares the magnitude response of the internal models used in odd-harmonic RC and odd-harmonic HORC for second (M=2) and third (M=3) order case; these have a nominal frequency of 60 Hz and a sampling period of 15 KHz. Fig. 4 also highlights the gain of the internal models designed for nominal frequency deviations of 59.5 and 60.5 Hz and their corresponding harmonics. It can be seen that the gain is higher for the odd-harmonic HORC (M=2 and M=3) compared with the odd-harmonic RC (M=1) for the same frequency variation. This improves the robustness against frequency changes and the performance under non-ideal operating conditions. However, internal models with high orders can decrease the robustness due to the elevated gains in the highest harmonics. Although this problem can be overcome by using a lower cut-off frequency in the low-pass filter H(z), this could cause performance decay because of the action reduction in the superior harmonics. For this reason, a tradeoff between the internal model order M and the filter bandwidth H(z) is required in order to achieve performance and stability robustness [18,19].
Based on the facts that frequency variations in the Colombian electric system are quite small (59.8-60.2) [23] and that it is desirable to keep the distortion as low as possible in the input current of the rectifier, the Odd Harmonic High Order internal model with M=2 (2ORC) has been experimentally validated as the controller with the best performance.
The odd internal model with the low-pass filter H(z) and M=2 becomes:
Furthermore, it is important to note that the odd internal model (eq. 8) and the standard repetitive controller are mostly of the same order, which results in a similar computational complexity during their implementations. This implies that standard internal models and second order odd harmonic internal models with same N parameter would perform almost the same number of multiplications and additions, and also use the same amount of memory during an experimental implementation.
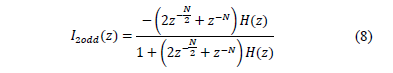
3.2. Repetitive controller structure
Each current control block shown in Fig. 2 has a corresponding repetitive controller, which is as the one shown in Fig. 5. In order to include one of the internal models that were defined in the previous section, i.e. I(z), Iodd(z), or I2odd(z) (equations (5), (7) and (8), respectively), repetitive control is usually implemented using the plug-in configuration presented in Fig. 5. As can be seen, the internal model (I(z), Iodd(z) or I2odd(z)) is added, as part of the existing controller Gc(z), and the filter Gx(z) is also incorporated. The compensator Gc(z) is used to stabilize the plant Gp(z) and to provide disturbance attenuation across the rectifier bandwidth. Additionally, compensator Gc(z) should offer good robustness margins, and filter Gx(z) is designed to ensure system stability in closed loop.
The transfer function of the plant is obtained from (eq. (1)-(3)), which performs the variable change and causes each phase to result in the following:

From the discretization of (9) the following can be obtained:

Control action in each phase results in:

with 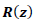 being the z-transform of
being the z-transform of 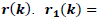
 .
and
.
and 
 which are the reference signals for
phase 1 and phase 2, respectively. Finally, dutty cycle
is calculated as
and sent to eah PWM generator, as seen in Fig.
2.
which are the reference signals for
phase 1 and phase 2, respectively. Finally, dutty cycle
is calculated as
and sent to eah PWM generator, as seen in Fig.
2.
3.3. Stability
The closed-loop system of Fig. 5 is stable if the following conditions are fulfilled [24]:
The closed-loop system without the repetitive controller is stable, which means the transfer function To(z) should be stable:

1.  , where H(z)
and Gx(z) should be chosen adequately.
, where H(z)
and Gx(z) should be chosen adequately.
Whole system dynamics, shown in Fig. 2, are divided into two parts: fast dynamics given by the current loop, and slow dynamics represented by the voltage loop. Therefore, to ensure the convergence of the whole system, two considerations are assumed: 1) the voltage loop provides very slow changes in the current reference, and 2) the current loop responds so fast that its dynamic behavior does not affect the evolution of the voltage loop. In order to obtain this behavior, the bandwidth of each loop should be properly selected in order to achieve a sufficient separation to differentiate between both dynamics. See reference [25] for a more detailed analysis on this topic.
3.4. Design of filter H(z)
Filter H(z) is used to limit the repetitive controller bandwidth, and, as such, it impacts performance, limiting the number of harmonics that will be taken into consideration. In general, the choice of filter bandwidth implies a trade-off between stability robustness and performance. Although numerous optimization techniques to define a conventional filter H(z) have been proposed, H(z) is chosen to be a null phase low-pass FIR filter [26].
3.5. Design of filter Gx(z)
In the event of a minimum phase systems, Gx(z) is usually selected as , while for non minimum phase systems, it is possible to use the approach proposed in [21]. Finally, the value of the gain kr requires a trade-off between stability robustness and steady state performance [27].
4. Voltage control loop
Voltage loop control is designed to achieve an active power balance in the rectifier and to provide the magnitude of the current reference for the current loops. Given that voltage at the rectifier output terminal has a waveform that is highly rippled, a low pass filter is usually applied to obtain a smoother signal. The purpose of this is to avoid the ripple propagation to the current reference id(t), which would negatively impact the harmonic distortion of the rectifier input current iL(t). In this work, the low pass filter has been replaced by an averaging filter that has been tuned at 60 Hz:

By using this filter, the average voltage
is calculated from the output voltage  .
.
Voltage loop structure is shown in Fig. 6. This structure is comprised of two basic components: a feedback control action, idfb, generated by a PI compensator, and a pre-feeding action idff. The PI controller in the feedback loop will regulate the average value of the output voltage to the desired value with zero error:
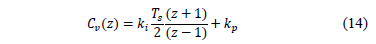
Moreover, the pre-feeding signal, idff, is designed in order to avoid sudden changes in voltage levels causing transients with high current peaks. This pre-feeding stage is calculated based on the rectifier power balance in steady state. As such, the balance between the AC active power and the DC power is given by:

where  is the peak value of the network voltage,
is the peak value of the network voltage,  is the peak value of the rectifier
input current,
is the peak value of the rectifier
input current,  is the average value of the capacitor voltage,
is the average value of the capacitor voltage, 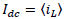 is the average value of the load current,
and
are the rectifier losses. On that basis, the
pre-feeding value can be computed by:
is the average value of the load current,
and
are the rectifier losses. On that basis, the
pre-feeding value can be computed by:

where  is a factor that weighs the
rectifier losses. As a result, the reference signal amplitude for the current
loop is calculated by:
is a factor that weighs the
rectifier losses. As a result, the reference signal amplitude for the current
loop is calculated by:

5. Experimental results
In this section the experimental results are presented and analyzed. Two different setups are defined for nominal and varying frequency conditions. A comparison of HORC and RC is provided in order to show the advantages of implementing the odd harmonic HORC.
5.1. Experimental setup
The utility network frequency is 60 Hz, thus defining a period of Tp=1/60 s. The sampling period is set to Ts=1/15000 s, which corresponds with the PMW switching frequency. As a result, the discrete period is N=Tp/Ts=250.
The
transfer function of the plant is obtained from (eq. 10) with L=300 mH and RL=0.1 ohms. The internal controller is Gc(z)=(6,293z-6,283)/(z-0.998), which
provides enough robustness margins. Filter H(z), which has a good robustness-performance tradeoff, is comprised of 


 .
Concurrently
.
Concurrently  with kr=0.7.
A PI controller for the voltage loop defined in (9) takes the values kp=0,01 and ki=0,7.
with kr=0.7.
A PI controller for the voltage loop defined in (9) takes the values kp=0,01 and ki=0,7.
For comparison purposes, a conventional
RC with internal model, as in (5), has been designed with  ,
,  ,
and
with kr=0,3.
,
and
with kr=0,3.
Results at nominal frequency are obtained with the rectifier connected to the grid, and results at different frequencies are acquired using an AC varying frequency voltage source from PowerSun. In both cases, a three phase autotransformer is used to provide Vin=20 Vrms to the rectifier. The three-phase rectifier is a power converter from Semikron, and control algorithms were implemented in an Intel PC with Matlab XPCTarget real time software. Bus dc voltage is Vc=80 V with a resistive load of 25 ohms.
5.2. Nominal frequency performance
Fig. 7 shows the response of the non-controlled rectifier. It can be seen that non-sinusoidal currents with a THD=34.4% are obtained. It is important to note that Fig. 7 also shows the distortion in the voltage network with 5th and 7th harmonics with a THD of 4.3 %. This distortion acts as a disturbance in the current loops.
Fig. 8 presents the results with the proposed odd harmonic HORC. It can be seen that currents now have a sinusoidal shape in the phase with the voltage source. The THD obtained is 2.2 %. Power factor is presented in Fig. 8 in which it can be seen that PF=1 was obtained.
These results show that odd harmonic HORC satisfies the control objectives, achieving a low THD and unitary power factor, even in the case of distortion in the voltage source. Based on its definition, conventional RC should also achieve the same performance. However, since HORC provides smaller robustness margins, the cut-off frequency of filter H(z) is usually smaller than the one selected for RC. This entails a slight performance reduction that appears as a small THD degradation. Fig. 9 shows the THD obtained with RC under the same conditions.
5.3. Varying frequency performance
These experiments use an AC voltage source that comes from PowerSun and has a configurable frequency. Fig. 10 depicts the current waveforms when the source frequency is 62 Hz and uses conventional RC. The distortion of the obtained currents can be seen with a THD=5 % with 5th and 7th harmonics. Also, the degradation of the power factor is now present with PF=0.98.
Using odd harmonic HORC yields, a significantly better performance can be seen in Fig. 11. The obtained THD and PF are 3.8 % and 1, respectively.
Similar behavior is expected at lower frequencies. Fig. 12 and Fig. 13 present the THD and phasor diagram results for 59 Hz for RC and HORC, respectively. It can be seen that HORC performs better with a lower THD and a smaller current phase deviation.
6. Conclusion
This work has proposed an odd harmonic HORC has for the current control loops in a three phase-PMW power rectifier. Experimental validation has shown that the proposed controller achieves high performance with THD=1.7% and a unitary PF. Compared to conventional RC, the HORC has the advantage of providing higher robustness against network frequency variations. This characteristic allows the rectifier to accomplish the more demanding standards of power quality, even under varying frequency conditions.
Despite being a high order controller, it was found that odd harmonic HORC has a similar computational burden when it was compared to a full- harmonic RC.
References
[1] Peña-Huaringa, O.J., Studying and simulating transformer configuration to improve power quality. Ingeniería e Investigación, 31, pp.125-130, 2011.
[2] Acha, E. and Madrigal, M., Eds., Power system harmonics, computer modeling and analysis, New York: Wiley, 2001.
[3] Etz, R., Patarau, T. and Petreus, D., Comparison between digital averafe current mode control and digital one cycle control for a bridgeless PFC boost converter, Design and Tehnology in Electronic Packaging (SIITME), IEEE 18th International Symposium for Design and Technology in Electronic Packaging (SIITME), pp. 211-215, 2012. DOI: 10.1109/SIITME.2012.6384378
[4] IEC 1000-3-2. Electromagnetic Compability. Part 3: Limits - Sect. 2: Limits for harmonic current emission (Equipment Input Current 16A per Phase), 1995.
[5] Rodriguez, J.R., Dixon, J.W., Espinoza, J.R., Pontt, J. and Lezana, P., PWM regenerative rectifiers: State of the art. Industrial Electronics, IEEE Transactions on, 52(1), pp. 5-22, 2005. DOI: 10.1109/TIE.2004.841149
[6] IEEE Recommended practices and requeriments for harmonic control in electrical power systems IEEE Std 519-1992, pp.1-112, 1993.
[7] Kazmierkowski, M.P. and Malesani, L., Current control techniques for three-phase voltage-source PWM converters: A survey. Industrial electronics, IEEE Transactions on, 45(5), pp. 691-703, 1998. DOI: 10.1109/41.720325
[8] Yuan, X., Merk, W., Stemmler, H. and Allmeling, J., Stationary-frame generalized integrators for current control of active power filters with zero steady-state error for current harmonics of concern under unbalanced and distorted operating conditions. Industry Applications, IEEE Transactions on, 38(2), pp. 523-532, 2002. DOI: 10.1109/28.993175
[9] Liu, F., Maswood, A., Kang, Y., Zhang, Y. and Duan, S., Proportional-resonant current control for three-phase three-level rectifier. In Power Engineering Conference, IPEC 2007. International, pp. 1018-1022, 2007.
[10] Cheng, Q.M., Cheng, Y.M., Xue, Y., Hu, X.Q. and Wang, Y.F., A summary of current control methods for three-phase voltage-source PWM rectifiers. Power System Protection and Control, 40(3), pp. 145-155, 2012.
[11] Longman, R.W., Iterative learning control and repetitive control for engineering practice. International Journal of Control, 73(10), pp. 930-954, 2000. DOI: 10.1080/002071700405905
[12] Zhou, K. and Wang, D., Digital repetitive controlled three-phase PWM rectifier. Power Electronics, IEEE Transactions on, 18(1), pp. 309-316, 2003. DOI: 10.1109/TPEL.2002.807150
[13] Ramos-Fuentes, G.A., Olm J.M. and Costa-Castelló, R., A survey of repetitive control in varying frequency conditions, Ingeniería e Investigación, 31(2), pp.29-37, 2011.
[14] Steinbuch, M., Repetitive control for systems with uncertain period- time, Automatica, 38, pp. 2103-2109, 2002. DOI: 10.1016/S0005-1098(02)00134-6
[15] Rahim, N.A., Green, T.C. and Williams, B.W., PWM ASIC Design for the three phase bidirectional buck converter, INT. J. Electronics, 1996. DOI: 10.1080/002072196136517
[16] Malinowski, M. and Kazmierkowski, M.P., CHAPTER 11 - Control of Three-Phase PWM Rectifiers, In Academic Press Series in Engineering, edited by Kazmierkowskir, M.P. and Blaabjerd, K., Academic Press, Burlington, Control in Power Electronics, pp. 419-459, 2002, ISBN 9780124027725, DOI: 10.1016/B978-012402772-5/50012-0.
[17] Siemens Industry, Inc. Harmonics in power systems. Causes, effects and control, USA, 2013.
[18] Ramos, G.A. and Costa-Castelló R. and Olm J.M., Digital repetitive control under varying frequency conditions. Lecture Notes in Control and Information Sciences. Springer-Verlag, Berlin, Germany. 446, 2013, 159 P. DOI: 10.1007/978-3-642-37778-5
[19] Pipeleers, G., Demeulenaere, B. and Sewers, S., Robust high order repetitive control: Optimal performance trade offs, Automatica, 44, pp. 2628-2634, 2008. DOI: 10.1016/j.automatica.2008.02.028
[20] Inoue, T., Practical repetitive control system design. Proc. 29th IEEE Conf. on Decision and Control, pp. 1673-1678, 1990.
[21] Tomizuka, M., Tsao, T.C. and Chew, K.K., Analysis and synthesis of discrete-time repetitive controllers, Meas. Control J. Dyn. Syst., 111, pp. 353-358, 1989. DOI: 10.1115/1.3153060
[22] Ramos, G.A., Costa-Castelló, R. and Olm, J.M., Analysis and design of a robust odd-harmonic repetitive controller for an active filter under variable network frequency, Control Engineering Practice, 20(9), pp. 895-903, 2012. DOI: 10.1016/j.conengprac.2012.05.009
[23] Colombia. Instituto Colombiano de Normas Técnicas y Certificación (ICONTEC). Norma Técnica Colombiana NTC 5001. Calidad de la Potencia Eléctrica. Límites y metodología de evaluación en puente de conexión común, 2008b.
[24] Griñó, R. and Costa-Castelló, R., Digital repetitive plug-in controller for odd-harmonic periodic references and disturbances, Automatica, 41(1), pp. 153-157, 2005. DOI: 10.1016/j.automatica.2004.08.006
[25] Costa-Castelló, R., Griñó, R., Parpal, R.C. and Fossas, E., High-performance control of a single-phase shunt active filter. Control Systems Technology, IEEE Transactions on, 17(6), 1318-1329, 2009. DOI: 10.1109/TCST.2008.2007494
[26] Tsao, T.C. and Tomizuka, M., Robust adaptive and repetitive digital tracking control and application to a hydraulic servo for noncircular machining, Journal of Dynamic Systems, Measurement, and Control, 116(1), pp. 24-32, 1994. DOI: 10.1115/1.2900676
[27] Hillerström, G. and Lee, R.C.H., Trade-offs in repetitive control, University of Cambridge, CUED/F-INFENG/TR 294, 1997.
G.A. Ramos, received his BSc in Electrical Engineering in 1999 and his MSc degree in Industrial Automation in 2006, both from the Universidad Nacional de Colombia, Bogotá, Colombia. He obtained his PhD in Automatics in 2012, from Universitat Politècnica de Catalunya, Barcelona, Spain. He is currently is an Associate Professor in the Electrical and Electronic Department, Facultad de Ingeniería, Universidad Nacional de Colombia. His research interests include: control theory, control applied to power converters, repetitive control and active disturbance rejection control. ORCID: 0000-0003-1393-6943
I.D. Melo Lagos, received his BSc in Telematics Engineering in 2008 from the University Distrital Francisco Jose de Caldas, Bogotá, Colombia, and his BSc in Electrical Engineering in 2010 from the Universidad Nacional de Colombia. In the years 2010-2015 he worked in the area of the design of power electronics equipment, in the CDP and Powersun groups. In 2015 he finished his MSc studies of in industrial automation at the Universidad Nacional de Colombia. His research interests include: control theory applied to power electronics. ORCID: 0000-0002-5818-5808
J.A. Cifuentes, received her BSc in Mechatronics Engineering in 2008, her MSc. degree in Industrial Automation in 2010, both from the Universidad Nacional de Colombia, Bogotá, Colombia. She was awarded a PhD in Industrial Automation from the Institute National des Sciences Apliqueés de Lyon (INSA), France and a PhD in Mechanical and Mechatronics Engineering from the Universidad Nacional de Colombia, Bogotá, Colombia in 2015. She is currently an Associate Professor in the program of Electrical Engineering, Facultad de Ingeniería, Universidad de la Salle. Her research interests include: Modeling and analysis of dynamic systems, Signal Processing, Biomedical Signal Classification, and Gesture Acquisition. ORCID: 0000-0001-7421-291X
Referencias
Peña-Huaringa, O.J., Studying and simulating transformer configuration to improve power quality. Ingeniería e Investigación, 31, pp.125-130, 2011.
Acha, E. and Madrigal, M., Eds., Power system harmonics, computer modeling and analysis, New York: Wiley, 2001.
Etz, R., Patarau, T. and Petreus, D., Comparison between digital averafe current mode control and digital one cycle control for a bridgeless PFC boost converter, Design and Tehnology in Electronic Packaging (SIITME), IEEE 18th International Symposium for Design and Technology in Electronic Packaging (SIITME), pp. 211-215, 2012. DOI: 10.1109/SIITME.2012.6384378
IEC 1000-3-2. Electromagnetic Compability. Part 3: Limits – Sect. 2: Limits for harmonic current emission (Equipment Input Current 16A per Phase), 1995.
Rodriguez, J.R., Dixon, J.W., Espinoza, J.R., Pontt, J. and Lezana, P., PWM regenerative rectifiers: State of the art. Industrial Electronics, IEEE Transactions on, 52(1), pp. 5-22, 2005. DOI: 10.1109/TIE.2004.841149
IEEE Recommended practices and requeriments for harmonic control in electrical power systems IEEE Std 519-1992, pp.1-112, 1993.
Kazmierkowski, M.P. and Malesani, L., Current control techniques for three-phase voltage-source PWM converters: A survey. Industrial electronics, IEEE Transactions on, 45(5), pp. 691-703, 1998. DOI: 10.1109/41.720325
Yuan, X., Merk, W., Stemmler, H. and Allmeling, J., Stationaryframe generalized integrators for current control of active power filters with zero steady-state error for current harmonics of concern under unbalanced and distorted operating conditions. Industry Applications, IEEE Transactions on, 38(2), pp. 523-532, 2002. DOI: 10.1109/28.993175
Liu, F., Maswood, A., Kang, Y., Zhang, Y. and Duan, S., Proportional-resonant current control for three-phase three-level rectifier. In Power Engineering Conference, IPEC 2007. International, pp. 1018-1022, 2007.
Cheng, Q.M., Cheng, Y.M., Xue, Y., Hu, X.Q. and Wang, Y.F., A summary of current control methods for three-phase voltage-source PWM rectifiers. Power System Protection and Control, 40(3), pp. 145-155, 2012.
Longman, R.W., Iterative learning control and repetitive control for engineering practice. International Journal of Control, 73(10), pp. 930-954, 2000. DOI: 10.1080/002071700405905
Zhou, K. and Wang, D., Digital repetitive controlled three-phase PWM rectifier. Power Electronics, IEEE Transactions on, 18(1), pp. 309-316, 2003. DOI: 10.1109/TPEL.2002.807150
Ramos-Fuentes, G.A., Olm J.M. and Costa-Castelló, R., A survey of repetitive control in varying frequency conditions, Ingeniería e Investigación, 31(2), pp.29-37, 2011.
Steinbuch, M., Repetitive control for systems with uncertain periodtime, Automatica, 38, pp. 2103-2109, 2002. DOI: 10.1016/S0005- 1098(02)00134-6
Rahim, N.A., Green, T.C. and Williams, B.W., PWM ASIC Design for the three phase bidirectional buck converter, INT. J. Electronics, 1996. DOI: 10.1080/002072196136517
Malinowski, M. and Kazmierkowski, M.P., CHAPTER 11 - Control of Three-Phase PWM Rectifiers, In Academic Press Series in Engineering, edited by Kazmierkowskir, M.P. and Blaabjerd, K., Academic Press, Burlington, Control in Power Electronics, pp. 419- 459, 2002, ISBN 9780124027725, DOI: 10.1016/B978-012402772- 5/50012-0.
Siemens Industry, Inc. Harmonics in power systems. Causes, effects and control, USA, 2013.
Ramos, G.A. and Costa-Castelló R. and Olm J.M., Digital repetitive control under varying frequency conditions. Lecture Notes in Control and Information Sciences. Springer-Verlag, Berlin, Germany. 446, 2013, 159 P. DOI: 10.1007/978-3-642-37778-5
Pipeleers, G., Demeulenaere, B. and Sewers, S., Robust high order repetitive control: Optimal performance trade offs, Automatica, 44, pp. 2628-2634, 2008. DOI: 10.1016/j.automatica.2008.02.028
Inoue, T., Practical repetitive control system design. Proc. 29th IEEE Conf. on Decision and Control, pp. 1673-1678, 1990.
Tomizuka, M., Tsao, T.C. and Chew, K.K., Analysis and synthesis of discrete-time repetitive controllers, Meas. Control J. Dyn. Syst., 111, pp. 353-358, 1989. DOI: 10.1115/1.3153060
Ramos, G.A., Costa-Castelló, R. and Olm, J.M., Analysis and design of a robust odd-harmonic repetitive controller for an active filter under variable network frequency, Control Engineering Practice, 20(9), pp. 895-903, 2012. DOI: 10.1016/j.conengprac.2012.05.009
Colombia. Instituto Colombiano de Normas Técnicas y Certificación (ICONTEC). Norma Técnica Colombiana NTC 5001. Calidad de la Potencia Eléctrica. Límites y metodología de evaluación en puente de conexión común, 2008b.
Griñó, R. and Costa-Castelló, R., Digital repetitive plug-in controller for odd-harmonic periodic references and disturbances, Automatica, 41(1), pp. 153-157, 2005. DOI: 10.1016/j.automatica.2004.08.006
Costa-Castelló, R., Griñó, R., Parpal, R.C. and Fossas, E., Highperformance control of a single-phase shunt active filter. Control Systems Technology, IEEE Transactions on, 17(6), 1318-1329, 2009. DOI: 10.1109/TCST.2008.2007494
Tsao, T.C. and Tomizuka, M., Robust adaptive and repetitive digital tracking control and application to a hydraulic servo for noncircular machining, Journal of Dynamic Systems, Measurement, and Control, 116(1), pp. 24-32, 1994. DOI: 10.1115/1.2900676
Hillerström, G. and Lee, R.C.H., Trade-offs in repetitive control, University of Cambridge, CUED/F-INFENG/TR 294, 1997.
Cómo citar
IEEE
ACM
ACS
APA
ABNT
Chicago
Harvard
MLA
Turabian
Vancouver
Descargar cita
CrossRef Cited-by
1. Muhammad Saqib Ali, Lei Wang, Hani Alquhayz, Obaid Ur Rehman, Guozhu Chen. (2021). Performance Improvement of Three-Phase Boost Power Factor Correction Rectifier Through Combined Parameters Optimization of Proportional-Integral and Repetitive Controller. IEEE Access, 9, p.58893. https://doi.org/10.1109/ACCESS.2021.3073004.
2. Johan Sebastian Sanchez-Choachi, Miguel Ángel Dávila, Cesar Leonardo Trujillo. (2018). Development of a high performance batteries charger with low THD, high power factor, and high efficiency. DYNA, 85(205), p.76. https://doi.org/10.15446/dyna.v85n205.60657.
3. Luis A. Garcia-Reyes, Aurelio Beltrán-Telles, Francisco Bañuelos-Ruedas, Manuel Reta-Hernández, Juan M. Ramírez-Arredondo, Rodolfo Silva-Casarín. (2022). Level-Shift PWM Control of a Single-Phase Full H-Bridge Inverter for Grid Interconnection, Applied to Ocean Current Power Generation. Energies, 15(5), p.1644. https://doi.org/10.3390/en15051644.
4. Mudarris, F. Danang Wijaya, Eka Firmansyah, Yohan Fajar Sidik, Musyaffa’ Ahmad, Doni Sigit R. (2023). Design of Controller Area Network (CAN) Communication for PWM Rectifier Control Hybrid Train. 2023 International Conference on Smart-Green Technology in Electrical and Information Systems (ICSGTEIS). , p.53. https://doi.org/10.1109/ICSGTEIS60500.2023.10424115.
5. Hoai Phong Nguyen, Thuan Thanh Nguyen, Minh Phuong Le, Minh Tan Tran, Cong Duy Pham. (2025). Design and implementation of three-phases energy storage system using DSP F28379D for laboratory research. HardwareX, 23, p.e00675. https://doi.org/10.1016/j.ohx.2025.e00675.
6. Wenzhou Lu, Wei Wang, Keliang Zhou, Qigao Fan. (2022). General High-Order Selective Harmonic Repetitive Control for PWM Converters. IEEE Journal of Emerging and Selected Topics in Power Electronics, 10(1), p.1178. https://doi.org/10.1109/JESTPE.2021.3101857.
Dimensions
PlumX
Visitas a la página del resumen del artículo
Descargas
Licencia
Derechos de autor 2016 DYNA

Esta obra está bajo una licencia internacional Creative Commons Atribución-NoComercial-SinDerivadas 4.0.
El autor o autores de un artículo aceptado para publicación en cualquiera de las revistas editadas por la facultad de Minas cederán la totalidad de los derechos patrimoniales a la Universidad Nacional de Colombia de manera gratuita, dentro de los cuáles se incluyen: el derecho a editar, publicar, reproducir y distribuir tanto en medios impresos como digitales, además de incluir en artículo en índices internacionales y/o bases de datos, de igual manera, se faculta a la editorial para utilizar las imágenes, tablas y/o cualquier material gráfico presentado en el artículo para el diseño de carátulas o posters de la misma revista.





























