Modeling attenuation and dispersion of acoustic waves in porous media containing immiscible non viscous fluids
Modelado de atenuación y dispersión de ondas acústicas en medios porosos que contienen fluidos inmiscibles no viscosos
DOI:
https://doi.org/10.15446/dyna.v83n199.56238Palabras clave:
Biot theory, attenuation, viscosity, saturation, porosity (en)Teoría de Biot, atenuación, viscosidad, saturación, porosidad (es)
Descargas
DOI: https://doi.org/10.15446/dyna.v83n199.56238
Modeling attenuation and dispersion of acoustic waves in porous media containing immiscible non viscous fluids
Modelado de atenuación y dispersión de ondas acústicas en medios porosos que contienen fluidos inmiscibles no viscosos
Alejandro Duitama-Leal a, Ovidio Almanza b & Luis Montes-Vides c
a Departamento de Matemáticas, Universidad de Cundinamarca, Bogotá,
Colombia, adulfisica@gmail.com
b Departamento de Física, Universidad Nacional de Colombia, Bogotá, Colombia.
oaalmanzam@unal.edu.co
c Departmento de Geociencias, Universidad Nacional de Colombia, Bogotá,
Colombia. lamontesv@unal.edu.co
Received. March 16th, 2016. Received in revised form. August 12th, 2016. Accepted. September 2nd, 2016.
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.
Abstract
This paper
reports the results of the propagation of P-waves in porous media, simulated by
solving the generalized Biot's equations in finite differences. In saturated
models, it was observed that when a wave advances, the maximum amplitude of the
spectrum is shifted to lower frequencies, and that this maximum amplitude and
its frequency are directly related. Besides this, the quality factor decreases
with porosity and saturation. Hence, attenuation becomes higher when porosity,
saturation, and frequency increase but tends asymptotically towards a constant
value. Although phase analysis is generally discarded, it does provide
interesting results. It was noted that the wave phase changes linearly with
frequency at a rate of change that increases linearly with travel time. This
rate increases with saturation but decreases slightly with porosity. This work
ignores spherical divergence or scattering and concentrates on intrinsic
attenuation caused by friction, particularly between fluids and solid
particles.
Keywords. Biot theory, attenuation, viscosity, saturation, porosity.
Resumen
Este artículo reporta resultados de la
propagación de ondas P en medios porosos, simulada solucionando en diferencias
finitas las ecuaciones generalizadas de Biot. En modelos saturados se observó
que cuando avanza la onda, la amplitud máxima del espectro se desplaza hacia
frecuencias menores, y que esta amplitud máxima y su frecuencia están
directamente relacionadas. Además, que el factor de calidad disminuye con la
porosidad y la saturación. Por ende, la atenuación aumenta con la porosidad, la
saturación y la frecuencia pero tiende asintóticamente a un valor constante. Se
observó que la fase de la onda cambia linealmente con la frecuencia a una rata
de cambio que aumenta linealmente con el tiempo de viaje. Esta rata aumenta con
la saturación pero disminuye ligeramente con la porosidad. Este trabajo ignora la
divergencia esférica y la retro dispersión, concentrándose en la atenuación
intrínseca causada por la fricción, en particular entre líquido y partículas
sólidas.
Palabras clave. Teoría de Biot; atenuación; viscosidad; saturación; porosidad.
1. Introduction
Attenuation is the exponential decay of traveling wave amplitude and dispersion is the change of velocity with frequency. These can be used to enhance seismic resolution and as direct hydrocarbon indicators. The intrinsic attenuation is quantified by the inverse of the quality factor Q-1 as the fraction of wave energy transformed to heat in each period, whereas the attenuation scattering Qscat-1 is due to energy scattered in all directions. The sum of both is known as total attenuation. In mild stratified sediments, the scattering losses are considered negligible depending on frequency range, varying the relation Q-1/Qscat-1 from 19 in sonic logs to 4 in VSP (Vertical Seismic Profile) [1]. In sedimentary environments, Q-1 values ranging from 10-2 to 10-1 across the seismic band (1-150 Hz) have been reported [1].
Despite scientific improvements, the physical phenomena related to the intrinsic and scattering attenuations in sedimentary rocks are not completely understood. Notwithstanding different flow regimes and frequency bands, it is possible to explain some aspects of wave attenuation with a single mechanism. wave induced fluid flow - WIFF. When a wave stresses an average element, pore fluids respond with different changes in their fluid pressures. As a consequence, fluids within the porous element start flowing, significantly attenuating the wave energy. It has been demonstrated that these fluid-flow waves are responsible for dispersion and attenuation at low frequencies (31-123 Hz) [2]. Additionally, the relative motion between the rock matrix and the fluids is intensified by the presence of fluid-fluid interfaces and their pressure gradients [3]. It has been demonstrated that WIFF causes significant attenuation in partially saturated Berea sandstone at low and high pressure [4]. The induced flows take place at distinct scales, the macroscopic scale phenomenon at low or high frequencies is known as "Biot loss" [5,6]. Microscopic mechanisms caused by micro-cracks or broken grain contact under stress and known as squirt flow have been proposed to explain measured attenuation at ultrasonic frequencies [7-9]. Also, mesoscopic mechanisms have been reported [10] to treat wave induced flow due to patchy saturation. Pride and Berryman [11,12] published research on mesoscopic losses occurring in the double-porosity model. At low rates of varying strain and at a larger length scale compared to typical pore size, the fluid pressure has enough time to equilibrate between the porous phases and consequently, the double porosity model is reduced to the Biot one porosity mechanism [13]. It is even believed that at seismic frequencies the main cause is the WIF; in homogeneous media, WIF becomes weaker and Biot loss could be sizeable. On the other hand, understanding the effects of saturation and viscosity on seismic response requires numerical simulations given that laboratory tests must be carried out with strains and frequencies set in the seismic domain. Hence, the propagation of acoustic waves in wet porous media was numerically simulated. Biot's equations were extended to porous media saturated with two immiscible fluids [14], solved in finite differences and coded in a C++ program. These equations include a complex quantity that represents the deviation from Poiseuille friction as the frequency increases, transforming the static viscosity coefficient into a dynamic complex term. Models with variable porosity and saturation were used to discriminate their separated effects of porosity and saturation. Spectral analysis using Fourier transform provided information about the behavior of amplitude and phase spectra of wavelets (although phase analysis is mostly disregarded) that characterize seismic response within these two parameters.
2. Theory
2.1. Wave propagation in porous media
The stresses and strains of the material inside a continuous elastic volume are connected by the Hooke's law, which only holds for some materials under certain loading conditions. Under these circumstances, the second-order tensors that represent stress and strain are related through a fourth-rank stiffness tensor.
Now, consider
a homogeneous and isotropic volume of rock 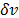 with porosity
with porosity  and density
and density 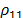 ,
which contains two immiscible fluids with saturation S and (S-1) and
respective densities
,
which contains two immiscible fluids with saturation S and (S-1) and
respective densities  and
and 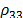 .
The displacements of the solid, and fluids 1 and 2 are designated by the
independent vectors
.
The displacements of the solid, and fluids 1 and 2 are designated by the
independent vectors 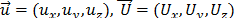 and
and  .
.
When a wave propagates across a media, the faces of the solid volume are under the stress tensor

and
the surfaces of fluids 1 and 2 are under
forces which are proportional to the fluids pressure  according to.
according to.
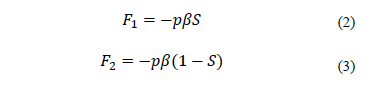
The minus sign indicates that the force is exerted in the opposite direction to the pressure.
The following strain tensor represents the deformed porous solid

The changes of volume in fluids 1 and 2 are
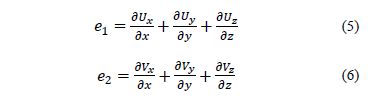
The kinetic energy of the system  per unit of volume is estimated by.
per unit of volume is estimated by.
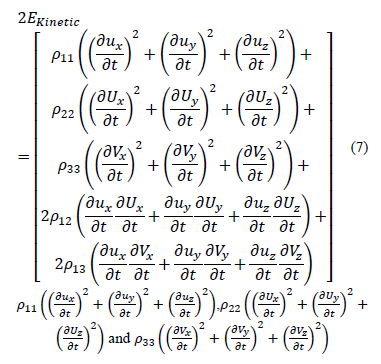
corresponds
to the kinetic energy of the matrix, and the kinetic energy of fluids 1 and 2, respectively. The mass coefficients  and
and  are apparent
densities which represent coupling parameters between the fluids and the solid,
so the last two terms correspond to their coupling energies. The weak
gas-liquid interaction was not taken into account. As a result, the friction is
only due to the relative motion between the solid and every fluid, and the
dissipation function
are apparent
densities which represent coupling parameters between the fluids and the solid,
so the last two terms correspond to their coupling energies. The weak
gas-liquid interaction was not taken into account. As a result, the friction is
only due to the relative motion between the solid and every fluid, and the
dissipation function  becomes.
becomes.

where 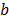 is the Darcy's coefficient of the fluid
component that relates the total friction force on the fluid with the average
fluid velocity and depends on the fluid's dynamic viscosity
is the Darcy's coefficient of the fluid
component that relates the total friction force on the fluid with the average
fluid velocity and depends on the fluid's dynamic viscosity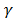 , the
permeability
, the
permeability  and the porosity
and the porosity  of the matrix, according to.
of the matrix, according to.

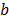 depends on the fluids
hence
depends on the fluids
hence , where
, where  and
and 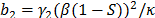 are the individual Darcy coefficients of each
fluid. After a certain frequency
are the individual Darcy coefficients of each
fluid. After a certain frequency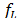 given later by equation (19), fluids behave as
a non-laminar or Poiseuille flow, hence D in equation (8) must be multiplied by
the factor
given later by equation (19), fluids behave as
a non-laminar or Poiseuille flow, hence D in equation (8) must be multiplied by
the factor
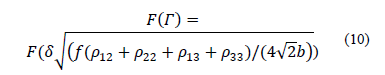
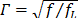 represents the ratio
between angular frequency and critical frequency
represents the ratio
between angular frequency and critical frequency  ,
, 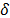 is a structure factor which depends on pore
geometry, and
is a structure factor which depends on pore
geometry, and  ,
,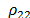 ,
,  and
and  are defined by.
are defined by.

The propagation of waves across the porous matrix saturated by the immiscible fluids is governed by the system of coupled equations.

The displacements vectors 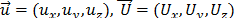 and
and  are completely described by the nine
independent equations 11, 12 and 13. In isotropic material, the transverse and
longitudinal waves are uncoupled and they obey independent equations of
propagation. The terms
are completely described by the nine
independent equations 11, 12 and 13. In isotropic material, the transverse and
longitudinal waves are uncoupled and they obey independent equations of
propagation. The terms 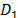 ,
,  ,
,  and
and  in equations 11, 12 and 13 are defined below.
in equations 11, 12 and 13 are defined below.
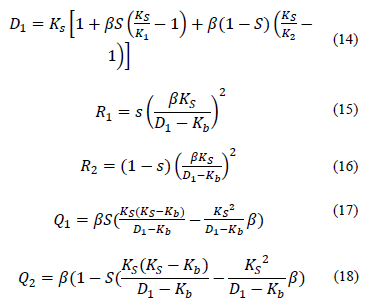
 is the shear modulus,
is the shear modulus,  is the Bulk Modulus of the Structure and
is the Bulk Modulus of the Structure and 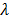 is the second Lame's parameter,
is the second Lame's parameter,  and
and 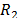 represent the pressure on fluids 1 or 2 required to displace the fluids into the
porous, and
represent the pressure on fluids 1 or 2 required to displace the fluids into the
porous, and  and
and  are physical constants that provide
information about the solid-fluids couplings.
are physical constants that provide
information about the solid-fluids couplings. 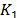 and
and 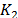 are the bulk modulus of the fluid 1 and 2, and
are the bulk modulus of the fluid 1 and 2, and 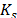 is the bulk modulus of the sand (grains).
is the bulk modulus of the sand (grains).
In a porous material with an
average pore diameter of d, the Poiseuille flow occurs below a certain
frequency  that defines the low frequency bandwidth [5]. Such
a frequency is given by.
that defines the low frequency bandwidth [5]. Such
a frequency is given by.
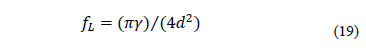
The longitudinal waves are decoupled from transverse waves, by applying the divergence operator on both sides of equations (11), (12) and (13) to finally obtain.
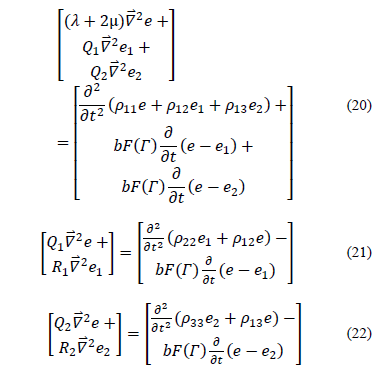
The set of equations 20, 21 and 22 rule the propagation of longitudinal waves in porous media containing fluids. The extension of this theory to the high-frequency range was developed by Biot [6], and since then it has been widely used in petroleum engineering.
A more detailed explanation of Biot's theory can be found in reference [14,15].
2.2. Attenuation and Dispersion
Intrinsic
seismic attenuation is characterized by the quality factor Q, defined in terms
of the mean stored energy  divided by
the energy lost
divided by
the energy lost  during a
cycle of sinusoidal deformation. The lost energy is absorbed by the medium as
heat energy. Q quantifies
the attenuation caused by fluid
movement and friction in pores, and is related to the phase angle
during a
cycle of sinusoidal deformation. The lost energy is absorbed by the medium as
heat energy. Q quantifies
the attenuation caused by fluid
movement and friction in pores, and is related to the phase angle  between stress
and strain, according to
between stress
and strain, according to

As is known, the Earth's crust preferentially attenuates higher frequencies, diminishing the seismic resolution.
Wavelets are formed by superposing monochromatic waves called frequency components of the wave, where each component travels with a velocity called phase velocity that depends on its frequency. Dispersion is the phenomenon by which each component has a different phase velocity that distorts the shape of the wave. When this occurs, the medium is referred to as dispersive.
3. Methodology
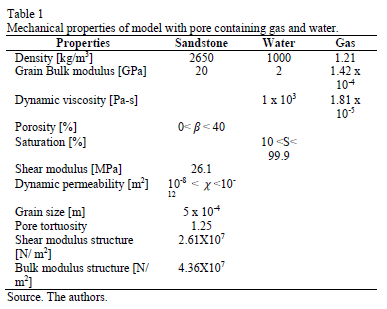
The system of simultaneous differential equations (20), (21) and (22), solved in the second order central finite difference scheme, was implemented in a C++ code. Porous sandstones were modeled as homogeneous isotropic porous media containing non-viscous fluids (gas and water). Each model with a different porosity and a distinct saturation according to its mechanical properties is listed in Table 1. To eliminate ghost reflections in the lateral and inferior regions bordering the model, non-reflecting borders were included by implementing Perfectly Matched Layers (PML) [16]. The efficiency of PML borders surrounding the model is observed in Fig. 1A containing three snapshots. the first at t=5 ms, the second at t=15 ms with spurious reflections on the borders, and the third at t=15 ms without reflections on PML borders. In order to circumvent geometric dispersion, the source generates a plane wave on the model simulating a 60Hz Ricker wavelet. In each simulation, the wave propagated in a 2D model with a depth of 2km and a width of 0.05 km formed grids that were 0.5 m high and 0.5 m thick. The downward wave was recorded at 20 points with a separation of 100 meters between one recording position and the next. The simulation time was 350 milliseconds and the sampling rate, 50 microseconds. According to equation (14), and taking into account the values listed in Table 1, the estimated critical frequency values are in kHz, hence the bandwidth of simulations is located in the seismic frequency range. To observe the isolated effect of porosity on attenuation and dispersion, some numerical simulations ran in fully saturated models each one with a different porosity. With that intention, homogeneous models saturated with water at 99.9% were created, with porosities varying of between 2.5% and 22.5% and with increases of 2.5%. Similarly, to observe the isolated effect of saturation on attenuation, other numerical simulations were run in constant porosity models with different saturations, ranging from 10% to 99.9%, with increases of 10%. For each simulation, the wavelets recorded in depth in each model, were spectrally decomposed by Fourier transform providing their respective amplitude and phase spectra. Besides the above, arrival times were estimated to find out the combined effect of porosity and saturation in P-wave velocity.
3.1. Analysis of results
Fig. 1B depicts a synthetic seismogram
formed by six superimposing wavelets recorded in depth in a 15% porosity
model of a porous sandstone which is
saturated with water at 99.9%, where the attenuation is manifested by a
reduction of the amplitudes, while the dispersion is manifested by changing the
waveforms. In a perfectly elastic homogeneous-isotropic medium, all frequency
components travel with the same phase velocity without energy loss and, as a
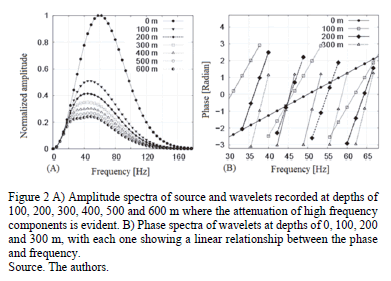
result, the wavelet holds its form while moving. The six wavelets of Fig. 1A were Fourier transformed and their amplitude spectra plotted in Fig. 2A,
indicating the depth at which each wavelet was recorded. The image shows the
amplitude spectrum diminishing in depth whereas the higher amplitude Am of each spectrum is
shifted toward low frequencies; from now on, the frequency of the maximum
component energy of each spectrum will be referred to as fm.
On the surface, fm is 60
Hz but at 100 m depth, it is 47 Hz. It reaches 45 Hz at 200 m; simultaneously the shape of the spectrum is
continuously modified until it becomes bi-modal at 600m. Given that the plane
wave does not suffer geometric dispersion, the above observed behavior is associated
entirely to the friction by the relative motion between the fluids and the pore
wall. Fig. 2B contains the phase spectra of wavelets recorded at depths of 100,
200 and 400 m. The phase spectra indicate that phase and frequency are related
by the expression , where the ratio of change of
phase with frequency
, where the ratio of change of
phase with frequency  increases in depth z. The above procedure,
including wave propagation, wavelet recording in depth, and spectral analysis,
was repeated for all numerical simulations.
increases in depth z. The above procedure,
including wave propagation, wavelet recording in depth, and spectral analysis,
was repeated for all numerical simulations.
Now, to quantify the impact of porosity on attenuation and dispersion, the wavelets recorded in depth and supplied by the simulation in each model were spectrally decomposed using the Fourier transform. As stated, each saturated model has a different porosity. From now on, the spectra of wavelets recorded in depth will be referred to as spectra in depth. Accordingly, the spectra in depth of each model were overlapped as shown in Fig. 2. Next, the logarithms of measured amplitudes at 40, 50, 60, 70, and 80 Hz were normalized by dividing each value by the maximum value, as shown in Fig. 3A. Each curve indicates that attenuation becomes stronger with porosity, which is explained by the fact that the pore surface, where friction occurs, is extended when porosity increases. Also, by comparing the curves according to frequency, it can be deduced that attenuation caused by porosity is strengthened when frequency increases.
This can be explained by the following
fact. At low frequencies, there is a
partial coupling between fluids and the solid but at higher frequencies, the
coupling breaks and friction increases together with the energy transfer rate.
In order to find the effects of porosity on dispersion,  were measured in phase
spectra in depth of each model with a different porosity. The summarized
results are shown in Fig. 3B. Fig. 2B shows that in a homogeneous-isotropic
saturated media,
were measured in phase
spectra in depth of each model with a different porosity. The summarized
results are shown in Fig. 3B. Fig. 2B shows that in a homogeneous-isotropic
saturated media,  increases with depth, whereas
Fig. 3B shows that
increases with depth, whereas
Fig. 3B shows that  becomes higher when porosity
increases, exacerbating the dispersion phenomena. The term
becomes higher when porosity
increases, exacerbating the dispersion phenomena. The term  might be considered a seismic
attribute and therefore a porosity indicator inside a fully saturated lithic
unit, relating their values directly with their porosities.
might be considered a seismic
attribute and therefore a porosity indicator inside a fully saturated lithic
unit, relating their values directly with their porosities.
On the other hand, the highest amplitudes
of all spectra in depth were estimated. Fig. 4A shows curves relating the
logarithm of the highest amplitudes 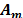 versus travel time and
porosity. Each curve shows an exponential decay of amplitude with the travel
time and a decay factor which increases with porosity. Although attenuation
increases with porosity, the lines tend asymptotically to a
limiting line established in this modeling by a porosity of about 22.5%. This
means that above this value, attenuation will remain constant no matter what
the value of porosity is.
versus travel time and
porosity. Each curve shows an exponential decay of amplitude with the travel
time and a decay factor which increases with porosity. Although attenuation
increases with porosity, the lines tend asymptotically to a
limiting line established in this modeling by a porosity of about 22.5%. This
means that above this value, attenuation will remain constant no matter what
the value of porosity is.
Fig. 1B illustrates that the maximum
amplitude 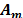 shifts to lower frequencies
when the depth increases. Therefore, the highest amplitudes (
shifts to lower frequencies
when the depth increases. Therefore, the highest amplitudes (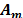 ) of all spectra in depth and their frequencies (
) of all spectra in depth and their frequencies ( ) were estimated and plotted in Fig. 4B. A numerical
regression indicates a linear relation between
) were estimated and plotted in Fig. 4B. A numerical
regression indicates a linear relation between 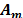 and
and  which is almost insensitive
to porosity. In a real case, the dispersion around the relationship would be
below estimation errors. The next step was to consider the quality factor Q, so
the amplitudes at 40, 50, 60, 70 and 80 Hz of all spectra in depth versus
porosity were plotted. Fig. 5A shows how amplitude decreases exponentially with
porosity and increases with frequency. It means that the higher frequency
components of waves are rapidly attenuated while the low frequency components remain. The
amplitudes of the 60Hz component were plotted in Fig. 5B, which shows the
decreasing effect of porosity on quality factor. Q tends asymptotically to a
constant value, as porosity increases. Values from Fig. 5A were used to build
the curves associated to components of 40, 50, 70 and 80 Hz. These curves
showed similar behavior
to the observed in Fig. 5B. The range of Q (from 35 to 80) observed in Fig. 5B points out that there is a sizeable attenuation in the seismic bandwidth.
which is almost insensitive
to porosity. In a real case, the dispersion around the relationship would be
below estimation errors. The next step was to consider the quality factor Q, so
the amplitudes at 40, 50, 60, 70 and 80 Hz of all spectra in depth versus
porosity were plotted. Fig. 5A shows how amplitude decreases exponentially with
porosity and increases with frequency. It means that the higher frequency
components of waves are rapidly attenuated while the low frequency components remain. The
amplitudes of the 60Hz component were plotted in Fig. 5B, which shows the
decreasing effect of porosity on quality factor. Q tends asymptotically to a
constant value, as porosity increases. Values from Fig. 5A were used to build
the curves associated to components of 40, 50, 70 and 80 Hz. These curves
showed similar behavior
to the observed in Fig. 5B. The range of Q (from 35 to 80) observed in Fig. 5B points out that there is a sizeable attenuation in the seismic bandwidth.
To establish the effect of porosity on P wave velocity, new simulations were run in saturated models with different porosity ranging from 2.5% up to 22.5% with a 2.5% variation each. The travel times estimated in depth displayed in Fig. 6A indicate that velocity decreases with porosity (from 3442 m/s in the 1% porosity model to 2093 m/s in the 25% porosity model). The observed variation in velocity coincides with reported velocity-porosity relationships obtained by numerical simulations to derive the elastic properties of model monomineralic consolidated sandstone [17] and empirical dataset of sandstone samples of varying porosity and clay content (from clean to 51% clay) whose velocities were measured at different pressures [18].
The observed velocity-porosity behavior in Fig. 6A was compared to the theoretical velocity models proposed by Wyllie & Gardner [19], Gassmann (1951) [20] and Biot [6], with all their curves plotted in Fig. 6B. The resulting curve shows a linear diminishing trend observed in laboratory research [2]. On one hand, the Wyllie & Gardner curve, which represents a time average equation and not a rigorous theoretical model, defines the upper limit of velocity-porosity relationship. On the other hand, Gassmann's velocity establishes the lower limit of velocity and coincides with Biot's velocity in case of a model without tortuosity, that is, entirely connected pores. In the presence of tortuosity, the velocity curve deviates from Gassmann's curve when porosity increases due to the fact that tortuosity affects solid-fluid coupling. The velocity of the rock matrix corresponds to the value where porosity becomes zero, settling around 3700 m/s. This result indicates that when the wave passes through a fully saturated medium, there is a delay in the journey that depends on porosity. Such behavior has also been observed in experimental data and field data [21].
Finally, the isolated effect of saturation in
the spectra of amplitude and phase was studied. Fig. 7A shows the amplitude
spectra of wavelets recorded in a 10% saturated model with a porosity of 10%.
On the surface 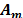 occurs when
occurs when  is 60 Hz, but as the wave propagates,
is 60 Hz, but as the wave propagates, 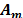 diminishes while its
diminishes while its  moves towards lower frequencies. This
behavior is accentuated when saturation
reaches 50% in same model seen in Fig. 7B, where a bi-modal shape appears in a
more attenuated spectrum. Fig. 7C shows a stronger effect due to a higher saturation. It can
thus be concluded that saturation strengthens both the phenomena of attenuation
and dispersion.
moves towards lower frequencies. This
behavior is accentuated when saturation
reaches 50% in same model seen in Fig. 7B, where a bi-modal shape appears in a
more attenuated spectrum. Fig. 7C shows a stronger effect due to a higher saturation. It can
thus be concluded that saturation strengthens both the phenomena of attenuation
and dispersion.
Simulations were run on models with porosities of 10%, 15%, 20%, 25% and
30%, with saturations of 10%, 20%, 30% and so on until reaching 99.9%. In each
spectra in depth, the quality factors at 60 Hz were estimated and the results,
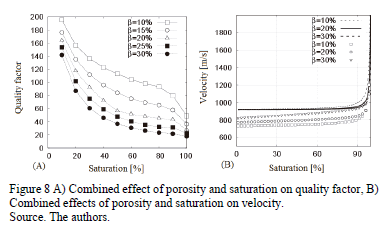
summarized in Fig. 8A, show that the quality factor decreases with saturation
and porosity. However, it can be noted
that the saturation effect on the quality factor is more intense for
saturations below 40%. Above this
value, a trend is depicted that is less steep. Furthermore, Fig. 8A shows that
the effect of porosity on the quality factor is steeper for lower values with a limiting Q curve of around 22%. In
Fig. 8B, the combined effect of porosity and saturation on velocity is
observed. When saturation is less than 90%, the propagation velocity remains
almost insensitive to saturation, but exceeding that value, velocity increases
rapidly until reaching full saturation. A similar behaviour of velocity with
water saturation in experimental tests has been reported [22] (Winkler and
Murphy, 1995). The extremely low bulk modulus of gas makes it feasible to
compress the rock-fluid aggregate, keeping an almost constant velocity. Thus,
velocity is mainly affected by porosity and to a lesser extent by saturation
except when saturation is almost full. Finally, the influence of saturation on  was studied by
was studied by
analyzing the phases observed in the previous simulations. The results
are shown in Figs. 9A, 9B and 9C and outline a linear relationship between
the increase of  and travel time. Slopes in the set of Figs.
9A, 9B and 9C show that
and travel time. Slopes in the set of Figs.
9A, 9B and 9C show that  decreases slightly with saturation.
Conversely, Fig. 3B shows that
decreases slightly with saturation.
Conversely, Fig. 3B shows that  increases with porosity. Porosity increases
the change of phase with frequency and simultaneously saturation slows this
effect down but only
increases with porosity. Porosity increases
the change of phase with frequency and simultaneously saturation slows this
effect down but only
4. Conclusions
The propagation of P-wave in porous media
that model porous sandstone containing gas and water was numerically simulated
allowing for the characterization of the effects of porosity and saturation on
velocity, attenuation, and dispersion. When a wave propagates in saturated
media, the maximum amplitude of the spectrum shifts to lower frequencies. As a
result, sizeable Biot's losses in seismic bandwidth were observed
with low Q values that contradict the belief regarding its absence. Attenuation
increases as porosity, saturation and frequency increase but it tends
asymptotically towards a limit value. Moreover, when porosity and saturation
increase, Q diminishes. Although usually discarded, the phase analysis did
provide interesting results. On one hand, the phase varies with frequency with
a rate that increases when wavelets propagate. On the other hand, this rate is
almost insensitive to saturation but increases with porosity. This term  might be considered a seismic
attribute and therefore a porosity indicator.
might be considered a seismic
attribute and therefore a porosity indicator.
Finally, a relationship between acoustic wave velocity and fully saturated porosity was established. When saturation is less than 90%, the propagation velocity remains almost constant, but when that value is exceeded, velocity increases rapidly until reaching full saturation.
Acknowledgements
The authors would like to thank Universidad Nacional de Colombia for the support given to this research, especially to the Graduate Program in Geophysics. This paper is a partial result obtained by the physicist Alejandro Duitama, while preparing his Master's thesis in Geophysics.
Bibliography
[1] Sams, M., Neep, J., Worthington, M. and King, M., The measurements of velocity dispersion and frequency-dependent intrinsic attenuation in sedimentary rocks. Geophysics, 62, pp. 1456-1464, 1997. DOI: 10.1190/1.1444249.
[2] White, J., Computed seismic speeds and attenuation in rocks with partial gas saturation. Geophysics, 40, pp. 224-232, 1975. DOI: 10.1190/1.1440520.
[3] Carcione, J., Helle, H. and Pham, N., White's model for wave propagation in partially saturated rocks: Comparison with poroelastic numerical experiments. Geophysics, 68, 1389-1398., 2003. DOI: 10.1190/1.1598132.
[4] Tisato, N., Quintal, B., Chapman, S., Madonna, C., Subramaniyan, S., Frehner, M., Saenger, E. and Grasselli, G., Seismic attenuation in partially saturated rocks. Recent advances and future directions. The Leading Edge, 33(6), pp. 648-655, 2014.
[5] Biot, M., Theory of propagation of elastic waves in a fluid-saturated porous solid, I. Low frecuency range. J. Acous. Soc. Am., 28, pp. 168-178, 1956. DOI: 10.1121/1.1908239.
[6] Biot, M., Theory of propagation of elastic waves in a fluid-saturated porous solid. II. Higher-frecuency range. J. Acous. Soc. Am., 28, pp. 179-191, 1956. DOI: 10.1121/1.1908239
[7] Dvorkin, J., Mavko, G. and Nur, A., Squirt flow in fully saturated rocks. Geophysics, 60, pp. 97-107, 1995. DOI: 10.1190/1.1443767.
[8] Mavko, G. and Nur, A., Wave attenuation in partially saturated rocks. Geophysics, 44, pp. 161-178, 1979. DOI: 10.1190/1.1440958.
[9] Williams, K., Jackson, D., Thorsos, E., Tang, D. and Shock, S., Comparison of sound speed and attenuation measured in sandy sediments to predictions based on the Biot theory of porous media. IEEE, J. Ocean. Eng., 27, pp. 413-428, 2002.
[10] Johnson, D., Theory of frequency dependent acoustics in patchy-saturated porous media. J. Acous, Soc. Am., 110, pp. 682-694, 2001. DOI: 10.1121/1.1381021.
[11] Pride, S. and Berryman, J., Linear dynamics of double porosity and dual-permeability materials. I. Governing equations and acoustic attenuation. Phys. Rev. E., 68, pp. 036603, 2003. DOI: 10.1103/PhysRevE.68.036603.
[12] Pride, S. and Berryman, J., Linear dynamics of double porosity and dual-permeability materials. II. Fluid transport equations. Phys. Rev. E., 60, pp. 4285-4299, 2003.
[13] Caspari, E., Qi, Q., Lopes, S., Gurevich, B., Rubino, J., Velis, D., Clenell, M. and Muller, T., Wave attenuation in partially saturated porous rocks - New observations and interpretation across scales. The Leading Edge, 33(6) pp. 606-614, 2014.
[14] Camarasa, M., Contribución a la teoría de Biot sobre propagación de ondas acústicas en sedimentos saturados en una mezcla de fluidos. Tesis Doctoral, Universidad Complutense de Madrid, Madrid, España,1992.
[15] Duitama, A., Simulación de la atenuación de frecuencias en ondas sísmicas primarias, MSc. Tesis, Departmento de Geociencias, Universidad Nacional de Colombia, Bogotá, Colombia, 2013.
[16] Zeng, Y., He, J. and Liu, W., The application of the perfectly matched layer in numerical modeling of wave propagation in poroelastic media. Geophysics, 6(4), pp. 1258-1266, 2001. Doi: 10.1190/1.1487073.
[17] Knackstedt, M., Arns, C. and Pinczewskiz, W., Velocity-porosity relationships, 1. Accurate velocity model for clean consolidated sandstones. Geophysics, 68, pp. 1822-1834, 2003.
[18] Han, D., Nur, A. and Morgan, D., Effects of porosity and clay content on wave velocities in sandstones. Geophysics, 51, pp. 2093-2107, 1986. DOI: 10.1190/1.1442062.
[19] Wyllie, M. and Gardner, L.W., Elastic wave velocities in heterogeneous and porous media, Geophysics, 21, pp 41-70, 1956. DOI: 10.1190/1.1438217.
[20] Gassmann, F., Uber die elastiziat poroser medien, Vier. der Natur. Gesellschaft, 96, pp 1-26, 1951.
[21] Korneev, V., Goloshubin, M., Daley, T. and Silin, G., Seismic low-frequency effects in monitoring fluid-saturated reservoirs. Geophysics, 69, pp. 522-532, 2004. DOI: 10.1190/1.1707072.
[22] Winkler, K. and Murphy, W., Acoustic velocity and attenuation in porous rocks, in T. Ahrens, ed. Rock physics and phase relations, Reference Shelf 3, AGU, pp 20-34,1955.
A. Duitama-Leal, is Physicist, and MSc. of Geophysics from Universidad Nacional de Colombia. Experience like instructor of physics and mathematics. Knowledge in geophysics and interest in research, particularly in numeric methods and simulation of physics and geophysics systems using the C++ language and parallel programming. In Geophysics, the topics are modeling of wave field, fluids mechanic and seismic theory inversion. ORCID. 0000-0002-5477-2191
O. Almanza-Montero, received the Dr, in Physic in the Universidad de Valladolid (Spain - 2000), his MSc. In Physic in the Universidad Nacional de Colombia. Currently he is professor in this University, from 1996. His works are focused in materials science such as semiconductor and antioxidant activity of some Colombian fruits as well. He is author of more than 50 paper published in different journals. Characterization techniques (XRD, EPR, IR, UV-vis) are methods he usually use. ORCID. 0000-0002-5141-6079
L. Montes-Vides, is Physicist from the Universidad Nacional de Colombia, MSc. in Engineering from the Universidad Nacional de Colombia in 1987 and Dr. in Science - Geophysics from the Universidade Federal do Pará (Brazil - 1998). At the Universidad Nacional de Colombia - sede Bogotá since 1990 as a lecturer in the following programs. undergratuate program in Geology, graduate programs in Master Science in Geophysics and Doctorate in Geosciences, all of them at the Faculty of Sciences. Research areas focused in Seismic prospecting, seismic inversion, seismic modeling and applied computing mathematics. Reviewer of following scientific journals. ESRJ, Revista da SBGf, J.Appl. Geophysics and CT&F. ORCID. 0000-0002-7470-9202
Referencias
Sams, M., Neep, J., Worthington, M. and King, M., The measurements of velocity dispersion and frequency-dependent intrinsic attenuation in sedimentary rocks. Geophysics, 62, pp. 1456- 1464, 1997. DOI: 10.1190/1.1444249.
White, J., Computed seismic speeds and attenuation in rocks with partial gas saturation. Geophysics, 40, pp. 224-232, 1975. DOI: 10.1190/1.1440520.
Carcione, J., Helle, H. and Pham, N., White’s model for wave propagation in partially saturated rocks. Comparison with poroelastic numerical experiments. Geophysics, 68, 1389-1398., 2003. DOI: 10.1190/1.1598132.
Tisato, N., Quintal, B., Chapman, S., Madonna, C., Subramaniyan, S., Frehner, M., Saenger, E. and Grasselli, G., Seismic attenuation in partially saturated rocks. Recent advances and future directions. The Leading Edge, 33(6), pp. 648-655, 2014.
Biot, M., Theory of propagation of elastic waves in a fluid-saturated porous solid, I. Low frecuency range. J. Acous. Soc. Am., 28, pp. 168- 178, 1956. DOI: 10.1121/1.1908239.
Biot, M., Theory of propagation of elastic waves in a fluid-saturated porous solid. II. Higher-frecuency range. J. Acous. Soc. Am., 28, pp. 179-191, 1956. DOI: 10.1121/1.1908239
Dvorkin, J., Mavko, G. and Nur, A., Squirt flow in fully saturated rocks. Geophysics, 60, pp. 97-107, 1995. DOI: 10.1190/1.1443767.
Mavko, G. and Nur, A., Wave attenuation in partially saturated rocks. Geophysics, 44, pp. 161-178, 1979. DOI: 10.1190/1.1440958.
Williams, K., Jackson, D., Thorsos, E., Tang, D. and Shock, S., Comparison of sound speed and attenuation measured in sandy sediments to predictions based on the Biot theory of porous media. IEEE, J. Ocean. Eng., 27, pp. 413-428, 2002.
Johnson, D., Theory of frequency dependent acoustics in patchysaturated porous media. J. Acous, Soc. Am., 110, pp. 682-694, 2001. DOI: 10.1121/1.1381021.
Pride, S. and Berryman, J., Linear dynamics of double porosity and dual-permeability materials. I. Governing equations and acoustic attenuation. Phys. Rev. E., 68, pp. 036603, 2003. DOI: 10.1103/PhysRevE.68.036603.
Pride, S. and Berryman, J., Linear dynamics of double porosity and dual-permeability materials. II. Fluid transport equations. Phys. Rev. E., 60, pp. 4285-4299, 2003.
Caspari, E., Qi, Q., Lopes, S., Gurevich, B., Rubino, J., Velis, D., Clenell, M. and Muller, T., Wave attenuation in partially saturated porous rocks – New observations and interpretation across scales. The Leading Edge, 33(6) pp. 606-614, 2014.
Camarasa, M., Contribución a la teoría de Biot sobre propagación de ondas acústicas en sedimentos saturados en una mezcla de fluidos. Tesis Doctoral, Universidad Complutense de Madrid, Madrid, España,1992.
Duitama, A., Simulación de la atenuación de frecuencias en ondas sísmicas primarias, MSc. Tesis, Departmento de Geociencias, Universidad Nacional de Colombia, Bogotá, Colombia, 2013.
Zeng, Y., He, J. and Liu, W., The application of the perfectly matched layer in numerical modeling of wave propagation in poroelastic media. Geophysics, 6(4), pp. 1258-1266, 2001. Doi: 10.1190/1.1487073.
Knackstedt, M., Arns, C. and Pinczewskiz, W., Velocity-porosity relationships, 1. Accurate velocity model for clean consolidated sandstones. Geophysics, 68, pp. 1822-1834, 2003.
Han, D., Nur, A. and Morgan, D., Effects of porosity and clay content on wave velocities in sandstones. Geophysics, 51, pp. 2093-2107, 1986. DOI: 10.1190/1.1442062.
Wyllie, M. and Gardner, L.W., Elastic wave velocities in heterogeneous and porous media, Geophysics, 21, pp 41-70, 1956. DOI: 10.1190/1.1438217.
Gassmann, F., Uber die elastiziat poroser medien, Vier. der Natur. Gesellschaft, 96, pp 1-26, 1951.
Korneev, V., Goloshubin, M., Daley, T. and Silin, G., Seismic lowfrequency effects in monitoring fluid-saturated reservoirs. Geophysics, 69, pp. 522-532, 2004. DOI: 10.1190/1.1707072.
Winkler, K. and Murphy, W., Acoustic velocity and attenuation in porous rocks, in T. Ahrens, ed. Rock physics and phase relations, Reference Shelf 3, AGU, pp 20-34,1955.
Cómo citar
IEEE
ACM
ACS
APA
ABNT
Chicago
Harvard
MLA
Turabian
Vancouver
Descargar cita
CrossRef Cited-by
1. Oleg Shapovalov, Thomas Heckel, Mate Gaal, Sabine Weiß. (2022). External Acoustical Damping on a Metallic Angle Wedge in a High Temperature Resistant Ultrasonic Probe. Acoustics Australia, 50(3), p.343. https://doi.org/10.1007/s40857-022-00270-9.
2. Omid Yousefian, R. D. White, Yasamin Karbalaeisadegh, H. T. Banks, Marie Muller. (2018). The effect of pore size and density on ultrasonic attenuation in porous structures with mono-disperse random pore distribution: A two-dimensional in-silico study. The Journal of the Acoustical Society of America, 144(2), p.709. https://doi.org/10.1121/1.5049782.
3. João Henrique Uliana, Everton Lucas Oliveira, Arthur de Araújo Ferreira, Willian Andrighetto Trevizan, Theo Zeferino Pavan, Tito José Bonagamba, Antônio Adilton de Oliveira Carneiro. (2023). Photoacoustic microscopy of sandstone reservoirs rocks. 2023 IEEE International Ultrasonics Symposium (IUS). , p.1. https://doi.org/10.1109/IUS51837.2023.10308378.
4. Catarina Baptista-Pereira, Jay N. Meegoda, Jitendra A. Kewalramani, Ellie Nadelmann, Trevor Elliott, Ashish D. Borgaonkar. (2025). Ultrasound applications in civil and environmental engineering. Academia Engineering, 2(4) https://doi.org/10.20935/AcadEng8000.
Dimensions
PlumX
Visitas a la página del resumen del artículo
Descargas
Licencia
Derechos de autor 2016 DYNA

Esta obra está bajo una licencia internacional Creative Commons Atribución-NoComercial-SinDerivadas 4.0.
El autor o autores de un artículo aceptado para publicación en cualquiera de las revistas editadas por la facultad de Minas cederán la totalidad de los derechos patrimoniales a la Universidad Nacional de Colombia de manera gratuita, dentro de los cuáles se incluyen: el derecho a editar, publicar, reproducir y distribuir tanto en medios impresos como digitales, además de incluir en artículo en índices internacionales y/o bases de datos, de igual manera, se faculta a la editorial para utilizar las imágenes, tablas y/o cualquier material gráfico presentado en el artículo para el diseño de carátulas o posters de la misma revista.