First approach to unilateral transfemoral amputees' contact mechanics
Primer acercamiento a la mecánica de contacto en amputados transfemorales unilaterales
DOI:
https://doi.org/10.15446/dyna.v84n202.58595Palabras clave:
finite element method, transfemoral amputation, cartilage stress state (en)método de elementos finitos, amputación transfemoral, estado de esfuerzos del cartílago (es)
Descargas
Recibido: 23 de junio de 2016; Revisión recibida: 14 de febrero de 2017; Aceptado: 20 de julio de 2017
Abstract
The stresses in the hip area have great importance because of their relationship to the health of the joint. Finite element models can predict contact between cartilages, however, contact patterns in unilateral transfemoral amputees have not yet been found in literature. We thus want to present an initial approach in the contact mechanics of the hip joint of these amputees. From an existing database, three transfemoral amputees who use prostheses were chosen. Their respective hips and femur were obtained from tomography, and so as their cartilages from their respective articular surfaces. Finite element models were created per patient and static bipedestation was analyzed. At the beginning of contact between cartilages, contact stresses were determined. The results showed that the stresses of the amputated side were higher than that of the non-amputated, in terms of average and peak contact stress. These were located in the anterior and superior zones, respectively.
Keywords:
finite element method, transfemoral amputation, cartilage stress state..Resumen
Los esfuerzos en la cadera son de gran importancia debido a su relación con la salud articular. Modelos de elementos finitos pueden predecir el contacto entre cartílagos, sin embargo, modelos de contacto en amputados transfemorales unilaterales, no han sido encontrados aún en la literatura. Se quiere presentar un acercamiento inicial en la mecánica de contacto de la articulación coxofemoral de dichos pacientes. De una base de datos existente, se eligieron tres amputados transfemorales usuarios de prótesis; se obtuvieron sus respectivas caderas y fémures a partir de tomografía, y los cartílagos de las respectivas superficies articulares. Se crearon modelos por elementos finitos por paciente y se analizó la bipedestación estática. Se determinaron los esfuerzos al inicio del contacto articular, observando resultados mayores para el lado amputado, tanto para los esfuerzos promedio como para los esfuerzos máximos de contacto; y estos se encontraron en la zona anterior y superior respectivamente.
Palabras clave:
método de elementos finitos, amputación transfemoral, estado de esfuerzos del cartílago..1. Introduction
Amputation is a surgical procedure in which a limb is removed because of an illness or injury. A way of improving the quality of life of people that had undergone amputation is through the use of orthopedic prostheses, which replace their lost limb and provide them the possibility of recovering mobility and help in their reintegration into society [1,2]. Lower limb amputation is categorized into: toe, ray, transmetatarsal, mid-foot, ankle-level, below the knee, through the knee, above knee and hip disarticulation [3]. Depending on the amputation’s location, different prosthesis is used.
In existing literature, studies of lower limb amputation are related to gait dynamics [4-7], socket design [8] and socket - stump interaction numerical models [9-11]. In addition to these, joints studies are associated with osteoarthritis (OA) development in the knee [12-14] and the hip [14,15], the influence of different sockets on the range of motion of the hip [16] and the effect of osteointegrated prosthesis on the hip joint moment [17].
Hip stresses are of great importance due to their relation to the joint’s health. Cartilage health, in particular, is influenced by the magnitude and direction of the resultant hip forces, the size of the weight-bearing surface and the stress distribution across the said surface [18]. There have been cases wherein some anatomical conditions like femoroacetabular impingement [19,20] causing osteoarthritis (OA) because of abnormal contact stresses [21]. Furthermore, there are also disagreements regarding the normal magnitudes and distribution of contact stress on one’s healthy hips [22]. For non-amputated subjects, finite element (FE) models have been developed as a way of understanding load distribution on the joint and predicting cartilage contact stresses on hips with and without pathological conditions [22-24]. Differences between healthy and dysplastic hips have been compared [25-27] and retroverted acetabula have been studied [28].
Computational methods can simulate hip joint mechanics and have thus been used to predict contact stresses [29-33]. Nonetheless, FE predictions of hip cartilage contact for unilateral transfemoral amputees have not been successfully found in literature. The objective of this study, therefore, is to develop a subject-specific numerical model to compare hip cartilage contact of unilateral transfemoral amputees between pathological and sound leg on standing position.
2. Materials and methods
As the first approach to this kind of models, a standing position model will be used, since it is not only the easiest load case but one that can predict if there is a stress difference on various sides. Three patients that had undergone unilateral transfemoral amputation were selected; their specific data is presented in Table 1. The patients were relatively active and did not have any additional physical, vascular, neurological or psychological condition that could affect the result of this study. The patients used a non-distal end support socket, a solid ankle cushioned heel (SACH) foot, and a mechanical monocentric knee prosthesis. In accordance to the ethics committee of Universidad Nacional de Colombia, proper and informed consent was given by each patient before any of the procedures took place
Source: The authors.Table 1: Patients’ characteristics and applied force.

2.1. Numerical models
2.1.1. Database and computed tomography
The database was composed by transfemoral amputees from Orthopraxis S.A. The parameters used for the scan were: SIEMENS/Emotion6 Scanner, 12mAs, 130 KV, 512x512 pxlmatrix, pixel size 0.758 mm, gantry tilt 0.00 and slice increment 1 mm; cross sections were obtained from the distal femur to about half hip. During the CT scan, the patients were in a laying supine position over the tomograph table and were not wearing their prosthetic socket or any additional element like socks or liners around their residual limbs.
2.1.2. Geometry reconstruction
From a previous study, the residual femur, the stump and the socket were reconstructed using a 3D and CT scanner. [11]. For each patient, cast molds were created by a technician, then scanned and reconstructed by NextEngine's Desktop 3D Scanner and ScanStudio™ software (Santa Monica, CA). From the tomographic information obtained, the non-amputated femur along with the hips were manually segmented from the image data using the VTK software. It is worth noting that the CT anatomical positions were maintained throughout the study to prevent the direction of the applied load from affecting the cartilage stresses.
For both legs, the femoral and acetabular cartilages were obtained by expanding their respective articular surfaces by 1 mm, Fig. 1. This expansion was well within the values reported in literature, which is specified to be from 0,93 to 2,3 mm [34-37]. The meshes were constructed using as reference the quantity of the elements of similar studies [21,25,26,38]. The layers of the cartilages were constructed with hexahedral elements using the Salome - Meca software. The cortical bone, the stump and the socket were discretized with tetrahedral elements. The trabecular bone was not included in the process since it yields little significance in terms of contact stresses [24]. The general representation of the geometries can be seen in Fig. 2.
Figure 1: Cartilage reconstruction.
Figure 2: Subject-specific models. a. Non-amputated assembly, b. Amputated assembly.
2.1.3. Materials
The material properties are assigned in ABAQUS V6.12; the cortical bone, the socket and the stump were modeled as homogeneous, isotropic materials with an elastic modulus of E=15𝐺𝑃𝑎, 𝐸=1.5𝐺𝑃𝑎 and 𝐸=25𝐾𝑃𝑎 respectively; their Poisson’s ratio are 𝑣=0.3 for the cortical bone and the socket, and 𝑣=0.475 for the soft tissue [11,39]. The cartilage was modeled as a homogeneous, isotropic, Neo-Hookean hyperelastic material. The Abaqus Neo-Hookean form was used in the process, with a shear modulus of 𝐺=13.6𝑀𝑃𝑎 and a bulk modulus of 𝐾=1359𝑀𝑃𝑎; the material constitutive parameters were calculated using eq (1) - (2) [40], 𝐶 10 =6.8𝑀𝑃𝑎 and 𝐷 1 =1.4𝑥 10 −9 𝑃𝑎 [22].


2.1.4. Contact properties, boundary conditions and loads
An explicit numerical model was developed using ABAQUS V6.12. The model was given general boundary conditions: no penetration and frictionless contact between the cartilages geometries [22] and a tie constraint between cartilage-bone and the bone-soft tissue to define the interfaces’ interactions.
2.1.5. Amputated model
This model was developed in four various steps. Donning: where the constraints were applied to the hip (in the pubis and superior face) and in the neck of the femur, a part of the ischium was removed to prevent contact between the stump and the pelvis. Finally, the donning procedure of the socket was done by applying a displacement vector (white arrows) on the socket, Fig. 3a. Stabilization: a 5-second step was then applied to allow the attenuation of the dynamic effects caused by the location of the socket and the acquisition of the final position of the soft tissue.
In this phase, there are no existing stimuli or additional boundary conditions, Fig. 3b. These two steps were done as per Lacroix and Ramirez [41]. Load: within 10 seconds of the process, the load described in Table 1 (black arrow) was applied in a caudocranial direction over the socket at the interface of the femoral prosthesis' extension, representing half of the patient weight, Fig. 3c. The constraints remain the same for this step. Contact: the displacement vector (white arrows) on the socket and the boundary condition (constraints) of the femur were eliminated, which then allowed contact between cartilages; a new boundary restriction was applied over the socket (constraints) to remove its lateral movements, Fig. 3d.
Figure 3: Amputated model boundary conditions. a. Donning, b. Stabilization, c. Load, d. Contact
2.1.6. Non-amputated models
These models were developed in two steps. Load: movement restrictions (constraints) were applied over the hip -pubis and superior faces. Afterwards, the loads (gray arrows) were applied in a caudocranial direction over the femoral condyles. This load is the same as described in Table 1, but were divided among the two condyles, Fig. 4. Stabilization: a 5-second step where no additional loads or boundary conditions were applied, allowing the stabilization of the model and the reduction of its internal energy.
Figure 4: Non-amputated model boundary conditions
2.1.7. Contact area and contact stresses
Cartilage contact stresses and contact area were evaluated on the acetabular cartilage. Contact area and peak contact stress were evaluated in the anteromedial (AM), anterolateral (AL), superomedial (SM), superolateral (SL), posteromedial (PM) and posterolateral (PL) regions of the acetabular cartilage [25], Fig. 5.
Figure 5: Anatomical regions on the acetabular cartilage.
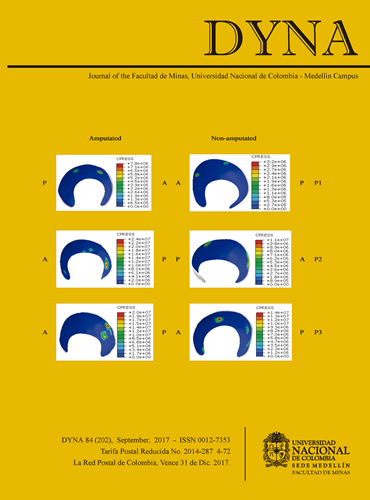
Overall, the amputated side proved to have higher stresses than the non-amputated one; however, the contact stress patterns in patients and their amputated and non-amputated sides were not constant, as can be seen in Fig. 6. As for contact pressure (CPRESS), it shows that there are some few localized stress zones present while the remaining cartilage does not show these - a common behavior in this type of stress distributions [23,27,41-44] since there are areas that have high load and some that have none. Due to the model's specific steps involved, the application time of the load varied between the amputated and the non-amputated sides. When the bone restriction was removed, the amputated models had almost immediate contact due to the stored energy, registering a time of 0.4 + -0.1 seconds to have contact, while registering 3.8±0.8 seconds contact for the non-amputated models, where the applied force was transferred progressively over the femur until contact happened.
Figure 6: Contact pressure (CPRESS) on acetabular cartilages during Load step. A: anterior, P: posterior. The units are Pa,
3. Results
The peak average and average stress were both determined in the first seconds of contact between cartilages; the average contact stresses were ~12 MPa for the amputated side and ~4 MPa for the non-amputated side. There were marked differences between the sides in both peak and average stresses in the PL and PM regions Fig. 7, as contact stresses at the posterior region were not present in the non-amputated side. The anterior region stresses were higher in the amputated side as compared to the non-amputated one, while the superior regions have also presented differences, although at a lower scale.
Figure 7: a. Average contact stresses, b. Peak contact stresses.
Stresses in the anterior region were the highest for the amputated side, while it was the superior region that registered the highest for the non-amputated one. However, both SL and SM were the regions with less variation in their stresses compared to the amputated one. Peak contact stress at the amputated side was higher than in the non-amputated side, Fig. 7, with the AL and the AM regions having the highest contact stresses. In contrast, it was the SL and the SM that had the highest contact stress in the non-amputated side.
Fig. 8 shows the total contact area of the acetabular cartilages in the contact and the stabilization steps. The contact areas for the non-amputated side was smaller than in the amputated one, and it shows that cartilage contact is always maintained throughout the step, even though the values show small iterative behaviors. In contrast, the contact areas in the amputated models have spaces where there is no contact between the surfaces, and the curves show growth behavior and decrease in time.
Figure 8: Contact area. a. Amputated, b. Non-amputated
The total acetabular cartilage surface area averaged 131.32 ± 40 mm2 for the amputated side; with the contact area percentage of around 20% for P2 and P3, and 17% for P1. In comparison, the surface area for the non-amputated side was 134,11 ± 17 mm2, with a contact area percentage of 15.4%, 14% and 11.3% for patients P1, P2 and P3 respectively.
4. Discussion
As expected, the main findings yielded some differences in the amputated and non-amputated side of each patient; however, changes to all the amputated and non-amputated sides were also observed in the contact mechanics (refer to Fig. 6.) These differences could be attributed to variations in bone and cartilage morphology [22,45], but other factors, such as stump and amputated femur longitudes, load directions, anatomical position of the patient and the distance covered by the socket upon positioning it, can also affect stress distribution. Nonetheless, it is normal for small regions to have concentrated stress while the rest of the zones have none. [21,22,24,25,27,28,44,46,47].
Direct comparison with past studies in terms of numerical values for contact stress or contact area is inappropriate in this case since we have not successfully found hip numerical models for transfemoral amputees as of writing. Nevertheless, we have found that some of our results have similarities with other published works as will be shown below. Peak normal stress results for patients P2 and P3 (24 MPa and 20 MPa), were akin to the stress values reported in pathological hips by Henak et al. [25] and [28], so as for acetabular dysplasia (30 MPa) and retroverted acetabula (25 MPa). The stress results of the amputated and non-amputated models did not exceed that of the peak stresses reported in literature. However, it is important to note that in the case of amputated models P2 and P3, the stress values found when they were in standing position were approximately the same to that of Anderson et al's results [28] in heel strike when climbing stairs or when rising from a seated position, indicating that amputees may be experiencing higher stresses in doing simple activities. The standard deviation in the contact stresses is high for all the patients and all sides, which can be explained by the fact that each of the models is unique and thus possess nonreplicable features.
During simulation, the contact area on the amputated side was mostly in the AL region. It was also in the AM, SL, SM, PL and PM regions but in lower proportions. As for the non-amputated side, in comparison, contact was primarily at the SL and AL regions, with some at the SM zone. This difference in both sides is likely caused by the residual energy stored in the stump during simulation, which then generates an iteration of contact. In general, the contact area on the amputated side was larger than in the non-amputated side, and there were no visible resemblances in the curves from between sides. Furthermore, similarities in contact area with previous studies were not found, except in the case of P1 where his amputated and non-amputated areas (374 mm2 and 309 mm2 respectively) were the closest to the average predicted value of a non-amputated hip (366.1 mm2) [24].
The models developed have several limitations that need to be discussed. First, the preliminary numerical models allowed us to observe that the internal energy stored in the residual soft tissue dislocated the hip in the standing position step. It was for this reason that the femur and socket constraints were applied to them. Moreover, because of the donning simulation, the soft tissue is represented as a unique volume, and the fibers that would have allowed control over the dislocation and that would have otherwise connected the hip and the femur, were not present. Adding muscle fiber or ligaments could have also helped prevent dislocation of the hip and made the numerical model more stable and fast, in terms of the model's completion. Second, the cartilage was assumed to be isotropic, nearly incompressible, and hyperelastic [21]. There are other cartilage models that might have allowed more accurate description of the tissue mechanical model - ie. the osmoporoviscoelastic models, [48], but poroelasticity models neglect the effects of inertia and are consequently not suitable for explicit analyses [49]. Finally, even though the models do not include the labrum, the FE model for the amputated side built in this study aims to progress toward a realistic interpretation of the transfemoral amputation. In contrast to other studies that evaluated donning of the socket without the articular joint [41,50], these models take into account the hip contact and the femoral and acetabular cartilages. There are other conditions that affect cartilage stresses -neck shaft angle, femoral anteversion angle and acetabular anteversion angle- as shown in [21], but for this specific case, our aim was to obtain a model where cartilage compression and socket donning are taking into consideration. The additional complexities explained above will be included in further studies.
4. Conclusions
Each individual is unique and thus each model has their respective differences and variations. The inclusion of the muscles that connect the hip and the femur and the understanding of their geometrical differences can change the model and make it more accurate. Our initial aim was satisfied, since the model was able to behave as expected. This study suggests that contact stress at the amputated side of the amputee are higher than that at the non-amputated side. And even though not all questions were answered by this study, there is no denying that it has generated additional issues that need resolutions through new analysis for a more complete understanding of these cases.
References
Referencias
Olivares-Miyares, A.L., Broche-Vázquez, L., Díaz-Novo, C., Garlobo-Castillo, L. y Sagaró-Zamora, R.. Análisis de la funcionabilidad de prótesis ortopédicas transfemorales. Revista Cubana de Ortopedia y Traumatología, [en línea]. 25(2), pp. 102-116, 2011. [Recuperado en 08 Octubre de 2012], Disponible en: http://scielo.sld.cu/scielo.php?script=sci_arttext&pid=S0864-215X2011000200001&lng=es&tlng=es.
Ramírez, J.F., Isaza, J.A., Mariaka, I. and Vélez, J.A., Analysis of bone demineralization due to the use of exoprosthesis by comparing Young’s Modulus of the femur in unilateral transfemoral amputees. Prosthet. Orthot. Int. 35, pp. 459-466, 2011. DOI: 10.1177/0309364611420478.
Marshall, C. and Stansby, G., Amputation. J. Biomech. 26, pp. 21-24. 2008. DOI: 10.1016/j.mpsur.2007.10.011.
Goujon-Pillet, H., Sapin, E., Fodé, P. and Lavaste, F., Three-dimensional motions of trunk and pelvis during transfemoral amputee gait. Arch. Phys. Med. Rehabil. 89, pp. 87-94, 2008. DOI: 10.1016/j.apmr.2007.08.136.
Bae, T.S., Choi, K., Hong, D. and Mun, M., Dynamic analysis of above-knee amputee gait, Clin. Biomech. 22, pp. 557-566, 2007. DOI: 10.1016/j.clinbiomech.2006.12.009.
Jaegers, S.M.H.J., Arendzen, J.H. and de Jongh, H.J., Prosthetic gait of unilateral transfemoral amputees: A kinematic study. Arch. Phys. Med. Rehabil. 76, pp. 736-743, 1995. DOI: 10.1016/S0003-9993(95)80528-1.
Helgason, B., Pálsson, H., Rúnarsson, T.P., Frossard, L. and Viceconti, M., Risk of failure during gait for direct skeletal attachment of a femoral prosthesis: A finite element study. Med. Eng. Phys. 31, pp. 595-600, 2009. DOI: 10.1016/j.medengphy.2008.11.015.
Colombo, G., Filippi, S., Rizzi, C. and Rotini, F., A new design paradigm for the development of custom-fit soft sockets for lower limb prostheses. Comput. Ind. 61, pp. 513-523, 2010. DOI: 10.1016/j.compind.2010.03.008.
Zhang, M., Mak, A.F. and Roberts, V.C., Finite element modelling of a residual lower-limb in a prosthetic socket: a survey of the development in the first decade. Med. Eng. Phys. [online]. 20, pp. 360-373, 1998. [accessed July 13, 2011]. Available at: http://www.ncbi.nlm.nih.gov/pubmed/9773689.
Portnoy, S., Yarnitzky, G., Yizhar, Z., Kristal, Oppenheim, A.U., Siev-Ner, I. and Gefen, A., Real-time patient-specific finite element analysis of internal stresses in the soft tissues of a residual limb: A new tool for prosthetic fitting, Ann. Biomed. Eng. 35, pp. 120-135, 2007. DOI: 10.1007/s10439-006-9208-3.
Ramírez-Patiño, J.F., Nivel de confort y distribución de esfuerzos en la Interfaz Socket – Muñón en amputados transfemorales - Repositorio Institucional UN, [en línea]. 2011. [consultado en: Noviembre 12, 2012]. Disponible en: http://www.bdigital.unal.edu.co/5486/
Lloyd, C.H., Stanhope, S.J., Davis, I.S. and Royer, T.D., Strength asymmetry and osteoarthritis risk factors in unilateral trans-tibial, amputee gait. Gait Posture. 32, pp. 296-300, 2010. DOI: 10.1016/j.gaitpost.2010.05.003.
Royer, T. and Koenig, M., Joint loading and bone mineral density in persons with unilateral, trans-tibial amputation. Clin. Biomech. 20, pp. 1119-1125, 2005. DOI: 10.1016/j.clinbiomech.2005.07.003.
Kulkarni, J., Adams, J., Thomas, E. and Silman, A., Association between amputation, arthritis and osteopenia in British male war veterans with major lower limb amputations. Clin. Rehabil. [online]. 12, pp. 348-353, 1998. Available at: http://www.ncbi.nlm.nih.gov/pubmed/9744670.
Struyf, P.A., van Heugten, C.M., Hitters, M.W. and Smeets, R.J., The prevalence of osteoarthritis of the intact hip and knee among traumatic leg amputees. Arch. Phys. Med. Rehabil. 90, pp. 440-446, 2009. DOI: 10.1016/j.apmr.2008.08.220.
Klotz, R., Colobert, B. and Botino, M.I., Permentiers, influence of different types of sockets on the range of motion of the hip joint by the transfemoral amputee. Ann. Phys. Rehabil. Med. 54, pp. 399-410, 2011. DOI: 10.1016/j.rehab.2011.08.001.
Tranberg, R., Zügner, R., Häggström, E. and Hagberg, K., Does osseointegrated transfemoral amputation prostheses increase the hip joint moment?. Gait Posture. 39(Supple), pp. S125-S126, 2014. DOI: 10.1016/j.gaitpost.2014.04.174.
Levy, J.H., Biomechanics: Principles, trends and applications, Nova Science, New York, [online]. 2010. Available at: http://www.ortopedska-klinika.si/upload/files/Biomechanics_poglavje.pdf.
Ng, K.C.G., Lamontagne, M., Labrosse, M.R. and Beaulé, P.E., Hip joint stresses due to cam-type femoroacetabular impingement: A systematic review of finite element simulations. PLoS One. 11, pp. e0147813, 2016. DOI: 10.1371/journal.pone.0147813.
Hellwig, F.L., Tong, J. and Hussell, J.G., Hip joint degeneration due to cam impingement: A finite element analysis. Comput. Methods Biomech. Biomed. Engin. 19, pp. 41-48, 2016. DOI: 10.1080/10255842.2014.983490.
Sánchez-Egea, A.J., Valera, M., Parraga-Quiroga, J.M., Proubasta, I., Noailly, J. and Lacroix, D., Impact of hip anatomical variations on the cartilage stress: A finite element analysis towards the biomechanical exploration of the factors that may explain primary hip arthritis in morphologically normal subjects, Clin. Biomech. 29, pp. 444-450, 2014. DOI: 10.1016/j.clinbiomech.2014.01.004.
Harris, M.D., Anderson, A.E., Henak, C.R., Ellis, B.J., Peters, C.L. and Weiss, J.A., Finite element prediction of cartilage contact stresses in normal human hips. J. Orthop. Res. 30, pp. 1133-1139, 2012. DOI: 10.1002/jor.22040.
Abraham, C.L., Maas, S.A., Weiss, J.A., Ellis, B.J., Peters, C.L. and Anderson, A.E., A new discrete element analysis method for predicting hip joint contact stresses. J. Biomech. 46, pp. 1121-1127, 2013. DOI: 10.1016/j.jbiomech.2013.01.012.
Anderson, A.E., Ellis, B.J., Maas, S.A., Peters, C.L. and Weiss, J.A., Validation of finite element predictions of cartilage contact pressure in the human hip joint. J. Biomech. Eng. 130, pp. 51008, 2008. DOI: 10.1115/1.2953472.
Henak, C.R., Abraham, C.L., Anderson, A.E., Maas, S.A., Ellis, B.J., Peters, C.L. and Weiss, J.A., Patient-specific analysis of cartilage and labrum mechanics in human hips with acetabular dysplasia. Osteoarthr. Cartil. 22, pp. 210-217, 2014. DOI: 10.1016/j.joca.2013.11.003.
Henak, C.R., Ellis, B.J., Harris, M.D., Anderson, A.E., Peters, C.L. and Weiss, J.A., Role of the acetabular labrum in load support across the hip joint. J. Biomech. 44, pp. 2201-2206, 2011. DOI: 10.1016/j.jbiomech.2011.06.011.
Abraham, C.L., Knight, S.J., Peters, C.L., Weiss, J.A. and Anderson, A.E., Patient-specific chondrolabral contact mechanics in patients with acetabular dysplasia following treatment with peri-acetabular osteotomy. Osteoarthr. Cartil. 25, pp. 676-684, 2017. DOI: 10.1016/j.joca.2016.11.016.
Henak, C.R., Carruth, E.D., Anderson, A.E., Harris, M.D., Ellis, B.J., Peters, C.L. and Weiss, J.A., Finite element predictions of cartilage contact mechanics in hips with retroverted acetabula. Osteoarthr. Cartil. 21, pp. 1522-1529, 2013. DOI: 10.1016/j.joca.2013.06.008.
Genda, E., Iwasaki, N., Li, G., MacWilliams, B.A., Barrance, P.J. and Chao, E.Y.S., Normal hip joint contact pressure distribution in single-leg standing—effect of gender and anatomic parameters. J. Biomech. 34, pp. 895-905, 2001. DOI: 10.1016/S0021-9290(01)00041-0.
Yoshida, H., Faust, A., Wilckens, J., Kitagawa, M., Fetto, J. and Chao, E.Y.S., Three-dimensional dynamic hip contact area and pressure distribution during activities of daily living. J. Biomech., 39, pp. 1996-2004, 2006. DOI: 10.1016/j.jbiomech.2005.06.026.
Brown, T.D. and DiGioia, A.M., III, A contact-coupled finite element analysis of the natural adult hip. J. Biomech., 17, pp. 437-448, 1984. DOI: 10.1016/0021-9290(84)90035-6.
Rapperport, D.J., Carter, D.R. and Schurman, D.J., Contact finite element stress analysis of the hip joint. J. Orthop. Res. Off. Publ. Orthop. Res. Soc., 3, pp. 435-446, 1985. DOI: 10.1002/jor.1100030406.
Ateshian, G.A., Henak, C.R. and Weiss, J.A., Toward patient-specific articular contact mechanics. J. Biomech., 48, pp. 779-786, 2015. DOI: 10.1016/j.jbiomech.2014.12.020.
Shepherd, D. and Seedhom, B., Thickness of human articular cartilage in joints of the lower limb, Ann. Rheum. Dis., [online]. 58, pp. 27-34, 1999. [accessed May 29th of 2013]- Available at: http://www.ncbi.nlm.nih.gov/pmc/articles/PMC1752762/.
Naish, J.H.H., Xanthopoulos, E., Hutchinson, C.E.E., Waterton, J.C.C. and Taylor, C.J.J., MR measurement of articular cartilage thickness distribution in the hip. Osteoarthr. Cartil. 14, pp. 967-973, 2006. DOI: 10.1016/j.joca.2006.03.017.
Li, W., Abram, F., Beaudoin, G., Berthiaume, M.-J., Pelletier, J.-P. and Martel-Pelletier, J., Human hip joint cartilage: MRI Quantitative thickness and volume measurements discriminating acetabulum and femoral head. IEEE Trans. Biomed. Eng., 55, pp. 2731-2740, 2008. DOI: 10.1109/TBME.2008.925679.
Mechlenburg, I., Nyengaard, J.R.R., Gelineck, J. and Soballe, K., Cartilage thickness in the hip joint measured by MRI and stereology – A methodological study. Osteoarthr. Cartil., 15, pp. 366-371, 2007. DOI: 10.1016/j.joca.2006.10.005.
Anderson, A.E., Ellis, B.J., Maas, S.A., Peters, C.L. and Weiss, J.A., Validation of finite element predictions of cartilage contact pressure in the human hip joint. J. Biomech. Eng., 130, pp. 51008, 2008. DOI: 10.1115/1.2953472.
Silver-Thorn, M.B., Steege, J.W. and Childress, D.S., A review of prosthetic interface stress investigations. J. Rehabil. Res. Dev., [online]. 33, pp. 253-266, 1996. [accessed July 13th of 2011]. Available at: http://www.rehab.research.va.gov/jour/96/33/3/pdf/silver-thorn2.pdf
Dassault Systèmes Simulia Corp, D.S.S. Corp, Abaqus 6.12 Documentation, Providence, RI, USA., 2012.
Lacroix, D. and Ramírez Patiño, J.F., Finite element analysis of donning procedure of a prosthetic transfemoral socket. Ann. Biomed. Eng., 39, pp. 2972-2983, 2011. DOI: 10.1007/s10439-011-0389-z.
Harris, M.D., Anderson, A.E., Henak, C.R., Ellis, B.J., Peters, C.L. and Weiss, J.A., Finite element prediction of cartilage contact stresses in normal human hips. J. Orthop. Res. 30, pp. 1133-1139, 2012. DOI: 10.1002/jor.22040.
Henak, C.R., Ellis, B.J., Harris, M.D., Anderson, A.E., Peters, C.L. and Weiss, J.A., Role of the acetabular labrum in load support across the hip joint. J. Biomech., 44, pp. 2201-2206, 2011. DOI: 10.1016/j.jbiomech.2011.06.011.
Henak, C.R., Ateshian, G.A. and Weiss, J.A., Finite element prediction of transchondral stress and strain in the human hip. J. Biomech. Eng., 136, pp. 21021, 2014. DOI: 10.1115/1.4026101.
Anderson, A.E., Ellis, B.J., Maas, S.A. and Weiss, J.A., Effects of idealized joint geometry on finite element predictions of cartilage contact stresses in the hip. J. Biomech. 43, pp. 1351-1357, 2010. DOI: 10.1016/j.jbiomech.2010.01.010.
Li, J., Stewart, T.D., Jin, Z., Wilcox, R.K. and Fisher, J., The influence of size, clearance, cartilage properties, thickness and hemiarthroplasty on the contact mechanics of the hip joint with biphasic layers. J. Biomech., 46, pp. 1641-1647, 2013. DOI: 10.1016/j.jbiomech.2013.04.009.
Russell, M.E., Shivanna, K.H., Grosland, N.M. and Pedersen, D.R., Cartilage contact pressure elevations in dysplastic hips: A chronic overload model. J. Orthop. Surg. Res., 1(6), pp. 1-11, 2006. DOI: 10.1186/1749-799X-1-6.
Van Donkelaar, C.C. and Wilson, W., Mechanics of chondrocyte hypertrophy. Biomech. Model. Mechanobiol., 11, pp. 655-664, 2012. DOI: 10.1007/s10237-011-0340-0.
Stops, A., Wilcox, R. and Jin, Z., Computational modelling of the natural hip: A review of finite element and multibody simulations. Comput. Methods Biomech. Biomed. Engin., 15, pp. 963-979, 2012. DOI: 10.1080/10255842.2011.567983.
Zhang, L. Zhu, M., Shen, L. and Zheng, F., Finite element analysis of the contact interface between trans-femoral stump and prosthetic socket, in: 2013 35th Annu. Int. Conf. IEEE Eng. Med. Biol. Soc., 2013, pp. 1270-1273. DOI: 10.1109/EMBC.2013.6609739.
Cómo citar
IEEE
ACM
ACS
APA
ABNT
Chicago
Harvard
MLA
Turabian
Vancouver
Descargar cita
Licencia
Derechos de autor 2017 DYNA

Esta obra está bajo una licencia internacional Creative Commons Atribución-NoComercial-SinDerivadas 4.0.
El autor o autores de un artículo aceptado para publicación en cualquiera de las revistas editadas por la facultad de Minas cederán la totalidad de los derechos patrimoniales a la Universidad Nacional de Colombia de manera gratuita, dentro de los cuáles se incluyen: el derecho a editar, publicar, reproducir y distribuir tanto en medios impresos como digitales, además de incluir en artículo en índices internacionales y/o bases de datos, de igual manera, se faculta a la editorial para utilizar las imágenes, tablas y/o cualquier material gráfico presentado en el artículo para el diseño de carátulas o posters de la misma revista.