Cálculo de susceptibilidad a deslizamientos mediante análisis discriminante. Aplicación a escala regional
Landslides susceptibility assessment using discriminant analysis. Application on a regional scale
DOI:
https://doi.org/10.15446/dyna.v84n201.61385Palabras clave:
Susceptibilidad a deslizamientos, análisis de riesgo, planificación del territorio (es)Landslide susceptibility, risk assessment, land planning (en)
Recibido: 6 de diciembre de 2016; Revisión recibida: 24 de abril de 2017; Aceptado: 12 de mayo de 2017
Resumen
En el presente artículo expone la aplicación, paso a paso, del método multivariado cuantitativo conocido como Análisis Discriminante, para la obtención de modelos de susceptibilidad a deslizamientos de tierra a escalas regionales. Como propuesta se incorporan variables de contexto dentro del análisis, que pretenden dar cuenta de la acción antrópica dentro del territorio. Se presenta el procedimiento detallado, se aplica a un área específica, obteniendo cinco funciones de susceptibilidad, las cuales se analizan en términos de rendimiento para seleccionar el mejor modelo. Como conclusión, se obtienen valores adecuados de rendimiento de los modelos, confirmando la utilidad del método como paso inicial en el cálculo de riesgo por deslizamiento a escala regional para la ordenación del territorio.
Palabras clave :
Susceptibilidad a deslizamientos, análisis de riesgo, planificación del territorio.Abstract
In this article, we present the stepwise application of the quantitative multivariate method known as Discriminant Analysis to obtain models of susceptibility to landslides at regional scales. As a proposal, context variables were incorporated into the analysis, which aim to account for anthropogenic action within the territory. The detailed procedure is presented, applied to a specific area, obtaining five susceptibility functions, which are analyzed in terms of performance to select the best model. In conclusion, adequate values of performance of the models are obtained, confirming the usefulness of the method as an initial step in the calculation of landslide risk at regional scale for land planning.
Keywords :
Landslide susceptibility, risk assessment, land planning.1. Introducción
Pese a la existencia de un marco de referencia robusto sobre Evaluación de Amenazas y Riesgos de Desastre, elaborado en los últimos 30 años, con teorías concretas, es poco común en nuestro medio contabilizar pérdidas, recolectar datos, y evaluar el riesgo sistemáticamente en términos numéricos. Como consecuencia de ello, no se dispone de opciones de priorización de recursos, al no conocer el riesgo o amenaza asociado a cada porción del territorio y por tanto resulta difícil proteger a las comunidades e inversiones, y reducir la vulnerabilidad frente a futuros impactos.
Una de las amenazas que mayores impactos genera en un entorno Andino como el nuestro, son los procesos de remoción en masa, que presentan un carácter recurrente y producen perdidas que, si bien son contenidas, presentan una tendencia repetitiva año tras año.
Un posible enfoque para analizar el fenómeno, desde un punto de vista cuantitativo, es en función de procesos sucesivos de cálculo que terminan en la zonificación de riesgo. Se inicia definiendo susceptibilidad como la predisposición espacial, intrínseca, del territorio a sufrir daño, lo cual en un escenario posterior debe relacionarse con la frecuencia de ocurrencia, dada por factores detonantes (amenaza), para finalmente, a través de un análisis de exposición y vulnerabilidad, obtener cuantificaciones de riesgo, en términos de pérdidas, métricas asociadas, o zonificaciones para la planificación territorial.
La ocurrencia de deslizamientos es el producto de las condiciones geológicas, hidrológicas y geomorfológicas y la modificación de éstas por procesos geodinámicos, vegetación, usos de la tierra y actividades humanas, así como la frecuencia e intensidad de las precipitaciones y la sismicidad.
Bajo este panorama, existe un fuerte componente antrópico, representado en factores como la localización y características de las carreteras, canales, tuberías, oleoductos y demás elementos, producto de la acción humana; presencia o ausencia de zonas duras o pavimentadas; las áreas de zonas verdes; la localización de sumideros y demás elementos de drenaje y los sitios de descarga de los diversos colectores de agua; alteración de la cobertura vegetal [11,15], entre otros importantes condicionantes que reflejan la presencia humana en el territorio y deben considerarse, preferiblemente de manera cuantitativa en un modelo de susceptibilidad.
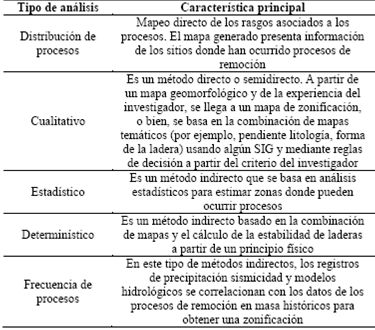
En general se distinguen cuatro principales métodos utilizados en la evaluación y confección de mapas de susceptibilidad del terreno a producir roturas de las laderas [8,16,14]: 1) determinísticos, 2) heurísticos, 3) estadístico-probabilísticos y 4) geomorfológicos, como se condensa en la Tabla 1.
Entre los métodos más conocidos están los modelos multivariantes. Estos analizan la interacción y dependencia de un conjunto de factores concurrentes, sobre la generación de deslizamientos. Los métodos más utilizados son la regresión múltiple y análisis discriminante [7,10,3,1]. El resultado es una serie de funciones basadas en la presencia/ausencia de deslizamientos que son combinación lineal de los factores de mayor significación estadística en la definición de la inestabilidad y consecuente generación de los movimientos de ladera.
Fuente: Elaboración propia, a partir de [4]Tabla 1: Descripción de los diferentes tipos de análisis
2. Análisis discriminante
El análisis discriminante, trata de dividir las laderas o unidades del terreno en dos poblaciones (estable e inestable) utilizando un conjunto de parámetros (variables) característicos de las mismas (por ejemplo, pendiente, litología, orientación, rugosidad, cubrimiento vegetal, entre otras variables disponibles). Esta técnica persigue la separación óptima de las dos poblaciones, minimizando la clasificación errónea de las laderas previamente identificadas como estables o inestables. Las variables independientes seleccionadas se combinan de forma lineal y la función discriminante adopta la forma: D = d1V1 + … + dnVn.
Donde Vi son las variables independientes de mayor significación estadística, Di son los coeficientes de clasificación estimados y D es el valor discriminante de la función.
Actualmente los sistemas de información geográfica SIG facilitan el manejo de grandes volúmenes de información y la aplicación de técnicas cuantitativas en la evaluación de la susceptibilidad [2,5,12]. Mediante los SIG, los factores analizados pueden obtenerse de forma automática, en algunos casos con un menor costo, gracias a los modelos digitales de elevaciones, permitiendo ser almacenados y analizados de forma digital.
En cuanto a metodologías ampliamente aceptadas, los métodos disponibles se dividen en métodos de tipo data-driven, utilizados para evaluación de susceptibilidad a deslizamientos [4] como se presentan en la Tabla 2, los cuales permiten, a partir de la combinación de factores que han generado deslizamientos en el pasado, y tratamientos de tipo estadístico, predecir de manera cuantitativa para áreas aún no afectadas que reúnan condiciones similares. La salida de estos métodos puede expresarse en términos de probabilidad.
Fuente: [4]Tabla 2: Métodos recomendados para evaluación de susceptibilidad a deslizamientos de tipo data-driven [4]

3. Aplicación del análisis discriminante: susceptibilidad a deslizamientos en una cuenca hidrográfica
En aras de proporcionar una metodología paso a paso sobre la aplicación del método Análisis Discriminante, apto para estudios de tipo regional, a continuación, se presenta la aplicación de la técnica al área de la Cuenca del río Chinchiná, en el Departamento de Caldas.
a) Inventario de deslizamientos
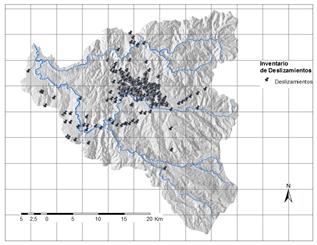
Se cuenta con un set total bruto de 893 puntos georreferenciados donde han ocurrido eventos de deslizamiento previamente, obtenidos a partir de la revisión detallada de registros, la base de datos SIMMA [13]. La Fig.1 muestra los puntos disponibles.
Desde el punto de vista numérico, extraer modelos a partir del inventario disponible, con concentración fuerte de datos en el área urbana, podría generar problemas de sesgo, los cuales llevarían a obtener modelos inapropiados. Adicionalmente, se busca un modelo aplicable a la zona rural de la cuenca; por ello se ha filtrado el conjunto de datos, descartando los registros que se encuentran dentro del perímetro urbano de los dos municipios principales de la cuenca: Manizales y Villamaría, para reducir la marcada influencia que se tiene hacia las áreas urbanas. El número total de puntos considerados, para la totalidad de la cuenca, considerando su situación rural, es de 234 eventos.
b) Factores de propensividad
A partir de la información disponible, se han seleccionado 17 factores potenciales de tres grandes grupos: 1. Distancia a elementos clave; 2. Suelos/Geología; 3. Factores derivados de la topografía. Los factores así obtenidos se explican brevemente en la Tabla 3 y su representación gráfica se presenta de la Fig.2 a la Fig.18.
Figura 1: Inventario de deslizamientos previos en la cuenca del río Chinchiná.
Fuente: Elaboración propiaTabla 3: Factores causales de deslizamiento en la Cuenca del río Chinchiná.

Figura 2: Mapa de coberturas.
Figura 3: Mapa de características geológicas.
Figura 4: Mapa de procesos geomorfológicos.
Figura 5: Modelo digital de elevaciones.
Figura 6: Pendiente del terreno.
Figura 7: Pendiente transformada del terreno.
Figura 8: Orientación de las laderas.
Figura 9: Curvatura del terreno.
Figura 10: Curvatura transversal del terreno.
Figura 11: Curvatura longitudinal del terreno.
Figura 12: Área de cuenca vertiente.
Figura 13: Longitud de cuenca vertiente.
Figura 14: Insolación del terreno.
Figura 15: Distancia a fallas y lineamientos.
Figura 16: Distancia a vías.
Figura 17: Distancia a centros poblados.
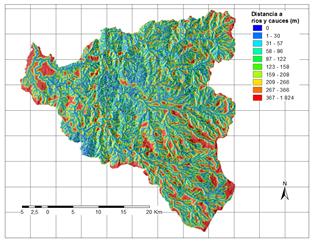
Figura 18: Distancia a ríos y cauces.
a) Muestra de análisis
Con la información disponible se conforma una muestra de datos de 234 eventos de deslizamiento, que constituyen uno de los dos grupos sobre los que se hará el análisis. El otro grupo está constituido por otros 234 puntos elegidos aleatoriamente en el área dónde no hay eventos registrados. En total se tienen 468 puntos que conforman la muestra de análisis constituida en dos grupos: estable (desl=0) e inestable (desl=1).
b) Función discriminante de susceptibilidad a deslizamientos
Es posible elaborar varios modelos a partir de diferentes combinaciones de variables. Un camino razonable es utilizar inicialmente todas las variables y generar un primer modelo para posteriormente valorar la exclusión de algunas de ellas en modelos posteriores. A continuación, se describen los pasos para construir un primer modelo por este método.
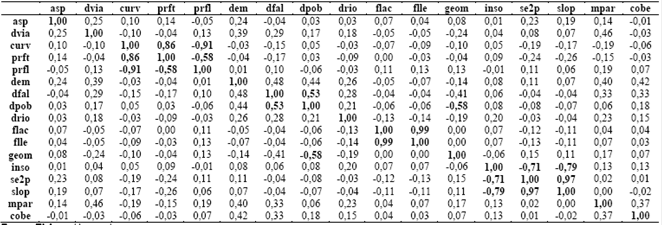
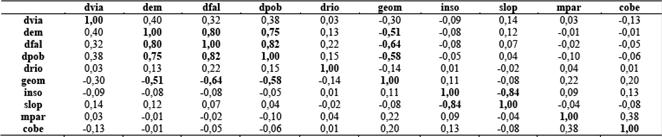
Un paso preliminar es hacer un análisis de correlaciones. Con el propósito de remover variables redundantes (altamente correlacionadas) de los datos, se calcula la matriz de correlaciones que aparece en la Tabla 4 La matriz ofrece una visión de la interrelación entre las variables de entrada.
Como puede notarse, existen algunos factores que presentan altas correlaciones; en este caso debe analizarse por pares qué variable es conveniente conservar y cual debe descartarse. Las variables con más fuerte correlación se muestran en la Tabla 5.
El test de igualdad de medias entre grupos mide el potencial de cada variable independiente antes de que el modelo sea creado. Cada test muestra el resultado de un análisis one-way ANOVA para la variable independiente usando la variable de agrupación como factor. Si el valor de significancia es mayor a 0.10, la variable probablemente no contribuye al modelo. Los valores Lambda de Wilks son otra medida del potencial de la variable. Valores pequeños indican que la variable es mejor discriminando entre grupos. Los valores de Lambda de Wilks y el F de Fisher para cada variable se presentan en la Tabla 6.
Fuente: Elaboración propiaTabla 4: Matriz de correlaciones.
Fuente: Elaboración propiaTabla 5: Variables con correlaciones altas.

Los gráficos correspondientes a los valores de la Tabla 6 permiten visualizar de mejor manera el grado de influencia de los factores de entrada en el modelo. En el caso del F de Fisher (Fig.19), para valores bajos, empiezan a perder influencia los factores; el caso del Lambda de Wilks (Fig.20) es en sentido inverso, a partir de cierto valor (alto) los factores ya no aportan. El punto de corte se establece en valores de significancia por encima de 0.10, en este caso, a partir de la variable prft.
Fuente: Elaboración propiaTabla 6: Test de igualdad de Media entre grupos.
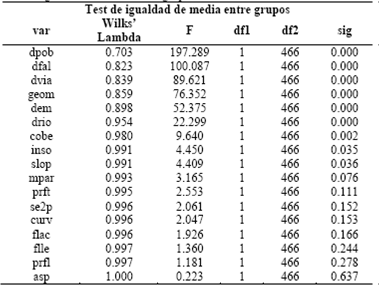
Figura 19: Test de igualdad de medias entre grupos (F de Fisher).
El análisis de varianza lleva a descartar las variables asp, prfl flle, flac, curv, se2p, pfrt, que aparecen en color azul en la Tabla 6, dado su bajo poder discriminante.
La correlación de los predictores o colinealidad se evalúa usando la matriz de covarianza entre grupos (Tabla 7). Una inspección de la correlación de las covarianzas muestra las correlaciones altas entre los predictores dem, dfal y dpob, y slop e inso.
Figura 20: Test de igualdad de medias entre grupos (Lambda de Wilks).
Ante esta situación, es conveniente hacer un razonamiento: Considérese por ejemplo una variable de cobertura vegetal y otra de elevación. La vegetación puede variar sistemáticamente según la elevación. Un supuesto de independencia condicional de estas dos capas no es razonable. En ese caso debe valorarse cómo son afectados los patrones de predicción si el supuesto de independencia condicional es violado [6].
Fuente: Elaboración propiaTabla 7: Correlación de covarianzas.
Dado el origen diferente de las variables dem, dpob y dfal, el hecho que ninguna de ellas se deriva de otra, y su alta influencia en el proceso discriminante de celdas estables e inestables (ver tablas y gráficas anteriores), se decide continuar el análisis con todas ellas, para posteriormente elaborar modelos alternativos descartando algunas y comparar los resultados. En el caso de slop e inso, se opta por probar con cada una también.
El test Box’s M es utilizado para probar la homogeneidad de las matrices de covarianza, chequea el supuesto de igualdad de covarianzas entre grupos. Los log determinantes (Tabla 8) son una medida de la variabilidad de los grupos. Valores altos corresponden a grupos más variables. Diferencias grandes en los valores indican que los grupos tienen diferentes matrices de covarianza.
Fuente: Elaboración propiaTabla 8: Chequeo de homogeneidad de covarianzas.

Cuando el valor Box’s M (Tabla 9) es significante (Sig.=0), se debe chequear el modelo discriminante mediante matrices separadas para verificar si se obtienen valores de clasificación diferentes. En este caso, los modelos con matrices separadas produjeron resultados de clasificación muy similares o en algunos casos inferiores a los obtenidos con un solo grupo.
Fuente: Elaboración propiaTabla 9: Test Box M.

Fuente: Elaboración propiaTabla 10: Lambda de Wilks para el modelo general. Fuente: Elaboración propia

Fuente: Elaboración propiaTabla 11: Valores propios y correlación para la función discriminante.

Fuente: Elaboración propiaTabla 12: Matriz de estructura del modelo.

El Lambda de Wilks (Tabla 10) es una medida de la manera en que cada función separa los casos en grupos. Es igual a la proporción de varianza total en los coeficientes discriminantes no explicada por diferencias entre los grupos. Pequeños valores de lambda indican gran poder discriminante de la función. El Chi-cuadrado asociado chequea la hipótesis de que las medias de las funciones son iguales entre grupos. Valores pequeños de Sig. Indican que la función discriminante tiene resultados mejores que el azar en la separación entre grupos.
La tabla de valores propios (Tabla 11) proporciona información sobre la eficacia de la función discriminante. Cuando existen dos grupos, la correlación canónica es la medida más útil en la tabla, y es equivalente a la correlación de Pearson entre los coeficientes discriminantes y los grupos.
Hay varias tablas que evalúan la contribución de cada variable al modelo, incluyendo los tests de igualdad de medias grupales, los coeficientes de la función discriminante y la matriz de estructura.
La matriz de estructura (Tabla 12) muestra la correlación de cada predictor con la función discriminante y constituye una prueba de la importancia que cada variable tiene dentro del modelo. El orden en esta matriz es igual al sugerido por el test de igualdad de medias grupales y es diferente del que aparece en la tabla de coeficientes estandarizados que constituye la ecuación del modelo lineal.
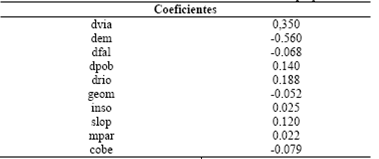
Los coeficientes estandarizados (Tabla 13) permiten comparar variables medidas en diferentes escalas. Coeficientes con valores absolutos altos corresponden a variables con alto poder discriminante. Puede observarse que dentro de las variables más influyentes individualmente se encuentran dpob, dem, dvia, slope y drio.
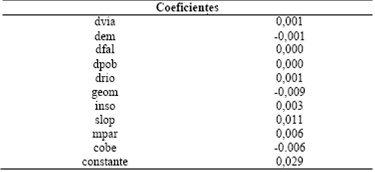
El modelo lineal obtenido con la función discriminante se ensambla con los coeficientes canónicos de la Tabla 14.
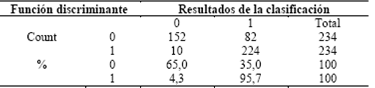
La Tabla 15 resume los resultados del modelo inicial en cuanto a capacidad de clasificación de casos. Puede leerse que el modelo acierta en la clasificación del 65% de las celdas estables, clasifica correctamente el 95.7% de las celdas inestables, y en total, tiene un acierto del 80.3% de casos.
Fuente: Elaboración propiaTabla 13: Coeficientes canónicos estandarizados. Fuente: Elaboración propia
Fuente: Elaboración propiaTabla 14: Coeficientes de la función discriminante. Fuente: Elaboración propia
Fuente: Elaboración propiaTabla 15: Resultados de clasificación del modelo inicial.
La ecuación lineal obtenida se ha aplicado a toda el área bajo estudio y sus valores se han normalizado entre 0 y 1. Este procedimiento hace que la asignación posterior de categorías de susceptibilidad sea más sencilla. El mapa resultado de esta clasificación se presenta a continuación (Fig.21). Se trata de un mapa ráster con valores entre cero y uno que refleja el grado relativo de susceptibilidad de cada celda del terreno.
Figura 21: Susceptibilidad mediante una función discriminante.
a) Diferentes modelos discriminantes probados
Se han elaborado siete modelos diferentes cambiando las variables incluidas en cada caso y se ha probado el desempeño en la clasificación de los datos. La configuración de cada uno de los modelos probados se presenta en la Tabla 16. El modelo MOD1 ya se presentó junto a la descripción del procedimiento en la Fig.21.
Los tres mejores modelos obtenidos fueron MOD1, MOD3 (Fig.22) Y MOD5, exhiben parámetros de rendimiento similares como se observa en la Tabla 17. El mejor modelo en capacidad de clasificación y sensibilidad es MOD3.
b) Rendimiento de los modelos obtenidos
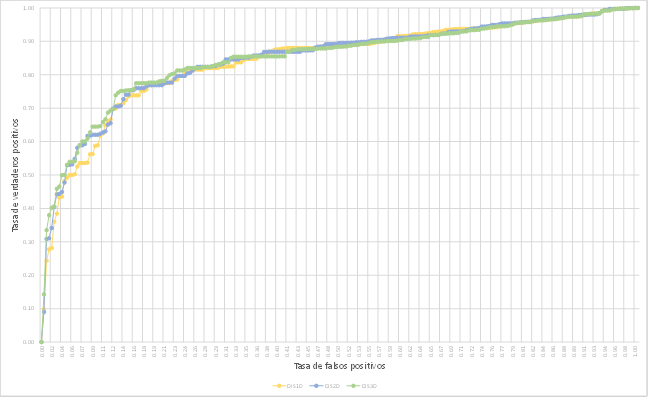
En cuanto a sus capacidades de clasificación, en la Fig.23 se presentan las curvas ROC obtenidas para cada modelo. La curva es un dibujo de la probabilidad de tener un verdadero positivo (un valor correctamente predicho) versus la probabilidad de un falso positivo (un valor incorrectamente predicho). Un modelo ideal muestra un valor del área bajo la curva AUC cercano a 1, mientras un valor cercano a 0,5 evidencia un inadecuado modelo.
Fuente: Elaboración propiaTabla 16: Diferentes modelos de función discriminante probados.
Figura 22: Modelo función discriminante MOD3.
Los valores del área bajo la curva para el caso de celdas inestables (deslizamientos), se muestran en la Tabla 17 bajo el nombre AUC_D; de allí se desprende que el modelo con mejor capacidad de clasificación es DIS03, con un valor AUC de 0.883, seguido muy de cerca por los otros dos modelos. En cuanto a clasificación de celdas estables, los valores AUC_E están cercanos a 0.5 en los tres casos, siendo deseables valores tendientes a cero. Sin embargo, para efectos de elección de un modelo de susceptibilidad a deslizamientos, es preferible aquel que acierte en clasificar correctamente celdas inestables que estables.
Fuente: Elaboración propiaTabla 17: Parámetros de rendimiento modelos discriminantes.
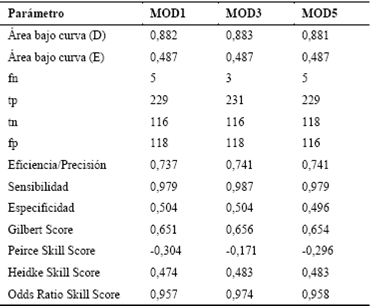
Figura 23: Curvas de rendimiento modelos discriminantes.
4. Conclusiones
Cuando se habla de planificación del territorio, se requiere una valoración o dimensionamiento como paso inicial para fines de gestión. Aunque en la literatura abundan enfoques cualitativos para valoración, y tradicionalmente se han obtenido modelos desde este enfoque, se prefiere el uso de análisis cuantitativos, pues permiten eliminar la subjetividad de los estudios, y hacen posible la comparación directa del nivel de susceptibilidad y amenaza entre áreas. De otro lado, es la única manera posible de hacer estimaciones posteriores de amenaza, en términos de probabilidad de ocurrencia, y de riesgo, en términos de niveles de pérdidas.
Un aspecto diferenciador de la metodología expuesta es la incorporación de factores de contexto, que reflejan la influencia antrópica dentro del territorio, aspecto fundamental cuando se aborda el tema de riesgo dado su carácter dinámico de construcción social.
La metodología planteada pretende interrelacionar variables para obtener zonificaciones y en ningún caso construir modelos que obedezcan a principios físicos, los cuales requieren otro enfoque. Se ha presentado una de las métricas posibles para obtener modelos de susceptibilidad en términos cuantitativos, lo cual constituye el primer paso en un análisis de riesgo por deslizamientos. Posteriormente deberá obtenerse una estimación de los umbrales detonantes y con ello un cálculo de amenaza, en términos de probabilidades de excedencia del umbral, para después analizar el modelo de exposición y vulnerabilidad y llegar al cálculo de riesgo en términos cuantitativos de pérdidas.
Aunque existen otras metodologías más sofisticadas para obtener modelos de susceptibilidad, los resultados obtenidos demuestran que siguiendo una serie de pasos lógicos, es posible llegar a zonificaciones aceptables para escalas de análisis de tipo regional, con precisiones del orden de 75% y sensibilidades altas.
Bibliografía
Referencias
Baeza, C. and J., Corominas. Assessment of shallow landslide susceptibility by means of multivariate statistical techniques. Earth Surface Processes and Landforms 26(12), pp. 1251-1263. DOI: 10.1002/esp.263. 2001.
Bianchini, S., Del Soldato, M., Solari, L., Nolesini, T., Pratesi, F. and Moretti, S., Badland susceptibility assessment in Volterra municipality (Tuscany, Italy) by means of GIS and statistical analysis. Environmental Earth Sciences. 75(889), pp. 1-14, 2016. DOI: 10.1007/s12665-016-5586-5
Carrara, A., Multivariate models for landslide hazard evaluation. Mathematical Geology, 15(3), pp. 403-426, 1983. DOI: 10.1007/BF01031290
Corominas, J., et al., Recommendations for the quantitative analysis of landslide risk. Bulletin of Engineering Geology and the Environment 73(2), pp. 209-263, 2014. DOI: 10.1007/s10064-013-0538-8
Chacón, J., Irigaray, C. y Fenández, T.,Metodología para la cartografía regional de movimientos de ladera y riesgos asociados mediante un sistema de información geográfica. III Simposio Nacional Sobre taludes y laderas inestables. La Coruña. 1, pp. 121-133, 1992.
Chung, C., Using likelihood ratio functions for modeling the conditional probability of occurrence of future landslides for risk assessment. Computers Geosciences, 32(8), pp. 1052-1068, 2006. DOI: 10.1016/j.cageo.2006.02.003 0.000.100.200.300.400.500.600.700.800.901.000.000.020.040.060.070.090.110.120.140.160.180.190.210.230.240.260.280.290.310.330.350.360.380.400.410.430.450.470.480.500.520.530.550.570.590.600.620.640.650.670.690.710.720.740.760.770.790.810.820.840.860.880.890.910.930.940.960.981.00Tasa de verdaderos positivosTasa de falsos positivosDIS1DDIS2DDIS3D Londoño-Linares / DYNA 84(201), pp. 278-289, June, 2017 289
Jones, F.O., Embody, D.R. and Peterson, W.L., Landslide along the Columbia river valley, Northestern Washington. Geological Survey Professional Paper, 367, pp. 1-94, 1961.
Lorentz, JF., Calijuri, ML., Marques, EG. And Baptista, AC., Multicriteria analysis applied to landslide susceptibility mapping. Natural Hazards. 83, pp. 41-52, 2016. DOI: 10.1007/s11069-016-2300-6
Myronidis, D., Papageorgiou, C. and Theophanous, S., Landslide susceptibility mapping based on landslide history and analytic hierarchy process (AHP). Natural Hazards. 81, pp.245-263, 2016. DOI: 10.1007/s11069-015-2075-1
Neuland, H., A prediction model of landslips. Catena, 3, pp. 215-230, 1976.
Persichillo, M.G., Bordoni, M. and Meisina, C., The role of land use changes in the distribution of shallow landslides. Science of the Total Environment. 574, pp. 924-937, 2017. DOI: 10.1016/j.scitotenv.2016.09.125
Santacana, N., Baeza, C., Corominas, J., de Paz, A. y Marturià, J., Análisis de la susceptibilidad del terreno a la formación de deslizamientos superficiales mediante el uso de un Sistema de Información Geográfica. Aplicación a La Pobla de Lillet (Pirineo Oriental). En: F.J. Ayala y J. Corominas (eds). Mapas de susceptibilidad a los movimientos de ladera con técnicas SIG. Fundamentos y aplicaciones en España. IGME. Madrid, pp. 55-82, 2003.
SGC. Sistema de Información de Movimientos en Masa SIMMA. Servicio Geológico Colombiano, 2016.
Soeters, R. and van Westen, C.J., Slope instability. Recognition, analysis and zonation. In: A.K. Turner and R.L. Schuster (Editors), Landslide: Investigations and mitigation. Special Report 247. Transportation Research Board. National Research Council. National Academy Press., Washington, D.C, pp. 129-177, 1996.
Suarez, J., Deslizamientos Volumen I: Análisis geotécnico. Publicaciones Universidad Industrial de Santander. Bucaramanga, Colombia. 2009, 582 P.
Van Westen, C.J., GIS in landslide hazard zonation: a review with examples from the Colombian Andes. In: Price, M.F. and Heywood, D.I. (eds.) Taylor and Francis, London, 1994, pp. 135-165.
Youssef, A., Pourghasemi, H., El-Haddad, B. and Dhahry, B., Landslide susceptibility maps using different probabilistic and bivariate statistical models and comparison of their performance at Wadi Itwad Basin, Asir Region, Saudi Arabia. Bulletin of Engineering Geology and the Environment, 75, pp. 63-78, 2016. DOI: 10.1007/s10064-015-0734-9
Cómo citar
IEEE
ACM
ACS
APA
ABNT
Chicago
Harvard
MLA
Turabian
Vancouver
Descargar cita
CrossRef Cited-by
1. Cleyver A. Rivera, Sivmny V. Valqui-Reina, Lenny F. García-Naranjo, Candy Lisbeth Ocaña-Zúñiga, Erick A. Auquiñivin-Silva, Sandy R. Chapa-Gonza, Dennis Cieza-Tarrillo, Cristhiam G. Vergara, Alex J. Vergara. (2025). Geospatial Landslide Risk Mapping Using AHP and GIS: A Case Study of the Utcubamba River Basin, Peru. Applied Sciences, 15(17), p.9423. https://doi.org/10.3390/app15179423.
Dimensions
PlumX
Visitas a la página del resumen del artículo
Descargas
Licencia
Derechos de autor 2017 DYNA

Esta obra está bajo una licencia internacional Creative Commons Atribución-NoComercial-SinDerivadas 4.0.
El autor o autores de un artículo aceptado para publicación en cualquiera de las revistas editadas por la facultad de Minas cederán la totalidad de los derechos patrimoniales a la Universidad Nacional de Colombia de manera gratuita, dentro de los cuáles se incluyen: el derecho a editar, publicar, reproducir y distribuir tanto en medios impresos como digitales, además de incluir en artículo en índices internacionales y/o bases de datos, de igual manera, se faculta a la editorial para utilizar las imágenes, tablas y/o cualquier material gráfico presentado en el artículo para el diseño de carátulas o posters de la misma revista.