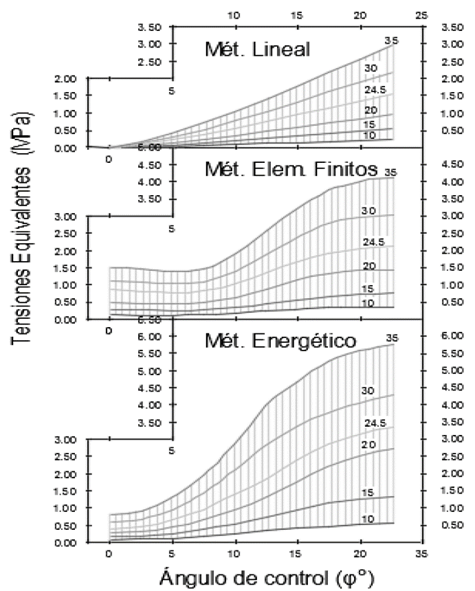
Método de cálculo para la determinación de las tensiones en volantes de rayos rectos
Calculation method for the determination of stresses in right-wing flywheels
DOI:
https://doi.org/10.15446/dyna.v85n204.64478Palabras clave:
sistemas hiperestáticos, tensiones equivalentes, volantes, llanta, rayos (es)hyper static systems, equivalent stress, flywheel, rim, rays (en)
Recibido: 27 de abril de 2017; Revisión recibida: 15 de octubre de 2017; Aceptado: 25 de noviembre de 2017
Resumen
En el trabajo se profundiza en dos métodos de cálculo de sistemas hiperestáticos aplicables para la evaluación de la resistencia de volantes de llantas y rayos los que se aplican al volante de un molino de martillos. Los resultados de los métodos analíticos se validaron mediante un Análisis de Elementos Finitos resultando diferencias inferiores al 10%. Las tensiones equivalentes en la llanta se aproximan a cero en el plano medio del rayo y aumentan a medida que se aleja del mismo, y a lo largo de los rayos se mantienen constante. Se apreció además que en todos los casos estudiados las tensiones equivalentes disminuyen a medida que el número de rayos aumenta ya que se incrementa la rigidez de los volantes. En el trabajo se obtienen nomogramas que permiten determinar la tensión equivalente en la llanta en función del número de rayos y la velocidad de operación.
Palabras clave:
sistemas hiperestáticos, tensiones equivalentes, volantes, llanta, rayos.Abstract
This research deepens on the methods to the solution of the hyper static systems applicable for the assessment resistance of flywheels which are applied to a flywheel of a hammer mill. The results of the analytical methods were validated through a Finite Element Analysis, the results show differences minors than 10%. The equivalent strength in the rim is almost zero in the middle plane of the beam and increases as it moves away from it, and remains constant throughout the rays. It was also observed that in all the studied cases the equivalent tension decreases when the number of rays increases because of the flywheels stiffness increases. Also, graphics tools are obtained to a fast determination of the equivalent tension in the rim according to the number of rays and the speed of operation.
Keywords:
hyper static systems, equivalent stress, flywheel, rim, rays.1. Introducción
Los volantes han sido utilizados desde el siglo XIX con la función de estabilizar el ciclo de trabajo de máquinas rotatorias como lo son: máquinas de vapor, motores de combustión interna, prensas y otras. En sus inicios, su diseño se realizó siguiendo criterios empíricos hasta principios del siglo XX cuando se desarrollan las ecuaciones principales para su diseño partiendo de los criterios de funcionamiento [1-4] y de resistencia mecánica [4-7].
1.1 Volantes tradicionales
Un volante convencional es un dispositivo mecánico giratorio Fig. 1, que almacena energía cinética en forma de rotación [1,2,4], la misma es proporcional al cuadrado de su velocidad de rotación, de ahí que para acumular energía se aumenta su velocidad y al consumirse la energía acumulada su velocidad se reduce. Esta forma de energía también se conoce como momento de inercia debido a que su acumulación y/o entrega se realiza mediante la aplicación de un momento torsional. Otra función de estos elementos es la de suavizar el flujo de energía entre una fuente de potencia y su carga, de ahí que se empleen en equipos con cargas irregulares de trabajo tales como motores de combustión interna, compresores reciprocantes, prensas punzonadoras y troqueladoras, martinetes, etc. [1-4].
Figura 1: Volantes almacenadores de energía cinética.
En la segunda mitad del siglo XX su utilización disminuyó debido a la generalización de los motores eléctricos que son más estables en su funcionamiento que los motores de combustión, sin embargo, a finales de siglo con el desarrollo de nuevos materiales y de la electrónica, su aprovechamiento como acumulador de energía ha despertado gran interés incrementando notable su utilización. [7-15]
1.2. Actualidad de los volantes
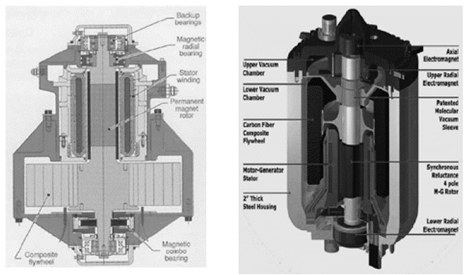
En la actualidad la obtención de nuevos materiales compuestos [8-11] y el desarrollo de la microelectrónica han permitido la aplicación de los volantes en campos como el aeroespacial [12], el desarrollo de vehículos eléctricos [13] y en el almacenamiento de energía proveniente de fuentes renovables [14], lo que ha dado lugar a los denominados almacenadores cinéticos de energía eléctrica KERS (Kinetic Energy Restore System) y los SUPS (Secondary Unit Power Supply) [3] que se muestran en la Fig. 2. Los KERS y los SUPS se conectan al sistema exterior a través de cables eléctricos al igual que una batería eléctrica. En la industria aeroespacial donde los requerimientos son mayores se minimizan las pérdidas por fricción al emplear cojinetes magnéticos de alto desempeño y trabajan en vacío [3,10, 11,15], la energía acumulada se puede mantener durante horas e incluso días y presentan gran compacidad con un alto intercambio de potencia por unidad de masa y una elevada velocidad de giro, las velocidades periféricas alcanzadas superan la velocidad del sonido para compensar la baja densidad de los materiales compuestos [9,11].
Figura 2: Volantes almacenadores cinéticos de energía eléctrica.
Estos dispositivos superan, en algunos aspectos a los sistemas clásicos de almacenamiento de energía como las baterías químicas, que tienen un proceso de carga lento, también se distinguen por su versatilidad ya que se adaptan fácilmente a cualquier necesidad energética mediante una adecuada regulación electrónica. En su contra, tienen pérdidas en la entrada y salida de energía debido al rendimiento eléctrico del motor.
La aplicación más destacable y reciente ha sido su empleo como suministro de energía eléctrica a satélites en la industria aeroespacial donde la energía proveniente de las placas fotovoltaicas durante las horas solares se almacena de forma similar a las baterías eléctricas, pero con menos peso y mayor fiabilidad. [12].
También se aplican en vehículos híbridos y eléctricos, cuya velocidad es discontinua y la energía cinética se perdería en forma de calor durante el frenado, siendo capaces de almacenar gran parte de la energía de frenado en un tiempo mínimo y devolverla en la aceleración posterior, fenómeno que se hace llamar frenado regenerativo [11,13].
Aunque las fallas en los volantes no son frecuentes deben prevenirse adecuadamente pues por sus dimensiones y condiciones de trabajo suelen ocurrir en forma de explosiones y tener graves consecuencias [16], sin embargo, se reconoce la dificultad de los métodos para la evaluación de su resistencia [17], trabajo que se desarrolla a través de modelos de elementos finitos por la carencia de métodos analíticos
El presente trabajo tiene como objetivo la aplicación de distintos métodos de solución para la obtención de las tensiones de manera rápida y efectiva a través de nomogramas para un volante como el que se menciona a continuación.
2. Materiales y métodos
2.1. Método de las deformaciones
El método es válido para un sistema de barras sometidas a tracción o compresión, el cálculo de los desplazamientos elásticos de los diferentes puntos del sistema de barras articuladas se analiza a través de las ecuaciones de la elástica, determinándose las tensiones axiales en todos los elementos del sistema y por la ley de Hooke se hallan las magnitudes de los alargamientos absolutos de los elementos. Para la solución de estos sistemas tiene gran importancia las relaciones geométricas entre los desplazamientos de los elementos que lo conforman, resultando la base para resolver los distintos grados de hiperestaticidad a través de las ecuaciones de compatibilidad según sea el caso.
2.2. Método energético aplicando el teorema del trabajo mínimo
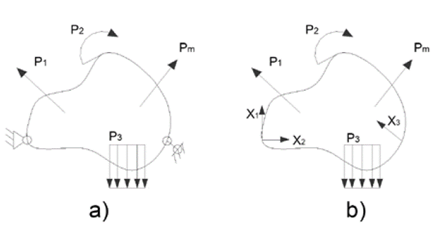
En el método energético aplicando el Trabajo Mínimo hay que considerar un sistema sobre el cual actúan un grupo de cargas exteriores P1, P2, P3, … , Pm y las reacciones de apoyo X1, X2, X3, … , Xn, tal y como se muestra en la Fig. 3. Si se cumple la Ley de Hooke y el Principio de Superposición de las Cargas se pueden hallar las reacciones de apoyo partiendo del Trabajo Mínimo (Teorema de Castigliano) que plantea que; la energía potencial de deformación que se acumula en el sólido elásticamente deformable será una función del sistema de cargas exteriores Pj y de las reacciones en los apoyos Xi, de manera que:
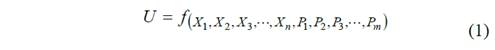
Como se conoce, los desplazamientos δi en las direcciones correspondientes a las reacciones de apoyo son iguales a cero, y se puede plantear como ∂U/∂Xi = 0. Por lo que planteando un sistema de ecuaciones se pueden determinar las reacciones en los apoyos X1, X2…Xn, y representa el desplazamiento en la dirección i, δi = ∂U/∂Xi = 0 que se puede expresar en función del desplazamiento provocado por una fuerza unitaria colocada en la posición de Xi, como δi = δii • Xi, si se deriva δi con respecto a la fuerza Xi, se obtendrá:
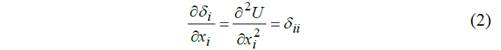
Se concluye que: En los sistemas isostáticos o hiperestáticos, las reacciones en los apoyos toman valores tales que la energía potencial de deformación del sistema alcanza un valor mínimo. Del mismo se desprende que al añadir a un sistema de ligaduras suplementarias, las reacciones en estas, se redistribuyen de manera que la energía potencial de deformación del sistema siempre disminuye.
Figura 3: Esquema de análisis del método del trabajo mínimo. a) Sistema isostático b) Sistema equivalente.
2.3. Determinación de las tensiones en un volante de rayos rectos aplicando el método de las deformaciones.
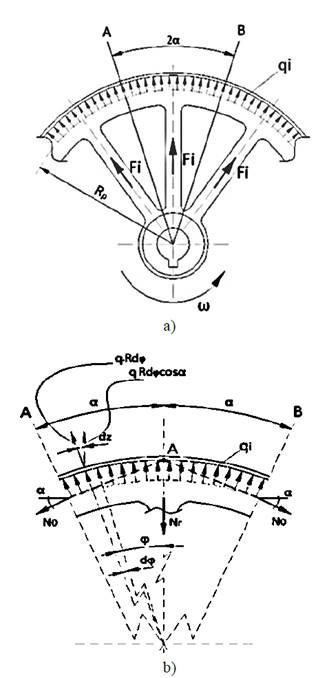
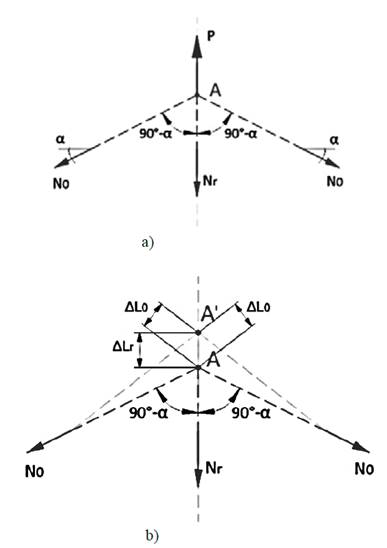
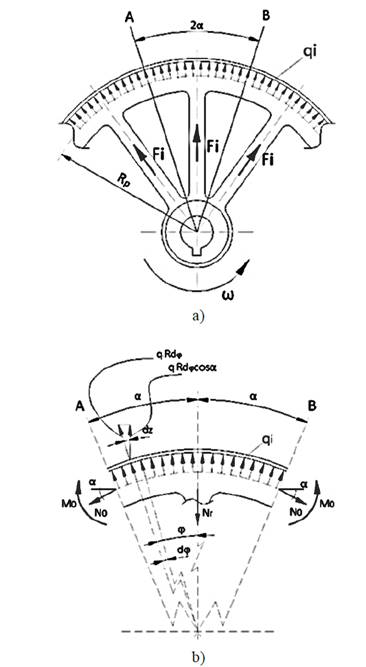
En esta sección se desarrolla el método para la determinación las tensiones en un volante por el método de las deformaciones, mediante el análisis de la llanta y los rayos como un conjunto de barras con todas las fuerzas externas actuando en un punto de concurrencia; las cargas actuantes son; las fuerzas de inercia uniformemente distribuida provocada por la masa de la llanta qi , y los rayos Fi , determinado por la velocidad de giro ( =cte. El diagrama de cuerpo libre de la Fig. 4, permitirá la determinación de las fuerzas interna, sin considerar los momentos que actúan en la llanta ya que el sistema se reduce a tres barras concurrentes en el punto imaginario A, dicho punto se obtiene de trazar un plano medio a través de uno de los rayos y trazar una línea tangente a la circunferencia primitiva indicada por Rp cortando perpendicularmente a los radios de las secciones A y B donde se están analizando. En la Fig. 4a se aprecia la sección a tratar y la distribución de la fuerza de inercia de la llanta y de los rayos provocada por la velocidad angular, y posteriormente se muestra una ampliación detallada de la sección analizada ver Fig. 4b.
Figura 4: Análisis realizado en un volante para la obtención de las fuerzas internas.
Aislando estas tres barras imaginarias que forman la llanta y el rayo, Fig. 5a y concentrando toda la fuerza de inercia en el punto A, se determina las deformaciones del sistema que provoca que dicho punto se desplace, Fig. 5b, la representación de esta deformación se encuentra exagerada para facilitar su comprensión.
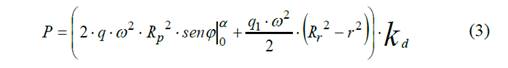
Donde
q, q1 - valor de la fuerza de inercia distribuida de la llanta y del rayo respectivamente.
( - velocidad angular.
α - ángulo de control para el tramo analizado
Rp, Rr, r - Radio primitivo, interior de la llanta y exterior del cubo respectivamente.
kd - coeficiente que tiene en cuenta las cargas dinámicas.
kd = (1,3….1,6)
Figura 5: Sistema de barras que forma en la llanta con el rayo.
Planteando las ecuaciones de la estática en el plano e igualando a cero la suma de las proyecciones sobre los ejes de todas las fuerzas que actúan sobre la parte analizada.

Debido a la simetría del sistema las fuerzas internas N0 de cada extremo son iguales. Trabajando con la otra ecuación la Ec. 4 se obtiene
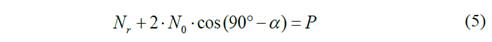
Se plantea la ecuación de compatibilidad de las deformaciones como ecuación suplementaria para resolver el grado de hiperestaticidad del sistema, donde la deformación de las barras de los extremos ΔL0 es la misma por simetría del sistema.
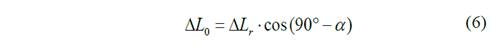
Aplicando la ley de Hooke en la ecuación de compatibilidad de las deformaciones se obtiene
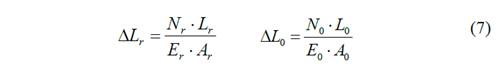
Sustituyendo en las ecuaciones anteriores en la Ec. 6.
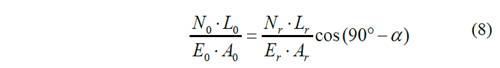
Para el caso a resolver, las áreas de las secciones transversales de la llanta y los rayos son iguales, el Módulo de Elasticidad no varía puesto que es el mismo material para todo el volante, y las longitudes a analizar son iguales o se pueden calcular a través de una función trigonométrica. Entonces se puede decir que:
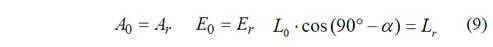
Sustituyendo Ec. 9 en Ec. 8, despejando y sustituyendo en Ec. 5 se obtienen Nr y No
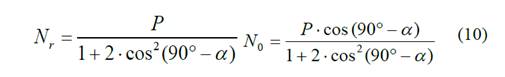
2.4. Determinación de las tensiones en un volante de rayos rectos aplicando el teorema del trabajo mínimo.
En esta sección se calculan las tensiones en el volante por el método energético anteriormente referido. Se conoce el valor de masa por unidad de longitud q (kg/m) de la llanta y la caracterización de la sección transversal; área y momento de inercia de la llanta A0, I0 respectivamente, n es el número de rayos cuya masa por unidad de longitud se define como q1 (kg/m) y área de la sección transversal del rayo A1, la velocidad de giro se define como ω y se considera constante para facilitar el estudio ver Fig. 6a.
Figura 6: Diagrama de cuerpo libre para el cálculo de las fuerzas internas Aplicando del Teorema del Trabajo Mínimo.
Por simetría en las secciones A y B no existen tensiones tangenciales, o sea, fuerzas internas de cortante. Solo existen fuerzas normales (No) y los momentos flectores (M0) por lo que en el tramo de llanta analizado solo actúan las fuerzas de inercia qi, N0, M0 y la fuerza que ejerce el rayo sobre la llanta Nr como se muestra en la Fig. 6b.
La fuerza de inercia qi se determina como:
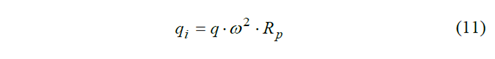
Donde
q-valor de la carga distribuida.
(-velocidad angular.
Rp -radio primitivo o medio de la llanta.
Para determinar las fuerzas que actúan en el volante se plantea el equilibrio de las fuerzas en la dirección del eje y-y obteniéndose fuerzas actuantes en el tramo analizado
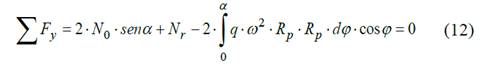
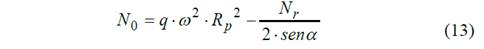
Donde
Nr - fuerza interna del rayo.
α - ángulo de control (variable que define el punto en el que se está calculando).
Existen dos incógnitas en la ecuación resultante por lo que se necesitan ecuaciones complementarias para determinar las fuerzas No , Mo y Nr estas se pueden obtener al aplicar el Teorema del Trabajo Mínimo.
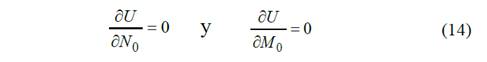
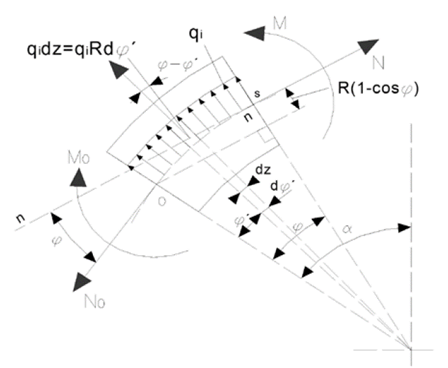
Partiendo de que los desplazamientos en estas direcciones son cero, hallando la energía potencial de deformación del sistema, y determinando las fuerzas internas que surgen en una sección cualquiera de la llanta y del rayo en función de q, No , Mo , Nr y (. La Fig. 7 se muestran las fuerzas internas N y Mf que actúan en una sección S.
Figura 7: Fuerzas internas N y M para una sección S cualquiera de la llanta.
Plateando las ecuaciones de equilibrio Σ Fn = 0 y Σ M0 = 0 se obtienen N y Mf .
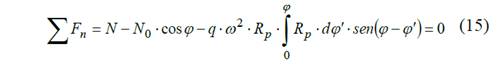
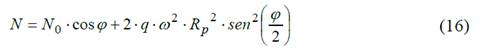
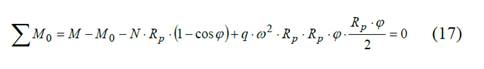
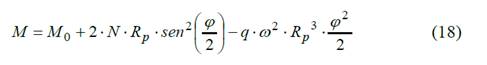
La fuerza interna N 1 en una sección cualquiera del rayo se obtiene del equilibrio del rayo Fig. 8.
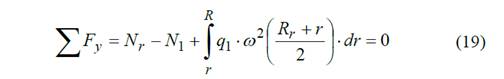
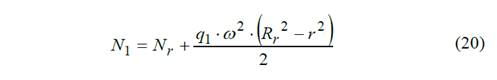
Donde
Rr - radio exterior del rayo (medido desde el centro hasta el radio interior de la llanta).
r - radio interior del rayo (medido desde el centro hasta el radio exterior del cubo).
Figura 8: Diagrama de cuerpo libre para la fuerza interna en la sección cualquiera del rayo.
La energía potencial de deformación del tramo analizado se determina como:
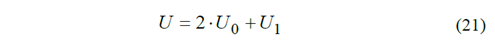
Donde
U - energía total de deformación.
U0 - energía de deformación de la llanta.
U 1 - energía de deformación del rayo.
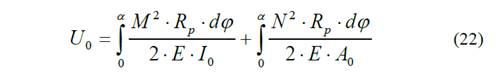
Donde
E - módulo de elasticidad de primer orden del material.
I0 - momento de inercia de la sección de la llanta.
A0 - área de la sección de la llanta.
φ - ángulo que representa la magnitud de la sección que se está analizando
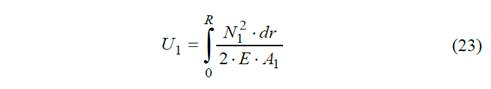
Donde
N1 - fuerza interna del rayo.
A1 - área de la sección transversal del rayo.
r - radio interior del rayo.
Obteniéndose la expresión general para la energía potencial de deformación.
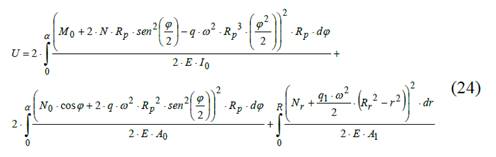
Derivando parcialmente esta función con respecto a N0 y M0 como se describe en la Ec. 14 y simultaneando las ecuaciones obtenidas con la Ec. 20 se obtiene
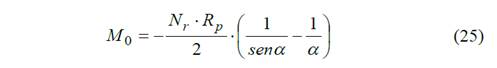
El signo negativo (-) indica que el momento M0 es contrario.
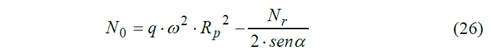
Para el caso del rayo la fuerza se determina como
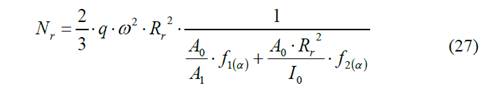
Donde
b, h - ancho y el espesor de la llanta respectivamente en (m).
El momento de inercia de la llanta I
0 se determina como el de una barra 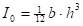
Las variables f1(α) y f2(α) son funciones que caracterizan la cantidad de rayos del volante
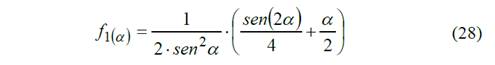
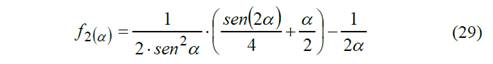
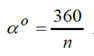 Ángulo entre rayos.
Ángulo entre rayos.
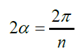 Valor en radianes.
Valor en radianes. 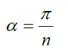
Con la fuerza del rayo Nr determinada por la Ec. 27, se puede calcular el momento flector en la sección transversal de la llanta M 0, por la Ec. 25, y del mismo modo la fuerza normal en la sección transversal de la llanta N 0, por la Ec. 26, la fuerza interna N y momento flector M que actúan en una sección cualquiera de la llanta n-n ver Fig. 7, se determinan por las expresiones 16 y 18 respectivamente, teniendo en cuenta que φ es la variable de control.
La tensión de tracción en una sección cualquiera ( de la llanta se halla por la expresión de la tensión en barras curvas (Ecuación de Winkler - Bach).
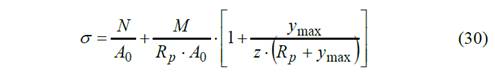
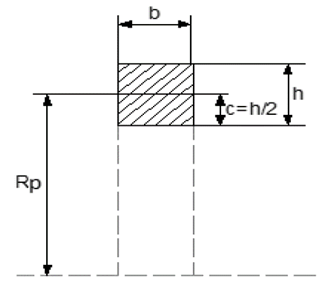
Para un volante de sección rectangular Fig. 9,
Figura 9: Representación de la sección rectangular de un volante.
Distancia del plano centroidal al borde más alejado de la llanta Ymáx (m).
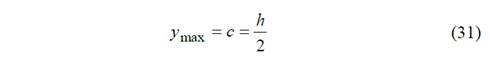
Parámetro geométrico de la sección según el grado de exactitud se aumenta el número de términos de la función.
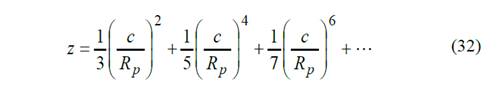
Con estos parámetros se pueden determinar las tensiones σ a medida que se varía el ángulo φ en una sección cualquiera S de la llanta, bajo la acción de una fuerza normal N y el momento flector M que también es función del ángulo φ.
La tensión en el rayo σ1 está dada por la fuerza interna de tracción producto a la inercia provocada por la acción de la llanta y del mismo rayo.
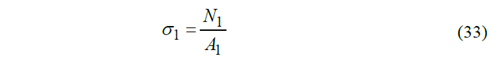
La fuerza interna en cualquier parte del rayo N1 es determinada como sigue
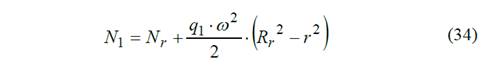
3. Resultados y discusión
3.1. Determinación de las tensiones aplicando el método de los elementos finitos
Para realizar los cálculos de las tensiones en el volante a través del Método de los Elementos Finitos se dibuja un modelo en 3D con un software CAD, analizándose un caso real. Para este estudio se ha seleccionado el volante de seis rayos de un molino de martillo perteneciente al área de recepción de materias primas de una fábrica de cemento, el cual es un elemento de gran porte y con características geométricas y de trabajos bien definidas lo que facilita su estudio, y luego se modela y simula por el método antes mencionado empleando el ANSYS 14.5. En el trabajo fueron analizadas diferentes variantes constructivas variando el número de rayos con el objetivo de poder llegar a conclusiones de las diferentes metodologías empleadas. A continuación, se muestran las propiedades del material empleado y el flujo de trabajo seguido ver Tabla 1 y los resultados obtenidos se muestran a continuación.
Fuente: Los autoresTabla 1: Propiedades del material empleado.


Caso de estudio analizando la influencia del número de rayos en las tensiones de la llanta:

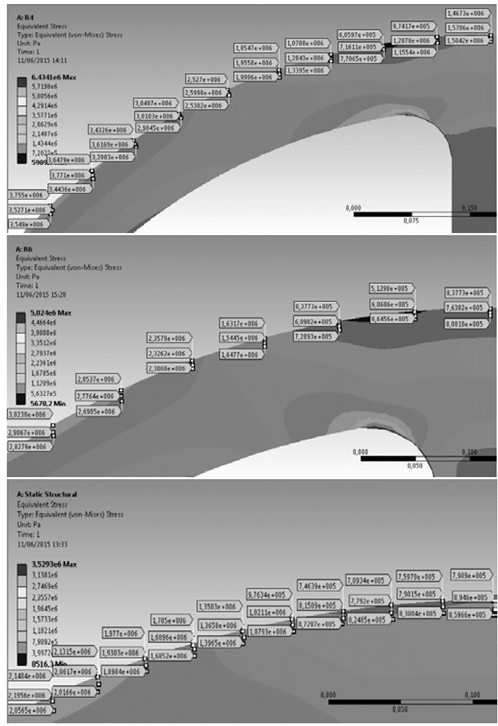
En la Fig. 10 se muestra campo de tensiones obtenido de los volantes luego del análisis realizado por ANSYS.
Figura10. Tensiones: equivalentes del Volante para 4,6 y 8 rayos, vista frontal.
En la Fig. 11 se muestra la zona de interés de la Fig. 10 en escala aumentada con el objetivo de facilitar la explicación de los resultados, comenzado por el volante de cuatro rayos, seis y ocho respectivamente.
Figura 11: Tensiones por la 4ta Teoría de Resistencia de Hubber-Von Mises-Hencky en la llanta.
La tensión de Von Mises obtenidas presentan valores extremos mínimos en la zona de transición rayos-llanta y se presentan los mayores en la zona intermedia entre dos rayos. Los valores de tensiones son menores a medidas que aumenta el número de rayos ya que la rigidez del sistema aumenta, un fenómeno similar se aprecia en la distribución prácticamente contante en las tensiones de los rayos por estar sometidos únicamente a tracción.
Para la obtención de las tensiones en las llantas se ha colocado probetas de control en puntos donde se habían calculado el ángulo φ en los métodos anteriores, para cada valor de ángulo se obtuvieron tres valores y se promediaron para graficar esta referencia con el fin de comparar con los demás métodos analizado y de esta forma validarlos.
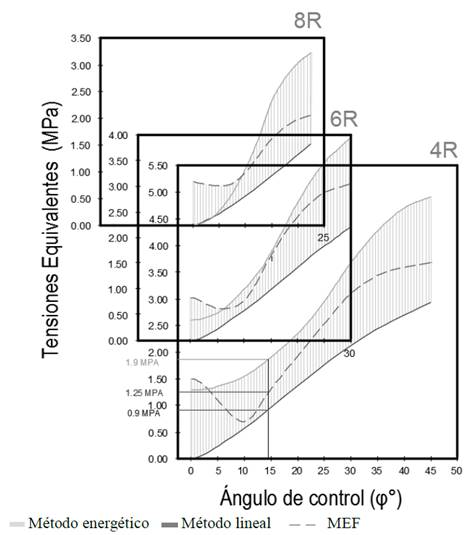
En la gráfica comparativa de la Fig. 12 se muestran las tensiones en el tramo analizado de la llanta con cuatro, seis y ocho rayos, también se muestran los resultados obtenidos por el Método Energético con el color gris claro, el gris oscuro representa los resultados por el Método de Elementos Finitos y el gris oscuro interrumpido los resultados del Método Lineal, estos resultados son obtenidos a 24.5 rad/s la velocidad de trabajo del volante bajo condiciones estables de trabajo. Se puede apreciar la clara influencia que tiene el número de rayos en el volante los que determina la rigidez del sistema, esto es corroborado por los tres métodos empleados para dicho cálculo.
Figura 12: Comparación de las Tensiones en la llanta.
Como se puede apreciar existen diferencias en cuanto al grado de exactitud de los diferentes métodos empleados, si se toma como base comparativa el Método de los Elementos Finitos por considerarlo como el de mayor exactitud. Se puede comprobar que al aplicar el Método Energético se sobre calculan las tensiones casi un 10%, lo mismo sucede al aplicar el Método Lineal donde los valores obtenidos también se encuentran por debajo de los resultados del patrón de comparación. Este error relativo de 10 % de las tensiones pueden fluctuar en dependencia del ángulo que se esté analizando debido al comportamiento del gráfico de tensiones por el Método de Elementos Finitos que es la referencia para cada caso ver Fig. 12. Estos errores relativos son en muchos casos manejable en la ingeniería debido a la complejidad del problema [17,18].
En los tres métodos de cálculo aplicados el comportamiento de la tensión equivalente es similar, se incrementa a medida que el ángulo de control crece, en el caso del Método Energético la tensión equivalente siempre es mayor a la calculada por el MEF lo que indica que siempre se estará del lado seguro al usarlo (se tiene una reserva de resistencia en los cálculos) por lo que es el método que se recomienda. Por otra parte, el Método lineal se encuentra siempre por debajo del MEF por lo que no es recomendado usarlo como método definitivo o decisorio.
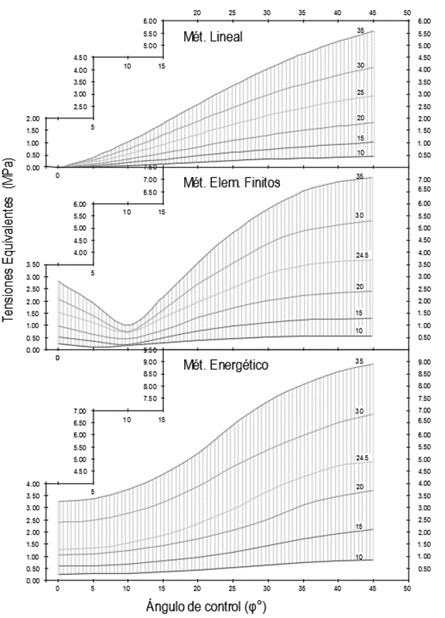
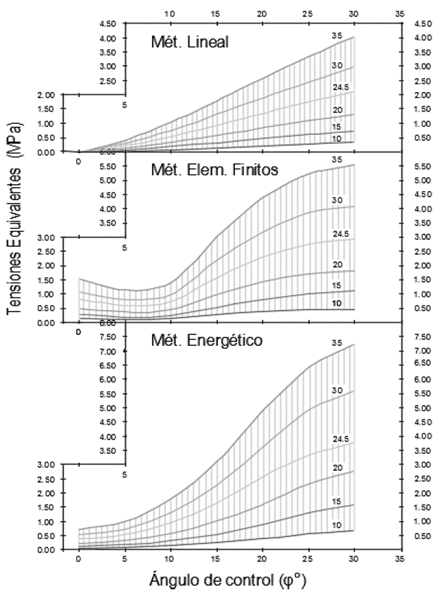
En esta sección se calculan las tensiones equivalentes en la llanta aplicando los tres métodos de cálculos tratados en el trabajo y se evalúan para las distintas variantes; volante con cuatro, seis y ocho rayos a velocidades de entre 10 y 35 rad/s para toda la amplitud del ángulo de control. Con los resultados se construyen los nomogramas mostrados en las Fig. 13, 14 y 15 que permiten determinar de forma rápida el comportamiento de la tensión equivalente en la llanta y sirven como herramienta para evaluar la resistencia de diseños preliminares de volantes si se conoce la velocidad de operación sin necesidad de desarrollar modelos complejos por elementos finitos.
Figura 13: Tensiones en una llanta de 4 rayos.
Figura 14: Tensiones en una llanta de 6 rayos.
Figura 15: Tensiones en una llanta de 8 rayos.
Un ejemplo se obtiene en el gráfico comparativo de la Fig. 12 donde para un volante de cuatro rayos que se desea conocer las tensiones equivalentes a una velocidad de 24.5 rad/s se obtiene que para el Método Energético el valor es 1.9 MPa, por el Método de los Elementos Finitos este valor sería de 1.25 MPa y empleando el Método Lineal 0.9 MPa.
4. Conclusiones
Los métodos analizados en este estudio permitieron comprobar que las tensiones equivalentes para los tres casos tratado: llanta de cuatro, seis y ocho rayos respectivamente, tienen una tendencia creciente a medida que el ángulo de control aumenta, y este comportamiento es similar en cada uno de los métodos analizados; Método Lineal, Método de Elementos Finitos, Método Energético y concordantes con los resultados de trabajos anteriores [17].
Los nomogramas desarrollados permiten al cálculo rápidos de las tensiones en volantes de 4,6 y 8 rayos rectos durante el diseño inicial de estos dispositivos, se recomienda la aplicación de los obtenidos por el método energético por tener un mayor margen de seguridad.
Bibliografía
Referencias
Norton, R. L. Diseño de máquinas: un enfoque integrado, 4a ed., México, Prentice Hall, 2011. pp. 34-50.
Norton, R. L. Diseño de maquinaria: síntesis y análisis de máquinas y mecanismos. 4a ed., México, McGraw-Hill, 2009. pp. 60-122.
Krack, M., Secanell, M., Mertiny, P. Rotor Design for High-Speed Flywheel Energy Storage Systems, 2ed., China, Intech, 2011. pp. 1-29. http://www.intechopen.com/books/energy-storage-in-the-emerging-era-ofsmart-grids/rotor-design-for-high-speed-flywheel-energy-storage-systems/
Bhandari V. B. Design of Machine Elements in Mechanical, 3a ed., New Delhi, Tata McGraw-Hill, 2010. pp. 77-112.
Mouleeswaran-Senthil, K. and Yogesh, K. Optimization of flywheel materials using geneticalgorithm. ACTA TECHNICA CORVINIENSIS – Bulletin of Engineering, Vol. 4, 2012. [15 de Abril 2014]. Disponible en: http://acta.fih.upt.ro/pdf/2012-4/ACTA-2012-4-04.pdf
Thirugnanam, A., Rakesh, L. and Rakesh, R. Computer Aided Design of Flywheel Using ‘C’ Program. Middle-East Journal of Scientific Research, 20(5), pp. 577-579, 2014. DOI: 10.5829/idosi.mejsr.2014.20.05.11337
Rathod-Balasaheb S. and Rajmane, M. A Case Study on Design of a Flywheel for Punching Press Operation. International Journal of Engineering and Advanced Technology (IJEAT), 3(4), 2014. [2 Julio 2014]. Disponible en: http://www.me.metu.edu.tr/courses/me418/index%20_files/flywheeldesignfor%20a%20punchpress.pdf
Krishnan. K. Chawla. Composite Materials Science and Engineering. 2a ed., New York, Springer‐verlag, 2001. pp.320-362.
Herbst, J., Manifold, S., Murphy, B., Price, J. et al., Design, Fabrication and Testing of 10 MJ Composite Flywheel Energy Storage Rotors. SAE Technical Paper 981282, 1998. DOI: https://doi.org/10.4271/981282.
DAI – Xingjian, ZHANG – Kai and ZHANG – Xiao. Design and test of a 300Wh composites flywheel energy storage prototype with active magnetic bearings, in International Conference on Renewable Energies and Power Quality (ICREPQ’11) ( 2011, Las Palmas de Gran Canaria, Spain). European Association for the Development of Renewable Energies, Environment and Power Quality (EA4EPQ) , Las Palmas de Gran Canaria, Spain, 2011, p. 6. DOI: https://doi.org/10.24084/repqj09.341
Ripoll-Masferrer Ll. Análisis y diseño de volantes de inercia de materiales compuestos, tesis (Doctorado en Ingeniería), España, Universidad Politécnica de Cataluña, 2005, 233 pp.
Christopher D. A., Beach R. Flysheel Technology Development Program for Aerospace Aplication. IEEE AES System Magazine, 13(6), pp. 9 – 14, 1998. DOI: 10.1109/62.683723
Álvarez J., Callejón I., Forns S., Bosch R., Salomón G., Küik J. Acumuladores cinéticos. Aplicación a vehículos de tracción urbana. Anales de ingeniería mecánica, 14(1), 2002. [16 Enero 2015]. Disponible en: http://www.asoc-aeim.es/anales.html
Jefferson C. M., Ackerman M. A. Flywheel Variator Energy Storage System. Energy Conversion and Management-Elsevier, 37(10), 1996. DOI: https://doi.org/10.1016/0196-8904(96)00007-6
Sudipta S., Abhik B., Sai-Tejesh G., Srikanth S.P. Computer aided design & analysis on flywheel for greater efficiency. International Journal of Advanced Engineering Research and Studies, (IJAERS). 1 (2), 2012. [fecha de consulta Nov 10 de 2017]. Disponible en: https://pdfs.semanticscholar.org/c38e/b66c612813ee4166181e56c8c3da0b9d2c17.pdf
Gallagher, Patrick, and Jonathan W. Gabrys. "Containment ring for flywheel failure." U.S. Patent No. 6,182,531. 6 Feb. 2001.
Dhengle, S. M., Bhope, D. D., & Khamankar, S. D. (2012). Investigation of stresses in arm type rotating flywheel. International Journal of Engineering Science and Technology (IJEST), 4 (2), 2012 [fecha de consulta Nov 20 de 2017]. Disponible en: https://www.idc-online.com/technical_references/pdfs/mechanical_engineering/Investigation%20Of%20Stresses%20In%20%20Arm%20Type%20Rotating%20Flywheel.pdf
Wilmer V., Mendoza R. and Triana G. Análisis estructural mediante simulación IAO en una estructura de carga y su validación, Revista INGE CUC. 8 (1), 2012. [fecha de consulta]. Disponible en: https://www.researchgate.net/publication/314211709_Analisis_estructural_mediante_simulacion_IAO_en_una_estructura_de_carga_y_su_validacion
López A. G., et al. Análisis de esfuerzos en un apero de tracción animal, empleando métodos experimentales y numéricos, Ingenierías. 9(33), 2006. [fecha de consulta]. Disponible en: http://ingenierias.uanl.mx/33/33_analisis.pdf
Cómo citar
IEEE
ACM
ACS
APA
ABNT
Chicago
Harvard
MLA
Turabian
Vancouver
Descargar cita
Licencia
Derechos de autor 2018 DYNA

Esta obra está bajo una licencia internacional Creative Commons Atribución-NoComercial-SinDerivadas 4.0.
El autor o autores de un artículo aceptado para publicación en cualquiera de las revistas editadas por la facultad de Minas cederán la totalidad de los derechos patrimoniales a la Universidad Nacional de Colombia de manera gratuita, dentro de los cuáles se incluyen: el derecho a editar, publicar, reproducir y distribuir tanto en medios impresos como digitales, además de incluir en artículo en índices internacionales y/o bases de datos, de igual manera, se faculta a la editorial para utilizar las imágenes, tablas y/o cualquier material gráfico presentado en el artículo para el diseño de carátulas o posters de la misma revista.