Herramienta de software para determinar constantes ópticas en celdas solares tipo película delgada
A software tool to determine optical constants in thin film solar cell
DOI:
https://doi.org/10.15446/dyna.v85n206.70003Palabras clave:
software, constantes ópticas, películas delgadas semiconductoras, celdas solares (es)manuscript software, optical constants, semiconductor thin films, solar cells (en)
Recibido: 25 de enero de 2018; Revisión recibida: 25 de julio de 2018; Aceptado: 2 de agosto de 2018
Resumen
En este trabajo se desarrolló una herramienta de software que permite determinar las propiedades ópticas de materiales semiconductores, esta herramienta es de utilidad para investigadores que trabajan en la caracterización de películas delgadas semiconductoras. El software calcula las constantes ópticas: índice de refracción (n), coeficiente de absorción (α) y brecha de energía prohibida (Gap), además del espesor aproximado de la película; con el programa desarrollado se calcularon las constantes ópticas de películas delgadas de ZnS, SnS:Bi y SnS2:Bi, que son usadas como capas buffer y absorbentes en celdas solares, en este trabajo se presentan los resultados obtenidos con una película de SnS2:Bi. El software fue creado en el lenguaje de programación Python dentro de una interfaz sencilla inglés-español y para desarrollarlo se tuvo en cuenta el método propuesto por Swanepoel, el cual toma como base el espectro de transmitancia experimental del material semiconductor.
Palabras clave:
software, constantes ópticas, películas delgadas semiconductoras, celdas solares.Abstract
In this work, it was developed a software tool that allows determining the optical properties of semiconductor materials, this tool is useful for researchers working on the characterization of semiconductor thin films. The software calculates the optical constants: index of refraction (n), coefficient of absorption (α) and prohibited energy gap (Gap), in addition to the approximate thickness of the film; with the developed program were calculated optical constants of thin films of ZnS, SnS:Bi, and SnS2:Bi, which are used as buffer layers and absorbers in solar cells, this paper presents the results obtained with a SnS2:Bi film. The software was created in the Python programming language within a simple English-Spanish interface and in order to develop it, the method proposed by Swanepoel, based on the experimental transmittance spectrum of the semiconductor material, was taken into account.
Keywords:
manuscript software, optical constants, semiconductor thin films, solar cells.1. Introducción
La creciente demanda mundial de energía ha guiado a los seres humanos a la búsqueda permanente de nuevos combustibles y fuentes alternativas de energía, principalmente las que provienen de fuentes naturales como la energía eólica, la mareomotriz y la solar, entre otras. La energía proveniente del Sol es una de las más utilizadas debido a sus grandes ventajas como disponibilidad en todos los lugares de la Tierra, no tiene costo, es silenciosa y es durable. La energía solar fotovoltaica encabeza la capacidad de generación de energía y se considera una nueva fuente de generación competitiva en muchos mercados emergentes en el mundo. La energía solar fotovoltaica fue la principal fuente de inclusión de capacidad de generación adicional en el año 2016 (48% más que en 2015) [1], debido en gran medida a la mejora en la competitividad, incremento en la demanda de energía eléctrica y a un mejor conocimiento del potencial de la energía solar fotovoltaica ya que los países tratan de reducir la contaminación y las emisiones de CO2.
En la actualidad cerca del 90% del mercado de la tecnología de celdas solares está dominado por materiales basados en silicio, el cual ha demostrado ser una tecnología robusta en los módulos fotovoltaicos, pero teniendo en cuenta el alto costo de las láminas de silicio, su probabilidad de reducción del mismo tiende a disminuir, lo que lleva a la búsqueda de nuevas tecnologías y nuevos materiales que además puedan ofrecer ventajas como mayor disponibilidad, estabilidad y menor toxicidad. Entre los materiales más estudiados se encuentran películas delgadas de CdTe, kesteritas (CZTS), SnS, Cu(In,Ga)Se2 y materiales compuestos como CuO/ZnO, CIS/TiO2 [2].
Uno de los aspectos relevantes al realizar la caracterización de películas delgadas es, sin lugar a dudas, la determinación de constantes ópticas [3]; la cual constituye una de las fases iniciales en el proceso de diseño de celdas solares usando películas delgadas semiconductoras. Aunque existen varios métodos para la determinación de las constantes ópticas [4] se encuentra que el método de Swanepoel [5] es uno de los mejores y más usados para caracterización óptica de películas delgadas semiconductoras, aislantes o dieléctricos sobre sustratos transparentes [6-8].
En un principio las envolventes máxima y mínima del espectro se solían realizar a mano, lo que conducía a considerables errores, por lo cual se plantea el uso de algoritmos para ordenadores. Un primer algoritmo se propone en [9], el cual usa interpolación por curvas de Bezier. De manera casi contemporánea, en [10] se presenta un algoritmo basado en aproximaciones parabólicas entre puntos sucesivos del espectro, el cual fue desarrollado en MATLAB. Posteriormente, en [11] se presenta una formulación programación no-lineal sin restricciones sobre el método de Swanepoel, el cual se resuelve mediante el uso del método del gradiente espectral. Finalmente, en [12] se realiza un proceso de suavizado del espectro seguido de una interpolación mediante polinomios de Hermite; sin embargo, los cálculos los realiza sobre el espectro de reflectancia. En nuestro trabajo se propone usar el cálculo a partir del espectro de Transmitancia.
Este trabajo pretende aportar al estudio de las energías renovables, específicamente en la caracterización óptica de los materiales semiconductores usadas en la fabricación de celdas solares tipo película delgada. Las propiedades ópticas de un material semiconductor se determinan a través del conocimiento de sus constantes ópticas.
El enfoque principal de este trabajo fue diseñar una herramienta de software que permita la caracterización óptica de los materiales semiconductores con el fin de determinar su índice de refracción (n), coeficiente de absorción (α) y brecha de energía prohibida (Gap).
2. Software desarrollado
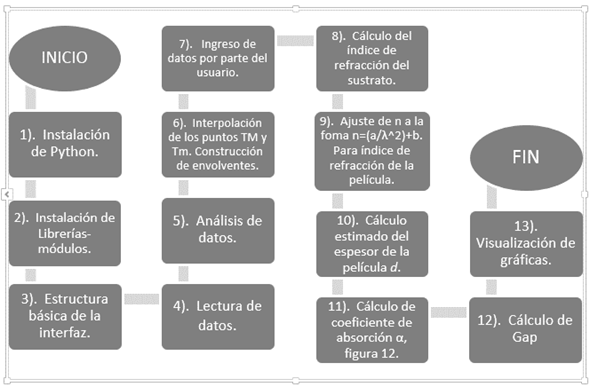
Las investigaciones, análisis de fórmulas y rutinas de código realizadas durante este trabajo dieron como resultado una herramienta de software creada en el lenguaje de programación Python, que lleva como nombre C.O.P.S® (Constantes Ópticas de Películas delgadas Semiconductoras); el software permite hallar las constantes ópticas de películas delgadas semiconductoras como índice de refracción, coeficiente de absorción y brecha de energía prohibida (gap) y una aproximación de su espesor, dentro de una interfaz sencilla inglés-español. Dentro de las librerías que se usaron para la construcción de la interfaz gráfica están entre otras: Tkinter, Matplotlib, Scipy, Numpy, todas con tareas específicas; en la Fig. 1 se presenta un diagrama donde se evidencia el proceso de construcción del software.
Figura 1: Diagrama de construcción del programa C.O.P.S.
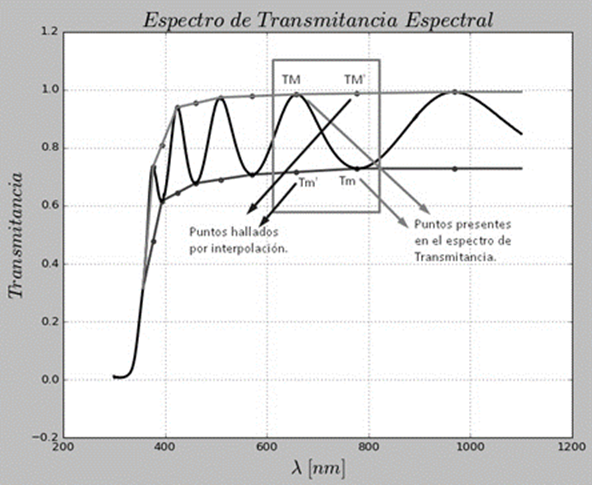
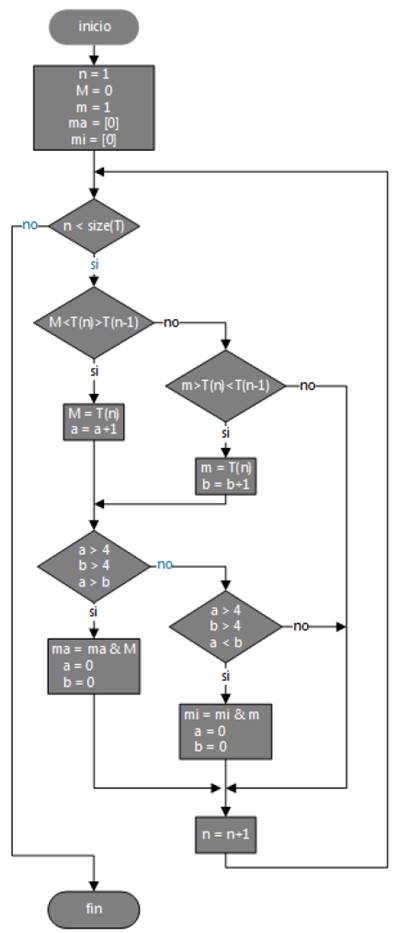
El desarrollo del software se basó en el método propuesto por Swanepoel [5] y en [13], que parte de medidas de espectros de transmitancia experimentales. Un primer paso es la creación de la rutina de código encargada de abrir un archivo de texto (.txt) donde está registrado un espectro de transmitancia experimental (Transmitancia en función de longitud de onda - T vs λ), para realizar un análisis riguroso de dichos datos del espectro; se realiza la detección de los puntos máximos y mínimos del espectro de transmitancia, una vez extraídos estos puntos con sus respectivos valores de longitud de onda (λ en nm) se procede a hacer una interpolación para hallar las envolventes máxima y mínima continuas (TM y Tm respectivamente). Con las envolventes se pueden hallar los puntos TM’ y Tm’, que son los valores de un máximo correspondiente a un mínimo dentro de la envolvente y viceversa. Los puntos TM’ y Tm’ se evidencian de una manera gráfica en la Fig. 2 y la rutina usada para el cálculo de los máximos y mínimos de transmitancia del espectro se presentan en la Fig. 3. En la rutina, T es el vector de transmitancia, ma es el vector de puntos máximos y mi es el vector de puntos mínimos.
Figura 2: Espectro de transmitancia mostrando los puntos TM’ y Tm’.
Figura 3: Rutina para el cálculo de los máximos y mínimos de transmitancia.
En el programa el usuario debe ingresar un valor de espesor (d) si lo tiene, además del índice de refracción del sustrato (s), si no es ingresado ninguno de estos valores el software hará los cálculos con el valor calculado automáticamente y el valor por defecto respectivamente. El cálculo de s, se calculará para muestras que el usuario decida no tomar este valor como constante a lo largo de todo el espectro de transmitancia como se presenta en la eq. (1).
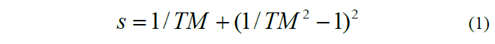
Donde TM son los valores correspondiste a los puntos máximos en la matriz de máximos y mínimos calculados luego de realizar la interpolación.
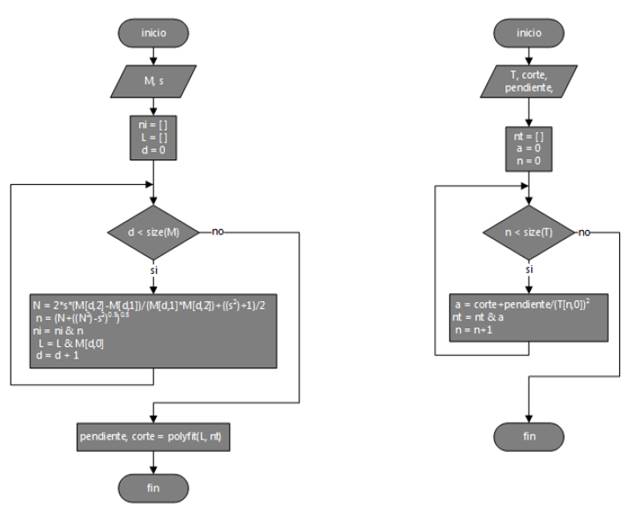
Para el cálculo del índice de refracción del material semiconductor (n), se tiene en cuenta la dispersión normal en el rango visible. Como las envolventes no existen en la zona de alta absorción no se puede hallar el índice de refracción de una forma analítica, por lo tanto, se aproxima por la ecuación Cauchy, eq. 2 [14].
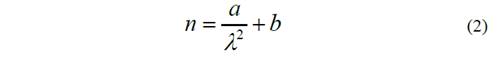
Este procedimiento se presenta en la imagen de flujo doble de la Fig. 4, donde M es una matriz con los máximos, mínimos y sus respectivas longitudes de onda y s es el índice de refracción del sustrato. Como resultado de este proceso se obtiene el índice de refracción de la película para todo el espectro en estudio denotado por nt.
Figura 4: Método para el cálculo del índice de refracción del semiconductor.
Una vez calculado el índice de refracción para todo el rango del espectro experimental se procede con el cálculo del espesor de película si el usuario no ha ingresado el valor previamente.
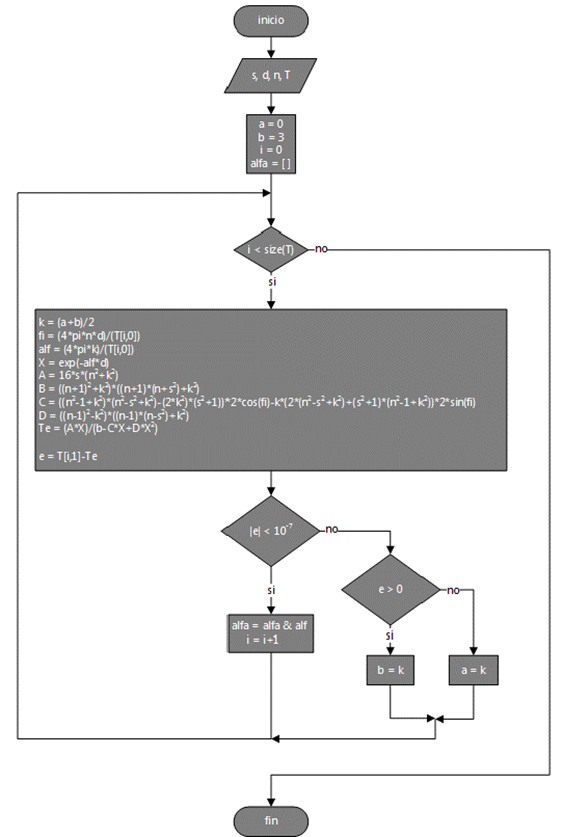
Para el cálculo del coeficiente de absorción α, se presenta el método de bisección de la Fig. 5, donde s es el índice de refracción del sustrato, d es el espesor de la película, n es el vector de índice de refracción de la película en el rango de espectro estudiado y T es la matriz de transmitancia. a y b se definen al inicio de dicha rutina y son los límites del rango de k. La expresión e=T[i,1]-Te se refiere a la diferencia entre el valor de la transmitancia experimental y el valor de transmitancia teórica calculado con el valor de k.
Figura 5: Rutina del método numérico para el cálculo del coeficiente de absorción.
Las iteraciones dentro de la rutina se realizan para cada valor de la longitud de onda hasta que el valor de e sea menor a 10-7, si esto se cumple durante n iteraciones se da por terminado el ciclo, si no, se procede a preguntar por el valor de e de nuevo, si este es mayor a cero (0) se asigna el valor de k a b y vuelve a realizarse el proceso con un nuevo rango de k y si por el contrario es menor a cero (0) se le asigna el valor de k a a y se realiza el mismo proceso; el método reduce el rango de k en un 50% por cada iteración.
En la Fig. 6 se muestra la estructura para el cálculo del Gap de los materiales semiconductores, en esta rutina T es la matriz de transmitancia, alfa es el vector de coeficientes de absorción, x es el vector hv, y es el vector (αhv)2 . En la rutina de la izquierda se crean los vectores hv y (αhv)2 y en la rutina de la derecha se halla la región de mayor pendiente sobre la cual se traza un recta paralela y su punto de corte con el eje x (hv) es el valor del Gap.
Figura 6: Método para el cálculo del Gap del semiconductor.
3. Comparación de resultados experimentales y simulados
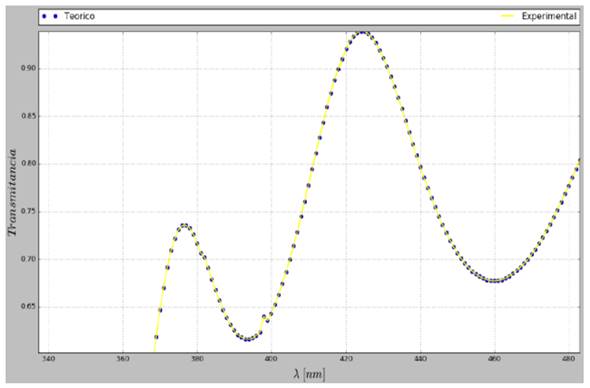
Para verificar la confiabilidad del programa desarrollado se compararon los datos experimentales con los datos obtenidos de forma teórica para el espectro de transmitancia retomando la ecuación propuesta por Swanepoel [5], eq. 3.
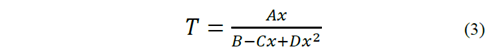
Con la que se puede reconstruir el espectro de transmitancia espectral experimental, en la Fig. 7 podemos ver en forma gráfica esta reconstrucción.
Figura 7: Espectros de transmitancia espectral experimental (línea amarilla) y teórico (puntos azules).
La gráfica del espectro espectral experimental se presenta dentro de la Fig. 7 como una línea continua de color amarillo, el teórico está representado por una sucesión de puntos azules; se puede observar que el espectro teórico se ajusta bastante bien al espectro experimental. De lo anterior se deduce que la aproximación que Swanepoel [5] propuso para reconstruir un espectro experimental de transmitancia, así como el software elaborado en este trabajo son adecuados para obtener valores confiables de las constantes ópticas de películas delgadas semiconductoras de espesor homogéneo.
Con el programa desarrollado se calcularon las constantes ópticas de películas delgadas de ZnS, SnS:Bi y SnS2:Bi, que son usadas como capas buffer y absorbente en celdas solares [15]. Como ilustración, enseguida se presentan los resultados obtenidos con una película de SnS2:Bi de espesor 638 nm.
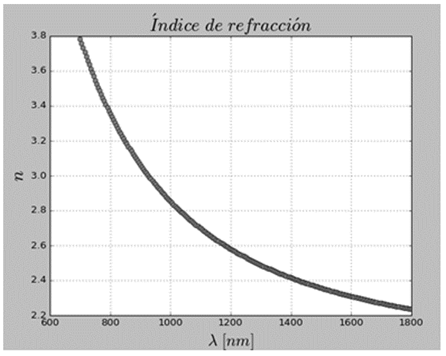
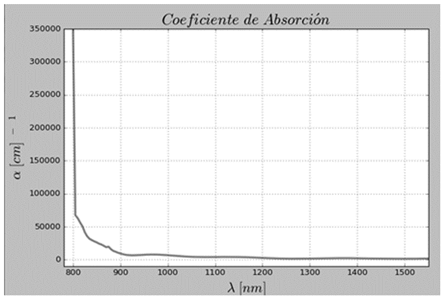
Los espectros y valores de las constantes ópticas obtenidos con el programa C.O.P.S. se compararon con los obtenidos para las muestras en [16] y se obtuvieron resultados muy similares, por ejemplo para el caso del Gap de la ilustración (Fig. 10), con el programa C.O.P.S. se obtuvo un Gap de 3,58 eV y en el trabajo [16] un Gap de 3,57 eV, el índice de refracción n varió entre 3,80 y 2,35 para λ entre 700 y 1500 nm (Fig. 8) y el coeficiente de absorción α del orden de 105 cm-1 en ambos casos (Fig. 9).
Figura 8: Índice de Refracción obtenido con el programa C.O.P.S.
Figura 9: Coeficiente de absorción obtenido con el programa C.O.P.S.
Figura 10: Gap obtenido con el programa C.O.P.S.
4. Manejo del programa C.O.P.S.
La interfaz de usuario de C.O.P.S. se hizo pensando en que personas que no conozcan muy bien el tema pero estén incursionando en él tengan la facilidad de utilizarla. A continuación se muestran las ventanas y comandos básicos que debe manejar el usuario del programa.
Aparece la ventana de inicio del programa (Fig. 11):
Figura 11: Entrando a C.O.P.S.
Luego se debe seleccionar el idioma (Fig. 12):
Figura 12: Selección de idioma.
Se genera la interfaz principal de C.O.P.S. (Fig. 13):
Figura 13: Ventana de interfaz principal de C.O.P.S.
En esta ventana seleccionando “Acerca de C.O.P.S.” se observa la siguiente ventana de Información del software (Fig. 14):
Figura 14: Ventana de información (“Acerca de C.O.P.S”).
En la ventana de la interfaz principal de C.O.P.S. también se encuentran las funciones principales del software: al presionar el botón “Calcular Constantes” ubicado dentro de la ventana de transición en la parte superior derecha se abrirá la ventana presentada en la Fig. 15 (también se puede acceder desde la misma ventana de transición dirigiéndose a la barra de menú en la opción desplegable “Archivo” luego opción “Calcular”).
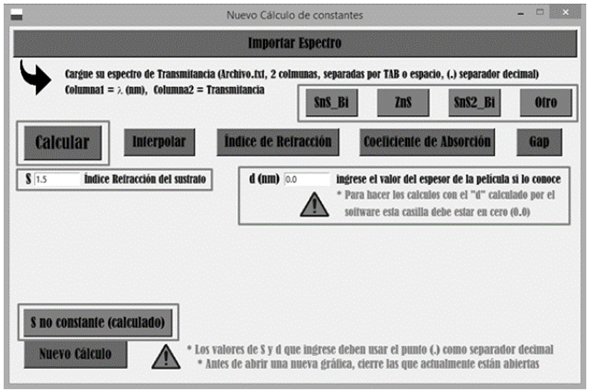
Figura 15: Ventana de cálculos de constantes ópticas.
En esta ventana el usuario puede ingresar dos valores: el espesor de la película d (en nm) y el índice de refracción del sustrato s que por defecto viene con un valor igual a 1,5 (para vidrio soda-lime).Si el usuario desea analizar el espectro ingresado y hacer que C.O.P.S. calcule un índice de refracción del sustrato no constante, debe pulsar el botón “s no constante (calculado)” ubicado en la parte inferior izquierda de esta ventana. El espesor es calculado automáticamente por el software empleando el método propuesto por Swanepoel [5], si el usuario tiene el dato de una medida de espesor que se haya realizado con anterioridad puede ingresarla y el programa ajusta los cálculos a este espesor (cada vez que ingrese un nuevo dato debe pulsar sobre el botón calcular). Si el usuario no ingresa ningún valor de espesor el software toma el valor que se calcula automáticamente, para hacer los cálculos, si después de oprimir “Calcular” con este valor por defecto desea ingresar un nuevo valor de espesor se podrá hacer y oprimir nuevamente el botón “Calcular”, de igual manera con el índice de refracción del sustrato.
El usuario también deberá seleccionar el tipo de compuesto del que se fabricó la película donde se presentan tres opciones: “ZnS, SnS:Bi y SnS2:Bi”, si otro compuesto se pulsa el botón “Otro”.
Una vez definidos estos valores con los que se desea calcular, se procede a cargar el espectro de transmitancia espectral como un archivo .txt (archivo generado por la mayoría de los espectrofotómetros comerciales) que bebe tener dos columnas: la primera con los valores de λ (en nm) y la segunda con los valores de la Transmitancia, separadas por espacio o Tabulación y utilizando el punto (.) como separador decimal en las cantidades que las componen.
Esta carga del archivo se hace por el botón que se encuentra en la parte superior de la ventana de cálculo “Importar Espectro” (Fig. 15), una vez seleccionado el archivo .txt que contiene el espectro de transmitancia experimental se procede a oprimir el botón “Calcular”, este proceso de cálculo toma alrededor de 0,5 a 2 segundos dependiendo la capacidad de cómputo del equipo donde se esté ejecutando C.O.P.S. Cuando el proceso de cálculo ha terminado la ventana de cálculo imprime el valor del espesor aproximado calculado de la película (d) y habilita los botones para poder ver las gráficas de la Interpolación (TM, Tm, λ), índice de refracción n, coeficiente de absorción α y Gap, como se muestra en la Fig. 16. Cada vez que un usuario abra una gráfica deberá cerrarla para abrir una nueva, esto evitará que las gráficas se sobrepongan dando lecturas erróneas; las gráficas se pueden mostrar aleatoriamente, una vez los botones estén habilitados no existe restricción en su orden.
Figura 16: Botones para exportar archivos .txt y visualizar gráficas de las constantes ópticas.
Luego de presionar un botón (“Interpolar”, “Índice de Refracción”, “Coeficiente de Absorción”, “Gap”) para visualizar su respectiva gráfica aparecerá en la parte inferior de la ventana de cálculos un botón correspondiente a cada gráfica con el mismo nombre, que permitirá al usuario extraer los datos de dicha gráfica en un archivo .txt,; adicional a esto cuando la gráfica se esté mostrando se podrá guardar en diferentes formatos como png, jpg, pdf. Los archivos .txt son guardados en el directorio que el usuario le indique y poseen su respectiva demarcación, es decir nombre para cada columna según el tipo de gráfica seleccionada.
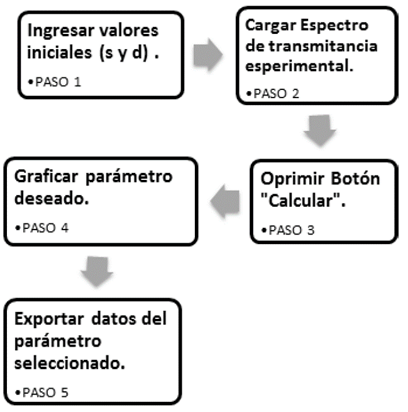
En la Fig. 17 se presenta el resumen del procedimiento que debe realizar el usuario para el cálculo de las constantes ópticas dentro del programa C.O.P.S.
Figura 17: Pasos para el cálculo de constantes ópticas en C.O.P.S.
5. Conclusiones
Se desarrolló una herramienta de software en el lenguaje de programación Python, la cual se nombró C.O.P.S. Se logró condensar todo dentro de un archivo .exe con el fin de ejecutarse sin la necesidad de tener instalado el lenguaje y sus múltiples librerías necesarias para el correcto funcionamiento de C.O.P.S. El software tomó como referencia el método propuesto por Swanepoel, que basa sus cálculos en medidas de transmitancia espectral experimentales. La herramienta permite hacer un ajuste automático para hallar los puntos máximos y mínimos de las envolventes del espectro de transmitancia experimental, para determinar las constantes ópticas de películas delgadas semiconductoras empleadas en la fabricación de celdas solares.
Se diseñó una interfaz gráfica de fácil manejo y multilenguaje (inglés-español), que permite al usuario entender de una manera sencilla los pasos que debe realizar para determinar las constantes ópticas a partir de un espectro de transmitancia tomado previamente y cargado en un archivo .txt, que es el formato que manejan los espectrofotómetros convencionales.
Se seleccionó el método de bisección para realizar las iteraciones en el cálculo de las constantes ópticas por facilidad y aplicabilidad, para este caso el método se ajustó correctamente y no consume una memoria computacional considerable, otros métodos numéricos pueden llegar a la respuesta en un tiempo más corto pero se debe tener cuidado en la selección de las condiciones para su evaluación ya que pueden alejar el valor esperado en vez de acercarlo en cada iteración.
El software desarrollado aporta a la caracterización y análisis para seleccionar las capas semiconductoras más adecuadas para la fabricación de celdas solares más eficientes. Se determinaron las constantes ópticas(n,α y Gap) de películas de diferentes compuestos: ZnS, SnS:Bi y SnS2:Bi con el programa C.O.P.S. y los resultados obtenidos se compararon con los reportados para las mismas películas en otro trabajo, comprobándose que los datos arrojados por C.O.P.S son confiables.
Referencias
Referencias
Renewables 2017 Global Status Report 2017 [Online]. [date of reference: October 1st of 2017]. Available at: http.//www.ren21.net
Ali, N., Hussain, A., Ahmed, R., Wang, M.K., Zhao, C., Ul-Haq, B. and Fu, Q.Y., Advances in nanostructured thin film materials for solar cell applications. Renewable and Sustainable Energy Reviews, 59, pp. 726-737, 2016. DOI: 10.1016/j.rser.2015.12.268
Mesa, F., Ballesteros, V. and Dussan, A., Cálculo de constantes ópticas de películas delgadas de Cu3BiS3 a través del método de Wolfe. Universitas Scientiarum, 19(2), pp. 123-131, 2014. DOI: 10.11144/Javeriana.SC19-2.ccop
Poelman, D. and Smet, P.F., Methods for the determination of the optical constants of thin films from single transmission measurements: a critical review. Journal of Physics D: Applied Physics, 36(15), pp. 1850-1857, 2003. DOI: 10.1088/0022-3727/36/15/316
Swanepoel, R., Determination of the thickness and optical constants of amorphous silicon. J. Phys. E: Sci. Instrum., 16, pp. 1214-1222, 1983. DOI: 10.1088/0022-3735/16/12/023
Shaaban, E.R., Yahia, I.S. and El-twally, E.G., Validity of Swanepoel's method for calculating the optical constants of thick films. Acta Physica Polonica A, 121, pp. 628-635, 2012. DOI: 10.12693/APhysPolA.121.628
Ilican, S., Caglar, M. and Çağlar, Y., Determination of the thickness and optical constants of transparent indium-doped ZnO thin films by the envelope method. Materials Science-Poland, 25(3), pp. 709-718, 2007.
Minkov, D.A., Gavrilov, G.M., Marquez, E., Fernandez-Ruano, S.M. and Stoynova, A.V., Development of algorithm for computer drawing envelopes of interference reflectance spectra for thin film specimens. Optik - International Journal for Light and Electron Optics, 132, pp. 320-328, 2017. DOI: 10.1016/j.ijleo.2016.12.063
McClain, M., Feldman, A., Kahaner, D. and Ying, X., An algorithm and computer program for the calculation of envelope curves. Computers in Physics, 5(1), pp. 45-48, 1991. DOI: 10.1063/1.168405
Minkov, D. and Swanepoel, R., Computer drawing of the envelopes of spectra with interference, Proceedings of the SPIE 1782: Thin Films for Optical Systems, 1993. DOI: 10.1117/12.141047.
Birgin, E., Chambouleyron, I. and Martı́nez, J.M., Estimation of the optical constants and the thickness of thin films using unconstrained optimization. Journal of Computational Physics, 151(2), pp. 862-880, 1999. DOI: 10.1006/jcph.1999.6224
Gavrilov, G.M., Minkov, D.A., Marquez, E. and Ruano, S.M.F., Advanced computer drawing envelopes of transmittance spectra of thin film specimens. International Advanced Research Journal in Science, Engineering and Technology, 3(9), 2016. DOI: 10.17148/IARJSET.2016.3931
Cómo citar
IEEE
ACM
ACS
APA
ABNT
Chicago
Harvard
MLA
Turabian
Vancouver
Descargar cita
Licencia
Derechos de autor 2018 DYNA

Esta obra está bajo una licencia internacional Creative Commons Atribución-NoComercial-SinDerivadas 4.0.
El autor o autores de un artículo aceptado para publicación en cualquiera de las revistas editadas por la facultad de Minas cederán la totalidad de los derechos patrimoniales a la Universidad Nacional de Colombia de manera gratuita, dentro de los cuáles se incluyen: el derecho a editar, publicar, reproducir y distribuir tanto en medios impresos como digitales, además de incluir en artículo en índices internacionales y/o bases de datos, de igual manera, se faculta a la editorial para utilizar las imágenes, tablas y/o cualquier material gráfico presentado en el artículo para el diseño de carátulas o posters de la misma revista.