REFLEXIÓN CUÁNTICA Y LA INTERACCIÓN DE ÁTOMOS ULTRA FRÍOS CON SUPERFICIES Y NANOESTRUCTURAS

QUANTUM REFLECTION AND THE INTERACTIONS OF ULTRACOLD ATOMS WITH SURFACES AND NANOSTRUCTURES

La reflexión cuántica se refiere a la reflexión de partículas por potenciales atractivos de largo alcance en regiones no clásicas del espacio de configuración donde no hay puntos clásicos de retorno. Los avances actuales en el campo de la nanotecnología y en los procesos de enfriamiento de átomos y moléculas permiten la creación de sistemas híbridos que involucran átomos ultra fríos y nanoestructuras, donde la reflexión cuántica puede jugar un papel importante.
En este trabajo presentamos una revisión de algunos aspectos fundamentales de la reflexión cuántica. Estos incluyen la descripción de la interacción entre partículas y superficies -cuyos orígenes se remontan a las fluctuaciones de vacío del campo electromagnético-, la caracterización de la reflexión cuántica cerca del umbral de energía, posibles aplicaciones para confinamiento y transporte de átomos ultra fríos, y la descripción de procesos de dispersión en un sistema híbrido básico: átomos interactuando con nanotubos.

Quantum reflection refers to the reflection of particles by attractive long-range potentials in nonclassical regions of coordinate space without reaching a classical turning point.

Recent advances in nanotechnology and in cooling processes of atoms and molecules give rise to the creation of hybrid systems involving ultracold atoms and nanostructures, where quantum reflection might play an important role. In this work we review some fundamental aspects of quantum reflection. These include the description of atom-surface interactions -which are originated from the vacuum fluctuations of the electromagnetic field-, the near-threshold characterization of quantum reflection, possible applications for trapping and guiding ultracold atoms, and the description of scattering processes in a basic hybrid system: ultracold atoms interacting with nanotubes.

Javier Madroñero

Physik Department, Technische Universität München, Munich, Alemania

Contacto: Javier Madroñero javier.madronero@mytum.de

(Recibido: 12/2010. Aceptado: 03/2011)

Cómo citar: Madroñero, J., Momento, 42, 1 (2011)

Resumen

La reflexión cuántica se refiere a la reflexión de partículas por potenciales atractivos de largo alcance en regiones no clásicas del espacio de configuración donde no hay puntos clásicos de retorno. Los avances actuales en el campo de la nanotecnología y en los procesos de enfriamiento de átomos y moléculas permiten la creación de sistemas híbridos que involucran átomos ultra fríos y nanoestructuras, donde la reflexión cuántica puede jugar un papel importante. En este trabajo presentamos una revisión de algunos aspectos fundamentales de la reflexión cuántica. Éstos incluyen la descripción de la interacción entre partículas y superficies — cuyos orígenes se remontan a las fluctuaciones de vacío del campo electromagnético —, la caracterización de la reflexión cuántica cerca del umbral de energía, posibles aplicaciones para confinamiento y transporte de átomos ultra fríos, y la descripción de procesos de dispersión en un sistema híbrido básico: átomos interactuando con nanotubos.

Palabras claves: Fuerza de Casimir, Dispersión, Sistemas híbridos.

Abstract

Quantum reflection refers to the reflection of particles by attractive long–range potentials in nonclassical regions of coordinate space without reaching a classical turning point. Recent advances in nanotechnology and in cooling processes of atoms and molecules give rise to the creation of hybrid systems involving ultracold atoms and nanostructures, where quantum reflection might play an important role. In this work we review some fundamental aspects of quantum reflection. These include the description of atom–surface interactions — which are originated from the vacuum fluctuations of the electromagnetic field —, the near–threshold characterization of quantum reflection, possible applications for trapping and guiding ultracold atoms, and the description of scattering processes in a basic hybrid system: ultracold atoms interacting with nanotubes.

Keywords: Casimir force, Scattering, Hybrid systems.

Introducción

Cuando una bola (macroscópica) cae hacia el piso bajo el efecto único de la gravedad inevitablemente termina en contacto con la superficie. El mundo nanoscópico está regido por las reglas que dicta la mecánica cuántica y a esas escalas no debe sorprendernos que una bola cuántica que es atraída hacia una superficie puede eventualmente reflejarse cuánticamente en una región donde no hay ningún punto clásico de retorno. Con los grandes avances alcanzados en la década de los 1990 en los procesos de enfriamiento de átomos y la creación de condensados de Bose–Einstein [1—3] y con los recientes desarrollos en el área de la nanotecnología es ahora posible combinar estas dos tecnologías y crear sistemas híbridos [4—6]. La comprensión de procesos fundamentales en sistemas híbridos básicos que involucran átomos a bajas temperaturas y nanoestructuras es el punto de partida en la búsqueda de un entendimiento bien fundado de sistemas híbridos en general. Efectos como la reflexión cuántica pueden jugar un papel importante en tales escenarios.

El origen de la interacción entre un átomo y una superficie en ausencia de fuerzas externas se remonta a las fluctuaciones del vacío del campo electromagnético [7] que generan un potencial atractivo para el átomo. Este potencial tiene un carácter electrostático (potencial de van der Waals) a distancias que son más cortas que las longitudes de las transiciones atómicas. En cambio efectos de retardación deben ser considerados para grandes distancias. Por ejemplo, para el caso de una superficie plana el potencial de van der Waals (vdW) tiene la forma —C₃/r³ [8], mientras que el potencial altamente retardado (AR) a grandes distancias es de la forma —C₄/r⁴ [7]. Para esta clase de potenciales en particular y para potenciales atractivos que son más singulares que —1/r² en general las propiedades de la reflexión cuántica a bajas energías han sido estudiadas intensamente [9–13] y dependen esencialmente de la longitud de umbral b y la longitud media de dispersión : el comportamiento de la amplitud de reflexión R cerca del umbral para una partícula de masa μ bajo la acción de un potencial atractivo de largo alcance esta dado en términos del valor asintótico del número de onda por [9, 11] |R| 1 — 2bk + (k²), y arg R π — 2k. Los parámetros b y dependen únicamente de las propiedades asintóticas del potencial a largas distancias más allá de una región semiclásica de distancias relativamente "pequeñas", donde funciones WKB con dirección de movimiento plenamente definida son soluciones bastante precisas de la ecuación de Schrödinger. Estas "pequeñas" distancias corresponden a regiones del espacio más allá del régimen cercano de unas pocas unidades atómicas donde los detalles de la estructura y de los constituyentes de la superficie son importantes. La interacción en esta región cercana es muy complicada y generalmente conlleva a procesos inelásticos o de adsorción. Sin embargo, las partículas que son reflejadas cuánticamente no se acercan lo suficiente a esta región y no se ven afectados por estos últimos procesos.

En esta contribución se hará una corta revisión de los aspectos más fundamentales de la reflexión cuántica y sus posibles aplicaciones. Entender la reflexión cuántica y sus posibles consecuencias requiere ante todo un conocimiento más que cualitativo de las fuerzas de interacción de las partículas con las superficies que las rodean.

Es así como vamos a empezar en la Sec. 1 con una breve descripción de estas interacciones en los pocos casos en que se conocen suficientemente bien. En la Sec. 2 trataremos los elementos teóricos de la reflexión cuántica para pasar luego a mostrar algunas posibles aplicaciones en las secciones siguientes. Concretamente, la Sec. 3 da cuenta de los avances teóricos logrados hasta ahora que exploran la posibilidad de usar la reflexión cuántica como un mecanismo para atrapar átomos fríos o para transportarlos a lo largo de guías de onda. La Sec. 4 revisa algunos aspectos de la interacción de átomos con nanotubos. Finalmente concluimos con la Sec. 4.

1. Potencial de Casimir y Polder

Un acercamiento puramente electrostático al problema de la interacción de átomos con superficies nos conduce al potencial de vdW. Sin embargo, no es posible con ello describir efectos de retardación. El tratamiento adecuado de estos efectos requiere la cuantización del campo electromagnético [7]. El hamiltoniano que describe el sistema es entonces

donde H_atom es el hamiltoniano del átomo no perturbado, H_campo es el potencial del campo cuantizado [7, 14], y el hamiltoniano de interacción en la aproximación de dipolo está dado en términos del operador de dipolo μ y el campo eléctrico E por

Los estados del sistema en términos de los estados |φ_j⟩ del átomo y de los estados |n_λk⟩ del campo¹ se expresan a través del producto tensorial |φ_i; n_λk⟩.

La corrección a los niveles atómicos de energía debidos a Hint se obtiene perturbativamente. Si el estado inicial del átomo es |φ_i⟩ y |0⟩ denota el estado de vacío del campo, la corrección a segundo orden (a primer orden la corrección es cero) es [7, 15]

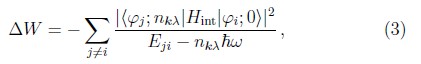
con E_ji = E_j — E_i la diferencia de energía entre los estados |φ_j⟩ y |φ_i⟩. E_ji caracteriza la frecuencia de transición ω_ji = E_ji/ entre estos estados mientras el inverso 1/E_ji determina las escalas de tiempo para estas transiciones y define las longitudes de transición λ_ji.

La expresión (3) es completamente general, válida para cualquier clase de átomo e independiente de la geometría y del material de la superficie. Aplicaciones específicas de (3) requieren en general aproximaciones adicionales. Por un lado, las frecuencias ω_ij se conocen de manera exacta para átomos hidrogenoides, mientras que para átomos de dos o más electrones grandes esfuerzos numéricos y experimentales proveen información parcial acerca de ellas [16, 17]. Esta dificultad se enfrenta típicamente considerando los casos límites de pequeñas y grandes distancias d entre el átomo y la superficie, es decir, los casos d << λ_ji (límite de vdW) y d >> λ_ji (límite AR), respectivamente. En el caso de vdW típicamente se pierde la dependencia de las transiciones E_ji y la suma sobre los niveles atómicos se simplifica en términos del valor esperado del dipolo eléctrico = ⟨φ_i|μ²|φ_i⟩. Para grandes distancias la corrección de la energía depende de la polarizabilidad estática del átomo

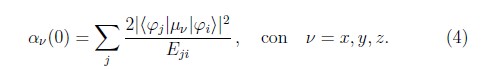
De otro lado, la expresión (3) requiere el conocimiento del campo eléctrico, el cual a su vez se determina a partir de las condiciones de frontera en la superficie. Debido a ello a la fecha se ha estudiado con cierto detalle la interacción tan sólo para geometrías relativamente sencillas, tales como superficies planas, cilíndricas o esféricas.

Superficie plana. Tal como se menciona arriba, los potenciales de vdW y AR tienen la forma —C₃/r³ y —C₄/r⁴, respectivamente. Las constantes C³ y C⁴ para el caso de una superficie perfectamente conductora dependen completamente de las propiedades del átomo y para el caso de un átomo en un estado esférico (α_d(0) := α_x(0) = α_y(0) = α_z(0)) están dadas por [18, 19]

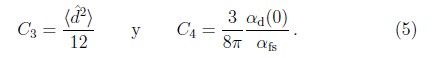
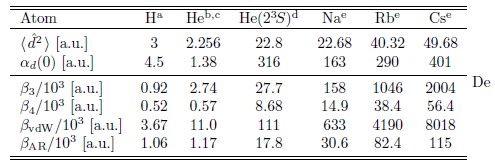
Ref. ^a[22]; ^b[23]; ^c[24]; ^d[25]; ^e[26]

Tabla 1. Valores explícitos en unidades atómicas de los valores esperados del operador de dipolo , de la polarizabilidad estática de dipolo α_d(0), y de las longitudes características β₃, β₄, β_vdW y β_AR para varias especies atómicas en su estado base (a menos que se indique de otra manera).

α_fs es la constante de estructura fina. Si el material de la superficie es un dieléctrico las constantes C₃ y C₄ adquieren correcciones que dependen de la dielectricidad ε del material [20, 21]. A partir de estas constantes se definen para una partícula de masa μ las longitudes características β_α, α = 3, 4, tales que . En la tabla 1 se muestran para algunas especies atómicas los valores de β₃ y β₄, los cuales pueden variar desde unos cuantos cientos hasta un par de millones de unidades atómicas.

Los resultados descritos en esta sección suponen que la superficie se encuentra a temperatura cero y en equilibrio térmico con el medio. Efectos debidos a temperaturas finitas y a desequilibrio térmico se han estudiado [27–30], pero no se tratarán aquí.

Esfera. Los potenciales de vdW y AR tienen la forma —C₆/r⁶ y —C₇/r⁷, respectivamente. Las intensidades C₆ y C₇ dependen del radio R de la esfera y están relacionadas con C₃ [31] y C₄ [32],

Cilindro. A diferencia de los casos anteriores, no es posible expresar de forma sencilla los límites vdW y AR del potencial de interacción con un cilindro conductor infinito. De todas formas la expresión exacta del potencial [15] se puede simplificar significativamente en estos límites. En estos casos el potencial puede escribirse como [33]

El símbolo x designa los límites vdW o AR, con α_vdW = 3 y α_AR = 4. Las longitudes características

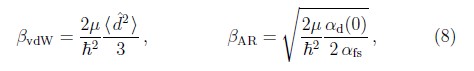
dependen, igual que en los casos anteriores, de las propiedades intrínsecas del átomo. En la tabla 1 se listan valores explícitos para hidrógeno, helio y átomos alcalinos. Los valores de β_vdW van desde pocos miles a millones de radios de Bohr, mientras que los valores de β_AR se encuentran en los límites de miles de radios de Bohr.

Las funciones f^x_m indican la influencia del radio del alambre y están definidas como

donde I_m^(α_x𔃀3) y K^(α_x𔃀3) son las derivadas de orden α_x — 3 de las funciones modificadas de Bessel I_m y K_m, respectivamente.

En el límite de grandes radios los dos límites respectivos reproducen los potenciales (5) como es de esperarse. En el límite de radios pequeños los dos casos tienen el comportamiento de series logarítmicas lentamente convergentes, las cuales no tienen uso en objetivos prácticos [34—36].

2. Reflexión cuántica y la aproximación semiclásica

La forma más sencilla de ilustrar el proceso de reflexión cuántica nos remite a cualquier curso elemental de mecánica cuántica: Uno de los primeros problemas que se resuelve allá es la ecuación de Schrödinger para una partícula de masa μ en un potencial unidimensional de paso V (r) = K⊃2₀/(2μ)Θ(r), donde Θ(r) es la función de paso de Heaviside. Una partícula lanzada desde r → +∞ con energía k²/(2μ) es modelada en este caso por una onda incidente e^—ikr. La solución de la ecuación de Schrödinger incluye en todo caso una onda transmitida Te^—iqr , y una onda reflejada Re^—ikr, donde T y R son las amplitudes de transmisión y reflexión, respectivamente. La probabilidad de reflexión en este caso esta dada por

Las propiedades de reflexión de partículas bajo la acción de potenciales atractivos de forma más general y que son más singulares que —1/r² tienen un comportamiento similar. La definición inequívoca de las amplitudes y probabilidades de transmisión a través de una región localizada del espacio de coordinadas requiere la existencia de soluciones unidireccionales de la ecuación de Schrödinger. Estás pueden ser obtenidas con la ayuda de funciones de onda WKB siempre y cuando éstas sean aproximaciones suficientemente precisas de las soluciones exactas. La función de onda WKB para una partícula incidente está definida por

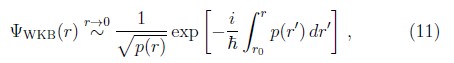
donde es el momento clásico local. Es común encontrar en la literatura que la aproximación WKB es válida cuando la longitud de onda de de Broglie λ = 2π/p(r) varia lentamente. Menos común, pero más precisa y apropiada es la condición para la aplicabilidad de la aproximación WKB en términos de la función de cuantalidad,

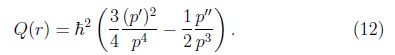
En este caso la aproximación WKB es válida cuando |Qj(r)| << 1 y es exacta cuando Q(r) = 0 [11].

Figura 1. Condiciones de frontera con funciones de onda WKB incidentes. La función de cuantalidad forma una "barrera cuántica" alrededor de r₀, donde tiene lugar la reflexión cuántica de una partícula con energía E_k = k²/(2μ).

Para potenciales que son más singulares que 1/r² la función de cuantalidad es pequeña cerca del origen y cero en la singularidad. También tiende a cero a grandes distancias y no es despreciable en la región alrededor de r₀, el punto de retorno asociado a la energía —E_k, E_k = k²/(2μ). r₀ suele interpretarse entonces como el lugar donde ocurre la reflexión cuántica. Como consecuencia de lo anterior se pueden modelar fácilmente condiciones de frontera absorbentes en el origen con funciones WKB incidentes (ver Fig. 1). En tales condiciones la amplitud de reflexión R es compleja y el comportamiento a bajas energías E = k²/(2μ) se resume en [9, 11]

o lo que es equivalente, R = e^—2iδ, δ —k, con = — ib. Igual que antes, b es la longitud de umbral. a es la longitud media de dispersión y es la longitud compleja de dispersión. Para el caso particular de potenciales atractivos homogéneos de la forma —C_α/r^α, α > 2, estas longitudes características se pueden expresar analíticamente en términos de la longitud característica β_α definida

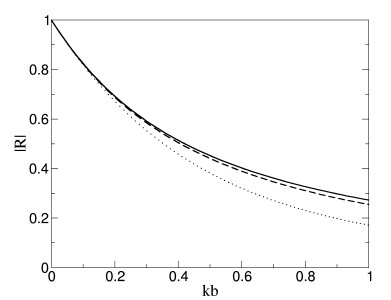
Figura 2. Amplitud de reflexión como función de kb para el potencial de paso (línea punteada), para el potencial retardado —C₄/r⁴ (línea a rayas) y para el potencial (15) con β₄4/β₃ = 1,0 (línea continua), donde b es la longitud de umbral asociada a cada potencial.

a partir de [11, 13]:

El comportamiento de la amplitud de reflexión más allá de bajas energías se muestra en Fig. 2 en términos de la variable adimensional kb para tres potenciales: el potencial de paso (línea punteada), el potencial AR —₄/r⁴ (línea a rayas) y el potencial

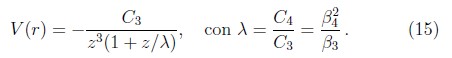
Para el potencial AR la longitud de umbral es b = β₄ (ver Ec. (14)), mientras que para el potencial (15) esta longitud se puede expresar en términos de las funciones de Bessel J₁(x) y Y₁(x) [10],

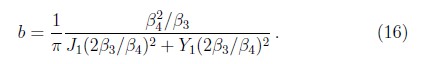
El potencial (15) reproduce los límites de vdW y AR de cortas y grandes distancias, respectivamente, y permite una transición suave entre estos límites. La longitud λ se puede interpretar como la longitud de transición entre estos dos límites. Se constituye así en una sencilla aproximación al potencial exacto que, sin embargo, permite reproducir las mediciones experimentales de reflexión cuántica. Ese es el caso, por ejemplo, en el trabajo de Shimizu [37], donde por primera vez se observó este efecto en átomos de neón interactuando con superficies de Silicio.

En la Fig. 2 vemos el comportamiento linear de |R| para valores de k cercanos a cero y que su valor es 1 en el umbral independientemente de la forma del potencial. En cambio, la probabilidad de reflexión depende drásticamente del potencial más allá de cierta energía. Para átomos ultra fríos interactuando con superficies tiene entonces la reflexión cuántica una importancia fundamental y en una primera aproximación es posible describirla con un simple modelo en el cual se remplaza el potencial exacto con una potencial de paso.

3. Atrapando y guiando átomos con reFLexión cuántica

Es de esperar que átomos ultra fríos confinados en una cavidad se mantengan alejados de las paredes de la cavidad debido al efecto de reflexión cuántica. Un estudio detallado y riguroso de este confinamiento es bastante complicado, puesto que, como se mencionó en la Sec. 1, el potencial de interacción se conoce tan solo para geometrías simples. A pesar de ello se han hecho algunas estimaciones del aumento de la probabilidad de supervivencia de átomos fríos debido a la reflexión cuántica en cavidades cúbicas [38] y a lo largo guías de onda cilíndricas [39].

3.1. Trampas cúbicas con reflexión cuántica.

Cómo dijimos antes, la primera dificultad se encuentra en la descripción del potencial. Para empezar consideremos un átomo atrapado entre dos paredes (ver Fig. 3(a)). Si z es la distancia que separa al átomo de la paredes, el potencial V (z) sufre una transición

Figura 3. (a) Átomo atrapado entre dos paredes separadas por una distancia 2L. La interacción se puede modelar en una primera aproximación por un potencial de paso. (b) Evolución temporal para la probabilidad de supervivencia de átomos ultra fríos de sodio (β₄/β₃ = 0.113) confinados entre dos paredes separadas una distancia 2L ≈ 10⁶ a.u. y bajo la acción del potencial (18) (línea continua). También se muestran los resultados obtenidos con el modelo del potencial de paso (línea punteada) y con la evolución libre de potencial (línea a rayas y puntos). (c) Densidad de supervivencia de una partícula a un tiempo escalado τ = 1 para el potencial (18) (línea continua) como función de β₄/β₃ en las mismas condiciones que (b). El círculo señala la densidad de probabilidad para β₄/β₃=0.113 (átomo de sodio). Para comparar se muestra también los resultados obtenidos con la potencial retardado —C₄/r⁴ (línea a rayas) y con el potencial de paso (línea punteada).

suave entre los límites de vdW y AR. Esta transición se puede modelar a través de una función de forma v(x) tal que v(x) 1 y v(x) x. El potencial se puede aproximar por

donde λ = C₄/C₃ es la longitud de transición entre los límites vdW y AR. Por ejemplo, la función v(x) = 1 + x reduce el potencial (17) al potencial de Shimizu (15) [37]. El potencial para un átomo entre dos paredes separadas una distancia L es entonces

Los átomos en el interior de una trampa se modelan por un paquete de ondas cuya dinámica está gobernada por la ecuación de Schrödinger dependiente del tiempo. Ésta, en términos de las variables adimensionales x = z/L y τ = t/t₀0, t₀ = 2ML²/, se reduce a

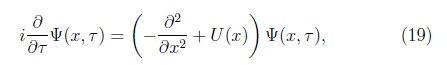
con U(x) = (t₀/)V(xL). Para fines prácticos el paquete de ondas inicial tiene la forma ψ(x,τ = 0) = Nexp(&8212;γ|x|)Θ(1—|x|), con N la constante de normalización. Sin embargo, el carácter tanto cuantitativo como cualitativo de los resultados que se presentan en esta sección son independientes de la forma de la función inicial. La energía del paquete de ondas está determinada por la constante adimensional γ y por la dimensión de la trampa: . Por lo tanto los valores de γ y L definen la temperatura de los átomos en la cavidad. La probabilidad de supervivencia en el interior de la cavidad es ρ(t) = ∫¹_—1dx|ψ(x,τ(|².

Ya en la Fig. 2 de la cercanía de las líneas sólida y a rayas podemos intuir que el efecto del potencial no retardado no es significativo en la interacción de átomos ultra fríos con superficies planas. Más aún, si los átomos son suficientemente fríos un potencial de paso con la longitud de umbral b = 1/K₀ escogida apropiadamente debería modelar suficientemente bien a los átomos en la cavidad. Este modelo propuesto originalmente por Jurisch y Friedrich [38] da cuenta del comportamiento de la probabilidad de supervivencia entre dos paredes. En este caso el potencial U(x) = σ²Θ(|x| — 1) y el sistema queda completamente caracterizado por el parámetro σ = L/b. La línea punteada en Fig. 3(b) muestra ρ(τ) para átomos de sodio (b = β₄ se encuentra definida en la tabla 1) en una trampa cuyas paredes se encuentran separadas una distancia 2L ≈ 10⁶ a.u. (σ≈30). El valor de γ = 5 garantiza que los átomos tienen una temperatura del orden de los nanokelvin [38] que son posibles de alcanzar experimentalmente [40]. El potencial (15) introduce algunas pequeñas correcciones al modelo anterior. La curva sólida de Fig. 3(b) es la densidad de probabilidad obtenida con (15) para átomos de sodio (β₄/β₃ = 0.113). Aunque el modelo del potencial de paso subestima en algo la probabilidad de supervivencia las diferencias con el resultado obtenido con el potencial de Shimizu o superan el 5% [41]. En cualquier caso alrededor del 50% de los átomos siguen

Tabla 2. Densidad de probabilidad para diferentes valores del parámetro σ = L/b después de un tiempo τ = 1. ρ(τ) es obtenido con el modelo de potencial de paso y típicamente subestima el valor obtenido con el potencial de Shimizu en un 5% aproximadamente.

confinados entre las paredes después de un tiempo τ = 1 (t ≈ 0,4s) y el valor de ρ(τ) es significativamente mayor que la supervivencia de átomos libres (línea a rayas y puntos en Fig. 3(b)). Al variar la especie atómica esta situación no cambia sustancialmente tal como lo indica Fig. 3(c) donde ρ(τ = 1) se presenta como función de β₄/β₃. Más aún, nuevamente aquí resulta evidente que el potencial AR (línea punteada) domina el proceso de reflexión cuando β₄ es mucho menor que β₃ y que el modelo del potencial de paso la subestima ligeramente.

Al ignorar los efectos del potencial debidos a las esquinas y a las aristas de una trampa cúbica el sistema tridimensional es separable. Ésta es una aproximación bastante significativa, sin embargo se puede asumir correcta si las dimensiones de la trampa y las separaciones típicas del átomo y las paredes son muy grandes comparadas con las dimensiones del átomo. En este caso la probabilidad de supervivencia ρ_3D resulta del producto de las probabilidades en cada dimensión. La tabla 2 resume esta probabilidad después de un tiempo τ = 1 para algunos valores de σ. Es de notar que en condiciones reales para átomos de sodio esta probabilidad es tres ordenes de magnitud superior al caso de una partícula libre.

3.2. Transporte de átomos a lo largo de guías de onda con la ayuda de reflexión cuántica.

Una guía de ondas cuadrada (circular) es una cavidad de lado 2L (radio L) en la cual los átomos se propagan libremente en la dirección z. Al igual que en el caso de las trampas cúbicas el potencial para átomos ultra fríos se puede modelar por un potencial de paso caracterizado por el parámetro σ = L/b. En unidades adimensionales (x → x/L, y → y/L, τ = t/t₀, t₀ = 2ML²/, los potencial para una guía cuadrada y cilíndrica son, respectivamente,

Cabe mencionar en el caso de las guías cuadradas que independientemente de la simplicidad de este potencial la ecuación de Schrödinger no es separable. Esto debido a las esquinas, en donde una función de onda plana puede transmitirse y reflejarse en cualquier dirección k con una amplitud a(k). La dependencia de los coeficientes a(k) de k no se puede expresar de manera analítica [39]. La tabla 3 resume los valores de la probabilidad de supervivencia en la guía para diferentes valores de σ. Al comparar la probabilidad ρ_cuad obtenida para la guía cuadrada con el cuadrado de la densidad de probabilidad unidimensional ρ²_1D (ver también la tabla 2) se nota que el efecto de la inseparabilidad originado en las esquinas es despreciable. Adicionalmente el factor de aumento de la probabilidad de confinamiento ρ_cuad/ρ_cuad^libre con respecto a una partícula libre aumenta con el parámetro σ. Más aún este factor es aparentemente independiente de la geometría de la guía, tal como se verifica al comparar con las probabilidades de confinamiento ρ_circ para una trampa circular.

Las dimensiones de una fibra hueca [42, 43] pueden ser del orden L ≈ 5 × 10 ⁵ a.u.. Un chorro de átomos de sodio (σ ≈ 30) a una temperatura T ≈ 14 μK se propaga a una velocidad de v ≈ 120mm/s y atraviesa la guía de onda de longitud 50mm en unos 0.4 s. Simplemente debido a la reflexión cuántica se espera entonces que la fracción de átomos que sobreviven al otro lado sea del orden del 30 %. Sin reflexión cuántica, es decir, ignorando la existencia de la interacción entre la superficie y los átomos, ésta sería tan sólo el 2%.

4. Dispersión de átomos ultra fríos por nanotubos

En esta sección consideramos un ejemplo básico de un sistema híbrido que involucra átomos y escalas nanométricas. Se trata de un

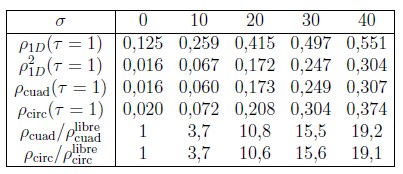
Tabla 3. Probabilidad de supervivencia de átomos en una guía de onda de geometría cuadrada (ρ_cuad) o circular (ρ_circ) para diferentes valores del parámetro σ = L/b después de un tiempo τ = 1. ρ_cuad se compara con el cuadrado de la densidad de probabilidad para átomos confinados entre dos paredes ρ_1D. Se muestra también los factores de incremento ρ/ρ^libre de la densidad de probabilidad en las guías cuadrada y circular. ρ^libre es la densidad de probabilidad para una partícula libre, es decir, para σ = 0.

átomo (o molécula) polarizable interactuando con un nanoalambre cilíndrico infinitamente largo y perfectamente conductor. A pesar de su aparente simplicidad, este sistema está lejos de ser trivial y, no obstante, entenderlo concienzudamente es un primer paso hacia la comprensión de sistemas más complejos que comprometen por ejemplo nanoredes usadas en experimentos actuales de difracción e interferencia de !tomos y moléculas [44, 45].

Debido a la simetría de traslación en la dirección paralela al eje del nanotubo, el problema de dispersión de un átomo en un nanoalambre es efectivamente bidimensional (2D). El tratamiento de este problema es muy diferente al de la bien conocida dispersión en tres dimensiones, en particular en el régimen de bajas energías [46, 47]. De todas formas el proceso de dispersión está dominado a bajas energías, al igual que en el caso tridimensional (3D), por la onda parcial s, aunque el comportamiento de la fase de dispersión cerca al umbral de energía difiere sustancialmente del caso 3D y está dado por

donde λ_E es la constante de Euler, λ_E = 0,577..... La cantidad a en (21) es la versión 2D de la longitud de dispersión [46–49], y

Figura 4. Parte real e imaginaria de la longitud de dispersión de átomos bajo la acción de la parte de vdW de la interacción con un nanotubo perfectamente conductor como función del radio R del nanotubo escalado con respecto a la longitud característica β = β_vdW (8).

se encuentra bien definida para potenciales que decaen más rápido que 1/r² a grandes distancias [47]. Cerca del umbral la amplitud de dispersión f(ø) (ø es el ángulo polar) y por lo tanto también la sección eficaz diferencial dλ/dø se encuentran completamente determinadas por la longitud de dispersión a:

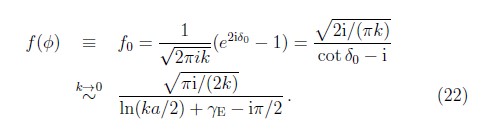
De esta forma, toda la información acerca del proceso de dispersión a bajas energías está contenido en la longitud de dispersión que se puede obtener de la función de onda parcial s de energía 0,

El problema entonces se reduce a la descripción precisa de esta función, lo cual nuevamente requiere el tratamiento adecuado del potencial de interacción cuyos límites vdW y AR son (7). Debido a la complejidad de este potencial [15] el uso de la forma exacta del potencial para fines prácticos no es posible. Tampoco se ha encontrado una forma analítica simple para pequeñas o grandes distancia tal como se explicó en la Sec. 1. En cambio, es necesario usar todos los términos de las expansiones en (7) para los límites respectivos. Afortunadamente, una jerarquía de aproximaciones permite determinar numéricamente estos límites tan precisamente como se quiera de una forma relativamente económica [33, 35].

La longitud de dispersión para el caso del potencial de vdW ha sido calculada [35, 36] y se reproduce en la Fig. 4 como función del radio R/β_vdW. La longitud de dispersión exhibe una dependencia linear con R para grandes valores de R. De hecho, en este límite el comportamiento de la longitud de dispersión es

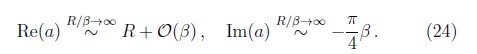
En particular, Im(a) se comporta en este límite exactamente como la longitud de dispersión de átomos con una pared plana [35]. El caso opuesto de tubos muy delgados (ver panel derecho de Fig. 4) muestra un comportamiento algo extraño: la longitud de dispersión tiende a cero cuando R → 0 y para valores de R cercanos a cero su comportamiento es aproximadamente [ln(R/β(]^—1. Esto tiene su explicación en la forma del potencial de vdW (7) para tubos ultra delgados que se comporta como V —r^—3(—ln[])^—1, con = R/β. Para potenciales homogéneos atractivos, —C_α/r^α, la longitud de dispersión a^(α) es proporcional a C¹^/(α—2)_α, es decir, es proporcional al coeficiente C_α cuando α = 3 [47]. Por lo tanto la forma del potencial para pequeños radios sugiere un comportamiento cercano a

Numéricamente se puede verificar que Re(a) tiende a 0 marginalmente más lento que (ln )^—1, mientras que Im(a) tiende a 0 marginalmente más rápido que (ln )^—1 para → 0 [35].

Un análisis similar se puede realizar con la parte AR del potencial (7). Una jerarquía análoga de aproximaciones permite una descripción precisa del potencial para fines prácticos, en particular para la descripción del proceso de dispersión. En este caso, una interpolación con la ayuda de una función de forma tal como se usó en la Ec. (17) permite aproximar el potencial exacto y de esta manera estudiar el papel del límite AR y del límite de vdW en el proceso de dispersión [33]. El resultado en este caso es que la parte AR del potencial domina prácticamente todo el proceso de interacción de átomos ultra fríos con nanotubos [33], tal como ocurrió en el caso de la interacción de átomos con superficies (ver Sec. 3).

Conclusiones

Las partículas ultra frías tienden a evitar el contacto con las superficies que la rodean. Esto no solo abre una ventana de posibilidades para atrapar y guiar átomos y moléculas ultra frías, sino que también se constituye en una consecuencia de un fenómeno fundamental de la naturaleza: las fluctuaciones del vacío del campo electromagnético. Si bien hemos alcanzado un entendimiento parcial acerca de algunos procesos en la interacción de átomos ultra fríos con superficies de geometrías sencillas, aún estamos lejos de entender, por ejemplo, complejos procesos de difracción, interferencia, reflexión, absorción de gases diluidos de átomos ultra fríos o de condensados de Bose–Einstein que se han empezado a observar en los laboratorios [44, 45, 50, 51]. Una cosa que nos queda bien clara de nuestras investigaciones es que en esta clase de procesos no podemos ignorar la interacción de Casimir y Polder. Más aún, ésta es fundamental y requiere un tratamiento bastante delicado que por ahora es posible solamente para algunas geometrías de la nanoestructura.

Agradecimientos

Este artículo es una revisión de parte del trabajo realizado con mis colaboradores de la "Technische Universtät München" durante los últimos años. Tanto por sus contribuciones directas como por discusiones fructíferas no puedo dejar de agradecer especialmente a Harald Friedrich, Martin Fink, Johannes Eiglsperger, Florian Arnecke, Alexander Jurisch y Patrick Raab. Igualmente agradezco a Diana Lozano por leer cuidadosamente este manuscrito.

¹ n_λk es el número de fotones con polarización λ y número de onda k.

Referencias

[1] M. H. Anderson, J. R. Ensher, M. R. Matthews, C. E. Wieman, and E. A. Cornell, Science 269, 198 (1995).

[2] C. C. Bradley, C. A. Sackett, J. J. Tollett, and R. G. Hulet, Phys. Rev. Lett. 75, 1687 (1995).

[3] K. B. Davis, M. O. Mewes, M. R. Andrews, N. J. van Druten, D. S. Durfee, D. M. Kurn, and W. Ketterle, Phys. Rev. Lett. 75, 3969 (1995).

[4] T. J. Kippenberg and K. J. Vahala, Science 321, 1172 (2008).

[5] F. Marquardt and S. M. Girvin, Physics 2, 40 (2009).

[6] M. Aspelmeyer, Nature 464, 685 (2010).

[7] H. B. G. Casimir and D. Polder, Phys. Rev. 73, 360 (1948).

[8] G. Vidali, G. Ihm, H.–Y. Kim, and M. W. Cole, Surf. Sci. Rep. 12, 135 (1991).

[9] R. Côté, H. Friedrich, and J. Trost, Phys. Rev. A 56, 1781 (1997).

[10] H. Friedrich, G. Jacoby, and C. G. Meister, Phys. Rev. A65, 032902 (2002).

[11] H. Friedrich and J. Trost, Physics Reports 397, 359 (2004).

[12] A. Jurisch and H. Friedrich, Phys. Rev. A 70, 032711 (2004).

[13] F. Arnecke, H. Friedrich, and J. Madroñero, Phys. Rev. A 74, 062702 (2006).

[14] H. Friedrich, Theoretical Atomic Physics (Springer, 2005).

[15] C. Eberlein and R. Zietal, Phys. Rev. A 80, 012504 (2009).

[16] J. Eiglsperger and J. Madroñero, Phys. Rev. A 80, 022512 (2009).

[17] Y. H. Jiang, R. Püttner, D. Delande, M. Martins, and G. Kaindl, Phys. Rev. A 78, 021401 (2008).

[18] G. Barton, Journal of Physics B: Atomic and Molecular Physics 7, 2134 (1974).

[19] M. Marinescu, A. Dalgarno, and J. F. Babb, Phys. Rev. A 55, 1530 (1997).

[20] D. Derjaguin, I. Abrikosov, and E. Lifschitz, Usp. Fiz. Nauk 64, 493 (1958).

[21] M. Antezza, L. P. Pitaevskii, and S. Stringari, Phys. Rev. A 70, 053619 (2004).

[22] S. Flügge, Handbuch der physik: Encyclopedia of physics. Vol. XXXV, Atoms I. Atome I, Handbuch der Physik (Springer, 1957) pp. 88–436.

[23] Z.–C. Yan, J. F. Babb, A. Dalgarno, and G. W. F. Drake, Phys. Rev. A 54, 2824 (1996).

[24] C. L. Pekeris, Phys. Rev. 115, 1216 (1959).

[25] Z.–C. Yan and J. F. Babb, Phys. Rev. A 58, 1247 (1998).

[26] A. Derevianko, W. R. Johnson, M. S. Safronova, and J. F. Babb, Phys. Rev. Lett. 82, 3589 (1999).

[27] M. Antezza, L. P. Pitaevskii, S. Stringari, and V. B. Svetovoy, Phys. Rev. A 77, 022901 (2008v.

[28] M. Antezza, L. P. Pitaevskii, and S. Stringari, Phys. Rev. Lett. 95, 113202 (2005).

[29] G. L. Klimchitskaya, U. Mohideen, and V. M. Mostepanenko, Rev. Mod. Phys. 81, 1827 (2009).

[30] V. Druzhinina, M. Mudrich, F. Arnecke, J. Madroñero, and A. Buchleitner, Phys. Rev. A 82, 032714 (2010).

[31] A. Derevianko, J. F. Babb, and A. Dalgarno, Phys. Rev. A63, 052704 (2001).

[32] G. Feinberg and J. Sucher, J. Chem. Phys. 48, 3333 (1968).

[33] M. Fink, J. Eiglsperger, J. Madroñero, and H. Friedrich, (2010), submitted.

[34] C. Eberlein and R. Zietal, Phys. Rev. A 75, 032516 (2007).

[35] M. Fink, A. Naranjo, F. Arnecke, J. Eiglsperger, H. Friedrich, J. Madroñero, P. Raab, and A. Wirzba, Phys. Rev. A 81, 062714 (2010).

[36] M. Fink, J. Eiglsperger, H. Friedrich, and J. Madroñero, The European Physical Journal D 63, 33 (2011).

[37] F. Shimizu, Phys. Rev. Lett. 86, 987 (2001).

[38] A. Jurisch and H. Friedrich, Physics Letters A 349, 230 (2006).

[39] J. Madroñero and H. Friedrich, Phys. Rev. A 75, 062902 (2007).

[40] T. A. Pasquini, Y. Shin, C. Sanner, M. Saba, A. Schirotzek, D. E. Pritchard, and W. Ketterle, Phys. Rev. Lett. 93, 223201 (2004).

[41] J. Madroñero and H. Friedrich, Phys. Rev. A 75, 022902 (2007).

[42] R. Dall, M. Hoogerland, K. Baldwin, and J. Buckman, Comptes Rendus de lÁcadémie des Sciences – Series IV – Physics 2, 595 (2001).

[43] X. Halliwell, H. Friedrich, S. Gibson, and K. Baldwin, Opt. Comm. 224, 89 (2003).

[44] M. Arndt, O. Nairz, J. Vos–Andreae, C. Keller, G. van der Zouw, and A. Zeilinger, Nature 401, 680 (1999).

[45] T. Juffmann, S. Truppe, P. Geyer, A. G. Major, S. Deachapunya, H. Ulbricht, and M. Arndt, Phys. Rev. Lett. 103, 263601 (2009).

[46] B. J. Verhaar, J. P. H. W. van den Eijnde, M. A. J. Voermans, and M. M. J. Schaffrath, Journal of Physics A: Mathematical and General 17, 595 (1984).

[47] F. Arnecke, H. Friedrich, and P. Raab, Phys. Rev. A 78, 052711 (2008).

[48] N. N. Khuri, A. Martin, J.–M. Richard, and T. T. Wu, J. Math. Phys. 50, 072105 (2009).

[49] C. Ticknor, Phys. Rev. A 81, 042708 (2010).

[50] T. A. Pasquini, M. Saba, G.–B. Jo, Y. Shin, W. Ketterle, D. E. Pritchard, T. A. Savas, and N. Mulders, Phys. Rev. Lett. 97, 093201 (2006).

[51] P. Schneeweiβ, Ph.D. thesis, Universität Túbingen (2011).