SOLUCIÓN DE LA ECUACIÓN DE SCHRÖDINGER PARA POTENCIALES UNI-DIMENSIONALES USANDO EL MÉTODO DE LA MATRIZ DE TRANSFERENCIA

SOLUTION OF SCHRÖDINGER'S EQUATION USING THE TRANSFER MATRIX METHOD FOR ONE-DIMENSIONAL POTENTIALS

El Método generalizado de Matriz de Transferencia (MMT) aparece como una alternativa de investigación a los fenómenos cuánticos dentro de materiales semiconductores y componentes opto electrónicos. En el presente trabajo el MMT es aplicado a los fenómenos de propagación de una partícula a través de un pozo o una barrera de potencial para el caso cuántico, deduciendo las relaciones de las amplitudes de dispersión mediante los coeficientes de la matriz de transferencia (transmisión y reflexión). Los resultados obtenidos son comparados con literatura relacionada, para así  determinar la veracidad y el alcance de el MMT, el cual a saber puede ser aplicado al estudio de muchos otros problemas de propagación de ondas y electrones, incluso en medios estratificados como cristales fotónicos.

The Generalized Method of Transfer Matrix (MMT) appears as an alternative to quantum phenomena research in semiconductor materials and optoelectronic components.
In this paper the MMT is applied to the propagation phenomena of a particle through a well or a potential barrier to the quantum case. The relations scattering amplitudes are deduced using the coefficients of the transfer matrix (transmission and reflection). The results are compared with related literature, to determine the accuracy and scope of the MMT, namely which can be applied to study many other problems of wave propagation and electrons, even in layered media as photonic crystals.

Jhon H. Vargas¹, Raúl E. Castiblanco¹, Maicol Cárdenas¹, John Morales¹²

¹Grupo de Campos y Partículas, Departamento de Física, Universidad Nacional de Colombia.

²Centro Internacional de Física

Contacto: Jhon H. Vargas: jhhvargasbe@unal.edu.co

Contacto: Raúl E. Castiblanco: recastiblancos@unal.edu.co

(Recibido: 02/2011. Aceptado: 04/2011)

Cómo citar: Vargas, J.H., Castiblanco, R.E., Cárdenas, M., Morales, J., Momento, 42, 23 (2011)

Resumen

El Método generalizado de Matriz de Transferencia (MMT) aparece como una alternativa de investigación a los fenómenos cuánticos dentro de materiales semiconductores y componentes opto electrónicos. En el presente trabajo el MMT es aplicado a los fenómenos de propagación de una partícula a través de un pozo o una barrera de potencial para el caso cuántico, deduciendo las relaciones de las amplitudes de dispersión mediante los coeficientes de la matriz de transferencia (transmisión y reflexión). Los resultados obtenidos son comparados con literatura relacionada, para así determinar la veracidad y el alcance de el MMT, el cual a saber puede ser aplicado al estudio de muchos otros problemas de propagación de ondas y electrones, incluso en medios estratificados como cristales fotónicos.[1]

Palabras claves: Matriz de Transferencia, Pozo y Barrera de Potencial, Coeficientes Transmisión y Reflexión

Abstract

The Generalized Method of Transfer Matrix (MMT) appears as an alternative to quantum phenomena research in semiconductor materials and optoelectronic components. In this paper the MMT is applied to the propagation phenomena of a particle through a well or a potential barrier to the quantum case. The relations scattering amplitudes are deduced using the coeficients of the transfer matrix (transmission and reflection). The results are compared with related literature, to determine the accuracy and scope of the MMT, namely which can be applied to study many other problems of wave propagation and electrons, even in layered media as photonic crystals.[1]

Keywords: Transfer Matrix, Potential Well and Barrier, Transmission and Reflection Coeficients

Introducción

El problema de la descripción del movimiento de partículas incidentes sobre un potencial arbitrario uni–dimensional es de gran interés teórico y práctico. En principio este problema ha sido resuelto en variada literatura [2, 3], sin embargo el método de matriz de transferencia (MMT), en contraste con los métodos convencionales de solución directa de la ecuación de Schrödinger, reduce el problema de frontera al cálculo del producto de matrices mediante la aproximación del potencial como un sistema de potenciales rectangulares adyacentes cuando se estudian sistemas periódicos. [4–7]

En este trabajo se describe la solución al problema del movimiento de un paquete de partículas a través de potencial de barrera y pozo. Así el MMT, consiste en determinar las amplitudes de transmisión y reflexión mediante condiciones de frontera a partir de las funciones de onda expresadas mediante la solución de la ecuación de Schrödinger.

Primero se ilustrará el método generalizado a través de una interface, determinando la matriz para este problema y revisando el sentido físico de cada uno de los coeficientes.[1]. Luego se analizan los resultados obtenidos para así contrastarlos, comparando el MMT, con los métodos tradicionales.[8].

Método Generalizado de Matriz de Transferencia para una Interface

Para demostrar la generalidad del método, consideramos la solución de la ecuación de onda independiente del tiempo descrita por la ecuación (1) cuyas soluciones en las regiones de potencial cero se muestran en la figura 1, en la región interior a la interface, la solución depende de la forma del potencial. Para el caso de una

Figura 1. Amplitudes del paquete de Ondas incidentes sobre una interface a un potencial arbitrario.

onda electromagnética incidente sobre una placa arbitraria de absorción, encontramos que la ecuación diferencial para cada región queda escrita de la forma.

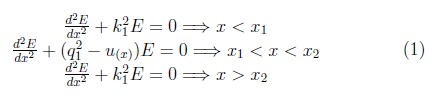
donde k₁ representa el vector de onda en las regiones de potencial cero para la barrera, y q la relación de dispersión, el comportamiento depende de la parte real e imaginaria del potencial. El campo eléctrico en las regiones I y II. toma la forma:

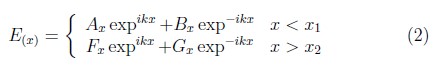
Ahora bien, conocida la solución de la ecuación de onda dentro de la región II, se evalúa e iguala, en los valores de frontera del campo eléctrico y su derivada en x₁ y x₂, obteniendo así un sistema de ecuaciones linealmente independientes 2 × 2, para cada interface, en general de la forma:

Donde los valores a₁, b₁, a₂, b₂, cumplen con la continuidad del campo elé7ctrico o de una función de onda arbitraria, y su derivada en dichas interfaces. Reescribiendo (3) en forma matricial.

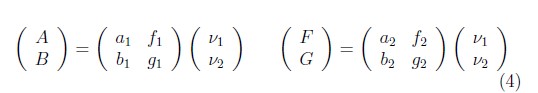
Es posible despejar el vector columna (ν₁ ν₂) y así encontrar una relación directa entre las amplitudes (A,B) y (F,G) para el caso de una barrera.

Así de acuerdo al MMT [1] entre las amplitudes A,B y F,G existe una relación lineal así:

Reescribiendo (5).

donde α, β, γ, δ son los elementos de la matriz de transferencia, que corresponden a los valores que toma la función de onda y su derivada en la frontera, los cuales cumplen.

Los elementos de esta matriz los podemos relacionar con los coeficientes de transmisión y reflexión para el caso típico cuando no hay incidencia por la derecha, es decir, G = 0: [8].

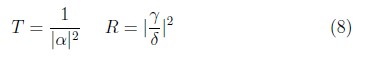
En nuestro caso de estudio tendremos que encontrar la matriz de transferencia para el caso de una barrera y pozo de potencial, ya que este problema es análogo al caso de una onda electromagnética con incidencia normal desde un medio con índice de refracción n₁, sobre una placa dieléctrica cuyo incide de refracción es n₂, y finalmente transmitida a un medio con indicie de refracción n₃. En este problema los índices de refracción son reales ya que la onda viaja a través de medios dieléctricos, este fenómeno se puede comparar con el caso cuántico como:

• primer caso Si la permitividad eléctrica de la placa ε₂ es mayor que la permitividad del medio incidente y transmitido, es decir, ε₂ > ε_1,3, este fenómeno cumple el mismo rol de una partícula incidente sobre un pozo potencial.
• segundo caso si ε₂2 < ε_1,3 este problema es análogo a una partícula incidiendo sobre una barrera de potencial. [9]

Como el objetivo primordial de este trabajo es encontrar la matriz de transferencia en el caso cuántico solo mencionamos el caso electromagnético como punto de referencia, aunque en el desarrollo de este escrito se comparan estos dos fenómenos de transmisión.

Pozo de Potencial

En esta sección discutiremos el potencial más simple sobre el cual se puede hacer incidir partículas en una región finita del espacio, potencial de pozo cuadrado, que se indica en la figura 2. con la función potencial descrita como:

Figura 2. Pozo de Potencial donde E > 0 > V₀

Considerando únicamente el caso donde E > V₀, donde se encuentra la solución de la ecuación de Schördinger para las tres regiones descritas en la figura 2, en este caso las partículas incidentes pueden ser escritas como ondas viajeras para la región I y III; así la solución propuesta para cada región será:

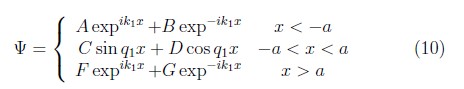
donde y y los valores de A, B, C, D, F, G son las amplitudes de la función de onda. Ahora evaluamos condiciones de frontera que debe cumplir la función de onda a cada lado del pozo, lo cual consiste en igualar las funciones y su primer derivada en los puntos de unión entre las distintas regiones.

Continuidad de la función de onda y su derivada en el punto x = —a

Continuidad de la función de onda y su derivada en el punto x = a

Matematicamente el MMT es tomar la solución completa de la ecuación de Schrödinger, sin reducir la solución de la ecuación de onda al caso particular del problema físico (como por ejemplo haciendo el coeficiente G = 0, para el caso típico cuando no hay partículas incidentes por la derecha del pozo, o también cuando la solución diverge para el caso de estados ligados). Ahora bien, combinamos las ecuaciones (13) y (14) multiplicando por sin q₁a y respectivamente, para luego sumarlas y despejar el coeficiente C obtenemos:

ahora para determinar D multiplicamos la ecuación (13) por cos q₁a y (14) por , sumando tenemos:

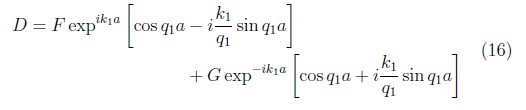
reemplazando (15) y (16) en la ecuación (11) se obtiene.

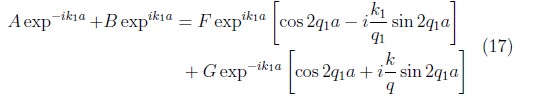
de igual forma reemplazando (15) y (16) en la ecuación de (12),se obtiene.

sumando las ecuaciones (17), (18), determinamos A.de la siguiente manera;

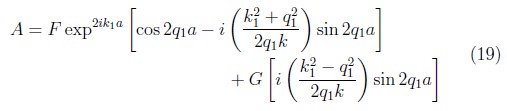
restando las ecuaciones (17) y (18) hallamos B así:

así es posible escribir las ecuaciones (19) y (20) de forma matricial como:

en la ecuación (21) se relaciona las amplitudes de la derecha–izquierda del pozo, mediante la matriz de coeficientes determinados al combinar las condiciones de frontera. Sin embargo debemos despejar los coeficientes F G de esta ultima ecuación para obtener así la matriz de transferencia (MT).

donde ,con la traspuesta de la matriz , aplicando esta relación encontramos los elementos de la matriz de transferencia (MT) descritos por la ecuación (6), para el pozo de potencial:

Es facil ver que el determinante de la matriz MT usando la ecuación (7) es 1.

Barrera de Potencial

En el caso de barrera de potencial, para encontrar la matriz de transferencia se debe solucionar la ecuación de Schördinger al igual que en el caso del pozo para tres regiones, cuyo potencial está escrito por

Para el caso de la barrera de potencial existen dos fenómenos interesantes de estudio: cuando la energía de las partículas incidentes es mayor a la barrera y cuando es menor. En ambos casos existe transmisión y reflexión.

Empecemos estudiando el caso donde E > V₀ (Ondas Viajeras)

Cuando las partículas incidentes tienen una energía mayor a la de la barrera, la solución a la ecuación de Schördinger para las tres

Figura 3. Barrera de Potencial

regiones es:

donde y siguiendo el procedimiento descrito en el caso del pozo de potencial, es posible obtener los elementos de la matriz de transferencia como:

es de resaltar que las MT para el caso de pozo y barrera cuando la energía de las partículas incidentes es mayor que el potencial E > V₀ guardan una estrecha similitud en cuanto a su forma, sin embargo difieren en los vectores de onda q₁ y q₁.

Continuación del estudio para el caso donde E < V₀

Ahora se analiza el caso de energías de las partículas incidentes son menores que la barrera de potencial, primero se propone la solución de la ecuación de Schördinger para las tres regiones como:

donde y , para encontrar la MT se aplican las condiciones de frontera en cada lado de los bordes de la barrera así.

Continuidad de la función de onda y su derivada en el punto x = –a

multiplicando la ecuación en (28) por ik y sumandola con (29), se obtiene el valor de A así;

al multiplicar la primer ecuación en (28) por –ik y sumandola con (29), es posible obtener B encontrando.

Continuidad de la función de onda y su derivada en x = a

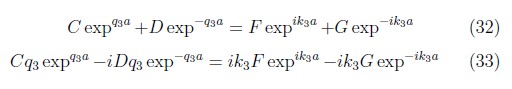
multiplicando (32) por q y luego por –q y sumandola con (33), es posible obtener C y D respectivamente obteniendo:

ahora reemplazando (34) y (35) en (30) se obtiene:

de igual modo reemplazando (34) y (35) en la ecuación (31) se determina que

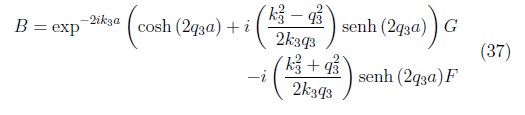
Escribiendo las ecuaciones (36) y (37) en forma matricial y encontrando la inversa de la matriz (2X2) encontramos los elementos de la matriz de transferencia para el caso de barrera de potencial con E < V₀, la cual guarda una similitud en la forma con las (MT) encontradas en los casos anteriores, pero con la diferencia en los vectores de onda, senos y cosenos por funciones hiperbólicas.

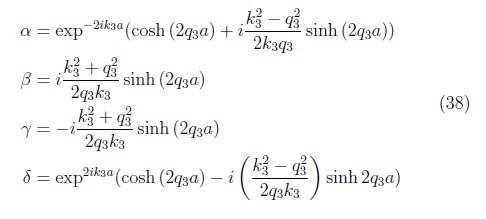
Análisis de resultados

A través de este cálculo, se pudo encontrar las matrices de transferencia para los dos casos estudiados, las cuales cumplen con las propiedades implícitas de una matriz de transferencia (MT); α = δ* y β = γ* , de modo que los elementos de la diagonal principal y secundaria de la (MT) son los correspondientes complejos conjugados, y el Det (MT) = 1, esta básicamente es la ley de conservación de la energía.

Transmitancia y Reflactancia para el Pozo de potencial

Para encontrar estos coeficse puede determinar el coeficiente de transmitancia para el pozo de potencial el cual esta dado por:

y para la reflactancia se tiene que

Al sustituir los vectores de onda k₁ y q₁ , de la solución de la ecuación de Schrödinger en las ecuaciones anteriores, y haciendo la sustitución y , obtenemos.

Notase que R + T = 1, para cualquier valor de energía y ancho de barrera. Como también hay casos en que T = 1 y R = 0, es decir el pozo es transparente, esto sucede cuando

En estas ecuaciones se observa que para específicos valores de a se obtiene una máxima transmitancia es decir todas las partículas atraviesan el pozo de potencial, de igual manera hay valores de energía asociadas a las partículas comparadas con la profundidad del pozo, que permite que se presente una transmitancia máxima, cabe resaltar que estos valores de energía son discretos pero dentro de un rango continuo, ya que la energía de dichas partículas es mayor que cero. Para el caso contrario se sabe (aunque no se mostró en el presente escrito(, que para este caso donde V₀ < E < 0 se tienen estados ligados de las partículas, es decir, pertenecen a un rango discreto de energía en donde no se presentan transmitancia ni reflactancia.

Transmitancia y reflactancia para la barrera de potencial

De igual manera que para el pozo de potencial, pero en esta ocasión utilizando el coeficiente que relaciona la transmitancia α y la reflactancia γ y δ de la martriz de transferencia (MT) relacionada en la ecuación (26) con E > V₀, y la ecuación (38) donde E < V₀, tenemos que la transmitancia y reflactancia cuando la energía de las partículas excede la barrera y el caso contrario son:

y para el caso de la refractancia

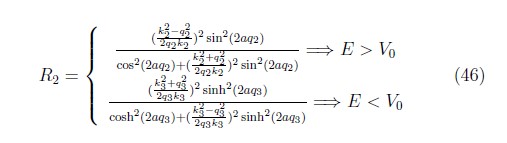
Se observa que para el caso de la barrera con E > V₀ estas ecuaciones son idénticas en su forma a la transmitancia y reflactancia para el pozo de potencial, cuya única diferencia son los vectores de onda provenientes de las soluciones de la ecuación de Schrödinger, ya que tanto en el pozo de potencial como para este caso, la energía es positiva y mayor al potencial.

Realizando el mismo procedimiento que para el pozo de potencial, donde relacionamos las variables implícitas. tenemos

De estas expresiones podemos analizar el caso para cuando k₂a = nπ (siendo n un número entero), el coeficiente de reflactancia vale R = 0 y la transmitancia T = 1 y por lo tanto todas las partículas atraviesan la barrera, esto sucede cuando:

La descripción del comportamiento físico de las ecuaciones (43) y (49) es análogo a lo que ocurre en óptica al analizar la interferencia de Frabri–Perot [9], es decir, el coeficiente de transmisión es igual a uno cuando el espesor de la barrera es igual a un múltiplo entero de longitudes de onda, para que exista una interferencia constructiva sobre el camino recorrido dentro de la barrera o el pozo bajo la condición η > 1. En la figura 4 se representa la transmitancia en función del ancho de la barrera o pozo de potencial.

Figura 4. Transmitancia según ancho de barrera o pozo

Para el caso de el pozo el valor minimo de la transmitancia está dado por , y con múltiplos enteros de la longitud de onda de . Para el caso de la barrera y , ambos casos con E > V₀.

Como acabamos de ver, ocurre interferencia para valores específicos de η > 1 dada por la expresión (50) y para valores específicos de a en (49). Pero falta analizar el comportamiento o la dependencia de la transmitancia con el ancho de la barrera de potencial para valores de η < 1. El coeficiente que describe esta situación es el encontrado en la ecuación (47), donde a diferencia de los casos anteriores no se obtienen patrones de interferencia por la dependencia con la función seno, si, un comportamiento tipo seno hiperbólico con los parámetros χ y η.

Cabe resaltar que al hacer tender la función seno hiperbólico → 0 la transmitancia tiende a ser cero, el cual es el análisis que predice la teoría clá también se obtiene el mismo resultado si se hace tender m → ∞, por lo tanto una partícula macroscópica no puede atravesar la barrera.

Ahora bien, analizando este coeficiente si hacemos tender el valor de a >> 1 el cuadrado del seno hiperbólico tiende a , en este caso la expresión (47) con η < 1, se puede aproximar a:

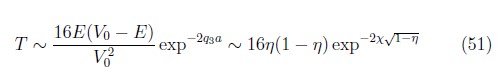
Con lo cual, al variar el parámetro a estamos variando implícitamente el parámetro χ, el cual está relacionado con la opacidad. Aquí nos encontramos frente a la notable predicción (en contraste con la mecánica clásica), que una partícula incidente sobre una barrera de potencial a una energía menor a la de la barrera posee una probabilidad T, de penetrar la barrera, es decir, que se produzca un efecto túnel.

En la figura 5 se puede ver la variación del coeficiente de transmisión, ya conocido, de un paquete de ondas o de partículas incidentes sobre un pozo (color rojo) o una barrera de potencial (color azul).

Se observa que el coeficiente de transmisión depende de la geometría de la barrera o del pozo, es decir, la opacidad χ de la barrera o pozo es pequeña, es decir menores a 3, es cuasi–transparente, la probabilidad de que las partículas incidentes se transmitan es relativamente mayor (parte a) y b) de la figura) donde los valores de η son menores a uno, en este caso existe la mayor probabilidad de ocurrir un efecto túnel para el caso de la barrera.

A medida que la opacidad χ aumenta (para valores de η > 0 en el caso del pozo de potencial), es posible encontrar un fenómeno de interferencia, para η > 1 encontramos interferencia en el caso de la barrera según el ancho a, cuyos valores (η_In) se muestran en la figura 5 (apartados c. y d.), los cuales se describen o se pueden encontrar a través de las ecuaciones (44) y (50) respectivamente.

Figura 5. Coeficiente de transmisión en función del parámetro η y χ

Para ambos casos; pozo y barrera de potencial, tenemos que para valores de η grandes el coeficiente de transmisión es 1 como caso limite. Para el pozo de potencial, se observa que para cualquier valor de η, siempre hay transmisión, esto es coherente, ya que las partículas incidentes sobre el pozo poseen valores de energías positivas y continuas, por lo cual, es más probable encontrarlas en dicha región.

Conclusiones

El método de la matriz de transferencia MMT es utilizado para calcular los coeficientes de transmitancia y reflactancia. Para ello como se vio en este escrito, se necesita conocer la solución de la ecuación de Schrödinger, el cálculo de los valores y vectores propios arrojados por esta ecuación caracterizan el sistema estudiado, en particular los sistemas cuánticos tienen gran similitud al caso electromagnético, principalmente en la interferencia sobre el camino recorrido sobre las interfaces dieléctricas. El MMT describe en términos de dichas soluciones, amplitudes de incidencia, transmisión y reflexión de ondas y/o partículas, relacionando así, estados iniciales y finales luego de interaccionar con una interfase.

Referencias

[1] A. Z. Khachatrian, Armenian J. Phys. 3, 178 (2010).

[2] P. Pereyra, The Transfer Matrix Method (Springer, 2010).

[3] S. Vatannia and G. Gildenblat, IEEE J. Quantum Elect. 32, 1093 (1996).

[4] J. Gain, M. Das Sarkar, and S. Sudakshina Kundu, Int. J. Eng. Sci. Tech. 3, 4954 (2011).

[5] L. Gómez Chico, El gas electronico confinado en sistemas semiconductores cuanticos., Ph.D. thesis, Universida Complutence de Madrid (1993).

[6] P. Pereyra, Ann. Phys. 320, 1 (2005).

[7] P. Pereyra and E. Castillo, Phys. Rev. B 65, 205120 (2002).

[8] D. Griffths, Introduction to quantum mechanics (Pearson Prentice Hall, 2005) p. 82.

[9] P. Markos and C. Soukoulis, Wave Propagation: From Electrons to Photonic Crystals and Left–Handed Materials (Princeton University Press, 2010).