EL MÉTODO DE ZHOU EN LA SOLUCIÓN DE ECUACIONES NO LINEALES DE TIPO LANE-EMDEN: UN CASO ESPECIAL
THE ZHOU’S METHOD FOR SOLVING THE NONLINEAR LANE-EMDEN TYPE EQUATIONS: A SPECIAL CASE
Keywords:
DTM, Ecuación de tipo Lane-Emden, esfera isoterma de gas, Método de Zhou, Teoría de corrientes termoiónicas (es)DTM, isothermal gas sphere, Lane-Emden type equation, Theory of thermionic currents, Zhou’s method. (en)
THE ZHOU'S METHOD FOR SOLVING THE NONLINEAR LANE–EMDEN TYPE EQUATIONS: A SPECIAL CASE
EL MÉTODO DE ZHOU EN LA SOLUCIÓN DE ECUACIONES NO LINEALES DE TIPO LANE–EMDEN: UN CASO ESPECIAL
Pedro P. Cárdenas, Diana M. Devia, Fernando Mesa
Grupo GEDNOL, Departamento de Matemáticas, Universidad Tecnológica de Pereira, Colombia
(Recibido: 06/2013. Aceptado: 08/2013)
Contacto:Diana M. Devia: dianadevia@gmail.com
Cómo citar: Cárdenas, P., Devia, D. & Mesa, F., Momento 47, 1 (2013)
Abstract
In this work we apply the differential transformation method (the Zhou's method) for solving some classes of Lane– Emden type equations as a model for the dimensionless density distribution in an isothermal gas sphere, which are nonlinear ordinary differential equations on the semi–infinite domain, as a special case ![]() = 0 and
= 0 and ![]() = 0 Differential transformation method may be considered as alternative and eficient for finding the approximate solutions of the initial values problems. Superiority of these methods by applying them on the some type Lane–Emden type equations was demonstrated. The power series solution of the reduced equation transforms into an approximate implicit solution of the original equation.
= 0 Differential transformation method may be considered as alternative and eficient for finding the approximate solutions of the initial values problems. Superiority of these methods by applying them on the some type Lane–Emden type equations was demonstrated. The power series solution of the reduced equation transforms into an approximate implicit solution of the original equation.
Keywords: DTM, isothermal gas sphere, Lane–Emden type equation, theory of thermionic currents, Zhou's method.
Resumen
En este trabajo aplicamos el método de transformación diferencial (método de Zhou) para resolver algunas clases de ecuaciones de tipo Lane–Emden como modelo para la distribución de densidad dimensional en una esfera de gas isoterma, las cuales son ecuaciones diferenciales no lineales en un dominio semi–infinito, como un caso especial ![]() = 0 y
= 0 y ![]() = 0 El método de transformación diferencial puede ser considerado como un método alternativo y eficiente para encontrar soluciones aproximadas de problemas de valor inicial. Se demostró la superioridad de estos métodos aplicándolo sobre algunas ecuaciones de tipo Lane–Emden. Las soluciones en series de potencias de la ecuación reducida transforman sobre una solución implícita aproximada de la solución general.
= 0 El método de transformación diferencial puede ser considerado como un método alternativo y eficiente para encontrar soluciones aproximadas de problemas de valor inicial. Se demostró la superioridad de estos métodos aplicándolo sobre algunas ecuaciones de tipo Lane–Emden. Las soluciones en series de potencias de la ecuación reducida transforman sobre una solución implícita aproximada de la solución general.
Palabras clave: DTM, Ecuación de tipo Lane–Emden, esfera isoterma de gas, Método de Zhou, Teoría de corrientes termoiónicas.
Introduction
Other classical nonlinear equation, which has been the object of much study is Lane–Emden's equation. This equation has the form:

with 0 > x ≥ 1 and the subject to initial conditions:

where α and β are constants and g(y) is a real–valued continuous function. The Equation 1 was used to model various problems, including the isothermal gas spheres and theory of thermionic currents.
Let us consider a spherical cloud of gas (see Fig. 1) and denote its hydrostatic pressure at a distance r1 from the centre by P. Let M(r1) be the mass of the spheres of radius r1, φ the gravitational

Figure 1. Spherical cloud of gas.
potential of the gas, and g the acceleration of gravity. Then, we have the following equations:

where G is the gravitational constant.
Thus, three conditions are assumed for the determination of φ and P:
![]()
where ρ is the density of the gas.

and
![]()
where γ and K are arbitrary constants.
Solving 4 and 6 with φ = 0 when ρ = 0 we have:
![]()
or
![]()
where n = 1/γ—1 and L = Kn. If this value of ρ is replaced into Equation 5, we obtain
![]()
where δ2 = 4πLG.
Now, since ![]() , by integration
, by integration ![]() , that is
, that is ![]()
If ρ is the central density, then φ0 must be zero, a change from the condition in the previous case where φ was zero only at the boundary of the sphere.
Poisson's equation is now replaced by:
![]()
where δ2 = 4πρ0G, Equation which is known as Liouville's equation. If we assume symmetry as before, Equation 1 in polar coordinates reduces to the following:

which replaces Equation 9.
If we let ![]() , then 11 becomes
, then 11 becomes

which is the solved subject to the boundary conditions y(0) = 0 and y'(0) = 0. The counterpart1 of 12 in which ey is replaced by e–y appears in Richardson's Theory of thermionic currents when one seeks to determine the density and electric force of an electron gas in the neighborhood of a hot body in thermal equilibrium.2
The Differential Transformation Method (DTM) is a semi–numerical–analytic method for solving ordinary and partial differential equations. The concept of the DTM was first introduced by Zhou in 1986.[1] Its main application therein is to solve both linear and non–linear initial value problems in electric circuit analysis. This technique constructs an analytical solution in the form of a polynomial. The Taylor series method is computationally expensive for large orders. The differential transformation method is an alternative procedure for obtaining analytic Taylor series solution of the differential equations. The series often coincides with the Taylor expansion of the true solution at point x0 = 0, in the initial value case. Although the series can be rapidly convergent in a very small region.
Many numerical methods were developed for this type of nonlinear ordinary differential equations, specifically on Lane–Emden type equations such as the Adomian Decomposition Method (ADM) [2, 3], the Homotopy Perturbation Method (HPM) [4, 5], the Homotopy Analysis Method (HAM) [4] and Bernstein Operational Matrix of Integration [6]. In this paper, we show superiority of the DTM by applying them on the some type Lane–Emden type equations. The power series solution of the reduced equation transforms into an approximate implicit solution of the original equation [7–10].
Description of Differential Transformation Method DTM
Differential transformation method of function y(x) is defined as follows:

In 13, y(x) is the original function and Y (k) is the transformed function and the inverse differential transformation is defined as:

In real applications, function y(x) is expressed by a finite series and Equation 14 can be written as:

Equation 15 implies that

is negligibly small. Here, n is decided by the convergence of natural frequency in this study.
The following theorems that can be deduced from Eqs. 13 and 14.
Theorem 1. If y(x) = f(x) ± g(x), then Y (k) = F(k) ± G(k).
Theorem 2. If y(x) = α1 f(x), then Y (k) = α1 F(k), α1 is a constant.
Theorem 3. If y(x) =![]() then Y (k) =
then Y (k) = ![]()
Theorem 4. If y(x) = g(x) h(x), then Y (k) = ∑kk1 =0 G(k1) H(k — k1).
Theorem 5. If y(x) = xn then Y (k) = δ(k — n), where

Theorem 6. (Cárdenas). If y(x) = xnf(x) with m ∈ N, then:

The proofs of Theorems are available in [1].
Numerical Examples
To illustrate the ability of the Zhou's method for the Lane–Emden type equation (Isothermal Gas Spheres), two examples are provided. The results reveal that this method is very effective.
Problem 1
To solve y'' + 2/x y' + ey = 0 subject to y(0) = y'(0) = 0. First, multiplying both sides by x we have:
![]()
using Theorems 3, 4 and 6:

where,

for all k ≥ 1.
Now, from the initial conditions y(0) = y'(0) = 0 we have:
![]()
Substituting Eq. 22 into Eq. 18 and by recursive method, the results are listed as follows:
For k = 1 we have:

for k = 2 we have:
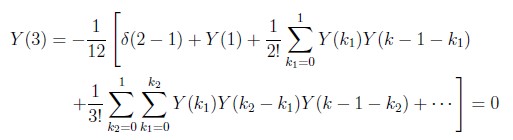
and then, Y(3)=0
for K=3 we have

Now, as Y(2) = —1/6 and S1=S2=S3= ... =0, then Y(4) = 1/4X5X6 = 1/120
For k=4 we have:
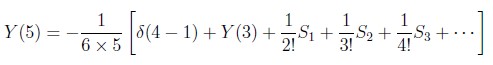
in this case as Y(3) = 0 and S1=S2=S3= ... =0, then Y(5) = 0
here the lector can see that:

For k = 5 we have:

Now, we can see:

and then:

for k = 6 we have:

here,

and

and so,
S2 = S3 = ... = 0.
Consequently, Y(7) = 0.
For k = 7 we have:

here

and

Consequently,
S3=S4= ... = 0.
Finally,

Therefore using 15, the closed form of the solution can be easily written as:

A series solution obtained by Wazwaz [3], Liao [2], Ramos [5] and Davis [8] by using ADM, HAM, MHAM and series expansion

Table 1. Comparison between Zhou's method and Wazwaz.
Respectively

Table 1 shows the comparison of y(x) obtained by the DTM (method proposed in this work) and those obtained by Wazwaz. The resulting graph of the isothermal gas spheres equation in comparison to the present method and those obtained by Wazwaz is shown in fig. 2.
Problem 2
To solve y'' + 2/x y' + e–y = 0 subject to y(0) = y'(0) = 0. Multiplying both sides by x:
![]()
As before, using theorems 3, 4 and 6 we have:
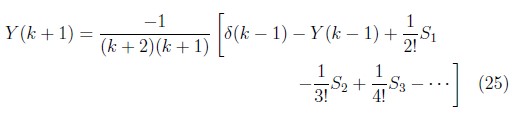

Figure 2. Comparison between DTM and solution by Wazwaz.
where S1, S2 and S are as 19, 20 and 21 respectively for all x ≥ 1.
Now, from the initial conditions y(0) = y'(0) = 0 we have:

Substituting Eq. 26 into Eq. 25 and by recursive method, the results are listed as follows:
For k = 1, 2, 3, 4, 5, we have respectively

So on, we can use 15 and the closed form of the solution can be easily written as:


Figure 3. Comparison between DTM and solution by Batiha [12].
A solution obtained by Yahya [11] by using the power series method respectively:

We can see the Fig. 3 and compare with [12], the results are very accurate because the error is minimal between the two methods.
Conclusion
In this work, we presented the definition and handling of one–dimensional differential transformation method or DTM. Using the differential transformation, differential equations can be transformed to algebraic equations and the resulting algebraic equations are called iterative equations. This method has applied to solve some classes of Lane– Emden type equations as a model for the dimensionless density distribution in an isothermal gas sphere, which are nonlinear ordinary differential equations on the semi–infinite domain. The figures and table clearly show the high eficiency of DTM to solve nonlinear equations in comparison with other analytical methods.
Acknowledgment
The authors gratefully acknowledge the support of the Department of Mathematics of the Universidad Tecnológica de Pereira and the group GEDNOL.
References
[1] J. K. Zhou, Differential Transformation and Its Applications for Electrical Circuits (Huarjung University Press, Wuuhahn, China, 1986).
[2]S. Liao, Appl. Math. Comput. 142, 1 (2003).
[3]A.–M. Wazwaz, Appl. Math. Comput. 118, 287 (2001).
[4] S. Iqbal and A. Javed, Appl. Math. Comput. 217, 7753 (2011).
[5] J. Ramos, Chaos Soliton Fract. 38, 400 (2008).
[6] N. Kumar, R. K. Pandey, and C. Cattani, ISRN Astron. Astrophys. 2011, 1 (2011).
[7] S. Chandrasekhar, An Introduction to the Study of Stellar Structure, Dover Books on Astronomy Series (Dover Publications, Incorporated, 1967).
[8] H. Davis, Introduction to Nonlinear Differential and Integral Equations, Dover Books on Mathematics Series (Dover Publications, 1962).
[9] C. Khalique and P. Ntsime, New Astron. 13, 476 (2008).
[10] S. S. Motsa and S. Shateyi, Math. Probl. Eng. 2012, 1 (2012).
[11] Y. Q. Hasan, ACMA 118, 191 (2012).
[12] B. Batiha, Int. J. Math. Analysis 3, 1953 (2009).
1For details, see H. Davis, Introduction to Nonlinear Differential and Integral Equations, Dover, New York, USA. (1962), pag: 379–380.
2The Emission of Electricity from Hot Bodies, 2d.ed, London, 1921, 320.
How to Cite
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Download Citation
Article abstract page views
Downloads
License
Those authors who have publications with this journal, accept the following terms:
a. The authors will retain their copyright and will guarantee the publication of the first publication of their work, which will be subject to the Attribution-SinDerivar 4.0 International Creative Commons Attribution License that permits redistribution, commercial or non-commercial, As long as the Work circulates intact and unchanged, where it indicates its author and its first publication in this magazine.
b. Authors are encouraged to disseminate their work through the Internet (eg in institutional telematic files or on their website) before and during the sending process, which can produce interesting exchanges and increase appointments of the published work.



















