RECONSTRUCCIÓN EXPERIMENTAL PARA LOS GRADOS DE LIBERTAD DE POLARIZACIÓN Y CAMINO: UN PASO HACIA LA CODIFICACIÓN DE DOS QUBITS EN UN SOLO FOTÓN

EXPERIMENTAL RECONSTRUCTION FOR POLARIZATION AND PATH DEGREES OF FREEDOM: A STEP TOWARDS ENCODING TWO QUBITS IN A SINGLE PHOTON

Con el fin de codificar  más información,  las aplicaciones cuánticas buscan aumentar la dimensionalidad  del espacio de Hilbert. En este artículo, reportamos nuestros esfuerzos para codificar dos qubits en un solo fotón utilizando los grados de libertad de polarización y camino. En particular, se presenta la reconstrucción  experimental  de qubits de polarización y se propone un montaje experimental para producir estados arbitrarios de camino  y  polarización.

In order to carry more information, quantum applications search for increasing the useful Hilbert space in which to encode information. In this paper, we report our efforts to encode two qubits in one single photon using the polarization and path degrees of freedom. In particular, we report the experimental state reconstruction of polarization qubits and we propose an experimental setup to produce arbitrary states of path and polarization.

Omar Calderón, David Jiménez, David Guzmán, Alejandra Valencia

Laboratorio de óptica cuántica, Departamento de física, Universidad de los Andes, A.A 4976, Bogotá, Colombia.

(Recibido: Febrero/2014. Aceptado: Marzo/2014)

Contacto: Omar Calderón o.calderon31@uniandes.edu.co

Cómo citar: Calderón, O., Jiménez, D., Guzmán, D. & Valencia, A. Momento. 48, 92 (2014)

Resumen

Con el fin de codificar más información, las aplicaciones cuánticas buscan aumentar la dimensionalidad del espacio de Hilbert. En este artículo, reportamos nuestros esfuerzos para codificar dos qubits en un solo fotón utilizando los grados de libertad de polarización y camino. En particular, se presenta la reconstrucción experimental de qubits de polarización y se propone un montaje experimental para producir estados arbitrarios de camino y polarización.

Palabras clave: Fotones individuales, Tomografía, Qubit de polarización, Qubit de camino

Abstract

In order to carry more information, quantum applications search for increasing the useful Hilbert space in which to encode information. In this paper, we report our efforts to encode two qubits in one single photon using the polarization and path degrees of freedom. In particular, we report the experimental state reconstruction of polarization qubits and we propose an experimental setup to produce arbitrary states of path and polarization.

Palabrasclave: Single photons, Tomography, Polarization qubit, Path qubit

Introducción

Hoy en día se conoce como qubit a la unidad básica de información que puede ser manipulada en cualquier algoritmo de computación cuántica y físicamente corresponde a un sistema cuántico de dos niveles. En particular cuando se trabaja con fotones, cualquiera de sus grados de libertad, la polarización [1], los modos espaciales [2], el momento angular orbital [3] o sus tiempos de llegada a fotodetectores [4], pueden ser utilizados en la implementación de qubits. Inclusive se pueden considerar varios de estos grados de libertad para la formación de múltiples qubits en un solo fotón [5].

En cualquier montaje experimental que busque implementar tareas de computación cuántica se distinguen al menos dos procesos importantes: La preparación del estado que va ha ser afectado por algún proceso o algoritmo cuántico y la reconstrucción del estado resultante. Para el caso de variables discretas, esta reconstrucción se logra mediante un procedimiento estándar de tomografía del estado cuántico (en inglés, standard quantum state tomography SQST) que en el caso de N qubits consiste en proyectar el operador densidad en las 3N bases completamente factorizadas del espacio de Hilbert del sistema [6]. Típicamente, todas las medidas necesarias para lograr la reconstrucción del estado se obtienen mediante medidas proyectivas sobre las diferentes bases consideradas. En el caso estándar se realizan 2^N — 1 medidas independientes.

El presente documento busca reportar nuestros esfuerzos para codificar experimentalmente dos qubits de información en un solo

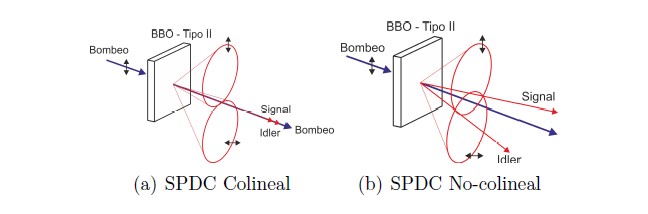
Figura 1. Conversión paramétrica espontánea mediante un cristal no–lineal tipo II.

fotón utilizando las variables de polarización y camino. El contenido se estructura de la siguiente manera: en la primera parte se hace una discusión sobre la fuente de fotones individuales y los montajes experimentales utilizados en la preparación del estado de los qubits, luego se describe el proceso de tomografía cuántica estándar en las variables de polarización y camino que permite reconstruir experimentalmente el estado del fotón.

Generación de fotones individuales

Un tópico de interés en los últimos años, debido a su aplicación en tareas de óptica cuántica, ha sido la implementación de fuentes de fotones individuales por demanda, en este contexto los puntos cuánticos, los centros NV del diamante, iones en cavidades, circuitos superconductores y procesos ópticos no lineales como el decaimiento paramétrico espontáneo se han propuesto como posibles fuentes de fotones [7–9].

En el presente trabajo consideramos la generación de fotones individuales mediante el proceso de conversión paramétrica espontánea o SPDC por sus siglas en inglés. A grosso modo, en este proceso se bombea un cristal no lineal con un láser para producir pares de fotones llamados signal e idler que están correlacionados en tiempo, energía, momento y polarización, por lo que típicamente son utilizados como qubits enredados en cualquier combinación de estos grados de libertad [10]. El proceso SPDC puede implementarse en el laboratorio en la configuración colineal o no–colineal dependiendo si el fotón signal y el foton idler son paralelos o no con el haz de bombeo como se ven en las Figuras 1(a) y 1(b) respectivamente.

La correlación temporal entre signal e idler permite que dichos pares sean utilizados para construir una fuente no–clásica de fotones, debido a que uno ellos anuncia la existencia del otro, esto es lo que se conoce como una fuente de fotones anunciados (HSP) [11]. Para el trabajo reportado en este documento utilizamos un cristal BBO tipo II, de 1 mm de espesor que se bombea con un diodo láser cuya longitud de onda es de 405 nm. La Figura 2 muestra el montaje experimental para las fuentes de fotones anunciados basadas en SPDC colineal y no–colineal que utilizamos en nuestros experimentos. Una detección en el foto–detector anunciador revela la presencia de su gemelo que estará listo para ser preparado en un estado particular. Para garantizar que dicha fuente de fotones produce en verdad un solo fotón cada vez que se tiene una detección en el anunciador es necesario realizar una medida de la correlación de segundo orden [12]. En particular, esta medida para nuestra fuente ha sido reportada en otro manuscrito [13].

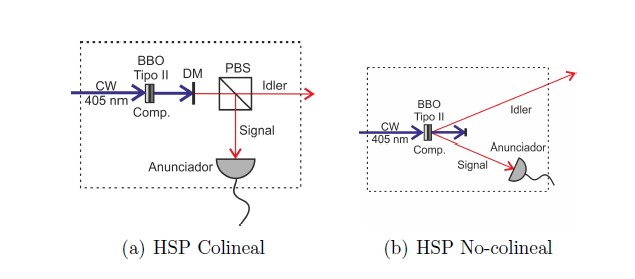
Figura 2. Diferentes configuraciones de las fuentes de fotones anunciados utilizados en los experimentos. En el caso colineal se utiliza un espejo dicróico DM para detener el bombeo y un divisor de haz de polarizacón para separar los rayos signal e idler. Comp es un cristal compensador para hacer indistinguibles temporalmente los fotones.

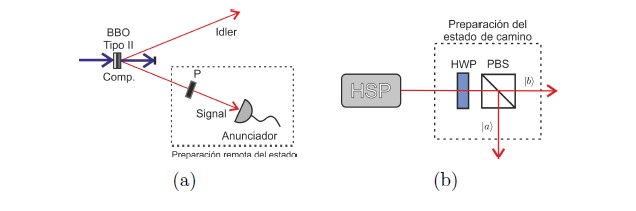
Figura 3. Esquema del montaje experimental que permite la preparación del estado de un qubit en un fotón (a) de polarización |φ_pol⟩ = sin (θ) |H⟩ jHi + cos(θ) |V⟩ , mediante la selección remota que se realiza variando el ángulo del polarizador. (b) de camino |φ_cam⟩ = α |a⟩ + β |b⟩, mediante la variación del ángulo de la HWP, se pueden ajustar los valores de α y β.

Preparación del estado cuántico: Codificando información en fotones individuales

La Figura 3(a) muestra el montaje para preparar remotamente estados de un qubit de polarización en el fotón idler de la forma

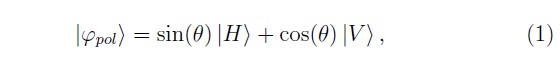
donde |H⟩ y |V⟩ corresponden a las polarizaciones horizontal y vertical respectivamente. Esto se realiza cambiando únicamente el ángulo θ del polarizador ubicado en el fotón anunciador signal. Para preparar qubits puros en polarización es necesario proyectar el fotón signal en un estado particular para obtener el estado deseado en el fotón idler. Formalmente, el proyector asociado al estado del fotón signal se puede escribir como

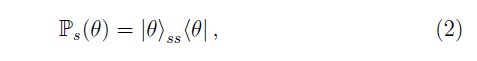
donde |θ⟩_s = cos(θ) |H⟩_s + sin(θ) |V⟩_s y θ es el ángulo del polarizador, esto implica que el estado del fotón idler anunciado por el fotón signal puede escribirse como

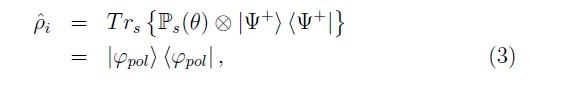
en donde hemos definido

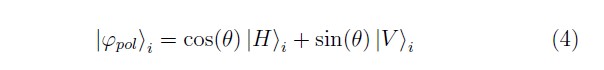
y es el estado de dos fotones que se obtiene del proceso SPDC con nuestras condiciones experimentales. Note que la Ecuación (4) corresponde con el estado de la Ecuación (1) que es justamente el que deseamos preparar.

Por otra parte, si consideramos el estado del fotón idler independientemente de lo que suceda con el fotón signal, o en otras palabras ignorando la existencia de este último, se tiene que el estado del fotón idler esta dado por

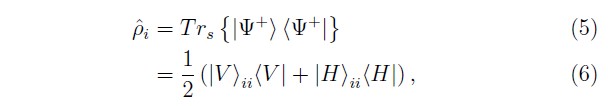
que corresponde a una mezcla estadística. Vale la pena resaltar que el estado dado por la Ecuación (4) se obtiene mediante una medición proyectiva, mientras aquel de la Ecuación (6) es el estado del fotón idler sin haber realizado ninguna medición.

Qubit en camino

Cuando un fotón pasa a través de un divisor de haz, este puede ser reflejado o transmitido de tal forma que el estado después del divisor puede ser escrito como una superposición de la siguiente forma

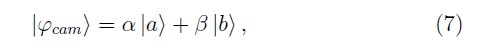
donde |a⟩ denota el camino de reflexión, |b⟩ el de transmisión y α y β las amplitudes de probabilidad respectivas. La Ecuación (7) representa lo que entendemos en este contexto por un qubit de camino. Debemos entonces contar con un montaje experimental que nos permita controlar las variables α y β para preparar un estado arbitrario. En la Figura 3(b) se ilustra este montaje experimental, que consta de la fuente de fotones anunciados HSP, una lámina de media onda HWP y un divisor de haz de polarización PBS. Rotando la HWP es posible controlar el estado de polarización que incide en el PBS y de esta forma las variables α = cos(ζ) y β = sin(ζ), donde ζ es el ángulo de la HWP.

Reconstrucción del estado cuántico

En general el estado arbitrario de un qubit se representa como una matriz 2 X 2 de entradas complejas, sin embargo debido a sus propiedades de norma y hermiticidad dicha matriz puede parametrizarse con tres valores reales y por tanto escribirse como

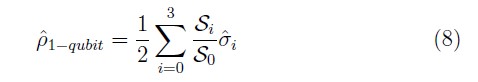
donde las cantidades

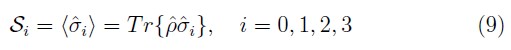
se conocen como los parámetros de Stokes y experimentalmente se relacionan con el valor esperado de los operadores de medida en cada una de las bases en las cuales se puede proyectar el estado. Además, σ₀ es el operador identidad, mientras que σ_j≠0 coinciden con los operadores de espín de Pauli σ_x, σ_y y σ_z.

La reconstrucción del estado se logra mediante la realización de medidas proyectivas [14] para determinar experimentalmente los parámetros de Stokes S_i que en el caso de un qubit se definen como

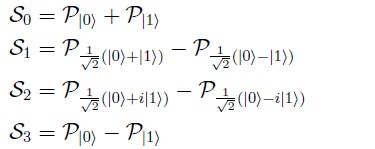
donde P es la probabilidad de medir el estado de proyección

Tomografía en variables de polarización

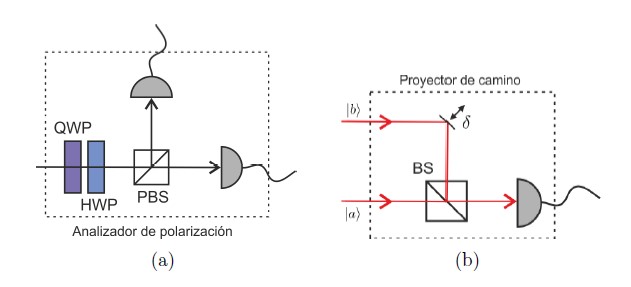
Figura 4. (a) Montaje experimental para proyectar un estado arbitrario |φ_pol⟩ de polarización en cada una de las bases asociadas a los operadores . (b) Esquema del proyector de camino de un fotón, consta de un espejo móvil que introduce un desfase δ en uno de los caminos y un divisor de haz (BS) 50/50. Este permite la proyección sobre estados arbitrarios de camino como los de la Ecuación (13).

El análisis de la polarización de un qubit se realiza utilizando el montaje de la Figura 4(a), que consta de una lámina de cuarto de onda (QWP), una lámina de media onda (HWP), un divisor de haz de polarización (PBS) y dos foto–detectores. Los estados de proyección que se requieren se obtienen rotando las láminas de onda en los ángulos que se relacionan en la Tabla 1 y las probabilidades P se determinan de los conteos de fotones que registran los detectores.

Efectuando la preparación remota de los estados |H⟩ y |V⟩ en el montaje experimental de la Figura 5 y el protocolo de tomografía descrito se logró reconstruir los estados que pueden verse en las Figuras 6(a) y 6(b) respectivamente. En cada caso, la fidelidad

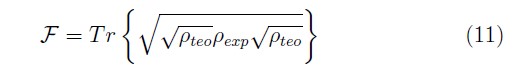
fue aproximadamente del 95 %

Tabla 1. Estados de proyección, operadores asociados y los ángulos correspondientes que se deben usar en el analizador de polarización de la Figura 4(a) para efectuar su medida.

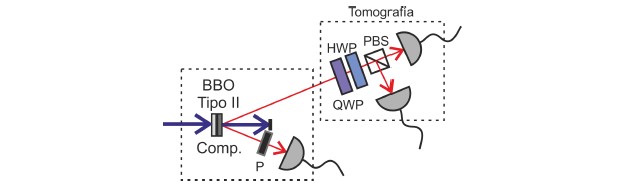
Figura 5. Montaje experimental utilizado para preparar y reconstruir un estado arbitrario |φ_pol⟩ de polarización.

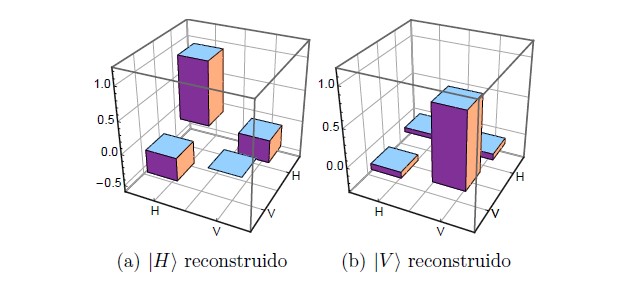
Figura 6. Tomografía de los estados |H⟩ y |V⟩ preparados mediante el método de selección remota.

Tomografía en variables de camino

De forma similar a la tomografía en variables de polarización, es necesario definir el operador de proyección de camino, para ello construimos el proyector [15]

sobre los estados base {|m⟩} requeridos para la realizar la tomografía que vienen dados por |a⟩, |b⟩,

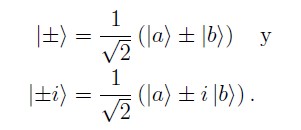
La Figura 4(b) muestra un esquema de lo que sería el proyector de camino de un fotón. Para ello se utiliza un "desfasador" δ (que en la práctica es un espejo móvil conectado a un cristal piezo–eléctrico) y un divisor de haz (BS), este montaje permite hacer proyecciones sobre un estado arbitrario de la forma

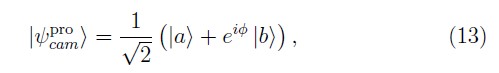
donde ø = δ + π/2 y π/2 es la fase adicional debida a la reflexión en el BS.

Debido a la interferencia de los dos posibles caminos que puede seguir el fotón en el proyector, la probabilidad de detección dependerá del valor de ø, la Figura 8(a) muestra el comportamiento te!rico de la probabilidad P(ø), de que el detector de la Figura 4(b) haga click como una función del desfase ø. La Tabla 2 resume los valores que debe tener dicho ø para efectuar la proyección del estado en la base correspondiente. Conviene resaltar que no se requiere de la interferencia de las alternativas de camino en la entrada del BS para medir los estados |a⟩ y |b⟩. Por ejemplo, para realizar la proyección sobre el estado |a∠, es suficiente contar los fotones que salen del proyector cuando se bloquea el camino jbi y viceversa. El montaje experimental para preparar y reconstruir el estado de un solo fotón en camino puede verse en la Figura 7, vale la pena comentar que corresponde a un interferómetro de Mach–Zehnder, lo que se podría considerar la entrada del interferómetro se utiliza

Tabla 2. Estados de proyección de camino, los operadores y los desfasamientos correspondientes que se deben realizar para efectuar el proceso de tomografía. Es importante resaltar que para medir los estados |a⟩, |b⟩ no se requiere de la interferencia de los caminos de entrada al BS, basta contar los fotones a la salida del proyector cuando se bloquea el camino #contrario" del estado que quiere medirse.

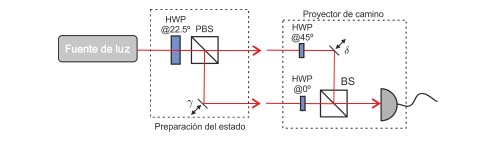
Figura 7. Interferómetro de Mach-Zehnder siendo utilizado como montaje experimental para preparar y reconstruir el estado de camino de un solo fotón.

para la preparación del estado de camino, mientras que uno de los espejos (al que se le conecta un cristal piezo–eléctrico) y el divisor de haz de la salida forman el proyector de camino para hacer la tomografía completa. Las HWPs que se utilizan sirven para garantizar que la polarización de los dos caminos sea la misma y de esta forma se de la interferencia en el divisor de haz de salida.

En la Figura 8(b) se muestra el interferograma experimental obtenido utilizando como fuente de luz un diodo láser a 808 nm. En particular se observa el cambio en la intensidad de la luz de salida como función del voltaje en el piezo–eléctrico que mueve el espejo desfasador con una visibilidad del 50 %. No obstante, esta visibilidad es muy baja para garantizar que el interferómetro funcione con un solo fotón, esto porque la diferencia de caminos no puede ser mayor que la longitud de coherencia de los dos fotones que se producen por SPDC que para nuestras condiciones experimentales es apenas de 60µm. Sin embargo el comportamiento

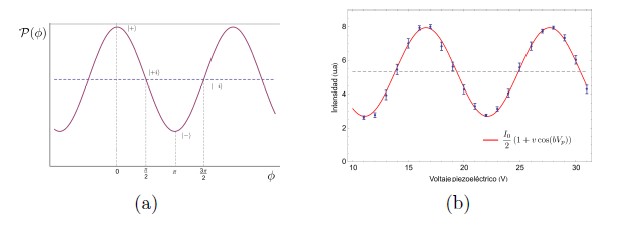
Figura 8. (a) Muestra la relación entre la probabilidad de detección del fotón y el desfase ø = δ + π/2, en particular se pueden ver los valores de ø requeridos para proyectar los estados de las bases dadas en la Tabla 2. (b) Gráfica de la intensidad medida como función del voltaje en el cristal piezo–eléctrico V_p y su ajuste correspondiente I₀(1 = v cos(bV_p))/2. I₀, b y v son parámetros de ajuste.

experimental es muy cercano al teórico, representado en la Figura 8(a), luego es posible asociar un voltaje de piezo–eléctrico a cada desfase y por tanto tener los estados de proyección que permiten realizar la tomografía del estado de camino.

Dos qubits en un solo fotón

En esta sección se pretende discutir sobre un posible montaje experimental que permita codificar dos qubits de información en una sola entidad de luz. Teniendo en cuenta que ya se ha ganado cierta experiencia en la manipulación de la polarización y el camino que puede tomar un fotón, lo más natural es que intentemos utilizar estos dos grados de libertad para codificarlos como qubits en el mismo fotón y producir estados generales de la forma

en donde

es un estado de polarización de la luz y los estados |a⟩, |b⟩ son los estados de camino. En particular, la Figura 9 muestra un esquema de la propuesta experimental que permite la preparación de dichos estados [16]. Todo lo que se requiere son tres láminas media onda

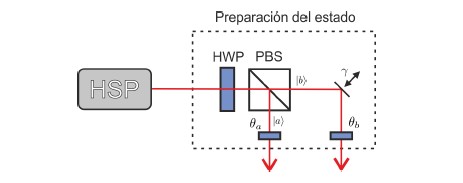
Figura 9. Esquema del montaje experimental que permite la generación del estado de dos qubits asociados al mismo fotón. Las variables de fase γ y polarización θ_a y θ_b, permiten la preparación de una gran variedad de estados de dos qubits.

HWPs para manipular los ángulos θ, θ_a y θ_b, un divisor de haz de polarización (PBS)y un espejo para introducir una fase entre los dos caminos γ. Por ejemplo, si las HWPs se fijan de tal forma que θ = π/8, θ_a = 0, θ_b = π y la posición del espejo introduce γ = 0 o γ = π se obtienen los estados de Bell en camino y polarización

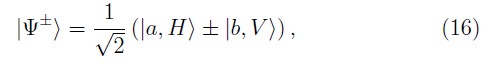
pero cambiando θ_a = π, θ_b = 0, se obtienen los otros dos estados de Bell

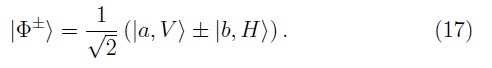
Utilizando los valores adecuados de θ, θ_a y θ_b y se pueden preparar por un lado, estados separables, pero también se pueden obtener estados enredados con una componente arbitraria de polarización.

Conclusiones y perspectivas

Utilizando el proceso de conversión paramétrica espontánea para producir fotones individuales anunciados y mediante el uso de elementos ópticos lineales se logró la implementación de montajes experimentales para la preparación de estados de un qubit tanto de polarización como de camino en un solo fotón. Asimismo, se implementaron los montajes y los procesos para realizar la reconstrucción completa del estado del qubit en cada una de las variables consideradas, en particular, se reportó la reconstrucción del estado de un qubit en polarización y se mostraron los avances para la reconstrucción del estado del qubit en la variable de camino. Por otra parte, se describió la propuesta de un montaje experimental para producir estados arbitrarios de polarización y camino codificados en el mismo fotón, actualmente se está trabajando en el diseño e implementación de las medidas para realizar la tomografía completa de dichos estados.

Referencias

[1] P. G. Kwiat, E. Waks, A. G. White, I. Appelbaum, and P. H. Eberhard, Phys. Rev. A 60, R773 (1999).

[2] N. J. Cerf, M. Bourennane, A. Karlsson, and N. Gisin, Phys. Rev. Lett. 88, 127902 (2002).

[3] G. Molina-Terriza, J. P. Torres, and L. Torner, Nat. Phys. 3, 305 (2007).

[4] R. T. Thew, A. Acín, H. Zbinden, and N. Gisin, Phys. Rev. Lett. 93, 010503 (2004).

[5] Y.-H. Kim, Phys. Rev. A 67, 040301 (2003).

[6] U. Fano, Rev. Mod. Phys. 29, 74 (1957).

[7] B. Lounis and W. E. Moerner, Nature 407, 491 (2000).

[8] S. Benjamin, Science 290, 2273 (2000).

[9] Sanders, Barry, Vuckovic, Jelena, and Grangier, Philippe, Europhys. News 36, 56 (2005).

[10] Y. Shih, Rep. Prog. Phys. 66, 1009 (2003).

[11] C. K. Hong and L. Mandel, Phys. Rev. Lett. 56, 58 (1986).

[12] L. R., The Quantum Theory of Light, edited by O. Oxford (Oxford Science Publications, 2000).

[13] D. Guzmán, O. Calderón, and A. Valencia, "Temporal second order correlation functions for different type of sources" (2013), en preparación.

[14] D. F. V. James, P. G. Kwiat, W. J. Munro, and A. G. White, Phys. Rev. A 64, 052312 (2001).

[15] S.-Y. Baek and Y.-H. Kim, Phys. Lett. A 375, 3834 (2011).

[15] J. Ahrens, P. Badziag, A. Cabello, and M. Bourennane, Nat. Phys. 8, 592 (2012).