Evidencias empíricas de regularidades estadísticas y leyes de potencia en los genomas de Arabidopsis thaliana, Oriza sativa y Mus musculus
Empirical evidences of statistical regularities and power laws in the genomes of Arabidopsis thaliana, Oriza sativa and Mus musculus
Palabras clave:
Genómica, leyes de potencia, Arabidopsis thaliana, Oriza sativa, Mus musculus. (es)Genomics, Power law, Arabidopsis thaliana, Oriza sativa, Mus musculus (en)
11Bióloga, M.Sc., Candidata a Ph.D. en Ciencias Agropecuarias, Universidad Nacional de Colombia, sede Palmira. A.A. 237. Valle del Cauca. Docente Universidad del Cauca.mialmanzap@palmira.unal.edu.co. 2 Ingeniera Bioquímica. Ph.D. en Biotecnología de Plantas. Docente Universidad Nacional de Colombia, sede Palmira. A.A. 237. Valle del Cauca. Autor para correspondencia.klopezl@palmira.unal.edu.co. 3 Biólogo. Ph.D. en Biología. Docente Universidad del Valle. pedro.moreno@univalle.edu.co 4Ingeniero de Sistemas. Universidad del Cauca. ctellez@unicauca.edu.co
La masiva cantidad de datos biológicos provenientes de las disciplinas ómicas y su aprovechamiento en el mejoramiento genético vegetal requiere de nuevos abordajes teóricos y estadísticos que describan de forma satisfactoria principios generales en los genomas. El total de secuencias de los genes de los genomas vegetales de Arabidopsis thaliana y Oriza sativa y del genoma animal Mus musculus fueron extraídas y depuradas de la base de datos pública del Genebank mediante el diseño de algoritmos en lenguaje de programación Python. Se analizaron las distribuciones de las variables frecuencia de uso y tamaño de los genes, exones e intrones por cromosoma y entre genomas. Los resultados señalaron que las variables presentan patrones de comportamiento no lineales en forma de ley de potencia que difieren estadísticamente entre los genomas pero no entre los cromosomas de un mismo genoma. Además, el análisis aportó evidencias respecto al tamaño promedio constante de las secuencias de exones y de los genes simples por cromosoma y entre genomas. Los hallazgos sugieren: primero, que el genoma se auto-organiza de la misma manera en los cromosomas independientemente del tamaño o número de genes que estos contengan, y, segundo, que tanto los cromosomas como sus elementos constituyentes: genes, exones e intrones han evolucionado conjuntamente. El estudio señala que las leyes de potencia cumplen un papel amortiguador en las leyes de variación biológica y proporcionan medidas cuantitativas de la organización de las secuencias de ADN que definen la identidad de un genoma. La regularidad estadística de estas medidas genéticas tiene potenciales aplicaciones en el incremento del valor predictivo de los actuales modelos de mejoramiento genético vegetal.
Palabra clave: Genómica, leyes de potencia, Arabidopsis thaliana, Oriza sativa, Mus musculus.
The huge quantity of biological data arising from the omics disciplines and their benefit in plant breeding require of new theoretical and statistical approaches in order to get a satisfactory description of the genomes general principles. The total number of sequences in the genes of A. thaliana and O. sativa plant genomes and in M. musculus animal genome was obtained from the public data base of the Genebank through algoritms designed in Python programming language. The variables distribution use frequency and gene size, exons and intrones per chromosome and among genomes were analyzed. The results indicated that variable distribution show non lineal patterns of behavior in a power law form, which are statistically different among genomes but no among the chromosomes of the same genome. In the same manner the analysis gave evidences about the constant mean size of the exons sequences and the single genes per chromosome and among genomes. These findings suggest that, first, the genome is self-organized in the same way in the chromosomes independently of the size or the number of genes being contained; second, so the chromosomes as their constituent elements: genes, exones and intrones, have evolved all together. The study points out that the power laws have a buffer roll in the biological variation laws and provide DNA sequences organization quantitative measurements which are defining the identity of the genome. The statistical regularity of these genetic measurements has potential applications in the predicted value increase of the actual models of genetic plant breeding.
Key words: Genomics, Power law, Arabidopsis thaliana, Oriza sativa, Mus musculus
Los mayores avances en el mejoramiento genético vegetal del siglo XXI se darán cuando se comprenda cómo extraer información de la ingente cantidad de datos biológicos postgenómicos provenientes de la aplicación de las nuevas tecnologías masivas, automatizables y cada vez menos costosas de la biología molecular. Mientras las secuencias de genes y genomas disponibles en las bases de datos crecen exponencialmente, la comprensión de la función de los genes lo hace linealmente. El reto principal del análisis de datos es encontrar regularidades estadísticas o patrones estructurales de organización y de función en los genomas, independientemente de que estos sean de vegetales o animales, procariotas o eucariotas o provengan de poblaciones, ecosistemas o metagenomas.
La detección de patrones forma parte del paradigma de las nuevas disciplinas denominadas ómicas y de la teoría de sistemas esbozada a mediados del siglo XX que en la época actual se presenta en los artículos científicos como System Biology o Network Biology, términos en inglés que aún no tienen un consenso de cómo deben ser traducidos al español. La idea fundamental es que a través del descubrimiento de regularidades y principios en el diseño de los componentes de los sistemas biológicos, y de la comprensión cuantitativa de su funcionamiento por medio del modelamiento y la simulación, es posible elucidar funciones biológicas y predecir cómo cambian frente a perturbaciones endógenas y exógenas para, finalmente, desarrollar experimentos precisos y efectivos para el mejoramiento de características de interés en los seres vivos (Barreto, 2008).
Los estudios de los genomas eucariotas secuenciados hasta el momento señalan dos aspectos importantes: el primero, la existencia de una intricada irregularidad topológica en la distribución de las secuencias codificantes y no-codificantes a lo largo de los cromosomas y en el contenido informacional de estas cuyo significado biológico aún dista de ser entendido por completo; y el segundo, la necesidad de cambiar de mentalidad y de herramientas informáticas para el tratamiento de datos biológicos a escala genómica. Estos aspectos son aún más críticos en genomas vegetales, en donde se aplican enfoques, recursos e infraestructura desarrollados para el genoma humano y para otros genomas eucariotas y procariotas, y no se consideran las características particulares de éstos, tales como alta plasticidad genética, metabolismo secundario complejo y su papel como cultivos.
Por otra parte, según Barreto (2008) en Colombia existen grupos con buen dominio en biología molecular pero muy pocos en genómica. Siendo esta última fundamental para tamizar e identificar genes y encontrar soluciones prácticas para el mejoramiento genético de cultivos comerciales y el desarrollo de servicios de diagnóstico de enfermedades y control de calidad de los cultivos vegetales y crianza de animales.
Los estudios comparativos y exhaustivos de los genomas de organismos modelo son la base teórica de las herramientas de análisis de la genómica, disciplina centrada en el estudio de la secuencia, la estructura y función del genoma. La idea subyacente de la genómica comparativa es que lo que es cierto para una especie es cierto para todas o al menos para muchas otras. Además, cuanta más información se tiene de un organismo más fácil es estudiarlo a otros niveles. La importancia del estudio de estos organismos radica en entender no sólo cómo funcionan en particular, sino en extrapolar los resultados obtenidos a un modelo general.
Las regularidades estadísticas o patrones se reconocen sólo cuando los sucesos se estudian en diversos organismos, los cuales operan de forma diferente pero mostrando características comunes. El estudio comparativo de organismos modelo alejados filogenéticamente permite identificar características esenciales evolutivamente conservadas a través de las especies, mientras que el estudio de organismos cercanos permite la comparación y descripción detallada de características específicas o variables de la especie (Simpson, 2002). Arabidopsis thaliana y O. sativa son las dos únicas plantas modelo actualmente secuenciadas y con anotaciones disponibles en las bases de datos públicas, mientras que el genoma del ratón M. musculus es el organismo modelo de los animales incluyendo el genoma humano, particularmente porque junto con Drosophila melanogaster son los organismos de los cuales se dispone de gran cantidad de información con verificación experimental en diferentes niveles de análisis.
El objetivo general del estudio es proponer nuevos abordajes teóricos estadísticos que describan de forma satisfactoria características estadísticas generales en los genomas. El objetivo específico del estudio es discernir estadística y biológicamente las variables frecuencia de uso y longitud de los genes y sus componentes (exones e intrones) en cromosomas y genomas. La estrategia consistió en resumir los datos en términos de las medidas de tendencia central (posición y dispersión) y analizar si se ajustaban a una función de distribución de probabilidad conocida.
Los datos. Las secuencias completas de los genes con sus respectivas secuencias de exones e intrones por cromosoma de los genomas vegetales de Arabidopsis thaliana y Oryza sativa (arroz) y el genoma animal de Mus musculus (ratón) fueron obtenidas directamente de los archivos en formato gbk disponibles vía ftp en la base de datos pública Genebank perteneciente al Centro Nacional de Información Biotecnológica NCBI (http://ftp. ncbi.nih.gov/genomes/) en marzo del 2009.
Con el lenguaje de programación Python se desarrollaron algoritmos para extraer y depurar las secuencias de ADN del formato gbk a un formato Fasta. Todo el estudio se realizó en un ambiente Linux. La información se organizó en tres archivos Fasta por cromosoma (secuencias de genes, exones e intrones) para facilitar el manejo de la información de las secuencias y alcanzar mayor rapidez de procesamiento. Los genes que contenían nucleótidos desconocidos (representados por la letra N) en sus secuencias o con longitudes menores de 20 nucleótidos fueron excluidos del estudio. El estudio consideró todos los genes de los cromosomas de los genomas vegetales (A. thaliana: 2n = 10; O. sativa: 2n = 24) y solamente los 19 cromosomas autosómicos de M. musculus: 2n = 42.
El genoma de M. musculus fue el genoma de referencia para validar la estrategia de análisis estadístico debido a que la información biológica de una buena cantidad de sus secuencias ha sido obtenida experimentalmente (Mouse Genome Sequencing Consortium, 2002; 2009). Los cromosomas sexuales fueron excluidos porque presentan características estructurales, genéticas y anatómicas particulares que podrían ocasionar sesgos estadísticos (Gu et al., 2000). Los genes extraídos por genoma del total registrado en la base de datos pública fue de 81.59%, 94.81% y 95.53% para M. musculus, y O. sativa, respectivamente.
Las variables analizadas fueron cantidad de secuencias (genes, exones e intrones) y tamaño o longitud (total de nucleótidos) de estas, por cromosoma y por genoma. El análisis estadístico se realizó en dos etapas: la primera, consistió en analizar las variables en términos de totales, promedios y porcentajes, y la segunda etapa, en analizar la estructura de distribución de las variables por conjunto de secuencias, por cromosoma y por genoma mediante la construcción de histogramas de frecuencias. En todos los casos, las transformaciones de las distribuciones fueron hechas con logaritmo común, las ecuaciones de regresión se obtuvieron por el método de mínimos cuadrados, la medida de ajuste de las rectas de regresión se determinó mediante el coeficiente de determinación (R2) y la significancia estadística de las pruebas fue p < 0.05.
Los conteos por gen fueron: longitud del gen, longitud de cada exón e intrón, número de exones e intrones y longitud total de los exones e intrones, mientras que los conteos por cromosoma y por genoma, fueron: longitud total de los genes, exones e intrones y cantidad de genes, exones e intrones.
Este estudio muestra que aunque la longitud total de los genes en cada genoma vegetal es aproximadamente 90% más pequeña que la del genoma animal de M. musculus, los tres genomas presentan regularidades estadísticas entre los cromosomas de un mismo genoma y entre genomas. Regularidades estadísticas que en su mayoría no habían sido detectadas en genomas vegetales. El Cuadro 1 indica que la longitud total de los genes de A. thaliana y O. sativa equivale al 8.3% (67.953.362 nucleótidos) y 11.1% (90.892.843 nucleótidos), respectivamente, de la longitud total de los genes (819.954.023 nucleótidos) de M. musculus, y además, los tres genomas contienen relativamente el mismo número de genes. Las evidencias moleculares soportan la explicación que el incremento de tamaño de los genomas de las especies superiores está asociado a procesos de poliploidía pleiotropía y epigénesis. Estos procesos constituyen fuerzas evolutivas cruciales en la regulación génica, ya que una vez que los genomas poseen mayor tamaño, la aparición de nuevos fenotipos resultaría de la alteración de los mecanismos de control de la maquinaria genética preexistente y no de la formación de novo de nuevos genes (Otto y Whitton, 2000; Rakyan et al., 2001; Osborn et al., 2003; Rodin y Rigs, 2003). Las investigaciones en evolución génica señalan que el 70% de las angiospermas han tenido al menos una ronda de duplicación total del genoma mientras que en los vertebrados se han propuesto por lo menos dos rondas de duplicación genómica para explicar la redundancia génica existente en los mamíferos (Mable, 2003; Gallardo et al., 2003; Furlong y Holland, 2004; Comai, 2005).
La proporción de nucleótidos pertenecientes a secuencias de exones e intrones difiere notablemente entre los genomas. El genoma de A. thaliana es el que contiene la mayor proporción de nucleótidos asociados a secuencias de exones. Obsérvese en el Cuadro 1 que en el genoma de A. thaliana, el 72.2% de nucleótidos (49.086.976 nucleótidos) pertenecen a secuencias de exones, mientras que el 27.8% (18.866.386 nucleótidos) pertenecen a secuencias de intrones. En contraste, estos porcentajes en O. sativa fueron cercanos al 50% (48.4% y 51.6% de nucleótidos relacionados con secuencias de exones y de intrones, respectivamente) y en M. musculus, menos del 7% de nucleótidos de la región génica estaban asociados a secuencias de exones (6.9% y 93.1% de nucleótidos relacionados con secuencias de exones y de intrones, respectivamente). Los porcentajes mencionados para el genoma de M. musculus concuerdan con las afirmaciones de Rogic et al. (2008), Taft y Mattick (2003) y Mattick (2004) respecto al predominio del ADN nocodificante en las especies más evolucionadas. Estos investigadores argumentan que la gran cantidad de nucleótidos asociados a secuencias de intrones en genomas superiores es debida al rol que tienen los intrones como mecanismo paralelo de control de la expresión genética. La existencia de intrones en el genoma pareciera facilitar la fusión, duplicación y reordenamiento de segmentos de genes. Según Gilbert (1978; 1987) los intrones presentan puntos de propensión que incrementan el barajamiento splicing de exones y por lo tanto, la eficiencia del contenido genético informacional de los genes y la formación de nuevos genes. Por otro lado, Angeline (1996) y André y Teller (1996) han determinado teórica y experimentalmente que los intrones pareciera que protegieran a los exones de los efectos destructores del cruzamiento en programación genética.
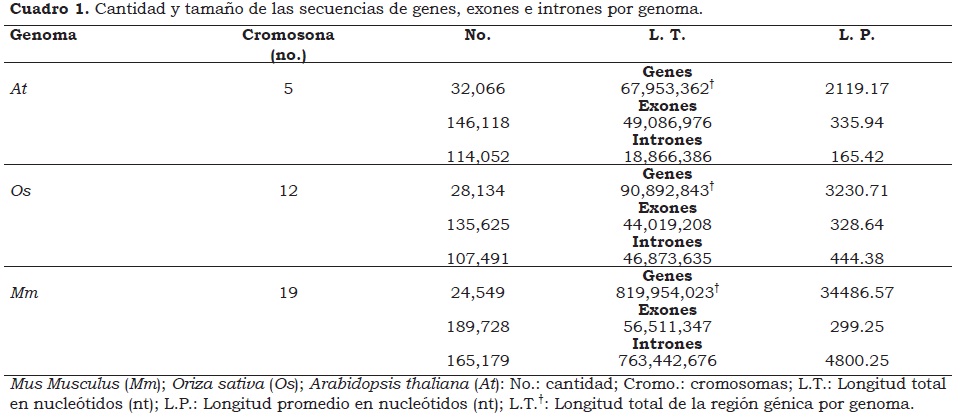
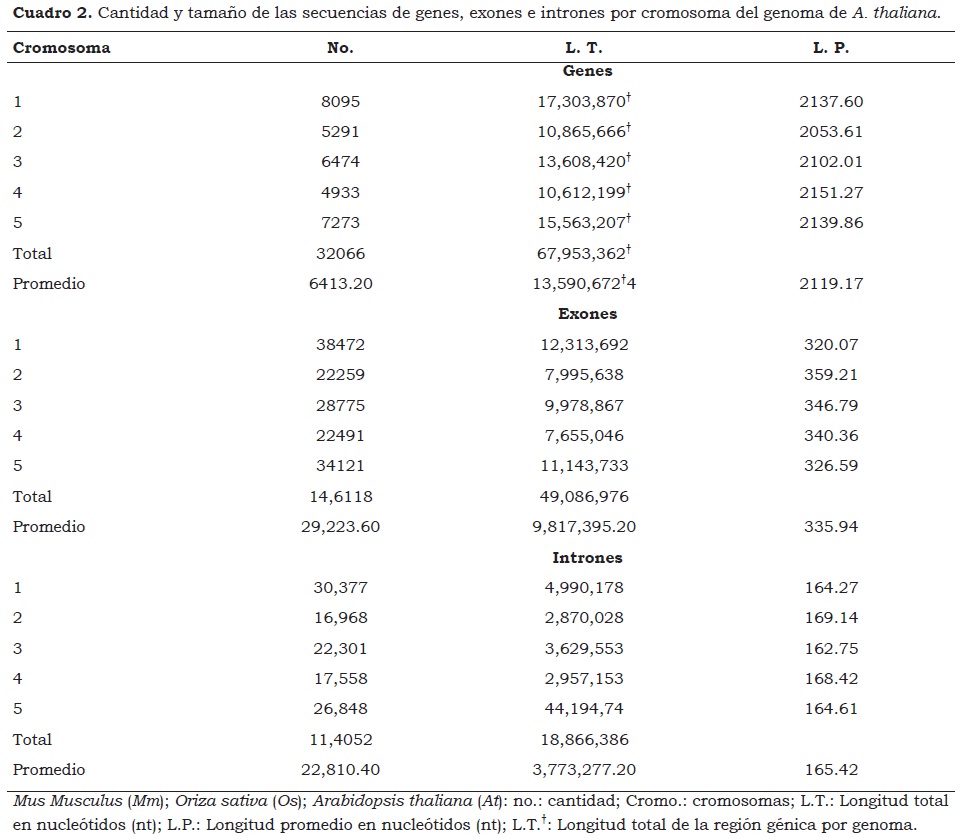
Lo interesante del análisis y primer hallazgo de este estudio es que las proporciones de nucleótidos pertenecientes a secuencias de exones e intrones encontradas por genoma no fueron estadísticamente diferentes entre los cromosomas de un mismo genoma. Esta afirmación se puede verificar en el Cuadro 2 que muestra el tamaño total de las secuencias de exones e intrones por cromosoma del genoma de A. thaliana; por ejemplo, la proporción de nucleótidos perteneciente a secuencias de exones para cada cromosoma del genoma de A. thaliana fue la siguiente: 71.2, 73.6, 73.3, 72.2 y 71.6%, cromosomas 1 al 5, respectivamente. Estos datos sugieren reglas estructurales evolutivas comunes entre los cromosomas de un mismo genoma.
Otro hallazgo importante reveló que aunque la proporción de nucleótidos pertenecientes a secuencias de exones es significativamente diferente entre genomas, la longitud promedio de los exones no difiere estadísticamente entre todos los cromosomas ni entre los genomas estudiados. Los datos en el Cuadro 1 indican que el tamaño promedio de las secuencias de exones en el genoma de A. thaliana es de 338.6 mientras que en O. sativa y en M. musculus es de 328.6 y 299.3, respectivamente. Estos valores no difieren significativamente de los obtenidos por cromosoma a través de los genomas. En el genoma de A. thaliana, la longitud promedio de los exones por cromosoma varía de 320.1 nucleótidos (cromosoma 1) a 359.2 nucleótidos (cromosoma 2) (Cuadro 2). Promedios similares de longitud de los exones se observan entre los cromosomas de los genomas de O. sativa y de M. musculus (datos no mostrados).
En contraste, la longitud promedio de los genes y de los intrones es específica para cada genoma pero se mantiene estadísticamente constante a través de los cromosomas del genoma respectivo. La longitud promedio de los genes e intrones de A. thaliana fue de 2.119.2 y 165.8 nucleótidos, respectivamente (Cuadro 1) y esas longitudes no varían estadísticamente a través de los cromosomas (Cuadro 2). El tamaño promedio de los intrones de O. sativa es aproximadamente tres veces más grande que el de A. thaliana y aproximadamente diez veces más pequeño que el de M. musculus (Cuadro 1). Comparaciones de tamaño de secuencias de exones e intrones entre especies de aves y mamíferos señalan que los exones no han sufrido cambios significativos en su longitud, mientras que los intrones presentan diferencias significativas entre especies, siendo los de las aves más cortos que los de los mamíferos (Hughes, 1999; Hughes y Hughes, 1995; Waltari y Edwards, 2002). Además, la longitud promedio de los exones obtenida en este estudio fue consistente con la revelada por Deutsch y Long (1999) al comparar muestras de secuencias de diez organismos modelo eucariotas (promedio 338.7 nucleótidos). Estos mismos investigadores indican que el tamaño del intrón disminuye a medida que las especies descienden en la escala filogenética y está directamente relacionado con el tamaño del genoma.
Cabe destacar que la longitud promedio de las secuencias de los genes, los exones y los intrones obtenidas para cada genoma fueron consistentes con las reportadas oficialmente por el Genebank (2009).
Genes simples versus genes interrumpidos
Un examen detallado de los genomas indica que están constituidos por dos categorías de genes: genes simples GS (genes constituidos solamente por un exón = genes sin intrones) y genes interrumpidos o fragmentados GI (genes constituidos por dos o más exones = genes constituidos por uno o más intrones). Los genomas vegetales contienen mayor cantidad de genes simples, en comparación con el genoma animal y los nucleótidos de estos genes ocupan proporciones importantes de la longitud total de las secuencias de genes de los genomas vegetales respectivos. El genoma de A. thaliana contiene 33.8% (10.836 genes) de genes simples mientras que el genoma de O. sativa y de M. musculus contienen el 26 y 18.8% de genes simples, respectivamente (Cuadro 3). Estos resultados indican que por cada GS hay 2 GI en A. thaliana, 3 GI en O. sativa y 4.3 GI en M. musculus.
Los genes simples de A. thaliana ocupan el 22.6% (15.324.888 nucleótidos) del total de nucleótidos de las secuencias de genes (67.953.362 nucleótidos) mientras que los genes simples de O. sativa ocupan el 8.3% y los de M. musculus, únicamente el 0.7% (Cuadro 3). Estos resultados indican que por cada nucleótido de un GS hay 3.4 nucleótidos en un GI del genoma de A. thaliana, 11 nucleótidos en un GI de O. sativa y 141 nucleótidos en GI de M. musculus.

El análisis de los genes simples revela dos hallazgos importantes (Cuadro 3): primero, la proporción de genes simples y longitud ocupada por estos no presentan diferencias significativas a través de los cromosomas de un mismo genoma; por ejemplo, del total de genes de los cromosomas de A. thaliana, 8095, 5291, 6474, 4933 y 7273 genes, cromosomas 1 al 5 respectivamente, el 31.3, 38.4, 34.8, 34.3 y 32%, respectivamente son genes simples. Segundo, el tamaño promedio de un gen simple no difiere estadísticamente a través de todos los cromosomas de los genomas estudiados (por ejemplo, el tamaño promedio de los genes simples en A. thaliana varía de 1306,4 nucleótidos cromosoma 1- a 1476,9 nucleótidos cromosoma 2) siendo el tamaño promedio de un GS en A. thaliana de 1414.3 nucleótidos, mientras que O. sativa es de 1029.1 nucleótidos y en M. musculus es de 1253 nucleótidos.
En contraste, el tamaño promedio de los genes interrumpidos es específico para cada genoma pero al igual que en los genes simples, este promedio no difiere estadísticamente entre los cromosomas del genoma respectivo. El tamaño promedio de un GI es significativamente más bajo en el genoma vegetal que en el genoma animal (Cuadro 3).
Este estudio demuestra que aunque la cantidad de genes interrumpidos es aproximadamente la misma en los tres genomas (21230, 20819 y 19931 genes interrumpidos, A. thaliana, O. sativa y M. musculus, respectivamente) (Cuadro 3), las diferencias subyacen en la distribución de las frecuencias de uso de exones y en la longitud promedio de uso de las secuencias de los genes interrumpidos en cada genoma. Este resultado aporta evidencias a lo sugerido por Levine y Tijan (2003) respecto a que la complejidad genética no se basa en la aparición de nuevos genes, sino en la progresiva y más elaborada regulación de la expresión de los existentes; pareciera que las especies eucariotas hubieran optado por la reutilización de genes para cumplir sus tareas, pues sería más económico modificar y aumentar el número de pequeñas secuencias control, que duplicar y mutar secuencias de genes (Mattick et al., 2001).
Distribuciones de Ley de Potencia en genes interrumpidos
Al ordenar los genes interrumpidos de acuerdo con la frecuencia creciente de uso de exones se origina una distribución que se ajusta a una ley cuantitativa de escalamiento o Ley de Potencia que resultó ser específica para cada genoma. Esta distribución proporciona una descripción sencilla de la organización jerárquica de los genes en el genoma, cuyos parámetros expresados en la ecuación se pueden utilizar como descriptores específicos de la estructura de cada genoma. Este resultado permite concluir que la composición de exones de los genes interrumpidos en un genoma contiene información relevante sobre la identidad de una especie.
La Figura 1 ilustra la distribución de la variable frecuencia de uso de exones de los genes interrumpidos en los genomas de A. thaliana, O. sativa y M. musculus. Nótese, en primera instancia, la regularidad estadística expresada en líneas rectas decrecientes de la distribución de los genes interrumpidos en los genomas y que esta distribución en una gráfica bilogarítmica obedece a una ley de potencia (recuadro en la Figura 1). Los coeficientes de determinación (R2) altos indican que las variables están altamente correlacionadas y confirman la presencia de la Ley de Potencia. En segunda instancia, la distribución de genes interrumpidos de cada genoma ocupa un lugar distinto en el espacio de coordenadas, definido por ecuaciones estadísticamente diferentes, lo que indica una firma genómica para cada especie.

La interpretación de la Figura 1 es inmediata: muchos GI utilizan pocos exones, mientras que muy pocos GI utilizan muchos exones y la proporción de unos y otros está relacionada por una ley de escalamiento con exponentes específicos (la pendiente) para cada genoma; por lo tanto, la frecuencia de GI según el número de exones que contiene un genoma no es al azar, obedece a una ley cuantitativa específica expresada por la ecuación que aparece en la Figura 1. Según Lus-Combe et al. (2002), las leyes de potencia proveen una descripción matemática concisa de una importante propiedad biológica: el dominio completo de los genes con pocos exones sobre todo el genoma. Además, la Figura 1 señala que los genes interrumpidos del genoma animal son más fragmentados que los del genoma vegetal. Esto debido probablemente a una mayor eficiencia en términos del barajamiento o splicing de genes y por ende del contenido genético informacional.
Otra evidencia que corrobora la afirmación de que los genes interrumpidos no se distribuyen al azar en el genoma, se encontró al analizar la cantidad y longitud de las secuencias de genes, exones e intrones que constituyen los genes interrumpidos. Ambas variables decrecen paralelamente en forma de ley de potencia a medida que se incrementa el número de exones por gen interrumpido. Muchos genes interrumpidos utilizan pocos exones y presentan promedios de longitud bajos pero ocupan gran parte de la longitud total de las secuencias de genes interrumpidos y pocos genes interrumpidos que utilizan muchos exones y presentan altos promedios de longitud ocupan una mínima parte de la longitud total de los genes interrumpidos. Las transformaciones de las variables y especificidad de las ecuaciones que se presentan en las Figura 2, Figura 3 y Figura 4 de los genomas de A. thaliana, O. sativa y M. musculus, respectivamente, ilustran de manera irrefutable las anteriores afirmaciones.

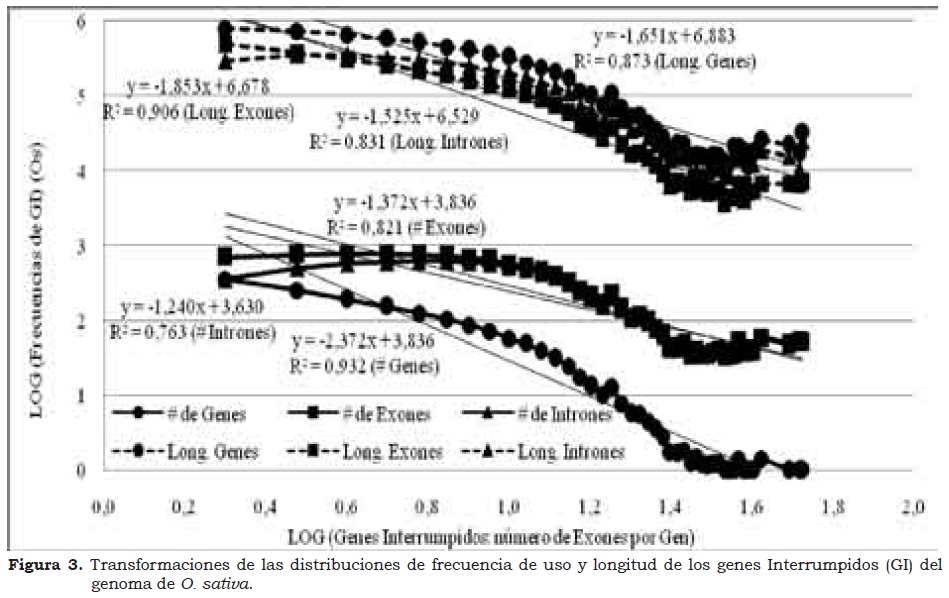

En conclusión, en la distribución en forma de leyes de potencia de los genes interrumpidos están contenidas otras leyes de potencia (de mayor magnitud) como son las distribuciones de cantidad y longitud de las secuencias que constituyen los exones e intrones. Cuanto más podamos distinguir la distribución en forma de leyes de potencia de variables que caractericen las secuencias de ADN de los genomas, más información tendremos sobre las regularidades estadísticas comunes entre y dentro de genomas. Probablemente, en un futuro, con la sumatoria de leyes de potencia de distintas variables analizadas en un conjunto de genes interrumpidos será posible obtener un perfil genético preciso del genoma al cual pertenece.
Finalmente, el hallazgo más importante del análisis de las variables frecuencia de uso de exones y longitud total de las secuencias de los genes interrumpidos mostró que el comportamiento de estas variables no presentó diferencias significativas a través de los cromosomas de un mismo genoma. A manera de demostración, en las Figura 5a y Figura 5b se observa que la forma de la distribución de ley potencia de las variables es similar en los cinco cromosomas del genoma de A. thaliana. Esta simetría fue aún más evidente en los recuadros de la Figura 5 que presenta las transformaciones de las distribuciones y, lo que es aún más importante, las ecuaciones por cromosoma no mostraron diferencias estadísticamente significativas de la ecuación obtenida para el genoma y que se presentó en la Figura 1.

Significado matemático de la distribución de uso y tamaño de los genes interrumpidos
Los comportamientos de Ley de Potencia de las distribuciones de las frecuencias de uso de exones y tamaño de los GI y de sus componentes generaron un sistema de ecuaciones matemáticamente simple que expresa relaciones únicas, precisas e invariantes entre los cromosomas y el respectivo genoma. Estas ecuaciones señalan que existen constantes estadísticas que relacionan de manera específica estas variables en cada genoma. Las constantes revelan que dichas secuencias no son independientes sino el resultado de sus relaciones que se expresan en formas de ley de potencia. Es decir, evidencian la existencia de un sistema que articula las secuencias de genes e indican que hay coherencia y regularidad en la aparición de estas secuencias en cada genoma.
De las ecuaciones se obtienen dos parámetros, el primero, la constante que depende del tipo de secuencia y del genoma y el segundo, el coeficiente de regresión o pendiente de la ecuación que corresponde al exponente en la gráfica bilogarítmica. La pendiente negativa denota el sentido inverso de la relación entre la cantidad de secuencias y la frecuencia de uso o longitud de estas secuencias, tanto en cromosomas como en genomas; por ejemplo, los genes más utilizados son los que contienen menor número de exones y en promedio son más pequeños pero ocupan la mayor parte de la longitud total de los genes. Así mismo, la pendiente muestra que el cambio por término medio de uso y longitud de las secuencias es menor en el genoma animal que en los genomas vegetales.
Las diferencias estadísticamente no significativas de las pendientes de las ecuaciones que definen cada variable a través de los cromosomas y el genoma respectivo son la evidencia empírica que mejor refleja la característica de invarianza de escala en el sentido estadístico: independiente de la escala de observación se conserva la forma de la función. Intuitivamente, la invarianza implica patrones de comportamiento similares en la distribución de las variables a través de los cromosomas y del genoma. Los cromosomas son autosimilares estadísticamente o invariantes al cambio de escala. Esto significa que el genoma se autoorganiza de la misma manera en los cromosomas, independientemente del tamaño o del número de genes, exones o intrones que estos contengan. Cada cromosoma manifiesta las propiedades estadísticas globales del genoma al cual pertenece. La pendiente denota el grado de irregularidad que permanece constante a diferentes escalas.
La principal conclusión de este sistema de ecuaciones es que existe una regularidad estadística no lineal entre la cantidad y el tamaño de las secuencias de los genes y sus componentes (los exones e intrones) que varía con el tipo de genoma y que se repite estadísticamente de manera similar a través de los cromosomas del respectivo genoma.
La interpretación matemática de estas leyes es irrefutable: lo que es válido para el genoma es válido para los cromosomas o viceversa. Cada cromosoma manifiesta las propiedades estadísticas globales del genoma al cual pertenece.
Significado biológico de la frecuencia de uso y tamaño de los genes interrumpidos
Biológicamente, las leyes de potencia indican que ni los genes ni sus componentes se distribuyen aleatoriamente en los cromosomas o en los genomas. Tanto las secuencias de genes como las de exones de cada genoma tienen asociada una cantidad escalar que representa su aptitud de adaptación o capacidad para soportar determinada cantidad de variación sin perder su identidad. Esta afirmación valida lo sugerido por Kosak y Groudine (2004) respecto a que la organización lineal de los genes en los cromosomas no es aleatoria y por Duboule y Morata (1994) en cuanto a que la organización física de los genes en los cromosomas es importante para su correcta activación y el desarrollo normal de sus funciones.
Las leyes de potencia actúan como fuerzas que pueden fusionar grupos de genes con el único fin de mantener la integridad y especificidad de cada genoma. Estudios recientes con microarrays muestran agrupaciones contiguas de genes coexpresados en A. thaliana (Williams y Bowles, 2004), en Drosophila (Boutanaev et al., 2002; Spellman y Rubin, 2002) y en nematodos y mamíferos (Lercher et al., 2002). Se han detectado agrupaciones de genes con funciones metabólicas o housekeeping (Halligan et al., 2004; Lercher et al., 2002), genes vecinos o próximos con patrones de expresión similares (Spellman y Rubin, 2002) o complejos génicos en tejidos específicos (Boutanaev et al., 2002). Los genes homeóticos se presentan agrupados en módulos en los cromosomas y se expresan casi en el mismo orden en todos los organismos estudiados (Veraksa et al., 2000).
Los estudios mencionados señalan que estas agrupaciones de genes contienen regiones codificantes y no-codificantes extraordinariamente conservadas tanto en su composición de nucleótidos como en su posición y orientación entre las especies. La coexpresión parece ser ventajosa y una razón para el mantenimiento de la sintenia. Sintenia que se manifiesta en la regularidad estadística de número, tamaño y frecuencia de uso de los genes y sus componentes manteniendo la forma de la distribución a través de sus cromosomas, pero diferenciándose cuantitativamente de manera precisa entre genomas.
La similaridad de la forma mas no de la ecuación de las distribuciones de frecuencia de uso y tamaño a través de genomas cercanos filogenéticamente como los genomas vegetales o lejanos filogenéticamente como M. musculus, avalan la hipótesis de algunos análisis genómicos comparativos que sostienen que las drásticas diferencias en el desarrollo de los diversos phyla son debidas al uso diferencial de productos génicos conservados estructural y funcionalmente más que a la invención de proteínas de novo (Carroll, 1995; 2000; Gellon y McGinnis, 1998).
La interpretación más simple de las regularidades estadísticas encontradas sería que la estructura de los cromosomas y por ende del genoma de una especie, se mantiene a expensas de una distribución específica de las variables de frecuencia de uso y tamaño de los genes y sus componentes según una Ley de Potencia. Las distribuciones en forma de esta Ley estudiadas en otros fenómenos biológicos, económicos o sociales se interpretan como mecanismos amortiguadores que en cierto grado ordenan y moldean los cambios genéticos en los genomas.
- A modo de síntesis, en la primera aproximación estadística general del estudio se presentan evidencias de una estructura estadística lineal del genoma que se refleja en sus cromosomas y se relaciona con el número y tamaño de sus genes y los componentes de estos últimos, los exones e intrones. En la segunda aproximación, que es un análisis detallado de la frecuencia de uso y tamaño de las secuencias, la estructura de estas dos simples variables se torna compleja y solamente puede ser analizada en términos de Leyes de Potencia, la interpretación biológica de estas leyes es contundente, lo que es válido para el genoma es válido para los cromosomas y que ambos análisis, el lineal y el no lineal, son necesarios para interpretar la estructura y organización de los genomas.
- Los resultados muestran que es posible modelar el comportamiento aparentemente aleatorio de los nucleótidos en las secuencias y de las secuencias en los cromosomas mediante el análisis de la distribución de frecuencias de las variables frecuencia de uso de exones y longitud de las secuencias de los genes interrumpidos.
- El abordaje teórico, la deducción de las ecuaciones y las interpretaciones biológicas y matemáticas, así como las comparaciones entre los genomas seleccionados son contribuciones de este estudio al desarrollo estadístico de las disciplinas ómicas en general, y en particular, sirven para paliar la escasez de estos análisis en los programas de mejoramiento genético vegetal de inmenso potencial biotecnológico.
- De este trabajo queda pendiente por definir cómo las regularidades estadísticas analizadas están asociadas a determinadas funciones matemáticas y biológicas, tal y como se observa en otros sistemas sociales o económicos e inclusive biológicos. Inicialmente, comparando grupos génicos de especies ubicadas a diferentes distancias filogenéticas, lo que permitiría detectar regiones funcionales importantes para distintos grupos de especies (Boffelli et al., 2003; 2004; Clark, 2001).
Los autores expresan sus agradecimientos al grupo de investigación en Biología Molecular y Cáncer, BIMAC de la Universidad del Cauca. Así mismo a la profesora de matemáticas Lorena Silva, de la Universidad del Cauca y al profesor M.Sc. Germán álvarez por sus valiosas discusiones y comentarios en el desarrollo de esta investigación.
André, D.; Teller, A. 1996. A study in program response and the negative effects of introns in genetic programming. En: Genetic Programming: proceedings of the first annual conference. 12-20, MIT, Press.
Angeline, P. 1996. Two self-adaptative crossover operators for genetic programming. En: Advances in genetic programming 2: 89-110, MIT, Press.
Barreto, E. 2008. Bioinformática: una oportunidad y un desafío. Rev. Colomb. Biotecnol. 10(1):132 - 138.
Boffelli, D.; McAuliffe, J.; Ovcharenko, D.; Lewis, K. D.; Ovcharenko, I.; Pachter, L.; Rubin, E.M. 2003. Phylogenetic shadowing of primate sequences to find functional regions of the human genome. Science 299: 1391 - 1394.
Boffelli, D.; Nobrega, M. A.; Rubin, E.M. 2004. Comparative genomics at the vertebrate extremes. Nat Rev. Genet 5: 456 - 465.
Boutanaev, A. M.; Kalmykova, A. I.; Shevelyov, Y. Y.; Nurminsky, D. I. 2002. Large clusters of co-expressed genes in the Drosophila genome. Nature 420:666 - 669.
Carroll, R. L. 1995. Homeotic genes and the evolution of arthropods and chordates. Nature 376:479 - 485.
Carroll, R. L. 2000. Towards a new evolutionary synthesis. Trends in Ecology and Evolution. 15:27 - 32.
Clark, A. 2001. The search for meaning in noncoding DNA. Genome Res. 11:1319 - 1320.
Comai, L. 2005. The advantages and disadvantages of being polyploidy. Nat. Rev. Gen. 6: 836-846.
Deutsch, M.; Long, M. 1999. Intron-exon structures of eukaryotic model organisms. Nucleic Acids Researc. 27 (15): 3219- 3228.
Duboule, D.; Morata, G. 1994. Colinearity and functional hierarchy among genes of the homeotic complexes. Tends Genet. 10: 358-364.
Furlong, R.F.; Holland, P.W.H. 2004. Polyploidy in vertebrate ancestry: Ohno and Beyond. Biological Journal of the Linnean Society. 82: 425-430.
Gallardo, M.H.; Bickham, J.W.; Kohler, N.; Honeycutt, R.L. 2003. Gradual and quantum genome size in the hystricognath rodents. Journal of evolutionary Biology. 16: 163-169.
Gellon, G.; McGinnis, W. 1998. Shaping body plans in development and evolution by modulation of hox expression patterns. Bioessays. 20:116 - 125.
Gilbert, W. 1978. Why genes in pieces?. Nature. Vol, 271 (9): 501.
Gilbert, W. 1987. The exon theory of genes. Cold Spring Harbor Symposia on Quantitative Biology. Volumen LII: evolution of catalytic function: 907-913.
Gu, Z.; Wang, H.; Nekulenko, A.; Li, W.L. 2000. Densities, length proportions, and other distributional features of repetitive sequences in the human genome estimated from 430 Mb of genomic sequence. Gene. 259: 81-88.
Kosak, S.T.; Groudine, M. 2004. Form follows function: the Genomic organization of cellular differentiation. Genes Dev. 18:1371 - 1384.
Halligan, D. L.; Eyre-Walker, A.; Andolfatto, P.; y Keightley, P. D. 2004. Patterns of evolutionary constrains in intrónica and intergenic DNA of Drosophila. Genome Res 14:273 279.
Hughes, A.L. (1999). Adaptative evolution of genes and genomes. Oxford University Press, Oxford, Reino Unido. 288 p.
Hughes, A. L.; Hughes M. K. 1995. Small genomes for better flyers. Nature 377:391.
Kosak, S. T.; Groudine, M. 2004. Form follows function: The genomic organization of cellular differentiation. Genes Dev. 18:1371 - 1384.
Lercher, M. J.; Urrutia, A. O.; Hurst, L. D. 2002. Clustering of housekeeping genes provides a unified of gene order in the human genome. Nat. Genet. 31:180 - 183.
Levine M.; Tijan R. 2003. Transcriptional regulation and animal diversity, Nature. Vol 424, 10.
Lus-Combe, N.M. et al., 2002. The dominance of the population by selected few: powerlaw behavior applies to a wide variety of genomics properties. Disponible en: http://genomebiology.com/2002/3/8/research/0040.1
Mable, B.K. 2003. Breaking down taxonomic barriers in polyploidy research. Trends in plant Science. 8: 582-590.
Mattick, J.S. 2004. RNA Regulation: a new genetics? Nature Reviews Genetics, 5.316- 323.
Mattick, S.; John, Y.; Gagen, M. J. 2001. The evolution of a controlled multitasked gene Network: The role of introns and other Noncoding RNA in the development of complex organism. Molecular Biology Evolution 18(9): 1611-1630.
Mouse Genome Sequencing Consortium. 2002. Initial sequencing and comparative analysis of the mouse genome. Nature. 420: 520-562.
Osborn, T.C.; Pires, J.C.; Birchler, J.A.; Auger, D.L.; Chen, Z.J.; Lee, H.; Comai, L.; Madlung, A.; Doerge, R.W., Colot, V.; Martiesen, R.A. 2003. Understanding mechanisms of novel gene expression in polyploids. Trends in Genetics. 19: 141- 147.
Otto, S.P.; Whitton, J. 2000. Poliploid incidence and evolution. Annu. Rev. Genet. 34, 401-437.
Rakyan, V.K., Preis, J., Morgan, H.D., Whitelaw, E. 2001. The marks, mechanisms and memory of epigenetic states in mammals. Biochem. J. 356, 1-10.
Rodin, S.; Riggs, A. 2003. Epigenetic silencing maya id evolution by gene duplication. Journ. Mol. Evol. 56, 718-729.
Rogic, S.; Mackworth, A.K.; Qullette, B.F. 2008. Evaluation of gene finding programs on mammalian sequences. Genome Res. 11, 817-832.
Simpson, P. 2002. Evolution of development in closely related species of flies and worms. Nat. Rev. Genet. 3:907 - 917.
Spellman, P. T. y Rubin, G. M. 2002. Evidence for large domains of similarly expressed genes in the Drosophila genome. J. Biol 1:5.
Taft, R. J. y Mattick, J. S. 2003. Increasing biological complexity is positively correlated with the relative genome-wide expression of non-protein-coding DNA sequences. Disponible en: http://www.arxiv.org/aba/q-bio.GN/0401020
Veraksa, A.; Del Campo, M.; y McGinnins, W. 2000. Developmental patterning genes and their conserved Functions: from model organisms to humans. Mol. Genet .Metab. 69:85 - 100.
Waltari, E. y Edwards, S. V. 2002. Evolutionary dynamics of intron size, genome size, and physiological correlates in archosaurs. The American Naturalist 160:539 - 552.
Williams, E. J. y Bowles, D. J. 2004. Coexpression of neighboring genes in the genome of Arabidopsis thaliana. Genome Res. 14:1060 - 1067.
Cómo citar
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Descargar cita
Visitas a la página del resumen del artículo
Descargas
Licencia
Derechos de autor 2010 Acta Agronómica

Esta obra está bajo una licencia internacional Creative Commons Atribución-NoComercial-SinDerivadas 4.0.
Política sobre Derechos de autor:Los autores que publican en la revista se acogen al código de licencia creative commons 4.0 de atribución, no comercial, sin derivados.
Es decir, que aún siendo la Revista Acta Agronómica de acceso libre, los usuarios pueden descargar la información contenida en ella, pero deben darle atribución o reconocimiento de propiedad intelectual, deben usarlo tal como está, sin derivación alguna y no debe ser usado con fines comerciales.



























