Mecánica estadística, neodarwinismo y la prefiguración de las ciencias de la complejidad

RESUMEN

En este articulo pretendo mostrar que: 1. Para los fundadores del neodarwinismo, Fisher y Wright, existía una relación muy estrecha entre la física y la biología. 2. El deseo de matematizar la genética de poblaciones buscaba darle al evolucionismo el estatus de “ciencia dura”,  al mismo nivel que la física de Boltzmann y Maxwell. 3. Este esfuerzo estuvo orientado a mostrar que la evolución por selección natural no se opone a las leyes termodinámicas que rigen la evolución de los sistemas físicos. 4. La metáfora que presenta a los seres vivos como “demonios de Maxwell” anticipó aspectos de las modernas teorías evolutivas que recurren a las ciencias de la información y la termodinámica de sistemas complejos adaptativos  desarrolladas por Prigogine en 1970 y Kauffman en 1993. 5. Para finalizar presento un contraste entre Darwin y Einstein que permite esclarecer mejor los puentes y conexiones bidireccionales que se establecen entre la biología y la física.

Abstract

This paper aims to illustrate: 1. for the founders of population genetics, Fisher and Wright, there was a close relationship between physics and biology. 2. The mathematics of population genetics aimed at placing evolutionary theory as a “hard science” at the same level as Boltzmann and Maxwell´s physics. 3. This effort showed that the concept of evolution by natural selection does not contradict the laws of thermodynamics that rule the evolution of physical systems. 4. The metaphor that represents living beings as “Maxwellian demons” anticipated some aspects of the present day evolutionary theories that recur to the thermodynamic of complex adaptive systems as developed by Prigogine (1970) and Kauffman (1993). 5. To conclude, I contrast Darwin and Einstein in order to clarify how can be understood today the bridges and bidirectional connections between physics and biology.

Statistical Mechanics, Neo-Darwinism and the Prefiguration of the Science of Complexity

EUGENIO ANDRADE¹. ¹Profesor Titular, Departamento de Biología. Universidad Nacional de Colombia, Bogotá D.C., Colombia leandradep@unal.edu.co

Presentado 28 de septiembre de 2009, aceptado 27 de octubre de 2009, correciones 28 de mayo de 2010.

---

En este artículo pretendo mostrar que: 1. Para los fundadores de la genética de poblaciones, Fisher y Wright, existía una relación muy estrecha entre la física y la biología. 2. El deseo de matematizar la genética de poblaciones buscaba darle al evolucionismo el estatus de -ciencia dura-, al mismo nivel que la física de Boltzmann y Maxwell. 3. Este esfuerzo estuvo orientado a mostrar que la evolución por selección natural no se opone a las leyes termodinámicas que rigen la evolución de los sistemas físicos. 4. La metáfora que paradójicamente presenta a los seres vivos como -demonios de Maxwell- anticipó aspectos de las teorías evolutivas modernas que recurren a las ciencias de la información y la termodinámica de sistemas complejos adaptativos desarrolladas por Prigogine en 1970 y Kauffman en 1993. 5. Para finalizar presento un contraste entre Darwin y Einstein que permite esclarecer mejor los puentes y conexiones bidireccionales que se establecen entre la biología y la física.

Palabras clave: Boltzmann, demonios de Maxwell, entropía, información, sistemas complejos adaptativos.

---

This paper aims to illustrate: 1. that for the founders of population genetics, Fisher and Wright, there was a close relationship between physics and biology. 2. The mathematics of population genetics aimed at placing evolutionary theory as a -hard science- at the same level as Boltzmann and Maxwell’s physics. 3. This effort showed that the concept of evolution by natural selection does not contradict the laws of thermodynamics that rule the evolution of physical systems. 4. The metaphor that paradoxically represents living beings as -Maxwellian demons- anticipated some aspects of the present day evolutionary theories that recur to the thermodynamic of complex adaptive systems as developed by Prigogine, 1970, and Kauffman, 1993. 5. To conclude, I contrast Darwin and Einstein in order to clarify, how can be understood today, the bridges and bidirectional connections between physics and biology.

Key words: Boltzmann, complex adaptive systems, entropy, information, Maxwell’s demons.

---

1. SIGLO XIX

Laplace. Al despuntar el siglo XIX se consolidaba el triunfo de la revolución newtoniana que consideraba que todos los eventos en el universo estaban regidos por una ley absoluta, universal, eterna e inmutable. Los modelos de la mecánica explicaban los cambios en posición y movimiento (momentum) de una partícula por acción de una fuerza externa ejercida sobre ella. Bastaba con aceptar la existencia de corpúsculos indivisibles y fuerzas. En este sentido el formalismo newtoniano debía dar cuenta del universo en su conjunto.

Sin embargo, la ciencia de la complejidad comienza a gestarse cuando surgen sospechas bien fundadas de que el mundo natural no se conforma a un modelo simple. Por ejemplo, Laplace aceptó que aunque la ley universal mecánica es anterior a todas, tal vez no era suficiente y que por tanto se debía también admitir la existencia de una ley estadística. Según Laplace, una aproximación fundada en poblaciones o conjuntos inmensos de partículas indivisibles dejaba intacta el principio de causalidad propio del sistema mecánico, es decir el pasado como causa del presente y este como causa del futuro, pero debido a que es imposible calcular la posición y el movimiento de todas las partículas debemos limitarnos a inferencias estadísticas. Usar la estadística es manejar la ignorancia, lo cual no altera el sueño de lograr una descripción completa de universo que permita hacer predicciones hacia el futuro y reconstrucciones del pasado. El universo se comporta de un modo determinista y eventualmente podría ser captado por una mente infinita. Esta metáfora denominada -demonio de Laplace- se expresa en la siguiente cita tomada del tratado de Laplace sobre la probabilidad.

Debemos imaginar el estado presente del Universo como el efecto del estado anterior y como la causa del estado que seguirá-. ... -Un ser inteligente que en un instante dado, pudiera conocer todas las fuerzas que animan la Naturaleza, y la respectiva situación de los seres que la componen, si, además, fuera suficientemente inmenso para someter esos datos al análisis, podría condensar en una única fórmula los movimientos de los cuerpos más grandes del Universo así como los del átomo más liviano, nada sería incierto para dicho ser, y tanto el futuro como el pasado, estarían presentes ante sus ojos- (De Laplace, 1985; Stewart, 1996. p. 16).

Todavía no hay una ruptura con el sistema mecánico puesto que la ley universal es absoluta, el problema es nuestra ignorancia que se manifiesta en azar e incertidumbre, y por tanto la invitación es a desarrollar la tecnología y las máquinas de computo para hacer el sueño determinista o la predicción a futuro y la reconstrucción del pasado, posibles. Laplace representa el sueño reduccionista, según el cual las predicciones sobre el mundo físico, biológico y social podrían reducirse a un computo de posición y momento de las partículas indivisibles constitutivas del universo. Pero la utilidad de la estadística que él legó como instrumento para manejar la incertidumbre anticipó la preocupación sobre si la naturaleza misma de las leyes del mundo que pretende describir son o no estadísticas. Problema resuelto en el siglo XX a favor de las leyes estadísticas.

1.2. DARWIN

Considerado en su época por Boltzmann como el más grande hombre de ciencia del siglo XIX, se propuso dar una explicación racional a la evolución de las formas de vida. Su tesis en los puntos que nos interesan para esta discusión podría resumirse de la siguiente manera.

a. Existe un desarrollo gradual de la vida desde formas muy simples a formas cada vez más diferenciadas y adaptadas a su entorno. El concepto de gradualidad en el cambio era para Darwin una postura innegociable, puesto que de acuerdo a la cosmovisión newtoniana de su época era la única manera como se podía introducir un principio de cambio. Los presupuestos del sistema mecánico quedaban intactos si se postulaba que el cambio era un desplazamiento gradual y mínimo del estado de equilibrio, el cual era nuevamente instaurado por acción de la selección natural. No obstante cuando se acepta un alejamiento así sea mínimo del equilibrio, se abre tímidamente una puerta hacia la aceptación de la complejidad.

b. Este desarrollo no sigue una trayectoria única trazada de acuerdo a un plan, sino que a partir de ancestros comunes se va abriendo y ramificando permanentemente por causas que desconocemos y que en este sentido podemos atribuirlas al azar (Fig. 1). Aquí Darwin traza una línea de demarcación con las teorías inspiradas en la filosofía natural que veían la evolución de la vida como consecuencia de un plan de la naturaleza en el que se minimizaban las desviaciones y no había lugar a la introducción de verdaderas innovaciones. La aceptación de un azar a nivel epistémico colocó a Darwin en una posición difícil que lo llevó a pensar en la posibilidad de un azar ontológico, aunque nunca lo defendió abiertamente. No obstante, la cercanía a esta posición lo coloca en un punto cercano a la aceptación de la complejidad.

c. Existe en la economía de la naturaleza una lucha y competencia por los recursos (fuentes de energía) que lleva a que el más fuerte sobreviva y deje descendencia, y el más débil perezca. Este principio debe, según Darwin, su inspiración a los trabajos de Malthus sobre el crecimiento de las poblaciones humanas en el contexto de la revolución industrial inglesa a finales del siglo XVIII y principios del XIX. Este es el concepto de selección natural que aunque fue definitivo para dar una explicación racional de la evolución, se consideró como una ley económica aplicable a los seres vivos, pero no necesariamente deducible de los postulados de la física, lo cual la hacia sospechosa en algunos círculos. No obstante, distanciarse de una física esencialmente newtoniana en su momento constituía un avance importante que expresaba su dilema entre mantenerse fiel al newtonianismo o buscar un tipo de aproximación diferente. Paradójicamente en su momento la aceptación del paradigma de la economía clásica inspirada en Smith en vez de alejarlo de Newton lo acerca aún más este punto de vista. Pero hoy en día la aproximación económica está más cercana a los teorías de sistemas termodinámicos lejos del equilibrio y de la complejidad que de la visión clásica del siglo XIX.

d. Como resultado de la selección natural las formas más adaptadas de vida incrementan su número en la población. Aunque Darwin rechazó la idea de que existe una única línea de progreso evolutivo, aceptó de acuerdo al espíritu de su época que cada linaje o rama del árbol de la vida manifiesta una tendencia clara y definida hacia estados de mayor adaptación o ajuste a las condiciones del medio ambiente. La adaptación es un componente fundamental del darwinismo. Pero en cuanto existen numerosos linajes divergentes adaptados a condiciones locales muy especificas y no una única vía hacia la adaptación, Darwin parece colocarse en el punto de ruptura con el paradigma newtoniano clásico aunque no se atrevió a expresarlo explícitamente.

1.3. BOLTZMANN Y MAXWELL

Hacia el siglo XIX se concibió un modelo extremadamente simple de evolución aplicable a un sistema físico y que para Boltzmann y Maxwell deberían arrojar luces sobre la evolución de los seres vivos, y cuyo desarrollo debía acercar el darwinismo a las interpretaciones de la física. El modelo buscaba explicar en términos estadísticos, el fenómeno del flujo de calor entre un compartimiento caliente y uno frió hasta alcanzar un estado de equilibrio térmico. Considerando que un gas es una población de moléculas, la temperatura medida sobre el sistema macroscópico se explicaría por una distribución estadística de las velocidades de las partículas. La velocidad promedio de las partículas para condiciones específicas de volumen, presión y composición química corresponde a la temperatura medible del sistema en su conjunto. De esta manera, la propiedad macroscópica se explica como una propiedad estadística de lo micro, pero existe, sin embargo, una tendencia espontánea hacia al desorden molecular, a alcanzar estados de equilibrio en el que el movimiento azaroso de las partículas genera una homogeneidad en las propiedades macroscópicas. Un sistema físico en condiciones de cerramiento es decir, al amparo de posibles perturbaciones externas evoluciona espontáneamente hacia un estado de equilibrio, y este es simplemente el estado más probable. Hay más modos de obtener estados desordenados, de desorden molecular que estados ordenados, por esta razón se presentan con una probabilidad mucho mayor. La evolución tiende al equilibrio, a los más probable, al desorden de lo micro, en otras palabras hacia el incremento de entropía. El incremento de entropía quiere decir que en el equilibrio no es posible extraer energía libre utilizable, puesto que el movimiento azaroso de las partículas en todas las direcciones posibles impide aprovechar su energía cinética para ejecutar un trabajo.

No obstante, la semilla de las teorías actuales de la complejidad se encuentra en un análisis minucioso de las consecuencias del trabajo de Boltzmann y Maxwell. Este último se preguntó sobre la posibilidad de revertir un proceso que tiende a desordenarse e incrementar la entropía. Además le preocupaba que siendo la entropía una derivación estricta de leyes estadísticas aplicables a los grandes números, qué pasaría con sistemas compuestos de un número relativamente bajo de partículas, donde por simple error de muestreo podríamos esperar incluso la aparición de configuraciones ordenadas con grados de probabilidad no despreciables. La cita siguiente es interesante por que no solo resume su concepto sobre lo que se denomino el demonio de Maxwell sino porque permite contrastarla con la cita precedente de Laplace (Fig. 2).

Si tenemos un gas confinado en un recipiente cerrado compuesto por dos cámaras separadas por un pequeño orificio y en equilibrio con su entorno, la única manera como se generaría un desequilibrio térmico entre los dos compartimientos sería por la acción de un ser (esencialmente finito) dotado de facultades tan agudas que puede distinguir cada molécula en su recorrido, y capaz de hacer lo que hasta el presente es imposible para nosotros ...Si este ser, que es capaz de ver moléculas individuales, abre y cierra el orificio que separa las dos cámaras, de modo que permite únicamente a las moléculas más rápidas pasar de A a B, y a las más lentas de B a A, lograría aumentar la temperatura de B y disminuir la temperatura de A, sin gasto de trabajo en contradicción con la segunda ley de la termodinámica (Maxwell, 1871 en Brillouin, 1951 traducido por E. Andrade en Andrade, 2003).

A partir de estas discusiones, Thompson argumentó que la imagen del demonio permite entender a los organismos como seres que sienten, eligen y actúan de modos muy sutiles, creando gradientes o distribuciones heterogéneas de materia. De ahí surgió la idea de que lo más similar a un demonio de Maxwell sería un ser vivo que violaría la segunda ley. Si los seres vivos no se acomodan a las leyes generales de la física, entonces obedecerían a principios únicamente aplicables a ellos. Obviamente esta conclusión no se podía satisfacer puesto que no podemos proponer una ley para los sistemas físicos y otra para la vida, la búsqueda de la unificación debería proseguir.

No obstante, Maxwell estaría indicando que además de las leyes mecánicas newtonianas y de las leyes estadísticas debería ser posible incluir algo así como el manejo y procesamiento de información para poder ejecutar las tareas de un hipotético demonio. Maxwell no solo abrió la vía hacia la complejidad con este hipotético y paradójico experimento mental, sino que además postuló abiertamente que el azar no es solamente una consecuencia de la incertidumbre sobre nuestro conocimiento de las partículas del universo sino que también existe una impredicción debido a la naturaleza de las cosas. Es decir, anunció la existencia de eventos naturales altamente sensibles a las condiciones del medio que hacen imposible la predicción de los estados futuros del mismo. Se rebela contra el determinismo newtoniano de un modo muy tímido, pero certero. Propone que lejos del equilibrio termodinámico se dan comportamientos descriptibles como bifurcaciones impredecibles, como si el sistema de su propia gana hubiera hecho una elección que para nosotros es inescrutable. Aunque Maxwell no desarrolló modelos experimentales que permitieran poner en evidencia este comportamiento azaroso en el momento de -decidir- una bifurcación, estos fueron desarrollados un siglo después por Prigogine.

La propuesta de Maxwell sin pretenderlo tendió un puente entre la teoría darwiniana y los modelos de la mecánica estadística por cuanto el primero esta basado en procesos de ramificación permanente que ocurren en los linajes de un modo azaroso, afirmación hecha en 1859 cuando todavía no había suficientes elementos para justificarla desde la física. Aunque Maxwell intuyó esta congruencia, todavía había que esperar los desarrollos del siglo XX para que realmente ganara un consenso amplio en la comunidad científica.

--2 SIGLO XX
--2.1 MECÁNICA ESTADÍSTICA Y NEODARWINISMO

El siglo XIX llegó a su fin dejando pendiente la discusión sobre a quien creerle si a Boltzmann o a Darwin, en otras palabras sobre si el universo y por tanto nosotros mismos estamos regidos por una ley de acuerdo a la cual cada vez estamos más cerca de una muerte térmica, donde no habrá posibilidades para la vida y menos aun para la cultura humanas, o si por el contrario se impone una ley darwiniana que impulsa hacia estados de mayor progreso, perfeccionamiento y diversificación de las manifestaciones de la vida, y por ende de la cultura y la sociedades humanas. Una discusión sobre la prevalencia de la muerte o la vida, no podía dejar de tener hondas repercusiones sociales y culturales.

Aunque la evolución del universo y de la vida se mueve en direcciones opuestas, la una hacia el desorden creciente, la entropía y la muerte térmica, y la otra hacia una organización y adaptación creciente, deberían ser consideradas como las dos caras de una misma moneda. Ronald Fisher contribuyó a resolver el presunto antagonismo entre la segunda ley de la termodinámica y el evolucionismo darwiniano, proponiendo que ambas son manifestaciones especificas de una ley más general que hace que mientras el mundo de la vida -asciende- en organización y complejidad, el universo se degrada o -decae- en términos energéticos. Darwin y Boltzmann personifican las dos tendencias del universo en que vivimos, la selección natural hala hacia arriba, explotando los gradientes de fitness debido a que paradójicamente, el universo decae a causa de la explotación de los gradientes energéticos. El hecho de que ambas leyes tengan la misma presentación estadística es indicio o sospecha de que pueden ser explicadas por una ley más general. Así como el cambio de dirección de las fuerzas por acción de una polea, (cuando una baja la otra sube), manteniendo el punto de suspensión fijo e inamovible como la ley universal que los explica a ambos. La prueba de que ambas leyes, la del aumento de entropía y la del aumento de fitness a lo largo de la evolución son la misma, se encuentra en su isomorfismo axiomático y matemático. Dos sistemas que son matemáticamente isomorfos deben obedecer a una ley más general. Ronald Fisher en las primeras décadas del siglo XX se preguntó sobre como resolver la aparente contradicción entre la existencia de una ley darwininiana hacia la evolución diversificante que genera formas más complejas y adaptadas, y la evolución del universo hacia un estado de equilibrio donde al no haber energía aprovechable tampoco habría lugar para la vida. Su respuesta fue argüir que debía existir una ley más general que explique la evolución física y biológica simultáneamente. La convicción de que debía existir esta ley más general se derivaba del hecho de que tanto la teoría de Boltzmann y la evolutiva se podrían explicar usando el mismo formalismo matemático.

Si dos teorías aparentemente disímiles poseen la misma estructura formal deben corresponder a casos específicos de una misma ley. Fisher se dedico a construir tal teoría isomorfa que conocemos como genética de poblaciones y cuya formulación se identifica con el surgimiento del neodarwinismo. Ronald Fisher logró convertir la genética de poblaciones en una ciencia -dura- al orientar sus esfuerzos hacia el cumplimiento de los siguientes objetivos:

1. Considerar las poblaciones o agregados de organismos, como conglomerados compuestos por un número muy alto de genes.

2.Proponer una teoría estadística de la selección natural isomorfa a las utilizadas en la teoría de los gases de Boltzmann.

3.Explicar la evolución en términos de cambios en las frecuencias génicas en la población.

Para tal efecto Fisher construyó su teoría a partir de los siguientes postulados.

1. Los genes son unidades atómicas y no interactúan entre ellos.

2.Los genes tienden a mutar y a dispersarse aleatoriamente en las poblaciones.

3.Los genes actúan independientemente y contribuyen aditivamente a la Fitness.

4.La adaptación obedece a una ley estadística.

5.La selección natural induce cambios en la composición genética de las poblaciones.

6.La evolución conduce a estados de equilibrio en ambientes constantes.

7. El valor de Fitness siempre aumenta.

Fisher, 1958 [1930], modeló la evolución como un cambio en las frecuencias génicas en la población que va de estados de amplia variación genética y poca adaptación a estados de menor variación genética y mayor adaptación, representados como el escalamiento de un pico adaptativo donde la amplitud corresponde a la variación y la altura a la adaptación (Fig 3; Fig 4). Es un modelo estadístico que permite prever una solución única para cualquier población que evolucione por variación aleatoria y selección natural en condiciones de medio ambiente estables.

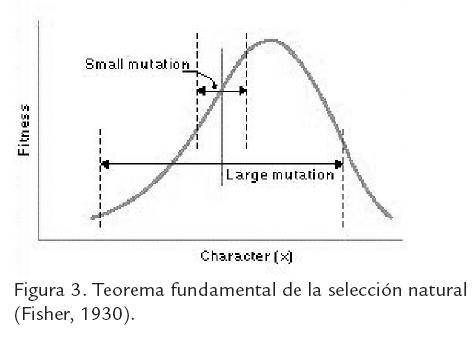
La simplicidad de este modelo fue criticada por Wright, 1930, quien consideró que la suposición de que los genes actuaban independientemente como entidades separadas era incorrecta. Para Wright el efecto de la interacción génica conducía a un modelo de -paisaje adaptativo con múltiples picos- que da cuenta de la complejidad del proceso evolutivo (Fig. 5).

Wright (Wright, 1986a; Wright, 1986b) corrigió el teorema fundamental de Fisher, diciendo que la tasa de incremento de fitness para cualquier población en cualquier momento es igual a su varianza genética, incluyendo los efectos de la mutación, migración, cambios ambientales y del muestreo aleatorio. De esta manera se muestra que los estados de equilibrio ocurren únicamente a nivel local en pequeñas subpoblaciones o demes; es decir que no hay el equilibrio global que caracteriza a una población numerosa panmíctica. El equilibrio está descrito como un estado cambiante shifting balance, que solamente se estabiliza cuando se escala el pico más alto. Pero la trayectoria que describe los desplazamientos del equilibrio global, permite entrever que lo que Wright tenía en mente era un proceso que transcurre lejos del equilibrio, treinta años antes de que Prigogine propusiera una descripción y formalización del comportamiento de los sistemas lejos del equilibrio.

Así como Maxwell anticipó las formulaciones de Prigogine, Wright anticipó las de Kauffman, 1993, quien formalizó la evolución de sistemas complejos adaptativos utilizando la imagen de paisajes rugosos con numerosos picos distribuidos aleatoriamente, a partir de datos genéticos que en la época de Wright era desconocidos. Para una misma población de organismos que evoluciona en un medio ambiente estable hay más de una solución posible y la impredicción aumenta si se tiene en cuenta las variaciones del medio ambiente.

2.2. ¿EXISTE O NO EL TIEMPO?

Boltzmann y Darwin coincidieron en señalar que existe el tiempo como una dimensión de la realidad, que permite decir que en los procesos de transformación sean físicos o biológicos es posible hablar de estados pasados, un presente y uno o varios estados futuros, que se suceden respetando el principio de una continuidad causal. Esta perspectiva de lo temporal como flecha con dirección hacia el futuro no fue de fácil aceptación entre los físicos. Por esta razón este recuento histórico debe detenerse a examinar el pensamiento y la influencia de Einstein en estas discusiones sobre la posibilidad de leyes generales que expliquen la aparición y evolución de sistemas complejos.

Para Einstein, no hay tiempo ni espacio absolutos sino un continuo espacio-tiempo que es inseparable de la materia. Niega la visión newtoniana de un espacio y tiempo absolutos que es anterior a la existencia misma de la materia, es decir no cree que el espacio sea un compartimiento infinito en el cual se colocan o ubican las partículas indivisibles de materia, ni tampoco que el tiempo sea un flujo que transcurre de modo constante independientemente de los procesos naturales que se dan. Por el contrario para Einstein el espacio y el tiempo no existen en cuanto tal, sino como un continuo cuya geometría está determinada por la cantidad de materia del universo. Es decir, no hay espacio, ni tiempo, puesto que no existen por separado, y seria mejor concebir el espacio-tiempo como dependiente de la materia.

Por otra parte, Einstein propuso la existencia de un límite a la velocidad con que se puede transmitir información de un punto a otro en el espacio, dado por la velocidad de la luz. Se trata de un límite que transforma la estructura del espacio-tiempo, y que por otra parte conduce a aceptar un tiempo local para cada observador particular (Fig. 6). Por el contrario, para Galileo la transmisión de señales a velocidad infinita permitía postular la existencia de un tiempo universal único. La idea de tiempos locales para cada observador es la base para el internalismo, mientras que el concepto de un tiempo global único es congruente con el externalismo. Es decir, no puede existir un observador que esté recibiendo señales desde todas las regiones del universo en un instante determinado, es imposible físicamente observar el universo desde afuera, el -demonio de Laplace- es una imposibe teórico. Los observadores naturales, físicamente posibles, son necesariamente locales puesto que ven el universo desde adentro y manejan información parcial para tratar de hacerse una imagen de él.

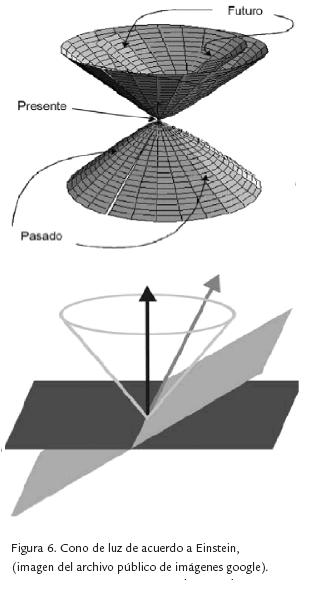
Las disecciones del espacio/tiempo en planos de simultaneidad dependen del observador, es relativa al sistema de referencia, pero esta relatividad se sustenta en un absoluto, el cono de luz que siempre es el mismo para todos los observadores. Para entender en qué consiste el cono de luz, imaginemos nuestra posición actual en el espacio-tiempo como un punto que tiene dependencia causal con todas las señales recibidas desde otras zonas del espacio-tiempo que han llegado al punto presente en cuestión. Como las señales no se pueden desplazar a una velocidad mayor que la de la luz, a medida que miramos hacia el pasado es mayor la zona del espacio desde la cual provienen señales luminosas que captamos en el presente, y así entre más tiempo haya transcurrido, más señales han podido alcanzarnos desde regiones más amplias del espacio, sin embargo nunca podremos recibir señales de regiones ubicadas en el espacio-tiempo por fuera del dicho cono de luz. El cono de luz se cierra del pasado al presente para rematar en el punto del espacio-tiempo en que nos ubicamos aquí y ahora. Es decir habrá regiones muy alejadas en el universo desde las cuales la luz no ha alcanzado a llegar y por tanto están causalmente desconectadas con los fenómenos que percibimos en el instante presente. Igualmente, a partir del presente el cono se abre hacia el futuro cubriendo las zonas del espacio-tiempo que pueden ser influidas causalmente por lo que ocurre aquí ahora.

Este era el absoluto que buscaba Einstein, pues aunque los planos de simultaneidad varíen para cada observador las leyes físicas son las mismas para todos. En conclusión, ante un conjunto de observadores, cuyos diferentes planos de simultaneidad son igualmente validos, se impone la negación de un único tiempo cósmico, evolutivo e irreversible. La democracia de observadores en la teoría general de la relatividad (TGR) conduce a la negación del tiempo cósmico, afirmando la imposibilidad de establecer una simultaneidad absoluta. O mejor aún, habría tantos tiempos que ninguno sería más fundamental que los otros, por esta razón Einstein sostuvo que el tiempo es «tan solo una ilusión». Einstein afirmó que la sensación subjetiva de un tiempo psicológico nos permite ordenar nuestras impresiones y decir que un acontecimiento precede a otro, pero es un capricho utilizar un reloj para conectar cada instante de tiempo con un número, o considerar el tiempo como un continuo unidimensional (Prigogine y Stengers, 1984; Prigogine y Stengers, 1986).

Hacia 1949 Einstein, volvió a trabajar sobre el tema del tiempo y trató de derivar la segunda ley de la termodinámica a partir de la mecánica y la probabilidad, con el fin de explicar la asimetría temporal, tal como lo había intentado Boltzmann. Pero su búsqueda del tiempo y de la irreversibilidad, chocó contra su propia formulación de la TGR según la cual no hay ningún fundamento objetivo para la percepción del flujo del tiempo. Por tanto al final de su vida se ratifica en su posición cuando escribió en 1955, Michele Besso acaba de dejar este mundo antes de mí. Para nosotros físicos convencidos, esto no tiene importancia, puesto que la distinción entre pasado, presente y futuro es una ilusión (cit. Prigogine y Stengers, 1984; Prigogine y Stengers, 1986).

Pero si el tiempo es una ilusión, lo que nosotros llamamos tiempo esta contenido en el pre-sente, y éste en el pasado referido a las condiciones iniciales del universo. Por tanto, para poder anticipar el estado futuro de un sistema basta con conocer las condiciones iniciales.

Para los filósofos y científicos evolucionistas, la postura de Einstein era una abstracción propia de la ciencia que al negar la experiencia vivida y la subjetividad, dejaba de lado lo que nos es más preciado, la vida misma. Esta -ilusión- psicológica es prueba de que no todo estaba dado desde el comienzo (en las condiciones iniciales), sino que la duración trae consigo creación e innovación. La evolución trae las sorpresas que depara la libertad, nuevas situaciones que no estaban contenidas en el libreto original, el azar va de la mano con la creación abriendo posibilidades hacia el futuro.

Pero preguntémonos, ¿es irreconciliable el evolucionismo con la física de Einstein?, ¿la TGR excluye necesariamente una perspectiva evolucionista?, ¿por qué según Einstein la multiplicidad de tiempos locales era incompatible con un tiempo global? Mientras que para Einstein el orden matemático de la naturaleza es una verdad que se acepta a priori, para los evolucionistas no existe un orden matemático absoluto, porque daría lugar a un determinismo que impide la aparición de innovaciones evolutivas. El orden matemático es una aproximación hacia la cual la evolución nos acerca, pero no corresponde a una condición de partida porque si así fuera la evolución seria como la ejecución de un algoritmo, donde no hay innovación sino una secuencia de operaciones lógicas. Einstein aceptó la existencia de leyes universales y desechó con vehemencia la idea de que en la naturaleza se den comportamientos azarosos, cuestionó la misma existencia de leyes estadísticas, puesto que para él todo estaba determinado por las condiciones iniciales del universo.

Usted cree que Dios juega a los dados, mientras que yo creo en la existencia de leyes y de orden en un mundo al que, de una manera brutalmente especulativa, estoy tratando de comprender (Einstein 1944, carta a M. Born, citada por Paz 2006).

Por el contrario filósofos evolucionistas como Peirce se preguntaron sobre si las leyes de la naturaleza son o no el resultado de la evolución, sobre la causa la ley de la causalidad, o sobre la evolución de las leyes de la naturaleza.

If the laws of nature are results of evolution, this evolution must proceed according to some principle, and this principle will itself be of the nature of a law. But it must be such a law that it can evolve or develop itself (Peirce, 1958).

Estos dos modos de pensar tan opuestos como complementarios, parecen ser una constante en la historia de la ciencia. Por otra parte al interior de la biología esta misma discusión se manifestó en la polémica entre preformismo y epigénesis. A la pregunta sobre como aparece y se transmite la forma de los seres vivos, los preformistas (siglo XVIII) y genétistas (siglo XX) sostenían que la forma de los seres vivos estaba preescrita en el germen, o determinada por las condiciones iniciales especificadas en los genes. Por el contrario para los epigenétistas, los seres vivos adquieren la forma en un proceso de interacciones en que intervienen factores genéticos, epigenéticos, embriológicos, ambientales, conductuales..., etc.

Por otra parte Einstein vio en el evolucionismo una especulación filosófica que lo alejaba del rigor del formalismo matemático. El antievolucionismo de Einstein era una manera de decir que el estudio de los procesos de cambio impide descubrir la invarianza de las leyes absolutas, que una vez encontradas mostrarían cómo todo estaba contenido en las condiciones iniciales. Para Einstein, todas las acciones de nuestra vida y de la vida en el universo están determinadas por las condiciones iniciales presentes en el big bang. Habría una evolución sin libertad, ni azar, una predeterminación desde el comienzo, un acto único de creación en el pasado. Si existe una ley universal absoluta la unificación es posible y por tanto no habría lugar a las ciencias de la complejidad.

2.3. COSMOLOGÍA EVOLUCIONISTA

He mencionado el interés de Einstein por la búsqueda de leyes universales, así como el caso de Fisher quien concibió la evolución biológica en términos de genética de poblaciones como complementaria con la segunda ley de la termodinámica, mostrando que dos leyes antagónicas pueden explicarse como casos particulares de una ley más general que habría que descubrir.

Después de Einstein las observaciones sobre la radiación cósmica de fondo se interpretaron como el producto de un universo en expansión, en el que la entropía actual (S), aumenta menos rápido que la entropía máxima posible (Smáx), debido a que la simetría del equilibrio se rompió cuando la materia y la radiación se desacoplaron aproximadamente cien mil años después del big bang. Vamos más despacio, distingamos en la evolución cósmica dos grandes etapas, la era de la radiación y la era de la materia. Las condiciones explosivas del universo primitivo hicieron que la energía almacenada en forma de radiación excediera la contenida en forma de materia. Si algo de materia atómica logró subsistir en esta era, lo hizo de una forma excepcional y microscópica suspendida como contamínante en una nube densa de radiación brillante, en un espacio inundado por fotones, luz, rayos X y gama, que constituían un plasma homogéneo y carente de estructura. En esta era la radiación y la materia estaban estrechamente acopladas en equilibrio térmico. A medida que la expansión avanzaba en el tiempo el contenido de energía radiante decreció más rápido que el contenido en forma de materia. Este desequilibrio ocasionó que la radiación palideciera dando lugar a un desacople entre materia y radiación que rompió con la simetría existente 100.000 años después del big bang. Una vez establecida la era de la materia los átomos aparecen distribuidos por todas partes, y la brillante bola de fuego se fue enfriando dando lugar a un universo transparente; las inestabilidades gravitacionales hicieron que la materia colapsara en agregados de gran masa que dieron lugar a las primeros racimos de estrellas.

El contenido de información y los cambios de entropía tenían un valor cero en una etapa temprana de la evolución del universo cuando la radiación y la materia estaban equilibradas y todo era homogéneo y aburrido; el cambio de entropía era cero incluso cuando el universo sufrió una expansión adiabática en ausencia de fuentes de radiación significativas (Fig. 7). Después del desacople apareció la materia atómica y se destruyó el equilibrio requiriéndose dos temperaturas para especificar la evolución cósmica, una para la temperatura de la radiación (Tr) y otra para la de la materia (Tm). Había dos escenarios posibles: 1) que el decrecimiento en la Tm fuera mucho más rápido debido a que el intercambio de energía entre la radiación y las partículas atómicas no se compensa con la velocidad de expansión de las partículas, y por tanto Tr>Tm. 2) que la materia intergaláctica no aglomerada hubiera sufrido un calentamiento, en los primeros 1.000 millones de años después del desacople, y por tanto tendríamos Tm>Tr. Pero, independientemente de si Tm fue mayor o menor que Tr, la diferencia entre las dos ha divergido estableciendo un gradiente térmico a nivel cósmico que proporciona las condiciones adecuadas para la evolución y los incrementos de información. Por tanto, un universo en expansión da lugar a estados lejos del equilibrio que permiten que tanto el desorden, S, como el orden, I, aumenten simultáneamente (Layzer, 1988; Chaisson, 2001).

No existe un acuerdo acerca de la edad del universo (10 a 20 mil millones de años), ni tam-poco de la velocidad real de la expansión en cuanto a si está desacelerando, acelerando, o es constante, pero si hay consenso en cuanto a que se está expandiendo a una velocidad suficiente como para producir regiones ricas en gradientes de energía aprovechable y por tanto aumentos de complejidad.

El potencial para el crecimiento de orden (Smax-S), ha aumentado desde el inicio de la era de la materia. Por consiguiente, la expansión del Universo es la fuente última de energía libre que promueve la evolución y aparición de orden en el cosmos. La energía libre seria el motor de la evolución. El concepto de evolución desbordó la biología, apoderándose de la física y la cosmología, para convertirse en un poderoso factor unificador de la ciencia. Después de Einstein la cosmología se hizo evolucionista alejada de una causalidad determinista. La TGR, dio lugar a la teoría de la expansión del universo, que parte de reconocer su historicidad y temporalidad orientada en una dirección, hecho que Einstein no admitía puesto que había concebido un modelo estable del universo. Sin embargo, su teoría fue mucho más allá de sus propias previsiones prefigurándose quizás como el Darwin de la física.

Prigogine cree que la ciencia del siglo XXI se dedicará a explorar el mecanismo del devenir y la evolución. Se refiere a la manera como se dan y suceden la serie de bifurcaciones que hoy en día se asocian independientemente a las teorías sobre el origen del vida y la cosmología. Podemos aceptar sin reparos que todo en el universo (rocas, estrellas, galaxias, supergalaxias...) evolucionan en una misma dirección, hacia el envejecimiento. Se trata de un universo abierto en el que la direccionalidad del tiempo juega el papel central (Prigogine, 1999).

Igualmente, es imposible concebir la vida y la cosmología sin procesos irreversibles que definen un tiempo que fluye, en el que la evolución transita por fases de aumento de orden y complejidad. De acuerdo a la previsión de Bergson, en la flecha del tiempo cósmico coexiste una multiplicidad de tiempos vividos. Chaisson, 2001, utiliza una flecha del tiempo para resaltar las características más sobresalientes de la historia cósmica, desde el comienzo del universo hasta el presente, señalando las fases que corresponden a los mayores incrementos de complejidad y orden. La direccionalidad del curso del tiempo, no implica una visión determinista hacia necesarios incrementos de complejidad, puesto que en todo momento se presentan bifurcaciones y surgen posibilidades imprevistas. En todo momento se conjugan factores azarosos y deterministas en un escenario cósmico en el que la flecha del tiempo nos guía en el curso de la evolución. La flecha no tiene intención antropomórfica sino mostrar que cualquier tipo de sistema, galaxias, microorganismos, invertebrados, mamíferos, computadores, sociedades humanas, a lo largo del tiempo se han vuelto más complejos (Fig. 8).

Por tanto si hay tendencias definidas orientadas a producir sistemas inteligentes, pero nada indica que su mayor expresión necesariamente tuviera que revestir la forma especifica de lo humano. Ilya Prigogine introdujo la irreversibilidad en la ciencia. En los sistemas lejos del equilibrio térmico no hay estabilidad a las perturbaciones y se presentan puntos de bifurcación, poniendo en evidencia que existen muchas posibilidades, o ramas que dan lugar a la aparición de nuevas estructuras. Si la dirección del tiempo esta dada por los incrementos de entropía, la irreversibilidad tiene un papel constructivo. En los puntos de bifurcación el sistema -elige- una rama, esta escogencia es probabilística ya que si se repite el experimento, el sistema puede -elegir- otra rama. Estas elecciones dependen de las evaluaciones que el sistema hace de su entorno y condiciones inmediatas haciéndole preferir en cada caso una opción dejando la otra. La evolución de la vida corresponde a una sucesión de bifurcaciones, y por tanto el futuro no esta predeterminado.

2.4. LA EVOLUCIÓN COMO ENTROPÍA

En el caso de la biología la búsqueda de una teoría unificada ha sido el propósito de varios autores como Brooks y Wiley, 1988, que consideran que la segunda ley de la termodinámica permite demarcar una teoría unificada de la biología. Pero si queremos ser consecuentes con las prescripciones de Einstein, podríamos preguntarnos si existe una ley más general que la segunda ley y para ello tendríamos que imaginar el estado del universo, antes de que apareciera la segunda ley o tendencia universal al aumento de entropía. El puente entre la física y la biología queda bien cimentado con la explicación de la evolución biológica en términos de aumentos de entropía. El concepto clásico de entropía fue propuesto para sistemas de gases en expansión en un recipiente cerrado, hasta alcanzar el equilibrio, en condiciones de cerramiento, pero superando este modelo, Brooks parte del modelo de expansión de la materia inspirado por la cosmología, según el cual el espaciotiempo se expande más rápidamente de lo que lo hace la materia. En consecuencia, aparece la segunda ley de la termodinámica y los aumentos de entropía nunca conducen al estado de equilibrio puesto que la materia en lugar de repartirse uniformemente se agrega por colapsos gravitatorios y su dispersión es por tanto heterogénea. Teniendo en cuenta que el universo se expande a mayor velocidad que la materia, está heterogeneidad se intensifica en función del tiempo. De esta forma se genera una diferencia entre la entropía máxima que puede ser alcanzada por el universo y la entropía real, y conforme transcurre el tiempo, esta diferencia se incrementa debido que el aumento en la entropía máxima, (expansión del universo), es más rápido que el aumento en la entropía real, (expansión de la materia), lo que representa un aumento del desequilibrio. Esta diferencia se traduce en creación de gradientes de energía libre aprovechables que dan lugar a la organización. Los sistemas en la cercanía del equilibrio tienden a aumentar el desorden microscópico, que se traduce en aumento de la homogeneidad macroscópica a medida que se aproximan al equilibrio y maximizan sus valores de entropía interna. Por contraste, los sistemas lejos del equilibrio, como el universo, tienden a aumentar el orden, la diversificación y a pesar de que su entropía aumenta, cada vez están más lejos de los valores de entropía máxima alcanzable. En ambos casos se dan aumentos de entropía, pero mientras en los primeros el aumento corresponde a los valores de entropía interna: ΔSi> 0, y dado el cerramiento ΔSe= 0; en los segundos ΔSe+ ΔSi> 0, donde ΔSe>>ΔSi

Pero, ¿existe realmente un paralelismo entre la evolución de la vida en la tierra y la evolución del universo en expansión? La vida y el universo son sistemas desequilibrados, la primera por ser un sistema abierto dependiente de una fuente de energía estable y continua, y el segundo aunque considerado en su totalidad es un sistema cerrado, genera gradientes de energía libre producidos en la expansión. Por tanto, es plausible que la Figura 9 que representa la variación de la entropía máxima Smáx y la real Sobs contra el tiempo, en un universo en expansión logre captar algunos aspectos aplicables a la evolución de sistemas abiertos como la vida (Fraustchi, 1982).

Layzer, 1988, sostiene que simultáneamente se dan incrementos de entropía y de orden, puesto que el orden equivale a la diferencia entre la entropía máxima alcanzable Smáx, y la actual Sobs. Para el caso de sistemas termodinámicos cerrados, (Smáx), es constante, pero en el caso de la evolución de la vida y del universo crece con el tiempo. Entre mayor sea la brecha entre la entropía máxima alcanzable y la observada mayor es el orden, (Q), que presenta el sistema, o mayor es su alejamiento de la aleatoriedad, de acuerdo con:

Q = 1 - (S_obs/S_máx), (Landsberg, 1984). La entropía es una medida de la dispersión, en el caso de un gas, se refiere a la distribución de las partículas en un recipiente cerrado, pero en el caso de la evolución biológica se refiere a la distribución en un espacio de posibilidades, en donde todos los microestados posibles están representados; por ejemplo, en un hipercubo n-dimensional de secuencias génicas, genotipos, etc. En ambos casos la expansión obedece a fenómenos aleatorios, como el movimiento de las partículas del gas o la mutación genética. En las primeras etapas de la expansión del universo, el equilibrio termodinámico tiende a prevalecer, pero cuando se rompe la simetría y ocurre la expansión se instaura el desequilibrio porque la velocidad con que tiende a restablecerse el equilibrio en menor que la tasa de expansión. En consecuencia la expansión cósmica produce diferencias de temperaturas y gradientes energéticos. Este proceso genera un orden estructural que se pone de manifiesto en una jerarquía de sistemas gravitatorios que hacen que la masa del universo no se distribuya uniformemente en el espacio.

En el caso de la evolución biológica, se da un proceso jerárquico de organización que presenta dos aspectos complementarios: diferenciación, (especialización y diversificación de partes), e integración, (la formación de nuevos agregados en los que la estructura y función de las partes están subordinadas y reguladas por la estructura y función del agregado; Layzer, 1988). Para comprender el giro que Brooks le da al concepto de entropía, es importante percatarse de que el espacio fase, microestados y macroestados descritos en esta teoría no corresponden a arreglos termodinámicos clásicos derivados del estudio de gases ideales, sino a estructuras, configuraciones, disposiciones, ordenamientos, etc. (Brooks y Wiley, 1988).

Se trata por tanto de una interpretación más general de la segunda ley. En otras palabras, se habla de entropías concebidas como arreglos o configuraciones estructurales; entre más diversidad estructural posean los organismos, mayor será la entropía o complejidad. Una de las conclusiones deducibles de este análisis es que aunque el proceso evolutivo parece representar una reducción en entropía, está reducción es relativa al sistema de referencia. En realidad, la evolución incrementa la entropía, tal como lo exige la segunda ley; pero la evolución no incrementa la entropía a la tasa más rápida posible, debido a que la disipación tiene lugar en el mundo real donde actúan restricciones. Por consiguiente, con respecto a la tasa más alta posible, Smáx, la entropía observada, Sobs, parece decrecer. En este sentido, la evolución es un proceso entrópico en aparente contradicción con el sentido común. La evolución se caracteriza por un aumento en complejidad, organización y orden que da la ilusión de un comportamiento neguentrópico. Esta paradoja se resuelve si se concibe la evolución como un proceso lejano del equilibrio, caracterizado por un espacio fase en incremento y por una tendencia a la expansión que va retrasada con respecto al máximo de entropía. En otras palabras, la diversidad existente es mucho menor que la diversidad posible.

Un observador colocado al interior de un sistema en expansión ve que a medida que transcurre el tiempo, la diversidad genética observada se va retrasando con respecto a la entropía máxima siempre en aumento. En este caso, el observador también se mueve, puesto que el máximo de entropía y el espacio fase aumentan con el tiempo. Cuando el máximo de entropía se incrementa a una velocidad mayor que la diversidad existente observada, el observador concluye que la evolución se comporta entropicamente, dando lugar a una complejidad y organización crecientes. La descripción correspondiente a la Figura 9 es realista, al postular que a lo largo del tiempo ha habido una tendencia al incremento total en diversidad. En este modelo, el orden de un sistema aumenta con el número de microestados accesibles, siempre y cuando la entropía real existente u observada aumente a una tasa menor que el máximo posible de entropía (Brooks y Wiley, 1988). En este caso, toda la diversidad no proviene de la fluctuación original, sino sobre todo de las perturbaciones azarosas que se han ido generando a lo largo de los procesos de estructuración y organización. Según este modelo, los sistemas, valores o propiedades por encima de la entropía máxima no son posibles, mientras que los intermedios son accesibles, pero dada la existencia de restricciones se accede a las nuevas configuraciones (el adyacente posible) siguiendo el camino marcado por la curva. Acceder bruscamente a esta zona sin respetar las restricciones representa una condición patológica del sistema que lo conduce a estados más cercanos a su aleatorización o destrucción.

La localización del observador es crucial y conduce a interpretaciones antagónicas. Mientras que desde la perspectiva clásica externalista del siglo XIX el aumento de entropía es incompatible con la evolución biológica, desde una visión internalista del siglo XX, ambas perspectivas convergen y armonizan entre sí. La especiación se puede entender como un proceso de aumento de entropía como resultado de la tendencia a la expansión de la población en el espacio de genotipos posibles de modo análogo a la expansión de los gases. Igualmente, el valor máximo de la expansión no puede ser alcanzado, ya que la población se encuentra limitada por la escasez de recursos y las restricciones estructurales (genéticas y de desarrollo), que como vimos limitan el rango de estructuras accesibles. Además la reproducción sexual mantiene cohesionados a los individuos impidiendo la formación de líneas clónales independientes, como ocurre en organismos de reproducción asexual, cuyas poblaciones tienden a ser mucho más heterogéneas; el sexo mantiene la cohesión y cuando está se pierde como consecuencia de la tendencia a expandirse, la población se subdivide en demes locales que pueden dar lugar a especiación. El enfoque de Brooks es compatible con el neo-darwinismo, en cuanto sostiene que la variación es independiente de las condiciones del medio, puesto que corresponde a la entropía del sistema. La tendencia espontánea a la diversificación, a aumentar la variabilidad dentro de las restricciones genéticas, al desarrollo y ecológicas, equivale a una expansión en el espacio de posibilidades, que da lugar a la tendencia a incrementar la entropía.

Así, Brooks reinterpreta a Darwin desde la óptica de la termodinámica lejos del equilibrio, donde el estado de máxima entropía equivaldría al de máxima diversificación, el cual nunca se alcanza. Si no existieran restricciones de ningún tipo y todo el espectro de posibilidades realmente llegara a existir, el sistema no sería ordenado.

El aumento en el grado de expansión o diversificación a lo largo del tiempo, está evidenciado por ejemplo en los números promedios de genes existentes en los diferentes grupos, para procariotas alrededor de 5.000, eucariotas invertebrados alrededor de 10.000 y vertebrados alrededor de 25.000 genes. La expansión brusca en el número de genes y variantes alélicas, genera una expansión exponencial del espacio genotípico. Este fenómeno permite entender mejor la existencia de variaciones neutras. La diversidad real o el valor real de entropía está dado en mayor proporción por las variaciones neutras, por lo tanto la evolución es el resultado de la tendencia al aumento de la variación neutra que facilita acceder a posibles variantes adaptativas.

It is commonly supposed that the production of physical entropy in the world is something which could further only the global equilibration of the Universe as a whole, when viewed as an isolated system. Here I take a different view, and suggest how necessary increases in entropy production in nonequilibrium situations can be used to explain the origin of complexity locally, thereby finding the Second law of thermodynamics to be a final cause of the origin of information because it provides the motivation for all dynamics in isolated, but non-equilibrated, systems (Salthe, 2004).

CONCLUSIÓN

Adoptando la actitud de Einstein, creo que la búsqueda de una teoría unificada debe continuar, en este sentido.El objetivo último de las teorías de la complejidad es demostrar que a pesar de todo era posible la simplificación o la explicación basada en un único sistema formal. Pero la unificación requiere aceptar el carácter temporal asociado a la evolución del universo. La temporalidad nos presenta la naturaleza como una transición de -potencialidades- a -actualidades-, a causa de las interacciones, en otras palabras aceptar que todos los sistemas en cuanto -observadores naturales- participan en la creación continúa de la realidad, hecho que lleva a que no pueda ser explicada por un único sistema formal, sino más bien por un lógica de tipo semiótico. Por tanto la evolución aunque dirigida y orientada hacia una mayor complejidad es abierta e impredecible. En este sentido las teorías de la complejidad son bienvenidas. Cabe la pregunta sobre si la ley de evolución y cambio es una ley que evoluciona, y en caso afirmativo, surge la pregunta sobre si esta ley de cambio, cambia de acuerdo a una ley absoluta. Si la respuesta es positiva el sueño de Newton y Einstein sigue vigente, si no, las teorías de la complejidad y el cambio deben tener la primacía. Pero la pregunta precedente, lejos de poderse responder afirmativamente, más bien nos conduce a una regresión infinita que en principio es irresoluble y por tanto las teorías de la complejidad siempre tendrán vigencia, contribuyendo al avance del conocimiento hacia niveles mayores de generalidad y de profundidad matemática simultáneamente.

Las discusiones precedentes motivan una reflexión sobre las relaciones entre la física y la biología. La biología se ha considerado tradicionalmente como una ciencia -blanda- con respecto a la física, debido a la creencia de que es imposible descubrir leyes generales aplicables a la materia por medio del estudio de los organismos debido a que estos representan apenas una parte muy pequeña del universo, un caso muy especifico de la materia organizada.

Biology is marginal because –the living world constituting but a tiny and very special part of the universe– it does not seem likely that the study of living things will ever uncover general laws applicable outside the biosphere- (Monod, 1971).

Pero por el contrario, si la irreversibilidad, el desequilibrio, la apertura y la indeterminación son condiciones más generales que las de reversibilidad, equilibrio, cerramiento y determinación, entonces los sistemas físicos clásicos corresponden a los casos más específicos, y la biología estaría reflejando con mayor propiedad la condición más general y universal. La física clásica asumió una posición determinista donde el control, la predicción y la certeza eran posibles siempre y cuando se conocieran las condiciones iniciales. La biología al referirse a los organismos como sistemas abiertos, o dependientes parcialmente de las condiciones de entorno no puede prometer ningún tipo de predicción determinista, a lo más que podría aspirar es a la predicción estadística, renunciando a la certeza y las posibilidades mismas del control. La física cuántica, la termodinámica lejos del equilibrio y la biología convergen a medida que se han hecho más indeterministas. Como afirma Prigogine el fin de la certeza da la posibilidad misma de la innovación y de la evolución. Siempre habrá algo inesperado desde el entorno que afecta al mismo objeto de estudio y por tanto la física se verá en dificultades para explicar no solo la vida sino los sistemas abiertos en un contexto determinado.

Einstein, entre otros, y sin preverlo contribuyó a tender puentes entre la materia y la vida, es el fruto de haber sido fiel a su criterio de objetividad.

A mí me basta con el misterio de la eternidad de la Vida, con el presentimiento y la conciencia de la construcción prodigiosa de lo existente, con la honesta aspiración de comprender hasta la mínima parte de razón que podamos discernir en la obra de la Naturaleza (Einstein, 1980).

Para concluir, lejos de contraponer a Darwin con Einstein, digamos que el primero nos hizo solidarios con la vida y el segundo con el universo que la generó. Ambos persiguieron la simplicidad expresada en leyes universales y esa actitud les permitió alcanzar la mayor estatura científica en sus respectivos siglos, pero desde la perspectiva de las teorías de la complejidad podemos captar que la convergencia entre ambas posturas se debe a que resaltan la imposibilidad de satisfacer plenamente el sueño de la simplicidad.

BIBLIOGRAFÍA

ANDRADE LE. Los demonios de Darwin. Semiótica y Termodinámica de la Evolución Biológica. Bogotá, D.C. Colombia. UNIBIBLOS; 2003.

BRILLOUIN L. Maxwell s demon cannot operate: Information and Entropy I. J Appl Phys. 1951;22:334-337.

BROOKS D, WILEY EO. Evolution as Entropy. Chicago: University of Chicago Press; 1988.

CHAISSON EJ. Cosmic Evolution. The Rise of Complexity in Nature. Cambridge, Massachusetts: Harvard University Press; 2001.

DARWIN CH. (1859). The origin of species by means of natural selection or preservation of favored races in the struggle for life. Nueva York, N.Y.: Collier Books; 1962.

DARWIN C. Carta a Asa Gray, 26 de noviembre de 1860. The Life and Letters of Charles Darwin. 1860; Vol II p. 68. Free Public Domain Book from the Classic Literature Library. Disponible en http://charles-darwin.classic-literature.co.uk/the-life-and-letters-of-charles-darwin-volume-ii/

DE LAPLACE PS. Ensayo Filosófico sobre las probabilidades. Madrid: Alianza Editorial, S.A.; 1985.

EINSTEIN A. 1944. Carta a Max Born, citada por Paz, J.P. 2006. Einstein contra la Mecánica Cuántica. Departamento de Física -Juan José Giambiagi-, FCEyN, UBA, Buenos Aires, Argentina. Disponible en http://www.df.uba.ar/~paz/borges/einstein.pdf

EINSTEIN A. Mi Visión del Mundo. Edición de Carl Seelig. Tusquets Editores. Barcelona. 1980.

FISHER R. The Genetical Theory of Natural Selection. Oxford: Oxford University Press. 2 end rev. ed., New York: Dover, (1930); 1958.

FRAUSTCHI S. Entropy in an Expanded Universe. Science. 1982;217:593-599.

KAUFFMAN S. The Origins of Order: Self-Organization and Selection in Evolution. Oxford: Oxford University Press; 1993.

LANDSBERG PT. Is equilibrium always an entropy maximum? J Stat Phys.1984;35:159-169.

LAYZER D. Growth of order in the universe. En: Weber BH, Depew DJ, Smith JD, editores. Entropy, Information and Evolution: New Perspectives on Physical and Biological Evolution. Editado por., and. Cambridge: MIT Press; 1988; p. 23-40.

MONOD J.Chance and Neccessity. Trans. A. Wainhouse. New York: Knopf; 1971.

PEIRCE CS. Collected Papers of Charles Sanders Peirce. Vols.1-8. Cambridge, MA: Harvard University Press; 19311958.

PRIGOGINE I, STENGERS I. Order out of Chaos. Man s dialogue with nature. Toronto-New York: Bantam Books; 1984. p. 213-217.

PRIGOGINE I, STENGERS I. La Nueva Alianza. Metamorfosis de la Ciencia. Alianza Universidad; 1986. p. 302-305.

PRIGOGINE I. The arrow of time. Conferencia inaugural en el taller -The Chaotic Universe- presentada por el premio Nobel Ilya Prigogine cuando la Ciudad de Pescara le otorgó la ciudadanía honoraria. ©IcraNetwork; 1999.

SALTHE S. The Spontaneous Origin of New Levels in a Scalar Hierarchy. Entropy. 2004; 6:327-343.

STEWART I. ¿Juega Dios a los dados? Barcelona: Grijalbo Mondadori;1996.

WRIGHT S. Review of the Genetical Theory of Natural Selection by R.A. Fisher. J Hered. 1930;21:349-356.

WRIGHT S. Evolution in Mendelian Populations. Genetics 1931; 16: 97-159. Reimpreso en Sewall Wright, Evolution: Selected Papers. Provine WB, editor. Chicago: University of Chicago Press; 1986a. p. 98-160.

WRIGHT S. The Roles of Mutation, Inbreeding, Crossbreeding and Selection in Evolution. Proceedings of the Sixth Annual Congress of Genetics 1932; 1: 356-366. Reimpreso en Sewall Wright, Evolution: Selected Papers. Provine WB, editor. Chicago: University of Chicago Press; 1986b. p. 161-177.