Desigualdad y leyes de potencia
Palabras clave:
desigualdad, leyes de potencia, ley de Pareto, procesos estocásticos, proceso de Yule. (es)DESIGUALDAD Y LEYES DE POTENCIA
Yalila Aljure Jiménez*
Jorge Andrés Gallego**
* Magíster en Economía, se desempeña como Analista Sectorial en Correval. E-mail: yaljure@correval.com. Dirección de correspondencia: Cll. 34 No. 6-65 (Bogotá, Colombia).
Estudiante de Doctorado en Ciencias Políticas (New York University). E-mail: jorge.gallego@nyu.edu. Dirección de correspondencia:19 W. 4th st., New York, NY, 10009 (New York, Estados Unidos).
Los autores agradecen los comentarios y sugerencias de Andrés Álvarez, Juan Pablo Herrera, Andrés Rosas, Jorge Restrepo, dos jurados anónimos, y en general, del Departamento de Economía de la Pontificia Universidad Javeriana.
Este artículo fue recibido el 7 de julio de 2008, la versión ajustada fue recibida el 28 de febrero de 2010 y su publicación aprobada el 20 de marzo de 2010.
Resumen
Para algunos, la distribución del ingreso es el primer ejemplo de una ley de potencia, regla empírica según la cual una variable aleatoria alcanza valores altos con una probabilidad baja y valores bajos con una alta probabilidad. En este artículo se verifica si la distribución del ingreso de los colombianos más ricos se ajusta a una ley de potencia. Igualmente, considerando el proceso de Yule (1925), y en general, la teoría de los procesos estocásticos, se formula un modelo teórico cuyo objetivo es explicar por qué el ingreso se distribuye de acuerdo con una ley de potencia. La esencia del modelo es que la riqueza presenta un efecto acumulativo, por tanto, a mayor nivel de ingreso, mayor probabilidad de incrementarlo.
Palabras clave: desigualdad, leyes de potencia, ley de Pareto, procesos estocásticos, proceso de Yule. JEL: C13, C12, O15.
Abstract
For some, the income distribution is the first example of a power law, empiric rule whereof an random variable reaches high values with a low probability and low values with a high probability. This article corroborates if the income distribution of the richest Colombians adjusts to a power law. Similarly, considering Yule´s process (1925), and in general, stochastic processes´ theory, a theoretical model, whose objective is to explain why income is distributed according to a power rule, is formulated. The essence of the model is that wealth presents an accumulative effects, therefore, at a higher income level, higher the probability of increasing it.
Key words: inequality, power laws, Pareto´s law, stochastic processes, Yule´s process. JEL : C13, C12, O15.
Résumé
Pour certains, la distribution du revenu est un exemple typique d´une loi de puissance. Une règle empirique selon laquelle une variable aléatoire atteint des valeurs supérieures avec une faible probabilité et des valeurs inférieures avec une forte probabilité. Dans cet article on vérifie si la distribution des revenus des colombiens les plus riches s´adapte à une loi de puissance. Également, on tient en compte du processus de Yule (1925), et en général, de la théorie des processus stochastiques. On formule un modèle théorique dont l´objectif est d´expliquer pourquoi les revenus sont distribués conformément à une loi de puissance. Ce modèle montre essentiellement que la richesse a un effet cumulatif : à un plus grand niveau de revenu la probabilité de l´augmenter sera plus grande.
Mots clés : inégalité, lois de puissance, loi de Pareto, processus stochastiques, processus de Yule. JEL : C13, C12, O15.
¿Qué tienen en común la desigualdad económica y la distribución del número de especies entre géneros en biología? En principio, parecería no haber una relación clara; pero no es así. Existen muchos géneros conformados por pocas especies, mientras que pocos géneros tienen muchas especies; de forma similar, muchas familias tienen un ingreso bajo, mientras que pocas familias tienen un ingreso alto. ¿Será posible que esta analogía permita a los economistas, con base en los adelantos de los biólogos, entender mejor los orígenes de la desigualdad?
¿Cuáles son las causas de la desigualdad? ¿Qué factores la atenúan y cuáles la acentúan? ¿Existen patrones o regularidades empíricas y estadísticas comunes a la distribución del ingreso en diferentes sociedades y en distintos momentos del tiempo? Pareto (1897, 1906) fue uno de los primeros en teorizar sobre este tema. En sus propias palabras:
La sociedad no es homogénea, y aquellos que no cierren sus ojos deliberadamente deben reconocer que los hombres difieren notablemente los unos de los otros desde el punto de vista físico, moral e intelectual. (...) A estas desigualdades de los seres humanos per se corresponden las desigualdades económicas y sociales, que observamos entre toda la gente, desde los tiempos más antiguos hasta el presente, en cualquier lugar del mundo, y de tal forma que esta característica siempre está presente (Pareto, 1906, 281, traducción propia).
De hecho, el estudio sistemático que Pareto hiciera de la desigualdad constituye un hito en el análisis de las leyes de potencia, campo de la estadística matemática y aplicada, de amplia divulgación en los últimos años1. Diversos fenómenos de las ciencias naturales y de las ciencias sociales pueden ser descritos satisfactoriamente por medio de este tipo de leyes, dando paso a una interesante retroalimentación entre disciplinas. Por ejemplo, adelantos en el estudio de los terremotos han ayudado a algunos a entender mejor las fluctuaciones económicas (Gabaix et al., 2003). Este trabajo apunta en una dirección similar, ya que se propone que el entendimiento de ciertos fenómenos biológicos puede servir como guía para comprender la desigualdad.
Este artículo tiene dos objetivos primordiales. En primer lugar, verificar si la distribución del ingreso en Colombia sigue una ley de potencia, una regla simple que ha explicado empíricamente la distribución del ingreso en un importante número de países y en distintos periodos. Si lo anterior se cumple, es posible identificar qué porcentaje de la población colombiana es dueña de los ingresos más altos de la sociedad. Esta ley es bastante importante porque mide el desequilibrio que existe en un rango primordial del ingreso.
El segundo objetivo es construir un modelo teórico que permita entender cuáles son los mecanismos que hacen de la desigualdad un fenómeno persistente. El modelo que se presenta es una aplicación del proceso de Yule (1925), el cual fue concebido originalmente para explicar la distribución del número de especies entre géneros en biología. La esencia del modelo propuesto es que la probabilidad de que una familia aumente su ingreso, es creciente en su nivel original de riqueza; es decir, la riqueza atrae cada vez más riqueza. Además, factores como la imperfección del mercado crediticio, el grado de movilidad social o el enfoque de la política económica, explican si la desigualdad es mayor o menor entre los más ricos.
Este artículo se compone de cuatro secciones. En la primera se define el concepto de ley de potencia y se presentan algunas de sus propiedades principales; en particular, la relación existente entre las leyes de potencia, la distribución del ingreso y la ley de Pareto. En el segundo apartado se realiza un ejercicio empírico –usando como muestra la Encuesta de Calidad de Vida de 2003 realizada por el Departamento Nacional de Estadística (DANE)–, en el cual se analiza, si la distribución del ingreso en Colombia se ajusta a una ley de potencia. Se identifica que esto ocurre en ocho de las nueve regiones que componen la encuesta, pero no a nivel nacional. En la tercera parte se formula un modelo teórico cuyo propósito es explicar por qué el ingreso se distribuye de esta forma y qué factores atenúan o acentúan la desigualdad. Por último, en la cuarta sección se discuten las principales conclusiones y recomendaciones del estudio.
¿QUÉ ES UNA LEY DE POTENCIA?
Hace ya más de un siglo Vilfredo Pareto (1897, 1906), en su Cours d´Economie Politique y en su famoso Manual de economía política, sugirió que el ingreso más alto de la economía tiende a distribuirse de acuerdo con una ley. Algunos la llaman la regla 80/20, según la cual el 20% de la población concentra el 80% de la riqueza de una nación. En términos generales, la aseveración de Pareto es que en todos los países y en todos los tiempos, una fracción pequeña de la sociedad, controla una porción alta de la riqueza. Este es, quizás, el primer ejemplo propuesto y analizado sistemáticamente de una ley de potencia (power law), que en los últimos años ha atraído la atención de científicos de diversas disciplinas.
Los términos distribución de potencia (power law distribution), ley de Zipf y ley de Pareto2, son usados para describir eventos en los cuales una variable aleatoria alcanza valores altos con poca frecuencia, mientras que los valores medianos o bajos son mucho más comunes. Por ejemplo:
- Hay pocas ciudades grandes y muchos pueblos pequeños, en relación con el número de habitantes.
- Hay pocas palabras que se utilizan con mucha frecuencia en un texto, mientras otras se usan pocas veces.
- En la luna, la frecuencia de los cráteres pequeños es alta, mientras que los cráteres grandes son menos frecuentes.
- Usando la escala de Richter, son pocos los grandes terremotos, pero muy frecuentes los movimientos telúricos de baja intensidad.
- Existen pocos géneros biológicos con muchas especies, y muchos géneros con pocas especies como subconjunto.
Así sucesivamente, se pueden encontrar otros fenómenos naturales y sociales en los cuales la variable de interés, sigue una distribución de potencia. En el caso de la distribución del ingreso, y como lo observara Pareto, la frecuencia de personas o familias con ingresos bajos es alta, mientras que la de individuos con ingresos altos es baja.
Características de una ley de potencia
Cuando la probabilidad de alguna variable se distribuye de acuerdo con una ley de potencia, su función de distribución se define como:
 |
[1] |
Siendo p(x) la probabilidad (frecuencia) de que la variable tome un valor de x; α el exponente de la distribución (el cual tiene que ser mayor que 1, de lo contrario al normalizar la función ésta no converge); x la variable que se quiere analizar y C una constante que depende del tipo de evento.
Tomando logaritmos a ambos lados de (1), se observa que para una ley de potencia
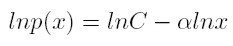 |
[2] |
Lo cual implica que en una gráfica con escala logarítmica, la relación entre lnp(x) y lnx, es descrita por una recta cuya pendiente negativa es α.
En la práctica, saber con certeza si una variable se distribuye como una distribución de potencia es difícil. Sin embargo, es posible inferirlo, y es lo que se pretende realizar en la siguiente sección de este artículo.
Leyes de potencia y la ley de Pareto
¿Qué relación existe entre una ley de potencia y la ley de Pareto? En particular, ¿qué papel juega α en el entendimiento de la desigualdad en la distribución del ingreso? Para responder a estas preguntas, es útil emplear la distribución acumulada complementaria (CDF) de potencia. Si P(x) es la distribución acumulada complementaria, entonces:
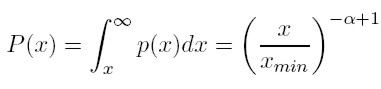 |
[3] |
Siendo xmin el menor valor a partir del cual se satisface la ley de Pareto. Este término será clave en el análisis posterior. De acuerdo con la anterior definición, el exponente es la pendiente de dicha función, de forma que cuanto más grande sea α, mayor será la frecuencia acumulada P(x) de algún valor x.
En la Gráfica 1 se presenta la distribución acumulada complementaria (ecuación 3) en escala logarítmica, que es igual a:
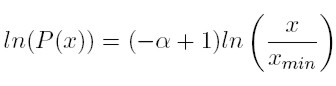 |
[4] |

Siendo (−α + 1) claramente la pendiente de la línea recta que se observa. En este sentido, y de acuerdo con lo definido hasta el momento, en la medida en que el parámetro α tome un valor más alto, la probabilidad acumulada será mayor, ya que la probabilidad acumulada complementaria será menor. A manera de ejemplo, si P(x) representa la probabilidad acumulada de que un hogar tenga un ingreso mayor a 5 millones de pesos, si α es mayor, la probabilidad acumulada de que una familia tenga dicho ingreso también lo será.
En otras palabras, cuánto más se aproxime a 1 el parámetro α, menor será la probabilidad de que un hogar tenga un ingreso mayor que x. Esto significa que un menor implica una mayor desigualdad en la distribución del ingreso de los más ricos3.
Una pregunta interesante que se desprende de la ley de Pareto es: ¿en dónde se encuentra la mayor parte de x (valores del ingreso) con relación a la frecuencia relativa (población)? La anterior ecuación permite estimar la población que tiene un nivel de ingreso mayor que cierto valor x. Ahora se desea establecer cuál es el porcentaje del ingreso que posee dicha población.
x1/2 corresponde al nivel de ingreso que divide a la distribución complementaria de potencia (ecuación 3) en dos partes. La primera, es el porcentaje de la población que tiene un ingreso mayor que xmin, pero menor que x1/2; la segunda parte, es la población cuyo ingreso está por encima de x1/2. Por lo tanto, x1/2 satisface las siguientes condiciones:
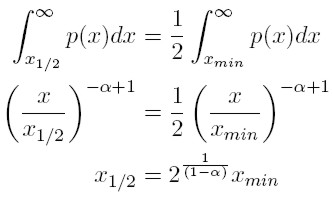 |
[5] |
Este ingreso representa el nivel medio de la distribución del ingreso, y con base en él, es posible calcular el ingreso agregado de la población cuyos ingresos son superiores a x1/2, usando el valor esperado de la distribución complementaria de potencia (para x mayor a x1/2). Así, la fracción del ingreso total controlada por el 50% más rico, es:
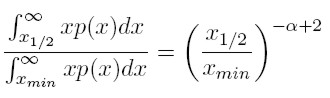 |
[6] |
Asumiendo4, que α > 2 es evidente que el 50% más rico controlará una fracción menor de la riqueza, cuánto más alto (alejado de 2) sea α.
De manera general, se requiere conocer la fracción del ingreso en manos de la población cuyo ingreso es superior x (siendo x ≥ xmin). De forma similar a como se derivó la ecuación anterior, esta fracción está definida de la siguiente forma:
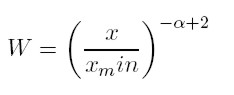 |
[7] |
En este caso, W es la fracción del ingreso en manos de la población cuyo ingreso es superior a x (nuevamente, es necesario asumir que α es mayor que 2, porque solamente así las integrales convergen). Despejando x / xmin en (3) y (7) y reordenando, se encuentra una ecuación que establece qué fracción del ingreso total es controlada por la fracción más rica de la sociedad:
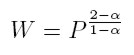 |
[8] |
Como α > 2 y P ∈ (0, 1), diferenciando (8) se aprecia que si α disminuye, aumenta la fracción del ingreso (W) en manos la fracción (P) más rica de la sociedad. De hecho, de (8), es claro que la famosa regla paretiana del "80/20", para la cual W = 0, 8 y P = 0, 2, el parámetro α debe ser igual a 2, 16. Este sería el valor de la potencia consistente con la observación del siglo XVIII de Pareto.
Así, la ley de Pareto es un caso particular de una ley de potencia. Entender las propiedades fundamentales de los sistemas generadores de leyes de potencia, puede ser un mecanismo para entender la emergencia y la evolución de la desigualdad en una sociedad.
Estimación del parámetro
El exponente α se puede estimar por varios métodos: un primer método es graficar los datos y calcular la pendiente; otro es utilizar mínimos cuadrados ordinarios (MCO), pero en este caso el estimador es sesgado. Por esta razón, la literatura especializada en el tema5 recomienda estimar este parámetro usando máxima verosimilitud, ya que el resultado es un estimador asintóticamente eficiente, es decir: (i) es consistente, (ii) se distribuye asintóticamente y (iii) tiene una matriz de covarianzas asintóticas.
La ecuación que resulta para estimar el parámetro por el método de máxima verosimilitud (MLE) es:
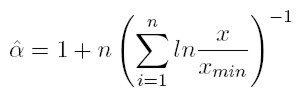 |
[9] |
n es el número de observaciones y xmin es el menor nivel de la variable, a partir del cual se cumple la ley de potencia. El error estadístico de este parámetro, estimado por máxima verosimilitud, es de acuerdo con Newman (2005):
 |
[10] |
Con base en estos resultados se calculará la estimación de la ley de potencia para el caso colombiano.
ANÁLISIS EMPÍRICO DE LA DISTRIBUCIÓN DEL INGRESO EN COLOMBIA
El objetivo de esta sección es verificar empíricamente si los ingresos de los hogares más ricos de Colombia se distribuyen de acuerdo con la ley de Pareto. El ingreso disponible de los hogares es un ingrediente básico de cualquier economía y en la medida en que se pueda medir el porcentaje de hogares dueños de los ingresos más altos, es posible entender cuál es el patrón distributivo que se presenta en la sociedad, lo cual puede ayudar en el diseño de políticas públicas que mejoren el nivel de vida de las personas.
En esta sección se examina el conjunto de datos que componen la Encuesta de Calidad de Vida del DANE, la cual viene efectuándose desde 1991. Esta encuesta se realiza con el objetivo de medir variables relacionadas con ingresos, egresos, educación y algunas otras variables sociodemográficas de los hogares.
Para este trabajo se utilizó la ECV de 2003. Como se muestra en el Cuadro 1, ésta es representativa a nivel nacional y para las 9 regiones en Colombia. La muestra de la encuesta es de 24.090 hogares, que expandida a nivel nacional, representa 11.194.108 hogares. En el caso especial de Bogotá, la ECV es representativa a nivel de localidad, pero para propósitos de este trabajo los datos no se analizaron a dicho nivel.

En el Cuadro 2 se presentan las principales estadísticas descriptivas de la variable "ingresos del hogar", para cada una de las 9 regiones. Como se puede apreciar, se presenta una gran dispersión en los datos, es decir, los ingresos disponibles de los hogares colombianos presentan una gran variabilidad frente al ingreso promedio del país. Este fenómeno se presenta en mayor magnitud en Bogotá y San Andrés.
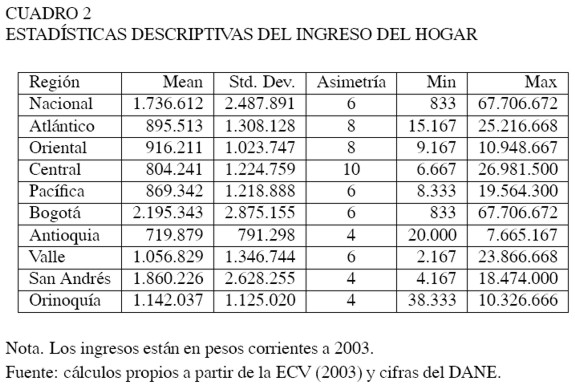
Por otro lado, el estadístico de forma, el coeficiente de asimetría6, indica que en todas las regiones se presenta una asimetría hacia la derecha, en especial, en la región Central. Esto significa que el porcentaje de hogares con ingresos más altos es relativamente pequeño. En otras palabras, esto podría indicar que existe una concentración de ingresos alta en todo el país.
Histogramas: una primera aproximación a la ley de Pareto
Como se mencionó anteriormente la firma clásica de una ley de potencia es el histograma construido a partir de los datos en una escala logarítmica, que debe ser, aproximadamente, una línea recta con pendiente negativa.
Para comprobar esto sobre los ingresos disponibles de los hogares colombianos, el primer paso fue normalizar la muestra con respecto a un rango de ingreso (Δx). La normalización se realizó dividiendo el número de hogares (n) que se encuentran dentro de un intervalo (Δx) del ingreso, de manera que sólo quede una observación por cada nivel de ingreso. La normalización de los datos es importante porque así la muestra se vuelve independiente del número de clases que se decida tomar para construir el histograma.
El histograma representa con claridad la distribución acumulada complementaria de potencia, ya que se construye de tal forma que el vértice del diagrama es la razón entre el nivel de ingreso y el número de hogares que tiene este nivel, y la directriz es el nivel de ingreso presentado de forma ordenada (de menor a mayor). En este sentido, la línea recta con pendiente negativa estaría reflejando la existencia de un gran porcentaje de hogares con niveles de ingresos no tan altos y un pequeño porcentaje de hogares con ingresos relativamente altos.
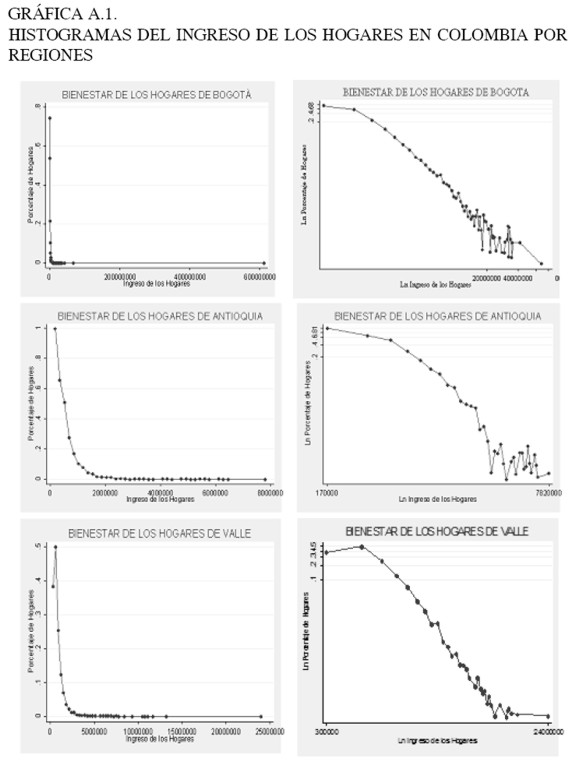
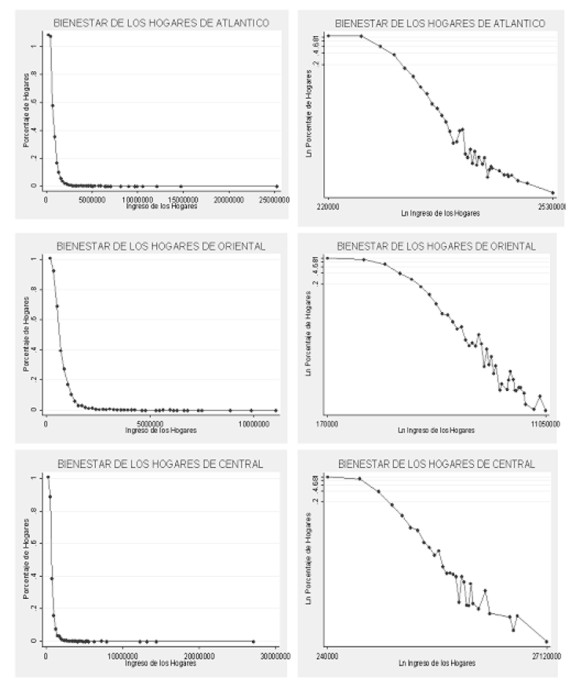
En las Gráficas 2A y 2B se presentan los histogramas construidos para los ingresos disponibles de los hogares a nivel nacional7. En el panel de la izquierda se encuentra el histograma simple y en el de la derecha un histograma con escala logarítmica.


Se puede observar en el histograma con escala logarítmica la línea recta con pendiente negativa, indicando que la distribución de los ingresos en el caso de Colombia podría ajustarse a la ley de Pareto. Sin embargo un histograma no es suficiente para determinar este tipo de resultados, ya que éste es un análisis puramente subjetivo y altamente sesgado.
Los histogramas con escala logarítmica construidos para este estudio (ver Anexo 1), muestran un ruido en la cola de la distribución, reflejando el hecho de que la distribución de potencia no se presenta a lo largo de toda la muestra, sino a partir de un valor mínimo del ingreso xmin. Por tanto, es importante determinar cuál es este valor mínimo desde el cual se cumple la ley de potencia.
Estimando el valor mínimo xmin y el parámetro α
Johnson (1937), tras encontrar que el ajuste de la distribución de Pareto con diferentes datos no siempre es la mejor, y que el exponente α puede variar, concluye: "No se puede negar que Pareto desarrolló un criterio fundamental. Encontró una descripción simple del esquema de la distribución del ingreso en los segmentos altos, y una limitación más interesante en el rango de la desigualdad medida en la distribución" (traducción propia).
Johnson, al igual que otros autores, demuestra que la distribución de Pareto se ajusta en los niveles más altos de ingreso. La razón es que existe un marcado sesgo en la distribución de los ingresos, que según Pareto, se debe a las habilidades inherentes de las personas para sobrevivir. Aquellos con habilidades menores al nivel mínimo de supervivencia desaparecen o son soportados por otros, y aquellos con fuertes habilidades tenderán a posicionarse en una sociedad, obstaculizando la redistribución de los ingresos.
Teorías más recientes, como las de Reed (2001), Levy (2001) y Fenner et al. (2005), explican por qué la ley de Pareto tan sólo se presenta en la cola de la distribución de los ingresos, a partir de un proceso estocástico multiplicativo. En un proceso estocástico multiplicativo de inversión, la tasa de retorno varía aleatoriamente y los ingresos futuros dependen de la inversión inicial. Estos autores asumen que sólo las personas que poseen un nivel de ingreso mayor a un ingreso mínimo (xmin), pueden participar en un proceso estocástico multiplicativo de inversión. El retorno de estas inversiones se ajusta perfectamente a una distribución de Pareto, bajo el supuesto de que el mercado en el cual se transan los distintos activos es eficiente.
Considerando lo anterior, puede verificarse teóricamente que la distribución del ingreso se ajusta a una ley de potencia a partir de un valor mínimo (xmin). No se trata tan sólo de tomar arbitrariamente un valor xmin a partir del cual la distribución de los ingresos se comporta como una distribución de Pareto, sino de estimar el valor del ingreso a partir del cual se sabe teóricamente que los hogares pueden acceder a ciertos beneficios económicos más que suficientes. Sin embargo, hace falta una teoría consistente que explique la emergencia de xmin, pues los modelos existentes, incluyendo el que se presentará más adelante, lo asumen de forma ad hoc.
De esta manera, es necesario estimar un valor xmin que permita hacer un buen ajuste de los datos con la distribución de Pareto, además de una buena estimación del parámetro α. Si se escoge un valor de xmin muy bajo, es probable que se presente un sesgo en el parámetro estimado, y se asuma una distribución de Pareto que no existe. Por otro lado, si se escoge un valor de xmin muy alto, se excluye información importante y se podría rechazar la hipótesis de que la distribución es de Pareto.
Para estimar el valor xmin existen varias maneras. Newman (2004) y Clauset et al., (2006) recomiendan la prueba de Kolmogorov-Smirnov, en la que se busca minimizar la distancia entre la distribución observada y aquella con la que se quiere hacer el ajuste. Además, este método es sensible a pequeñas desviaciones en el valor de xmin.
El estadístico de Kolmogorov-Smirnov se define como:
 |
[11] |
Siendo S(x) la distribución complementaria observada en los ingresos de los hogares (para cada una de las 9 regiones de la ECV), y P(x) la distribución complementaria de potencia (ecuación 3). En este caso, D es la distancia absoluta entre estas dos distribuciones. Si esta comparación refleja una diferencia significativamente grande, la hipótesis nula de igualdad de distribuciones se rechaza; es decir, los ingresos disponibles de los hogares no se ajustan adecuadamente a una distribución de Pareto.
La idea fundamental es encontrar el valor de xmin, que minimice la máxima distancia entre S(x) y P(x). En el Cuadro 3 se presentan tanto los valores de xmin, estimados para todo el país y para cada una de las 9 regiones, como el parámetro correspondiente a este valor. Se utilizó el método de simulación bootstrap para verificar la consistencia de los parámetros.
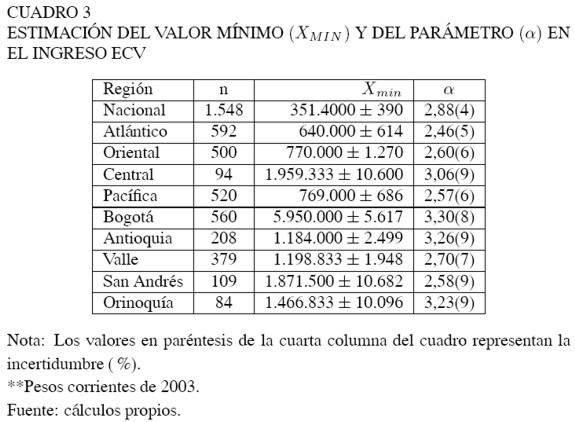
A partir de un muestreo aleatorio de tamaño n sobre los datos observados, se estimaron los parámetros xmin y α. Este proceso se realiza un número grande de veces, y se toma la desviación estándar de los parámetros calculados. En el Cuadro 3 se puede observar que el xmin está acompañado de un valor de incertidumbre calculado a partir del proceso bootstrap, y al igual que para el parámetro α se presenta su error entre paréntesis.
Los valores de xmin y α presentados para cada una de las regiones y a nivel nacional, permiten hacer una comparación relativa sobre la distribución de los ingresos. En lo que se refiere al parámetro α la población que exhibía una mayor inequidad entre los más ricos era Atlántico; en este caso de acuerdo con la ley de Pareto, el 5% de sus hogares más ricos, concentraban el 38,9% del ingreso en el rango más alto (ver ecuación 7). El mismo ejercicio para Bogotá muestra que en 2003, el 5% de la población era dueña del 18% de los ingresos de la población más rica de la ciudad. Estos resultados indican, siguiendo la teoría de Levy (2001), que eran más los hogares en Bogotá que podían hacer inversiones y lucrarse de actividades distintas al trabajo.
Así, el valor xmin refleja el nivel de ingreso disponible que debían tener los hogares para formar parte de la dinámica de inversión que se presentaba en la región. En Bogotá este valor era de 5,9 millones de pesos, lo que indica que los hogares por debajo de este ingreso mensual se encontraban dentro de una dinámica de salario y consumo, es decir, hogares por debajo de este nivel de ingreso no podían acceder a otro tipo de actividades (por ejemplo, inversiones en activos fijos), que además del salario, produjeran algún tipo de renta. En el caso de Atlántico, este valor fue de 640 mil pesos mensuales, que comparado con el valor xmin de Bogotá, es casi 10 veces menor. Esto indica que en el Atlántico la remuneración salarial y el consumo, son mucho menores. Además, los hogares en el Atlántico poseen menores posibilidades de mejorar sus niveles de ingreso, frente a las oportunidades a las que puedan acceder los hogares en Bogotá.
Reed (2002) estimó el parámetro α para algunos países por el método de máxima verosimilitud, y encontró que para Canadá el parámetro estimado era 4,16, mientras que para Sri Lanka era 2,09. Al comparar estos valores con Colombia, se evidencia que Canadá presenta una mejor distribución de los ingresos en el rango más alto, mientras que Sri Lanka presenta una mayor concentración de los ingresos en la cola de la distribución.
Al hacer la misma comparación, pero ya no a través de α sino a través de un indicador de desigualdad como el coeficiente de Gini, se encuentra que de los tres países mencionados, la nación con menos desigualdad es Sri Lanka, seguida de Canadá y finalmente Colombia –que como ya se comentó, se encuentra dentro del conjunto de países más desiguales del mundo. Esto simplemente refleja que el coeficiente de Gini y el parámetro de la ley de potencia, miden aspectos distintos de la distribución del ingreso8.
Por lo tanto, recordando que la ley de Pareto es una medida de desigualdad sólo para la parte más alta de la distribución del ingreso, el 5% de la población en Canadá concentraba menos ingresos en comparación con Colombia y Sri Lanka. En otras palabras, en Canadá un mayor porcentaje de la población tiene acceso a recursos que les permiten realizar distintos tipos de inversión y verse beneficiados de los retornos que estas actividades producen, logrando así que el ingreso disponible mensual no sólo dependa del salario y del consumo.
En esta sección se presentaron los resultados que se obtuvieron a través de los distintos procesos para estimar xmin y α. Se realizó una primera interpretación de estos resultados, revelando que el Gini y el parámetro α no son medidas de desigualdad comparables, ya que:
- Evalúan rangos del ingreso diferente.
- La ley de Pareto surgió como explicación del sesgo positivo que se presenta en los ingresos.
- La ley de Pareto es una regularidad empírica que va más allá de la simple comparación entre los ingresos disponibles de los hogares.
¿Los datos se ajustan a la ley de Pareto?
Las herramientas estimadas en la sección anterior ayudan a identificar cuál es la mejor forma de ajustar los datos a una distribución de potencia, pero no dicen mucho sobre si realmente siguen está distribución. Las dos pruebas de bondad de ajuste más usadas son la chi cuadrada (χ2) y la prueba de Kolmogorov-Smirnov (K-S). La prueba χ2 es muy simple de usar, pero tiene varios inconvenientes relacionados con la construcción del histograma, mientras que la prueba de K-S utiliza la distribución observada en los ingresos de los hogares.
Para no cometer un juicio erróneo sobre la distribución que siguen los datos aquí presentados, se utiliza nuevamente el estadístico de Kolmogorov-Smirnov para contrastar la hipótesis nula de que los ingresos disponibles de los hogares, en su rango más alto, se ajustan a la distribución de Pareto. Para esto, Kolmogorov (1933) suministró una tabla para su prueba estadística, la cual supone que la distribución esperada (distribución de Pareto) es independiente de los datos observados.
En el Cuadro 4 se puede ver que el estadístico calculado a partir de la ecuación 9 para todas las regiones y a nivel nacional (columna 5), es menor que el valor de la tabla de Kolmogorov (columna 6), de manera que no se puede rechazar la hipótesis nula. Hasta el momento se estaría diciendo que los ingresos de los hogares colombianos se distribuyen de acuerdo con la ley de Pareto a partir de un valor mínimo xmin.
Sin embargo, no es del todo cierto que los ingresos disponibles de los hogares sean independientes de la distribución de Pareto, ya que los parámetros (xmin y α) fueron estimados a partir de los datos, de forma conjunta. En estas circunstancias, el estadístico de K-S presenta una menor tasa de rechazó que la esperada.
Lilliefors (1967) suministra una tabla para contrastar el estadístico de KS, la cual asume que los parámetros son estimados a partir de los datos observados, utilizando el método de máxima verosimilitud. Esta tabla se obtuvo con el método de Monte Carlo, el cual se basa en la generación de un número grande de distribuciones de potencia con parámetros aleatorios. Para cada caso se calculó la prueba estadística de K-S y los percentiles que representan los grados de significancia de la prueba, y se construyó la tabla que permite contrastar la hipótesis nula.
En la columna 8 del Cuadro 4 se presentan los valores estimados por Lilliefors, los cuales permiten hacer el contraste en cada una de las 9 regiones y a nivel nacional. Como se puede observar el estadístico calculado (columna 5) es mayor que el valor presentado en la tabla de Lilliefors, para la región del Valle y a nivel nacional. Por tanto, se rechaza la hipótesis nula de que los ingresos disponibles de los hogares de los departamentos que conforman la región del Valle y el agregado nacional, en su rango más alto, se ajustaran en 2003 a la distribución de Pareto.
Este resultado podría explicarse en parte porque la base de datos utilizada para hacer el estudio no es la más apropiada, a pesar de que la ECV es representativa a nivel nacional. Para este tipo de estudios se recomienda utilizar información de la declaración de renta de las personas naturales, listas publicadas sobre las personas con mayores ingresos en el país, o bases que incorporen la cola derecha de la distribución del ingreso. Es importante resaltar que la hipótesis nula sólo resulto rechazada en dos de los diez casos, lo cual permitiría inferir que en su gran mayoría, las regiones colombianas cumplían una ley de potencia en 2003. Sin embargo, la divergencia entre los resultados regionales, y el resultado nacional, plantea un interrogante que todavía no es posible responder.
En el siguiente apartado se interpretará la ley de Pareto sobre los ingresos disponibles de los hogares en Colombia, a pesar de que la hipótesis nula se rechazara en dos casos utilizando la tabla de Lilliefors. No obstante, es importante recordar que la hipótesis nula no se rechaza utilizando el estadístico tradicional de K-S y la estimación del parámetro se hizo a través del método máxima verosimilitud.
Interpretación de los resultados
Pareto (1897), en su trabajo Cours D´Economie Politique, argumenta que la riqueza depende, en cierto grado, del talento de cada persona. No todos los individuos poseen, por ejemplo, la misma habilidad para hacer negocios; no todos tienen un mismo nivel de riqueza inicial; y no todos tienen la misma suerte. En cierto grado, la distribución de la riqueza depende de factores que no son redistribuibles.
En la Gráfica 3 se presenta la curva de Pareto para los ingresos disponibles de los hogares colombianos mayores a $3.514.0009 en 2003. De acuerdo con el razonamiento de Pareto, estos son los hogares que poseen cierto grado de talento, condiciones iniciales y suerte, que les permiten posicionarse económicamente dentro de la sociedad.
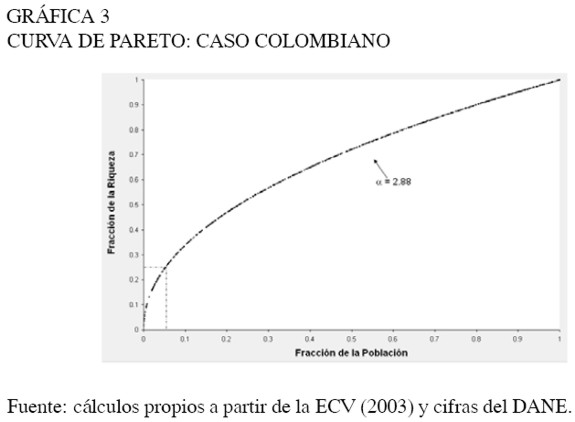
Se puede observar que 5% de los hogares "exitosos" en Colombia poseían 25% de la riqueza. Se comentó anteriormente que Reed (2001) calculó la ley de Pareto para países como Canadá y Sri Lanka, utilizando el método de máxima verosimilitud. En el caso de Canadá el autor encontró que 5% de la población "exitosa" concentraba 13% de la riqueza y en el caso de Sri Lanka que 5% de la población "exitosa" concentraba 78% de la riqueza.
Bajo la reflexión de Pareto esto indicaría que hay un mayor número de personas con un nivel suficiente de riqueza inicial, habilidad o suerte, en países como Canadá, que en países latinoamericanos como Colombia. Lo anterior tiene sentido si se considera que Canadá tiene indicadores de calidad de vida muy superiores e instituciones no tan polarizadas como las existentes en Colombia. Estos son factores que en cierta medida promueven fuentes de ingreso diferentes a los salarios. Además, y como se verá más adelante, seguramente la movilidad social juega un papel preponderante en la persistencia de la desigualdad. Así, la mayor desigualdad en el segmento más rico de la población colombiana, frente a la canadiense, probablemente es una consecuencia de la menor movilidad social que existe en Colombia.
En la Gráfica 4 se presenta la distribución complementaria de los ingresos de los hogares en Colombia, con dos curvas de ajuste. Se incluyó el ajuste de acuerdo con la estimación por máxima verosimilitud, y su equivalente a partir de mínimos cuadrados ordinarios. Es fácil ver que la curva de ajuste construida a partir del método de mínimos cuadrados ordinarios10 está más distanciada que la construida con el método de máxima verosimilitud. Este resultado no es sorprendente debido a los sesgos que presenta el método de MCO. Sin embargo, este ejercicio se llevó a cabo para comparar los resultados obtenidos con otros ejercicios empíricos, como los de Clementi y Gallegatti (2005a), Sitabhra (2005), entre otros.
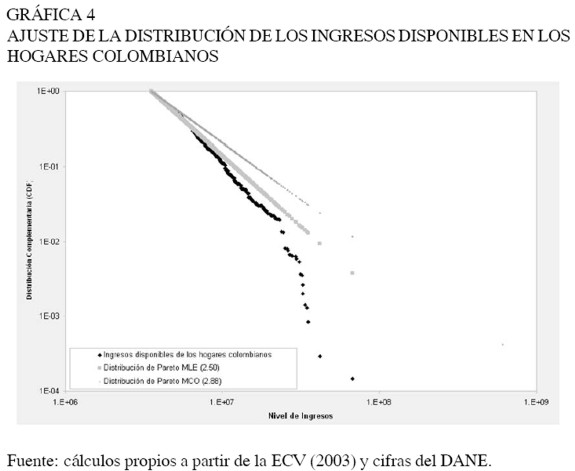
En el trabajo "Pareto´s Law of Income Distribution: Evidence for Germany, the United Kingdom, and the United States", Clementi y Gallegatti (2005b) encuentran que 5% de la población más rica en Estados Unidos, concentraba 17% de la riqueza. En el caso del Reino Unido el mismo 5% concentraba el 9,3%, y en el caso de Alemania el 13%. En otro artículo, estos autores realizaron el mismo ejercicio para Italia, y encontraron que 5% de la población más rica concentraba 27,4%.
Dado el valor α de 2,50 estimado por el método de MCO para el caso colombiano, el 5% de los hogares colombianos concentra el 37% de la riqueza. Este resultado muestra el mismo patrón encontrado en la comparación con Canadá. Estos son países que en términos de indicadores socioeconómicos presentan mejores niveles que Colombia, por tanto mejores oportunidades para que los hogares o las personas incrementen sus ingresos a partir de actividades diferentes al trabajo. Además, es probable que la movilidad social sea mayor que en Colombia.
¿QUÉ CAUSA LA DESIGUALDAD?
Amartya Sen (1997) argumenta que diferentes tipos de contingencias conducen a una variación sistemática en el ingreso, categorizadas en cinco fuentes de variación. La primera es la heterogeneidad de las personas (personal heterogeneities), refiriéndose a características físicas como la edad, el género, las inhabilidades, la tendencia a enfermarse, entre otras, que hacen que las necesidades entre un individuo y otro sean muy diferentes. Por ejemplo, si un individuo tiende a enfermarse requerirá más ingresos monetarios que otro que no se enferma tanto.
La segunda fuente corresponde a la diversidad ambiental (enviromental diversities): diferentes climas, por ejemplo, influyen en lo que una persona puede conseguir a partir de cierto nivel de ingreso.
La tercera fuente es la variación que existe en el clima social (variations in social climate). Aquí, Sen menciona la capacidad que posee un individuo para convertir sus ingresos o recursos en algo productivo, bajo la influencia de ciertas condiciones sociales. Por ejemplo, si un individuo se encuentra en una sociedad en la que las condiciones incluyen una cobertura adecuada de salud, de educación, con bajos niveles de criminalidad y violencia, muy probablemente mejorará su situación personal, lo cual incrementaría su productividad vía capital humano.
Una cuarta fuente son las diferentes perspectivas que existen según la comunidad en la que se vive (differences in relational perspectives). Sen con esto quiere hacer referencia a que las necesidades varían de una sociedad a otra dependiendo de las costumbres y convenciones que se tengan.
La quinta y última fuente, se refiere a la distribución que existe dentro de un hogar, de modo que los ingresos obtenidos por uno o más miembros de este núcleo, tienen que ser compartidos por partes iguales por todos los miembros, tanto los que tienen ingresos como los que no. De modo que el bienestar de la familia en términos monetarios, depende del número de miembros que componga ese hogar.
Con lo anterior, Sen teoriza acerca de las fuentes de la desigualdad, basándose en factores circunstanciales, sociales, económicos e inherentes al individuo, que en últimas no son capturados por simples estadísticas.
Muchas teorías se han construido para explicar la desigualdad y su relación con el crecimiento económico. Según Barro (1999), estas teorías se dividen en cuatro categorías: las relacionadas con imperfecciones del mercado de crédito, con política económica, malestar social y tasas de ahorro.
La imperfección en los mercados de crédito es más preocupante en economías pobres, en las que el acceso es limitado, ya que para tener un aval crediticio se requiere de algún bien como garantía. Así, los hogares con pocos recursos renuncian a hacer cualquier tipo de inversión, abriendo más la brecha existente entre pobres y ricos.
Por otro lado, las malas políticas económicas generan corrupción, haciendo que los recursos de la economía se desvíen en actividades de lobby y compra de votos, mas no en políticas redistributivas, ni en programas que ayuden a que los individuos de pocos recursos accedan a educación, salud y mejor trabajo, reforzando de este modo la desigualdad económica.
La exclusión social de determinados grupos de la población motiva al excluido a involucrase en actividades delictivas, lo cual conduce a un gasto de recursos y hace que la productividad económica se reduzca. Se produce un malestar social y por ende, más inequidad, de manera que se crea un círculo vicioso de desigualdad social.
Otras teorías de la desigualdad se han enfocado en el individuo, aislándolo de factores macroeconómicos. Stiglitz (1969) examina cómo la función de consumo, la heterogeneidad en las habilidades y la reproducción de un individuo pueden ser la causa de diferentes niveles de ingreso.
Trabajos como el de Ocampo, Sánchez y Tovar (2000) muestran que según la literatura colombiana hasta 2000, el principal determinante de la desigualdad en Colombia, en términos de ingreso laboral urbano e ingreso de los hogares, era el relacionado con las diferencias en dotaciones educativas y sus retornos (Bonilla, 2008).
Asimismo, Núñez y Sánchez (1998a), Robbins (1997) y Mesa y Gutiérrez (1996), al comparar tendencias recientes en la distribución del ingreso en Colombia, muestran que el aumento de la desigualdad de la década de los noventa es una consecuencia del incremento en la demanda de trabajadores calificados. De esta manera, choques estructurales, como la apertura económica, explican los cambios en la demanda relativa de trabajadores calificados frente a trabajadores no calificados, explicando también los cambios en los salarios relativos y su subsecuente efecto sobre la distribución del ingreso. Lo que parece quedar claro de estos estudios, naturalmente, es la importancia de la educación como determinante del ingreso.
Por su parte, Attanasio, Goldberg y Pavnik (2002) sugieren que la apertura tuvo un impacto negativo en la distribución del ingreso a través de tres canales: incrementos en los retornos a la educación superior, cambios en los salarios industriales que afectaron sectores que inicialmente tenían salarios bajos y una fracción alta de trabajadores no calificados, y un desplazamiento de la oferta laboral hacia sectores informales.
Para el periodo de 1976 a 1997, Núñez y Sánchez (1998b) descomponen la desigualdad en los ingresos laborales urbanos en Colombia, con el objetivo de determinar empíricamente cuáles eran los factores que contribuían a dicha desigualdad. Los autores concluyen que la educación es el factor que más incide en la desigualdad salarial. Además de la educación, otras variables importantes en esta descomposición son la posición ocupacional, el género, si el empleo es público o privado, si se es jefe de hogar, si el empleo es de tipo parcial o temporal, o si se vive en la ciudad. Si bien este ejercicio empírico presenta una importante descomposición de los factores que explican la desigualdad, es importante reconocer que cerca de 50% de la distribución del ingreso no es explicada por los factores incluidos. Naturalmente, esto concuerda con la posición de Sen (1997) según la cual algunos de los principales determinantes de la desigualdad son difíciles de cuantificar.
Birchenall (2007), por su parte analiza la relación entre la distribución del ingreso y las variables macroeconómicas, para el caso colombiano. Utilizando variables como el PIB, la tasa de desempleo, la tasa real de devaluación, el crecimiento de la oferta monetaria, el crecimiento fijo de la inversión, la tasa de inflación, la tasa real de interés y el crecimiento real de las reservas monetarias, el autor encuentra que todas estas variables afectan la distribución del ingreso, siendo la inflación la que mayor impacto tiene. Tanto en el corto como en el largo plazo, una mayor inflación reduce el ingreso sectorial y educativo para todos los grupos en la población. Bernal, Cárdenas, Núñez y Sánchez (1997) también encontraron que la inflación y el desempleo afectan negativamente la distribución del ingreso en el caso colombiano.
A continuación, por medio de un modelo teórico, se busca explicar cómo estos y otros factores causan desigualdad y hacen de su distribución una ley de potencia.
Un modelo generador de leyes de potencia
Una familia que acumule a través del tiempo y de generación en generación, una gran cantidad de dinero, poder y estatus social, es una dinastía. Los Medici en Florencia durante el Renacimiento, los Carolingios en Francia entre los siglos VIII y X, o los Túdor en Inglaterra entre los siglos XVI y XVII, son apenas tres ejemplos de dinastías que no sólo detentaron el poder político durante vastos periodos, sino que también amasaron importantes fortunas que se fueron transmitiendo de generación en generación.
La esencia del modelo de distribución del ingreso que se formula en esta sección es que en la sociedad existe un conjunto de dinastías, cada una poseedora de un ingreso determinado, el cual permite caracterizarlas como familias ricas. Por supuesto, unas familias son más ricas que otras, y en el tiempo, dependiendo del nivel de movilidad social que exista en la economía, nuevas dinastías emergerán.
Diferentes factores explican la rapidez o lentitud con la que emerge una nueva dinastía (familia rica):
1. La imperfección del mercado crediticio, que en mayor o en menor medida origina barreras a la entrada a las familias de bajos ingresos, que buscan formar parte del proceso de inversión y acumulación de capital.
2. El enfoque de la política económica, que en muchos casos responde a los intereses de las clases privilegiadas, en perjuicio de las necesidades de redistribución.
3. La ausencia de movilidad social, materializada en la incapacidad de ciertos mecanismos como la educación, para brindar oportunidades de progreso.
4. La naturaleza misma de la función consumo, que hace que las familias de altos ingresos cada vez puedan ahorrar más, y por tanto, participar en mayor medida en procesos en los que cuales el retorno a la inversión es creciente en la cantidad invertida.
En el modelo propuesto, estos factores jugarán un rol clave al momento de explicar la persistencia de la forma en la que se distribuye el ingreso.
Se considera yi como la riqueza de la dinastía i, y se asume que esta riqueza es superior a cierto nivel mínimo necesario para considerar a una familia una dinastía y0, por tanto, yi ≥ y0, para toda dinastía i. En el tiempo, el dinero fluye entre las dinastías, pero la probabilidad de que un dólar fluya a una dinastía en particular, depende de la riqueza que ésta tenga, mediante un mecanismo que se explicará más adelante.
Se asume adicionalmente que nuevas dinastías pueden aparecer y que el dinero fluye a una tasa constante por unidad de tiempo. En aras de simplificar el análisis, se supondrá que cada segundo un dólar fluye hacia una familia. Una vez m dólares han fluido, es decir, una vez una cantidad m de tiempo ha transcurrido, emerge una nueva dinastía. Es decir, un nuevo individuo o grupo familiar supera el umbral y0, siempre que m dólares se hayan distribuido entre las familias que originalmente habían estado por encima de este umbral.
De esta manera, m es un indicador de qué tanta movilidad social existe en la economía. Si m es alto, mucho dinero fluye, y por ende, mucho tiempo transcurre, antes de que una nueva familia pueda empezar a considerarse "rica"; es decir, existe poca movilidad social e intergeneracional. Sucede todo lo contrario si m es bajo. Una interpretación equivalente puede darse a este parámetro en términos del grado de imperfección del mercado crediticio, del nivel de plutocracia11 o de la relación entre ingreso, ahorro y consumo.
Se define un periodo como la cantidad de tiempo existente entre la aparición de una d inastía y otra. De esta manera, si en un momento determinado existen t dinastías, entonces en la sociedad han transcurrido t periodos. Los periodos son de igual longitud, y corresponde a la cantidad m de dinero que fluye. Así, en un periodo en particular, la economía "produce" y0 + m dólares, dado que y0 es la riqueza con la que empieza la nueva dinastía.
pi es la probabilidad de que el siguiente dólar que fluirá en la economía llegue a una dinastía con ingreso yi, y se define como:
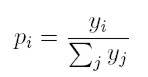 |
[12] |
De esta manera, la probabilidad de que el siguiente dólar vaya a una familia rica en particular, es simplemente la proporción de la riqueza total en manos de esa dinastía. Esto hace que dicha probabilidad sea creciente en la riqueza relativa de una familia. Los más ricos tienen una probabilidad mayor de hacerse más ricos, o en otros términos, la riqueza atrae más riqueza.
Algunos argumentos económicos sustentarían esta hipótesis. Por ejemplo, si la inversión presenta un proceso estocástico multiplicativo, en el que la tasa de retorno es creciente en el monto invertido, en el tiempo los que tengan mayor capacidad de inversión acumularán más. Este fenómeno se reforzaría de generación en generación si la riqueza y las habilidades se transmiten de padres a hijos. También, si el mercado crediticio es imperfecto, ya que los más ricos tendrían una capacidad mayor de endeudamiento porque cumplirán con mayor facilidad los requerimientos de capital exigidos por el sector financiero. Este mayor endeudamiento puede significar una tasa de retorno de la inversión también más alta.
Como la riqueza se distribuye de manera no simétrica entre las dinastías (precisamente como consecuencia de la definición de pi), no todas las t dinastías tendrán el mismo nivel de riqueza. De hecho, θ t y corresponde a la fracción de dinastías cuya riqueza es igual a y cuando existen t dinastías (o lo que es lo mismo, en el periodo t). De esta manera, el número total de dinastías existentes en este periodo es θ t y t y la riqueza total acumulada en la economía es
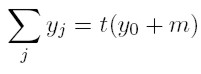 |
[13] |
El lado izquierdo de la igualdad es la sumatoria de la riqueza entre las familias ricas, mientras que el lado derecho simplemente es el número de periodos transcurridos (que en este modelo es equivalente al número de dinastías), multiplicado por la cantidad de dinero que fluye en cada periodo.
Se ha dicho que entre el establecimiento de la dinastía t y la aparición de la t + 1, una cantidad m de dólares fluye en el sistema. Por esta razón, la probabilidad de que una dinastía con riqueza yt obtenga un dólar en dicho periodo de tiempo es
 |
[14] |
La segunda igualdad surge de reemplazar (12) el denominador del lado derecho de (13). Se deba ahora considerar las dinastías cuya riqueza el periodo t es igual a y. Del total de dinastías en este periodo, una fracción θ t y tiene este nivel de riqueza, y el número total es θ t y t. De esta manera, el número esperado de dinastías de este tipo, que adquiere un dólar entre la aparición de una dinastía y otra es
 |
[15] |
Si (14) representa el número de dinastías cuya riqueza es y en el periodo t y que reciben exactamente un dólar más durante este periodo, a su vez representa el número en el que decrece, para el periodo t + 1, la categoría de dinastías precisamente con esta riqueza, porque ahora todas estas familias tendrán una riqueza igual a y + 1. Pero este número de dinastías en la categoría y no sólo decrece; también crece, porque aquellas familias cuya riqueza en t es y − 1, y que reciben un dólar durante este proceso, formarán parte de la categoría y en el periodo t + 1. De hecho, el número esperado de familias ricas que experimentan este cambio es
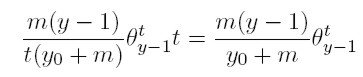 |
[16] |
Así, (14) y (15) representan, respectivamente, el número en el que decrece y crece la categoría de dinastías cuya riqueza es y.
Dado que el interés principal es la distribución del ingreso entre las familias, por lo menos dentro del conjunto de las más ricas (que es el grupo en el cual empíricamente se cumple la ley de potencia), es necesario saber cuántas dinastías en el periodo t + 1 (cuando hay igual número de dinastías) tienen una riqueza equivalente a y. Sumando (15) y restando (14) al periodo t, este número es:
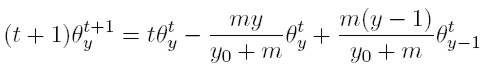 |
[17] |
O de manera equivalente:
 |
[18] |
El modelo aquí presentado define un proceso estocástico en el que el número (y por ende la proporción) de familias con un ingreso determinado, es una variable aleatoria que evoluciona en el tiempo. De hecho, (17) es la ecuación maestra del proceso estocástico que aplica para todos los niveles de riqueza con una excepción: el de aquellas familias cuya riqueza es apenas la mínima necesaria para ser consideradas una dinastía (y0). De hecho, el número esperado de familias con este ingreso en el periodo t + 1 es:
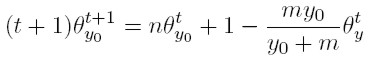 |
[19] |
La intuición detrás de (18) es simple. El lado izquierdo es el número de dinastías en dicho periodo (t + 1), multiplicado por la fracción del total que tienen un ingreso de y0. El lado derecho, por su parte, es el número de dinastías con dicho ingreso en el periodo anterior (tθ t y 0 ), más la nueva dinastía que emerge, menos el número total de dinastías cuyo ingreso en t era y0, pero que en el transcurso de este periodo ganan un dólar adicional.
¿Qué ocurre en el largo plazo? Es decir, dado que t es el número de dinastías, pero a la vez es el número de periodos, ¿qué ocurre a medida que t crece?
Si lím t→∞ θ t y = θ y, es decir, la fracción de familias con ingreso y converge a un valor fijo si t crece indefinidamente, (18) se convierte en: θ y 0 = 1 − (m / y0+ m ) y0 θ y0.
Y simplificando,
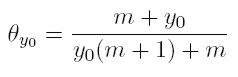 |
[20] |
De esta manera, la condición (19) representa la fracción de familias cuyo ingreso es apenas el necesario para ser consideradas dinastías, en la distribución estacionaria. Con un argumento similar, (17) se convierte en 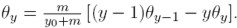
Ecuación que implica 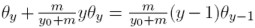 y resolviendo, se halla la distribución estacionaria para las dinastías cuyo ingreso es y:
y resolviendo, se halla la distribución estacionaria para las dinastías cuyo ingreso es y:
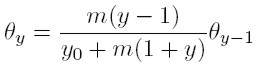
Para facilitar la iteración, se multiplica el lado derecho de esta igualdad por m / m, para obtener:
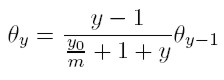
E iterando, se obtiene:

Y así sucesivamente hasta llegar a:

Que es equivalente a:
 |
[21] |
Como

Entonces (8) se convierte en:
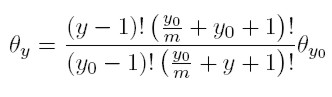 |
[22] |
Matemáticamente y por definición, si n es un número natural, su función gamma asociada es12 Γ(n) = (n − 1)!.
Por lo tanto, escribiendo (21) en término de funciones gamma, la proporción estacionaria de familias con ingreso y es:
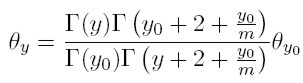 |
[23] |
Por otro lado, existe una relación entre las funciones gamma y la función beta, definida por: B(a, b) = ∫ 1 0 z a − 1 (1 − z) b−1 dt.
Es posible demostrar que:
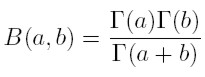 |
[24] |
Como (31) es equivalente a:

Entonces, combinando (31) y (33), es posible escribir la fracción de dinastías con ingreso y en término de funciones beta:

Resulta interesante expresar dicha fracción de esta manera, porque una importante propiedad de la función beta B(a, b) es que, manteniendo constante b e incrementando a, la función sigue una ley de potencia de la forma B(a, b) ∼ a−b. En este caso, en la cola de la distribución θy ∼ y −(2+ (y0 / m )).
De esta manera, el coeficiente de la ley de potencia en el modelo es α = 2 + (y0 / m). Por definición, tanto m como y0 son positivos, por lo tanto α siempre es mayor que dos. Este resultado es consistente con las estimaciones de la sección 2. Cuanto más se acerque a 2 este exponente de la ley de potencia, mayor será la desigualdad entre los ricos.
Por lo tanto, en el modelo, una menor movilidad social (mayor m) acentúa la desigualdad. De esta manera, diversos factores económicos explicarían una mayor o menor desigualdad entre los ricos, teniendo como canal de transmisión la movilidad social. Por ejemplo, si el mercado crediticio en una región (o país) es más imperfecto que en otra(o), menor movilidad social existirá y por tanto habrá más desigualdad, de acuerdo con el modelo. Si la plutocracia es más acentuada en un lugar que en otro, probablemente esto también iría en detrimento de la movilidad social, con su respectivo impacto sobre la distribución del ingreso. Por último, si la inversión sigue un proceso estocástico multiplicativo, de tal forma que la tasa de retorno sea una función creciente del monto invertido, es probable que la movilidad intergeneracional sea baja, de tal forma que de generación en generación, el capital y la riqueza se transmitan dentro de las dinastías, perpetuando la desigualdad.
También es claro que α decrece y tiende a 2 conforme disminuye y0. Este parámetro mide el ingreso con el cual aparece una nueva dinastía o familia rica. Por lo tanto, cuánto más bajo sea este ingreso, mayor será la desigualdad. Si las nuevas dinastías empiezan con un nivel menor de riqueza, probablemente esto favorezca, en el largo plazo, a las que inicialmente tenían un nivel alto.
De esta manera, el modelo presentado en esta sección pretende explicar el origen de la ley de potencia en la distribución del ingreso de los más ricos en una sociedad. El argumento básico del modelo es que la probabilidad de que una dinastía en particular obtenga más dinero, es creciente en su nivel de riqueza. El ingreso atrae más ingreso, de forma similar a como una ciudad grande atrae más habitantes, como un género con muchas especies tiene una probabilidad mayor de crear una nueva especie, o como es muy probable que un artículo muy citado, vuelva a serlo.
CONCLUSIONES Y RECOMENDACIONES
A partir de la Encuesta de Calidad de Vida de 2003 realizada por el DANE, en este trabajo se verificó si los ingresos disponibles de los hogares en Colombia, en su parte más alta, se distribuyen de acuerdo con la ley de Pareto. Estimando el parámetro por el método de máxima verosimilitud y utilizando la prueba tradicional de Kolmogorov-Smirnov, se encontró que no se rechaza la hipótesis nula de que los ingresos disponibles de los hogares se ajustan a la distribución de Pareto. Sin embargo, esta prueba no es suficiente para confirmar la hipótesis nula, ya que K-S asume independencia entre la distribución observada y la esperada. En este caso, los parámetros de la distribución de Pareto se estimaron a partir de la distribución de los datos observados en la ECV. Por lo tanto, fue necesario corregir la prueba utilizando la tabla de Lilliefors, la cual determinó que los ingresos disponibles de los hogares en la región Valle y a nivel nacional, no se ajustan a la distribución de Pareto. En los ocho casos restantes no se rechazó la hipótesis nula.
La mayoría de los estudios aplican el método mínimos cuadrados para estimar el parámetro exponencial de la distribución de Pareto y utilizan pruebas tradicionales de bondad de ajuste como la χ2, la prueba de K-S y el mismo R cuadrado de la regresión lineal. Estos métodos no son los más indicados debido a los diferentes tipos de sesgos que se presentan en el momento de calcular los resultados. Adicionalmente, el valor mínimo del ingreso (xmin) debe ser estimado por algún método estadístico que no permita cometer ningún tipo de error. La estudios económicos referenciados, seleccionaron el (xmin) con base en el histograma construido con los datos observados de los ingresos o simplemente identificando un valor mínimo del ingreso a partir de políticas fiscales.
A pesar de que el ajuste de la distribución de Pareto se rechaza en dos de los ocho casos utilizando la tabla de Lilliefors, los resultados permitieron construir una medida relativa de la riqueza para Colombia, encontrando que países como Canadá, Estados Unidos, Italia y Alemania, presentan una mejor distribución en la parte más alta de los ingresos. Esta medida relativa de riqueza también permitió concluir que el coeficiente de Gini y el parámetro no son medidas de desigualdad comprables, ya que: (i) evalúan diferentes rangos del ingreso, (ii) la ley de Pareto surge como explicación al sesgo positivo que presenta la distribución del ingreso, y (iii) la distribución de Pareto no es una simple comparación de ingresos.
El análisis empírico hecho en este artículo permite concluir que en ocho de las nueve regiones colombianas la distribución del ingreso de los más ricos, se ajusta a una ley de Pareto. Sin embargo, y como era de esperar, esta distribución es más desigual en algunas regiones que en otras. Seguramente este patrón también se observa a nivel global, entre naciones. Por tanto, inmediatamente surgen diversos interrogantes: ¿por qué el ingreso sigue una distribución de potencia? ¿Qué factores económicos, políticos y sociales perpetúan esta distribución? ¿Por qué en algunas regiones la distribución es más desigual?
El modelo teórico presentado intenta responder algunos de estos interrogantes. Tomando como dada la desigualdad en la distribución del ingreso, ésta persiste porque la probabilidad de que una familia aumente su riqueza, es creciente en el nivel inicial de ingreso que dicha familia tenga. Este fenómeno se exacerba cuando más baja sea la movilidad social, más plutócrata sea el gobierno o más imperfecto sea el mercado crediticio.
En cuanto a las recomendaciones, es necesario reconocer que la base de datos utilizada para hacer este tipo de estudios no es la más apropiada, a pesar de que la ECV es una base representativa a nivel nacional. Deberían utilizarse bases de datos como la declaración de renta de las personas naturales, la lista de las personas con mayores ingresos en el país, o bases de datos que ciertamente incorporen la cola derecha de la distribución de los ingresos. Es importante resaltar que la hipótesis nula sólo resultó rechazada en dos de los diez casos, utilizando las pruebas más exigentes recomendadas por la literatura especializada. Esto representa un avance con respecto a la mayoría de estudios empíricos realizados a nivel mundial en este campo.
Sitabhra (2005) realizó la estimación del parámetro α para distintos periodos, con lo cual concluyó que hay una correlación entre los ingresos de un periodo y otro, y pudo hacer inferencias acerca de la evolución de la desigualdad. Para Colombia sería muy interesante evaluar el parámetro exponencial de la ley de Pareto para distintos periodos. Por un lado, sería posible encontrar correlaciones entre los niveles de ingreso de un periodo y otro, lo cual corroboraría el proceso estocástico multiplicativo en los rendimientos de los inversionistas. Por otro lado, sería interesante analizar la correlación del parámetro con el coeficiente de Gini o algún otro indicador económico, que permita hacer inferencias sobre las causas de una mayor o menor concentración del ingreso en el rango más alto.
NOTAS AL PIE
1 Newman (2004) ofrece una excelente introducción a este tema.
2 Ver Newman (2005).
3 "De los más ricos" porque como se verá más adelante, la ley de potencia se satisface para aquellos que tienen un ingreso superior a cierto nivel mínimo xmin<; es decir, no se cumple para todos
4 Este supuesto cobrará validez empírica más adelante. De hecho, matemáticamente es necesario asumir esto porque de lo contrario, las integrales de (5) divergen.
5 Ver, por ejemplo, Clauset et al., (2006).
6 El coeficiente de asimetría es igual a cero cuando la distribución es simétrica, positivo cuando existe asimetría a la derecha y negativo cuando existe asimetría a la izquierda.
7 En el Anexo 1, se presentan las parejas de histogramas para cada una de las 9 regiones de la ECV.
8 Las verdaderas relaciones entre el exponente α y el coeficiente de Gini, son un problema interesante a resolver en futuras investigaciones.
9 Pesos corrientes.
10 La regresión lineal por el método de máxima verosimilitud presenta un coeficiente de determinación R2 de 0,82.
11 Es decir, qué tanto favorece a las clases privilegiadas la política económica.
12 De hecho, en general, la función gamma es una extensión de la función factorial de los números naturales, a los números reales, y más aun, a los números complejos.
13 Ver Newman (2004).
ESTIMACIÓN DEL EXPONENTE α POR MÁXIMA VEROSIMILITUD13
Considérese la siguiente distribución de potencia:

Normalizando la constante C, para que ∑ n i=1 p(xi) = 1, la distribución de potencia se convierte en:
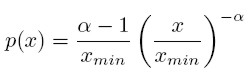
Dado un conjunto de datos de n observaciones xi ≥ xmin , se quiere saber cuál es el valor estimado del parámetro α.
La probabilidad de que los datos se distribuyan como una distribución de potencia, dado un valor del parámetro α es:

Esta probabilidad se conoce como verosimilitud de los datos dado un modelo.
Comúnmente se trabaja es con el logaritmo de esta probabilidad:

Al derivar el logaritmo de verosimilitud con respecto al parámetro e igualar a cero, se obtiene el estimador por máxima verosimilitud:
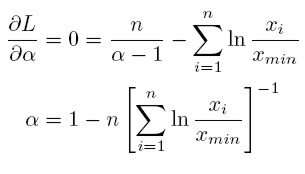 |
[25] |

REFERENCIAS BIBLIOGRÁFICAS
[1] Attanasio, O., Goldberg, P.K. y Pavcnik, N. (2004). Trade reforms and wage inequality in Colombia. Journal of Development Economics, 74(2), 331-366.
[2] Barro, R.J. (2000). Inequality and Growth in a Panel of Countries. Journal of Economic Growth, 5(1), 5-32.
[3] Bernal, R., Cárdenas, M., Núñez, J. y Sánchez, F. (1997). Macroeconomic Performance and Inequality in Colombia. Bogotá: Departamento Nacional de Planeación.
[4] Birchenall, J. (2007). Income Distribution and Macroeconomics in Colombia. Journal of Income Distribution, 16(2), 351-387.
[5] Bonilla, L. (2008). Diferencias regionales en la distribución del ingreso en Colombia. Bogotá: Banco de la República.
[6] Champernowne, D. G. (1953). A model of Income Distribution. The Economic Journal, 63(250), 318-351.
[7] Clauset, A., Shalizi, R.C. y Newman, M. (2006). Power-law Distributions in Empirical Data. SIAM Review, 51, 661-703. doi: 10.1137/070710111. Recuperado de: http://arxiv.org/PS_cache/arxiv/pdf/0706/0706.1062v2.pdf.
[8] Clementi, F. y Gallegati, M. (2005a). Power law Tails in the Italian Personal Income Distribution. Physica A: Statistical Mechanics and its Applications, 30(2- 4),427-438. Recuperado de http://129.3.20.41/eps/mic/papers/0505/0505005.pdf.
[9] Clementi, F. y Gallegati, M. (2005b). Pareto´s Law of Income Distribution: Evidence for Germany, the United Kingdom, and the United States. En: Chatterjee, A., Yarlagadda, S., and ChakrabartiB.K. (2005). Econophysics of Wealth Distributions (pp. 3-14). Milan: Springer-Verlag Italia. Recuperado de http://arxiv.org/abs/-physics/0504217.
[10] Fenner, T., Levene, M. y Loizou, G. (2005). A Stochastic Evolutionary Model Exhibiting Power-Law Behaviour with an Exponential Cutoff. Physica A: Statistical Mechanics and its Applications, 355(2-4), 641-656.
[11] Gabaix, X., Gopikrishnan, P., Plerou, V. y Stanley, H.E. (2003). A Theory of Power-Law Distributions in Financial Market Fluctuations. Nature, 423, 267-270.
[12] Hayakawa,M. (1951). The Application of Pareto´s Lawof Income to Japanese Data. Econometrica, 19, 174-183.
[13] Johnson, N.O. (1937). The Pareto Law. The Review of Economic Statistics, 19(1), 20-26.
[14] Kolmogorov, A. (1933). Grundbegriffe der Wahrscheinlichkeitsrechnung. Bulletin (New Series) of the American Mathematical Society, 37, 1, 91-92.
[15] Levy, M. (2001). Market Efficiency, the Pareto Wealth Distribution, and the Lévy Distribution of Stock Returns. En: Durlauf, S., Blume, L. (Eds.), The Economy as an Evolving Complex System III. Oxford University Press. Recuperado de http://www.emh.org/Levy01.pdf.
[16] Lilliefors, H. (1967). On the Kolmogorov-Smirnov Test for Normality with Mean and Variance Unknown. Journal of the American Statistical Association, 62, 399-402.
[17] Lydall, H.F. (1959). The Long-Term Trend in the Size Distribution of Income. Journal of the Royal Statistical Society. Series A (General), 122(1), 1-46.
[18] Majunder, A. y Chakravarty, S.R.N. (1990). Distribution of Income: development of a New Model and its Application to U.S. Income Data. Journal of Applied Econometrics, 5(2), 189-196.
[19] Mesa, F. y Gutierrez, J. (1996). Los efectos no considerados de la apertura económica en el mercado laboral industrial. Bogotá: Departamento Nacional de Planeación.
[20] Newman, M.E.J. (2005). Power laws, Pareto Distributions and Zipf´s law. Contemporary Physics, 46(5), 323-351.
[21] Newman, M.E.J. (2005). The Power of Design. Nature, 405, 25-26.
[22] Núñez, J. y Sánchez, F. (1998a). Educación y salarios relativos en Colombia: evolución, determinantes e implicaciones para la distribución del ingreso, 1976-1995. Bogotá: Departamento Nacional de Planeación.
[23] Núñez, J. y Sánchez, F. (1998a). Descomposición de la desigualdad del ingreso laboral urbano en Colombia: 1976-1997. Bogotá: Departamento Nacional de Planeación.
[24] Ocampo, J.A., Sánchez, F. y Tovar, C. (2000). Mercado Laboral y Distribución del Ingreso en Colombia en los Años Noventa. Revista de la Cepal, 72, 53-78.
[25] Pareto, V. (1897). Cours d´Economie Politique. Lausanne: Rouge. doi: 10.1177/000271629700900314.
[26] Pareto, V. (1906)[1971]. Manual of Political Economy. New York: Kelley .
[27] Reed, W.J. y Hughes, B.D. (2002). From Gene Families and Genera to Incomes and Internet File Sizes: Why Power Laws are so Common in Nature. Physical Review E, 66, 6, 1-4. Recuperado de: http://llacolen.ciencias.uchile.cl/∼vmunoz/download/papers/rh02.pdf.
[28] Reed,W.J. (2001). The Pareto Law of Incomes-an Explanation and an Extension. Physica A, 319, 469-486. doi: 10.1016/S0378-4371(02)01507-8.
[29] Rhodes, E.C. (1950). Distribution of Incomes in the United Kingdom in 1938 and 1947. Econometrica, 17(66), 146-158.
[30] Robbins, D. (1997). Liberación comercial y salarios en Colombia. Bogotá: Departamento Nacional de Planeación.
[31] Sen, A.K. (1997). From Income Inequality to Economic Inequality. Southern Economic Journal, 64(2), 383-401.
[32] Sitabhra, S. (2006). Evidence for Power-Law Tail of the Wealth Distribution in India. Physica A, 359, 555-562.
[33] Stiglitz, J.E. (1969). Distribution of Income and Wealth among Individuals. Econometrica, 37(3), 382-397.
[34] Vuong, Q.H. (1989). Likelihood Ratio Test for Model Selection and Non-Nested Hypotheses. Econometrica, 57(2), 307-333.
[35]Wold, H.O.A. yWhite, P. (1957). A Model Explaining the Pareto Distribution of Wealth. Econometrica, 25(4), 591-595.
[36] Yamamoto, K., Yamamoto, H., Miyazima, S., Ohtsuki, T. y Fujihara, A. (2005). The Power-Law Exponent and the Competition Rule of the High Income Model. Practical Fruits of Econophysics, 5, 349-353. doi: 10.1007/4-431-28915-1_64.
[37] Yule, G.U. (1925). A Mathematical Theory of evolution based on the conclusions of Dr. J.C. Willis. Philosophical Transaction of the Royal Society of London B, 213(402-410), 21-87.
Cómo citar
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Descargar cita
Visitas a la página del resumen del artículo
Descargas
Licencia
Derechos de autor 2010 Cuadernos de EconomíaCuadernos de Economía a través de la División de Bibliotecas de la Universidad Nacional de Colombia promueve y garantiza el acceso abierto de todos sus contenidos. Los artículos publicados por la revista se encuentran disponibles globalmente con acceso abierto y licenciados bajo los términos de Creative Commons Atribución-No_Comercial-Sin_Derivadas 4.0 Internacional (CC BY-NC-ND 4.0), lo que implica lo siguiente:



















