Estimación de la utilidad en riesgo de una empresa de transmisión de energía eléctrica considerando variables económicas
Palabras clave:
riesgo de mercado, utilidad en riego, valor en riesgo, transmisión de electricidad. (es)ESTIMACIÓN DE LA UTILIDAD EN RIESGO DE UNA EMPRESA DE TRANSMISIÓN DE ENERGÍA ELÉCTRICA CONSIDERANDO VARIABLES ECONÓMICAS
Santiago Medina Hurtado1
Jorge Aníbal Restrepo Morales2
1 Doctor en Estadística. Profesor asociado de la Facultad de Minas, Universidad Nacional de Colombia. Director del grupo de Investigación en Ingeniería Financiera y Gestión Empresarial. E-mail: smedina@unal.edu.co. Dirección de correspondencia: Calle 23 sur No. 28-49 Urbanización Vilanova. (Envigado, Colombia).
2 MBA, candidato a Doctor en Internacionalización de la Empresa. Profesor asociado en la Universidad Autónoma de las Américas y la Institución universitaria Tecnológico de Antioquia. Líder del Grupo RED-Tecnológico de Antioquia. E-mail: jrestrepo@tdea.edu.co Dirección de correspondencia: Calle 32B No. 69c-22. (Belén-Medellín, Colombia). Este artículo fue recibido el 12 de diciembre de 2011, la nueva versión el 24 de enero de 2012 y su publicación aprobada el 26 de febrero de 2012.
Este artículo fue recibido el 12 de diciembre de 2011, la nueva versión el 24 de enero de 2012 y su publicación aprobada el 26 de febrero de 2012.
Resumen
Este artículo presenta una aproximación metodológica para la cuantificación de posibles pérdidas económicas en una empresa de transmisión de energía, causadas por la volatilidad de las siguientes variables macroeconómicas: tasa representativa del mercado (TRM), índices de precios al consumidor (IPC), índice de precios al productor (IPP), depósitos a término fijo (DTF) y la London Interbank Basic Operational Rate (Libor). La exposición se mide a partir del cálculo de la utilidad en riesgo (EaR), utilizando la distribución de probabilidad de las utilidades de la empresa. Las distribuciones de probabilidad y los procesos estocásticos identificados para los factores de riesgo están integrados a las cuentas del estado de resultados que son afectadas; después, mediante Simulación Montecarlo, se pueden cuantificar los efectos de la volatilidad de cada factor sobre los estados financieros de la empresa, lo cual permite tomar decisiones administrativas o cubrimiento de riesgos.
Palabras clave: riesgo de mercado, utilidad en riego, valor en riesgo, transmisión de electricidad.
JEL: G17, E47, G32.
Abstract
This paper presents a methodological approach to quantification of potential economic losses caused by the macroeconomic variables following: money exchange rate (TRM for its initials in Spanish), consumer price index (CPI), producer price index (PPI), fixed term deposits (DTF for its initials in Spanish), and London Interbank Basic Operational Rate (Libor), on a power transmission company. Exposure is measured calculating the Earning at risk (EaR) over the probability distribution of the company profits. The Probability distribution functions and the stochastic processes of each risk factor were identified and integrated into the financial statement, then, using Monte Carlo simulation the potential losses of each risk factor over the company financial statements were identified in order to take management decisions or hedge risks.
Keywords: market risk, earning at risk, value at risk, electric transmission.
JEL:G17, E47, G32.
Résumé
Cet article présente une approche méthodologique pour la quantification des pertes économiques dans une entreprise de transmission d'énergi, causées par la volatilité de quelques variables macroéconomiques : taux représentatif de marché (TRM), indice des prix à la consommation (IPC), indice d'prix à la production (IPP), dépôts à terme fixe (DTF) et le taux LIBOR. L'exposition est mesurée à partir du calcul de la valeur à risque (EAR), en utilisant la distribution de probabilité des bénéfices de la firme. Les distributions de probabilités et les processus stochastiques définis pour les facteurs de risque sont intégrés dans les comptes de résultat qui sont affectées, puis la simulation Monte Carlo il est possible de quantifier les effets de la volatilité de chaque facteur sur les états financiers de la l'entreprise, ce qui permet prendre des décisions de gestion ou de la couverture des risques.
Mots clés : risque de marché, utilité d'irrigation, valeur à risque, transmission de l'électricité.
JEL : G17, E47, G32.
INTRODUCCIÓN
Puede definirse el riesgo como la posibilidad de que un evento determinado se presente en el futuro ocasionando un daño o detrimento que afecte negativamente un objetivo específico. El riesgo, por lo general, se mide valorando la desviación que se puede presentar con respecto a un determinado objetivo. Desde una perspectiva financiera, la literatura, en su gran mayoría, coincide en agrupar los riesgos en tres categorías básicas: los riesgos operacionales, inherentes a las pérdidas acaecidas como consecuencia de fallas en procesos o sistemas al interior de la organización, o por factores externos tales como errores humanos, fallas en procesos, caídas de los sistemas, entre otras. Los riesgos de mercado hacen referencia a la exposición a los movimientos adversos de los precios de los diferentes activos que se transan en un mercado: acciones, monedas, títulos, o mercancías como el algodón y la energía eléctrica. Por último, están los riesgos de crédito, que es la exposición a que un deudor o cliente no cumpla con sus obligaciones contractuales (Jorion, 2007). No obstante esta gruesa clasificación, existen otras categorías de riesgo tales como el riesgo regulatorio, el riesgo reputacional, el riesgo jurídico y social, el riesgo tecnológico, el riesgo político, entre otros que también juegan un papel muy importante en el desempeño de la empresa y sobre los cuales existe muy poca literatura para su tratamiento (Holton, 2004).
El valor en riesgo, (VaR) es una técnica que consiste en la medición probabilística del riesgo al que está expuesto un portafolio de inversión. La génesis de esta herramienta se remonta a 1952, cuando Roy y Markowitz, de forma independiente, publicaron sus mediciones de riesgo asociados al concepto de volatilidad de los rendimientos continuos. A partir de entonces se han presentado numerosos aportes a la metodología desde la teoría de portafolios, y en especial a partir de la cuantificación de suficiencia de capital para mitigar posibles pérdidas. En los años noventa, J.P. Morgan, con su metodología Risk Metrics (JP Morgan, 1996), propone una medición estructurada del riesgo de mercado usando el índice VaR.
VaR es una estimación estadística definida como la máxima pérdida potencial que puede sufrir una cartera de activos durante un periodo de tiempo y con un determinado nivel de confianza, producto de variaciones en los precios de mercado. El concepto de VaR, inicialmente propuesto en el sector financiero para la medición de los riesgos de mercado, se extendió a la cuantificación del riesgo de crédito y, rápidamente, al riesgo operativo. Todo lo anterior impulsado por los acuerdos de Basilea, firmados por los bancos centrales de los países industrializados desde el año 1988 (Basel I, 1988) como un marco de referencia para la gestión de riesgos en el sector financiero.
Posteriormente, a mediados de los años noventa, se plantea la necesidad de aplicar el concepto en un contexto más amplio, de tal forma que se consideren todos los factores de riesgo de una empresa y cualquier sector económico. Se aborda la problemática de la gestión y cuantificación del riesgo desde un enfoque corporativo (AS/NZS 4360, 1999; Vaughan, 1997). En Colombia, el Instituto de Normas Técnicas (Icontec) emite la norma NTC 5254 (2004), que recoge todo el marco de referencia de gestión de riesgos planteado en la anterior norma. A nivel internacional, la Organización Internacional de Estandarización emite la norma ISO 31000 (2008) como un marco de referencia para la administración de riesgos.
La cuantificación de riesgos como una etapa del modelo de gestión es abordada mediante la modelación de las distribuciones de probabilidad de los factores de riesgo de la empresa, para medir su impacto en el desempeño corporativo (JP Morgan, 1999). Los factores de riesgo son agregados en los estados financieros (el estado de resultados y el flujo de caja de la empresa) mediante un proceso de Simulación Montecarlo, que permite obtener la función de distribución de probabilidad de la utilidad, el flujo de caja o el capital de la empresa. Esto permite cuantificar a priori diversas medidas de riesgo que ilustran las posibles pérdidasen las utilidades, el efecto sobre la liquidez de la empresa o el capital corporativo. Para ello se construyen indicadores de riesgo tales como: el EaR (utilidad en riesgo), EPSaR (utilidad por acción a riesgo), FCaR (flujo de caja libre a riesgo) o el CaR (capital a riesgo), estimados periódicamente para observar la evolución frente a la exposición a riesgo de la empresa a lo largo del tiempo, con el objeto de diseñar estrategias de planeación estratégica, operación o cubrimiento.
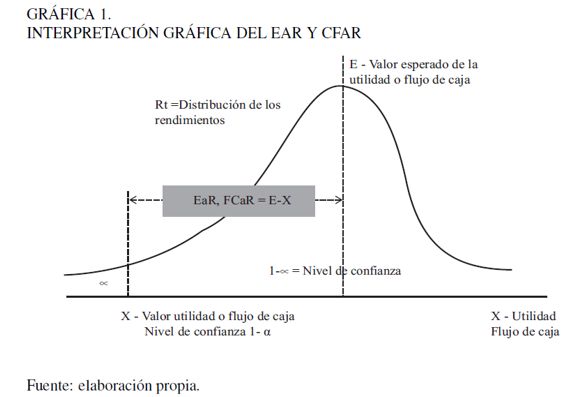
La Gráfica 1 es una representación del concepto VaR, EaR o CFaR, que muestra, para un nivel de confianza del 95 %, que el EaR o CFaR se determina por la distancia entre el valor esperado -también puede ser un valor de referencia, por ejemplo un valor presupuestado para el siguiente periodo- y el valor límite leído en la distribución de probabilidad al nivel de confianza dado.
Desde un enfoque de cuantificación de riesgo corporativo, si estamos interesados en la liquidez, por ejemplo, la idea es medir la capacidad de la empresa para cubrir sus obligaciones financieras de corto plazo: en qué rango se moverán los niveles de flujo de efectivo y los niveles de probabilidad asociados, y cuál es el impacto que tienen los diferentes factores de riesgo sobre la liquidez. Este análisis permite, entonces, identificar y medir aquellos factores críticos en la generación de efectivo, con el fin de tomar decisiones orientadas a mitigar los efectos negativos sobre la liquidez. En una perspectiva de riesgo, las proyecciones financieras son tratadas como variables aleatorias, y el objetivo es determinar la función de distribución de probabilidad de los índices que permiten realizar la planeación financiera del negocio.
En un principio es posible modelar factores de riesgo tales como la tasa de interés, la tasa de cambio, el precio de materias primas, la tasa de crecimiento del mercado, etc., sobre los cuales existe información histórica y para lo cual se han planteado diferentes modelos de cuantificación. Lo más usual es incorporar en el análisis cuantitativo del riesgo corporativo factores de mercado, de crédito y operativos sobre los cuales exista información. (Knop, 2004; Vilariño, 2001; Jorion, 2007).
No obstante, con otro tipo de factores de riesgo (como es el caso del riesgo político, el riesgo regulatorio, el conflicto armado, el riesgo imagen, el riesgo jurídico, el fraude, entre otros), el modelamiento es más difícil por las complejidades que esto implica, ya que, primero se debe entender adecuadamente el fenómeno e identificar las variables asociadas y sus relaciones, y, segundo, trasladar el efecto de sus cambios a los estados financieros. Lo anterior plantea actualmente interesantes retos de investigación para la comunidad académica y empresarial. Son varias las aproximaciones realizadas desde la estadística y la inteligencia artificial para tratar este tipo de riesgos, como lo son los árboles bayesianos y la lógica difusa (Sand, 2008; Medina, 2010).
Desde un enfoque de mercado, el análisis corporativo puede considerar, entre otras, las siguientes variables: el índice de precios al consumidor (IPC), la tasa de depósitos a término fijo (DTF), la tasa representativa del mercado (TRM), el índice general de la Bolsa de Colombia (IGBC), las tasas de interés, los precios de materias primas, las tasas de los bonos del tesoro americano, los precios del petróleo. Cada empresa debe identificar previamente cuál de estas variables impacta sus resultados, para ello puede usar la metodología de identificación planteada en la norma ISO 31000.
Este trabajo presenta una aproximación metodológica para la estimación del riesgo corporativo, calculando el indicador de riesgo EaR de una empresa de transmisión de energía eléctrica. Está estructurado en cuatro apartes incluida la introducción. En la segunda parte se presenta el marco conceptual, que incluye las definiciones y el análisis e identificación de los procesos estocásticos para las variables TRM e IPC, el ajuste de las distribuciones de probabilidad de la serie de tiempo de las variables macroeconómicas IPP, DTF y LIBOR. En la tercera parte se explica el modelo de simulación agregado, para finalmente presentar los resultados y las principales conclusiones.
ANÁLISIS E IDENTIFICACIÓN DE PROCESOS ESTOCÁSTICOS
Como se indicó previamente, el interés de este trabajo se enfoca en obtener las relaciones que permiten capturar la dinámica del comportamiento de la serie de tiempo de los factores de riesgo previamente identificados. Para este caso se consideran las variables: IPC, TRM, IPP, DTF y LIBOR. La elección de estas variables obedece a su impacto en el valor de mercado de las diferentes posiciones, activas o pasivas, que mantiene la empresa con el propósito de cumplir con las propuestas de valor emanadas de su objeto social. Por ejemplo, la TRM y la LIBOR afectan de forma directa el monto de los créditos que la empresa presenta en dólares; el IPP incide en el valor de los insumos utilizados en producción; el IPC impacta tanto los ingresos como los egresos corporativos, y la DTF los créditos contratados en moneda local. En esta sección se detallará la obtención del proceso estocástico de la serie para la TRM y la IPC. Para IPP, DTF y LIBOR se ajustan distribuciones de probabilidad.
Proceso estocástico de la tasa representativa del mercado
La TRM es un indicador económico que revela el nivel diario de la tasa de cambio oficial en el mercado spot de divisas colombiano. Corresponde al promedio aritmético simple de las tasas promedio ponderadas de compra y venta de divisas de las operaciones interbancarias y de transferencias desarrolladas en las ciudades de Bogotá D.C., Medellín, Cali y Barranquilla, por los intermediarios plenos del mercado que se encuentran autorizados en el estatuto cambiario, es decir: bancos comerciales, corporaciones financieras F.E.N. y Bancoldex (Superfinanciera).
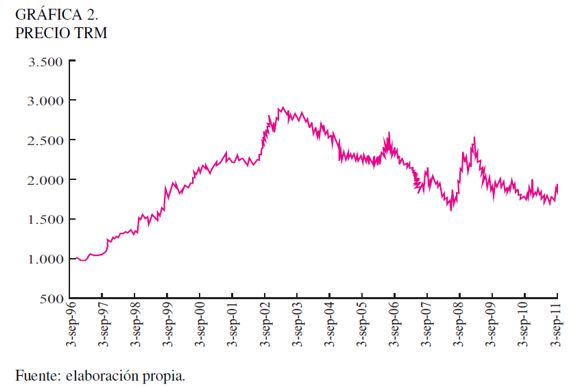
En la Gráfica 2 se visualiza cómo a lo largo de la serie de tiempo se han presentado dos diferentes tendencias: en el primer periodo, comprendido entre septiembre de 1996 y marzo de 2003, converge un escenario de devaluación; el segundo escenario inicia a mediados de 2003 y va hasta octubre de 2011, y presenta una fuerte reevaluación causada por diferentes fenómenos macroeconómicos tales como el aumento de la competitividad del mercado colombiano, el incremento de las exportaciones, la mejora de la calificación de riesgo país, las inversiones de extranjeros, el lavado de activos, entre otras.
Un proceso estocástico se define como una colección de variable aleatorias Xt para t = 1, 2, 3, coordenadas de acuerdo con el parámetro discreto t o tiempo. Así, los modelos estocásticos de series temporales conciben una serie temporal dada (Xt), como una colección de observaciones muéstrales en el tiempo.
Las leyes probabilísticas que rigen cualquier proceso estocástico se describen ampliamente y sin ambigüedades mediante las funciones de distribución de probabilidad asociadas a la variable. Para fines prácticos; los procesos pueden describirse mediante sus momentos, entre los cuales se destacan: la media, la función de autocovarianza y la función de autocorrelación.
Existe abundante literatura referida a la determinación del proceso estocástico de la TRM o de otros activos cuyo precio depende fuertemente de las expectativas de los agentes. Además, se han desarrollado innumerables investigaciones para determinar cuál será el valor de la TRM al final de un periodo, con resultados muy desalentadores, debido en gran medida a la fuerte intervención que los agentes y los mercados tienen en la formación de precios de la TRM, que no es fácil de capturar. La Gráfica 3 muestra los rendimientos logarítmicos de la serie TRM (Ecuación 1).
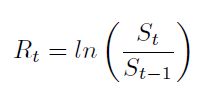 | [1] |
Como se puede observar, estos rendimientos producen una distribución más simétrica de los puntos alrededor de cero; aunque se observan periodos de baja y alta variación en los rendimientos (conglomerados de volatilidad), lo que implica la necesidad del uso de modelos de volatilidad dinámica para su modelamiento. Esta característica es propia de las series de tiempo económicas y financieras.
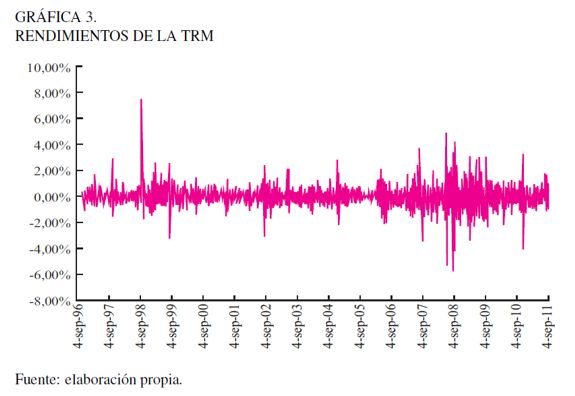
El proceso estocástico más simple supone que los rendimientos pueden explicarse mediante la relación:
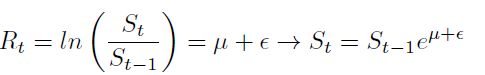 | [2] |
En la relación anterior, el precio de mañana depende inicialmente del precio de hoy, más una componente aleatoria asociada a la media del proceso y un error aleatorio; se pueden derivar procesos más complejos, dependiendo de los supuestos asociados a los parámetros 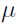 y
y 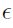 , como es el caso del movimiento browniano geométrico. Se supone inicialmente que la media del proceso
, como es el caso del movimiento browniano geométrico. Se supone inicialmente que la media del proceso 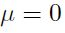 y los errores
y los errores 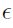 se distribuyen normal,
se distribuyen normal, 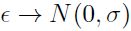 .
.
Movimiento Browniano Geométrico (MBG)
Como se describió, el rendimiento del activo puede ser explicado por dos componentes: 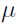 y
y 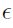 .
. 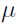 es la tasa promedio de rendimiento del activo, es determinístico y está asociado por lo general al rendimiento libre de riesgo; además, se asume constante y crece en función del tiempo dt.
es la tasa promedio de rendimiento del activo, es determinístico y está asociado por lo general al rendimiento libre de riesgo; además, se asume constante y crece en función del tiempo dt.
El segundo elemento 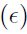 , representa el cambio aleatorio del precio del activo y, en general, se debe a factores externos como el impacto de noticias inesperadas. En el modelo browniano supone que
, representa el cambio aleatorio del precio del activo y, en general, se debe a factores externos como el impacto de noticias inesperadas. En el modelo browniano supone que 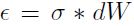 , donde
, donde 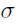 es la volatilidad de los rendimientos, dW contiene la aleatoriedad del precio del activo y se asume que es un proceso de Wiener con las siguientes propiedades: dW es derivado de una distribución normal con media cero y varianza dt. Esto es:
es la volatilidad de los rendimientos, dW contiene la aleatoriedad del precio del activo y se asume que es un proceso de Wiener con las siguientes propiedades: dW es derivado de una distribución normal con media cero y varianza dt. Esto es:
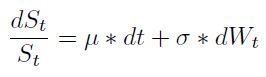 | [3] |
Se puede escribir 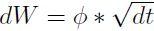 , donde
, donde 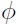 es una variable derivada de la distribución normal estándar con media cero y varianza unitaria.
es una variable derivada de la distribución normal estándar con media cero y varianza unitaria.
La ecuación diferencial que define el movimiento del precio del activo se define como:
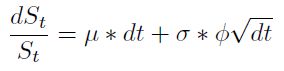 | [4] |
Si se aplica 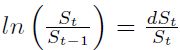 , obtenemos un modelo de dinámica de precios que permite generar caminos aleatorios del proceso de simulación para la TRM:
, obtenemos un modelo de dinámica de precios que permite generar caminos aleatorios del proceso de simulación para la TRM:
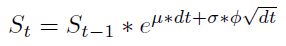 | [5] |
Supuestos. El parámetro 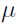 se asume normal (el precio se distribuye lo normal) y constante; sin embargo, en modelos más complicados
se asume normal (el precio se distribuye lo normal) y constante; sin embargo, en modelos más complicados 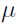 puede ser una función de S y t. El parámetro
puede ser una función de S y t. El parámetro 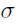 se asume contante pero pueden utilizarse modelos de volatilidad dinámica para capturar la volatilidad de los rendimientos de una manera más adecuada. Los errores se distribuyen normales
se asume contante pero pueden utilizarse modelos de volatilidad dinámica para capturar la volatilidad de los rendimientos de una manera más adecuada. Los errores se distribuyen normales  con media cero y desviación típica
con media cero y desviación típica 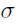 (Hull, 2006).
(Hull, 2006).
Análisis de volatilidad
La volatilidad de los rendimientos logarítmicos de la TRM no es constante, como se puede ver en la Gráfica 3, donde se evidencian periodos en los cuales existe baja volatilidad y otros donde esta es mayor (agrupamientos de volatilidad), lo que introduce un sesgo al modelo de precios antes descrito si asumimos que la volatilidad es contante, pues no se cumple uno de los supuestos sobre los cuales se basa el MBG. Es necesario establecer un modelo estocástico para la volatilidad, que describa el comportamiento de los cambios de la serie de tiempo. Este modelo se puede integrar al modelo de precio de la ecuación (5) para obtener una aproximación al verdadero comportamiento de la serie TRM.
En la primera etapa de la modelación de la TRM se realizaron pruebas de ajuste a su serie mensual de rendimientos logarítmicos históricos 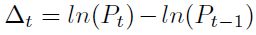 con el fin de corroborar la hipótesis de normalidad de la serie.
con el fin de corroborar la hipótesis de normalidad de la serie.
Como se muestra en el Cuadro 1, el valor P = 0, 0000 < 0, 05; 0, 01 es decir, para niveles alfa de 0, 01 y 0, 05 existe evidencia para rechazar la hipótesis nula de que los datos se ajustan a la distribución normal con una confiabilidad del 95% y 99 %, respectivamente.
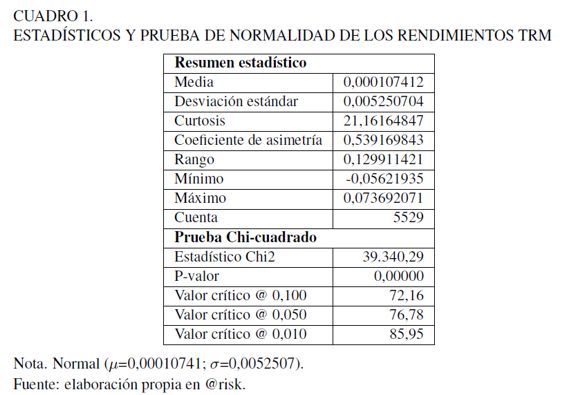
Al calcular la función de autorrelación parcial entre los rendimientos, se evidencia que existe una estructura de autorrelaciones subyacente en los datos. De forma similar, las pruebas Ljung-Box-Pierce (1970, 1978) y la prueba ARCH de Angle (1982) proporcionaron autocorrelación significativa, lo que robustece la propuesta de uso de modelos de volatilidad dinámicos.
Posteriormente, se realizaron pruebas de ajuste de modelos de volatilidad dinámica tipo ARCH (Modelo autoregresivo de heterocedasticidad condicional) y GARCH (Modelos autoregresivos de heterocedasticidad condicional generalizados) (Hull, 2006; Vilariño 2001). Las ecuaciones que recogen el dinamismo de la volatilidad se presentan a continuación:
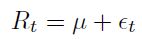 | [6] |
Los rendimientos Rt son iguales a una constante más una perturbación aleatoria incorrelacionada. La varianza pronosticada 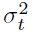 es igual a una constante más los promedios ponderados de previas varianzas (efecto Garch) y de los errores al cuadrado (efecto ARCH), esto es:
es igual a una constante más los promedios ponderados de previas varianzas (efecto Garch) y de los errores al cuadrado (efecto ARCH), esto es:
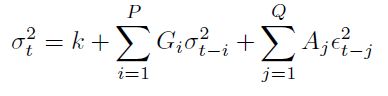 | [7] |
Los resultados obtenidos para los parámetros del modelo se encuentran disponibles en el Cuadro 2.
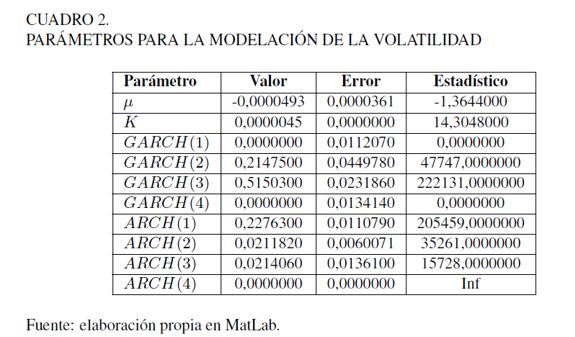
El estadístico T está normalmente distribuido con media cero y varianza unitaria. El valor 1,65 corresponde a un nivel de confianza del 95% para la prueba de significancia de los parámetros del modelo. En general, el estadístico T > 1, 65 indica que los parámetros del modelo son significativos. Son varios los modelos que podemos utilizar según el Cuadro 2, pero para efectos de simplicidad utilizaremos un modelo GARCH(0, 1) o ARCH(1)(1, 65 < 205.459)
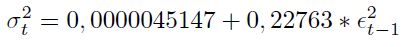 | [8] |
Partiendo de lo anterior, se procede a incorporar el modelo de volatilidadARCH(1) en la ecuación [5], donde la volatilidad 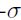 será el modelo dinámico obtenido en [8]. La relación [9] será usada en el proceso de simulación de caminos aleatorios de la TRM. El parámetro μ define la tendencia del proceso, valores negativos generan caminos aleatorios con tendencia negativa y valores positivos generan caminos con tendencia al aumento.
será el modelo dinámico obtenido en [8]. La relación [9] será usada en el proceso de simulación de caminos aleatorios de la TRM. El parámetro μ define la tendencia del proceso, valores negativos generan caminos aleatorios con tendencia negativa y valores positivos generan caminos con tendencia al aumento.
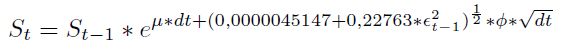 | [9] |
Siendo St el dato actual de TMR (o simulado); St−1 es el dato antrior de TRM (partiendo de valores históricos); 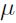 es la media aritmética de los rendimientos logarítmico;
es la media aritmética de los rendimientos logarítmico; 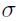 es la volatilidad dinámica de los rendimientos y
es la volatilidad dinámica de los rendimientos y 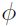 es el componente aleatorio distribuido N(0, 1).
es el componente aleatorio distribuido N(0, 1).
Finalmente, se exponen los resultados de 10 simulaciones de precios para 730 días. La generación de caminos aleatorios de precios son indispensables para la cuantificación del riesgo de tipo de cambio en los estados financieros. La Gráfica 4 muestra los caminos aleatorios que puede tomar la TRM en cada simulación.
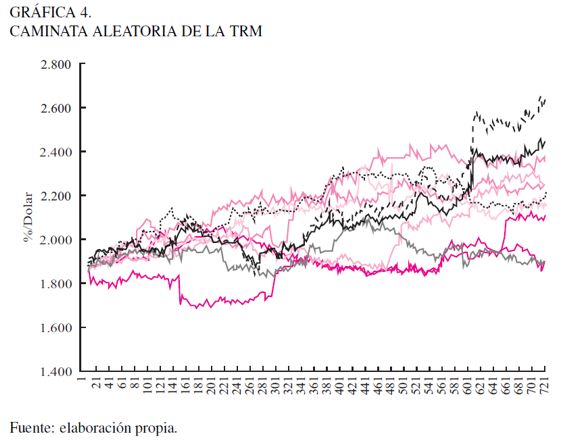
Proceso estocástico del índice de precios al consumidor
El IPC mide la variación de los precios de bienes y servicios de consumo final correspondientes a una canasta típica en la que se incluyen los servicios educativos, de salud, de alimentos y combustible, entre otros. El estudio de esta variable es de gran importancia para las empresas de transmisión energética, ya que, para el cálculo de la remuneración por transmisión de energía, el Estado colombiano, a través de la Comisión Reguladora de Energía y Gas, estableció los parámetros para calcular dicho valor, entre los que se encuentra el IPC (vigente del último mes) y la TRM (modelada anteriormente), entre otros (CREG 011, 2009).
Por lo anterior, el análisis, la modelación y el pronóstico de esta serie es imprescindible para cuantificar el efecto que esta tiene sobre las utilidades y los flujos de caja, y como guía en el proceso de la toma de decisiones. Para el IPC se probaron diferentes modelos de pronóstico con el fin de poder predecir, a un nivel de significancia del 95% y con un horizonte de tiempo de tres años, su comportamiento. La serie utilizada contempla un periodo de 10 años, con una periodicidad mensual que inicia el 01 de enero de 1997 y termina el 01 de octubre de 2011.
El análisis de series de tiempo parte de la identificación de sus componentes básicas, a saber: la tendencia T, la estacionalidad E, los ciclos C y su componente irregular I; por lo tanto, los valores de la serie Yt serán una función de las compo nentes, esto es:
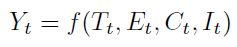 | [10] |
Para la identificación de dichos componentes, en general, se parte del análisis gráfico de la serie y se utilizan modelos matemáticos para su explicación. El análisis gráfico permite elaborar una representación simplificada de las características más importantes que contiene la serie, relacionadas con su evolución en el tiempo, es decir, identificar los movimientos sistemáticos y diferenciarlos de las fluctuaciones irregulares.
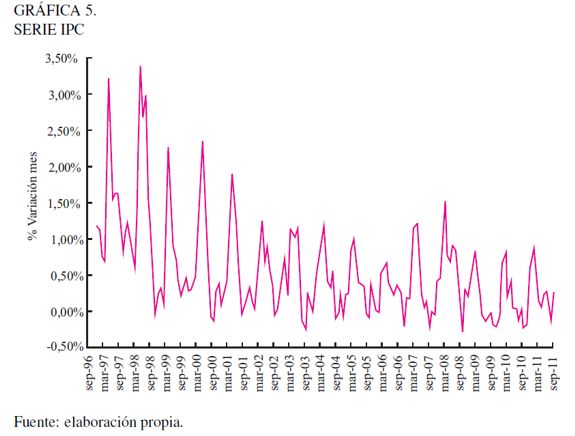
En la Gráfica 5 se puede ver el comportamiento mensual del IPC en Colombia. El análisis gráfico muestra que la serie de tiempo presenta una componente de tendencia (T) descendente hasta el año 2003 y a partir de allí presenta una estabilidad, además, se pueden identificar oscilaciones periódicas dentro de cada año o componente estacional (E). En el periodo de 1996 hasta 2000, la serie presenta una mayor variabilidad, comparada con la de los siguientes años. A partir del año 2000, se observa algo de estabilidad en la serie. Este patrón podría representar un factor de tipo oscilante caracterizado por movimientos en torno a la tendencia que se repiten cada determinados años o ciclos (C).
Sin embargo, el comportamiento cíclico de la serie no es muy claro. La serie también presenta variaciones o picos irregulares (componente irregular -I) para los cuales es difícil encontrar sus causas; estas variaciones no influyen de manera drástica en el comportamiento de la serie (Makridakis 1998). La detección de componentes de tendencia y estacionalidad descarta el hecho de que podamos utilizar un modelo dinámico para la simulación como el MBG, debido a que este genera caminos aleatorios.
La serie de precios del IPC no es estacionaria en media ni en varianza, es decir, los datos no se mueven alrededor de la media igual a cero, los picos están dispersos y no son constantes; además, se verificó que la volatilidad cambia a lo largo del tiempo, lo cual sugiere que para la modelación se requerirá de una transformación. Para la transformación de la serie se tuvo en cuenta la relación entre media y desviación típica anual del IPC, además de estimar la componente de tendencia con base en el método de media móvil de 12 meses de periodo estacional (Gráfica 6). Lo que permite que la serie sufra variaciones importantes en su evolución y que el promedio se adapte a las circunstancias cambiantes.
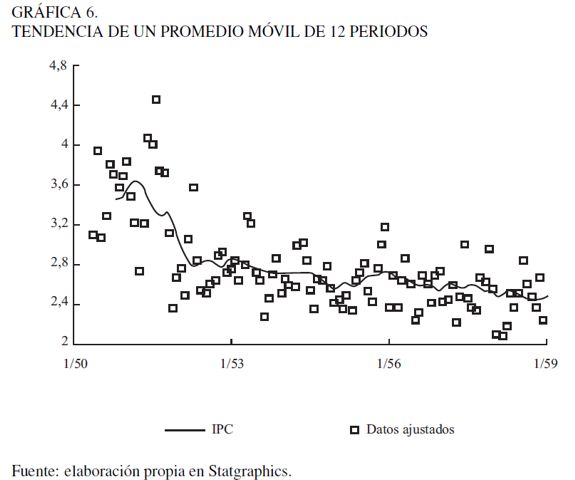
Con la prueba (PACF) se descartó la posibilidad de que la serie se pueda considerar ruido blanco, lo que implica una nueva transformación para remover la no estacionalidad de la serie. Para la transformación se utilizó el método Box-Cox (1964), el cual consiste en introducir una transformación de la variable a pronosticar con el objetivo de satisfacer la suposición de normalidad de un modelo de regresión. La transformación es de la forma (transformación potencia), donde 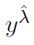 es estimada con los datos históricos.
es estimada con los datos históricos.
Más específicamente, la transformación está definida por 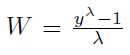 si
si 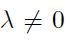 y
y 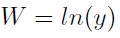 si
si 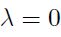 ; donde
; donde 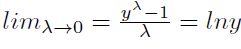 .
.
Con la ayuda del programa MatLab se encontró que el Lambda que minimiza el coeficiente de variación corresponde a 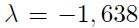 . El coeficiente de variación corresponde a la división entre la desviación estándar y la media de cada una de las series anuales desde 1997 hasta 2011, obteniendo una transformación de la forma:
. El coeficiente de variación corresponde a la división entre la desviación estándar y la media de cada una de las series anuales desde 1997 hasta 2011, obteniendo una transformación de la forma:
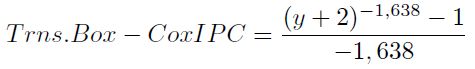 | [11] |
Posteriormente, para la serie de tiempo transformada se procedió a seleccionar diferentes tipos de modelos de pronóstico, con el fin de comparar su desempeño mediante diferentes índices de ajuste. En términos generales la predicción se realizó teniendo en cuenta los siguientes aspectos:
- Los modelos seleccionados se aplican a series con tendencia.
- Integración multiplicativa de componentes, ya que la relación entre la media y desviación típica anual del IPC sigue una tendencia creciente.
- Se utiliza un conjunto de datos para la validación del modelo (holdout set).
- El periodo estacional se considera de 12 meses.
- Los modelos se seleccionan considerando el error en el grupo de validación RMSE y MAPE, entre otros.
Los modelos seleccionados fueron:
- (A) ARIMA(0, 0, 1)x(0, 1, 1)12.
- (B) Suavización Exponencial Lineal de Brown con alpha = 0, 0977.
- (C) Suavización Exponencial Lineal de Holt con alpha = 0, 1068 y beta = 0, 0356.
- (D) Suavización Exponencial Simple con alpha = 0, 1768.
- (E) Promedio Móvil Simple con 12 rezagos.
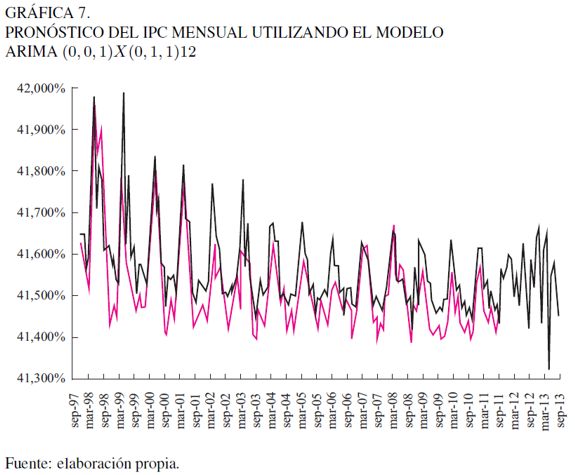
La variable de entrada es el modelo IPC trasformado; el número de observaciones es 123; el intervalo de la serie es mensual; los rezagos de la estacionalidad son 12 y el ajuste estacional es multiplicativo. Con esta información se compararon los resultados de los análisis descritos anteriormente, para decidir acerca del modelo que mejor representa el comportamiento del IPC. En la Gráfica 7 se muestra el pronóstico del IPC para 36 meses utilizando el modelo ARIMA(0, 0, 1)x(0, 1, 1)12 (RMSE = 0, 00077 y MAPE = 5, 00720).
Para simular la serie de precios del IPC fue necesario incluir en la fórmula el error aleatorio con las características de un ruido blanco 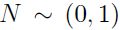 , partiendo del supuesto de que los errores de un modelo ARIMA se deben distribuir de la siguiente forma:
, partiendo del supuesto de que los errores de un modelo ARIMA se deben distribuir de la siguiente forma:
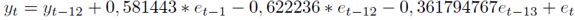 | [12] |
Donde:
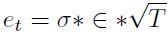 | [13] |
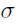 es la desviación estándar móvil de la serie IPC con rezagos de 12 meses;
es la desviación estándar móvil de la serie IPC con rezagos de 12 meses; 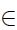 sigue una distribución normal N(0, 1) y permite generar el aleatorio del proceso de simulación y
sigue una distribución normal N(0, 1) y permite generar el aleatorio del proceso de simulación y 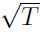 es el intervalo de tiempo para la simulación, para este caso T = 1.
es el intervalo de tiempo para la simulación, para este caso T = 1.
Con estos parámetros se obtiene la fórmula para el proceso de simulación
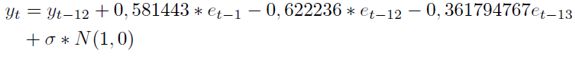 | [14] |
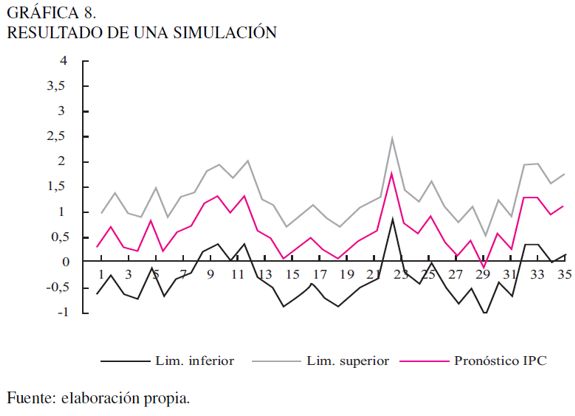
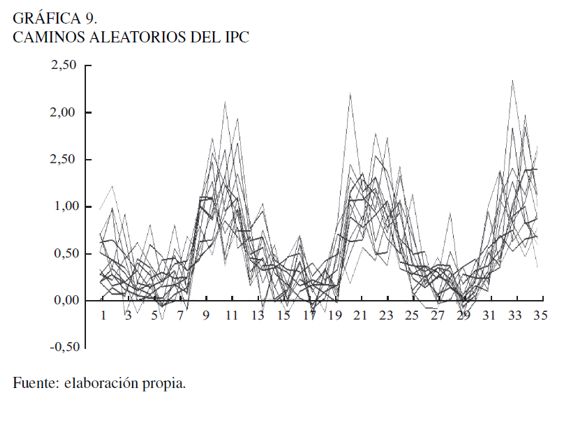
En la Gráfica 8 se observa la simulación de los 36 meses; representa un solo camino aleatorio con sus respectivos intervalos al 95% de confianza. La Gráfica 9 muestra algunos de los diferentes caminos que puede tomar el IPC con cada iteración. Los datos simulados muestran que nuestro modelo captura las componentes de tendencia y estacionalidad presentes en la serie histórica.
Distribuciones de probabilidad de las series Índice de Precios al Productor, Tasa de Depósitos a Termino Fijo y Tasa LIBOR
Para las series de tiempo relativas al IPP, DTF y LIBOR la simulación se realizará partiendo de las distribuciones de probabilidad ajustadas a las series de tiempo. En un proceso de Simulación Montecarlo es factible utilizar diferentes modelos para capturar la dinámica de los factores de riesgo, como también emplear modelación estocástica o las distribuciones de probabilidad de la serie. El error de asumir un modelo estocástico o una distribución de probabilidad para la serie de datos histórica de cada factor de riesgo está asociado a la sobrevaloración o subvaloración del riesgo o estimación de las pérdidas potenciales en el momento de realizar el análisis de la utilidad o los flujos de caja. Por ello, es necesario realizar un análisis estadístico metódico que permita capturar las características de la serie de tiempo.
En términos generales, el riesgo no se mide directamente sobre los precios Pt, ya que si obtenemos su histograma de frecuencia, éste por lo general tiene formas irregulares, lo cual dificulta ajustar una función de distribución de probabilidad teórica de los datos financieros. Por ello, es frecuente realizar transformaciones a los precios con el fin de normalizar las variaciones. Esta transformación permite construir un histograma de frecuencias del factor de riesgo que, por lo general, aparece más normalizado que el de la serie original. Las transformaciones más utilizadas para este caso son: calcular los rendimientos logarítmicos o los rendimientos aritméticos de acuerdo a la caracterización de la serie. El rendimiento aritmético o discreto se calcula con la siguiente relación:
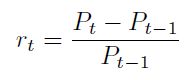 | [15] |
La tasa de rendimiento logarítmica o continua se define en términos de logaritmos del cociente de precios para un horizonte largo de tiempo:
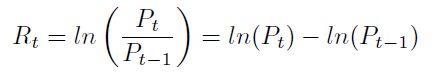 | [16] |
Cuando los cambios de precios 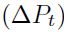 no son muy grandes de un periodo a otro, o la frecuencia de medición del precio es pequeña (diaria, horaria), las diferencias entre ambas rentabilidades no es significativa
no son muy grandes de un periodo a otro, o la frecuencia de medición del precio es pequeña (diaria, horaria), las diferencias entre ambas rentabilidades no es significativa 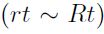 , sin embargo, cuando se presentan cambios bruscos o extremos en los precios o la frecuencia de medición de los precios es grande (mes, año), las diferencias entre ambas rentabilidades es significativa, con lo cual debemos tener cuidado.
, sin embargo, cuando se presentan cambios bruscos o extremos en los precios o la frecuencia de medición de los precios es grande (mes, año), las diferencias entre ambas rentabilidades es significativa, con lo cual debemos tener cuidado.
Desde el punto de vista económico, la rentabilidad logarítmica podría ser más significativa que la rentabilidad aritmética, porque ello asegura que el precio del recurso nunca será negativo, como ocurre normalmente en el mercado. Por el contrario, si se asume normalidad para las rentabilidades aritméticas, se permite que el comportamiento de los precios sea negativo. Por otra parte, cuando se compara la volatilidad y se presenta el caso de que los cambios de precios 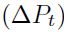 de un periodo a otro son muy grandes, por lo general, la magnitud de la volatilidad
de un periodo a otro son muy grandes, por lo general, la magnitud de la volatilidad 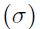 de los rendimientos logarítmicos es menor que la volatilidad estimada con rendimientos aritméticos y esto podría tener efectos importantes a la hora de medir los riesgos.
de los rendimientos logarítmicos es menor que la volatilidad estimada con rendimientos aritméticos y esto podría tener efectos importantes a la hora de medir los riesgos.
Otro elemento a considerar en el uso de rendimientos logarítmicos está asociado a las series de tiempo, en las cuales es posible encontrar rendimientos negativos o con valor cero durante un periodo (por ejemplo el IPC, IPP y tasa de devaluación, para las cuales en algún mes el cambio puede ser negativo). En este caso, podemos sumar uno (1) a cada término de la serie, para luego proceder al cálculo de las rentabilidades y realizar el análisis.
Índice de Precios al Productor (IPP)
El IPP mide las variaciones que muestran los precios de bienes y servicios intermedios, es decir, de aquellos consumidos en el proceso de producción, tales como las materias primas. Como esta serie de tiempo puede tener valores negativos para un mes específico, se le suma a cada dato el valor 1 (tasa IPP + 1), para que no se presente dificultad con el cálculo de la rentabilidad. Se tomó la serie de valores mensuales del IPP, desde 30-09-96 hasta el 31-10-11, y se le calcularon los retornos aritméticos y logarítmicos (Cuadro 3).
Al comparar los resultados de volatilidad, se puede ver que la diferencia entre ambas no es significativa (0,8% al mes). En este caso, para los posteriores análisis se usarán los rendimientos logarítmicos. En el Cuadro 3 se pueden observar, además, las medidas de tendencia central, medidas de variabilidad y medidas de forma.
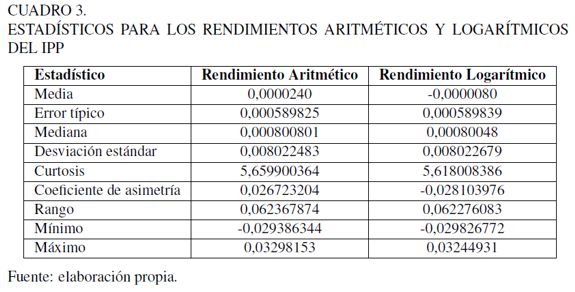
El coeficiente de asimetría y la Curtosis se pueden utilizar para determinar si la muestra se aproxima a una distribución normal. Los valores de Curtosis, alrededor de 3, indican similitud significativa de los datos con la distribución normal. El IPP tiene una Curtosis de 5,66, valor cercano a 3, no obstante se debe verificar su ajuste mediante una prueba estadística. Por otra parte, una distribución simétrica tiene coeficiente de asimetría 0, y para el caso del IPP los datos se distribuyen simétricamente alrededor de la media.
La prueba de bondad de ajuste Chi-Cuadrado tienen P-value igual a 0,43 y 0,39, para las distribuciones Logistic y Normal, respectivamente. Por lo tanto, se puede aceptar que los datos del IPP se ajustan a ambas distribuciones a un nivel de confianza del 95 %. En el Cuadro 4 se muestran los resultados
.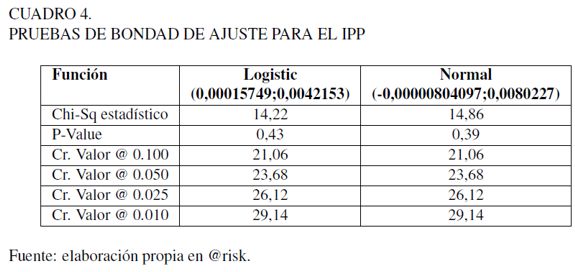
Para efectos de la simulación se utilizará la distribución logística, cuya función acumulativa está dada por:
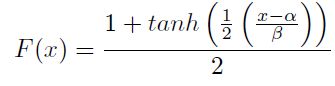 | [17] |
Donde 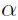 y
y 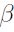 son los parámetros de la distribución. La inversa de la relación [17] es definida como
son los parámetros de la distribución. La inversa de la relación [17] es definida como 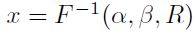 ; siendo R un valor aleatorio distribuido U(0, 1) y permite derivar valores aleatorios de x distribuidos en forma logística.
; siendo R un valor aleatorio distribuido U(0, 1) y permite derivar valores aleatorios de x distribuidos en forma logística.
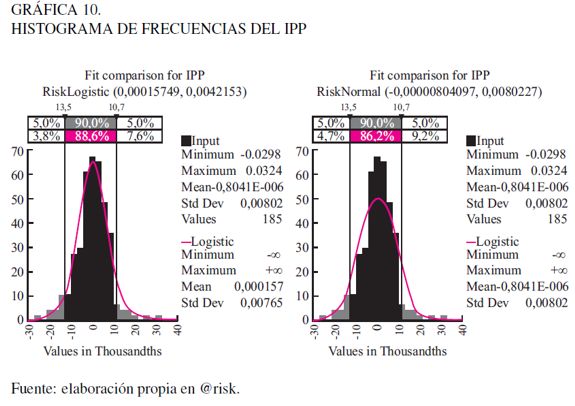
En la Gráfica 10 se muestra el histograma de la frecuencia en perspectiva del ajuste a una distribución normal.
Con los valores derivados de la distribución de probabilidad logística se puede obtener los valores específicos de IPP para un mes usando la relación:
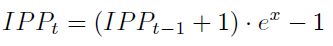 | [18] |
DTF
La DTF es un indicador que recoge el promedio semanal de la tasa de captación de los certificados de depósito a término de 90 días (CDTs 90) de los bancos, corporaciones financieras de ahorro y vivienda y compañías de financiamiento comercial, el cual es calculado por el Banco de la República. A la serie de valores históricos de la DTF desde 01-04-96 hasta el 31-10-11 (valores semanales) se le calcularon los rendimientos aritméticos y logarítmicos, que arrojaron los resultados del Cuadro 5.
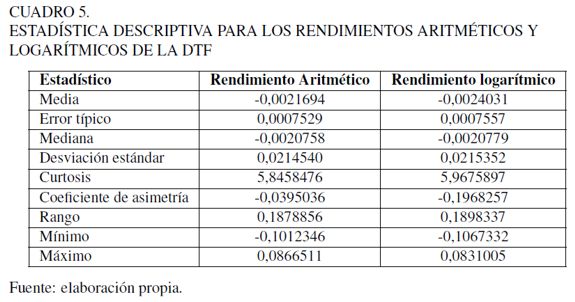
Para efectos de la simulación, se tomaron los rendimientos continuos y se verificó el ajuste de los datos a alguna distribución de probabilidad paramétrica. El Cuadro 5 indica que las medidas de forma se alejan de la distribución normal (curtosis mayor de 3 y asimetría). En el Cuadro 6 se muestran los resultados de la prueba Chi-cuadrado para las distribuciones logística y normal. Si se compara el estadístico de prueba (Chi-Sq Statistic,) 63,64 y 108,53, para la distribución logística y normal, respectivamente, estos valores son mayores que el nivel crítico a diferentes niveles de confianza (Cr. Value @ 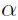 ). Lo anterior indica que hay evidencia estadística de que los datos no se ajustan a ninguna de las distribuciones, además de que el valor P es igual a cero.
). Lo anterior indica que hay evidencia estadística de que los datos no se ajustan a ninguna de las distribuciones, además de que el valor P es igual a cero.
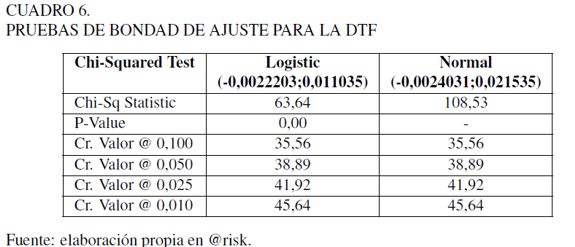
En la Gráfica 11 se muestra el histograma de la frecuencia y el ajuste de las distribuciones.
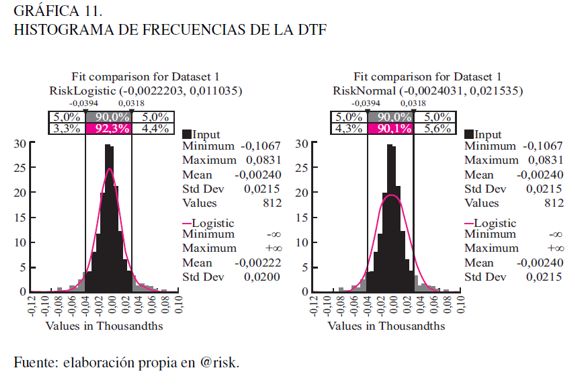
Como se observa en la Gráfica 11, en las colas de la distribución también puede evidenciarse una frecuencia mayor que la que indica la distribución teórica respectiva, lo que tiene un efecto importante en la cuantificación de riesgos. En el caso de la DTF, significa que si aumenta la tasa DTF, los riesgos de pagar mayores flujos de dinero vía intereses por endeudamiento son mayores que los que se pronostican utilizando la distribución teórica.
En este punto del análisis se puede hacer uso de la distribución empírica, es decir, de aquella que surge directamente a partir de los datos de la distribución. Esta es definida por la pareja de puntos E(Xi, Pi), los cuales son determinados directamente del histograma de frecuencias. Otra opción es utilizar una distribución que se ajuste mejor a las colas, por ejemplo la distribución t, que tiene colas más pesadas que la normal. Para este caso, dado que el ejercicio es metodológico, se usará la distribución logística, porque es la que más se ajusta a los datos, aun cuando no pase las pruebas de bondad de ajuste.
LIBOR 6M
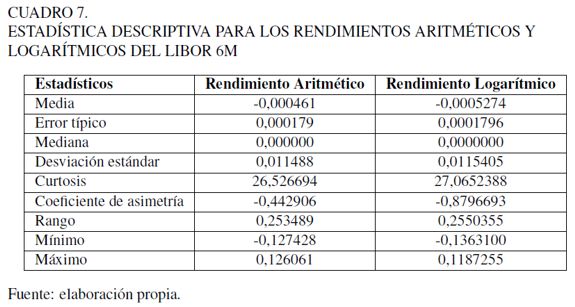
La tasa LIBOR 6M es la tasa de interés anual vigente para los préstamos interbancarios de primera clase en Londres. Se calcularon los rendimientos aritméticos y logarítmicos a la serie de valores históricos diarios de la tasa LIBOR desde 1-04-96 hasta el 31-10-11. En el Cuadro 7 se resumen los principales estadísticos.
Al comparar ambos resultados, rendimiento y volatilidad, la diferencia entre ellos no es significativa. En este caso, podemos utilizar los rendimientos logarítmicos. En el Cuadro 7 se observan, además, medidas de tendencia central, medidas de variabilidad y medidas de forma. El coeficiente de asimetría (swekness) y la Curtosis presentan diferencias significativas con la distribución normal: en el caso de la asimetría se exhibe una cola larga hacia la izquierda de la distribución (-0,879) y la Curtosis muestra gran cantidad de datos centrados en torno a la media (27,065).
En el Cuadro 8 se revelan los resultados obtenidos de la prueba de bondad de ajuste chi-cuadrado para las distribuciones logística y normal. En ambos casos el valor - p que determina la significancia del ajuste es igual a cero, lo que indica que los datos no se ajustan a las distribuciones seleccionadas (para que la prueba sea aceptada debe cumplirse que el estadístico 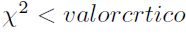 ).
).
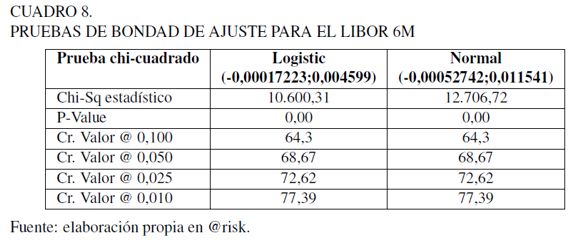
La Gráfica 12 muestra el histograma de frecuencias y el ajuste de las distribuciones. Como se indica, la distribución logística captura mejor el comportamiento de los datos pero estadísticamente no se ajusta dada su alta curtosis.
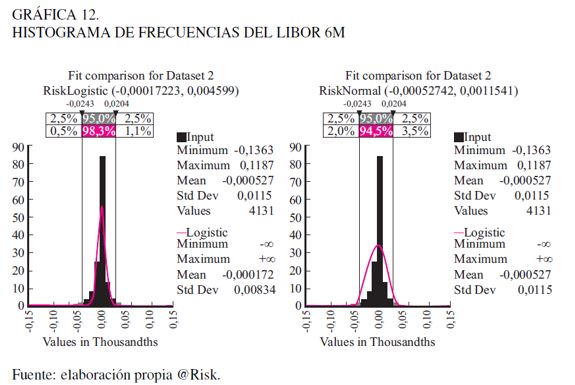
En el caso del modelamiento de la tasa Libor procederemos a utilizar la distribución empírica, que es definida por la pareja de puntos E(Xi, Pi), los cuales son extraídos de la tabla del histograma de frecuencias de la Gráfica 13 y el Cuadro 9.
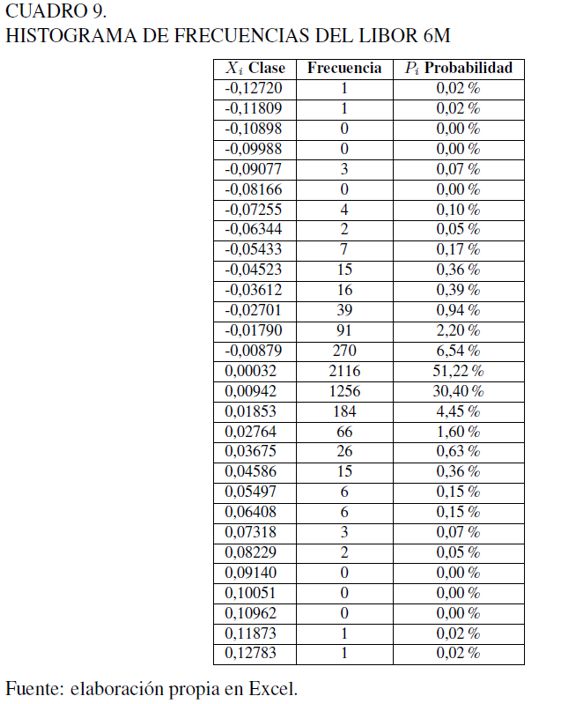
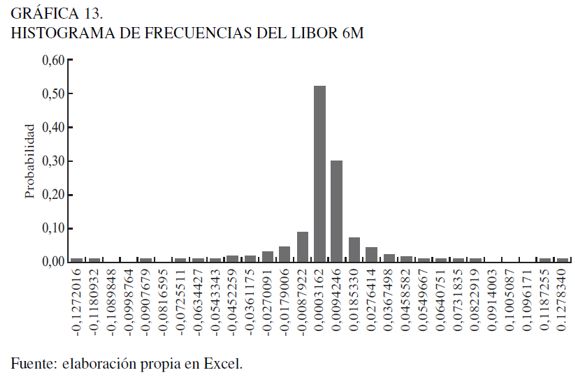
Usando los valores derivados de la distribución de probabilidad empírica en el proceso de simulación, podemos luego obtener los valores específicos de la tasa anual LIBOR con la relación:
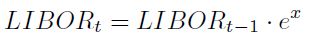 | [19] |
MODELO DE SIMULACIÓN AGREGADO
(Montecarlo estructurado)
Una vez modeladas las series de precios (mediante procesos estocásticos o distribuciones de probabilidad), que para efectos de este trabajo son los factores de riesgo de mercado relacionados con el negocio de la transmisión de energía (TRM, IPC, DTF, IPP y LIBOR 6M), es posible iniciar el análisis del cálculo de las distribuciones de probabilidad de las utilidades y los flujos de caja, identificando los recursos de la empresa que son afectados por su variación. Es necesario, entonces, contar con el modelo financiero de la empresa o los estados financieros pronosticados (estado de resultados, flujo de caja y balance), sobre los cuales se identifican las cuentas que son afectadas por la variación de cada uno de los factores de riesgo, esto es, se debe conocer la posición, activa o pasiva, que la empresa mantiene en préstamos en dólares o en pesos y asociados a qué tipo de tasas; además, cuáles costos de los insumos que utiliza son afectados por el IPC y el IPP.
La Simulación Montecarlo consiste en obtener escenarios de rendimientos o precios de un activo mediante la generación de números aleatorios correlacionados que repliquen las distribuciones de probabilidad o los procesos estocásticos definidos para cada uno de los factores de riesgo. La inclusión de estos valores en los estados financieros permite observar el impacto de su variación en algún aspecto específico de la empresa asociado con la rentabilidad, la liquidez o el endeudamiento.
El proceso de simulación permite construir las distribuciones de probabilidad para todo tipo de indicador financiero, lo que hace posible realizar un análisis bajo riesgo de cualquier aspecto de la empresa, esto es, que sería posible trasladar el análisis financiero tradicional realizado en términos determinísticos a un ambiente de incertidumbre. Por otra parte, es interesante establecer cuáles son las variaciones máximas en algunos indicadores financieros a un determinado nivel de probabilidad si las cosas van mal, tal como se indica en la Gráfica 1. La comunidad académica y empresarial por lo general hace referencia a la utilidad, el flujo de caja y el capital de la empresa como indicadores de riesgo corporativo (VaR Corporativo), sin embargo, este análisis puede ser extendido a cualquier indicador, tal como la rentabilidad del activo, el margen operativo, el valor de la empresa, entre otros.
El proceso de Simulación Montecarlo Estructurado (Jorion 2007), para el análisis de riesgo de la empresa, incluye los siguientes pasos:
- Calcular los rendimientos de cada factor de riesgo e identificar sus distribuciones de probabilidad o los procesos estocásticos con sus parámetros.
- Calcular las correlaciones entre los factores de riesgo.
- Construir el modelo financiero e identificar las cuentas que son afectadas por los diferentes factores de riesgo.
- Aplicar la descomposición de Cholesky de tal manera que
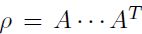 , donde
, donde 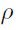 es la matriz de correlacione y A es la matriz cuadrada de Cholesky.
es la matriz de correlacione y A es la matriz cuadrada de Cholesky. - Generar números aleatorios
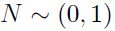 independientes.
independientes. - Generar números aleatorios correlacionados
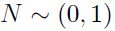 haciendo uso de la matriz A.
haciendo uso de la matriz A. - Alimentar los procesos estocásticos o las distribuciones de probabilidad inversas con los números aleatorios correlacionados.
- Generar series de precios aleatorios.
- Alimentar el modelo financiero con los precios generados aleatoriamente y construir el histograma de frecuencias de los indicadores financieros.
- Realizar un análisis estadístico y un análisis de sensibilidad del indicador financiero.
Reparametrización por Descomposición de Cholesky
La descomposición de Cholesky se usa en la Simulación Montecarlo para representar sistemas con variables que están correlacionadas (Stewart, 1998). Por definición, una matriz simétrica definida positiva (por ejemplo la matriz de correlaciones) puede ser descompuesta como el producto de una matriz triangular inferior (matriz de Cholesky) y la traspuesta de esta matriz:
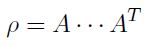 | [20] |
Si se parte de la matriz de correlaciones entre variables es posible obtener la matriz A de Cholesky, la cual puede ser aplicada a una matriz de números aleatorios independientes para generar una matriz de números aleatorios correlacionados. Estos números aleatorios correlacionados replican la correlación histórica existente entre los factores de riesgo y se usan para alimentar los procesos estocásticos o distribuciones de probabilidad para la generación de precios aleatorios. Para nuestro caso la matriz A de Cholesky se muestra en el Cuadro 10.
Si se tiene una matriz de números aleatorios independientes Rindmxn (m es cantidad de números aleatorios independientes y n es el número de factores de riesgo) y la matriz de Cholesky, Anxn, correspondiente a los factores de riesgo considerados, se puede obtener una serie de números aleatorios correlacionados que alimentaran el modelo de simulación realizando la multiplicación matricial:
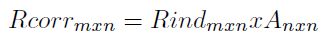 | [21] |
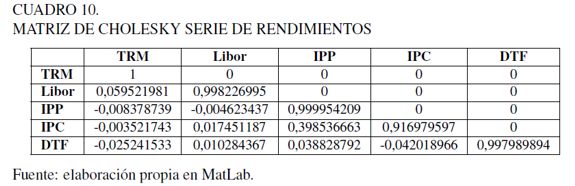
Para nuestro caso la matriz de correlaciones entre endimientos utilizadas se indican en el Cuadro 11.
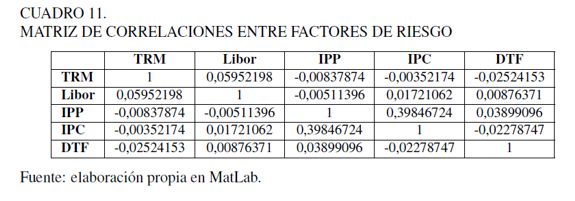
ANÁLISIS DE RESULTADOS
La aplicación de la metodología se realizará tomando como base la empresa colombiana de servicios públicos Interconexión Eléctrica S.A. (ISA), la cual se encuentra enfocada en el desarrollo de proyectos de infraestructura eléctrica en Latinoamérica. Directamente, o a través de sus filiales y subsidiarias, participa en negocios relacionados con el transporte de energía eléctrica, transporte de telecomunicaciones, construcción de proyectos de infraestructura, concesiones viales y administración de mercados energéticos.
Para la cuantificación del riesgo corporativo con un indicador tipo VaR, se requiere realizar un pronóstico de la situación financiera de la empresa mediante la proyección de los estados financieros (estado de resultados, flujo de caja y balances) para el próximo periodo. Para realizar el pronóstico, se recurrirá a la consulta en línea de la información financiera y las notas a los estados financieros publicados para los años 2008, 2009 y 2010. (ISA, 2010), posteriormente se procede a construir un modelo financiero de la empresa para el año 2011.
El análisis parte de identificar los recursos de que dispone la empresa, que están relacionados en las cuentas activas, pasivas y de resultado. Luego, es necesario seleccionar aquellas posiciones con exposición a los factores de riesgo explicados previamente. El modelo financiero incorpora diferentes modelos cuantitativos ajustados a dichos factores de riesgo. En términos muy generales, el modelo financiero concentra la información expuesta en el Cuadro 12, extraída de los informes financieros del año 2010 (ISA 2010).
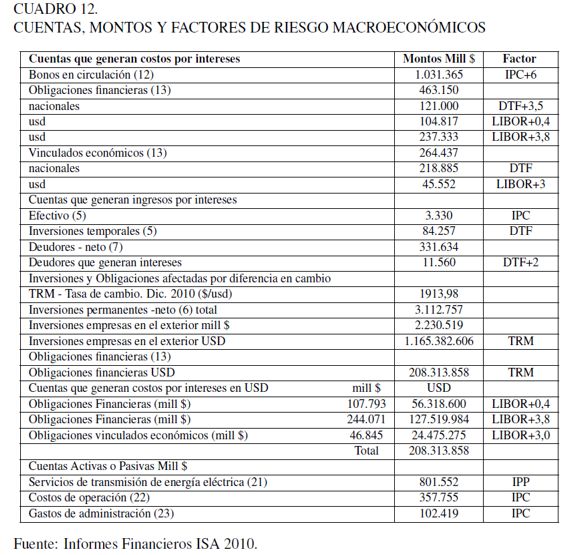
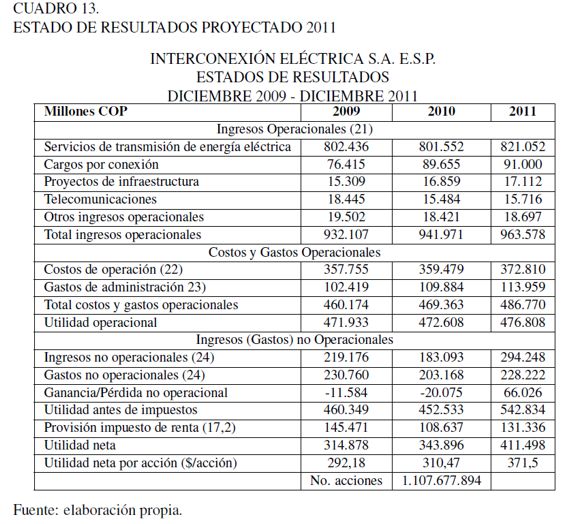
Adicionalmente, el Cuadro 12 indica las diferentes posiciones, activas y pasivas, de la empresa y los factores de riesgo identificados. Los valores entre paréntesis equivalen a las notas a los estados financieros extraídas del informe financiero del grupo ISA para el año 2010. Con la información anterior, más los indicadores financieros, se realiza un pronóstico de la situación financiera para el periodo 2011, incorporando en los modelos el efecto de los factores de riesgo. Una muestra del modelo de estado de resultados y la proyección para el año 2011 se indica en el Cuadro 13.
La simulación de los diferentes factores de riesgo sobre el modelo financiero se convierte en la base para calcular la distribución de probabilidad de la utilidad (Gráfica 14), que a su vez permite obtener la utilidad bajo riesgo.
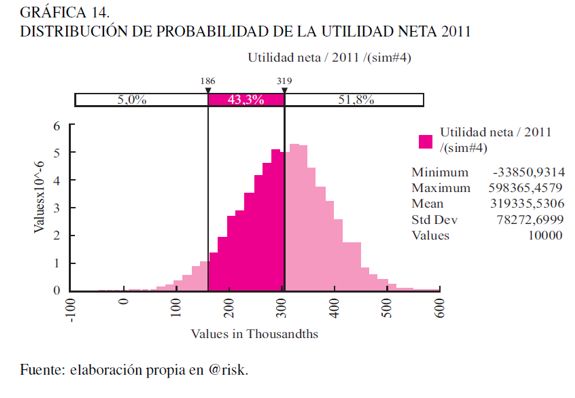
En la Gráfica 14 se visualiza cómo el valor esperado de utilidad para el año 2011 asciende a la suma de 319.335 millones COP3 -y esta puede disminuir hasta 186.000 mil COP, con un 95% de confianza-. La pérdida máxima de utilidad para el grupo ISA a un 95% de confianza es de EaR = 319.335−186.000 = 133.335 millones COP.
Según lo expresado en líneas anteriores es factible, por medio de la simulación, obtener la función de distribución de probabilidad de cualquier indicador financiero. Para la ilustración del presente análisis se utilizara la utilidad proyectada.
Análisis de sensibilidad de la utilidad
Entre los análisis más importantes a la hora de construir modelos de simulación figuran los análisis de sensibilidad (Gráfica 15), que permiten medir el efecto de los factores de riesgo sobre las utilidades, el flujo de caja o el capital. El impacto sobre un aspecto específico se puede dimensionar por medio de indicadores de correlación y regresión, proceso que permite identificar los factores de riesgo críticos que perturban el negocio, facilitando a los estrategas de la empresa diseñar medidas preventivas que pueden involucrar la negociación de pólizas, la cobertura con instrumentos financieros derivados como: las opciones, los forward o los swaps, entre otros, y, paralelamente, disminuir los niveles de exposición a los factores de riesgo más representativos o mejorar su gestión.
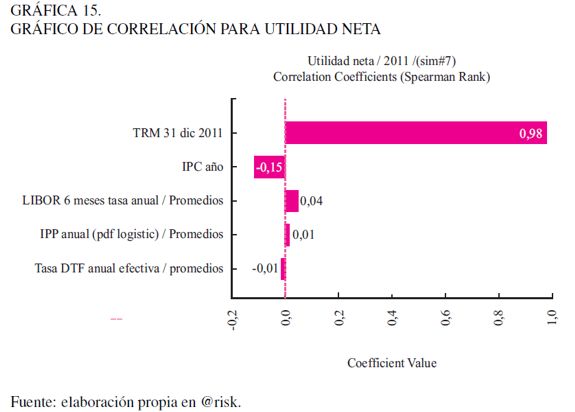
Para el caso particular del grupo ISA, se identifica como principal factor de riesgo sobre las utilidades a la tasa de cambio, fundamentalmente por el alto volumen de las inversiones transnacionales realizadas por el grupo en los últimos años. Como los mayores costos financieros se derivan de la deuda en dólares, una tendencia devaluacionista de la TRM acarrearía un efecto positivo, como producto de la ganancia de valor de las inversiones respecto al peso.
En orden de importancia, aparece como segundo factor de riesgo el IPC, por su relación de causalidad con todos los costos de la empresa. Abordando los demás factores de riesgo del análisis, como por ejemplo la tasa LIBOR, se presenta un efecto positivo sobre la utilidad, entre otros, porque esta tasa permite valorar la deuda en USD, en cuyo caso intervienen dos factores de riesgo: tasa de cambio e interés; el efecto positivo se deriva de la tendencia revaluacionista del dólar.
CONCLUSIONES
Uno de los resultados significativos del presente análisis muestra el importante efecto de la TRM sobre las operaciones realizadas en el exterior, respecto a las utilidades y la valorización de las inversiones. De aquí se desprende la posibilidad de que la empresa de transmisión obtenga ingresos provenientes del exterior o en su defecto de realizar el pago por operación local en moneda extranjera, estrategias que ubican a las empresas en una posición de riesgo por el hecho de maniobrar en entornos económicos dinámicos propios de cada una de los países en los cuales se realice la operación.
Para fines ilustrativos, el análisis se realizó tomando como referencia el dólar americano, para todas las inversiones realizadas del grupo ISA; sin embargo, desde un punto de vista práctico es necesario incluir cada una de las tasas de cambio de los países donde se realicen operaciones, esto es: Ecuador, Perú, Venezuela, Brasil, Chile, Argentina y Panamá, porque esto permitirá ponderar por país la exposición al riesgo por la TRM y definir mecanismos de cobertura para las pérdidas potenciales cuantificadas en cada moneda.
Aun cuando este análisis abarca un aspecto amplio de factores de riesgo asociado a variables macroeconómicas, es menester recordar que las operaciones de la empresa y por tanto la permanencia del negocio están expuestos a factores de riesgo tales como: los riesgos de mercado circunscritos al precio de las acciones (tanto para las inversiones de la empresa como para los accionistas), el precio de las materias primas, las tasas de cambio, las tasas de interés y otros tipos de riesgo no menos importantes y más complejos tales como los riesgos sociales, el conflicto armado, el riesgo legal y tributario, el riesgo regulatorio o jurídico, el riesgo operativo, etc.
La configuración del panorama de exposición de la empresa es identificado mediante un adecuado modelo de gestión de riesgos dentro del cual se encuentran los modelos de cuantificación de las pérdidas potenciales. En este sentido, la metodología propuesta es un complemento de los modelos de gestión de riesgos donde se identifican previamente los factores de riesgo; sin embargo, llegar hasta la cuantificación de las pérdidas potenciales que cada uno de los riesgos mencionados puede generar a la empresa, en muchos casos, no es fácil y asocia retos para la comunidad académica y empresarial, por ejemplo, ¿cómo puede cuantificarse la pérdida potencial asociada a los riesgos jurídicos?
Los análisis planteados resultan claves en el momento de pensar en planes de expansión, consolidación en los mercados, inversiones en confiabilidad del sistema, coberturas, etc., es decir, la metodología planteada puede servir de base para los procesos de toma de decisiones, ya que está asociada a los efectos de los factores de riesgo sobre los indicadores financieros como el flujo de caja, las utilidades o el capital corporativo, y permite obtener los posibles escenarios de pérdida en los mercados regionales.
Es necesario resaltar el hecho de que la metodología presentada aquí toma en cuenta el indicador de utilidad y cuantifica la pérdida máxima esperada EaR dado un determinado nivel de confianza. Sin embargo, es factible medir el efecto de la volatilidad en cualquier indicador financiero de la empresa, tal como: la rentabilidad, el costo del capital, el valor económico agregado, entre otros. Por otro lado, es posible llevar el análisis precedente todavía más lejos, si se considera la empresa como un portafolio de inversión con diferentes posiciones activas y pasivas y nuestro interés está en cómo balancear los montos mantenidos para disminuir la posición en riesgo.
Por último, es de resaltar que la metodología aquí presentada es recursiva y tiene un enfoque práctico; demanda que los profesionales que trabajen en estas áreas cuenten con adecuadas habilidades financieras, estadísticas, matemáticas y de sistemas, pues considera un enfoque cuantitativo de los diferentes factores de riesgo que apoyan el modelo de administración basado en riesgos. Si bien los desarrollos de estas metodologías están enfocados al sector financiero, desde solo hace recientes años el sector real se ha percatado de la importancia de la identificación y cuantificación de riesgos.
NOTAS AL PIE
3 COP: abreviatura para Peso colombiano, según norma ISO 4217.
REFERENCIAS BIBLIOGRÁFICAS
[1] AS/NZS 4360 (1999). Administración de Riesgos. Estándar Australiano.
[2] Engle, R.F. (1982).Autorregresive Conditional Heterocedasticity with Estimates of the Variance of the U.K. Inflation. Econométrica, 50(4), 987-1008.
[3] Basel I. (1988). International convergence of capital measurement and capital standards. Basel Committee on Banking Supervision.
[4] Box, G.E.P. y Cox, D.R. (1964). An analysis of transformations. Journal of the Royal Statistical Society, Series B 26(2), 211-252.
[5] Box, G. E. P. y Pierce, D. A. (1970). Distribution of Residual Autocorrelations in Autoregressive - Integrated Moving Average Time Series Models. Journal of the American Statistical Association, 65, 1509-1526.
[6] CREG (2009). Metodología de remuneración actividad de Transmisión. Bogotá: Comisión de Regulación de Energía y Gas.
[7] Holton, G.A. (2004). Defining risk. Financial Analyst Journal, 6, 19-25. Recuperado de: http://www.riskexpertise.com.
[8] Hull, C. J. (2006). Options, Futures and Other Derivates. New York: Prentice Hall.
[9] Instituto de Normas Técnicas (2004). Norma Técnica Colombiana para la Gestión de riesgos NTC 5254. Bogotá: Instituto de Normas Técnicas (Icontec).
[10] ISA (2010). Informe Financiero ISA S.A. E.S.P. Recuperado de: http://www1.isa.com.co/irj/portal/anonymous?NavigationTarget=navurl://a435be0c1e60a7fb92c4dce716f408b8
[11] ISO 31000 (2008). Draft: Risk management- Principles and guidelines on implementation. International Organization for Standardization.
[12] Jorion, P. (2007). Value At Risk-The New Benchmark For Managing Financial Risk. New York: McGraw-Hill.
[13] JP Morgan. (1996). Risk Metrics TM, Technical Document. Risk Metrics Group. New York: Bank JP Morgan.
[14] JP Morgan. (1999). Corporate Metrics. The benchmark for corporate risk managements. Technical Document. New York: Bank JP Morgan.
[15] Knop, R. Ordovás, R. y Vidal, J. (2004). Medición de riesgos de mercado y de crédito. Barcelona: Ariel Económica.
[16] Ljung G. M. y Box G. E. P. (1978). On a Measure of a Lack of Fit in Time Series Models. Biometrika 65(2), 297-303.
[17] Makridakis, S., Mcgee, V. E. y Wheelwrigt, S. (1998). Forecasting: methods and applications. New York: John Wiley & Sons.
[18] Markowitz, H.M. (1952). Portfolio Selection. The Journal of Finance, 7(1), 77-91.
[19] Medina S. (2010). Modeling of Operative Risk Using Fuzzy Expert Systems. En Michael Glykas (Ed.), Fuzzy Cognitive Maps Advances in Theory, Methodologies, Tools and Applications. Atenas: Ed. Springer.
[20] Sand, K. (2008). Application of Bayesian networks in distribution system risk management. Probabilistic Methods Applied to Power Systems, PMAPS '08. Proceedings of the 10th International Conference on Sintef Energy Research, Trondheim.
[21] Stewart, G. W. (1998). Basic decompositions, Society for Industrial and Applied Mathematics. En Matrix Algorithms (Vol. 1). Philadelphia: PA USA.
[22] Vaughan, E. J. (1997). Risk management. Londres: John Wiley & Sons.
[23] Vilariño, S. A. (2001). Turbulencias Financieras y Riesgos de Mercado. Madrid: Prentice Hall.



