Income distribution in the Colombian economy from an econophysics perspective
Distribución de ingresos en la economía colombiana desde la perspectiva de la econofísica
Distribuição de rendas na economia colombiana desde a perspectiva da econofísica
DOI:
https://doi.org/10.15446/cuad.econ.v35n69.44876Palabras clave:
Econophysics, income distribution, Colombian economy, Boltzmann-Gibbs distribution, Pareto distribution (en)Econofísica, distribución de ingresos, economía colombiana, distribución de Boltzmann-Gibbs, distribución de Pareto (es)
Econofísica, Distribuição da renda, Economia colombiana, Distribuição Boltzmann-Gibbs, Distribuição Pareto (pt)
En el marco de la econofísica se ha demostrado recientemente que es posible analizar sistemas económicos como modelos termodinámicos en equilibrio. En este artículo aplicamos métodos de termodinámica estadística para analizar la distribución de ingresos dentro del sistema económico colombiano. Utilizando datos de encuestas aleatorias, demostramos que la distribución de ingresos presenta dos fases particulares. La primera corresponde a cerca del 90% del grupo analizado y se caracteriza por una distribución exponencial del tipo Boltzmann-Gibbs. La segunda fase, en la que están incluidos los entrevistados con ingresos más altos, se puede describir mediante una o dos distribuciones de potencias: distribuciones de Pareto.
https://doi.org/10.15446/cuad.econ.v35n69.44876
Income distribution in the Colombian economy from an econophysics perspective
Distribución de ingresos en la economía colombiana desde la perspectiva de la econofísica
Distribution des revenus dans l'économie colombienne dans la perspective de l'éconophysique
Distribuição de rendas na economia colombiana desde a perspectiva da econofísica
Hernando Quevedo a
María N. Quevedo b
a Professor and Researcher at the National Autonomous University of Mexico and Adjunct Professor and Researcher at the University of Rome. Email: quevedo@nucleares.unam.mx, Institute of Nuclear Sciences, National Autonomous University of Mexico, Mexico City, Mexico.
b Professor at the Universidad Militar Nueva Granada. Email: maria.quevedo@unimilitar.edu.co; Facultad de Ciencias Básicas y Aplicadas, Departamento de Matemáticas, Universidad Militar Nueva Granada, Bogotá, D. C., Colombia.
We thank the Vicerrectoría de Investigaciones of the Universidad Militar Nueva Granada for financially supporting the project CIAS1168 of 2013. This work was partially supported by DGAPA-UNAM, grant No. 113514 and Conacyt-Mexico, grant No. 166391.
Sugerencia de citación: Quevedo, H., & Quevedo, M. N. (2016). Income distribution in the Colombian economy from an econophysics perspective. Cuadernos de Economía, 35(69), 691-707. doi: 10.15446/cuad.econ.v35n69.44876.
Abstract
Recently, in econophysics, it has been shown that it is possible to analyze economic systems as equilibrium thermodynamic models. We apply statistical thermodynamics methods to analyze income distribution in the Colombian economic system. Using the data obtained in random polls, we show that income distribution in the Colombian economic system is characterized by two specific phases. The first includes about 90% of the interviewed individuals, and is characterized by an exponential Boltzmann-Gibbs distribution. The second phase, which contains the individuals with the highest incomes, can be described by means of one or two power-law density distributions that are known as Pareto distributions.
Keywords: Econophysics, income distribution, Colombian economy, Boltzmann-Gibbs distribution, Pareto distribution.
JEL: A12, C02, C49, D10, D31.
Resumen
En el marco de la econofísica se ha demostrado recientemente que es posible analizar sistemas económicos como modelos termodinámicos en equilibrio. En este artículo aplicamos métodos de termodinámica estadística para analizar la distribución de ingresos dentro del sistema económico colombiano. Utilizando datos de encuestas aleatorias, demostramos que la distribución de ingresos presenta dos fases particulares. La primera corresponde a cerca del 90% del grupo analizado y se caracteriza por una distribución exponencial del tipo Boltzmann-Gibbs. La segunda fase, en la que están incluidos los entrevistados con ingresos más altos, se puede describir mediante una o dos distribuciones de potencias: distribuciones de Pareto.
Palabras clave: econofísica, distribución de ingresos, economía colombiana, distribución de Boltzmann-Gibbs, distribución de Pareto.
JEL: A12, C02, C49, D10, D31.
Résumé
Dans le cadre de l'éconophysique, il a été récemment démontré qu'il était possible d'analyser des systèmes économiques comme des modèles thermodynamiques en équilibre. Dans cet article nous utilisons des méthodes de thermodynamique statistique pour analyser la distribution des revenus dans le système économique colombien. En utilisant des données d'enquêtes aléatoires, nous démontrons que la distribution des revenus présente deux phases particulières. La première correspond à près de 90 % du groupe analysé et se caractérise par une distribution exponentielle de type Boltzmann-Gibbs. La seconde phase, dans laquelle sont inclues les personnes interrogées avec des revenus plus élevés, peut être décrite par une ou deux distributions de puissances : distributions de Pareto.
Mots-clés : Éconophysique, Distribution du revenue, Économie colombienne, Distribution Boltzmann-Gibbs, Distribution Pareto.
JEL : A12, C02, C49, D10, D31.
Resumo
No marco da econofísica, ficou demonstrado recentemente que é possível analisar sistemas econômicos como modelos termodinâmicos em equilíbrio. Neste artigo, aplicamos métodos de termodinâmica estatística para analisar a distribuição de renda dentro do sistema econômico colombiano. Utilizando dados de pesquisas aleatórias, demonstramos que a distribuição de renda apresenta duas fases particulares: A primeira corresponde a cerca de 90% do grupo analisado e se caracteriza por uma distribuição exponencial do tipo Boltzmann-Gibbs; a segunda fase, na qual estão incluídos os entrevistados com renda mais alta, pode ser descrita mediante uma ou duas distribuições de potências: Distribuições de Pareto.
Palavras-chave: Econofísica, Distribuição da renda, Economia colombiana, Distribuição Boltzmann-Gibbs, Distribuição Pareto.
JEL: A12, C02, C49, D10, D31.
Este artículo fue recibido el 11 de noviembre de 2014, ajustado el 23 de junio de 2015 y su publicación aprobada el 1° de julio de 2015.
INTRODUCTION
Thermodynamics is a science based upon empirical facts and observations of different physical configurations, including simple laboratory systems, for example the ideal gas and the van der Waals gas, astrophysical compact objects, like planets, stars, black holes, etc., and even our complete Universe. All these systems can be considered under certain conditions as thermodynamic systems, the behavior and evolution of which must satisfy the well-known laws of classical thermodynamics (Callen, 1985). These laws can be considered as axioms of a mathematical model that can be applied to very different situations. Albert Einstein once expressed the potential of thermodynamics as a science in the following manner (Howard & Stachel, 2000): "Thermodynamics is the only physical theory of universal content, which I am convinced, that within the framework of applicability of its basic concepts will never be overthrown." This is one of the reasons why thermodynamics can be applied in very different and unexpected fields.
In particular, the idea of applying the laws of thermodynamics to economic systems had been discussed for a long time, but only recently was it possible to incorporate them into the context of the so-called econophysics (Stanley, 1996). Several methods of probability theory, which were successfully applied in statistical physics, have been adapted to attack actual problems in economics and finance. In a recent work, we have shown that, starting from an arbitrary function and using the methods of statistical thermodynamics, it is possible to propose models for economic systems within an econophysics framework (Quevedo & Quevedo, 2011). One of the first and most interesting results of econophysics is that certain economic parameters can be considered to be conserved thermodynamic variables, and their distributions among the agents of an economic system are described by means of quite simple probability functions. It was shown that the income distribution in several societies is basically characterized by the presence of two different phases (Bouchaud & Mézard, 2000; Chakraborti & Chakrabarti, 2000; Chatterjee, Yarlagadda & Chakrabarti, 2005; Chakrabarti, Chakraborti & Chatterjee, 2006; Dragulescu & Yakovenko, 2000, 2001, 2003; Silva & Yakovenko, 2005; Yakovenko, 2009). In other words, the population of all the societies analyzed within an econophysics framework can be split into two groups, each one characterized by a particular income probability distribution. The first group includes about 95% of the agents, mostly those with medium and low incomes, and corresponds to a Boltzmann-Gibbs distribution. The second group, which consists of around 5% of the agents with highest incomes, is characterized by a Pareto distribution. This unexpected result has been corroborated in the economies of several countries such as Australia, UK, Germany, India, the USA, etc. In addition, this result is considered as a contribution to the understanding of the economic parameter structures in those countries. The main goal of the present work is to analyze the income distribution of the available data in order to determine the distributions that prevail throughout the Colombian economy.
In most economic systems in which the existence of these two types of distributions has been established, the results are based upon the use of the tax refund data from which it is possible to derive approximate information about the income of a particular number of agents. A more recent study (Newby, Behr & Feizabadi, 2011) analyzes the data related to the personal income distribution obtained from the United States Census Bureau for the years 2006, 2007 and 2008. The results of this study directly show that the income distribution in the United States is characterized by the two groups corresponding to the Boltzmann-Gibbs and Pareto functions, as econophysics had previously predicted.
It should be mentioned that the results obtained in econophysics are based on simple statistical models in which, at the beginning, two agents are chosen randomly to perform an economic transaction (money interchange). The process is repeated and after a finite number of repetitions an equilibrium stated is reached that corresponds to a Boltzmann-Gibbs distribution. A recent study (Cerdá, Montoliu & Colom, 2013) with more complex models that were previously used in statistical physics with gas lattice automata has notably corroborated the results previously obtained using simple models. Additionally, this study allows additional factors to be considered in economic transactions, which means that more general results can be obtained.
Moreover, in statistical physics it is known that the power distribution (Pareto) is related to the intrinsic fractal structure of the physical systems. The results obtained in econophysics about the Pareto distribution raise the question of whether the income distribution in an economic system is also characterized by a fractal structure. This question was affirmatively answered by using a fractal theoretical model and data obtained from realistic economic systems (Eliazar & Cohen, 2014). This result once again shows the close relationship between statistical physics and realistic economic systems.
This work is organized as follows: in Section 2 we present a brief review of the main theoretical concepts which are necessary to carry out the data analysis, in Section 3 we analyze the income data for different periods and find out the probability distributions which prevail in the Colombian economic system, and in Section 4, we discuss our results and propose some tasks for future investigations.
THEORETICAL FRAMEWORK
One of the main assumptions of econophysics is that, under certain conditions and within a specific period of time, an economic system can be considered as being in a state of equilibrium. It has been shown that today economic systems exist that satisfy this condition and can be investigated within the framework of econophysics (Yakovenko, 2009). These systems obey the laws of thermodynamics and, in addition, can be treated within the framework of statistical thermodynamics (Quevedo & Quevedo, 2011), by means of which it is possible to develop specific models to describe the thermodynamic behavior of economic systems.
Although it is true that inside a realistic system there are many factors that play a relevant role, it is clearly impossible to analyze all of them. The fact that we can consider such a system as being in equilibrium allows us to apply the methods of probability theory and statistics in order to calculate average quantities which accurately describe the behavior of the system, under the conditions that follow from the assumption of equilibrium.
In particular, for equilibrium systems it is possible to define conserved quantities such as the total amount of money M that exists during a certain period of time. Of course, this assumption has been extensively discussed in the literature due to the fact that in realistic economic systems the issuing of money occurs quite frequently, leading to the result that the total amount of money is not conserved. Nevertheless, it is clear that in systems governed by free marketing, the general tendency is to maintain M constant in order to keep other phenomena under control like inflation or deflation. In this work, we will consider a system free of crisis that is economically stable, at least during a certain period of time, and therefore we can assure that the condition of M being constant is a reasonable, close-toreality assumption. It should be noticed that the conditions of stability and lack of crisis are essential in econophysics in order for an economic system to be considered as an equilibrium thermodynamic system. Otherwise, it is not possible to use either the Boltzmann-Gibbs distribution function (explained below) as the starting point of statistical thermodynamics, or the resulting laws of classical equilibrium thermodynamics.
Consider a system in which M is a conserved quantity. If the system consists of NT agents, the probability that an agent has a part m of M is determined by means of the probability distribution function P(m), which in the case of thermodynamic equilibrium, gives the Boltzmann-Gibbs distribution
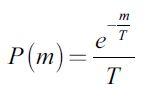 | [1] |
where T represents the average money per agent, T = M/NT (Yakovenko, 2009). A function which is very important for the understanding of the money distribution in a given economic system is the cumulative distribution function
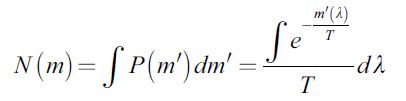 | [2] |
which represents the number of agents with an income greater or equal to m in the above equation. We introduced the function m' as the agent's amount of money which can depend on the additional parameter λ. This was shown in (Quevedo & Quevedo, 2011) where, in addition, the general function m' was analyzed in the case in which it depends on n so-called microeconomic parameters λ1,...,λn. For simplicity, in this work, we limit ourselves to the case of one single microeconomic variable.
The simplest example of a cumulative probability function is obtained for a lineal function m' = λ which yields
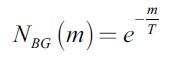 | [3] |
and corresponds to a Boltzmann-Gibbs cumulative function. Another example which is very important in econophysics is obtained from the logarithmic function, m' = c1 ln λ, c1 = const., and corresponds to the Pareto cumulative distribution function
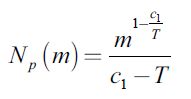 | [4] |
In general, it is possible to obtain a probabilistic model for any function m'(λ) and each of them could, in principle, have some application in econophysics. Nevertheless, the analysis of realistic economic systems has shown that if M is taken as money, income, or wealth, the corresponding cumulative distribution function corresponds basically either to the Boltzmann-Gibbs or to the Pareto cumulative functions. This result is schematically illustrated in Figure 1. The vertical axis represents the cumulative function, and the horizontal axis is its argument. There is a first phase that covers most of the graphic and corresponds to the Boltzmann-Gibbs cumulative function. The second phase is for higher values and is described by a Pareto cumulative function.

This kind of behavior with different phases has been corroborated in the income distributions of several economic systems world-wide. It is considered to be one of the most interesting results obtained in econophysics during this field's short existence. It is, therefore, interesting to ask the question of whether the Colombian economic system shows similar behavior to other countries such as Germany, India, the USA, etc.
DATA ANALYSIS
Unfortunately, in Colombia it is not possible to access statistical data about income per agent as in the case of Germany. Neither it is possible to freely use tax revenue data, as in the case of the USA, from which one can construct reliable data about the number of persons with certain income.
In Colombia, public access data is very limited. Nevertheless, there are studies based on the so-called Gran Encuesta Integrada de Hogares (GEIH) which is a nation-wide probabilistic poll used by the Departamento Administrativo Nacional de Estadística (DANE)1 to deliver specific, coherent and efficient information to national and international organizations. One of the questions that must be answered in the GEIH is the approximate income of each individual in Colombian pesos (COP). Although, at a first sight, this kind of data does not seem to be very reliable, we decided to analyze it as it was the only data available. First, we carried out a filtering of the data, removing those answers that were obviously wrong and could alter the statistics. For instance, some people declare a negative income. Moreover, we did not consider answers stating a total monthly income ranging from zero to ten thousand COP, because this amount would clearly be insufficient to cover the minimum living expenses which in Colombia correspond to about 150,000 COP per month.
To analyze the data we fix the quantity mi (i = 1,2,...,k) and determine the number of individuals ni who declared to have a monthly income of mi COP. In Table 1, we present an example of the data for the second quarter of 2010 (2010-II). For the complete analysis of this quarter we used a total of 843 different values for m. For the sake of comparison we notice that the average exchange rate of the Colombian peso in the period from 2010 to 2012 remained rather stable and was around 1875 COP per 1 USD.

We also analyzed data corresponding to different quarters contained between the years 2010 and 2012. Table 2 shows an example of the data. It is interesting to note that the number of persons n(m) for a fixed m is quite stable during this period, which is an indication that the system can be considered as being in equilibrium.
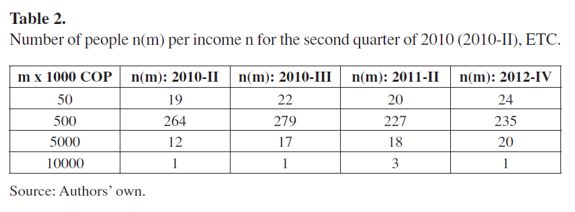
Calculating the total number of individuals in the poll
 | [5] |
one can determine the cumulative function
 | [6] |
which represents the number of agents with an income equal or greater than mi. In all the analyzed cases, the number of subdivisions k was greater than 800 and the total number of individuals NT was always greater that ten thousand.
According to Eq.(2), the analysis of (6) allows us to determine the probability distribution function. To illustrate this procedure we plot N(mi) vs. mi, using a logarithmic scale for the sake of clarity. In Figure 2, we present several examples for different quarters between 2010, 2011 and 2012. On the same graph, we also present the exponential function exp(-m/106) with a normalized argument and a second vertical axis to facilitate comparisons. The analysis of the data corresponding to other quarters leads to similar results. It can be seen that in the graphs (a), (b) and (c), the exponential curves (red lines) seem to have two different regions. In fact, this is not so, and there is only one region with common exponential behavior. The second region on the right-hand side of the plot appears because the number of available points (mi) to be plotted is less that the number of points on the left-hand side of the plot.
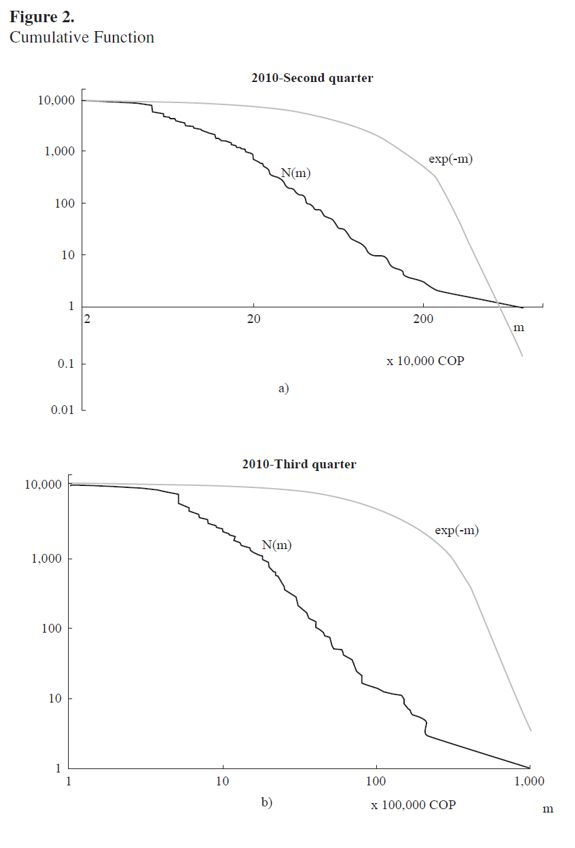

The obvious result of this study is that there are different phases in the behavior of the cumulative function. In the first phase, the exponential distribution coincides quite well with the income distribution. However, as the value of m increases, the difference becomes more noticeable, indicating that the Boltzmann-Gibbs distribution cannot be applied in this region. Instead, a power distribution seems to be more appropriate to reproduce the behavior of the curve. Finally, in the region with higher values of m, the trend changes again, and can still be modelled by a power distribution. To corroborate this behavior, we consider in detail the 2010 second quarter case.
Figure 3 primarily shows in (a) the region that can be approximated by exponential distribution. This approximately corresponds to 90% of the individuals in the poll and includes all income of approximately 1.5 million COP. The second graph in Fig. 3b contains two right lines that reproduce the cumulative probability function in two different regions, together representing about 10% of the individuals with the highest income. In this way, we see that this part of the graph corresponds to two different Pareto distributions. One can calculate the slopes of the right lines and determine the Pareto indices in this way
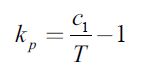 | [7] |

Which, in the case under consideration, corresponds to kp = 2.5 and kp = 0.5, respectively (cf. Fig. 3). Since the parameter T can be calculated as
 | [8] |
it is possible to find the value of the constant c1 that enters the function m' = c1 ln λ and determines the relationship between the Pareto distribution and the microeconomic parameter λ. Moreover, the explicit value of T for different quarters can be used as an approximate criterion to test the equilibrium condition imposed for the present analysis in an econophysics framework. Straightforward computation gives to the results shown in Table 3.

It can be seen that the average income T oscillates around the approximate value 850,000 COP with no drastic modifications, indicating that the equilibrium assumption is a considerably good approximation.
It is worth mentioning that the analysis of data corresponding to other quarters leads to similar results in terms of the behavior of the cumulative probability function. The first Boltzmann-Gibbs phase always represents between 85% and 90% of the individuals, and contains all the income values less than 1,5 million Colombian pesos.
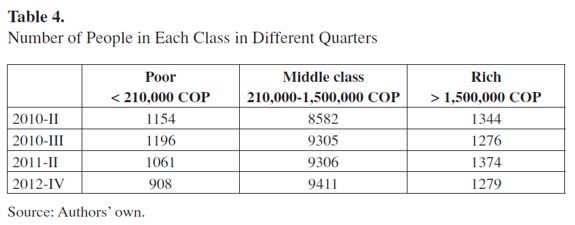
In addition, we can perform complementary analysis that takes into consideration the income distribution in different economic classes. According to DANE the poverty limit in Colombia is about 210,000 COP. In addition, our results show that the Pareto distribution, which characterizes the rich class, begins at an income of around 1.5 million COP. Then, we can split the Colombian income distribution structure into three classes as shown in Table 4. The number of people in each class is indicated for several quarters within the 2010-2012 period. The numbers do not show drastic changes during the two-year period, except perhaps for the number of poor people in the last quarter of 2012, which shows a decrease of around 10%.
CONCLUSIONS
In this work, we applied the results of econophysics relating to income distribution to the Colombian economic system. First, we supposed that the total income M is a conserved quantity, at least during a certain period of time, so that it is possible to consider the economic system determined by the income as an equilibrium thermodynamic system. As a consequence, we can apply the laws of thermodynamics, as developed in econophysics about two decades ago (Stanley, 1996), and also the method of statistical thermodynamics that we suggested in a recent work (Quevedo & Quevedo, 2011).
We used the data obtained in the GEIH by means of which it is possible to determine the number of individuals ni with an income of mi Colombian pesos. With this data it was possible to calculate the cumulative probability function N(m). In econophysics, it has been shown that, in several contemporary economies, the function N(m) possesses two different phases determined by the Boltzmann-Gibbs (exponential) and the Pareto (power) distributions. In the case of the Colombian economic system, we have found similar behavior with some specific peculiarities.
Practically, in all the economic systems analyzed so far, the phase determined by the Boltzmann-Gibbs distribution function corresponds to about 95% of the population. In the Colombian system, however, this boundary is located between 85% and 90%. The remaining part cannot be described by only one Pareto distribution, as in all the other economies, but by two distributions with different Pareto indices. The individuals who declare a monthly income of up to 1,5 million Colombian pesos belong to the Boltzmann-Gibbs phase. All the incomes greater than this value are located within the phase described by the Pareto distributions, the first of which extends to include incomes ranging between 8 and 15 million. In this case, the value of the Pareto index is about 2.5. The second Pareto phase includes the highest incomes, reaching values of one hundred million COP, with a Pareto index situated around 0.5. In some quarters, however, the last phase disappears and the entire region, with approximately 10% of the higher incomes, can be represented by a distribution with a Pareto index of about 2.5.
The most important result of the present analysis is that the income distribution the Colombian economic system is characterized by behavior similar to that found in other economic systems. The peculiarity of the Colombian system is that the Pareto distribution contains between 10% and 15% of the higher incomes, in contrast to other economic systems where this value is 5% or less.
FOOTNOTES
1 El Departamento Administrativo Nacional de Estadística (DANE) is the Colombian government official agency whose purpose is to contribute to national development by producing and disseminating reliable, relevant, timely and high quality statistical information, always intended to support decision-making.
REFERENCES
[1] Bouchaud, J. P., & Mézard M. (2000). Wealth condensation in a simple model of economy. Physica, A 282, 536.
[2] Callen, H. B. (1985). Thermodynamics and an introduction to thermostatics. New York: John Wiley & Sons, Inc.
[3] Cerdá, J., Montoliu, C., & Colom, R. J. (2013). LGEM: A lattice Boltzmann economic model for income distribution and tax regulation. Mathematical and Computer Modelling, 57, 1648.
[4] Chakrabarti, B. K., Chakraborti, A., & Chatterjee, A. (Eds.) (2006). Econophysics and sociophysics. Berlin: Wiley-VCH.
[5] Chakraborti, A., & Chakrabarti, B. K. (2000). Statistical mechanics of money: How saving propensity affects its distribution. The European Physical Journal, J. B 17, 167.
[6] Chatterjee, A., Yarlagadda, S., & Chakrabarti, B. K. (Eds.) (2005). Econophysics of wealth distributions. Milan: Springer Verlag.
[7] Dragulescu, A., & Yakovenko, V. M. (2000). Statistical mechanics of money. The European Physical Journal, J. B 17, 723.
[8] Dragulescu, A., & Yakovenko, V. M. (2001). Exponential and power-law probability distributions of wealth and income in the United Kingdom and the United States. Physica, A 299, 213.
[9] Dragulescu, A., & Yakovenko, V. M. (2003). Statistical mechanics of money, income, and wealth: A short survey. In Modeling of Complex Systems: Seventh Granada Lectures (pp. 661-180), AIP Conference Proceedings.
[10] Eliazar, I., & Cohen, M. H. (2014). Hierarchical socioeconomic fractality: The rich, the poor, and the middle-class. Physica, A 40230.
[11] Howard, D., & Stachel, J. (2000). Einstein: The formative years, 1879-1909. Boston: Birkhauser.
[12] Newby, M., Behr, A., & Feizabadi, M. S. (2011). Investigating the distribution of personal income obtained from recent U. S. data. Economic Modelling, 28, 1170.
[13] Quevedo, H., & Quevedo, M. N., (2011). Statistical thermodynamics of economic systems. J-Therm, 676495.
[14] Silva, A. C., & Yakovenko, V. M. (2005). Temporal evolution of the 'thermal' and 'superthermal' income classes in the USA during 1983-2001. The European Physical Journal, Lett. 69, 304.
[15] Stanley, H. E. (1996). Anomalous fluctuations in the dynamics of complex systems: From DNA and physiology to econophysics. Physica, A 224, 302.
[16] Yakovenko, V. M. (2009). Econophysics, statistical mechanics approach to. In R. A. Meyers (Ed.), Encyclopedia of Complexity and System Science. Springer: New York.
Referencias
Bouchaud, J. P., & Mézard M. (2000). Wealth condensation in a simple model of economy. Physica, A 282, 536.
Callen, H. B. (1985). Thermodynamics and an introduction to thermostatics. New York: John Wiley & Sons, Inc.
Cerdá, J., Montoliu, C., & Colom, R. J. (2013). LGEM: A lattice Boltzmann economic model for income distribution and tax regulation. Mathematical and Computer Modelling, 57, 1648.
Chakrabarti, B. K., Chakraborti, A., & Chatterjee, A. (Eds.) (2006). Econophysics and sociophysics. Berlin: Wiley-VCH.
Chakraborti, A., & Chakrabarti, B. K. (2000). Statistical mechanics of money: How saving propensity affects its distribution. The European Physical Journal, J. B 17, 167.
Chatterjee, A., Yarlagadda, S., & Chakrabarti, B. K. (Eds.) (2005). Econophysics of wealth distributions. Milan: Springer Verlag.
Dragulescu, A., & Yakovenko, V. M. (2000). Statistical mechanics of money. The European Physical Journal, J. B 17, 723.
Dragulescu, A., & Yakovenko, V. M. (2001). Exponential and power-law probability distributions of wealth and income in the United Kingdom and the United States. Physica, A 299, 213.
Dragulescu, A., & Yakovenko, V. M. (2003). Statistical mechanics of money, income, and wealth: A short survey. In Modeling of Complex Systems: Seventh Granada Lectures (pp. 661-180), AIP Conference Proceedings.
Eliazar, I., & Cohen, M. H. (2014). Hierarchical socioeconomic fractality: The rich, the poor, and the middle-class. Physica, A 40230.
Howard, D., & Stachel, J. (2000). Einstein: The formative years, 1879-1909. Boston: Birkhauser.
Newby, M., Behr, A., & Feizabadi, M. S. (2011). Investigating the distribution of personal income obtained from recent U. S. data. Economic Modelling, 28, 1170.
Quevedo, H., & Quevedo, M. N., (2011). Statistical thermodynamics of economic systems. J-Therm, 676495.
Silva, A. C., & Yakovenko, V. M. (2005). Temporal evolution of the 'thermal' and 'superthermal' income classes in the USA during 1983-2001. The European Physical Journal, Lett. 69, 304.
Stanley, H. E. (1996). Anomalous fluctuations in the dynamics of complex systems: From DNA and physiology to econophysics. Physica, A 224, 302.
Yakovenko, V. M. (2009). Econophysics, statistical mechanics approach to. In R. A. Meyers (Ed.), Encyclopedia of Complexity and System Science. Springer: New York.
Cómo citar
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Descargar cita
CrossRef Cited-by
1. Lijie Cui, Chuandong Lin. (2020). Lattice–Gas–Automaton Modeling of Income Distribution. Entropy, 22(7), p.778. https://doi.org/10.3390/e22070778.
2. Alexander Santos Niño, Wilder Arleht Angarita Osorio, José Luis Alvarado Martínez. (2024). Estudio de la dinámica de préstamos y depósitos en un sistema económico cerrado a partir de modelos cinéticos de distribución . Cuadernos de Economía, 43(91), p.327. https://doi.org/10.15446/cuad.econ.v43n91.99851.
3. Wilson A. Rojas, Alexander Zamora. (2025). THERMOSTATISTICAL EVALUATION OF ECONOMIC ACTIVITY. MOMENTO, (71), p.38. https://doi.org/10.15446/mo.n71.121535.
4. Lijie Cui, Chuandong Lin. (2023). Kinetic modeling of economic markets with heterogeneous saving propensities. International Journal of Modern Physics C, 34(08) https://doi.org/10.1142/S0129183123501061.
Dimensions
PlumX
Visitas a la página del resumen del artículo
Descargas
Licencia
Derechos de autor 2016 Cuadernos de EconomíaCuadernos de Economía a través de la División de Bibliotecas de la Universidad Nacional de Colombia promueve y garantiza el acceso abierto de todos sus contenidos. Los artículos publicados por la revista se encuentran disponibles globalmente con acceso abierto y licenciados bajo los términos de Creative Commons Atribución-No_Comercial-Sin_Derivadas 4.0 Internacional (CC BY-NC-ND 4.0), lo que implica lo siguiente:




















