DETECCIÓN Y AISLAMIENTO ROBUSTO DE FALLAS MEDIANTE OBSERVADORES CON ENTRADAS DESCONOCIDAS
Keywords:
Diagnóstico de fallas, Observadores con entradas desconocidas, Estabilidad. (es)Downloads
En el presente artículo se muestra una metodología de diseño de observadores con entradas desconocidas para la solución del problema de Detección de Fallas. La técnica propuesta se basa principalmente en la observación de señales de error conocidas como residuos, las cuales se obtienen mediante la diferencia entre la salida actual del sistema y la salida estimada. Un observador con entradas desconocidas tiene la particularidad de que su vector de error de estimación tiende a cero asintóticamente, sin considerar la presencia de las entradas desconocidas o perturbaciones en el sistema. El algoritmo de detección se aplica satisfactoriamente en un sistema hidráulico de nivel de líquido tanto en simulación como en tiempo real.
DETECCIÓN Y AISLAMIENTO ROBUSTO DE FALLAS MEDIANTE OBSERVADORES CON ENTRADAS DESCONOCIDAS
ROBUST FAULT DETECTION AND ISOLATION USING UNKNOWN INPUTS OBSERVERS
JUAN ANZUREZ MARÍN
Profesor Titular, Facultad de Ingeniería Eléctrica Universidad
Michoacana de San Nicolás de Hidalgo sede Morelia, Michoacán México, janzurez@jupiter.umich.mx
NUN PITALÚA DÍAZ
Profesor Titular, Departamento de Ingeniería Industrial, universidad de Sonora,
México npitalua@gmail.com
Recibido para revisar junio 27 de 2008, aceptado diciembre 12 de 2008, versión final febrero 6 de 2009
RESUMEN: En el presente artículo se muestra una metodología de diseño de observadores con entradas desconocidas para la solución del problema de Detección de Fallas. La técnica propuesta se basa principalmente en la observación de señales de error conocidas como residuos, las cuales se obtienen mediante la diferencia entre la salida actual del sistema y la salida estimada. Un observador con entradas desconocidas tiene la particularidad de que su vector de error de estimación tiende a cero asintóticamente, sin considerar la presencia de las entradas desconocidas o perturbaciones en el sistema. El algoritmo de detección se aplica satisfactoriamente en un sistema hidráulico de nivel de líquido tanto en simulación como en tiempo real.
PALABRAS CLAVE: Diagnóstico de fallas, Observadores con entradas desconocidas, Estabilidad.
ABSTRACT: A technique for design of unknown inputs observers is presented, applied to the solution of fault detection problem. The proposed technique is mainly based on observation of error signals known as residuals, which are obtained by taking away actual input from estimated input. In an unknown inputs observer the state estimation error vector approaches zero asymptotically, regardless the presence of the unknown inputs or perturbations in the system. Diagnosis algorithm was satisfactorily tested in a hydraulic liquid level system in simulation as well as real time.
KEYWORDS: Fault detection, Unknown Input Observers, Stability.
1. INTRODUCCIÓN
El objetivo de la detección y aislamiento de fallas es hacer un sistema más inteligente; permitiendo que éste se desenvuelva cuando ha ocurrido una falla y tenga la posibilidad de recuperarse de ella. El proceso de detección y aislamiento de fallas cuenta con varios niveles. El primer nivel es la detección de la falla, el cual indica simple y sencillamente que ha ocurrido una falla en alguna parte del sistema. El siguiente
nivel es el aislamiento de la falla el cual indica específicamente la localización de la misma en el sistema. El nivel final es la identificación de la falla en el cual se indica la magnitud y naturaleza de ésta [1]. El alcance del presente artículo es la detección y aislamiento de la falla.
La detección de fallas basadas en observadores implica la comparación de la salida actual del sistema con la calculada por un observador. Este enfoque requiere de un modelo del sistema además que los estados que involucran los
sensores
de salida de interés sean detectables [2]. Entonces, la salida del sistema y la
salida del observador se restan para producir una señal conocida como residuo,
de tal manera que, idealmente este residuo siempre deberá ser cero y cualquier
perturbación en esta señal es considerada para detectar la presencia de las
fallas [5]. El propósito de los observadores con entradas desconocidas (UIO) es
producir una salida estimada 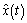 que asintóticamente
alcance el estado actual
que asintóticamente
alcance el estado actual 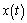 mientras rechaza los
efectos de ruido y errores de modelado en el sistema. Esto se logra permitiendo
que la salida del sistema afecte a la salida del observador, así como a la entrada
[1].
mientras rechaza los
efectos de ruido y errores de modelado en el sistema. Esto se logra permitiendo
que la salida del sistema afecte a la salida del observador, así como a la entrada
[1].
La generación de residuos es por lo tanto la tarea más importante de las técnicas de diagnóstico basadas en el modelo. El desacoplar las perturbaciones es un enfoque dominante para la generación de dichos residuos. Aunque el vector de entradas desconocidas es una matriz de distribución que se supone conocida. Basados en la información de esta matriz las entradas desconocidas (perturbaciones) se pueden desacoplar de los residuos.
Una de las aplicaciones importantes de los observadores con entradas desconocidas es en la detección robusta de fallas [1], [10]. Por ejemplo en [10] Demetriou utiliza un observador con entradas desconocidas para sistemas vector de segundo orden particularmente de sistemas mecánicos como son las suspensiones de automóviles.
En el presente trabajo se plantea el uso de la estructura de un observador con entradas desconocidas de orden completo, propuesto por Chen y Patton en [1], en un sistema hidráulico no lineal de dos tanques interconectados; esto debido a la libertad de diseño que presenta para la generación de los residuos con el objeto de realizar una detección robusta de fallas en sensores.
2. OBSERVADOR CON ENTRADAS DESCONOCIDAS (UIO)
La detección de fallas puede desarrollarse mediante la observación de la señal residual la cual es obtenida mediante la diferencia entre la salida actual del sistema y la salida estimada por el observador, de la siguiente manera:
 (1)
(1)
El diseño de UIO para una clase de sistemas en los cuales las incertidumbres se pueden resumir como un término aditivo de perturbaciones desconocidas en la dinámica del sistema descrito por:
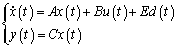 (2)
(2)
donde 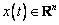 es el vector de
estado,
es el vector de
estado, 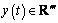 es el vector de
salida,
es el vector de
salida,  es el vector de
entradas conocidas y
es el vector de
entradas conocidas y  es el vector de
entradas desconocidas (perturbaciones).
es el vector de
entradas desconocidas (perturbaciones).  son matrices conocidas,
de dimensión apropiada.
son matrices conocidas,
de dimensión apropiada.
De esta manera, la estructura para un observador con entradas desconocidas de orden completo está descrito por:
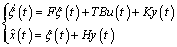 (3)
(3)
donde 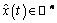 es el vector de estado
estimado y
es el vector de estado
estimado y  es el vector de estado
del observador de orden completo y
es el vector de estado
del observador de orden completo y  son matrices diseñadas
para lograr el desacoplamiento de las entradas desconocidas y otros
requerimientos de diseño. El observador descrito en (3) se ilustra en
la Figura 1.
son matrices diseñadas
para lograr el desacoplamiento de las entradas desconocidas y otros
requerimientos de diseño. El observador descrito en (3) se ilustra en
la Figura 1.

Figura 1. Estructura del observador de orden completo con
entradas desconocidas
Figure 1. Unknown Input Observer Structure
Así, un observador es definido como de entradas desconocidas
(3) (UIO) para el sistema (2), si su vector de error de estimación,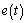 , tiende a cero asintóticamente, sin considerar la presencia
de las entradas desconocidas o perturbaciones en el sistema.
, tiende a cero asintóticamente, sin considerar la presencia
de las entradas desconocidas o perturbaciones en el sistema.
Donde, el error de estado estimado está definido por:
 (4)
(4)
Y está gobernado por la siguiente ecuación:
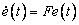 (5)
(5)
De esta manera si F es Hurwitz, 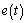 tiende a cero
asintóticamente es decir,
tiende a cero
asintóticamente es decir, 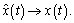 Para lo cual se
cumplen las siguientes relaciones:
Para lo cual se
cumplen las siguientes relaciones:
 (6)
(6)
donde  .
.
Entonces, el diseño del UIO se lleva acabo mediante la solución de (6) y además haciendo que los valores propios de F sean estables. Antes de mencionar las condiciones necesarias y suficientes para la existencia de un UIO es necesario mencionar dos lemas [1].
Lema 1. La ecuación  tiene solución si y sólo si
tiene solución si y sólo si

Y una solución especial es
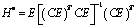 .
.
Lema 2. Sea

Entonces la detectabilidad del par 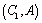 , es equivalente a la del par
, es equivalente a la del par  .
.
Observación 1: La detectabilidad
es una condición más débil que la observabilidad. Un par  es detectable cuando
todos los modos no observables para este par son estables.
es detectable cuando
todos los modos no observables para este par son estables.
Teorema 1 Las condiciones necesarias y suficientes para que el observador (3) sea un UIO para el sistema definido en (2) son:

- el par
 sea detectable, donde
sea detectable, donde
 (7)
(7)
Prueba: Suficiencia De acuerdo con el lema 1, la ecuación  tiene solución cuando la condición (i) se satisface. Una
solución especial, para H es
tiene solución cuando la condición (i) se satisface. Una
solución especial, para H es

En este caso la matriz dinámica del sistema es:
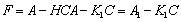
La cual puede ser estabilizada mediante la selección adecuada de la matriz de ganancias K1 debido a la condición (ii). Finalmente, el resto de las matrices del observador (3) pueden ser obtenidas mediante (6). Así, el observador (3) es un UIO para el sistema (2).
Necesidad: Debido a que el
observador (3) es un UIO del sistema (2), la ecuación  tiene solución. Esto
guiado por el hecho de que la condición (i)
se cumple de acuerdo al Lema 1. En general, la matriz H para la ecuación anterior se puede calcular como
tiene solución. Esto
guiado por el hecho de que la condición (i)
se cumple de acuerdo al Lema 1. En general, la matriz H para la ecuación anterior se puede calcular como
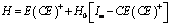
donde,  es una matriz
arbitraria y
es una matriz
arbitraria y  es la matriz inversa
izquierda de
es la matriz inversa
izquierda de  , la cual se obtiene como
, la cual se obtiene como

Sustituyendo la solución para H en (6)  , la matriz dinámica F entonces es:
, la matriz dinámica F entonces es:
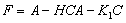


También, usando la ecuación (7) para los primeros dos términos de la derecha podemos reescribir la ecuación anterior como:


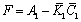
Donde
 .
.
Puesto que la matriz F es estable, el par  es detectable y el
par
es detectable y el
par  también es detectable
de acuerdo al Lema 2.
también es detectable
de acuerdo al Lema 2.
Observación 2: El máximo número de perturbaciones que pueden ser desacopladas no pueden ser mayor que el número de mediciones independientes.
Entonces, uno de los pasos más
importantes para el diseño del UIO es estabilizar  , mediante la selección adecuada de
, mediante la selección adecuada de 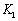 , cuando el par
, cuando el par  es detectable.
es detectable.
El algoritmo de diseño de un UIO se presenta a continuación en la Figura 2.

Figura 2(a). Algoritmo para el diseño de un UIO (primera parte)
Figure
2(a). UIO design algorithm (first part)
La Figura 2(a) muestra el caso
sencillo cuando el par  es observable entonces
directamente se obtienen los valores de las ganancias F y K del observador (3).
La figura 2(b) muestra la parte complicada desde el punto de vista de cálculo;
es decir describe la parte del algoritmo en la que el par
es observable entonces
directamente se obtienen los valores de las ganancias F y K del observador (3).
La figura 2(b) muestra la parte complicada desde el punto de vista de cálculo;
es decir describe la parte del algoritmo en la que el par  es no observable, de
tal forma que se tiene que construir una matriz de transformación que lleve al
sistema a la forma canónica observable entonces verificar si la parte
observable del mismo es estable para poder continuar con el procedimiento de
diseño del UIO en caso contrario detenerlo.
es no observable, de
tal forma que se tiene que construir una matriz de transformación que lleve al
sistema a la forma canónica observable entonces verificar si la parte
observable del mismo es estable para poder continuar con el procedimiento de
diseño del UIO en caso contrario detenerlo.

Figura 2(b). Algoritmo para el diseño de un UIO (segunda parte)
Figure
2(b). UIO design algorithm (second part)
3. AISLAMIENTO DE FALLAS EN SENSORES
La tarea principal de la detección de fallas robusta es la generación de residuos que sean robustos ante la incertidumbre del sistema. Para detectar una falla en particular, el residuo debe ser sensible a dicha falla. Entonces es posible tener en un sistema tanto fallas en sus sensores como en actuadores. En el presente trabajo sólo se aborda el problema de detección de fallas en sensores.
De tal manera que, en el diseño de un esquema de aislamiento de fallas en sensores se supone que todos los actuadores están libres de falla, entonces las ecuaciones del sistema se pueden escribir como:
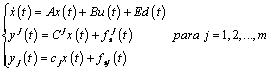 (8)
(8)
donde  es el j-ésimo renglón de la matriz
es el j-ésimo renglón de la matriz 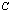 ,
, 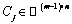 se obtiene a partir de
la matriz
se obtiene a partir de
la matriz 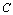 quitando el j-ésimo renglón
quitando el j-ésimo renglón  ,
, 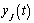 es el j-ésimo componente de
es el j-ésimo componente de  y
y  se obtiene a partir
del vector
se obtiene a partir
del vector  sin considerar el j-ésimo componente
sin considerar el j-ésimo componente 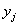 .
.  Representa la falla en
el sensor j.
Representa la falla en
el sensor j.
De acuerdo con esta descripción
es necesario construir un generador de  residuos basados en
UIO de la forma (9):
residuos basados en
UIO de la forma (9):
 (9)
(9)
Para los cuales se deben satisfacer las matrices de parámetros (10).
 (10)
(10)
De la ecuación (9) es fácil de ver que cada residuo esta manejado por todas las entradas y sólo una salida, lo cual se indica en el esquema de la Figura 3. Por lo tanto, cuando todos los actuadores están libres de falla y ésta ocurre en el j-ésimo sensor, el residuo debe satisfacer la condición lógica de aislamiento (11).
 (11)
(11)
donde 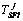 son los umbrales de
aislamiento.
son los umbrales de
aislamiento.

Figura 3. Esquema de aislamiento de fallas en sensores
Figure
3. Sensors fault Isolation scheme
4. RESULTADOS EXPERIMENTALES
La aplicación experimental en el presente trabajo está basada en un sistema dinámico no lineal, conocido como Sistema Hidráulico de Dos Tanques (SHDT) [3], [8]. Este prototipo de laboratorio se muestra en la Figura 4 y está formado por dos tanques de almacenamiento de líquido interconectados, dos sensores ultrasónicos de nivel, dos electro-válvulas industriales para el control del flujo de líquido y una bomba de suministro constante de líquido a la entrada.

Figura 4. Sistema hidráulico de dos tanques
Figure 4. Two tanks hydraulic system
El modelo matemático del sistema está descrito por (12):
 (12)
(12)
donde hi, wi y vi; i=1,2, son los niveles del i-ésimo tanque, el factor de apertura de la i-ésima electro-válvula y el voltaje de entrada a la i-esima electro-válvula respectivamente; At es el área de sección transversal de cada tanque; T, Ke1, Ke2 son las constantes de tiempo y las ganancias estáticas de las válvulas respectivamente; fe es el flujo de entrada constante al tanque 1 además fs1 y fs2 modelan las fallas en los sensores de nivel 1 y 2 respectivamente.
Recientemente la investigación en el área del diagnóstico de fallas se ha enfocado hacia los sistemas no lineales [5], [6], [7]. Tradicionalmente el problema del diagnóstico de fallas para sistemas dinámicos no lineales ha sido tratado en dos pasos; primero, se obtiene el modelo lineal en un punto de operación y posteriormente se aplica alguna técnica específica para generar los residuos, por ejemplo, filtros de Kalman, observadores, espacios de paridad, estimación de parámetros, etc. [1], [8] En este caso de estudio se emplean los observadores de entradas desconocidas.
Por ejemplo, para el sistema de aplicación (SHDT) tomando como punto de operación 25-25 (25cm en tanque 1 y 25 cm en tanque 2), el modelo (2) queda definido mediante las siguientes matrices:

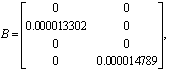
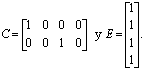
Para
iniciar el procedimiento de diseño, primero se procede a verificar las
condición i) del Teorema 1 (Figura
2a), de lo cual se observa que el  y
y  . A continuación, las matrices T, H y A1 se define como:
. A continuación, las matrices T, H y A1 se define como:
 ,
, y
y
 .
.
La
condición ii) del Teorema 1 (caja de
decisión de la Figura
2(a)) se satisface puesto que el par  es observable, es
decir el rango de la matriz de observabilidad es pleno, por lo tanto el UIO se
puede construir utilizando los siguientes valores de F y K.
es observable, es
decir el rango de la matriz de observabilidad es pleno, por lo tanto el UIO se
puede construir utilizando los siguientes valores de F y K.

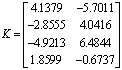 .
.
Sustituyendo estos valores en ecuación (9) se diseñan los observadores con entradas desconocidas para generar los residuos correspondientes con el objetivo de detectar fallas en sensores.
Los resultados obtenidos del diseño del UIO para el sistema SHDT se muestran en la figura 5(a), (b) y (c). El escenario del diagnóstico desde el punto de vista de simulación se plantea bajo dos condiciones: Condiciones normales o libres de fallas y en condiciones de falla, tanto en el sensor 1 como en el sensor 2 del sistema.

Figura
5(a). Residuos para el sistema libre de fallas
Figure
5(a). Residuals for the system faults free

Figura
5(b). Residuos para fallas en el sensor 1
Figure
5(b). Residuals
for fault in the sensor 1

Figura
5(c). Residuos para fallas en el sensor 2.
Figure
5(c). Residuals for faults in the sensor 2.
Como se mencionó en la sección 2.2 se debe diseñar un UIO por cada una de las salidas del sistema bajo el esquema de diagnóstico de fallas en sensores (Figura 3). Analizando cada uno de los renglones de la matriz de salida una combinación el sistema no es observable por esta razón sólo de diseñan tres UIOs.
La Figura 5(a) muestra los residuos del sistema cuando éste se encuentra libre de fallas, se observa que los mismos se mantienen en cero para todos los UIO, después del tiempo de estabilización. En la Figura 5(b) se muestra que para una falla en el sensor 1 se activan los residuos de los UIO 2 y 4 es decir, se viola la condición dada en (11). Asimismo, para una falla en el sensor 2 del sistema se activan los residuos de los tres UIOs. Un aspecto importante de esta aplicación es el diagnóstico de fallas en tiempo real, para realizar esta prueba se provocó una falla en el sensor 1 del SHDT y el resultado se muestra en la Figura 6, obsérvese la semejanza con la respuesta (residuos) obtenida en simulación para el mismo caso, Figura 5(b), en la cual aparecen activos los residuos de los UIO 2 y 4.

Figura 6. Residuos cuando falla el sensor 1 del sistema
hidráulico de dos tanques en tiempo real
Figure 6. Residuals in real time to fault in the sensor
1 of two tank hydraulic system.
5. CONCLUSIONES
En el presente trabajo se muestra el diseño de observadores con entradas desconocidas (UIO) aplicados al problema del diagnóstico de fallas. Se emplea como ejemplo de aplicación un sistema hidráulico de dos tanques, el algoritmo de diagnóstico se probó tanto en simulación como en tiempo real. De acuerdo a los resultados satisfactorios obtenidos, es posible suponer que el diseño de UIOs es una buena herramienta de solución al problema de diagnóstico para sistemas de los cuales se conoce su modelo matemático, razón por la cual está técnica se clasifica dentro de las conocidas como basadas en el modelo. Una de las desventajas de las técnicas basadas en el modelo, es precisamente las incertidumbres que se presentan en los mismos; para lo cual se pueden aplicar otras técnicas, por ejemplo redes neuronales; sin embargo, para sistemas cuya dinámica es lenta esta técnica como se muestra en los resultados presenta excelentes resultados.
REFERENCIAS
[1] CHEN J. AND PATTON R., Robust Model-Based Fault Diagnosis for Dynamic Systems, Kluwer Academia Publishers, Boston, 1999.
[2] RIDENOUR J. AND ZAK S., Observer Based Fault Detection and Isolation, Technical Report Advancing Technology Through Collaboration, 2004.
[3] BEGOVICH O., SÁNCHEZ E. AND MALDONADO M., Real-Time nonlinear system regulation via TS fuzzy control, 18th International Conference of North American Fuzzy Information Processing Society, USA, Cat. 99TH8397, ISBN 0-78035211-4, pp. 645-649, 1999.
[4] YONG YANG CAO AND PAUL M. FRANK, Stability analysis and synthesis of nonlinear time-delay systems via linear Takagi-Sugeno fuzzy models, Automatica, Fuzzy Set and Systems, Vol. 124, 2001, pp. 213-229.
[5] CASTILLO B. AND ANZUREZ J., Model-Based fault diagnosis using sliding mode observers to Takagi-Sugeno fuzzy model, Proceeedings of the 2005 IEEE International Symposium on Intelligent Control, Cyprus , 2005, pp. 652-657.
[6] ANZUREZ J. AND CASTILLO B., An application of sliding mode observer to fault diagnosis, XXVI International Congress of electronic engineering ELECTRO 2004, México, pp. 103-108, 2004.
[7] ANZUREZ J. AND CASTILLO B., An application of sliding mode observer to fault diagnosis, XXVI International Congress of electronic engineering ELECTRO 2004, México, pp. 103-108, 2004.
[8] ANZUREZ J. AND CASTILLO B., The fault diagnosis problem: Sliding mode fuzzy dedicated observers approach, 2006 IEEE International Conference on Fuzzy Systems, Vancouver, B.C. Canada , 2006, pp. 6672-6678.
[9] PATTON R. AND PAUL M. FRANK AND RON N. CLARK, Issues of Fault Diagnosis for Dynamic systems, Springer, 2000.
[10] MICHAEL A. DEMETRIOU, UIO for fault detection in vector second order systems, Proceedings of the American Control Conference, Arlington, USA , 2001, pp. 1121-1126.
How to Cite
IEEE
ACM
ACS
APA
ABNT
Chicago
Harvard
MLA
Turabian
Vancouver
Download Citation
Article abstract page views
Downloads
License
Copyright (c) 2009 DYNA

This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.
The author of a paper accepted for publication in any of the journals published by the School of Mines will yield all the property to the National University of Colombia rights free of charge, within which include article: the right to edit, publish, reproduce and distribute both print and digital media, as well as including in an article in international indexes and / or databases, likewise, it enables the publisher to use images, tables and/or graphic material presented in Article for designing covers or posters of the magazine. By assuming the economic rights of the article, it may be reproduced partially or totally in any printed or digital media without express permission of the same.
















