FINDING FUZZY IDENTIFICATION SYSTEM PARAMETERS USING A NEW DYNAMIC MIGRATION PERIOD-BASED DISTRIBUTED GENETIC ALGORITHM
Keywords:
on-line identification, Takagi-Sugeno-Kang fuzzy model, distributed genetic algorithm, cluster. (es)Downloads
FINDING FUZZY IDENTIFICATION SYSTEM PARAMETERS USING A NEW DYNAMIC MIGRATION PERIOD-BASED DISTRIBUTED GENETIC ALGORITHM
DETERMINANDO LOS PARÁMETROS DE UN SISTEMA DE IDENTIFICACIÓN DIFUSA USANDO UN NUEVO ALGORITMO GENÉTICO DISTRIBUIDO BASADO EN PERIODO MIGRATORIO DINÁMICO
MARCO ANTONIO CASTRO
Departamento
de Sistemas y Computación, Instituto Tecnológico de La Paz, Cuba, mcastroliera@acm.org
FRANCISCO HERRERA
Departamento
de Automática y Sistemas Computacionales, Universidad Central Martha Abreu de
Las Villas, Cuba herrera@uclv.edu.cu
Recibido para revisar agosto 27 de 2008, aceptado enero 23 de 2009, versión final febrero 20 de 2009
ABSTRACT: This paper presents a distributed genetic algorithm with dynamic determination of the migration period. The algorithm is especially well suited for the on line estimation of a fuzzy identification system parameters, using heterogeneous clusters. The results of the optimization of a TSK (Takagi-Sugeno-Kang) system for the identification of a biotechnological (fermentative) process including the solutions quality and speedup analysis are presented. Comparative results using static and dynamic migration periods on the genetic algorithm are also presented.
KEYWORDS: on-line identification, Takagi-Sugeno-Kang fuzzy model, distributed genetic algorithm, cluster.
RESUMEN: El presente trabajo, propone un tipo de algoritmo genético distribuido con determinación dinámica del período migratorio el cual se adapta especialmente para la determinación en línea de los parámetros de un sistema de identificación difusa y su implementación en clusters heterogéneos. Se presentan los resultados de la optimización de un sistema Takagi-Sugeno-Kang (TSK) para la identificación de un proceso biotecnológico (fermentativo). Se incluyen el análisis de la calidad de la solución, la aceleración que se obtiene al agregar nodos al cluster y la comparación del desempeño del algoritmo usando un periodo migratorio estático y dinámico.
PALABRAS CLAVE: identificación en línea, modelo borroso Takagi-Sugeno-Kang, algoritmo genético distribuido, clusters.
1. INTRODUCTION
The present work addresses two main aspects: the collaborative use of a specially adapted Distributed Genetic Algorithm [1] that runs on a low-cost parallel architecture known as a cluster; and a TSK fuzzy system [2] to solve a highly non-linear identification problem.
When combining fuzzy systems and genetic algorithms a synergy is created in which, as expressed by Zadeh [3], the main contribution of fuzzy logic is what may be called the calculus of fuzzy if-then rules, while genetic algorithms provide a methodology of systematized random search inspired by evolutionary processes in living species and proposed originally by John H. Holland [4].
One of our main motivations is the use of a low-cost parallel architecture that will allow us to address problems that demand a high computational cost without the need of acquiring parallel computers (shared memory) [5] that are too expensive for most educative and other scientific institutions at present.
Distributed genetic algorithms, also known as coarse-grained genetic algorithms and island model parallel genetic algorithms, are currently studied as one of the more scalable forms of parallel genetic algorithms [1,6,7].
These types of algorithms have been addressed having in mind the special limitations of the computer clusters when compared with parallel computers, particularly, the low inter-processor bandwidth.
Currently one of the most popular ways for parameter estimation in fuzzy systems is by means of artificial neural networks (ANN), however, by exploring alternatives for their implementation on computer clusters (distributed memory) [8,9] we find that due to the nature of the training process of the ANN when computing the new weights for a neuron, the precedent layers must be known. It turns to be complicated to limit the amount of data to be transferred between processors, which is the main bottleneck.
2. THE FUZZY MODELS STRUCTURE
Lets assume a TSK model with two input variables, x and s with three partitions each, gbell membership functions and lineal output functions.
The rule base for such a model has the following structure:
![]()
![]() (1)
(1)
With j varying from 1 up to the number of fuzzy sets that divide xt (three on our case) k varying form 1 up to the number of fuzzy sets that divide st (three on our case) and i varying from 1 to the number of fuzzy rules n on the rule base (nine on our case).
The gbell functions are of the form:
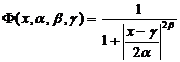
(2)
The predicted model´s output is given by:

(3)
Where the degree in which each rule is fulfilled is calculated using the T operator, (usually the product).
![]() (4)
(4)
3. TWO PHASE STRATEGY
The optimization process was divided into two stages; the first stage aims to find a set of coefficients (ai0, ai1, ai2) for the consequent part of the fuzzy rules set that minimize the total error calculated as:
![]()
(5)
Where n is the total training samples number, xc is the model´s calculated output, and xm the system´s measured output.
To conduct the first part of the optimization, fixed parameters were chosen for the generalized bell membership functions to create fuzzy sets that evenly divide the input variable space, for the assumed model case:

(6)
The second stage of the optimization process aims to find a set of membership-function parameters that minimize the maximum error given by:
![]()
(7)
The above mentioned parameters are used to find the output functions coefficients that minimize the resulting models total error given by (5).
For the second part of the optimization problem the best set of coefficients is fixed to try to find a set of parameters for the membership functions that minimizes the maximum prediction error given by (7).
4. HETEROGENEOUS CLUSTERS
We define a heterogeneous cluster as one in which the involved nodes have different architectures and processing speeds.
If the applied algorithm assumes a homogeneous cluster (one in which all the nodes have approximately the same computational power), and assigns the same amount of work load to each task, when the algorithm is executed on a heterogeneous cluster, the nodes with a higher computational power will have to wait until those that are slower have finished their processing before being able to perform migration, resulting on undesirable dead times on the faster nodes.
The chosen alternative to minimize this disadvantage is to dynamically determine the migration period for each sub-population in dependence of its execution time.
Figures 1 and 2 show the master and slave task portions of the new proposed algorithm.
With this new approach those sub-populations with an execution time below the average perform more iterations of the GA before the next migration, while those with a higher than average execution time perform fewer iterations.
This strategy progressively evens the execution times of all the sub-populations, so the waiting times decrease.
5. THE FERMENTATIVE PROCESS
To carry out a fermentative process a quantity of microorganisms (biomass) are suspended in a food rich medium (substratum).
This kind of process presents a highly non-lineal behavior that responds to a dynamic system following the general structure [10]:
![]()
(8)
where![]() is the vector formed by the two state variables [x,s], u is the input variable (Sin),
and b is the constant dilution rate D.
is the vector formed by the two state variables [x,s], u is the input variable (Sin),
and b is the constant dilution rate D.
We deal with a model with three input variables xt, st, and sin that represent the biomass, substrate, and input substrate concentration at instant t respectively. The model must determine the amount of biomass on the next instant (t+1).
For those processes like the studied case, where sin remains constant, the terms ai0 and ai3sin can be consolidated, giving us a simplified form of the rule base as given by (1).
Input variables x and s were divided into three fuzzy sets giving us a total of nine different fuzzy rules on the base. This mean we have to find a total of 18 parameters for the antecedent part of the rules and 27 coefficients for the consequent part.
The chromosome uses real representation on a 3 by 9 matrix that corresponds to the 3 output coefficients that each of the 9 lineal output functions requires.
490 samples were processed in total, taken from 10 different fermentative processes with different initial conditions.
6. GENETIC ALGORITHM PARAMETERS
Note that by varying the ![]() parameters we vary the
shape and position of the membership functions for the fuzzy sets that divide
the input variables thus we obtain different initial membership functions
within the ranges described by (9).
parameters we vary the
shape and position of the membership functions for the fuzzy sets that divide
the input variables thus we obtain different initial membership functions
within the ranges described by (9).
The chosen parameters for the first phase were:
Search ranges:
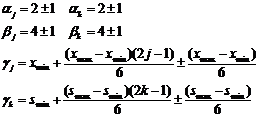 (9)
(9)
Population Size MU=600.
Maximum generations GMAX=160.
Tournament selection with tournament size Z=2.
Crossing probability PC=0.7
Uniform crossing parameter ![]() generated on (0,1).
generated on (0,1).
Uniform mutation, with mutation probability PM=0.2.
Search ranges: [-7,7] for ai0, [-4,4] for ai1 and [-2,2] for ai2.
Migration period MP=20.
Maximum migration period MPMAX=30.
Migration rate MR=2.
The chosen parameters for the second phase were:
Population Size IMU=300.
Maximum generations IGMAX=60.
Tournament selection with tournament size IZ=2.
Crossing probability IPC=0.7
Uniform crossing parameter ![]() generated on (0,1).
generated on (0,1).
Uniform mutation, with mutation probability IPM=0.2.
Migration period IMP=20.
Maximum migration period IMPMAX=30.
Migration rate IMR=2.
7. RESULTS
Several test where conducted to measure the quality of the obtained models, as well as the execution time behavior under different conditions.
The sample size for each set of conditions was 200 runs of the algorithm and where conducted on a heterogeneous parallel virtual machine with a fast-Ethernet switch and two types of nodes:
Type a) Pentium IV@2.8 GHz with 1024 KB cache and 512 MB DDR2 RAM@400 MHz
Type b) Pentium IV@2.0 GHz with 512 KB cache and 512 MB DDR2 RAM@266 MHz
7.1 Quality of the solutionTable 1 shows the error behavior with various sub-population numbers, where:
- SP is the number of sub-populations.
- ATE the average total error.
- AE the average per-sample error.
- AME the average maximum error.
The average execution time with the fore-mentioned parameters and a heterogeneous 18 nodes cluster was 220 seconds (using a node for each sub-population).
Figure 3 plots the prediction error of a typical model generated with 4 sub-populations, figure 4 shows a comparison of the predicted and measured outputs and figure 5 plots the prediction error of a typical model generated with 18 sub-populations.
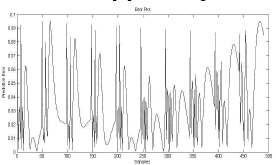
Figure 3. Prediction error, 4 sub-populations

Figure 4. Prediction error 18 sub-populations

Figure 5. Prediction quality, 18 sub-populations
To achieve lower run-times, while maintaining reasonably good solutions the following parameters were modified:
- Population Size MU=400.
- Maximum generations GMAX=120.
- Migration period MP=15.
- Maximum migration period MPMAX=20.
- Population Size IMU=200.
- Maximum generations IGMAX=30.
- Migration period IMP=15.
- Maximum migration period IMPMAX=20.
Over 1000 tests with 18 sub-populations, an estimated average total error of 14.81098 that represents an average per-sample error of 0.03023 was obtained; the estimated average maximum error was 0.08609.
Expression 10 is used to estimate the size of a sample when determining means over infinite populations.
![]()
(10)
Where n is the size of the sample, S2 is the estimated variance of the population and d is half the amplitude of the confidence interval. Using a Za value of 2.576, that corresponds to a 99% certainty level we can determine d using expression (11).
![]()
(11)
The execution times obtained using a cluster of 9 type (a) nodes are shown on table 3.
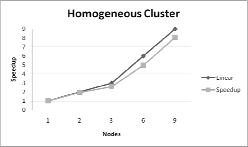
Figure 6 shows the comparative speedup against lineal acceleration under the above mentioned conditions.
The following times were obtained using the non-adaptive version of the algorithm on a heterogeneous cluster:
Table 4. Heterogeneous cluster non-adaptive version

The obtained execution times show that type a) nodes are much faster than type b) ones but the algorithm shows a quasi-lineal speedup behavior, because it considers every node as equal to the rest, therefore it is unable to take advantage of the faster nodes added on the later stages to the cluster (in fact we can observe comparing tables 3 and 4, that 9 nodes of type b ran faster than 18 mixed nodes). On the other hand, the adaptive version of the algorithm produced the following execution times:
Table 5. Heterogeneous cluster adaptive version
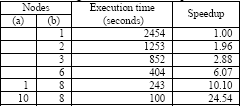
It is clear that, when adding faster nodes to an existing cluster, this version of the algorithm is able to exploit their higher computational power unlike the non adaptive version.
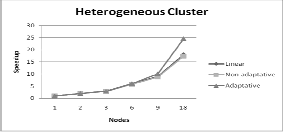
Figure 7 shows the comparative speedup of both algorithms against a lineal acceleration.
8. CONCLUSIONS
The proposed algorithm is able to generate adequate solutions for the identification problem.
The presented results show that the quality of the solution improves as the number of sub-populations increase; it is also evident that low execution times can be maintained while increasing the amount of sub-populations by adding nodes to the cluster.
The speedup tests for up to 18 nodes clusters show that, at least for this amount of processors, the algorithm can be scaled without considerable loss of performance.
It can be observed that when we add faster nodes to a cluster, hyper-lineal accelerations are obtained with the adaptive version of the algorithm whereas the non-adaptive version achieves only quasi-lineal speedups since it cannot take advantage of the faster nodes added to the cluster.
The algorithm can be easily adapted for the parametric optimization of different TSK Fuzzy models; the scope of application is vast but limited by the amount of data that needs to be exchanged between sub-populations for models with a very large number of parameters and large number of sub-populations.
However, these limitations can be reduced with the advent of new networking technologies such as gigabit- Ethernet.
The real limit for the number of sub-populations that the algorithm can exploit on fast-Ethernet networks for this specific problem remains to be empirically found, since for the moment on test runs with 18 nodes and up to 36 sub-populations that limit was not reached.
Source code of the application written in C for GNU/Linux and PVM 3.4 is available at [11].
REFERENCES
[1] NOWOSTAWSKI, M. Y P. RICARDO, Parallel Genetic Algorithm Taxonomy. Third International Conference of Knowledge-Based Intelligent Information Engineering Systems, 1999.
[2] CORDÓN, O., ET AL., Genetic fuzzy systems : evolutionary tuning and learning of fuzzy knowledge bases 2001, Singapore : World Scientific. xxv, 462.
[3] ZADEH, L.A., Foreword, en Genetic fuzzy systems: evolutionary tuning and learning of fuzzy knowledge bases, O. Cordon, et al., Editors. 2001.
[4] HOLLAND, J.H., Adaptation in Natural and Artificial Systems (1975) 6 ed. 2001, Michigan: MIT Press. 205.
[5] MATTSON, TIMOTHY G. ET AL., Patterns for Parallel Programming 2008, Addison Wesley. 355.
[6] ALBA, E. y J.M. TOYA, Analyzing Synchronous and Asyncrhonous Parallel Distributed Genetic Algorithms Future Generation Computer Systems, 2001. 17(4): p. 451-465.
[7] ALBA, E. AND M. TOMASSINI, Parallelism and Evolutionary Algorithms. IEEE Transactions on Evolutionary Computation, 2002. 6(5): p. 443-462.
[8] CRISTEA T. AND OKAMOTO T. "Parallelization methods for Neural Networks on different environments: Advantages and Disadvantages", Australian Journal for Intelligent Information Processing Systems, Elsevier IS/2, Special Issue on Information Systems, Authors, 1999.
[9] SUNDARARAJAN N. AND SARATCHANDRAN P. Parallel Architectures for Artificial Neural Networks: Paradigms and Implementations, 1998, Wiley-IEEE Computer Society Press, pp409.
[10] HERRERA FERNÁNDEZ, F., ET AL. Aplicación de las Técnicas de la Inteligencia Artificial en un Proceso Biotecnológico de Reproducción Celular (Embriogénesis Somática). 2003, Universidad Central "Marta Abreu" de Las Villas: Santa Clara, Libre. p. 38.
[11] CASTRO LIERA, MARCO A. http://sistemas.itlp.edu.mx/castroga/biomasa-full.tgz. biomass model generator source code 2006, Instituto Tecnológico de La Paz.
How to Cite
IEEE
ACM
ACS
APA
ABNT
Chicago
Harvard
MLA
Turabian
Vancouver
Download Citation
Article abstract page views
Downloads
License
Copyright (c) 2009 DYNA

This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.
The author of a paper accepted for publication in any of the journals published by the School of Mines will yield all the property to the National University of Colombia rights free of charge, within which include article: the right to edit, publish, reproduce and distribute both print and digital media, as well as including in an article in international indexes and / or databases, likewise, it enables the publisher to use images, tables and/or graphic material presented in Article for designing covers or posters of the magazine. By assuming the economic rights of the article, it may be reproduced partially or totally in any printed or digital media without express permission of the same.