OBSERVABILIDAD DE LA VELOCIDAD EN MOTORES DE INDUCCIÓN DE ALTO DESEMPEÑO DINÁMICO
Keywords:
Observabilidad No lineal, Control sin medida de velocidad, Motor de Inducción. (es)Downloads
En este artículo se muestran los resultados más importantes desarrollados en el análisis de la pérdida de la observabilidad de la velocidad para aplicaciones de Control de Motores de Inducción sin sensor de velocidad y trabajando en regímenes de velocidad cercanos a cero e incluyendo cero velocidad. Se describen el problema de control sin sensor de velocidad y las herramientas utilizadas para el análisis de la observabilidad; finalmente, se hace una revisión de los reportes de análisis de la Observabilidad del motor de inducción.
OBSERVABILIDAD DE LA VELOCIDAD EN MOTORES DE INDUCCIÓN DE ALTO DESEMPEÑO DINÁMICO
OBSERVABILITY OF THE SPEED IN INDUCTION MOTORS OF HIGH DYNAMIC PERFORMANCE
EDINSON FRANCO MEJIA
Ingeniero Electricista, M.Sc, en
Automática, Ph.D, Universidad del Valle, edinsonfm@univalle.edu.co
JOSE
MIGUEL RAMÍREZ
SCARPETTA
Ingeniero Electricista, M.Sc, en
Sistemas de Generación, Ph.D, Universidad del Valle, jomiram@univalle.edu.co
Recibido para revisar Marzo 23 de 2007, aceptado Noviembre 06 de 2007, versión final Enero 22 de 2008
RESUMEN: En este artículo se muestran los resultados más importantes desarrollados en el análisis de la pérdida de la observabilidad de la velocidad para aplicaciones de Control de Motores de Inducción sin sensor de velocidad y trabajando en regímenes de velocidad cercanos a cero e incluyendo cero velocidad. Se describen el problema de control sin sensor de velocidad y las herramientas utilizadas para el análisis de la observabilidad; finalmente, se hace una revisión de los reportes de análisis de la Observabilidad del motor de inducción.
PALABRAS CLAVE: Observabilidad No lineal, Control sin medida de velocidad, Motor de Inducción.
ABSTRACT: In this paper, the more important results obtained in the analysis of observability loss for Induction motors working in zero and proximities of zero speed are reviewed. The problems in Sensorless Control and the analytic tools to study the nonlinear observability for inductions motors are described; finally, important results reported about the observability of induction motors are analyzed.
KEYWORDS: Nonlinear Observability, Sensorless control, Induction Motor.
1. INTRODUCCIÓN
Hasta mediados de los 80's, la mayoría de los accionamientos eléctricos usaban el Motor de Corriente Directa (MDC); ahora, el Motor de Inducción (MI) ha remplazado en muchas aplicaciones al MDC; en los MI las corrientes rotóricas son inducidas, por lo que contrario al MDC no es necesario el uso de escobillas ni de anillos rozantes, esto hace su mantenimiento más simple y su operación más sencilla [4][5].
Otras características importantes del MI son: robustez, menor costo, confiabilidad, versatilidad y los rangos de velocidad y par considerables.
Para el control vectorial del MI es necesario conocer el estado magnético (flujo magnético) de la máquina, a partir de los 90's la información de flujo magnético en la máquina se obtuvo empleando estimadores y observadores en lugar de sensores [30].
Por otra parte, para controlar la velocidad del MI la información de posición y velocidad en el eje del rotor se hace en algunos casos empleando decodificadores incrementales; estos instrumentos presentan fallas recurrentes lo que hace necesario un programa de paradas de máquina para su mantenimiento y en caso de fallas generan sobrecostos adicionales en la producción.
El desarrollo de la teoría de estimación y de observadores permitió no solo observar el flujo magnético sino también la variable de velocidad del rotor en el MI a partir de los voltajes y corrientes en el estator, lo que además aumenta la robustez del sistema de control, generando una línea de investigación y desarrollo conocida como: “Sensorless Control” o Control Sin Sensor Mecánico.
En este trabajo se revisan los aportes en la Observabilidad del MI, en la sección dos del artículo se presenta la nomenclatura empleada, en la sección tres se presentan algunos de los modelos del MI y a nuestro parecer, los más empleados en los reportes del análisis de su observabilidad, en la sección cuatro se presenta una revisión del Control del Motor de Inducción sin Sensor de Velocidad (CMISV), en la sección cinco se presentan las herramientas conceptuales de análisis de observabilidad y en la sección seis se presenta el problema de observabilidad del MI y los principales aportes encontrados en la literatura para su solución.
2. NOMENCLATURA
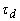 : Par motor;
: Par motor;
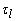 : Par de
carga;
: Par de
carga;
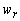 : Velocidad
angular del rotor;
: Velocidad
angular del rotor;
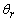 : Posición
del rotor;
: Posición
del rotor;
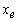 : Vector
de estado electromagnético (corrientes del estator-rotor, flujos del estator-rotor
o combinaciones de los anteriores);
: Vector
de estado electromagnético (corrientes del estator-rotor, flujos del estator-rotor
o combinaciones de los anteriores);
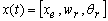 : Vector
de variables de estado del motor (
: Vector
de variables de estado del motor (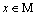 );
);
 : Espacio
de estados de dimensión “m” con una estructura
: Espacio
de estados de dimensión “m” con una estructura 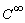 , con topología “Hausdorff “;
, con topología “Hausdorff “;
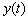 : Variable
de salida, (variables medidas del sistema, corrientes del estator),
: Variable
de salida, (variables medidas del sistema, corrientes del estator),  ;
;
(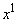 ,
,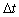 ): Trayectoria
o evoluciones del estado a partir del estado inicial
): Trayectoria
o evoluciones del estado a partir del estado inicial 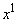 en el intervalo
en el intervalo 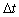 ;
;
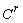 : Función
donde las primeras “r” derivadas existen y son continuas;
: Función
donde las primeras “r” derivadas existen y son continuas;
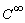 : Variedades
conectadas infinitamente diferenciables;
: Variedades
conectadas infinitamente diferenciables;
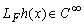 : derivada
Lie de
: derivada
Lie de 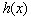 respecto
al funcional
respecto
al funcional 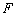 ;
;
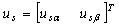 : Vector
de voltajes del estator;
: Vector
de voltajes del estator;
 : Vector
de voltajes del rotor;
: Vector
de voltajes del rotor;
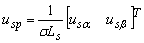 : Vector
de voltajes del estator escalados;
: Vector
de voltajes del estator escalados;
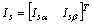 : Vector
de corrientes del estator;
: Vector
de corrientes del estator;
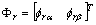 : Flujos
del rotor;
: Flujos
del rotor;
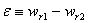 : Desviación
de medición de velocidad del rotor;
: Desviación
de medición de velocidad del rotor;
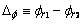 : Desviación
de medición de flujo del rotor;
: Desviación
de medición de flujo del rotor;
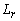 : Inductancia
del rotor;
: Inductancia
del rotor; 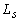 : Inductancia
del estator;
: Inductancia
del estator; 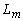 : Inductancia
mutua;
: Inductancia
mutua;
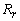 : Resistencia
del rotor;
: Resistencia
del rotor;  : Resistencia
del estator;
: Resistencia
del estator;
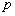 : Pares
de polos;
: Pares
de polos; 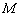 : Masa Inercial;
: Masa Inercial; 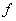 : Coeficiente
de fricción viscosa;
: Coeficiente
de fricción viscosa;
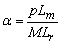 ,
, 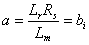 ,
, 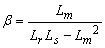 ,
, 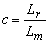 ,
, 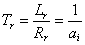 ,
, 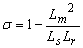 ,
, 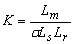 ,
, 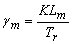 ,
, 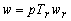 ,
, 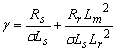 ;
; 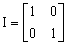 ,
, 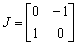
3. MODELOS DEL MOTOR DE INDUCCIÓN
El modelo natural del MI está representado en el conjunto de ecuaciones (1); para el caso de rotor devanado cortocircuitado y de jaula de ardilla el voltaje en terminales del rotor es cero.
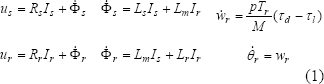
A partir de la ecuación (1), se construyen varias aproximaciones de modelos del MI, dependiendo significativamente del enfoque de solución de control que se aborde; generalmente, por la simetría del motor, el modelo trifásico se puede llevar a una representación más simple bifásica ortogonal. El modelo del MI más empleado por su simplicidad es el modelo de Park, para el cual se asumen las siguientes hipótesis de simplificación: la máquina es simétrica y equilibrada, la inducción en el entrehierro es sinusoidal, la permeabilidad magnética del núcleo es infinita, las pérdidas ferromagnéticas son despreciables y no se consideran el efecto piel, ni los efectos de las ranuras. Con estos supuestos, las ecuaciones electromagnéticas del MI en representación de espacio de estados se expresan como un sistema bilineal no lineal de la forma:
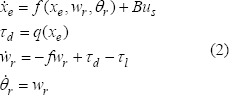
donde B es
una matriz de entrada, q es un producto vectorial de los estados y 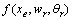 expresa
diferentes representaciones del motor dependiendo de los ejes de referencia
como
expresa
diferentes representaciones del motor dependiendo de los ejes de referencia
como 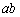 ,
, 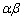 , ó
, ó 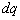 .
.
En la representación 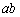 ( ó modelo
vectorial real) los ejes de referencias conservan su estado natural (fijo en
el estator, móvil para el rotor a la velocidad
( ó modelo
vectorial real) los ejes de referencias conservan su estado natural (fijo en
el estator, móvil para el rotor a la velocidad 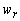 ), los
estados y las entradas son sinusoidales y dependen de la posición (en este
caso las entradas serán los voltajes estatóricos en ejes
), los
estados y las entradas son sinusoidales y dependen de la posición (en este
caso las entradas serán los voltajes estatóricos en ejes 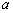 y
y 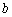 respectivamente,
respectivamente, 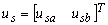 ; en la
representación
; en la
representación 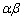 -ver ecuación
(3)- se elimina la dependencia explícita del modelo
-ver ecuación
(3)- se elimina la dependencia explícita del modelo 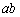 de la posición
del rotor -ángulo
de la posición
del rotor -ángulo 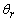 - a través
de una rotación del sistema de referencias del rotor, esta representación permite
pasar de un sistema con dos ejes de coordenadas a uno solo haciendo más simple
el modelo; por ejemplo, la dinámica del flujo ahora depende explícitamente
de la velocidad angular del rotor y no de la velocidad y la posición.
- a través
de una rotación del sistema de referencias del rotor, esta representación permite
pasar de un sistema con dos ejes de coordenadas a uno solo haciendo más simple
el modelo; por ejemplo, la dinámica del flujo ahora depende explícitamente
de la velocidad angular del rotor y no de la velocidad y la posición.
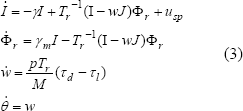
Ibarra et alia [18] presentan un sistema dinámico algebraico diferencial con restricciones algebraicas para determinar las dinámicas del MI que se denominan como indistinguibles (ver sección 5):
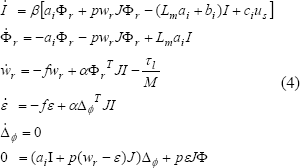
este modelo incluye
dos nuevas variables que son: la dinámica del error de las trayectorias de
velocidad del rotor 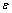 y la dinámica
del error de las trayectorias del flujo del rotor
y la dinámica
del error de las trayectorias del flujo del rotor 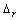 .
.
La representación
o modelo 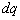 se obtiene
al orientar los ejes giratorios del modelo
se obtiene
al orientar los ejes giratorios del modelo 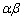 usualmente
a la velocidad angular (
usualmente
a la velocidad angular (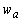 ) de la
alimentación; en algunos casos, se puede orientar el sistema de coordenadas
en la dirección de un vector de flujo.
) de la
alimentación; en algunos casos, se puede orientar el sistema de coordenadas
en la dirección de un vector de flujo.
4. CONTROL SIN SENSOR DE VELOCIDAD DEL MOTOR DE INDUCCIÓN
4.1 Problema
de CMISV
Consiste en determinar
las entradas 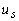 -ver ecuación
(1)- que permitan obtener un comportamiento dinámico deseado con una alta eficiencia
y mayor confiabilidad del sistema de control; en controladores de medio desempeño
dinámico y alto desempeño dinámico, para el CMISV se impone la necesidad de
disponer de observadores para el flujo del rotor y la velocidad angular e implementar
el control de velocidad solo a partir de mediciones de los voltajes y corrientes
del estator [3][26][31]. Por ser el MI un sistema no lineal, no se cumple el
principio de separación para el control con observador y es difícil establecer
un análisis completo de la estabilidad del control; además, para el MI la observación
y el control se dificultan por las variaciones paramétricas por lo que es necesario
tener controladores robustos. Por tanto, los investigadores se ven enfrentados
a un reto, resolver el problema de control y de observación no lineal del motor
MI simultáneamente. Se ha encontrado que la mayor limitante de las implementaciones
del CMISV es el bajo desempeño dinámico a bajas frecuencia y la pérdida de
observabilidad en estos regímenes de operación; las limitaciones de los esquemas
de CMISV se resumen así:
-ver ecuación
(1)- que permitan obtener un comportamiento dinámico deseado con una alta eficiencia
y mayor confiabilidad del sistema de control; en controladores de medio desempeño
dinámico y alto desempeño dinámico, para el CMISV se impone la necesidad de
disponer de observadores para el flujo del rotor y la velocidad angular e implementar
el control de velocidad solo a partir de mediciones de los voltajes y corrientes
del estator [3][26][31]. Por ser el MI un sistema no lineal, no se cumple el
principio de separación para el control con observador y es difícil establecer
un análisis completo de la estabilidad del control; además, para el MI la observación
y el control se dificultan por las variaciones paramétricas por lo que es necesario
tener controladores robustos. Por tanto, los investigadores se ven enfrentados
a un reto, resolver el problema de control y de observación no lineal del motor
MI simultáneamente. Se ha encontrado que la mayor limitante de las implementaciones
del CMISV es el bajo desempeño dinámico a bajas frecuencia y la pérdida de
observabilidad en estos regímenes de operación; las limitaciones de los esquemas
de CMISV se resumen así:
- La velocidad se hace no observable a frecuencia de excitación cero [1] [7] [18]; Canudas et al. (2000); Ibarra et al. (2004)).
- Una incorrecta
estimación
del flujo o el par, si
 no se conoce
con precisión, lleva a un pobre desempeño a baja velocidad.
no se conoce
con precisión, lleva a un pobre desempeño a baja velocidad. - El control preciso de la velocidad depende generalmente
de la constante
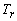 , se encuentran
reportes de buen control hasta un mínimo de velocidad del rotor de 0.002pu
[21].
, se encuentran
reportes de buen control hasta un mínimo de velocidad del rotor de 0.002pu
[21]. - Inestabilidad en estado estable a baja velocidad, particularmente bajo frenado regenerativo.
4.2 Estimadores,
observadores y filtros
Para reducir los problemas
de estabilidad a baja velocidad, mejorar la convergencia de la estimación y
reducir la sensibilidad a las variaciones paramétricas, se han diseñado estrategias
de control con: observadores de Kalman [28] o algunas de sus variantes, identificación
paramétrica [25], estimadores de flujo y parámetros [10][2], observadores de
flujo y velocidad no lineales [9], observadores de flujo y velocidad
usando modos deslizantes [16] ó usando modos deslizantes adaptables, entre
otros. Para casos donde los ruidos son débiles la aproximación determinística
de los observadores clásicos es suficiente, pero cuando los niveles de ruido
son considerables o son de naturaleza estocástica, es necesario aumentar la
precisión de las variables estimadas utilizando filtros estocásticos como el
filtro de Kalman [19]; las investigaciones muestran muy buenos comportamientos
de estas aproximaciones, la mayor limitación está en el peso computacional.
4.3 Estrategias
de Control
Históricamente las
técnicas de control del MI más empleadas son el control Voltaje-frecuencia
(U/f) y el Control por Campo Orientado (en Ingles la sigla es FOC),
estas técnicas se han extendido al CMISV centrando los esfuerzos en los problemas
de observación y estimación como se mencionó en el párrafo inmediatamente anterior.
Otra técnica menos convencional pero importante para la solución del CMISV
es la técnica de planitud (“flatness"), desarrollada por los investigadores
del Centro de Automática y Sistemas (CAS:``Centre Automatique et Systemes")
de la Escuela de Minas de París [23], los investigadores estudian
las propiedades de planitud del MI, desarrollaron un CMISV con algoritmo de
planitud y manifiestan problemas de observación en cercanías de singularidades
[24].
Hacia finales de los 90's y lo corrido de esta década aparece otra estrategia de CMISV basados en explotar las “saliencias" e inyección de señales [14][6]; por saliencias se entienden: los armónicos debidos a los ranuras (“slots''), las asimetrías en el diseño, la saturación, y la excentricidad dinámica. Particularmente los trabajos de Holtz y de Lorentz [14][6] muestran soluciones al CMISV realizando cambios geométricos en el rotor del MI induciendo saliencias mecánicas. Franco et al. [11][12] desarrollan un modelo completo del MI considerando las saliencias inducidas reportadas en [6].
4.4 CMISV a frecuencias de excitación
bajas
En la última década
se han reportado algunos esfuerzos por resolver el problema del control a
velocidad cero o frecuencia cero, Huangang et alia [17] reportan un método
de control vectorial práctico para el MI a través de técnicas de integración
del término 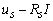 para una aplicación
de un puente grúa de 40 toneladas, el cual requiere torques cuya frecuencia
fundamental está entre 2 y 3 hz aproximadamente. Maes et alia [22] presentan
la combinación de la técnica de Control Directo del Par (DTC) [29] con
un observador adaptable, reportan haber alcanzado buenos desempeños dinámicos
a cero velocidad pero en la gráficas de prueba estos resultados no son contundentes
y no están soportados en resultados analíticos formales.
para una aplicación
de un puente grúa de 40 toneladas, el cual requiere torques cuya frecuencia
fundamental está entre 2 y 3 hz aproximadamente. Maes et alia [22] presentan
la combinación de la técnica de Control Directo del Par (DTC) [29] con
un observador adaptable, reportan haber alcanzado buenos desempeños dinámicos
a cero velocidad pero en la gráficas de prueba estos resultados no son contundentes
y no están soportados en resultados analíticos formales.
Rodic y Karen [27] presentan un diseño en el que combinan un DTC con la técnica de modos deslizantes y reportan haber empleado técnicas de optimización del flujo para mejorar la respuesta dinámica del par del MI, los resultados muestran buenos desempeños a cero velocidad pero el rizado en el par eléctrico introducido por el control por modos deslizantes es aún indeseable. Este problema es mejorado por Lascu et alia [20] introduciendo el concepto más general de estructura variable y el control del actuador usando técnicas de modulación del vector espacial, sus resultados son prometedores, reportan mejoras considerables en el rizado del par a cero velocidad y buen comportamiento dinámico a cero velocidad; Lascu et alia [21] muestran progresos en términos de desempeños dinámicos y estáticos, muestran mejoras en las técnicas de estimación de la resistencia del estator; sin embargo y a pesar de trabajar en cero velocidad manifiestan la presencia del rizado en las variables de velocidad y par electromagnético. Otros resultados muy importantes fueron presentados por Holtz y Quan [15] en los que reportan buenos desempeños dinámicos operando hasta 0.25 Hz y usando la técnica de inyección de señal.
Las dos siguientes secciones presentan las herramientas teóricas para analizar formalmente la observabilidad no lineal que permiten explicar las limitaciones del CMISV a frecuencia cero y bajas velocidades.
5. OBSERVABILIDAD NO LINEAL
Como se ilustró en
las ecuaciones (2) a (4), el MI es inherentemente no lineal, por lo tanto el
análisis de la observabilidad que se aplica se apoya en la teoría desarrollada por
Hermann y Krener [13], para entenderlo se revisarán primero los conceptos fundamentales
de la teoría de observabilidad. El análisis de observabilidad no lineal se
basa en el concepto de indistiguibilidad del estado 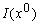 , considerando
el sistema no lineal descrito por:
, considerando
el sistema no lineal descrito por:

se dice que dos
estados 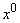 y
y 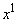 del SN son indistinguibles (
del SN son indistinguibles (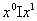 : l denota
indistinguibilidad) si para cada entrada admisible
: l denota
indistinguibilidad) si para cada entrada admisible 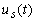 en el intervalo
de tiempo
en el intervalo
de tiempo 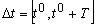 las salidas
correspondientes son idénticas. El SNL es observable en
las salidas
correspondientes son idénticas. El SNL es observable en 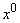 si
para cualquier par de estados
si
para cualquier par de estados 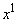 y
y 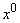 (
(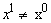 ), para
cada entrada admisible
), para
cada entrada admisible 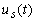 en
en 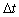 , las evoluciones
del sistema generan diferentes salidas y a partir de las salidas es posible
distinguir claramente el estado
, las evoluciones
del sistema generan diferentes salidas y a partir de las salidas es posible
distinguir claramente el estado 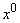 , lo que
implica que l
, lo que
implica que l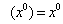 ; el sistema
(5) es globalmente observable si lo anterior se cumple para todo estado
en el espacio de estados, i.e. para todo
; el sistema
(5) es globalmente observable si lo anterior se cumple para todo estado
en el espacio de estados, i.e. para todo 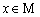 se cumple que l
se cumple que l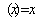 (ver Figura
1, esquina superior derecha).
(ver Figura
1, esquina superior derecha).
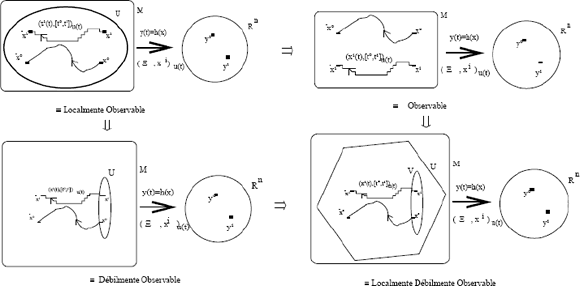
Figura
1. Relaciones de Observabilida
Figure 1. Observability Relationships
La observabilidad
global del sistema implica que alguna entrada distingue puntos de 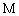 ; sin embargo,
esta noción es muy relajada y puede no ser muy útil porque para determinarla
puede ser necesario atravesar una distancia considerable o por un largo tiempo
para distinguir entre dos puntos de
; sin embargo,
esta noción es muy relajada y puede no ser muy útil porque para determinarla
puede ser necesario atravesar una distancia considerable o por un largo tiempo
para distinguir entre dos puntos de 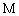 . En otros
casos se emplean conceptos locales (los cuales son más fuertes), como el de
indistinguibilidad en una región cerrada
. En otros
casos se emplean conceptos locales (los cuales son más fuertes), como el de
indistinguibilidad en una región cerrada 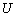 del espacio
del espacio 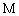 ; este concepto
puede ser demasiado restrictivo, pues es posible que este subespacio
; este concepto
puede ser demasiado restrictivo, pues es posible que este subespacio 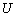 no sea completo y que no
no sea completo y que no
Represente adecuadamente
el espacio de estados. Se define entonces el concepto de Observabilidad Local “relajando” el
subespacio de estados 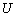 como un
subespacio abierto en
como un
subespacio abierto en 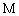 ; el sistema
es Localmente Observable (LO) en
; el sistema
es Localmente Observable (LO) en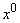 si para
cada vecindad abierta
si para
cada vecindad abierta 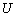 de
de 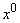 ,
, 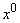 es U-Indistinguible
(i.e. l
es U-Indistinguible
(i.e. l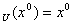 ) y el sistema es LO si esto se
cumple para todo
) y el sistema es LO si esto se
cumple para todo 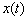 en
en 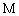 (Ver Figura 1, esquina
superior izquierda).
(Ver Figura 1, esquina
superior izquierda).
Para relajar la condición de observabilidad, se incluye un concepto denominado "débil", la idea es permitir que se pueda distinguir entre dos estados vecinos alejándose (de ser necesario)
Considerablemente
de la vecindad. Se define que el SNL es Débilmente Observable (DO) en 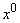 si existe
si existe
una vecindad 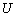 de
de 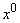 tal que l
tal que l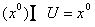 , y en general,
el sistema es DO si lo anterior se
, y en general,
el sistema es DO si lo anterior se
cumple para cada 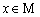 (ver Figura
1, esquina inferior izquierda).
(ver Figura
1, esquina inferior izquierda).
Es probable que
sea necesaria una evolución lejos de 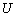 para distinguir
puntos de
para distinguir
puntos de 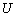 , se define
un concepto no tan débil introduciendo una restricción a la evolución posible
de los estados en un subespacio o vecindad abierta
, se define
un concepto no tan débil introduciendo una restricción a la evolución posible
de los estados en un subespacio o vecindad abierta 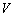 de
de 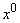 contenida
en
contenida
en 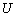 , se dice
que el sistema es Localmente Débilmente Observable (LDO) en el estado
, se dice
que el sistema es Localmente Débilmente Observable (LDO) en el estado 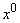 si existe
una vecindad abierta
si existe
una vecindad abierta 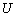 de
de
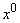 tal que
para alguna vecindad abierta
tal que
para alguna vecindad abierta 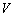 de
de 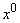 contenida
en
contenida
en 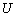 , el estado
, el estado 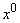 es Indistiguible
en
es Indistiguible
en 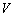 , (l
, (l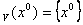 ) y en general,
es LDO si lo anterior se cumple para cada estado en el espacio de estados (
) y en general,
es LDO si lo anterior se cumple para cada estado en el espacio de estados (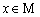 ) (ver Figura
1, esquina inferior derecha).
) (ver Figura
1, esquina inferior derecha).
En la figura 1 las relaciones de observabilidad local, localmente débil y débil son transitivas pero no recíprocas (ver el sentido de las flechas).
La observabilidad localmente débil a pesar de no ser la más fuerte tiene la ventaja sobre las demás que permite ser probada a través de un instrumento algebraico conocido como la condición de rango [13].
El concepto de indistinguibilidad del estado y en general el de observabilidad son conceptos que desde el enfoque práctico no son útiles pues pueden implicar esperar largas evoluciones de los estados; esto implica que para sistemas con estados de dinámicas rápidas las evoluciones transitorias no sean observables lo cual será una limitante para aplicaciones de altos desempeños dinámicos. Normalmente los ingenieros de control conocen la vecindad de los estados que se desea distinguir (regiones de operación limitadas ya sea por la física en sí de los elementos: rangos, regiones de trabajo, etc., ó por restricciones físicas: saturaciones de los actuadores, condiciones extremas de los procesos, etc.) siendo útil desde este enfoque para el análisis de observabilidad utilizar un concepto local; sin embargo, las restricciones en términos de vecindades es muy fuerte por cuanto el espacio de observación deberá estar muy limitado. La herramienta más útil que se puede considerar, desde el enfoque de aplicación, es el concepto de observabilidad localmente débil ya que por un lado nos permite restringir el espacio de distinguibilidad, por otro lado nos permite garantizar que las evoluciones del estado están muy próximas a los puntos de trabajo, y por otro lado si se logra mostrar que esta propiedad de observabilidad localmente débil se cumple al menos para todo el espacio de estado de trabajo, se podrá garantizar la observabilidad del sistema o proceso bajo estudio.
La condición de rango
(Teorema 3 en [13] - instrumento que permite estudiar la Observabilidad Localmente
Débil-) para el sistema (5) es una prueba suficiente que consiste en calcular
el rango del subespacio de observabilidad de 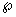 que se
muestra en la siguiente ecuación:
que se
muestra en la siguiente ecuación:
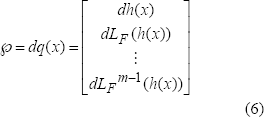
donde, 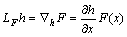 es la rata
de cambio con respecto al tiempo de la función escalar de salida
es la rata
de cambio con respecto al tiempo de la función escalar de salida 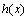 a lo largo
de las trayectorias del sistema (5);
a lo largo
de las trayectorias del sistema (5); 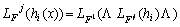
donde 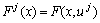 para alguna
para alguna 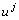 constante
constante 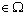 y
y 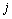 es cualquier
entero real positivo.
es cualquier
entero real positivo.
Teorema: Si 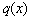 satisface
la condición de rango de observabilidad en
satisface
la condición de rango de observabilidad en 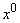 , entonces,
(6) es localmente débilmente observable en
, entonces,
(6) es localmente débilmente observable en 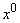 .
.
Es claro del teorema que la condición es suficiente, si no se cumple la condición de rango no implica que el sistema no sea observable.
6. OBSERVABILIDAD DEL MI
Las diferentes
aplicaciones reportadas muestran que existen problemas de observabilidad
en cercanías del
régimen de operación a bajas frecuencias de alimentación y/o para bajas velocidades (Asher,
2000). Estos problemas de pérdida de observabilidad han sido estudiados analíticamente
y reportados partiendo del modelo 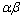 del MI
por Canudas et alia [7] y también a partir del modelo
del MI
por Canudas et alia [7] y también a partir del modelo 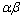 construyendo
un sistema de ecuaciones diferenciales algebraicas por Ibarra et alia [18].
construyendo
un sistema de ecuaciones diferenciales algebraicas por Ibarra et alia [18].
Del conjunto de ecuaciones (3), considerando que las corrientes y los voltajes son medidos, y que el flujo es estimado (u observado), se observa en ambas expresiones que la velocidad del rotor aparece multiplicada por el flujo; para conocer el valor de la velocidad considerando valores de velocidad y flujos constantes diferentes de cero, una simple solución puede implicar despejar la velocidad del producto; sin embargo, en la presencia de imprecisiones del flujo estimado se generan errores en la estimación de la velocidad. En el caso en que la velocidad es cercana a cero y cero, es imposible de las expresiones de corriente y flujo obtener información de la velocidad.
Canudas et alia
[7], basados en la prueba de rango del espacio de observación, revisan las condiciones
de observabilidad suficientes a partir del análisis de geometría vectorial
clásica para posteriormente analizar algunas condiciones bajo las cuales estas
son también necesarias; como resultados del análisis de las condiciones bajo
las cuales el MI no es localmente observable, asumiendo que 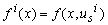 para algún
para algún 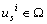 constante
y que la velocidad es constante, concluyen que es condición suficiente que
constante
y que la velocidad es constante, concluyen que es condición suficiente que 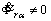 ó
ó 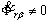 ; y segundo,
de la hipótesis de flujos constantes
; y segundo,
de la hipótesis de flujos constantes 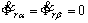 , que es
suficiente que
, que es
suficiente que  . Particularmente
analizan las condiciones de observabilidad cuando el MI está operando a bajas
frecuencias y estudian la posibilidad de encontrar entradas que hagan el sistema
observable [8]. Una conclusión muy importante en [7] es la relación física
dada en la curva de par v.s. velocidad del vector de flujo del rotor -ecuación
(7)- la cual expresa la región de pérdida de observabilidad.
. Particularmente
analizan las condiciones de observabilidad cuando el MI está operando a bajas
frecuencias y estudian la posibilidad de encontrar entradas que hagan el sistema
observable [8]. Una conclusión muy importante en [7] es la relación física
dada en la curva de par v.s. velocidad del vector de flujo del rotor -ecuación
(7)- la cual expresa la región de pérdida de observabilidad.
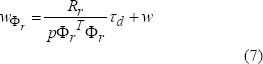
donde 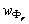 es la velocidad
angular del vector de flujo. Con la norma del flujo diferente de cero, y con
la derivada del flujo nula (
es la velocidad
angular del vector de flujo. Con la norma del flujo diferente de cero, y con
la derivada del flujo nula (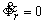 ó
ó  ), el par
electromagnético y la velocidad del rotor tienen signos opuestos, lo que equivale
a estar en modo de regeneración con corrientes en el estator estacionarias,
en esta situación la observabilidad de la velocidad en el MI se pierde; se
observa que en esta condición de pérdida de observabilidad la velocidad del
rotor no es necesariamente nula. Además, para valores estacionarios de velocidad
(
), el par
electromagnético y la velocidad del rotor tienen signos opuestos, lo que equivale
a estar en modo de regeneración con corrientes en el estator estacionarias,
en esta situación la observabilidad de la velocidad en el MI se pierde; se
observa que en esta condición de pérdida de observabilidad la velocidad del
rotor no es necesariamente nula. Además, para valores estacionarios de velocidad
(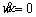 ) y con
el MI operando en vacío (
) y con
el MI operando en vacío (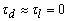 ), los modos
de operación a velocidad cercana a cero y cero quedan también configurados
en la región de pérdida de observabilidad cuando
), los modos
de operación a velocidad cercana a cero y cero quedan también configurados
en la región de pérdida de observabilidad cuando  .
.
Ibarra et alia [18] hacen una aproximación diferente para el análisis de pérdida de observabilidad del MI; a partir del modelo en ecuaciones diferenciales algebraicas -ecuación (4)-, presentan otro enfoque con el que proponen encontrar las trayectorias internas de indistinguibilidad para el MI. El análisis realizado es importante porque muestra que el sistema MI no es globalmente observable y deja planteado un problema basado en restricciones que es el eje principal de su artículo; igualmente caracteriza diferentes condiciones de operación local bajo las cuales el MI es detectable y observable (o no detectable y no observable) resaltando entre ellas que a frecuencia nula de la alimentación y que a velocidad nula, la observabilidad se pierde. Resumiendo, el planteamiento más relevante de este trabajo es que se muestra analíticamente que no es posible obtener observadores locales o globales para el CMISV; y además, los autores describen un procedimiento para calcular las trayectorias o evoluciones donde la observabilidad no se puede alcanzar.
7. CONCLUSIONES
Ibarra et. alia y Canudas et alia, han mostrado analíticamente como el MI pierde observabilidad de la velocidad a frecuencias de excitación nula. Se ha demostrado que la velocidad del MI no es ni localmente, ni globalmente observable y sr ha caracterizado la región y algunas condiciones para la pérdida de observabilidad del MI.
8. AGRADECIMIENTOS
Agradecimientos especiales a: Dr. Carlos Canudas-de-Wit (INPG-Francia), Dr. Gerardo Espinosa (DEPFI, UNAM México), Dr. Jaime Moreno (Instituto de Ingeniería, UNAM -México), la Universidad del Valle, Colciencias y a la embajada de Francia en Colombia por el apoyo recibido.
REFERENCIAS
[1] ASHER, G. M.. Sensorless induction motor drives. IEE Seminar on Advances in Induction Motor Control (Ref. 2000/072). 6, 1-5.
[2] Atkinson, D.J., P.P. Acarnley y J.W. Finch. Application of estimation
techniques in vector controlled induction motor drives. Power Electronics and
Variable-Speed Drives. pp. 358 363. Fourth International Conference on, London,
UK . 1991.
[3] Bodson, M., J. Chiasson y R. Novothak. Nonlinear speed observer for high-performance induction motor control. IEEE Transactions on Industrial Electronics. 42(4), 337343.
1995.
[4] Bose, B. K. Power electronics and motion control-technology status
and recent trends. IEEE Trans. on Industrial Application, 29(5). 902909. 1993.
[5] Power electronics and drives technology advances and trends. Industrial
Electronics, ISIE ’99. Proceedings of the IEEE International Symposium on p.
TU1. Bled, Slovenia. 1999.
[6] Briz, F., M.W. Dener, A. Diez y R. Lorentz. Measuring, modeling,
and decoupling of saturation-induced saliencies in carrier-signal injection-based
sensorless ac drives. Transactions on Industry Applications, IEEE. 37(5), 13561364.
2001.
[7] Canudas-De-Wit, C., A. Youssef, J. Barbot, P. Martin y F. Malrait. Observability conditions of induction motors at low frequencies. Conference on Decision and Control. Sidney-Australia. 2000.
[8] D. Lubineau, Commande non lineaire de moteur asynchrone avec observateur,
Thèse préparée au Laboratoire d`Automatique de Grenoble, Grenoble- Francia,
Avril 8 1999.
[9] M. Djemai, T. Boukhobza, J.P. Barbot, J.L. Thomas y S. Poullain, Rotor speed and flux nonlinear observer for speed sensorless induction motors, Control Applications, Proceedings of the 1998 IEEE International Conference on, 2, 848-852. 1998,
[10] Finch, J.W., D.J. Atkinson y P.P. Acarnley. Full-order estimator
for induction motor states and parameters. Electric Power Applications, IEE
Proceedings 145(3), 169179. 1998.
[11] Franco E., Amaya M., Ramírez S. J.M., A New Model For Induction
Motor With Induced Saliencies. IEEE International Conference on Industrial
Electronics and Control Applications. Nov-Dec., Quito-Ecuador. 2005
[12] Parametrización de un motor de inducción con saliencias inducidas para análisis estático y dinámico. II Congreso Internacional sobre uso racional y eficiente de la energía.
Articulo 02-121. Santiago de Cali, Noviembre 2-4 de 2006.
[13] Hermann, R. y A.J. Krener. Nonlinear controlabillity and observability.
IEEE Transactions on Automatic Control. AC-22 No 5, 728740. 1977
[14] Holtz, J. Sensorless control of induction motors drives. In: Proceedings
of the IEEE. Vol. 90-8. pp. 13591394. 2002.
[15] Holtz, J. y Quan. Drift- and parameter-compesated flux estimator
for persistent zero-stator-frequency operation of sensorless-controlled induction
motors. In: IEEE Transactions on Industry Applications. Vol. 39-4. pp. 10521060.
2003.
[16] Hren Alenka y Jezernik Karen. Robust Sliding Mode Control of Induction Motor Drive Without Speed Sensor. Proceedings of the 1998 IEEE International Conference on Control Applications. Trieste, Italy , 1-4 Sept. 1998.
[17] Huangang, Wang, Zhang Xiaoping, Xu Wenli y Yang Geng. The speed-sensorless
control of induction motors at zero frequency. Electrical Machines and Systems,
ICEMS 2001. Proceedings of the Fifth International Conference on 2, 1195 1198.
2001
[18] S. Ibarra-Rojas, J. Moreno y G. Espinosa-Pérez. Global observability analysis of sensorless induction motors. Automática,
vol. 40, p.p. 1079-1085. 2004.
[19] R. Kim, K Sul y M Park, Speed sensorless vector Control of Induction Motor using extended Kalman filter, IEEE Transactions on Industry Applications, 1225 - 1233. 1994.
[20] Lascu, C., Ion. Boldea y Frede Blaabjerg. Direct torque control
of sensorless induction motor drives: A sliding-mode approach. IEEE Transactions
on Industry Applications. 40(2), 582590. 2004.
[21] Very-low-speed variable-structure control of sensorless induction
machine drives without signal injection. IEEE Transactions on Industry Applications.
41(2), 591598. 2005.
[22] Maes, Jehudi y A. Melkebeek. Speedsensorless direct torque control
of induction motors using an adaptive flux observer. IEEE Transactions on Industry
Applicactions. 36(3), 778 784. 2000.
[23] Philippe Martin. Ph.D. Thesis: Contribution a l'étude es Systemes Différentiellemenet
Plats, Ecole des Mines de Paris, 1992.
[24] Philippe Martin y Pierre Rouchon. Flatness and Sampling Control of Induction Motors, 13th triennial World Congress, San Francisco, USA , 389-394. 1996.
[25] Moons, C. y B. de Moor. Parameter identification of induction motor
drives. Automática. 31(8), 11371147. 1995.
[26] Rashid, A. On induction motors control. IEEE Transactions on Control
Systems Technology, 5(3), 380382. 1997.
[27] Rodic Mirian and Karel Jezernik. Speed-Sensorless Sliding-Mode
Torque Control of an Induction Motor. IEEE Transactions on Industrial Electronics,
49(1), 8795. 2002.
[28] Salvatore L., Stasi S., y Tarchioni L. A new EKF-based algorithm for flux estimation in Induction Machines. IEEE Transactions on Industry Electronic (1993); 40(5): 496-504.
[29] Takahashi, I. y T. Noguchi. A new quick response and high-efficiency control strategy of an induction motor. IEEE Transactions on Industrial Applications, IA-22, 820827.
1986.
[30] Verghese, G. C. y S. R. Sanders. Observers for flux estimation
in induction machines. IEEE Transactions on Industrial Electronics. (35), 85 94.
1988.
[31] Zamora, J.L., A. García-Cerrada and A. Zazo. Rotor-speed estimator for induction motors using voltage and current measurements. Control Engineering Practice. 6, 369383.
1998.
How to Cite
IEEE
ACM
ACS
APA
ABNT
Chicago
Harvard
MLA
Turabian
Vancouver
Download Citation
Article abstract page views
Downloads
License
Copyright (c) 2008 DYNA

This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.
The author of a paper accepted for publication in any of the journals published by the School of Mines will yield all the property to the National University of Colombia rights free of charge, within which include article: the right to edit, publish, reproduce and distribute both print and digital media, as well as including in an article in international indexes and / or databases, likewise, it enables the publisher to use images, tables and/or graphic material presented in Article for designing covers or posters of the magazine. By assuming the economic rights of the article, it may be reproduced partially or totally in any printed or digital media without express permission of the same.
















