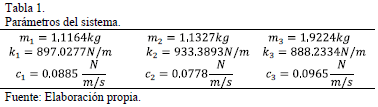Active vibration control in building-like structures submitted to earthquakes using multiple positive position feedback and sliding modes
Control activo de vibraciones en estructuras tipo edificio sometidas a sismos utilizando múltiple retroalimentación positiva de la posición y modos deslizantes
DOI:
https://doi.org/10.15446/dyna.v81n188.40097Keywords:
Modal analysis, Active vibration control, Earthquakes, Positive Position Feedback, Sliding mode control. (en)Análisis modal, Control activo de vibraciones, Sismo, Retroalimentación Positiva de la Posición, Modos deslizantes. (es)
Downloads
https://doi.org/10.15446/dyna.v81n188.40097
Active vibration control in building-like structures submitted to earthquakes using multiple positive position feedback and sliding modes
Control activo de vibraciones en estructuras tipo edificio sometidas a sismos utilizando múltiple retroalimentación positiva de la posición y modos deslizantes
Josué Enríquez-Zárate a & Gerardo Silva-Navarro b
a Sección de Mecatrónica, Centro de Investigación y de Estudios
Avanzados del I.P.N., México, D.F., México. enriquezz@cinvestav.mx
b Sección de Mecatrónica, Centro de Investigación y de Estudios
Avanzados del I.P.N., México, D.F., México. gsilva@cinvestav.mx
Received: October 2th, 2013. Received in revised form: May 9th, 2014. Accepted: September 28th, 2014.
Abstract
This work
deals with the structural and dynamic analysis of a building-like structure
consisting of a three-story building with one passive/active vibration
absorber. The base of the structure is perturbed using a shaker, providing
excitation forces and noisy excitations emulating ground transportation,
underground railways and earthquakes, quite common in Mexico City. It is
considered a realistic seismic record of 8.1Mw occurred at Mexico City,
containing some resonant frequencies of the structure. The mechanical structure
is modeled using Euler-Lagrange methodology and validated using experimental
modal analysis techniques. The active control scheme is synthesized to actively
attenuate the noise and vibration system response, caused by noisy excitation
forces acting on the base, by employing Multiple Positive Position Feedback and
Sliding Mode Control to improve the closed-loop system response and,
simultaneously, attenuate three vibration modes. Simulation and experimental
results describe the overall system performance.
Keywords: Modal analysis; Active vibration control; Earthquakes; Positive Position Feedback; Sliding mode control.
Resumen
Este trabajo
considera el análisis estructural y dinámico de una estructura tipo edificio de
tres pisos con un absorbedor de vibraciones pasivo/activo. La base de la
estructura se perturba con un generador de vibraciones, proporcionando fuerzas
de excitación y ruido emulando transporte terrestre, trenes subterráneos y sismos, comunes en la Ciudad
de México. Se considera un registro sísmico real de magnitud 8.1Mw, conteniendo
algunas frecuencias resonantes de la estructura. La estructura mecánica se
modela con la metodología de Euler-Lagrange y se valida con técnicas de
análisis modal experimental. El esquema de control activo se diseña para
atenuar la respuesta vibratoria del sistema, ocasionada por las fuerzas
armónicas que actúan en la base, empleando múltiple retroalimentación positiva
de la posición y control por modos deslizantes para mejorar la robustez del
sistema en lazo cerrado y atenuar tres modos de vibración. Resultados en
simulación y experimentales describen el desempeño del sistema completo.
Palabra Clave: Análisis modal; Control activo de vibraciones; Sismo; Retroalimentación Positiva de la Posición; Modos deslizantes.
1. Introducción
El estudio sobre el control de las vibraciones mecánicas en el diseño de edificios es un tema de investigación que actualmente es de gran interés sobre todo en las grandes ciudades. En particular, este trabajo de investigación se centra en el análisis de la respuesta de estructuras tipo edificio, que se encuentran perturbadas por fenómenos sísmicos.
Nuestra investigación se centra en las edificaciones de la Ciudad de México, debido a que por su tipo de suelo, la mayor parte está clasificada como zona lacustre y de transición, teniendo baja resistencia sísmica, y debido a esto las estructuras son más vulnerables y se encuentran afectadas por fenómenos como el ruido, transporte, trenes subterráneos y especialmente por sismos [1].
Las investigaciones recientes sobre el control de vibraciones en edificios, se refieren generalmente al uso de los esquemas pasivo, semiactivo y activo [2]. Los esquemas pasivos, conocidos como Tuned Mass Damper (TMD, por sus siglas en inglés), generalmente se encuentran limitados en su respuesta, debido a que se diseñan para la atenuación o minimización de una frecuencia o modo de vibración específico de la estructura. Los esquemas activos, denominados Active Mass Damper (AMD, por sus siglas en inglés), ofrecen un controlador en lazo cerrado para un amplio rango de frecuencias o modos de vibración. Generalmente este diseño agrega un grado de libertad y un actuador al modelo original de la estructura tipo edificio, añadiendo complejidad a la dinámica del sistema. La supresión o atenuación de las frecuencias vibratorias en el sistema se realiza agregando una fuerza de control proporcionada por un actuador electrohidráulico o electromecánico.
En este trabajo se considera una estructura tipo edificio de tres niveles, con excitación armónica y sísmica en la base, la cual se controla con un absorbedor de vibraciones pasivo/activo o híbrido y leyes de control basadas en múltiple retroalimentación positiva de la posición (MPPF, por sus siglas en inglés), en combinación con la técnica de control por modos deslizantes, para mejorar la robustez y minimización la respuesta dinámica del sistema.
2. Sistema completo
Se presenta el diseño y construcción a escala de una estructura tipo edificio de tres pisos sometida a perturbaciones del tipo sísmico. El objetivo consiste en analizar su respuesta dinámica, en simulación numérica y experimental, utilizando esquemas de control pasivo/activo para minimizar su respuesta frecuencial en lazo cerrado.
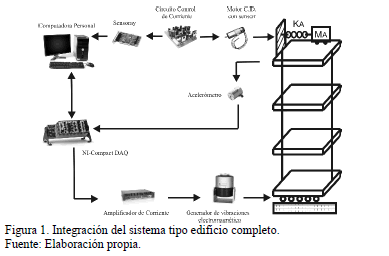
Específicamente, el sistema es una estructura tipo edificio a escala de tres pisos, diseñada y construida de aleación de aluminio. La altura máxima de la estructura, sin considerar el sistema de absorción de vibraciones es de 950 mm, con una base rectangular de 300x200 mm. La estructura completa se encuentra montada sobre un riel con rodamiento de bolas sin fricción y la base móvil se encuentra conectada directamente a un generador de vibraciones electromecánico modelo ET-139, el cual se utiliza para perturbar al sistema con componentes armónicos de baja frecuencia, obtenidos directamente del registro sísmico del temblor ocurrido en la Ciudad de México en 1985, con epicentro en la costa de Zihuatanejo, Michoacán [3]. El generador de vibraciones se controla por un amplificador de potencia Labworks®, modelo PA-138. Para propósitos de control se utiliza como variable de control en lazo cerrado la posición del sistema. Se utiliza un sistema de adquisición de datos NI-CompactDAQ de National Instruments®, chasis modelo NI-DAQ-9172 y módulo de acelerómetros modelo 9133 conectado vía USB a una computadora, para obtener la señal de un acelerómetro colocado en un piso de la estructura, que mide directamente la aceleración y procesa a través de las plataformas de Labview® y Matlab/Simulink® para calcular los desplazamientos (ver Fig. 1).
Por último, se considera que el actuador en el absorbedor pasivo/activo de vibraciones es un motor de cd, acoplado directamente a un sistema masa-resorte con una base móvil, soportada sobre una guía de bolas montada sobre el tercer piso de la estructura. El desplazamiento de la masa del absorbedor se mide con un decodificador óptico en la flecha del motor, señal que se emplea para determinar el valor de la fuerza requerida por la acción de control, por medio de la variación en su valor en corriente. Para el esquema de control retroalimentado se utiliza una tarjeta de adquisición de datos Sensoray® modelo 626. En la Fig. 1 se describe un diagrama esquemático de la integración del sistema completo y en la Fig. 2 se muestra el prototipo de la estructura experimental.
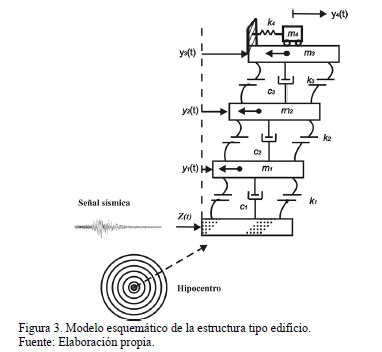
La estructura
tipo edificio consta de tres masas 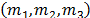 interconectadas cada una por cuatro columnas
flexibles en cada masa, expresado por medio de rigideces equivalentes
interconectadas cada una por cuatro columnas
flexibles en cada masa, expresado por medio de rigideces equivalentes 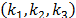 y
se considera amortiguamiento viscoso (lineal) equivalente
y
se considera amortiguamiento viscoso (lineal) equivalente 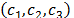 sobre cada grado de libertad (ver Fig. 3)
[4].
sobre cada grado de libertad (ver Fig. 3)
[4].
La fuerza de control se describe como 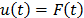 , que afecta directamente a un TMD, a
través de
, que afecta directamente a un TMD, a
través de 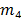 , para lograr los objetivos de control
deseados de atenuación y/o cancelación de vibraciones. La base de la estructura
está perturbada por un desplazamiento en la base
, para lograr los objetivos de control
deseados de atenuación y/o cancelación de vibraciones. La base de la estructura
está perturbada por un desplazamiento en la base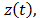 producida por una fuerza lateral de un
generador de vibraciones electromagnético conectado a la estructura. Las mediciones de la aceleración se obtienen usando un acelerómetro conectado
sobre la masa
producida por una fuerza lateral de un
generador de vibraciones electromagnético conectado a la estructura. Las mediciones de la aceleración se obtienen usando un acelerómetro conectado
sobre la masa 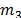 .
.
El
sistema primario y el TMD están formados por elementos mecánicos 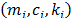 ,
, 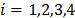 . Las vibraciones no deseadas que causan
el desplazamiento de la estructura se generan por el desplazamiento
. Las vibraciones no deseadas que causan
el desplazamiento de la estructura se generan por el desplazamiento 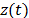 en
términos de la aceleración
en
términos de la aceleración 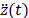 .
.
3. Registro sísmico de 1985
La señal
perturbadora 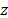 se
representa por un registro sísmico real ocurrido en la Ciudad de México el 19
de septiembre de 1985 en hora epicentro
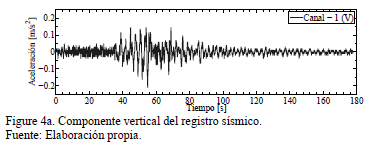
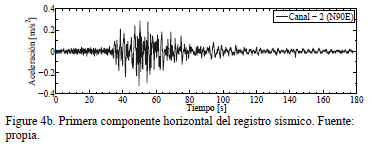
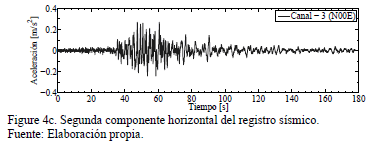
(GMT): 13:17:42,6. [3,5]. Esta señal sísmica se representa por tres
componentes (ver Figs. 4a,b,c), es decir, se tienen dos en el plano horizontal
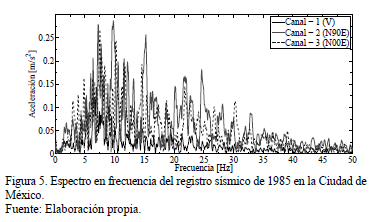
(llamadas longitudinal y transversal) y otra en sentido vertical [6,7]. La
respuesta espectral de las tres componentes se observa en la Fig. 5.
se
representa por un registro sísmico real ocurrido en la Ciudad de México el 19
de septiembre de 1985 en hora epicentro
(GMT): 13:17:42,6. [3,5]. Esta señal sísmica se representa por tres
componentes (ver Figs. 4a,b,c), es decir, se tienen dos en el plano horizontal
(llamadas longitudinal y transversal) y otra en sentido vertical [6,7]. La
respuesta espectral de las tres componentes se observa en la Fig. 5.
La respuesta en frecuencia corresponde a señales de baja frecuencia, las cuales tienen un fuerte impacto sobre estructuras (e.g., edificios, casas) de gran altura o de varios pisos y de gran masa, debido a que tienen períodos naturales de vibración largos [1]. Los sismos de mayor magnitud tienen mayor duración (cerca o superior a un minuto) y liberan más energía a bajas frecuencias. Las frecuencias altas muestran una mayor tendencia a atenuarse por encima de los 5 o 10 Hz, dependiendo de la distancia a la fuente sísmica y las condiciones geológicas del sitio. Las frecuencias más altas se registran en sitios de roca y en las cercanías de la fuente sísmica [8]. La estructura experimental es de baja altura y poca masa, y sus modos de vibración difícilmente son excitados por la señal sísmica real (Fig. 4). Por lo tanto, es conveniente escalar la componente de amplitud del registro sísmico real por una constante de veinte veces su valor, esto con la finalidad de excitar los primeros modos de vibración de la estructura, en el rango de frecuencias del registro sísmico real.
4. Estructura tipo edificio de tres niveles
Un modelo matemático simplificado para un edificio de tres pisos sometido a movimiento por aceleración en la base se obtiene como
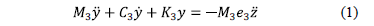
donde 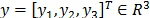 es el vector de coordenadas generalizadas de
desplazamientos relativos con respecto al marco de referencia principal,
es el vector de coordenadas generalizadas de
desplazamientos relativos con respecto al marco de referencia principal, 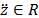 es la aceleración de la señal sísmica en la
base de la estructura y
es la aceleración de la señal sísmica en la
base de la estructura y 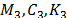 son matrices de masa, amortiguamiento y
rigidez de
son matrices de masa, amortiguamiento y
rigidez de 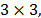 respectivamente. El vector
respectivamente. El vector 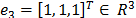 es el vector de influencia, que representa el
desplazamiento de cada masa debido al desplazamiento del suelo. Las matrices de
masa, rigidez y amortiguamiento para el edificio de tres pisos son
es el vector de influencia, que representa el
desplazamiento de cada masa debido al desplazamiento del suelo. Las matrices de
masa, rigidez y amortiguamiento para el edificio de tres pisos son
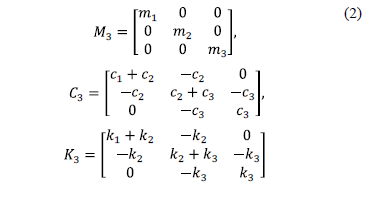
La matriz de masas 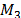 se determina a
partir de las masas (
se determina a
partir de las masas (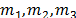 ) por cada piso del edificio. Los valores de la matriz de
rigidez
) por cada piso del edificio. Los valores de la matriz de
rigidez 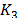 se obtienen
considerando las dimensiones y propiedades mecánicas del material en cada piso
del edificio.
se obtienen
considerando las dimensiones y propiedades mecánicas del material en cada piso
del edificio.
Para propósitos de análisis modal se considera amortiguamiento proporcional
o de Rayleigh [9,10], es decir, que 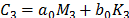 , donde
, donde 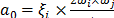 y
y 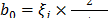 , con
, con 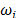 y
y  las
frecuencias resonantes de la estructura y
las
frecuencias resonantes de la estructura y 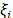 y
y 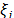 la
proporción de amortiguamiento en la estructura para los modos
la
proporción de amortiguamiento en la estructura para los modos 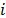 y
y 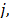 respectivamente.
respectivamente.
La estructura tipo edifico de tres pisos se perturba con una señal sísmica en su componente vertical (ver Figs. 4 y 5), reproducida con un generador de vibraciones electromagnético para amplitud y frecuencia variable en un tiempo de 179 s [3].
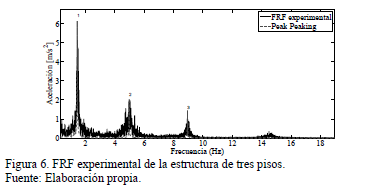
La función de respuesta frecuencial (FRF) experimental en la estructura se obtiene mediante la transformada rápida de Fourier (FFT, por sus siglas en inglés) y la aplicación de técnicas de análisis modal experimental como Peak Peaking (ver Fig. 6).
Los parámetros del sistema sin TMD ni control activo se presentan en la Tabla 1.
Los parámetros
de amortiguamiento se obtuvieron indirectamente, a partir de la FRF,
considerando el amortiguamiento modal 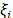 y
la frecuencia modal de la estructura
y
la frecuencia modal de la estructura 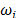 obtenidos experimentalmente. El
amortiguamiento modal es aproximado por medio de los métodos de Peak Peaking y Curve Fitting.
obtenidos experimentalmente. El
amortiguamiento modal es aproximado por medio de los métodos de Peak Peaking y Curve Fitting.
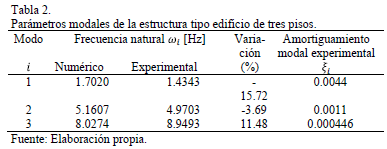
Una comparación de las frecuencias de resonancia obtenidos en forma experimental y numéricamente, se presentan en la Tabla 2, donde los resultados son muy cercanos para validar el modelo simplificado de la estructura tipo edificio de tres pisos en los primeros tres modos de vibración.
5. Estructura tipo edificio con TMD
En la
estructura tipo edificio mostrada en la Fig. 3 el TMD se representa en términos
de los parámetros  y
se diseña para atenuar una de las frecuencias de resonancia más críticas en el
sistema. En este caso el efecto del desplazamiento en la base
y
se diseña para atenuar una de las frecuencias de resonancia más críticas en el
sistema. En este caso el efecto del desplazamiento en la base 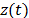 se
logra atenuar en la respuesta del
sistema primario, para un rango pequeño de frecuencias de excitación y bajo
condiciones de operación estables [2].
se
logra atenuar en la respuesta del
sistema primario, para un rango pequeño de frecuencias de excitación y bajo
condiciones de operación estables [2].
La principal desventaja de estos esquemas de control en lazo abierto es la ausencia o poca robustez con respecto a incertidumbres o parámetros desconocidos o variaciones en las frecuencias de excitación.
El edificio de
tres pisos con un TMD sobre la masa del tercer piso de la estructura, sometida
a un movimiento sísmico 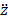 , de manera que el TMD se diseña para
compensar el segundo modo de vibración. Las ecuaciones de movimiento del
sistema de cuatro grados de libertad son
, de manera que el TMD se diseña para
compensar el segundo modo de vibración. Las ecuaciones de movimiento del
sistema de cuatro grados de libertad son
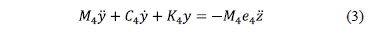
donde 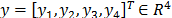 es el vector de coordenadas
generalizadas de desplazamientos relativos con respecto al marco de referencia
principal,
es el vector de coordenadas
generalizadas de desplazamientos relativos con respecto al marco de referencia
principal, 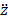 es la aceleración de la señal
sísmica en la base de la estructura y
es la aceleración de la señal
sísmica en la base de la estructura y 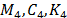 son las matrices de masa, rigidez y
amortiguamiento de
son las matrices de masa, rigidez y
amortiguamiento de 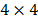 , respectivamente. En este caso
, respectivamente. En este caso 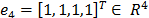 es el vector de influencia, que
representa el acoplamiento inercial entre los pisos de la estructura y el desplazamiento del suelo. Las matrices
de masa, amortiguamiento y rigidez se expresan como
es el vector de influencia, que
representa el acoplamiento inercial entre los pisos de la estructura y el desplazamiento del suelo. Las matrices
de masa, amortiguamiento y rigidez se expresan como
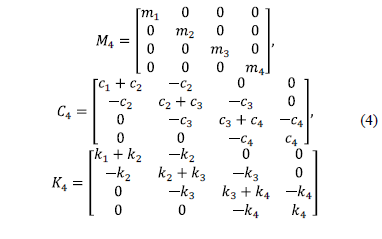
Para propósitos
de análisis modal se propone que el sistema posee amortiguamiento de tipo
proporcional, de manera que 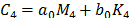 , donde
, donde 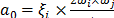 y
y 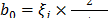 con
con 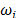 y
y  , las frecuencias modales de la estructura
y
, las frecuencias modales de la estructura
y 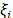 y
y 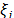 la
proporción de amortiguamiento en la estructura para los modos
la
proporción de amortiguamiento en la estructura para los modos 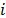 y
y 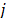 respectivamente.
respectivamente.
El TMD se
diseña para atenuar pasivamente la 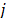 -ésima frecuencia a partir de la expresión
-ésima frecuencia a partir de la expresión 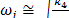 donde
donde  es
la
es
la 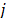 -th frecuencia de resonancia de la estructura
que será atenuada y
-th frecuencia de resonancia de la estructura
que será atenuada y 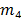 y
y 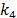 son
la masa y la rigidez equivalente del TMD. En particular, el TMD se diseña para
atenuar el segundo modo de vibración experimental, localizado en
son
la masa y la rigidez equivalente del TMD. En particular, el TMD se diseña para
atenuar el segundo modo de vibración experimental, localizado en  Hz.
Hz.
Los parámetros del edificio de tres pisos con TMD se proporcionan en la Tabla 3.
Los parámetros
de amortiguamiento se obtuvieron indirectamente, a partir de la FRF,
considerando el amortiguamiento modal 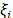 y
la frecuencia modal de la estructura
y
la frecuencia modal de la estructura 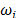 obtenidos experimentalmente. El
amortiguamiento modal se estima con los métodos de Peak Peaking y Curve Fitting.
La estructura tipo edificio de tres pisos con TMD se caracteriza aplicando un
movimiento armónico en el suelo, utilizando la componente vertical del registro
sísmico, que tiene una amplitud variable aproximadamente entre 0 y 0.20 m/s2 y frecuencias de excitación de 0 a 50 Hz (ver Fig. 5).
obtenidos experimentalmente. El
amortiguamiento modal se estima con los métodos de Peak Peaking y Curve Fitting.
La estructura tipo edificio de tres pisos con TMD se caracteriza aplicando un
movimiento armónico en el suelo, utilizando la componente vertical del registro
sísmico, que tiene una amplitud variable aproximadamente entre 0 y 0.20 m/s2 y frecuencias de excitación de 0 a 50 Hz (ver Fig. 5).
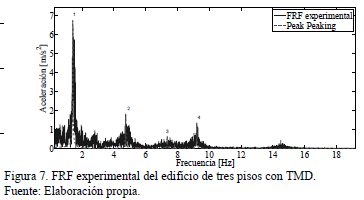
La FRF experimental se describe en la Fig. 7. Los resultados del análisis modal experimental se resumen en la Tabla 4, donde se puede apreciar un aproximamiento razonable con respecto a los resultados numéricos.
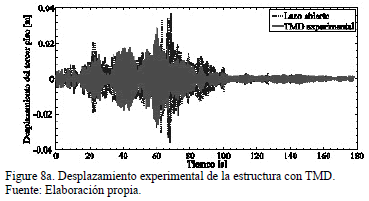
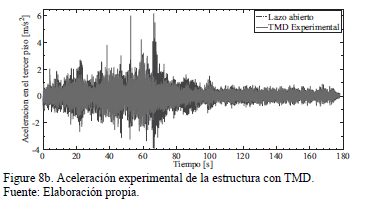
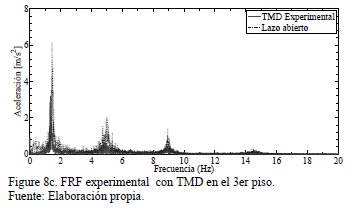
La respuesta dinámica experimental (desplazamiento y aceleración) en el tercer piso de la estructura tipo edificio con TMD, cuando se somete a movimiento sísmico en el suelo se muestra en las Figs. 8a,b,c.
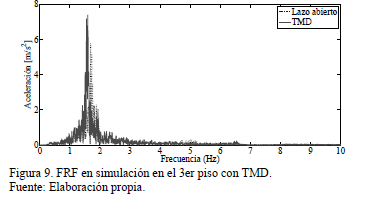
La respuesta del sistema cerca del segundo modo de vibración se atenúa en 39.78%. La FRF en simulación del tercer piso considerando el TMD se presenta en la Fig. 9. En este caso los últimos modos se reducen.
Dado que el TMD está diseñado para atenuar una frecuencia de resonancia específica se considera que esta solución no es lo suficientemente robusta para atenuar en forma simultánea varios modos de vibración en presencia de vibraciones con variación en las frecuencias de excitación y amplitud, como las frecuencias de una señal sísmica. Involucrando otros efectos no deseables como roll-off. Es por tal motivo, que aplicamos esquemas de control pasivo/activo de vibraciones con técnicas de retroalimentación positiva de posición.
6. Estructura tipo edificio con control pasivo/activo PPF
El esquema de
control por retroalimentación positiva de posición (PPF, por sus siglas en
inglés) se utiliza para compensar la respuesta del sistema en presencia de la
perturbación generada por la señal sísmica 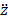 . Este controlador es ampliamente conocido
en la literatura como un método de control modal para atenuación de vibraciones
[9,11,12,14,15].
. Este controlador es ampliamente conocido
en la literatura como un método de control modal para atenuación de vibraciones
[9,11,12,14,15].
Este esquema de control agrega un grado de libertad adicional al sistema mecánico original, considerado como un absorbedor pasivo virtual o como un filtro de segundo orden. Los parámetros de este controlador se pueden obtener utilizando datos experimentales, lo que hace que la técnica PPF sea muy utilizada entre otro tipo de aplicaciones estructurales y de control [11]. El término de retroalimentación positiva de la posición significa que la coordenada de posición (desplazamiento) del sistema primario se retroalimenta positivamente al filtro y la coordenada de posición (desplazamiento) del compensador (sistema secundario) se retroalimenta positivamente al sistema primario [11].
Considere el
edifico de tres pisos con TMD colocado en el tercer piso, la aceleración del
suelo o señal sísmica 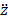 y
una fuerza de control activa
y
una fuerza de control activa 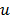 que
actúa sobre el TMD, que se representa como
que
actúa sobre el TMD, que se representa como
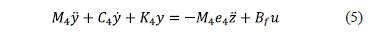
donde 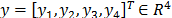 es
el vector de coordenadas generalizadas,
es
el vector de coordenadas generalizadas, 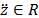 es
la aceleración del suelo generado por la señal sísmica en la base del sistema y
es
la aceleración del suelo generado por la señal sísmica en la base del sistema y 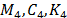 son
las matrices de masas, amortiguamiento y rigidez de 4x4, respectivamente. Aquí
son
las matrices de masas, amortiguamiento y rigidez de 4x4, respectivamente. Aquí 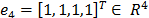 es
el vector de influencia que representa el acoplamiento inercial entre los pisos
y el movimiento del suelo. El control de fuerza
es
el vector de influencia que representa el acoplamiento inercial entre los pisos
y el movimiento del suelo. El control de fuerza  afecta directamente a la masa
afecta directamente a la masa 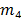 del
TMD y
del
TMD y 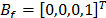 representa una matriz de entrada para el
sistema completo.
representa una matriz de entrada para el
sistema completo.
Note que el
sistema (5) es completamente controlable a partir de la fuerza de control 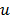 y
observable a partir del desplazamiento del TMD
y
observable a partir del desplazamiento del TMD 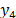 .
.
En nuestro
caso, la estructura mecánica tiene únicamente un sensor de movimiento
(aceleración) en el TMD (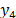 ) y una fuerza de control
) y una fuerza de control 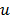 que
actúa directamente sobre su masa (
que
actúa directamente sobre su masa (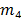 ). El esquema de control PPF para la
estructura tipo edificio de cuatro grados de libertad (5) resulta en el sistema
en lazo cerrado
). El esquema de control PPF para la
estructura tipo edificio de cuatro grados de libertad (5) resulta en el sistema
en lazo cerrado
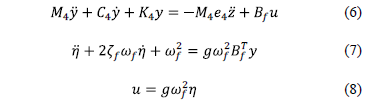
donde 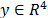 y
y 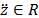 es
el movimiento del suelo. El absorbedor pasivo virtual
es
el movimiento del suelo. El absorbedor pasivo virtual 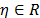 , con relación de amortiguamiento
, con relación de amortiguamiento 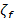 y
frecuencia natural
y
frecuencia natural 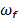 , se retroalimenta con el sistema primario
mediante
, se retroalimenta con el sistema primario
mediante 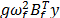 . La ley de control PPF se representa por
la fuerza de control
. La ley de control PPF se representa por
la fuerza de control 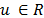 , donde
, donde 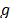 es
una ganancia de control.
es
una ganancia de control.
En forma compacta, el sistema en lazo cerrado se describe como
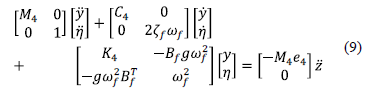
Observe
que la matriz de masa 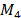 es
simétrica y definida positiva, por lo tanto, la matriz de masa completa en (9)
es también simétrica y definida positiva. La matriz de amortiguamiento
proporcional
es
simétrica y definida positiva, por lo tanto, la matriz de masa completa en (9)
es también simétrica y definida positiva. La matriz de amortiguamiento
proporcional 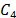 es
simétrica y definida positiva, y de igual forma, la matriz de amortiguamiento
completa tiene las mismas propiedades. Sin embargo, la matriz de rigidez
es
simétrica y definida positiva, y de igual forma, la matriz de amortiguamiento
completa tiene las mismas propiedades. Sin embargo, la matriz de rigidez 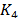 es
simétrica y definida positiva, y para garantizar la estabilidad asintótica en
lazo cerrado es suficiente el seleccionar constantes apropiadas
es
simétrica y definida positiva, y para garantizar la estabilidad asintótica en
lazo cerrado es suficiente el seleccionar constantes apropiadas 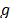 y
y 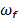 en
el control PPF, de tal forma que la matriz de rigidez en lazo cerrado sea
simétrica y definida positiva [9,12]. Para mostrar esto considere que
en
el control PPF, de tal forma que la matriz de rigidez en lazo cerrado sea
simétrica y definida positiva [9,12]. Para mostrar esto considere que
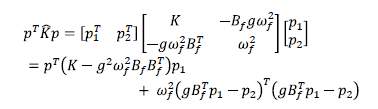
siendo el
segundo término siempre no negativo y para asegurar la estabilidad asintótica
en lazo cerrado, la matriz de rigidez 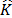 debe ser definida positiva, esto se obtiene
seleccionando
debe ser definida positiva, esto se obtiene
seleccionando 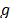 y
y 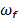 de
tal forma que la matriz
de
tal forma que la matriz 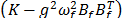 sea
definida positiva [9].
sea
definida positiva [9].
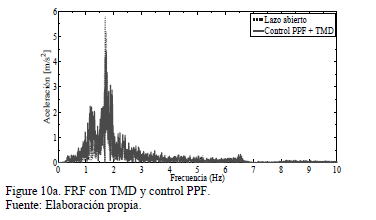
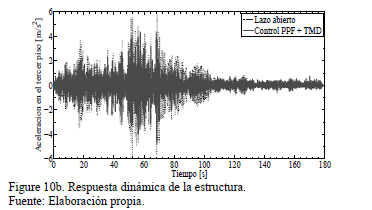
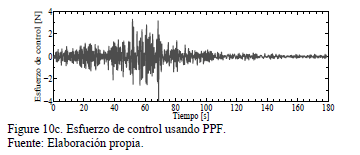
Las Figs.
10a,b,c describen los resultados numéricos aplicando el esquema de control
activo/pasivo de vibraciones (6)-(8). Los parámetros del control PPF son 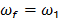 ,
, 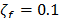 y
y 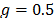 . La respuesta completa del sistema se
atenúa en alrededor del 49% con respecto a la dinámica de la estructura en lazo
abierto, con pequeños esfuerzos de control.
. La respuesta completa del sistema se
atenúa en alrededor del 49% con respecto a la dinámica de la estructura en lazo
abierto, con pequeños esfuerzos de control.
Para mejorar el desempeño de la respuesta vibratoria del esquema de control activo/pasivo usando TMD y control PPF, proponemos agregar múltiples controladores PPF para obtener mayor robustez para un amplio rango de frecuencias.
7. Estructura tipo edificio con un control MPPF y TMD
El control basado
en múltiple absorbedores pasivos virtuales (MPPF) es una extensión del control
PPF. El propósito de este esquema es agregar 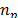 absorbedores pasivos virtuales conectados en
paralelo hacia el sistema primario, para atenuar las vibraciones [9,16].
absorbedores pasivos virtuales conectados en
paralelo hacia el sistema primario, para atenuar las vibraciones [9,16].
Considere el
edificio de tres pisos con TMD sobre el tercer piso, la aceleración del suelo 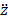 y
una fuerza de control activa operando sobre el TMD. El diseño de un control
MPPF para una estructura tipo edificio de cuatro grados de libertad (5) resulta
en un sistema en lazo cerrado de la forma
y
una fuerza de control activa operando sobre el TMD. El diseño de un control
MPPF para una estructura tipo edificio de cuatro grados de libertad (5) resulta
en un sistema en lazo cerrado de la forma
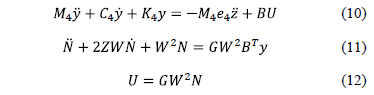
donde 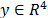 y
y 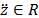 es
el movimiento en la base,
es
el movimiento en la base, 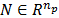 son
coordenadas de
son
coordenadas de 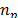 absorbedores pasivos virtuales, con matrices diagonales de relaciones de
amortiguamiento
absorbedores pasivos virtuales, con matrices diagonales de relaciones de
amortiguamiento 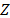 y
frecuencias naturales
y
frecuencias naturales 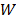 . En este caso
. En este caso 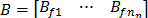 . La ley de control MPPF está representada
por la fuerza de control
. La ley de control MPPF está representada
por la fuerza de control 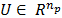 , donde
, donde 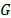 es
una matriz diagonal de ganancias de control.
es
una matriz diagonal de ganancias de control.
En forma compacta el sistema en lazo cerrado es expresado de la siguiente forma
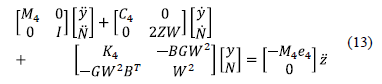
Note que la matriz 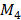 es simétrica y definida positiva, además
es simétrica y definida positiva, además 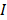 es la matriz
identidad y, entonces, la matriz de masa completa en (13) es también simétrica y
definida positiva. La matriz
es la matriz
identidad y, entonces, la matriz de masa completa en (13) es también simétrica y
definida positiva. La matriz 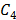 es simétrica y definida positiva, luego la
matriz de amortiguamiento completo es también simétrica y definida positiva. La
matriz de rigidez
es simétrica y definida positiva, luego la
matriz de amortiguamiento completo es también simétrica y definida positiva. La
matriz de rigidez 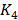 es simétrica y definida positiva, y para
garantizar la estabilidad asintótica en lazo cerrado resulta suficiente
seleccionar constantes adecuadas
es simétrica y definida positiva, y para
garantizar la estabilidad asintótica en lazo cerrado resulta suficiente
seleccionar constantes adecuadas 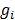 y
y 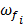 , de tal forma que
la matriz de rigidez en lazo cerrado sea simétrica y definida positiva [9].
Para mostrarlo considere
, de tal forma que
la matriz de rigidez en lazo cerrado sea simétrica y definida positiva [9].
Para mostrarlo considere 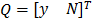 , con la forma cuadrática
, con la forma cuadrática
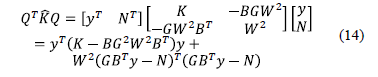
donde el
segundo término es siempre no negativo y con esto, para asegurar la estabilidad
asintótica en lazo cerrado, la matriz de rigidez 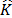 en
(14) debe ser definida positiva, que se obtiene seleccionando las matrices
en
(14) debe ser definida positiva, que se obtiene seleccionando las matrices 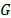 y
y 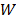 de
tal forma que
de
tal forma que 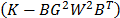 sea
definida positiva [3].
sea
definida positiva [3].
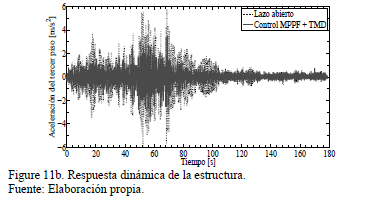
Las Figs.
11a,b,c, muestran los resultados numéricos del esquema de control pasivo/activo
(9)-(11). Los parámetros del control MPPF son 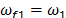 ,
, 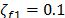 ,
, 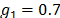 ,
, 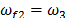 ,
, 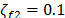 ,
, 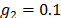 y
y 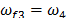 ,
, 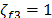 ,
, 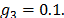 La
respuesta del sistema se atenúa aproximadamente en 54% con respecto a la
respuesta en lazo abierto, empleando esfuerzos de control muy pequeños.
La
respuesta del sistema se atenúa aproximadamente en 54% con respecto a la
respuesta en lazo abierto, empleando esfuerzos de control muy pequeños.
Para optimizar el desempeño del control MPPF, proponemos agregar un esquema de control PPF combinado con una componente de control basada en modos deslizantes para obtener una dinámica más robusta.
8. Estructura tipo edificio con un control TMD y PPF combinado con modos deslizantes
La técnica de control por modos deslizantes es un esquema de control robusto que puede utilizarse tanto para sistemas lineales como no lineales. Una característica importante de los controladores por modos deslizantes es su alta robustez, ante la presencia de incertidumbres no modeladas, como son las perturbaciones externas [13].
Para compensar en forma simultánea varios modos de vibración, un control PPF con modos deslizantes se expresa como
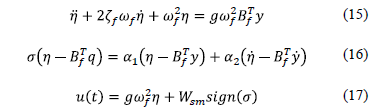
donde 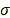 es
la superficie de conmutación, establecida en términos del error virtual
es
la superficie de conmutación, establecida en términos del error virtual 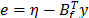 , con los parámetros positivos
, con los parámetros positivos 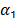 y
y 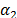 y
y 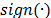 es
la función signum, que para
propósitos prácticos se aproxima por la función continua
es
la función signum, que para
propósitos prácticos se aproxima por la función continua
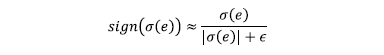
con un parámetro positivo 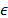 suficientemente pequeño, dependiendo de las
limitaciones físicas y ancho de banda del motor de cd.
suficientemente pequeño, dependiendo de las
limitaciones físicas y ancho de banda del motor de cd.
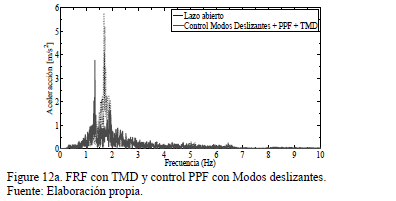
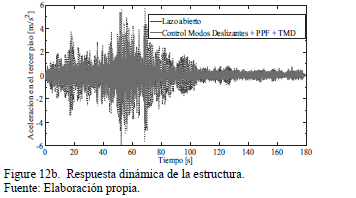
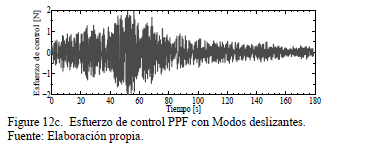
En las Figs.
12a,b,c se ilustran los resultados numéricos, aplicando el esquema de control
pasivo/activo de vibraciones (15)-(17). Los parámetros del control PPF con
modos deslizantes son 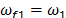 ,
, 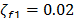 ,
, 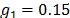 ,
,  ,
, 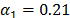 y
y 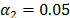 y
y 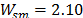 . Se observa la buena atenuación en la
respuesta frecuencial, aunque en este caso el esfuerzo de control es mayor,
debido al término del control por modos deslizantes.
. Se observa la buena atenuación en la
respuesta frecuencial, aunque en este caso el esfuerzo de control es mayor,
debido al término del control por modos deslizantes.
En general, el controlador PPF combinado con modos deslizantes resulta más sencillo de implementar que el controlador MPPF, produciendo una mejor respuesta y empleando esfuerzos de control ligeramente mayores, pero añadiendo robustez ante las perturbaciones exógenas desconocidas, como realmente ocurre en los sismos.
9. Conclusiones
Se utiliza un absorbedor pasivo/activo con esquemas de control por retroalimentación positiva de la posición y modos deslizantes para una estructura tipo edificio de tres pisos, perturbada en su base por un registro sísmico de magnitud 8.1 Mw, que afectó a la Ciudad de México en 1985. El desempeño del sistema completo, en lazo abierto y lazo cerrado, se valida a través de resultados en simulación y experimentales. Los resultados son satisfactorios, debido a que los esquemas de control atenúan altamente la respuesta del sistema en presencia de la señal excitadora, utilizando pequeños esfuerzos de control y recurriendo únicamente a la retroalimentación de la posición del TMD.
Referencias
[1] Meli, R. y Bazán, E., Diseño sísmico de edificios. México: Editorial LIMUSA, 2013.
[2] Gómez, G., Marulanda, J. and Thomson, P., Control systems for dynamic loading protection of civil structures. DYNA, 75 (155), pp. 77-89, 2008.
[3] Centro de Instrumentación y Registro Sísmico, A.C. Datos del registro sísmico del temblor de la Ciudad de México en 1985. [Online] Disponible en: www.cires.org.mx
[4] Rios-Gutiérrez, M. and Silva-Navarro, G., Active vibration control in building-like structures using piezoelectric actuators and positive acceleration feedback. DYNA, 80 (179), pp. 116-125, 2013.
[5] Auvinet G. y Mendoza M.J., Comportamiento de diversos tipos de cimentación en la zona lacustre de la Ciudad de México durante el sismo del 19 de septiembre de 1985. Proc. Symposium: Los Sismos de 1985; Casos de Mecánica de Suelos, 1986.
[6] Schmidt-Díaz, V. y Quirós-Serrano, C. Caracterización de los registros acelerográficos obtenidos en el laboratorio de ingeniería sísmica de la Universidad de Costa Rica. Ingeniería, 17 (1), pp. 27-41, 2007.
[7] Kappos, A.J. and Anastasios, G.S., Protection of buildings from earthquake-induced vibration, en Crocker M.J. In: Handbook of Noise and Vibration Control, Wiley, 2007.pp. 1393-1403. https://doi.org/10.1002/9780470209707.ch117
[8] Santana, G., Sismo de Cóbano 25 de marzo de 1990 efectos sobre suelos y edificaciones, Costa Rica: Univ. de Costa Rica, Inst. Inv. en Ingeniería, Lab. de Ing. Sísmica, 1990.
[9] Cabrera-Amado, A. and Silva-Navarro, G., Semiactive vibration absorption in a rotor-bearing system using a PPF control scheme, Proc. International Conference on Noise and Vibration Engineering ISMA2012+USD2012, pp. 209-221, 2012.
[10] Gawronski, W.K., Advanced structural dynamics and active control of structures. NY: Springer-Verlag, 2002.
[11] Inman, D.J., Tarazaga, P.A. and Salehian, A., Active and passive damping of structures, Proc. International Congress on Sound and Vibration ICSV13, pp. 1-8, 2006.
[12] Friswell, M.I. and Inman, D.J. The relationship between positive position feedback and output feedback controllers. Smart Materials and Structures, 8, pp. 285-291, 1999. https://doi.org/10.1088/0964-1726/8/3/301
[13] Utkin, V.I., Sliding modes in control and optimization. Berlin: Springer-Verlag, 1992. https://doi.org/10.1007/978-3-642-84379-2
[14] Baz, A. and Poh, S., Optimal vibration control with modal positive position feedback. Optim. Control Appl. Meth., 17 (2), pp. 141-149, 1996. https://doi.org/10.1002/(SICI)1099-1514(199604/06)17:2<141::AID-OCA566>3.0.CO;2-D
[15] Baz, A. and Hong, J.T., Adaptive control of flexible structures using modal positive position feedback. International Journal of Adaptive Control and Signal Processing, 11 (3), pp. 231-253, 1997. https://doi.org/10.1002/(SICI)1099-1115(199705)11:3<231::AID-ACS435>3.0.CO;2-8
[16] Moon K.K. and Seok H., Active vibration control of smart grid structure by multiinput and multioutput positive position feedback controller. Journal of Sound and Vibration, 304 (1-2), pp. 230-245, 2007. https://doi.org/10.1016/j.jsv.2007.02.021
J. Enríquez-Zárate, es Ing. en Cibernética de la Universidad del Sol, Cuernavaca, México, con grado de MSc en Ing. Eléctrica - Mecatrónica, y de Dr en Ing. en Diseño Mecánico, ambos obtenidos en la UNAM, Mexico D.F, México. Actualmente realiza una estancia Posdoctoral en la Sección de Mecatrónica en el CINVESTAV-IPN, México, con intereses de investigación en absorbedores de vibraciones activo/pasivo y semi-activo en estructuras mecánicas (edificios, plataformas marinas, eólicos), diseño mecánico y control de sistemas no lineales.
G. Silva-Navarro, es Ing. Mecánico (Diseño Mecánico e Ingeniería Térmica) con grado de MSc. en Inge. Eléctrica (Control) ambos obtenidos en el Instituto Tecnológico de la Laguna, Torreón, México, y con grado de Dr. en Ing. Eléctrica (Control Automático) obtenido en el CINVESTAV-IPN, México. Actualmente es investigador titular en la Sección de Mecatrónica en el CINVESTAV-IPN. México, con intereses de investigación en mecatrónica, absorbedores de vibraciones activo/pasivo para sistemas mecánicos, estructuras inteligentes, máquinas rotativas, diseño mecánico y control de sistemas no lineales.
References
Meli, R. y Bazán, E., Diseño sísmico de edificios. México: Editorial LIMUSA, 2013.
Gómez, G., Marulanda, J. and Thomson, P., Control systems for dynamic loading protection of civil structures. DYNA, 75 (155), pp. 77-89, 2008.
Centro de Instrumentación y Registro Sísmico, A.C. Datos del registro sísmico del temblor de la Ciudad de México en 1985. [Online] Disponible en: www.cires.org.mx
Rios-Gutiérrez, M. and Silva-Navarro, G., Active vibration control in building-like structures using piezoelectric actuators and positive acceleration feedback. DYNA, 80 (179), pp. 116-125, 2013.
Auvinet G. y Mendoza M.J., Comportamiento de diversos tipos de cimentación en la zona lacustre de la Ciudad de México durante el sismo del 19 de septiembre de 1985. Proc. Symposium: Los Sismos de 1985; Casos de Mecánica de Suelos, 1986.
Schmidt-Díaz, V. y Quirós-Serrano, C. Caracterización de los registros acelerográficos obtenidos en el laboratorio de ingeniería sísmica de la Universidad de Costa Rica. Ingeniería, 17 (1), pp. 27-41, 2007.
Kappos, A.J. and Anastasios, G.S., Protection of buildings from earthquake-induced vibration, en Crocker M.J. In: Handbook of Noise and Vibration Control, Wiley, 2007.pp. 1393-1403. https://doi.org/10.1002/9780470209707.ch117
Santana, G., Sismo de Cóbano 25 de marzo de 1990 efectos sobre suelos y edificaciones, Costa Rica: Univ. de Costa Rica, Inst. Inv. en Ingeniería, Lab. de Ing. Sísmica, 1990.
Cabrera-Amado, A. and Silva-Navarro, G., Semiactive vibration absorption in a rotor-bearing system using a PPF control scheme, Proc. International Conference on Noise and Vibration Engineering ISMA2012+USD2012, pp. 209-221, 2012.
Gawronski, W.K., Advanced structural dynamics and active control of structures. NY: Springer-Verlag, 2002.
Inman, D.J., Tarazaga, P.A. and Salehian, A., Active and passive damping of structures, Proc. International Congress on Sound and Vibration ICSV13, pp. 1-8, 2006.
Friswell, M.I. and Inman, D.J. The relationship between positive position feedback and output feedback controllers. Smart Materials and Structures, 8, pp. 285-291, 1999. https://doi.org/10.1088/0964-1726/8/3/301
Utkin, V.I., Sliding modes in control and optimization. Berlin: Springer-Verlag, 1992. https://doi.org/10.1007/978-3-642-84379-2
Baz, A. and Poh, S., Optimal vibration control with modal positive position feedback. Optim. Control Appl. Meth., 17 (2), pp. 141-149, 1996. https://doi.org/10.1002/(SICI)1099-1514(199604/06)17:2<141::AID-OCA566>3.0.CO;2-D
Baz, A. and Hong, J.T., Adaptive control of flexible structures using modal positive position feedback. International Journal of Adaptive Control and Signal Processing, 11 (3), pp. 231-253, 1997. https://doi.org/10.1002/(SICI)1099-1115(199705)11:3<231::AID-ACS435>3.0.CO;2-8
Moon K.K. and Seok H., Active vibration control of smart grid structure by multiinput and multioutput positive position feedback controller. Journal of Sound and Vibration, 304 (1-2), pp. 230-245, 2007. https://doi.org/10.1016/j.jsv.2007.02.021
How to Cite
IEEE
ACM
ACS
APA
ABNT
Chicago
Harvard
MLA
Turabian
Vancouver
Download Citation
CrossRef Cited-by
1. Fernando Gómez, Wen Yu. (2021). Discrete-time tri-directional active control of building structures. Engineering Structures, 243, p.112689. https://doi.org/10.1016/j.engstruct.2021.112689.
2. J. Enríquez-Zárate, L. Trujillo, C. Hernández, Claudia N. Sánchez. (2019). Numerical and Evolutionary Optimization – NEO 2017. Studies in Computational Intelligence. 785, p.187. https://doi.org/10.1007/978-3-319-96104-0_10.
3. Josue Enríquez‐Zárate, Guillermo Valencia‐Palomo, Francisco‐Ronay López‐Estrada, Gerardo Silva‐Navarro, José Antonio Hoyo‐Montaño. (2020). Efficient predictive vibration control of a building‐like structure. Asian Journal of Control, 22(4), p.1411. https://doi.org/10.1002/asjc.2015.
4. P. Aguilar-Álvarez, G. Valencia-Palomo, J. Enríquez-Zárate, J. Morales-Valdez, O. Hernández-González. (2023). Vibration Control Using a Positive Position Feedback-based Predictive Controller Applied to a One-Bay Three-Story Scaled Shear Frame. Journal of Vibration Engineering & Technologies, 11(3), p.873. https://doi.org/10.1007/s42417-022-00613-w.
Dimensions
PlumX
Article abstract page views
Downloads
License
Copyright (c) 2014 DYNA

This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.
The author of a paper accepted for publication in any of the journals published by the School of Mines will yield all the property to the National University of Colombia rights free of charge, within which include article: the right to edit, publish, reproduce and distribute both print and digital media, as well as including in an article in international indexes and / or databases, likewise, it enables the publisher to use images, tables and/or graphic material presented in Article for designing covers or posters of the magazine. By assuming the economic rights of the article, it may be reproduced partially or totally in any printed or digital media without express permission of the same.