Published
Convergence analysis of the variables integration method applied in multiobjetive optimization in the reactive power compensation in the electric nets
DOI:
https://doi.org/10.15446/dyna.v82n190.43697Keywords:
Heuristic optimization, evolutionary algorithms, power factor (es)Downloads
DOI: https://doi.org/10.15446/dyna.v82n190.43697
Convergence analysis of the variables integration method applied in multiobjetive optimization in the reactive power compensation in the electric nets
Análisis de la convergencia del método de integración de variables aplicado en la optimización multiobjetivos de la compensación de potencia reactiva en redes de suministro eléctrico
Secundino Marrero-Ramírez a, Ileana González-Palau b & Aristides A. Legra-Lobaina c
a Instituto Superior Minero Metalúrgico, Moa, Cuba,
smarrero@ismm.edu.cu
b Instituto Superior Minero Metalúrgico, Moa, Cuba,
igonzalez@ismm.edu.cu
c Instituto Superior Minero
Metalúrgico, Moa, Cuba, alegra@ismm.edu.cu
Received: May 27th, 2014. Received in revised form: January 16th, 2015. Accepted: February 23th, 2015.
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.
Abstract
This research deals with the use of a calculus method in
multi-criteria optimization. A modification do the algorithm of variable
integration was carried out, in order to establish a terminal criterion during
the multi-objective optimization of the reactive power compensation, in
electric supply nets. It demanded the
use of heuristic techniques, where the existence of high number of nodes,
guided the research towards methods able to minimize the required processing
time to find a solution, without affecting the quality of the results, and the
convergence of the process, in spite of the high number of present members
within the total population to be evaluated.
Key words: Heuristic optimization, evolutionary algorithms, power factor.
Resumen
La
investigación trata sobre el uso de un método de cálculo en la optimización
multicriterial. Se llevó a cabo una modificación al algoritmo de integración de
variables, para establecer un criterio de parada durante la optimización
multiobjetivo en la compensación de potencia reactiva en redes de suministro
eléctrico. Se requirió el uso de
técnicas heurísticas, donde la existencia de un elevado número de nodos,
condujo la investigación hacia métodos capaces de minimizar el tiempo de
proceso requerido, para encontrar una solución, sin afectar la calidad de los
resultados y la convergencia de los procesos, a pesar del elevado número de
miembros presentes en la población total a ser evaluada
Palabras clave: Optimización heurística, algoritmo evolutivo, factor de potencia.
1. Introducción
Los problemas de optimización pueden ser formulados en términos de encontrar el valor de un conjunto de variables de decisión, para lo cual una función objetivo o un conjunto de ellas pueden alcanzar un valor mínimo o máximo, considerando restricciones. Estos problemas, en un número considerable suelen ser no linealizables, lo que dificulta la obtención de un óptimo global. Ello ha exigido la creación de procedimientos que permitan lidiar con estas dificultades durante la búsqueda de buenas soluciones que pueden ser no óptimas pero si satisfactorias.
La solución a los problemas de optimización combinatoria multiobjetivo se aplica hoy en diferentes campos de los sistemas energéticos donde la inteligencia artificial permite superar las dificultades de la programación matemática clásica a través de técnicas como la optimización difusa por enjambre de partículas con factor de constricción -c (EPSO- c) donde se integran elementos de la optimización difusa, inteligencia de grupo y estrategias evolutivas [14,15].
Las técnicas heurísticas cada vez tienen mayor aplicación en los estudios de calidad de energía como se muestra en [6], el pronóstico de demanda a través de modelos no lineales [13] y en balance de cargas para la eficiencia energética [15]
Entre los métodos heurísticos más utilizados hoy para los problemas relacionados con la compensación de la potencia reactiva, se encuentran los Algoritmos Genéticos (AG), donde se destacan autores como Aydogan [3], Furong [4], y Hernández [12]. Esta técnica utiliza como procedimiento general, un primer paso que consiste en la búsqueda de una población inicial que cumpla con las restricciones del problema (individuos admisibles) y la evaluación de la función objetivo en cada individuo de esta población.
Durante el segundo paso, se efectúa la generación de nuevos individuos, evaluación de la función objetivo y las restricciones, donde se sustituyen los "peores" individuos de la población por los "mejores" (entre los nuevos individuos generados). Estos dos pasos se repiten hasta que se encuentra una población final.
Es importante aclarar que en los Algoritmos Genéticos no se obtiene una solución óptima, sino que se busca un conjunto de soluciones próximas al óptimo o soluciones eficientes.
El problema que será abordado, surge cuando se tienen múltiples capacitores para ser situados en un conjunto de nodos candidatos de un sistema de suministro eléctrico y se requieren encontrar soluciones óptimas con técnicas heurísticas para su distribución en el menor tiempo posible de búsqueda, empleando una función objetivo multicriterial [7,16]. Esta tarea puede ser tratada como minimizar la distancia de Tchevichef (que existe entre un valor calculado y el valor deseado) para un conjunto de indicadores técnico económico seleccionados dentro de la función objetivo [10], lo que facilita la mejora selectiva de los parámetros de explotación y permite maximizar el valor actual neto (VAN), a través de la reducción de las pérdidas.
2. Materiales y métodos
Las técnicas metaheurísticas hoy se perfilan como una buena alternativa para resolver el problema de gestión óptima de la potencia reactiva, entendido como operación, localización y dimensionado óptimo del banco de compensación. Entre ellas, los algoritmos genéticos se destacan por su rapidez de cálculo y su sencillez.
La gestión de potencia reactiva en el sistema de suministro eléctrico, es una de las estrategias que incrementa la seguridad del sistema mediante la disminución de las pérdidas y la mejora de la estabilidad de tensión. Entre las acciones que esto exige se encuentran: seleccionar la ubicación de las fuentes de generación de potencia reactiva (etapa de planificación) y decidir la asignación de la inyección de potencia reactiva en función de la demanda en la red (etapa de operación).
Durante la planificación de potencia reactiva así como en la asignación por nodos, es necesario emplear métodos de optimización con distintos objetivos y restricciones. Los objetivos comprenden, el uso de funciones de coste, que pueden ser asociadas a costes fijos y variables derivados del funcionamiento, la dimensión del banco de compensación de reactivo, así como de los costes asociados a las pérdidas en el sistema y su relación con del combustible. Otros objetivos se pueden relacionar con las desviaciones de las consignas de tensión en los nodos del sistema, los márgenes de estabilidad de tensión [1], o incluso se puede emplear una función multiobjetivo como combinación de varios objetivos.
Para resolver el problema expuesto anteriormente en presencia de una red eléctrica de gran dimensión, se necesita la utilización de un algoritmo que permita la búsqueda de la población y su mejora en el menor tiempo posible de convergencia, sin tener que recurrir a la búsqueda exhaustiva o al análisis de un volumen elevado de la población [9, 10], a partir de un criterio de parada que garantice una población final de soluciones eficientes y satisfaga las exigencias del evaluador y las restricciones. Este problema, en la actualidad también ha sido abordado por el método de colonia de hormigas [17,18] con resultados satisfactorios en la convergencia.
2.1. Optimización multiobjetivo de la compensación de potencia reactiva en redes industriales
Como función objetivo (FO) para la compensación de la potencia
reactiva [7, 10] en cada nodo  del sistema, se
utiliza:
del sistema, se
utiliza:
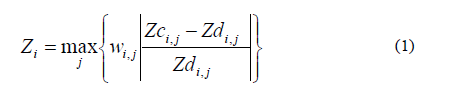
Dónde:
Zi - Valor de la
función parcial del nodo i, donde se cumple que 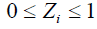 ya que
ya que

 - Coeficiente de peso en el nodo i para cada indicador j,
- Coeficiente de peso en el nodo i para cada indicador j,  , donde
, donde

Zci,j , Zdi,j - Valor calculado y deseado en el nodo i para el indicador j.
Dentro de los posibles indicadores j a utilizar, se encuentran la tensión en los nodos, el factor de potencia en los nodos, total de distorsión armónica de tensión, total de distorsión armónica de corriente, las pérdidas activas totales de la red (PT) y el valor actualizado neto (VAN), entre otros.
En este sentido, es necesario aclarar que la función implementada permite reducir el número de indicadores a criterio del evaluador, utilizando el coeficiente de peso wij que al tener el valor de cero, anula el indicador j ó permite dar mayor o menor prioridad a este, en la búsqueda de las soluciones.
2.2. Método de integración de variables
Con frecuencia surgen dificultades en la aplicación de los algoritmos genéticos a los problemas de optimización, donde en dependencia de la naturaleza de la función objetivo, pueden ser generados códigos de solución muy malos, combinando bloques de códigos buenos y se produce una pérdida de diversidad genética de la población.
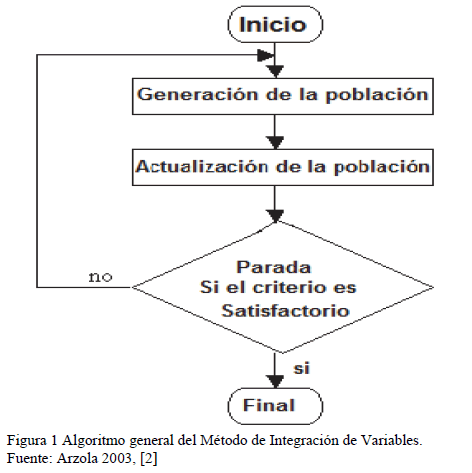
Con el propósito de superar las deficiencias antes señaladas, se han desarrollado métodos heurísticos que mantienen algunas características comunes con los Algoritmos Genéticos y evitan sus deficiencias como se muestra en Arzola [2], con el método de integración de variables (MIV), que constituye una generalización de los AG y aporta toda una familia de algoritmos heurísticos de carácter evolutivo, donde no necesariamente se debe utilizar un solo código variable para describir las posibles soluciones, sino cualquier cantidad de ellos y cualquier conjunto de operadores para actualizar los miembros de la población. El algoritmo general del MIV aparece en la Fig. 1.
Los rasgos generales de este método consisten en: las posibles variantes de solución son codificadas en uno o más códigos variables, según un procedimiento característico para cada aplicación particular del método, se genera un juego de n soluciones próximas al óptimo y la selección del criterio de parada obedece en el caso general, a las particularidades de cada aplicación concreta, donde predominan las condiciones para lograr una cantidad dada de iteraciones sin modificaciones de la población, la diferencia entre la peor y la mejor solución de la población, inferior a un valor preestablecido, así como la generación de un número predeterminado de opciones de soluciones y condiciones mixtas.
Para la aplicación del Método de Integración de Variables se requiere de la definición de los siguientes problemas:
1. Un sistema de codificaciones para la representación de las posibles soluciones del problema estudiado. Esta es una de las tareas más importantes y complejas del método.
2. Creación de la población inicial.
3. Una función de calidad (fitness) que permita ordenar los códigos, de acuerdo a los valores de la función objetivo.
4. Operadores que permiten alterar la composición de los códigos de las soluciones en las poblaciones sucesivas.
5. Valores de los parámetros requeridos por el algoritmo utilizado (tamaño de la población, probabilidades asociadas con la aplicación de ciertos operadores, etc.)
6. Atendiendo a las características del problema planteado, donde el carácter discreto, no lineal y la dimensión del sistema a analizar, limita el empleo de otras técnicas clásicas de optimización. Por ello se plantea:
Minimizar la función objetivo 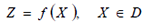 con las restricciones
con las restricciones 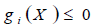 , i = 1, 2,... n
, i = 1, 2,... n
El problema a resolver lo podemos enunciar de la siguiente forma:
Donde D es el conjunto finito de las posibles T configuraciones del sistema eléctrico que se estudia, considerándose éste, un ejemplo del llamado Problema General de Optimización Discreta.
Como se ha definido, D es finito, entonces siempre se podrá aplicar el Método de Búsqueda Exhaustiva para encontrar las mejores configuraciones X.
Si T no es pequeño, entonces este método no proporciona la solución buscada (deseada) en un límite de tiempo adecuado. Sin embargo, podemos asegurar que la solución del problema existe y que debemos proponer un método de optimización que nos proporcione una solución factible en un periódo de tiempo conveniente.
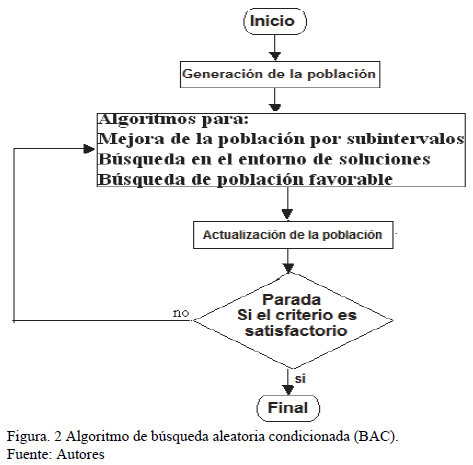
A pesar de las aplicaciones ya existentes del MIV, este puede ver limitada su aplicación debido a la no convergencia cuando la cantidad de posibles soluciones es elevada y esto exige su combinación con otros algoritmos que faciliten la búsqueda y reduzcan el tiempo de cálculo. Por ello se propone desarrollar una modificación del MIV que denominaremos Búsqueda Aleatoria Condicionada (BAC) y responde a las particularidades de la función objetivo y las restricciones del problema.
El método BAC sigue las ideas básicas del Método de Integración de Variables descrito en la Fig. 1 y en particular, reúne características del Método de Búsqueda Aleatoria del Extremo de una Función de un Código Variable. Este método esta compuesto por una serie de algoritmos con los cuales se realiza la búsqueda de la población inicial, su mejoramiento y reducción selectiva. En todos los casos se ha contemplado que esta operación de mejorar la población pueda ejecutarse tantas veces como se quiera con las siguientes estrategias:
Mejoramiento de la población por subintervalos. Esto se realiza con el objetivo de lograr una mayor diversidad en la población a todo lo largo del intervalo de existencia de soluciones.
Búsqueda en el entorno de las soluciones eficientes calculadas con el objetivo de encontrar otro miembro con mejor desempeño que la obtenida.
Búsqueda de una muestra de población favorable. A partir de las mejores características encontradas en la población ya calculada, se selecciona en dependencia de sus códigos, una subpoblación en el resto de la población aún no calculada para priorizar su evaluación.
La estructura de este algoritmo se presenta en la Fig. 2 y para su validación, se realizó el cálculo automatizado de las corridas de los flujos de potencia durante la optimización con el software DYCSE versión 1.0, [9] desarrollado en el Instituto Superior Minero Metalúrgico de Moa para el diseño y cálculo de sistemas eléctricos que utiliza la modelación del sistema propuesta en [11], donde se puede comprobar a través de un conjunto de simulaciones, como ocurre la convergencia del método propuesto al incorporar el algoritmo BAC a esta herramienta informática.
3. Caso de estudio
3.1. Sistema de suministro eléctrico de un taller mecánico
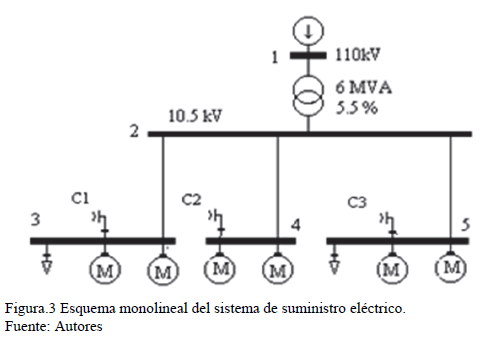
En el sistema de suministro de la Fig. 3, compuesto por tres nodos de carga, es necesario seleccionar de forma óptima los valores de los bancos de capacitores para reducir las pérdidas, considerando restricciones en las variaciones de voltaje (DV< 5%), valor del VAN positivo, los límites del cos j > 0.9 en el nodo de entrada y cos j > 0.75 en lo nodos de carga, partiendo de una variante base para el cálculo de la optimización, donde los valores del factor de potencia en los nodos de carga 3, 4 y 5 fueron elevados hasta 0.9 (ver Tabla 1). Para el cálculo económico se consideró el costo del Kvar = 15 CUC, el tiempo del proyecto de 10 años y la tasa de descuento 15%. El valor del VAN obtenido en la variante base es de 10000 CUC.
Para la validación del algoritmo durante la optimización, se realizaron las simulaciones del sistema, efectuándose primeramente una búsqueda exhaustiva en la población para obtener el patrón de calidad que permitiera evaluar soluciones con respecto al mejor valor encontrado en la misma, representada a través de Zexa que representa el mejor (mínimo) valor encontrado.
Luego se procedió a realizar experimentos con más de 40 muestras. Los resultados para cinco de estos ensayos aparecen en la Fig. 4, donde se observa el comportamiento de la relación Z/Zexa (relación del valor de Z calculada y el menor valor de Zexa = 0.728x10- 2 encontrado en la búsqueda exhaustiva para diferentes % de población evaluada, con respecto al total de individuos existentes.
En los experimento se le asignó un coeficiente de peso mayor (wi) a los indicadores factor de potencia y pérdidas totales en la función objetivo, como resultado se observó que al calcular el 5% de las configuraciones posibles, el error siempre era menor de un 2%.
En la Fig. 4 se puede observar que a pesar de iniciarse el proceso con individuos que tiene valores iniciales de Z diferentes en cada experimento, debido al grado de aleatoriedad que existe en el comienzo del proceso de búsqueda, siempre se alcanzó valores de buenas soluciones a partir de un 7%, lo cual se corrobora en la gráfica de la Fig. 5 realizada con los valores promedios obtenidos durante los 40 experimentos. De esto se puede deducir, que al arribar a la búsqueda en el entorno del 10 % de la población para este sistema, es posible obtener soluciones que garantizan las exigencias del proceso de mejora, al lograr valores cercanos al óptimo (soluciones eficientes o de Pareto), esto coincide con lo planteado por Arzola en [2].
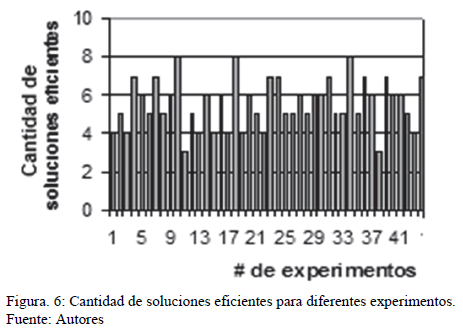
Es necesario señalar que en las simulaciones efectuadas, la aparición de soluciones eficientes cercanas a la mejor solución hallada en la búsqueda exhaustiva, superaron en la mayoría de los casos la cifra de cuatro (Fig. 6).
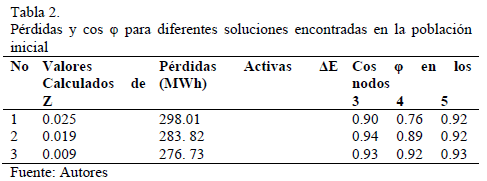
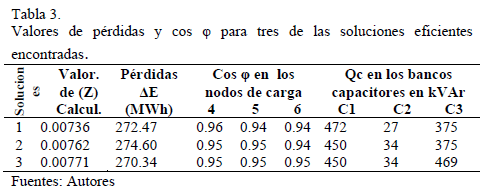
En la Tabla 2 se ofrecen valores de las soluciones encontradas en la población inicial para valores diferentes y alejados entre sí (con valores de Z alto, medios y bajos) que al ser comparados con la población final (Tabla 3) se puede observar, la mejora del factor de potencia en los nodos de carga y la reducción de las pérdidas en el sistema para tres de las mejores soluciones que garantizan en el nodo de entrada valores del factor de potencia entre 0.9 y 0.91, la reducción de pérdidas en valores superiores al 20% e incrementos del VAN en mas del 30% en comparación con la variante de base.
3.2. Análisis de resultados
Si bien los resultados obtenidos corresponden a este caso particular, la tendencia observada constituye una muestra de que es posible encontrar soluciones eficientes con el empleo de este algoritmo para volúmenes de población analizados, cercanos al 10%. También se debe señalar, que al combinar este resultado con los criterios de calidad preestablecidos para las soluciones eficientes y el comportamiento invariable del valor de Z en las iteraciones consecutivas cercanas a este %, se puede argumentar un criterio de parada efectivo. Entonces podemos afirmar que existe una vía eficaz para detener la búsqueda con una economía de tiempo importante.
En la Tabla 2 se muestra la evolución del algoritmo propuesto (BAC) para 3 valores de Z pertenecientes a la población inicial, aplicado para el ejemplo de la Fig. 3, donde existe un total de 8600 posibles configuraciones. De ellas, en la población inicial (PI) solo una tiene un valor bajo de Z = 0.009, que es el valor más cercano al mínimo valor de Z = 0.00728 encontrado en la búsqueda exhaustiva.
4. Conclusiones
En la estimación del error del algoritmo de optimización empleado, se realizaron experimentos de convergencia para la determinación del número de iteraciones necesarias, con vista a lograr soluciones óptimas en la población final.
Se observó en todos los casos, la obtención de soluciones eficientes al evaluar un número de población cercano al 10% del total de posibles soluciones. Sin bien, no se puede afirmar categóricamente que para cualquier caso tiene vigencia esta regularidad, en los experimentos realizados es posible considerar que transcurrido el número de iteraciones señalado en el análisis de poblaciones cercanas al 10%, se pueden alcanzar soluciones eficientes a pesar de la aleatoriedad presente en la búsqueda de los códigos de soluciones. También se evidenció que en un número considerable de los experimentos, al arribar al análisis del 10% de la población total, existían más de tres soluciones cercanas a los valores de la mejor solución encontrada en la búsqueda exhaustiva, además de observarse poca variabilidad de Z en este entorno, lo que permite establecer la parada en la búsqueda de soluciones eficientes.
El empleo del método de Búsqueda Aleatoria Condicionada permite generar poblaciones de soluciones y obtener convergencia en el problema de optimización de forma relativamente rápida y efectiva, lo que facilita evaluar diferentes opciones de conexión de los elementos correctores (secciones del banco de compensación y tap de trabajo en el transformador), para la selección de la variante más adecuada en la compensación de reactivo.
Bibliografía
[1] Alonso M.M., Gestión óptima de potencia reactiva en sistemas eléctricos con generación eólica. Tesis de PhD, Universidad Carlos III de Madrid. Madrid, España, 2010
[2] Arzola R.J., Simeon R.M. and Maceo, A., The integration of variables method: a generalization of genetic algorithm. Intensive workshop on optimal design of method. Paris. Francia. 2003.
[3] Aydogan, O., Jae Y.L. and Chanan, S., Post-outage reactive power flow calculations by genetic algorithms: Constrained optimization approach. IEEE Transactions on Power Systems, 20 (3), pp. 1226-1272, 2005.
[4] Li, F., Pilgrim, D.J. and Dabeedin, C., Genetic algorithms for optimal reactive power compensation on the national grid system. IEEE. Transactions On Power Systems, 20 (1), pp. 493-500, 2005. https://doi.org/10.1109/TPWRS.2004.841236
[5] García C., García E. y Villada F., Algoritmo evolutivo eficiente aplicado a la planeación de la expansión de sistemas de distribución. Revista Información Tecnológica, 23 (4), pp. 3-10, 2012. https://doi.org/10.4067/S0718-07642012000400002
[6] Gil, M.F., Manzano, A.F., Gómez, L.J. y Sánchez, A.P., Técnicas de investigación en calidad eléctrica: Ventajas e inconvenientes. DYNA, 79 (173), pp. 66-74, 2012.
[7] González, P.I., Legra, L.A., Marrero, R.S. y Arzola, R.J., Optimización de la compensación de potencia reactiva en redes de suministro eléctrico industrial con el empleo de de un algoritmo de criterios múltiples. Parte I Revista Energética [on line]. XXVII (2), pp. 40-44. 2006. Disponible en: http://revistascientificas.cujae.edu.cu/Revistas/Energetica/Vol-XXVII/2-3-2006/40-44Optimización
[8] González, P.I., Legra, L.A. y Marrero, R.S., Diseño y desarrollo del software DYCSE. Versión 1.0. Simposio Internacional Eléctrica. - SIE, Villa Clara, Cuba, 2003
[9] González, P.I., Выбор пaрaметров экономичеcки выгодной компенcaции реaктивной мощноcти // Зaпиcки Горного инcтитутa. РИЦ СПГГУ. CПб, 2011г Том. 194, pp. С 125-130. Pocиa
[10] González P. I; Я.Э. Шклярcкий. Оптимизaция компенcaции реaктивной мощноcти в cложных электричеcких cетях / // Зaпиcки Горного инcтитутa. РИЦ СПГГУ. CПб, 2011г Том. 194, pp. С 130-135. Pocиa
[11] González, P.I., Моделировaние электричеcкой cети и рacчет ее режимов при нaличии нелинейных иcкaжений // Нaучно-техничеcкие ведомоcти СПбГПУ. CПб, 2011г. N 4, pp. С. 162-170. Pocиa
[12] Hernández, G., Julio, A. y Nieva, G.J., Planificación de la compensación reactiva mediante programación evolutiva, Reunión de Verano de Potencia 2000, IEEE Sección México, Acapulco, México, 2000.
[13] Rueda, V.M., Velázquez, J.D, Franco, C.J., Avances recientes en la predicción de la demanda eléctrica usando modelos no lineales.DYNA, 78 (167), pp. 36-43, 2011.
[14] Schweickardt, G.A., Metaheurística FPSO- c. Multiobjetivo. Una aplicación para la planeación de expansión de mediano/largo plazo de un sistema de distribución eléctrica. Energética. (42) pp. 73-88. 2009. DOI: 10.15446/energética.
[15] Schweickardt, G.A., Eficiencia energética mediante el balance de fases en sistemas de distribución en baja tensión. Solución desde un enfoque metaheurístico. Energética (44) pp. 5-17, 2014. DOI: 10.15446/energética
[16] Sharaf, A.M. and El-Gammal, A.A.A., A novel discrete multi- objective particle swarm optimization (MOPSO) of optimal shunt power filter, IEEE/PES Power Systems Conference and Exposition, PSCE '09. pp. 1-7, 2009. DOI: 10.1109/PSCE.2009.4839957
[17] Stützle, T., Dorigo, M., A short convergence proof for a class of Ant Colony Optimization algorithms. IEEE Transactions on Evolutionary Computation, 6 (4), pp. 358-365, 2002. https://doi.org/10.1109/TEVC.2002.802444
[18] Gutjahr, W.J., ACO algorithms with guaranteed convergence to the optimal solution. Information Processing Letters, 82 (3), pp. 145-153, 2002. DOI: 10.1016/S0020-0190(01)00258-7
S. Marrero-Ramírez, graduado de Ing. Electrónica Industrial en 1983, del Instituto Politécnico de Kiev, Universidad Técnica de Ucrania, Ucrania, es Dr. en automatización en 1989 de la Universidad Estatal de Minas de Sant Petersburgo, Rusia. Es profesor principal de la carrera de Ingeniería Eléctrica y profesor de ingeniería de sistemas y automatización del Instituto Superior Minero Metalúrgico de Moa (ISMMM), Cuba. Su área de interés incluye eficiencia y calidad de la energía eléctrica y la automatización industrial.
I. González-Palau, graduada de Ing. Electricista del Instituto en 1983 de Minas de Moscu. Es Dra. en Ing. Eléctrica en 2011 de la Universidad Estatal de Minas de Sant Petersburgo, Rusia. Es coordinadora de la Carrera de Ing. Eléctrica y profesora de suministro eléctrico y calidad de energía eléctrica del ISMMM, Cuba. Su área de interés incluye optimización de sistemas eléctricos y calidad de la energía eléctrica.
A.A. Legra-Lobaina, graduado de Lic. en Educación Especialidad Matemática en 1981 del Instituto Superior Pedagógico Frank Pais de Santiago de Cuba. Dr. en Ciencias Técnicas del Instituto Superior Minero Metalúrgico de Moa, Cuba. Es Director del Centro de Estudios de Energía y Tecnología Avanzada de Moa y profesor en el Dpto. de Matemática del ISMMM, Cuba. Su área de interés incluye técnicas de optimización y sistemas computacionales.
How to Cite
IEEE
ACM
ACS
APA
ABNT
Chicago
Harvard
MLA
Turabian
Vancouver
Download Citation
License
Copyright (c) 2015 DYNA

This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.
The author of a paper accepted for publication in any of the journals published by the School of Mines will yield all the property to the National University of Colombia rights free of charge, within which include article: the right to edit, publish, reproduce and distribute both print and digital media, as well as including in an article in international indexes and / or databases, likewise, it enables the publisher to use images, tables and/or graphic material presented in Article for designing covers or posters of the magazine. By assuming the economic rights of the article, it may be reproduced partially or totally in any printed or digital media without express permission of the same.