Publicado
A reconstruction of objets by interferometric profilometry with positioning system of labeled target periodic
DOI:
https://doi.org/10.15446/dyna.v82n190.42616Palabras clave:
profilometry, optical metrology, surface topography, Mirau interferometer. (es)DOI: https://doi.org/10.15446/dyna.v82n190.42616
A reconstruction of objets by interferometric profilometry with positioning system of labeled target periodic
Reconstrucción de objetos por perfilometría interferométrica con sistema de posicionamiento de mira periódica
Néstor Alonso Arias-Hernández a, Martha Lucía Molina-Prado a, & Jaime Enrique Meneses-Fonseca b
a Grupo de Óptica Moderna, Universidad de Pamplona, Pamplona, Colombia.
nesariher@unipamplona.edu.co
b Grupo de Óptica y Tratamiento de Señales, Universidad Industrial
de Santander, Bucaramanga, Colombia. jaimen@uis.edu.co
Received: March 15th, 2014. Received in revised form: June 1st, 2014. Accepted: March 15th, 2015.
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.
Abstract
A method to extract 3D information using a white light
interferometer without using PZT is presented. Instead a positioning system
that uses the phase sensitivity of a target periodic is employed. The image treatment realized on the periodic
target permits to calculate the relative distance between Mirau objective and
object surface. Topographic reconstructions of objects with dimensions of some
tenths of millimeters were calculated with an accuracy of approximately 28
nanometers. Theoretical analysis and experimental results are shown.
Keywords: profilometry, optical metrology, surface topography, Mirau interferometer.
Resumen
En este
trabajo se presenta un método para extraer información 3D usando un microscopio
interferométrico, sin la necesidad de utilizar un dispositivo transductor
piezoeléctrico (PZT, por su siglas en inglés). En lugar de ello se utiliza un
sistema de posicionamiento que aprovecha la sensibilidad a la fase de una mira
periódica, que es registrada mediante el uso de un sistema de visión. El
procesamiento de la mira permite calcular la distancia relativa entre el
objetivo Mirau y el objeto. Reconstrucciones topográficas de algunas décimas de
milímetros fueron calculadas con una precisión de aproximadamente 28
nanómetros. Se presenta un análisis teórico y algunos resultados
experimentales.
Palabras clave: Perfilometría, metrología, óptica, topografía de superficie, interferometro Mirau.
1 Introducción
La interferometría con luz blanca es una técnica ampliamente utilizada
para medidas topográficas de alta resolución axial, sin contacto [1-5,14]. La
técnica básicamente divide un rayo de luz de una fuente de luz blanca en dos
haces separados. Un rayo es reflejado por la superficie del objeto a medirse
(Brazo muestra) mientras que el otro sigue un trayecto conocido de distancia
óptica constante (Brazo de referencia). Debido al ancho de banda espectral extendido de la fuente y la longitud
de coherencia corta, franjas de buen contraste se obtendrán únicamente cuando
los dos brazos del interferómetro estén próximos en longitud, cuya diferencia
sea menor a la longitud de coherencia de la fuente. Usualmente se utiliza un
PZT para variar la distancia óptica del brazo muestra del interferómetro. Las
variaciones de altura a través de la muestra pueden ser determinadas buscando
la posición que tiene el PZT cuando se obtiene el máximo contraste de
franjas. Este modo de operación es
conocido como modo de sensado del pico de
coherencia por barrido vertical. En
esta situación, el rango máximo axial de distancias para el análisis
topográfico es determinado por el máximo
desplazamiento del PZT. Un esquema
experimental tradicional puede incluir un objetivo tipo Mirau de 10X y un PZT
con desplazamiento máximo de 40 . Si se desea incrementar el máximo
desplazamiento, los dispositivos PZT presentan algunos inconvenientes, dentro
de estos se puede mencionar: alto costo y presencia de histeresis.
. Si se desea incrementar el máximo
desplazamiento, los dispositivos PZT presentan algunos inconvenientes, dentro
de estos se puede mencionar: alto costo y presencia de histeresis.
En publicaciones anteriores se ha demostrado la alta precisión y resolución de un sistema de posicionamiento que se obtiene al emplear una mira periódica [11,13]. La alta sensibilidad se obtiene al utilizar la información de fase espacial como elemento codificador de la posición espacial de la mira periódica. En el presente artículo se propone reemplazar el PZT utilizado para realizar el barrido axial en un microscopio interferométrico tipo Mirau del interferómetro.
En el presente trabajo se realiza inicialmente una descripción de la microscopía interferencial tipo Mirau, en donde se detalla el principio de funcionamiento del interferómetro. De igual forma se explica la metodología tradicional para el análisis de franjas interferométrica de luz policromática, utilizando como sistema de codificación de altura un sistema de posicionamiento basado en el rastreo de una mira periódica con un sistema de visión apropiado.
2. Sistema de microscopía interferencial tipo Mirau.
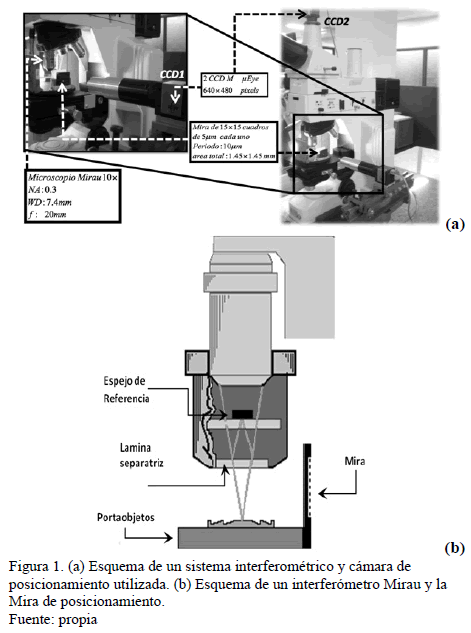
Un sistema de microscopía interferencial tipo Mirau está compuesto por un microscopio de reflexión, el cual tiene un objetivo interferométrico tipo Mirau, Fig. 1(a) y (b). El objetivo interferométrico Mirau está compuesto de una lámina semitransparente entre el objetivo y la muestra (lámina separatríz), y un espejo de referencia sobre el centro de su cara frontal. El funcionamiento del objetivo interferométrico es similar al de un interferómetro Michelson, con la diferencia que los dos brazos por donde la luz realiza su recorrido están en un mismo eje. De esta manera, cuando el haz atraviesa el objetivo, la lámina separatríz divide el frente de onda en dos: uno que se transmite hacia la muestra y el otro que es reflejado. El haz reflejado va al espejo de referencia, regresa a la lamina separatríz y se superpone con el reflejado por el objeto. Así, la correlación de los dos haces es vista por el objetivo. El contacto óptico se obtiene cuando la diferencia de camino óptico entre la lámina separatríz-espejo y la lámina semitransparente-objeto, es cero.
3. Análisis de franjas de interferencia de luz policromática.
Al utilizar el sistema mostrado de la Fig. 1(a) y (b) con luz
policromática, las reflexiones sobre la muestra, ubicada en el portaobjeto, son
combinadas con las reflexiones provenientes del espejo de referencia,
localizado en el objetivo Mirau. El campo eléctrico  que
llega al detector es la superposición de la luz que proviene de la muestra y el
espejo de referencia,
que
llega al detector es la superposición de la luz que proviene de la muestra y el
espejo de referencia,
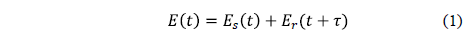
Donde 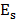 y
y  son
respectivamente las amplitudes ópticas del haz señal y del haz referencia. Mientras
que,
son
respectivamente las amplitudes ópticas del haz señal y del haz referencia. Mientras
que, 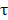 es el
tiempo de retraso debido a la diferencia de longitud en los caminos ópticos de
los dos haces. La intensidad registrada por el detector está dada por,
es el
tiempo de retraso debido a la diferencia de longitud en los caminos ópticos de
los dos haces. La intensidad registrada por el detector está dada por,

donde 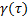 es el grado
complejo de coherencia mutua, que se expresa como,
es el grado
complejo de coherencia mutua, que se expresa como,

En general, el grado complejo de coherencia mutua incluye los efectos de coherencia espacial y temporal. Para un interferómetro de división de amplitud con el microscopio interferométrico Mirau en iluminación de Köhler, la coherencia espacial se puede despreciar. Así la coherencia mutua se reduce a la auto-coherencia o coherencia temporal, en este caso,
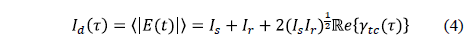
Donde,  es la
parte real del grado complejo de coherencia temporal de la fuente de luz. Su
forma normalizada está dada por
es la
parte real del grado complejo de coherencia temporal de la fuente de luz. Su
forma normalizada está dada por 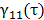 ,
,
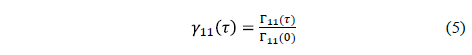 (5)
(5)
Donde  y el
subíndice 11, corresponde a un único punto de la fuente incoherente. El grado complejo de coherencia normalizado
de la fuente de luz es dado por la transformada de Fourier de la densidad
espectral de energía. Si la fuente de
luz es policromática y se asume una densidad espectral de energía gaussiana con
ancho espectral
y el
subíndice 11, corresponde a un único punto de la fuente incoherente. El grado complejo de coherencia normalizado
de la fuente de luz es dado por la transformada de Fourier de la densidad
espectral de energía. Si la fuente de
luz es policromática y se asume una densidad espectral de energía gaussiana con
ancho espectral  y
frecuencia media
y
frecuencia media  , el grado complejo de coherencia temporal
, el grado complejo de coherencia temporal 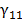 estará
dado por,
estará
dado por,

Donde  es una
constante. Teniendo en cuenta que
es una
constante. Teniendo en cuenta que  , se tiene que:
, se tiene que:

Así la ec. 4, se puede escribir como,

O

Donde  es
la intensidad de fondo,
es
la intensidad de fondo,  es
la función de contraste de las franjas o envolvente del patrón de franjas
observado. Esta función
es
la función de contraste de las franjas o envolvente del patrón de franjas
observado. Esta función  está dada por,
está dada por,
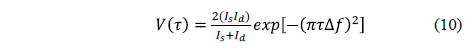
Si en el
sistema de la Fig. 2(a) y 2(b) el origen de coordenadas es tomado sobre un
punto  en
particular en la dirección axial, donde los dos caminos ópticos son iguales, y
la superficie de prueba es movida a lo largo del eje
en
particular en la dirección axial, donde los dos caminos ópticos son iguales, y
la superficie de prueba es movida a lo largo del eje  en
una serie de pasos de tamaño
en
una serie de pasos de tamaño 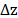 , entonces la intensidad sobre un punto
, entonces la intensidad sobre un punto 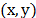 en
el plano de la imagen que corresponde a un punto del objeto de altura
en
el plano de la imagen que corresponde a un punto del objeto de altura 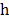 , se puede escribir como,
, se puede escribir como,

donde  e
e 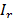 son las intensidades de los dos haces que
actúan independientemente,
son las intensidades de los dos haces que
actúan independientemente,  es el grado complejo de coherencia, la cual
corresponde a la visibilidad de la envolvente de la franjas de interferencia, y
es el grado complejo de coherencia, la cual
corresponde a la visibilidad de la envolvente de la franjas de interferencia, y  es la modulación cosenoidal donde
es la modulación cosenoidal donde  corresponde a la longitud de onda media de la
fuente,
corresponde a la longitud de onda media de la
fuente,  es la diferencia de longitud de los caminos
ópticos atravesados por los dos haces y
es la diferencia de longitud de los caminos
ópticos atravesados por los dos haces y 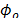 es la diferencia del corrimiento de fase
debido a las reflexiones sobre el divisor de haz, los espejos y posiblemente el
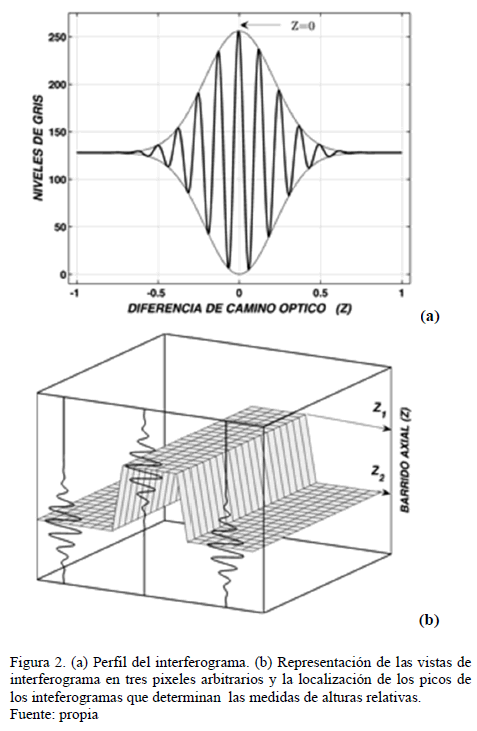
material de prueba. La Fig. 2(a),
muestra las variaciones de intensidad sobre el punto de la imagen cuando el objeto es barrido axialmente.
es la diferencia del corrimiento de fase
debido a las reflexiones sobre el divisor de haz, los espejos y posiblemente el
material de prueba. La Fig. 2(a),
muestra las variaciones de intensidad sobre el punto de la imagen cuando el objeto es barrido axialmente.
Se utiliza una
cámara (CCD2 en la Fig. 1(a)), ubicada en el plano imagen del sistema óptico
del microscopio, como mecanismo de registro del interferográma. Cada pixel de
la cámara tiene la posibilidad de registrar patrones de interferencia similares
a los de la Fig. 2(a) en la medida que el objeto es desplazado en la dirección  . Estos patrones de interferencia tienen
la posición del máximo de la envolvente en posiciones de barrido que depende de
la topografía de la superficie del objeto. De esta manera, de las posiciones
del máximo de la envolvente sobre el eje de barrido se obtiene la topografía
del objeto, ver Fig. 2(b).
. Estos patrones de interferencia tienen
la posición del máximo de la envolvente en posiciones de barrido que depende de
la topografía de la superficie del objeto. De esta manera, de las posiciones
del máximo de la envolvente sobre el eje de barrido se obtiene la topografía
del objeto, ver Fig. 2(b).
4. Detección de máximos
La detección de
máximos es una técnica que aprovecha la propiedad de los interferogramas
producidos por una fuente policromática. Según la ec. 9, las franjas se
encuentran moduladas por una envolvente 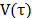 , presentando un máximo de intensidad en
puntos donde la diferencia de camino óptico es cero. Como se menciona en la
sección anterior, determinar la forma del objeto consiste en localizar la
posición del máximo de la envolvente del interferograma para cada punto del
objeto. Esto se realiza desplazando uno de los brazos del interferómetro Mirau,
de tal manera, que cada punto pase por el plano de contacto óptico. Este
desplazamiento se puede realizar moviendo el porta-objeto o moviendo el
objetivo y dejando fijo el porta-objeto. En el presente trabajo se deja fijo el
objetivo de microscopio y se desplaza el porta-objeto, sobre el cual se ha adherido una mira periódica para
determinar su posición axial, como se muestra en la sección siguiente.
, presentando un máximo de intensidad en
puntos donde la diferencia de camino óptico es cero. Como se menciona en la
sección anterior, determinar la forma del objeto consiste en localizar la
posición del máximo de la envolvente del interferograma para cada punto del
objeto. Esto se realiza desplazando uno de los brazos del interferómetro Mirau,
de tal manera, que cada punto pase por el plano de contacto óptico. Este
desplazamiento se puede realizar moviendo el porta-objeto o moviendo el
objetivo y dejando fijo el porta-objeto. En el presente trabajo se deja fijo el
objetivo de microscopio y se desplaza el porta-objeto, sobre el cual se ha adherido una mira periódica para
determinar su posición axial, como se muestra en la sección siguiente.
La cámara CCD2 registra los valores de la intensidad del interferograma, almacenando tanto el máximo del interferograma como el desplazamiento del portaobjeto, asociado al valor de intensidad máximo. Así se obtienen dos matrices: una con la información de los máximos de intensidad del interferograma y otra con las posiciones de desplazamiento del portaobjeto. La primera da una imagen en niveles de grises de los puntos del objeto focalizados y con la mayor reflectividad y la segunda brinda la información de altura del objeto discretizada en un número de niveles de grises, propio de la cámara utilizada.
5. Dispositivo experimental
La Fig. 1(a y b) muestra
como está conformado el sistema de microscopía interferencial Mirau, utilizado
en el presente artículo. Este está constituído por un microscopio de reflexión
metalográfico Eclipse 600, marca Nikon y un objetivo interferométrico tipo
Mirau de 10X de apertura numérica (NA) de 0.3 y de distancia de trabajo (WD) de
7.4mm, la cual está sincronizado a dos cámaras CCD monocromáticas de 640x480
pixeles de conexión USB, marca  . Una de estas
cámaras tiene como propósito registrar el interferograma (CCD2) y la otra
registrar la mira que está adherida al porta-objeto del microscopio (CCD1), ver
Fig. 1(a) . Tradicionalmente la muestra se ubica sobre un PZT y este sobre el
porta-objeto.
. Una de estas
cámaras tiene como propósito registrar el interferograma (CCD2) y la otra
registrar la mira que está adherida al porta-objeto del microscopio (CCD1), ver
Fig. 1(a) . Tradicionalmente la muestra se ubica sobre un PZT y este sobre el
porta-objeto.
La propuesta
implementada en el presente artículo remplaza el PZT por la mira periódica que
se ubica verticalmente sobre el porta-objeto, ver Fig. 1(a). La mira está constituída por un arreglo periódico de 15x15 cuadros de 5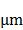 cada uno y de período 10
cada uno y de período 10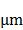 , constituyendo
así una mira de
, constituyendo
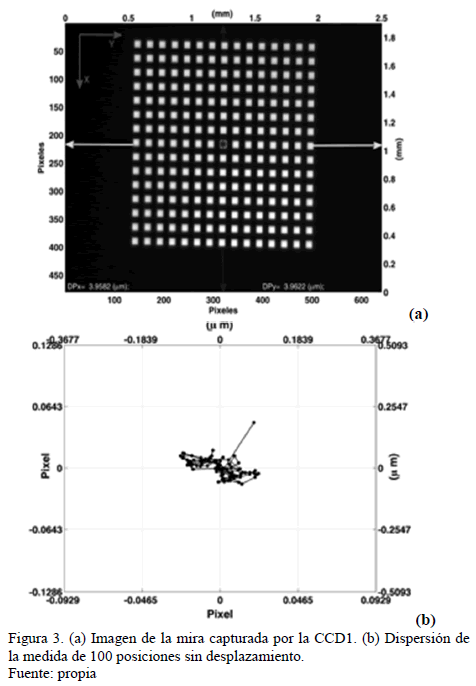
así una mira de 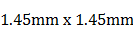 , ver Fig. 3(a).
, ver Fig. 3(a).
6. Calibración del sistema
Inicialmente se
realiza la calibración del sistema de posicionamiento, es decir, obtener la
resolución y rango de desplazamiento de la mira, la cual es observada por una cámara  monocromática de 640x480 pixeles(CCD1). Para
obtener una imagen ampliada de la mira se utiliza un objetivo de microscopio de
50mm de distancia focal, junto con un tubo extensor de 10cm aproximadamente.
Para evaluar la influencia del ruido y vibraciones del sistema se adquirieron
100 imágenes de la mira para una posición fija axial. Se calcularon las 100
posiciones del centro de la mira utilizando el método de codificación de fase.
Este método aprovecha la información de fase debido a la distribución regular
de los puntos para calcular el centro de cada uno. Como el centro de cada punto
debe tener una fase igual a un número entero de 2p, la posición se obtiene con precisión subpixel al
interpolar la fase. Este método es presentado en detalle en [11].
monocromática de 640x480 pixeles(CCD1). Para
obtener una imagen ampliada de la mira se utiliza un objetivo de microscopio de
50mm de distancia focal, junto con un tubo extensor de 10cm aproximadamente.
Para evaluar la influencia del ruido y vibraciones del sistema se adquirieron
100 imágenes de la mira para una posición fija axial. Se calcularon las 100
posiciones del centro de la mira utilizando el método de codificación de fase.
Este método aprovecha la información de fase debido a la distribución regular
de los puntos para calcular el centro de cada uno. Como el centro de cada punto
debe tener una fase igual a un número entero de 2p, la posición se obtiene con precisión subpixel al
interpolar la fase. Este método es presentado en detalle en [11].
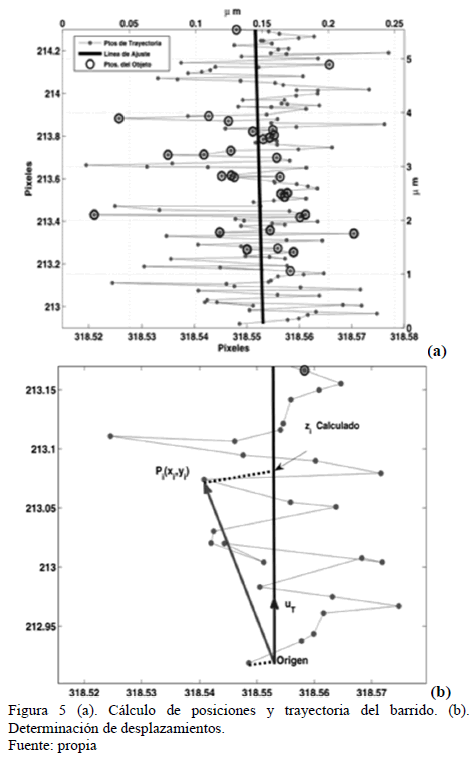
La desviación estándar de las coordenadas del centro los eje X y Y determinan la influencia del ruido en el cálculo de la posición axial usando la mira. De igual forma, se puede determinar el tamaño del pixel de la CCD1 en el plano de la mira, valor importante para calcular las coordenadas axiales en unidades métricas. Al desplazar el porta-objeto en dirección vertical y al usar el factor de conversión pixeles a milímetros sobre el plano de la mira, se puede establecer la dirección del eje de barrido. La Fig. 5(a) muestra los datos obtenidos para un desplazamiento vertical de 5.3 mm de la mira. De esta serie de datos se determina el eje de barrido, al realizar un ajuste por mínimos cuadrados, y el vector unitario del eje de barrido. Con el vector unitario se puede determinar la posición de cualquier posición de la mira al proyectar las coordenadas del centro sobre el eje de barrido, ver Fig. 5(b).
Del análisis de
los datos se obtuvo una desviación estándar de  en
X y
en
X y 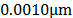 en
Y, como se puede observar en la Fig. 3(b) y el tamaño de pixel calculado es de
en
Y, como se puede observar en la Fig. 3(b) y el tamaño de pixel calculado es de  en
X y
en
X y  en
Y, ver en la Fig. 3(a). Esto implica que
el sistema es bastante estable, pudiéndose resolver dos posiciones axiales
consecutivos igual al doble de la desviación estándar, empleando la mira. Como
el sensor es de 640x480 pixeles, el campo de observación es de
en
Y, ver en la Fig. 3(a). Esto implica que
el sistema es bastante estable, pudiéndose resolver dos posiciones axiales
consecutivos igual al doble de la desviación estándar, empleando la mira. Como
el sensor es de 640x480 pixeles, el campo de observación es de 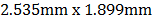 .
.
Para el cálculo del centro de la mira empleando la información de fase se requiere que la imagen de la mira en la CCD1 se observe completamente. Esto implica que la imagen de la mira ocupa una fracción de la superficie del sensor de la cámara CCD1, obteniéndose regiones libres en los extremos de la mira, como se observa en la Fig. 3(a). Esta región libre define el rango de traslación de la mira en los ejes X y Y. Debido a la disposición de la cámara CCD1, el rango de traslación en X define el rango de desplazamiento máximo del sistema de perfilometría, que corresponde a 0.449 mm. Para aplicaciones en donde sea necesario un mayor rango de desplazamiento es conveniente orientar la cámara, de tal forma, que la dirección de mayor número de pixeles coincida con la dirección de barrido. De esta manera, el uso de la mira permite un rango de desplazamiento o tamaño máximo del objeto de 449 micras con desplazamiento mínimo de 2.2 nm.
Por otro lado, para determinar el campo de observación de la cámara colocada en el interferómetro (CCD2), es decir el tamaño de la región transversal al eje óptico observada sobre el objeto, se realiza un procedimiento clásico de calibración. Este procedimiento consiste en realizar desplazamientos conocidos, empleando tornillos micrométricos, de un objeto que está siendo observado por el sistema de visión del interferómetro, al cual se facilite hacer el seguimiento de un punto particular de su superficie.
Esto permite obtener una función de asociación entre los pixeles en el
plano imagen y milímetros en el plano del objeto. En este caso como el
desplazamiento realizado es lineal, se encontró una recta de ajuste por mínimos
cuadrados, D , donde Dp es la distancia recorrida en
pixeles y Dm la distancia recorrida en mm. Esta ecuación permite determinar el
tamaño del pixel de observación de la cámara en el interferómetro (CCD2), bajo
la suposición de que el pixel posee una razón de aspecto 1. El tamaño del pixel
obtenido es
, donde Dp es la distancia recorrida en
pixeles y Dm la distancia recorrida en mm. Esta ecuación permite determinar el
tamaño del pixel de observación de la cámara en el interferómetro (CCD2), bajo
la suposición de que el pixel posee una razón de aspecto 1. El tamaño del pixel
obtenido es  , y el campo de observación es
, y el campo de observación es 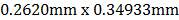 , ver Fig. 5 (a) y (b).
, ver Fig. 5 (a) y (b).
7. Resultados
La perfilometría con luz policromática fue implementada con base en la detección de máximos de intensidad explicada en las secciones 3 y 4. El método se implementó utilizando un sistema sincronizado de dos cámaras, una que registra las intensidades del interferograma y otra que registra la mira de posicionamiento. La imagen registrada de la mira permite obtener la posición en pixeles del centro de la mira, la cual es posteriormente convertida a mm mediante el proceso de calibración [11]. Mientras se realiza el barrido vertical, se almacenan dos matrices de igual tamaño en memoria (dimensiones que son determinadas por el sensor de la cámara que registra el interferograma): la matriz de los valores de intensidades máximas del interferograma y la matriz de posiciones de los máximos, las cuales son calculadas por el método de posicionamiento de la mira. Al realizarse el barrido completo, la matriz de intensidades máximas almacena el valor del máximo de intensidad obtenido en todo el recorrido y su correspondiente posición del centro de la mira, para cada posición en la imagen de la CCD2. La matriz de intensidades máximas brinda información de reflectividad de la superficie del objeto. La matriz de las posiciones de los máximos corresponde a la topografía de la superficie del objeto.
Utilizando como fuente de iluminación la lámpara halógena y aplicando el algoritmo de detección de máximos de intensidad sobre dos muestras (lente de Fresnel y una moneda de 500 COP), se obtuvieron la reconstrucción 3D de sus superficies. Las Figs 4 (a) y (b) muestra las matrices de máximos de intensidad y las Figs 4 (c) y (d) las matrices de las posiciones de los máximos en micras para las dos muestras analizadas. Para cada posición del centro de la mira se calcula la posición sobre el eje de barrido al realizar la proyección, ver Fig. 5(b). Para la lente de fresnel se realizó un barrido de 2 micras y para la moneda de 24 micras.
8. Conclusiones
Se implementó un sistema de microscopía
interferencial Mirau, que permite obtener la topografía de un objeto, con una
resolución axial de 0.028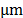 (tres desviaciones estandar) y una resolución
transversal de 5.45X10-4mm; sin la necesidad de utilizar un dispositivo de
posicionamiento piezoelectrico (PZT) para obtener las posiciones o medida de las alturas. El posicionamiento se logra utilizando el método de
posicionamiento de alta resolución basado en la recuperación de la fase
[11]. Para este esquema experimental, se
hace un análisis de franjas de interferencia de luz blanca. El nuevo esquema
implementado abre la posibilidad de ampliar el rango de desplazamiento,
permitiendo reconstruír objetos de dimensiones mayores que las permitidas por
un dispositivo piezoeléctrico convencional. En este caso, se utilizó una cámara
monocromática de 640X480 pixeles, un objetivo de microscopio de 50mm de
distancia focal, un tubo extensor de 10cm y una mira de 15x15 cuadros de 5
(tres desviaciones estandar) y una resolución
transversal de 5.45X10-4mm; sin la necesidad de utilizar un dispositivo de
posicionamiento piezoelectrico (PZT) para obtener las posiciones o medida de las alturas. El posicionamiento se logra utilizando el método de
posicionamiento de alta resolución basado en la recuperación de la fase
[11]. Para este esquema experimental, se
hace un análisis de franjas de interferencia de luz blanca. El nuevo esquema
implementado abre la posibilidad de ampliar el rango de desplazamiento,
permitiendo reconstruír objetos de dimensiones mayores que las permitidas por
un dispositivo piezoeléctrico convencional. En este caso, se utilizó una cámara
monocromática de 640X480 pixeles, un objetivo de microscopio de 50mm de
distancia focal, un tubo extensor de 10cm y una mira de 15x15 cuadros de 5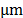 y
10
y
10 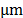 de
período. Se logra un desplazamiento de barrido máximo de 0.468mm, con
posibilidad de aumentar su rango de trabajo a 1.0858mm.
de
período. Se logra un desplazamiento de barrido máximo de 0.468mm, con
posibilidad de aumentar su rango de trabajo a 1.0858mm.
Agradecimientos
Néstor Alonso Arias Hernández y Martha Lucía Molina Prado, agradecen al Departamento de Ciencia, Tecnología e innovación - COLCIENCIAS Colombia, a la Universidad de Pamplona (Colombia) a través de la Vicerrectoría de Investigación y Extensión (Proyecto Interno PR130-00-012(GA160-BP-II-2013-2.1.2.2.1)) y a la Universidad Industrial de Santander (Colombia) por el apoyo financiero y logístico para la realización del presente trabajo. De igual forma Jaime Meneses agradece el apoyo brindado por la Universidad Industrial de Santander a través de la Vicerrectoría de Investigación y Extensión (Proyecto Interno 1343).
Referencias
[1] Caber, P.J., Interferometric profiler for rough surfaces, Appl. Opt., 32 (19), pp. 3438-3441, 1993. https://doi.org/10.1364/AO.32.003438
[2] Deck, L. and De Groot, P., High-speed noncontact profiler based on scanning white-light interferometry, Appl. Opt., 33 (31), pp. 7334-7338, 1994. https://doi.org/10.1364/AO.33.007334
[3] De Groot, P. and Deck, L., Surface profiling by analysis of white-light interferograms in the spatial frequency domain, J. of Mod. Opt. 42 (2), pp. 389-401, 1995. https://doi.org/10.1080/09500349514550341
[4] Sandoz, P., An algorithm for profilometry by white light phase shifting interferometry, J. Mod. Opt., 43 (8), pp. 1545-1554, 1996. https://doi.org/10.1080/09500349608232826 https://doi.org/10.1080/095003496154987
[5] Larkin, K.G., Efficient nonlinear algorithm for envelope detection in white light interferometry, J. Opt. Soc. Am., 13 (4), pp. 832-843, 1996. https://doi.org/10.1364/JOSAA.13.000832
[6] Takeda, M., Fourier-transform method of fringe-pattern analysis for computer-based topography and interferometry, J. Opt. Soc. Am., 72 (1), pp. 156-160, 1982. https://doi.org/10.1364/JOSA.72.000156
[7] Sandoz, P., Ravassard, J.C., Dembele, S. and Janex A., Phase sensitive vision technique for high accuracy position measurement of moving targets, IEEE Trans. Instrum. Meas., 49 (4), pp. 867-872, 2000. https://doi.org/10.1109/19.863940
[8] Sandoz, P., Bonnas, V. and Gharbi, T., High-accuracy position and orientation measurement of extended two-dimensional surfaces by a phase-sensitive vision method, Appl Opt., 41 (26), pp. 5503-5511, 2002. https://doi.org/10.1364/AO.41.005503
[9] Sandoz, P., Nanometric position and displacement measurement of the six degrees of freedom by means of a patterned surface element, Appl. Opt., 44 (8), pp. 1449-1453, 2005. https://doi.org/10.1364/AO.44.001449
[10] Sandoz, P., Zeggari, R., Prétet, J.L. and Mougin, C., Position referencing in optical microscopy thanks to sample holders with out-of-focus encoded patterns, Journal of Microscopy, 255 (3), pp. 293-303, 2007. https://doi.org/10.1111/j.1365-2818.2007.01745.x
[11] Arias, N., Suarez, M.A., Meneses, J. y Gharbi, T., Medida de la orientación, posición y desplazamiento en el plano de un objeto por codificación de fase, Revista BISTUA, ,7 (2), pp. 70-76, 2009.
[12] Galeano, J., Sandoz, P., Gaiffe, E., Prétet, J.L. and Mougin, C., Pseudo-periodic encryption of extended 2D surface for high accurate recovery of any random zone by vision, International Journal of Optomechatronics, 4 (1), pp. 65-82, 2010. https://doi.org/10.1080/15599611003660395
[13] Arias, N., Suarez, M.A., Meneses, J. and Gharbi, T. ,3D localization of a labeled target by means of a stereo vision configuration with subvoxel resolution. Opt. Exp., 18 (23), pp. 24152-24162, 2010. https://doi.org/10.1364/OE.18.024152
[14] Munera, N., Lora, G.J., Garcia-Sucerquia J., Evaluation of fringe projection and laser scanning for 3D reconstruction of dental pieces. DYNA, 79 (171), pp. 65-63, 2012.
N.A. Arias-Hernández, received the Bsc in Mathematical and Physics in 1994, from the Universidad Popular del Cesar, Colombia, the MSc degree in Physics in 2004, from the Universidad Industrial de Santander, Colombia, the PhD. degree in Natural Sciences (Physics) in 2010. He has worked as a professor and researcher for over fifteen years. Currently, he is a full professor in the Physics Program, Faculty of Natural Sciences, Universidad de Pamplona, Pamplona, Colombia. His research interests include: optics, image processing, optical design and optical metrology. ORCID: 0000-0002-9224-7654
M. L. Molina-Prado, received the Bsc. in Mathematic and Physics in 1994, from the Universidad Popular del Cesar, Colombia, the MSc degree in Physics in 2003, from the Universidad Industrial de Santander, Colombia, the PhD degree in Natural Sciences (Physics) in 2010, from the Universidad Industrial de Santander, Colombia. She has worked as a professor and researcher for over fifteen years. Currently, she is a full professor in the Physics Program, Faculty of Natural Sciences, Universidad de Pamplona, Pamplona, Colombia. Her research interests include: optics, speckle metrology and photorefractive crystals. ORCID: 0000-0002-3347-7986
J.E. Meneses-Fonseca, received the Bsc in Physics in 1990, from the Universidad Industrial de Santander, Colombia, the MSc degree in Physics in 1993, from the Universidad Industrial de Santander, Colombia, the PhD degree in Sciences Pour L'ingenieur in 1998, from the Université de Franche Comté, France. He has worked as a professor and researcher for over seventeen years. Currently, he is a full professor in the Physics Program, Faculty of Natural Sciences, Universidad Industrial de Santander, Bucaramanga, Colombia. His research interests include: optics, signal processing and optical metrology. ORCID: 0000-0001-5551-9959
Cómo citar
IEEE
ACM
ACS
APA
ABNT
Chicago
Harvard
MLA
Turabian
Vancouver
Descargar cita
Licencia
Derechos de autor 2015 DYNA

Esta obra está bajo una licencia internacional Creative Commons Atribución-NoComercial-SinDerivadas 4.0.
El autor o autores de un artículo aceptado para publicación en cualquiera de las revistas editadas por la facultad de Minas cederán la totalidad de los derechos patrimoniales a la Universidad Nacional de Colombia de manera gratuita, dentro de los cuáles se incluyen: el derecho a editar, publicar, reproducir y distribuir tanto en medios impresos como digitales, además de incluir en artículo en índices internacionales y/o bases de datos, de igual manera, se faculta a la editorial para utilizar las imágenes, tablas y/o cualquier material gráfico presentado en el artículo para el diseño de carátulas o posters de la misma revista.