Publicado
Encryption using circular harmonic key
DOI:
https://doi.org/10.15446/dyna.v82n190.42915Palabras clave:
Cryptografy, Circular harmonics, Fourier optics (es)Descargas
DOI: https://doi.org/10.15446/dyna.v82n190.42915
Encryption using circular harmonic key
Encriptación usando una llave en armónicos circulares
Jorge Enrique Rueda-Parada
Grupo Óptica Moderna, Facultad de Ciencias Básicas, Universidad de Pamplona, Pamplona, Colombia. jorgeenriquerueda@gmail.com
Received: April 2th, 2014. Received in revised form: February 2th, 2015. Accepted: February 20th, 2015
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.
Abstract
This work presents a study of variance to rotation key
encryption processors based on the Fourier transform. It was determined that
the key in rectangular coordinates allows a tolerance level of less than 0.2
degrees of rotation of the key in the decryption process. Thus, the solution is
to build the key in polar coordinates, by means of circular harmonics expansion;
in this way, the tolerance threshold rises to about 40 degrees of rotation of
the key in the decryption process. This solution is an added value for optical
encryption processors. I have developed a computational tool for simulations
and results obtained in this study.
Keywords: Cryptography, Circular harmonics, Fourier optics.
Resumen
En este
trabajo presento un estudio sobre la varianza a la rotación de la llave del
procesador de encriptación basado en la transformada de Fourier. Determiné que
la llave en coordenadas rectangulares permite un nivel de tolerancia inferior a
0.2 grados de rotación de la llave en el proceso de decriptación. Entonces la solución es construir la llave en
coordenadas polares, por medio de una expansión en armónicos circulares. De
esta manera, el umbral de tolerancia aumenta aproximadamente hasta 40 grados de
rotación de la llave en el proceso de decriptación. Esta
solución es un valor agregado para el procesador de encriptación óptico. He
desarrollado una herramienta computacional para las simulaciones y resultados
obtenidos en este estudio.
Palabras clave: Criptografía, Armónicos Circulares, Óptica de Fourier.
1. Introduction
Using optical processor encryption based on the Vander Lugt Correlator (VLC) [1], the image is encrypted due to the encryption key located on Fourier plane [2,4,5,6,9,10]. This processor uses a phase only key with random spatial distribution of the phase. Fig. 1 shows the optical arrangement encryption-decryption based on the VLC.
Encryption techniques
should have two equally important features: 1) resistance to attacks on the
encrypted information, and 2) they should allow recipient to decrypt the
information without difficulty. In previous works [6], we implemented this type
of encryption arrangement using the encryption-keys in rectangular coordinates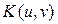 . Then, we observed that the decryption is a variant
operation with the rotation of the key. In practice, this variance is a problem
that needs to be solved. I propose a solution to the problem using a
decomposition of the key in circular harmonics.
. Then, we observed that the decryption is a variant
operation with the rotation of the key. In practice, this variance is a problem
that needs to be solved. I propose a solution to the problem using a
decomposition of the key in circular harmonics.
Fig. 2 shows a result of variance of the decryption operation with the rotation of a key in rectangular coordinates. A rotational variance encryption processor, due to rotation of the key may be measured in terms of the IOR parameter given by eq.(1):
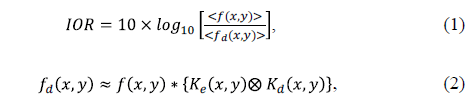
Where, 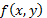 is
the input image and
is
the input image and 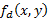 is the decrypted image,
is the decrypted image, 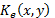 is
the encryption key, and
is
the encryption key, and  is the decryption key. * is the convolution
operator and
is the decryption key. * is the convolution
operator and 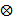 is the correlation operator. If IOR = 0 dB, meaning that the output image
is the correlation operator. If IOR = 0 dB, meaning that the output image is
approximately equal to the input image. Analyzing eq.(2), the system will
decrypt only if
is
approximately equal to the input image. Analyzing eq.(2), the system will
decrypt only if 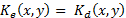 ,
then the operation
,
then the operation 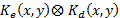 generates an autocorrelation peak that does
not distort the image
generates an autocorrelation peak that does
not distort the image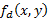 .
But if we rotate the key
.
But if we rotate the key  ,
then the result of the
,
then the result of the 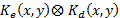 correlation will be a noise, which is
convolved with the image
correlation will be a noise, which is
convolved with the image 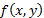 ,
and therefore the result is a distorted image. In this work, it was determined
that the level of this distortion depends on the angle of rotation of the
decryption key
,
and therefore the result is a distorted image. In this work, it was determined
that the level of this distortion depends on the angle of rotation of the
decryption key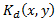 .
This occurs because the correlation product is variant with rotation functions.
.
This occurs because the correlation product is variant with rotation functions.
The results shown in Fig. 2 correspond to a key in
rectangular coordinates, and Fig. 3 is the corresponding calculation of IOR vs
the rotation angle of the same key. Note that rotation of 0.2 degrees,
corresponds to a value of IOR = 1.25dB, which corresponds to the image in Fig.
2(e), and here it is observed that 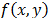 is highly
distorted. Now, for
angles greater than 0.2 degrees, the level of distortion is such that there is
no decrypted image, as with the result in Fig. 2(f). The solution is
then decomposed into harmonic circular key, and thus the operation of
decryption increases tolerance to rotation of the key
is highly
distorted. Now, for
angles greater than 0.2 degrees, the level of distortion is such that there is
no decrypted image, as with the result in Fig. 2(f). The solution is
then decomposed into harmonic circular key, and thus the operation of
decryption increases tolerance to rotation of the key  .
Furthermore, we can use IOR as a relative measure of the level of distortion of
the decrypted image. Thus, we can see in Fig. 3 that as we increase the angle
of rotation of the
.
Furthermore, we can use IOR as a relative measure of the level of distortion of
the decrypted image. Thus, we can see in Fig. 3 that as we increase the angle
of rotation of the 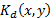 key,
the value of IOR increases.
key,
the value of IOR increases.
2. Encryption with circular harmonic key
An image can be expressed in polar coordinates for
circular harmonic components [7,8]. Then we can consider the key in polar
coordinates, so the key takes the form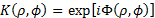 ,
where F must contain a distribution of random values. Thus, the key can be decomposed
into harmonic circular, as follows:
,
where F must contain a distribution of random values. Thus, the key can be decomposed
into harmonic circular, as follows:
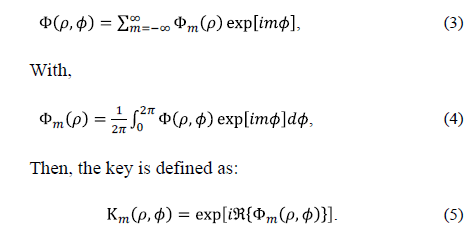
Where Â{-} is the real part of Fm. Fig. 4 is an example of decomposition into circular harmonics of m=1 order. Fig. 5 shows the decomposition of m=1 order, of an encryption key given in rectangular coordinates in Fig. 5(a).
2.1. Encryption-Decryption results with circular harmonics key
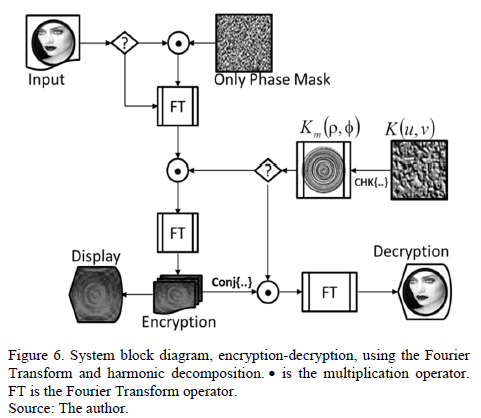
The block diagram of the cryptography system (Fig. 6) was implemented in Matlab(R2012b). Fig. 7 is a result of encryption-decryption using a key Km(r,f) (Fig. 5). These results indicate that the decryption operation increased the level of tolerance with respect to the case of the key in rectangular coordinates.
Fig. 7(b) shows the intensity of the encrypted image. Note that the intensity of the encrypted image has the appearance of a deterministic image. However, the values are totally random (see Fig. 8). The output of the processor delivers an array of complex values. So the encrypted image is composed of three parts: a real values matrix, an imaginary values matrix and a phase values matrix.
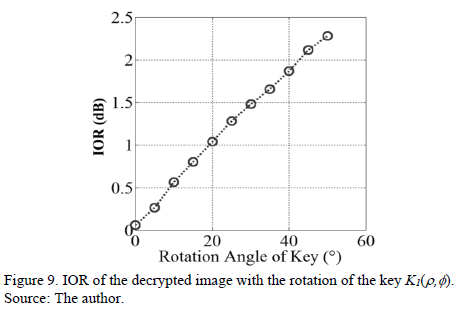
Fig. 9 is the relationship IOR between rotation angles of the decryption key. This analysis corresponds to Figs. 7(c)-(f). Note that for an output of IOR = 2dB, a rotation of the key » 41 degrees is necessary. Thus, tolerance decryption operation is much higher with respect to the key in case of rectangular coordinates. So then encryption with keys in polar coordinates is a solution to the problem of variance in the decryption of the optical arrangements, and is also useful for fully digital encryption.
The order of the harmonic decomposition can be handled as an additional variable that increases the difficulty of breaking the encryption information.
3. Conclusions
In sum, this study show that the encryption processor based on the Fourier transform is a variant with key rotation. It was demonstrated that a solution to this variance is to expand the key into circular harmonics. The proposed technique increases the tolerance of the processor with the rotation of the key. The key in rectangular coordinates allows a tolerance to rotation of about 0.2 degrees, while with the key in circular harmonics, tolerance increases to about 40 degrees. Thus, the decomposition of the key circular harmonics solves the particular problem of optical encryption processor based on the phenomenon of diffraction, because the decryption key must be physically positioned with high accuracy, as can be concluded from the simulation results presented in this report.
Furthermore, the proposed technique can also be used in digital encryption algorithms, considering that the encrypted image is not deterministic, as it appears to be if only the appearance of the encrypted image is observe. If we analyze the distribution of values of the amplitude and phase of the encrypted image, we find that these are really random. Failing that, the quality of the image encrypted with the key in circular harmonics can be an element of distraction to break the code attacks.
References
[1] Vanderlugt, A., Signal detection by complex spatial filter, IEEE IT-10, pp.139-146, 1964.
[2] Refregier, P. and Javidi, B., Optical image encryption based on input plane and Fourier plane random encoding, Opt. Lett. 20 (7), pp.767-769, 1995. https://doi.org/10.1364/OL.20.000767
[3] Matoba, O. and Javidi, B., Encrypted optical storage with angular multiplexing, Appl. Opt. 38 (35), pp.7288-7293, 1999. https://doi.org/10.1364/AO.38.007288.
[4] Lin, C., Shen, X., Tang, R. and Zou, X., Multiple images encryption based on Fourier transform hologram, Opt. Commun. 285 (6), pp.1023-1028, 2012. DOI: 10.1016/j.optcom.2011.10.046
[5] Tebaldi, M., Furlan W.D., Torroba, R. and Bolognini, N., Optical-data storage-readout technique based on fractal encrypting masks, Opt. Lett. 34 (3), pp. 316-318, 2009. https://doi.org/10.1364/OL.34.000316
[6] Rueda, J.E. and Romero, A.L., Optical cryptography using Fresnel diffraction and phase conjugation, Revista DYNA. Facultad de Minas, Universidad Nacional de Colombia, Sede Medellín, Colombia, 80 (181), pp. 25-30, 2013.
[7] Hsu, Y.N., Arsenault, H.H. and April, G., Rotation-invariant digital patter recognition using circular harmonic expansion, Appl. Opt. 21(22), pp. 4012-4015, 1982. https://doi.org/10.1364/AO.21.004012
[8] Gualdron O. and Arsenault H.H., Phase dirived circular harmonic filter, Opt. Commun. 104(1-3), pp.32-34, 1993. DOI: 10.1016/0030-4018(93)90100-J
[9] Hennelly, B. and Sheridan, J.T. Optical image encryption by random shifting in fractional Fourier domains. Optics Letters 28(4), pp.269-271, 2003. https://doi.org/10.1364/OL.28.000269
[10] Salazar, A., Rueda, J.E. and Lasprilla, M., Encriptación por conjugación de fase en un BSO utilizando señales ópticas de baja potencia, Revista Colombiana de Física 34 (2), pp.636-640, 2002.
J.E. Rueda-Parada, completed his BSc in Physics in 1993, an MSc Physics in 1996, and a PhD Physics in 2002, all of them from the Universidad Industrial de Santander, Colombia. He finished his postdoctoral studies in February 2015, at the Institute of Physics of São Carlos, University of São Paulo, Brazil. Currently, he is a full Professor at the Physics Department, Faculty of Basic Sciences, Universidad de Pamplona, Colombia. His research interests include: growth of mono-crystalline fibers, photorefractive optics, holography, wave mixing, and optical encryption and digital image processing.
Cómo citar
IEEE
ACM
ACS
APA
ABNT
Chicago
Harvard
MLA
Turabian
Vancouver
Descargar cita
CrossRef Cited-by
1. B. Lokesh Reddy, Anith Nelleri, Wei Liu. (2022). Single-Pixel Compressive Digital Holographic Encryption System Based on Circular Harmonic Key and Parallel Phase Shifting Digital Holography. International Journal of Optics, 2022, p.1. https://doi.org/10.1155/2022/6298010.
Dimensions
PlumX
Visitas a la página del resumen del artículo
Descargas
Licencia
Derechos de autor 2015 DYNA

Esta obra está bajo una licencia internacional Creative Commons Atribución-NoComercial-SinDerivadas 4.0.
El autor o autores de un artículo aceptado para publicación en cualquiera de las revistas editadas por la facultad de Minas cederán la totalidad de los derechos patrimoniales a la Universidad Nacional de Colombia de manera gratuita, dentro de los cuáles se incluyen: el derecho a editar, publicar, reproducir y distribuir tanto en medios impresos como digitales, además de incluir en artículo en índices internacionales y/o bases de datos, de igual manera, se faculta a la editorial para utilizar las imágenes, tablas y/o cualquier material gráfico presentado en el artículo para el diseño de carátulas o posters de la misma revista.