ESTUDIO DE CRISTALES FOTÓNICOS UNIDIMENSIONALES DE TRES MEDIOS CON EL MÉTODO DE ONDAS PLANAS
STUDY OF THREE MEDIA ONE-DIMENSIONAL PHOTONIC CRYSTALS WITH THE PLANE WAVE EXPANSION
Keywords:
Cristal fotónico, reflector de Bragg, tres medios. (es)Photonic crystal, Bragg reflector, Three media. (en)
Downloads
ESTUDIO DE CRISTALES FOTÓNICOS UNIDIMENSIONALES DE TRES MEDIOS CON EL MÉTODO DE ONDAS PLANAS
STUDY OF THREE MEDIA ONE-DIMENSIONAL PHOTONIC CRYSTALS WITH THE PLANE WAVE EXPANSION
Juan P. Vasco1, Herbert Vinck-Posada2
1Departamento de Física, Universidade Federal de Minas Gerais, Belo Horizonte MG, Brasi
2Departamento de Física, Facultad de Ciencias, Universidad Nacional de Colombia–Sede Bogotá, Bogotá, Colombia
(Recibido: 03/2012. Aceptado: 06/2012)
Contacto: Herbert Vinck–Posada hvinckp@unal.edu.co
Cómo citar: Vasco, J.P., Vinck–Posada, H., Momento 44, 1 (2012)
Resumen
En este trabajo presentamos un estudio teórico de las propiedades ópticas de un cristal fotónico unidimensional de tres medios, diseñado para obtener un buen rendimiento en una longitud de onda λ que es seleccionada arbitrariamente. Las autofrecuencias y los autoestados del campo electromagnético son obtenidos a través de una diagonalización numérica del operador de Maxwell en una base de ondas planas. Encontramos que es posible construir un reflector de Bragg obteniendo estados fuertemente localizados en una cavidad de longitud λ.
Palabras clave: Cristal fotónico, reflector de Bragg, tres medios.
Abstract
In this work we present a theoretical study of the optical properties of a three media one–dimensional photonic crystal designed to have a high effciency at a wavelength λ, which is chosen arbitrarily. The eigenfrequencies and the eigenstates of the electromagnetic field are obtained through a numerical diagonalization of the Maxwell operator in a plane wave basis. We find that it is possible to make a Bragg reflector obtaining strongly localized states in a cavity of length λ.
Keywords: Photonic crystal, Bragg reflector, Three media.
Introducción
Durante las dos últimas décadas, el estudio de las propiedades ópticas en metamateriales ha atraído la atención de un gran número de científicos, debido a sus potenciales aplicaciones en el campo de las telecomunicaciones [1], ingeniería [2] y estudio de física fundamental [3]. En particular, los cristales fotónicos prometen una revolución tecnológica en el área del procesamiento de la información completamente óptica, gracias a los interesantes efectos que producen sobre el flujo de la radiación electromagnética.
En analogía al potencial quántico periódico determinado por un cristal atómico, la función dieléctrica del cristal fotónico es periódica en el espacio, de esta manera, los estados permitidos (bandas de valencia y conducción) y prohibidos (band gaps) que en cristales atómicos son producidos por medio de fenómenos de interferencia constructiva y destructiva de la función de onda electrónica, respectivamente, en cristales fotónicos surgen como fenómenos de interferencia de las ondas electromagnéticas dispersadas en el cristal. AsÍ mismo, cuando se rompe la periodicidad del cristal fotónico a través de la introducción de impurezas o defectos (geométricos o de composición) se induce la localización del campo electromagnético alrededor de la impureza, permitiendo el confinamiento o guiado de modos de luz con alta eficiencia [4]. En este trabajo discutimos la posibilidad de confinar modos de radiación electromagnética en cavidades producidas aumentando el tamaño de una capa en un cristal fotónico de tres medios. El diseño del cristal se fundamenta en un análisis básico de las fases producidas en los fenómenos de reflexión en cada una de las interfases del sistema.
Método teórico
La dinámica del campo electromagnético, y por lo tanto sus estados estacionarios, están gobernados por la ecuación de onda electromagnética, que en el sistema MKS y bajo la consideración de medios lineales, no magnéticos e isotrópicos adquiere la siguiente forma para el campo H [5]:
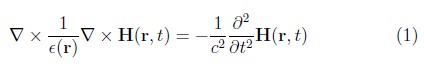
Si consideramos sólo un modo armónico en la dependencia temporal H(r,t) = H(r)eiωt, lo cual no es una gran restricción pues siempre es posible describir dependencias temporales complicadas a través de una combinación lineal adecuada de estos modos, la ecuación de onda 1 se reduce a la forma estacionaria:

Donde ![]() , conocido como el operador de Maxwell, es un operador Hermítico y semidedinido positivo [6]. De esta forma, el problema de encontrar los estados estacionarios de un sistema dieléctrico no homogéneo se reduce a resolver el problema de autovalores 2. Al imponer la periodicidad de la función dieléctrica ε(r + R) = ε(r) el sistema dieléctrico es llamado cristal fotónico, siendo R el vector de la red cristalina. De la teoría del estado sólido, la función de onda debe ser escrita como un estado de Bloch, que en este caso es representada por el campo magnético H:
, conocido como el operador de Maxwell, es un operador Hermítico y semidedinido positivo [6]. De esta forma, el problema de encontrar los estados estacionarios de un sistema dieléctrico no homogéneo se reduce a resolver el problema de autovalores 2. Al imponer la periodicidad de la función dieléctrica ε(r + R) = ε(r) el sistema dieléctrico es llamado cristal fotónico, siendo R el vector de la red cristalina. De la teoría del estado sólido, la función de onda debe ser escrita como un estado de Bloch, que en este caso es representada por el campo magnético H:
![]()
En el caso de un cristal fotónico de placas infinitas en el plano yz y dirección de periodicidad x, obtenemos:

Donde a es conocido como el parámetro de red. Dado que 1/ε(x) y HzP(x)son funciones periódicas, ellas pueden ser expandidas en una base de ondas planas cuya periodicidad es la misma de la red:
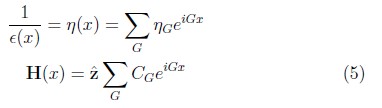
Siendo G = 2πm/a, con m un número entero, la magnitud del vector de la red recíproca. Substituyendo las expresiones 5 en 2, e integrando sobre la celda unitaria del cristal (en el intervalo [0, a]), obtenemos un sistema infinito de ecuaciones algebraicas para los CG que puede ser escrito como un problema de autovalores [7]:
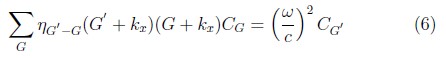
Mecanismo DBR para el cristal de tres medios
A diferencia de las cavidades metálicas y las fibras ópticas convencionales, donde los mecanismos de confinamiento y guiado corresponden a la reflexión especular y reflexión total interna, respectivamente, el mecanismo de confinamiento asociado a los cristales fotónicos, conocido como reflexión de Bragg distribuida o DBR (distributed Bragg reflection), se basa en fenónemos de interferencia constructiva e interferencia destructiva de las ondas electromagnéticas involucradas. De esta manera, en una cavidad de cristal fotónico, por ejemplo, las múltiples reflexiones en la interfases del sistema interfieren constructivamente en la región de la cavidad e interfieren destructivamente fuera de ella, produciendo modos de radiación fuertemente localizados [4]. Adicionalmente, el mecanismo DBR es altamente eficiente en todo el espectro electromagnético.
Nuestro análisis preliminar consiste, por lo tanto, en estudiar las múltiples reflexiones provenientes de las interfases de una distribución periódica de tres medios, con el fin de inducir interferencia constructiva para una longitud de onda particular que en el vacío tenga un valor λ, obteniendo así un espejo dieléctrico de alta eficiencia, conocido como espejo de Bragg. La figura 1 muestra el esquema
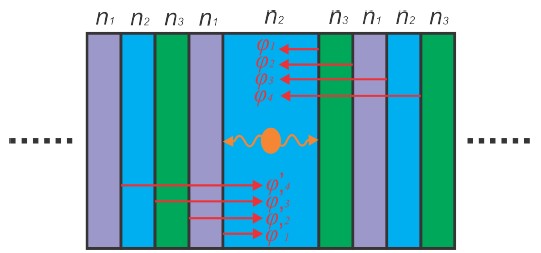
Figura 1. Análisis de fases para cada una de la reflexiones en la interfases del cristal, los ni corresponden a los índices de refracción de cada uno de los medios.
sugerido. En el centro se encuentra un material de índice de refracción n2 y longitud λ/n2 rodeado por distribuciones periódicas de medios con índices n2, n2 y n3. Las fases φ1, φ'1, φ2, φ'2, φ3, φ'3, φ4 y φ'4 pueden ser escritas en radianes como:
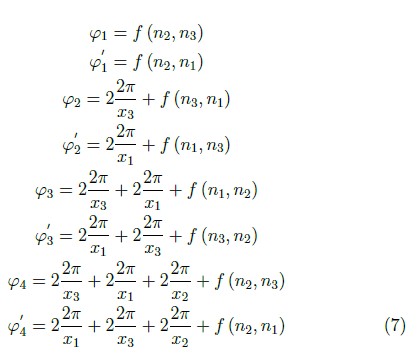
Donde xi corresponde a la longitud del medio y el factor de 2 es producido debido a que la onda recorre el medio dos veces: camino de ida y regreso. La función f(ni, nj) se define como:

En este artículo nos limitaremos a estudiar el caso x1 = 2 y x2 = x3 = 4 y, en el cual obtenemos φi = φi—3 y φ'i = φ'i—3 para i ≥ 4. El propósito de esta elección es cumplir la condición ![]() , con m entero, y reducir el problema a tres fases independientes en cada uno de los extremos de la cavidad. Bajo estas condiciones las relaciones 7 se reducen a:
, con m entero, y reducir el problema a tres fases independientes en cada uno de los extremos de la cavidad. Bajo estas condiciones las relaciones 7 se reducen a:
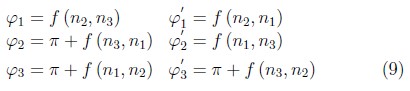
Las expresiones 9 representan fenómenos de interferencia constructiva cuando n2 > n1 > n3, es decir, un caso de defecto dieléctrico (mayor índice de refracción). En este punto es claro el por qué de la elección de un defecto de longitud λ/n2: los espejos reflejan con alta eficiencia la radiación cuya longitud de onda en el vacío sea λ, por lo tanto, al menos un modo cuya longitud de onda sea λ debe ser confinado.
Resultados
Con el fin de estudiar los modos que se confinan en la cavidad fueron considerados 30 espejos n2n3n1 al lado izquierdo y 30 espejos n3n1n2 al lado derecho de ésta con λ = 0.9a. Nótese que el sistema completo corresponde a un cristal fotónico de tres medios al que se le ha aumentado el tamaño de una capa cada 60 periodos, por lo tanto, desde la teoría de cristales fotónicos, es posible la localización de estados electromagnéticos en esta región defectiva o de impureza [6]. El parámetro de red asociado al sistema corresponde a la suma de las longitudes de los 60 espejos y la longitud de la cavidad, obteniendo de esta forma una supercelda periódica [8].
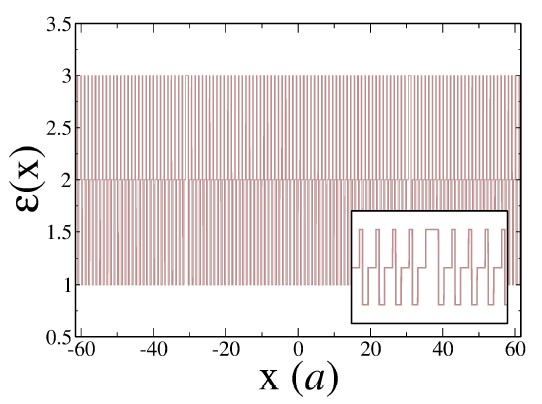
Figura 2. Función dieléctrica considerada con ε1 = n12 = 2, ε2 = n22 = 3 y ε3 = n32 =. El defecto λ se muestra amplificado en la parte inferior derecha.
La figura 2, donde se ha graficado la función dieléctrica del sistema, muestra este hecho. En la parte inferior derecha se muestra el defecto λ amplificado.
Las autofrecuencias y autoestados del sistema fueron calculados resolviendo numéricamente la ecuación de autovalores 6 con una base de 601 ondas planas, que es suficiente para obtener una buena convergencia de las autofrecuencias. La figura 3 muestra el diagrama de bandas en la primera zona de Brillouin, donde la frecuencia se ha escrito en unidades de ωa/2πc, siendo a el parámetro de red del cristal fotónico no defectivo. En efecto, surgen modos permitidos con velocidad de grupo nula en los dos primeros band gaps del cristal, significando modos altamente localizados. Las distribuciones de intensidad del campo eléctrico |E|2 para el modo fundamental (izquierda) y primer excitado (derecha) se muestran en la figura 4.

Figura 3. Diagrama de bandas del cristal fotónico en unidades de ωa/2πc. Un estado es permitido en el primer band gap del sistema (rojo), y otro estado es permitido en el segundo band gap )azul).
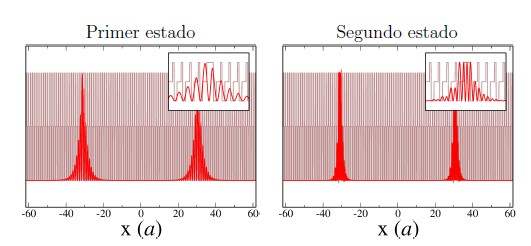
Figura 4. Intensidad del campo eléctrico |E|2 superpuesta con la función dieléctrica en la supercelda para los dos primeros estados localizados en la cavidad.
Bajo las condiciones en la cuales fue diseñado el cristal, se espera la localización de un modo cuya frecuencia este asociada a un modo de longitud de onda λ = 0.9a en el vacío, que en las unidades ωa/2πc corresponde a un valor de a/)λ/a') = 0.7478, donde a' = λ(1/2n1 + 1/4n2 + 1/4n3). El valor encontrado a través de la solución de la ecuación 6 fue de 0.7554, el cual es bastante cercano (1% de diferencia), teniendo en cuenta la aproximación de supercelda que determina una distribución periódica e infinita de defectos. Además de esto, la frecuencia del modo se encuentra en el medio del band gap fotónico, significando un alto grado de confinamiento del estado electromagnético [9]. En la figura 4 (derecha) puede comprobarse visualmente que en efecto el modo contiene una longitud de onda en la cavidad. Nótese, sin embargo, que existe otro estado en el primer band gap del sistema, cuyo origen es atribuido al mismo tipo de fenómenos de interferencia, pero como puede verse de las figuras 3 y 4, la frecuencia del modo no se encuentra en el centro del band gap y el decaimiento del modo es más lento fuera de la cavidad que para el caso del primer excitado, por lo tanto el confinamiento para este valor de frecuencia no es eficiente.
Conclusiones
La reflexión de Bragg distribuida es un mecanismo altamente eficiente bajo el cual es posible la localización y guiado de modos fotónicos en estructuras periódicas dieléctricas o cristales fotónicos. En el desarrollo de este trabajo mostramos la posibilidad de diseñar un cristal fotónico unidimensional con tres medios para localizar modos de luz en una cavidad λ. Nuestros resultados numéricos concuerdan con los esperados físicamente a través de un análisis simple de fases e interferencia de ondas electromagnéticas.
Referencias
[1] M. Petrovich, F. Poletti, A. van Brakel, and D. Richardson, Optics Express 16, 4337 (2008).
[2] C. Ren, J. Tian, S. Feng, H. Tao, Y. Liu, K. Ren, Z. Li, B. Cheng, and D. Zhang, Optics Express 14, 10014 (2006).
[3] N. Masahiro, K. Tanabe, S. Iwamoto, and Y. Arakawa, Optics Express 18, 8144 (2010).
[4] P. R. Villeneuve and M. Piché, Progress in Quantum Electronics 18, 153 (1994).
[5] K. Sakoda, Optical Properties of Photonic Crystals, 2nd ed. (Springer, 2004).
[6] J. D. Joannopoulos, S. G. Johnson, and J. N. Winn, Photonic Crystals: Molding the Flow of Light, 2nd ed. (Princenton University Press, 2008).
[7] J. P. Vasco, Caracterización y control de las propiedades ópticas en cristales fotónicos, Tech. Rep. (2011).
[8] L. Wu, F. Zhuang, and S. He, Physical Review E 67 (2003)
[9] A. Yariv and P. Yeh, Photonics: Optical Electronics in Modern Communications, sixth ed. (Oxford University Press, 2006).
How to Cite
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Download Citation
Article abstract page views
Downloads
License
Those authors who have publications with this journal, accept the following terms:
a. The authors will retain their copyright and will guarantee the publication of the first publication of their work, which will be subject to the Attribution-SinDerivar 4.0 International Creative Commons Attribution License that permits redistribution, commercial or non-commercial, As long as the Work circulates intact and unchanged, where it indicates its author and its first publication in this magazine.
b. Authors are encouraged to disseminate their work through the Internet (eg in institutional telematic files or on their website) before and during the sending process, which can produce interesting exchanges and increase appointments of the published work.




















