ENTRELAZAMIENTO Y TRANSICIONES DE FASE EN UN BEC DE POLARITONES EXCITÓNICOS CONFINADOS EN UNA NANOCAVIDAD DE CRISTAL FOTÓNICO *

ENTANGLEMENT AND PHASE TRANSITIONS IN A EXCITON-POLARITON BEC CONFINED IN A PHOTONIC CRYSTAL NANOCAVITY

En este trabajo estudiamos un sistema de polaritones excitónicos con_nado en punto cuántico embebido en una nanocavidad de cristal fotónico. Usando un estado separable del tipo BCS, para el subsistema excitónico confinado en el punto cuántico, y un estado coherente, para el modo electromagnético con_nado en la nanocavidad, se calcula la energía del estado base para el sistema de N polaritones excitónicos. También se realiza una caracterización de las coherencias cuánticas del sistema calculando discordia y entrelazamiento a partir de la llamada matriz densidad de pares. Finalmente, introduciendo temperatura y campo magnético en nuestro modelo, podemos evidenciar la señal de una posible transición de fase en las correlaciones cuánticas del sistema.

In this work we study a polariton-exciton system confined in photonic crystal nanocavity with embedded quantum dot. Using a separable state of the type BCS, for the matter subsystem, product by a coherent state, for the photonic mode, we compute the ground state energy of N polaritons. Also, we characterize the quantum coherence in the system using entanglement and discord, calculated both from the pair density matrix. Finally, we introduce temperature and magnetic field to our model and we obtain signatures of phase transitions in the quantum correlations of the system.

Guillermo A. Guirales¹, Herbert Vinck-Posada², Boris A. Rodríguez¹

¹Instituto de Física, Facultad de Ciencias Exactas y Naturales, Universidad de Antioquia UdeA; Calle 70 No. 52-21, Medellín–Colombia.

²Departamento de Física, Facultad de Ciencias, Universidad Nacional de Colombia, Sede Bogotá, Carrera 30 Calle 45–03, CP111321, Bogotá, Colombia.

(Recibido: 11/2013. Aceptado: 12/2013)

Contacto: Guillermo A. Guirales: gguiral@fisica.udea.edu.co

Cómo citar: Guirales, G.A., Vinck–Posada, H., Rodríuez, B.A.,Momento 47, 77 (2013)

Resumen

En este trabajo estudiamos un sistema de polaritones excitónicos confinado en punto cuántico embebido en una nanocavidad de cristal fotónico. Usando un estado separable del tipo BCS, para el subsistema excitónico confinado en el punto cuántico, y un estado coherente, para el modo electromagnético confinado en la nanocavidad, se calcula la energía del estado base para el sistema de N polaritones excitónicos. También se realiza una caracterización de las coherencias cuánticas del sistema calculando discordia y entrelazamiento a partir de la llamada matriz densidad de pares. Finalmente, introduciendo temperatura y campo magnético en nuestro modelo, podemos evidenciar la señal de una posible transición de fase en las correlaciones cuánticas del sistema.

Palabras clave: Entrelazamiento, operador de densidad de pares, transición de fase cuántica, BEC de polaritones, discordia cuántica.

Abstract

In this work we study a polariton{exciton system confined in photonic crystal nanocavity with embedded quantum dot. Using a separable state of the type BCS, for the matter subsystem, product by a coherent state, for the photonic mode, we compute the ground state energy of N polaritons. Also, we characterize the quantum coherence in the system using entanglement and discord, calculated both from the pair density matrix. Finally, we introduce temperature and magnetic field to our model and we obtain signatures of phase transitions in the quantum correlations of the system.

Keywords: Entanglement, pair density operator, quantum phase transition, polariton BEC, quantum discord.

Recientemente, el gas de polaritones excitónicos confinado en heteroestructuras semiconductoras y nanocavidades de cristal fotónico, ha surgido como una alternativa prometedora para el condensado de Bose–Einstein (BEC) en sistemas de estado sólido.[1, 2] Las fuertes correlaciones cuánticas presentes en este sistema lo hacen un candidato único para el estudio de entrelazamiento y transiciones de fase cuánticas [3] —i.e., cambios cualitativos en las propiedades del estado base del sistema—. En este trabajo, consideremos un sistema formado por un punto cuántico embebido en una cavidad de cristal fotónico, tal que los excitones producidos por bombeo óptico, confinados por el potencial del punto, se acoplan via la interacción radiación—materia con alguno de los modos fotónicos de la cavidad. Adicionalmente, consideramos un campo magnético en la dirección de crecimiento del punto cuántico. Sistemas modelo pueden encontrarse en [4—6].

Siguiendo el trabajo pionero de Nozières y Compte [7], Kamide y Ogawa en el 2010 establecieron el diagrama de transiciones de fase para un gas de electrones y huecos confinados en un pozo cuántico.[8] En este trabajo se determinan las diferentes fases del sistema: plasma electrón—hueco, BEC de fotones, excitones o polaritones, BCS de excitones, etc, en términos de la densidad de pares electrón—hueco. En estudios previos realizados en nuestro grupo [4, 9, 10] sobre excitones confinados en puntos cuánticos, con y sin interacción con un modo confinado de luz, se ha observado un comportamiento propio de sistemas que exhiben un cambio de fase: escalamiento con el número de partículas de la energía del estado base en función de la constante de acople o el campo magnético, y además se ha encontrado un valor de temperatura para el cual el sistema polaritónico muestra un cambio en la estructura de su estado base exhibiendo claramente una transición de fase cuántica.

En este trabajo se estudian las señales de estas transiciones de fase cuánticas en las correlaciones cuánticas del sistema. En particular, nos interesan las correlaciones dadas por la discordia [11] y el entrelazamiento [12] en este sistema de muchos cuerpos.

Sistema polaritónico

El hamiltoniano del sistema, sin considerar posibles efectos de disipación y coherencia, es:

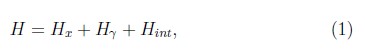
en donde H_x representa la parte excitónica, H_γ representa la parte fotónica y H_int es la parte de interacción electrón–hueco–fotón. Usando segunda cuantización tanto para las excitaciones de materia como del campo electromagnético, podemos escribir más detalladamente cada uno de los términos anteriores y visualizar todas las interacciones en este sistema [4, 13]:

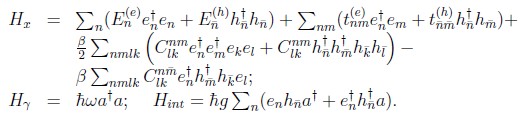
En las expresiones anteriores e_n(e_n^†, y a(a^†) son los operadores de aniquilación (creación) para electrones, huecos y el modo fotónico respectivamente. En son las energías uniparticulares, t_nm representa términos de energía de potencial adicionales como campo magnético, etc. son los elementos de matriz, entre los respectivos estados de una partícula, del potencial de interacción de Coulomb determinado por la constante de acople β. es la energía del modo confinado de la nanocavidad y g la constante de acople dipolar de la interacción radiación—materia. Dentro de las aproximaciones usuales en esta clase de sistemas: aproximación de masa efectiva, aproximación dipolar y de onda rotante, este es el hamiltoniano más completo y general que puede escribirse. Por otro lado, como estado base del sistema introducimos el producto directo de un estado coherente del modo con un estado BCS de pares electrón—hueco de la forma

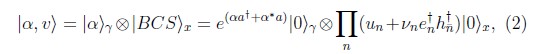
donde |α|² es el número medio de fotones del estado coherente, vn, son los parámetros variacionales del estado BCS que representan la probabilidad de creación o no de un par y |0⟩_γ(x) son los respectivos estados de vacío tanto de campo como de materia. Siguiendo un típico proceso variacional en términos de los parámetros v_n sujetos a la restricción de que el número de excitaciones N_p es constante, se introduce el potencial químico μ, como multiplicador de Lagrange, y se minimiza la energía . De esta forma se obtienen las llamadas ecuaciones de Gap [10]:

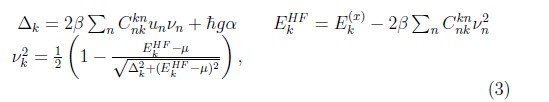
las cuales deben resolverse de forma autoconsistente. Siendo Δ_k el gap de energía, E_k^HF la energía de Hartree–Fock y v_k las ocupaciones del estado k del par.

En el caso de temperatura finita es posible hacer una generalización del anterior procedimiento, introduciendo el operador de densidad

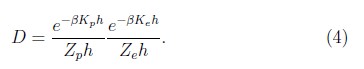
En donde y K_eh se expresa en términos de las energías uniparticulares y las funciones de gap. El lector que desee obtener los detalles de las expresiones teóricas y el cálculo computacional puede referirse a [10, 14].

Negatividad y discordia

La negatividad, , y la discordia, , miden las correlaciones cuánticas presentes en el estado del sistema. Por un lado, la negatividad ofrece información sobre el entrelazamiento o separabilidad de un estado cuántico. Así, una negatividad distinta de cero asegura que el sistema es no separable y por lo tanto entrelazado, mientras que una negatividad igual a cero indica la posibilidad de separabilidad. Sin embargo, sólo en sistemas bipartitas de baja dimensionalidad —2 X 2 o 2 X 3— el criterio es necesario y suficiente para medir el entrelazamiento. En sistemas de mayor dimensionalidad la negatividad es tan un sólo un testigo del entrelazamiento [12, 15]. Por la naturaleza del estado (2) no hay entrelazamiento entre los pares excitónicos con el modo del campo, por lo que calcularemos el entrelazamiento entre un par electrón–hueco.

Por otro lado, la discordia [11, 16] mide cuanto más de correlaciones cuánticas sobre las las correlaciones clásicas hay en las correlaciones totales de un sistema, tal que . La ventaja de calcular la discordia es que, salvo problemas prácticos, me permite afirmar con certeza si existen o no correlaciones cuánticas en el sistema. Como en el caso de la negatividad, la discordia es facilmente computable para una familia de estados de sistemas bipartitas 2X2 llamados estados X.

Estos estados tienen la particularidad de que la forma general de su matriz densidad tiene elementos sobre las diagonales principal y secundaria, y obligatoriamente cero en las otras entradas.

Para calcular la negatividad se debe partir de un sistema formado por subsistemas A y B cuya matriz densidad total se puede escribir ρ = ρ_A ⊗ ρ_B = {ρ_μm,υn}, tal que los índices μ, υ pertenecen al subsistema A y los índices m, n al subistema B. Entonces se introduce la matriz traspuesta parcial respecto a alguno de los subsistemas, supongamos A, como ρ^TA tal que ρ^TA = {ρ_υm,μn}. De acuerdo a los resultados de Vidal [17], la negatividad se escribe finalmente como

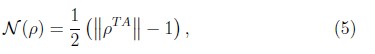
donde es la norma del operador ρ^TA.

Por otro lado, la discordia para un estado X se calcula según [18]:

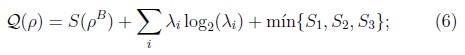
en donde las funciones S, S₁, S₂ y S₃ son funciones de entropía y λ_i los autovalores de la matriz densidad del sistema.

Aplicación al sistema polaritónico

La matriz densidad de pares del subsistema electrón—hueco usando el estado (2) es

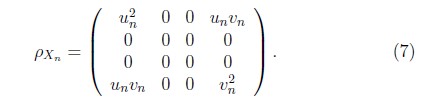
El subíndice n etiqueta el estado del n–ésimo par en el estado BCS. De esta forma usando el anterior estado en la ecuación de la negatividad (5) se obtiene:

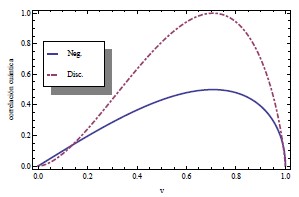
Figura 1. Negatividad y discordia en función de la ocupación del par vk. Se observa que ambas cantidades tienen un comportamiento cualitativo semejante para el estado BCS.

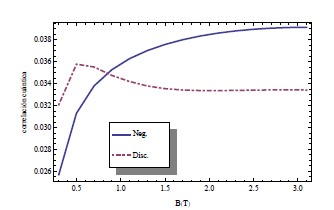
Figura 2. Negatividad y discordia por par excitónico en función de un campo magnético aplicado medido en teslas.

Finalmente, para la discordia (6) se encuentra:

En las siguientes figuras se muestran los cálculos de negatividad y discordia para el n–ésimo par en función de la ocupación —Fig. 1—, de un campo magnético externo aplicado —Fig. 2— y de la temperatura —Fig. 3. Detalles de los cálculos y los parámetros usados junto con un análisis detallado de los resultados se publicarán en extenso en otro trabajo. Sin embargo, se están usando parámetros realistas para estos sistemas. Esto nos permite predecir que para una temperatura crítica de aproximadamente T_c ≈ 2,2meV ≈ 25,5 K el sistema presenta una transición de fase cuántica —ver Fig. 3— que se ve reflejada en sus correlaciones cuánticas.

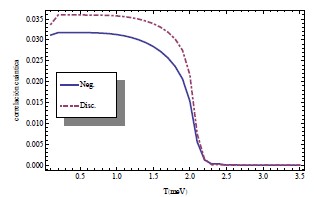
Figura 3. Negatividad y discordia por par excitónico en función de la temperatura medida en meV. Para una temperatura crítica de T_c ≈ 2,2meV puede observarse una transición cuántica de fase.

Conclusiones

En este trabajo se han calculado las correlaciones cuánticas para un sistema de polaritones excitónicos confinados en un sistema de nanocavidad—punto cuántico. Para un estado separable del tipo BCS producto directo estado coherente, la negatividad y la discordia de un par electrón–hueco muestran cualitativamente el mismo comportamiento. Sin embargo, existe un comportamiento no monótono de la discordia para bajos campos magnéticos —ver Fig. 2— y bajas temperaturas —ver Fig. 3—. En nuestros resultados se observa una clara transición de fase en las correlaciones cuánticas del sistema, lo que permitiría caracterizar las diferentes fases del sistema a través de sus correlaciones.

Agradecimientos

G.G agradece el apoyo de COLCIENCIAS a través de una Beca de Doctorado Nacional. H.V–P agradece el soporte parcial de COLCIENCIAS dentro del proyecto código 110156933525 y del Grupo de Óptica e Información Cuántica de la Universidad Nacional de Colombia, Sede Bogotá. Finalmente, G.G y B.A.R. agradecen al CODI, Universidad de Antioquia por su apoyo parcial dentro del Proyecto de Sostenibilidad del Grupo de Física Atómica y el proyecto de Mediania Cuantía E01620.

Referencias

[1] J. Kasprzak, M. Richard, S. Kundermann, A. Baas, P. Jeambrun, J. M. J. Keeling, F. M. Marchetti, M. H. Szymanska, R. Andre, J. L. Staehli, V. Savona, P. B. Littlewood, B. Deveaud, and L. S. Dang, Nature 443, 409 (2006).

[2] H. Deng, H. Haug, and Y. Yamamoto, Rev. Mod. Phys. 82, 1489 (2010).

[3] S. Sachdev, Quantum Phase Transitions (Cambridge University Press, 201).

[4] H. Vinck–Posada, B. A. Rodríguez, P. S. S. Guimaraes, A. Cabo, and A. González, Phys. Rev. Lett. 98, 167405 (2007).

[5] P. C. Cárdenas, N. Quesada, H. Vinck–Posada, and B. A. Rodríguez, J. Phys.–Condens. Mat. 23, 265304 (2011).

[6] A. Faraon, A. Majumdar, D. Englund, E. Kim, M. Bajcsy, and J. Vuckovic, New J. Phys. 13, 055025 (2011).

[7] C. Comte and P. Nozières, J. Phys. France 43, 1083 (1982).

[8] K. Kamide and T. Ogawa, Phys. Rev. Lett. 105, 056401 (2010).

[9] B. A. Rodríguez, A. González, L. Quiroga, F. J. Rodríguez, and R. Capote, Int. J. Mod. Phys. B 14, 71 (2000).

[10] H. Vinck–Posada, B. A. Rodriguez, and A. Gonzalez, Superlattice. Microst. 43, 500 (2008).

[11] H. Ollivier and W. H. Zurek, Phys. Rev. Lett. 88, 017901 (2001).

[12] R. Horodecki, P. Horodecki, M. Horodecki, and K. Horodecki, Rev. Mod. Phys. 81, 865 (2009).

[13] H. Vinck, B. A. Rodriguez, and A. Gonzalez, Physica E 35, 99 (2006).

[14] J. Blaizot and G. Ripka, Quantum Theory of Finite Systems (Mit Press, 1986).

[15] A. Peres, Phys. Rev. Lett. 77, 1413 (1996).

[16] M. Ali, A. R. P. Rau, and G. Alber, Phys. Rev. A 81, 042105 (2010).

[17] G. Vidal and R. F. Werner, Phys. Rev. A 65, 032314 (2002).

[18] B. Li, Z.–X. Wang, and S.–M. Fei, Phys. Rev. A 83, 022321 (2011).