ESTUDIO DE LAS PROPIEDADES DE ENTRELAZAMIENTO ENTRE LUZ Y MATERIA INCLUYENDO DETECTORES EN UN SISTEMA MICROCAVIDAD PUNTO CUÁNTICO

STUDY OF THE ENTANGLEMENT PROPERTIES BETWEEN LIGHT AND MATTER INCLUDING DETECTORS IN A MICROCAVITY-QUANTUM DOT SYSTEM

En trabajos recientes [1, 2], los autores incluyen detectores en una propuesta hamiltoniana para modelar procesos de experimentos en un sistema microcavidad punto cuántico. En nuestro trabajo, estudiamos las propiedades de entrelazamiento entre luz y materia como función de la constante de acople del campo con los detectores ei y el tiempo t, y analizamos el caso de los estados cuánticos protegidos.

In recent works [1, 2] the authors include detectors in a hamiltonian proposal to model processes for experiments in a microcavity-quantum dots system. In our work, we study the entanglement properties between light and matter as a function of the coupling constant with detectors ei and time t, and we analyze the case of protected quantum states.            

Álvaro Montaña-Guerrero, Herbert Vinck-Posada

Departamento de Física, Facultad de Ciencias, Universidad Nacional de Colombia Grupo de (Óptica e Información Cuántica, C.P. 111321, Bogotá, Colombia
Álvaro Montana-Guerrero: amontanag@unal.edu.co

(Recibido: Abril/2015. Aceptado: Agosto/2015)

---

Resumen

En trabajos recientes [1, 2], los autores incluyen detectores en una propuesta hamiltoniana para modelar procesos de experimentos en un sistema microcavidad punto cuántico. En nuestro trabajo, estudiamos las propiedades de entrelazamiento entre luz y materia como función de la constante de acople del campo con los detectores ε_i y el tiempo t, y analizamos el caso de los estados cuántico protegidos.

Palabras clave: Detector, Punto cuántico, Entrelazamiento, Negatividad.

---

Abstract

In recent works [1, 2] the authors include detectors in a hamiltonian proposal to model processes for experiments in a microcavity-quantum dots system. In our work, we study the entanglement properties between light and matter as a function of the coupling constant with detectors ε_i and time t, and we analize the case of protected quantum states.

Keywords: Detector, Quantum dot, Entanglement, Negativity.

---

Introducción

La introducción de detectores en un sistema cuántico como un modelo teórico es de gran importancia para entender el rol de estos en la medida, y su posible influencia en el sistema que se quiere observar. Como primera aproximación, en recientes trabajos, los autores [1, 2] introducen en distintos sistemas cuánticos una serie de N detectores modelados como sistemas de dos niveles. Los detectores se incluyen con una propuesta hamiltoniana y un correspondiente valor de emisión espontánea en la ecuación maestra. Sin embargo, es necesario encontrar en que rango de valores de los parámetros, los detectores permiten medir sin alterar dramáticamente el sistema bajo estudio. Medir el posible entrelazamiento, es un primer paso para cuantificar el efecto de los detectores sobre el sistema.

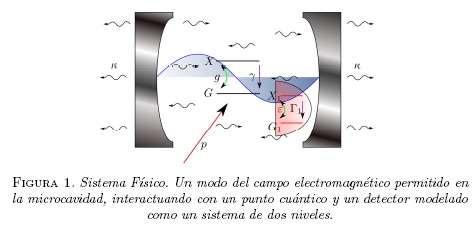
Sistema Físico

El sistema físico bajo estudio corresponde a un átomo de dos niveles interactuando con un modo del campo electromagnético permitido en una microcavidad, en el cual se introduce un detector, como se observa esquemáticamente en la figura (1). Sin tener en cuenta el detector, al iniciar un bombeo incoherente sobre el átomo a una tasa p, el átomo puede pasar del estado base |G) al estado excitado |X). En este punto puede ocurrir: una emisión espontanea del átomo a una tasa γ, lo que conlleva a que el átomo retorne al estado base |X, n) → |G,n), o, el acople átomo-campo a una tasa g y la subsecuente emisión de un foton que queda confinado en la microcavidad |X, n - 1) → |G, n). Sin embargo la microcavidad no es perfecta, por lo tanto algunos fotones pueden escapar a una tasa κ. [3].

Introducimos el detector dentro de la microcavidad, modelado también como un átomo de dos niveles. Este puede acoplarse con el modo del campo a una tasa ε y puede decaer espontáneamente a una tasa Γ₁. A diferencia del átomo, el detector no es afectado de manera directa por el bombeo incoherente p, como se observa en las figuras (1,2). Dado que es un modelo para un detector, deseamos que no afecte el sistema átomo-campo, así que en principio ε < g.

Sin embargo, se estudiará un rango más amplio. Cabe aclarar que el valor de la constante ε, no puede ser demasiado pequeña, dado que sería equivalente a no tener el detector y no es un comportamiento deseado.

Al continuar el bombeo incoherente sobre el átomo, observamos en la figura (2) los niveles de energía permitidos para nuestro sistema. Nuevos niveles son permitidos tales como |G,α_i,n),|X,α_i,n) con α_i = G₁, X₁, que corresponden al detector en su estado base y excitado respectivamente.

Ecuación maestra

La ecuación maestra que describe el sistema, con el operador L definido como L_c(O) = (2cOc^† - c^†cO - Oc†c), es descrita por:

Donde el hamiltoniano H corresponde a la suma del hamiltoniano usual de Jaynes-Cummings [4], y el hamiltoniano de interacciones con N detectores modelados como sistemas de dos niveles <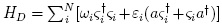 [1, 2]. Cada detector tiene una constante de acople con el campo, y una energía propia h ω. En la ecuación maestra se observan los términos de bombeo p, decaimiento espontáneo 7 y perdida por espejos κ, y los términos de decaimiento espontaneo Γ_i de cada detector. En este caso, solo se trunca el número de detectores a N=1. Los operadores de creación y destrucción (o de escalera) fotonico, de materia y del detector, están definidos respectivamente como:

El operador N = a^†a + σ^†σ + ς^†ς conmuta con el hamiltoniano [H, N] = 0, lo que permite utilizar la base de estados desnudos . A este número N lo llamaremos número de variedad, y si por ejemplo, se afirma que se truncaría a un valor N = 2, esto implicaría que solo estados con valores de variedad de excitación menores o iguales a este número se tomaran. Para el anterior ejemplo los máximos niveles permitidos corresponderían a 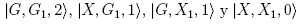en la figura (2).

Negatividad: Una medida de entrelazamiento.

El entrelazamiento consiste en la no separabilidad de un sistema físico en sus subsistemas constituyentes. La negatividad de Peres surge como un cuantificador para establecer la separabilidad de la matriz densidad. Para calcular esta, se toma la transpuesta parcial de la matriz densidad p sobre un subsistema p_S1. Luego, se calcula la traza parcial sobre uno de los subsistemas. Esto resulta en un nuevo operador hermético p^T1 :

La regla formula que una condición necesaria para la descomposición de p, es que ninguno de los autovalores del operador p^T1 sea negativo. Se define entonces la negatividad como:

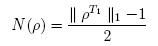
Finalmente, este se puede reducir a la suma del valor absoluto de los autovalores negativos de la matriz p^T1:

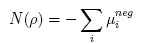
Hay que tener en cuenta que la cuantificación del grado de entrelazamiento es un problema abierto para sistemas multipartitos [5].

Regímenes bajo estudio

Dado que el modelo tiene bastantes parámetros, es necesario encontrar regímenes para estudiar el problema de una manera general. La pérdida de fotones por espejos κ, puede ser comparada con el mecanismo disipativo asociado a la materia, el cual correspondería a un promedio entre el bombeo p y su correspondiente decaimiento espontáneo γ [3]. Por lo tanto compararemos los valores κ con (p + γ)/2. Al no incluir el detector, existen tres regímenes para los parámetros en los cuales el sistema tiene distintos comportamientos:

i) Cuando la microcavidad es ineficiente permite una gran pérdida de fotones que permanecían dentro de esta, por lo tanto se cumple:

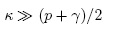
Este caso no se tomaría bajo estudio, dado que todos los fotones se escaparían de la microcavidad y no tendría una aplicación útil un sistema tan ineficiente.

ii) Cuando el bombeo p sobre la materia es alto comparado con la pérdida por espejos κ, es posible llegar a niveles altos de energía en el sistema, como se puede deducir en la figura (2):

En principio, la microcavidad sería útil para confinar un número grande de fotones.

iii) Al ser el bombeo p comparable con la pérdida de fotones κ, habría una cota en los niveles que se podrán alcanzar. Si niveles altos son poblados por el bombeo p, se retornará a niveles bajos por medio de κ. Un número pequeño de fotones permanecerían en la microcavidad, y en este caso:

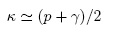
El acople entre el campo y la materia g, es del orden de meV, y la energía ω_χ es del orden de eV. Asignamos los siguientes valores g=1 meV, ω_χ = 1000 meV. El valor del detonan Δ es 5 meV, lo que evidencia una cuasi-resonancia entre el campo y la materia. Finalmente el valor γ = 0.1 refleja que en situaciones prácticas esta emisión espontanea es ineficiente [3]. Los valores de p y κ se variarán para estudiar los regímenes ii) e iii).

Resultados

En la figura (3) se observan dos columnas de graficas que corresponden a las poblaciones p_in,in para los regímenes ii) e iii) respectivamente. Para la primera columna se tiene p = 15 y κ = 0.1, y para la segunda p = 1 y κ = 0.5. En la primera fila de graficas el detector no se ha introducido. Observamos que para la gráfica superior izquierda, dado que el bombeo es alto, los niveles poblados corresponden a niveles altos, ya que niveles bajos como |G, 0), |X, 0) y |X, 1) están poco poblados, en orden a la conservación de la probabilidad Tr{p} = 1. En el otro caso, en la gráfica superior derecha se observa que al ser el bombeo p comparable con la perdida por espejos κ, el nivel |X, 0) queda altamente poblado al transcurrir un tiempo bastante grande.

Cuando se introduce el detector tomando una constante de acople con el campo ε = 1 y un tasa de emisión espontanea γ = 0.1, se obtienen la fila inferior de graficas en la figura (3). Al comparar las gráficas de la columna izquierda, que pertenecen al régimen κ << (p + γ)/2, se observa que las poblaciones de los estados en los cuales el detector está en su estado excitado |α₁, X₁, n) con α₁ = G, X, son poco apreciables. Esto significa que el detector está afectando poco al sistema átomo-campo. Los valores de negatividad encontrados para este régimen no son apreciables.

Sin embargo, se deduce algo importante al comparar las gráficas de la columna derecha que pertenecen al régimen κ ≄ (p + γ)/2. El detector está interactuando de manera no despreciable con el sistema átomo-campo, dado que niveles como |X, X₁, 0) y |G, X₁, 0) están poblados, y el nivel |X, G₁, 0) (que anteriormente se denotaba |X,0) al no ser tenido en cuenta el detector), sufre un gran cambio. Esto nos permite decir, en principio, que puede haber entrelazamiento en este régimen. Por esta razón calcularemos la negatividad para el régimen κ ≄ (p + γ)/2.

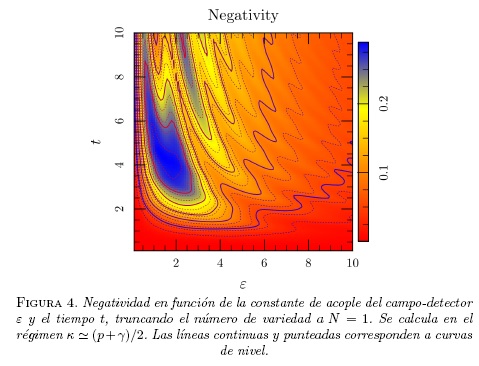
En este régimen existen dos opciones, la primera cuando el número de variedad (del cual se habló en la sección de la ecuación maestra) es truncado a N = 1, y los demás casos cuando N ≥ 2.:

i) En el primer caso que se observa en la figura (4) para valores de la constante de acople del detector con el campo ε en un rango de 0 a 4, la negatividad existe, y más aún permanece en un lapso de tiempo bastante apreciable. Esto significa que hay entrelazamiento entre el detector y el átomo, lo cual no permitiría utilizar el argumento de un detector, dado que en principio se desea que el detector afecte lo menos posible el sistema átomo-campo. Por ejemplo, para valores de ε = 0.5 el entrelazamiento ya es apreciable.

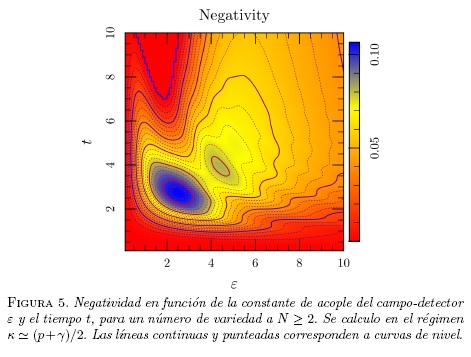
ii) En el segundo caso que se observa en la figura (5), la forma funcional de la negatividad es igual para valores N ≥ 2. En esta se observa que aunque el máximo valor de la negatividad es menor al máximo valor del caso anterior, es distinta de cero en una gran región.

Para valores de ε y tiempo t entre 1 y 4 respectivamente, la negatividad es máxima. Para un valor ε = 5 la negatividad tiene otro pico. Aunque en estos casos de ε ≥ 1 el acople campo-detector es muy grande, no hay razón para obviarlos. Tal vez el caso que es más interesante y que necesita más atención se presenta desde ε = 0.5, donde la negatividad comienza a aumentar de manera suave, y por ende, existe el entrelazamiento átomo-detector. En este caso el acople es pequeño, como para suponer que el detector está afectando poco al sistema átomo-campo, pero este valor de negatividad demuestra que hay entrelazamiento.

Conclusiones

La aproximación del detector como un átomo de dos niveles que interactúa con un modo del campo electromagnético, es buena si el valor de la constante de acople ε es menor que el valor de la constante de acople átomo-campo g. Tal vez el caso que es más interesante y que necesita más atención se presenta desde ε = 0.5 en el régimen κ ≄ (p + γ)/2, donde la negatividad comienza a aumentar de manera suave, y por ende, existe el entrelazamiento átomo-detector. Desde este punto, es necesario ver si el entrelazamiento aumenta al introducir más detectores. Por otra parte no se observa un claro entrelazamiento en el régimen κ << (p + γ)/2, el cual podría ser cuantificado utilizando otras medidas de entrelazamiento distintas a la negatividad de Pares.

Agradecimientos

Este trabajo ha sido financiado por Colciencias dentro del proyecto con código 110156933525, contrato número 026-2013 y código HERMES 17432. Por otra parte, reconocemos el apoyo técnico y computacional del Grupo de (Óptica e Información Cuántica de la Universidad Nacional de Colombia, Sede Bogotá.

---

Referencias

[1] E. del Valle, A. Gonzalez-Tudela, F. P. Laussy, C. Tejedor, and M. J. Hartmann, Phys. Rev. Lett. 109, 183601 (2012).

[2] A. Gonzalez-Tudela, F. P. Laussy, C. Tejedor, M. J. Hartmann, and E. del Valle, New Journal of Physics 15, 033036 (2013).

[3] J. I. Perea, D. Porras, and C. Tejedor, Phys. Rev. B 70, 115304 (2004).

[4] Gerry and P. L. Knight, Introductory Quantum Optics (Cambrige University Press, 2005).

[5] J. P. R. Cuartas, Decoherencia Cuántica: Sistemas Atómicos y Mesoscopicos (Tesis para optar al título de Físico, 2008).

[6] S. M. Barnett and P. M. Radmore, Methods in Theoretical Quantum Optics (Oxford Science Publications, 2005).