REVIEW OF NEW PHYSICS SEARCHES AT LHCb EXPERIMENT
RESEÑA DE BÚSQUEDA DE NUEVA FÍSICA EN EL EXPERIMENTO LHCb
DOI:
https://doi.org/10.15446/mo.n51.56230Keywords:
LHCb, New Physics, Bmeson decays. (en)LHCb, Nueva física, desintegraciones de mesones B. (es)
Downloads
In this document we present an experimental status of beyond Standard Model searches using data samples collected by the LHCb experiment during the LHC-Run1.
En este documento se presenta el estatus de búsqueda de física más allá del Modelo Estandar usando datos recolectados por el experimento LHCb durante el primer periodo de operación de LHC.
REVIEW OF NEW PHYSICS SEARCHES AT LHCb EXPERIMENT
RESEÑA DE BÚSQUEDA DE NUEVA FÍSICA EN EL EXPERIMENTO LHCb
Diego A. Milanés, Jairo A. Rodriguez
Universidad Nacional de Colombia, Sede Bogotá, Colombia.
(Recibido: Octubre/2015. Aceptado: Diciembre/2015)
Abstract
In this document we present an experimental status of beyond Standard Model searches using data samples collected by the LHCb experiment during the LHC-Run1.
Keywords: LHCb, New Physics, B-meson decays.
Resumen
En este documento se presenta el estatus de búsqueda de física más allá del Modelo Estándar usando datos recolectados por el experimento LHCb durante el primer periodo de operación de LHC.
Palabras clave: LHCb, Nueva física, desintegraciones de mesones B.
Introduction
The Large Hadron Collider Beauty experiment (LHCb experiment) is one of the four main particle detectors which operate in the Large Hadron Collider (LHC), at CERN. It is gratifying to mention that Universidad Nacional de Colombia is an associate member institution of the experiment since mid 2014, represented by the authors of this review. The LHCb experiment is a single-arm forward spectrometer, design to capture almost half of heavy hadrons produced cross-section in pp collisions at the TeV-scale [1]. Its design, excellent tracking and particle identification performance, and the large data samples collected, makes of this detector the best scenario, at present, to study processes involving b- and c-hadrons and their decays. Some of these decays help us to measure the Cabibbo-Kobayashi-Maskawa (CKM) matrix elements [2] which is the sector of the Standard Model of Electroweak interactions (SM) [3-6] where differences between matter and antimatter are accounted for. It is precisely the full experimental stablishment of this sector the one of the main goals of experiments like the B-factories [7, 8] and LHCb. In addition, the measurement of observables sensitive to virtual particles and the comparison with SM prediction represents an indirect way to search for physics beyond the SM or New Physics (NP).
Beyond the SM and heavy hadron physics
The SM have been extensively and successfully tested for almost half century by now. Its most recent achievement was the discovery, by the ATLAS and CMS collaborations at CERN [9, 10], of a particle which properties are as expected for the SM Higgs boson. This particle closes the SM circle, and we can confidentially say that the spectrum of the SM is now complete. Despite this tremendous success, it is well know that there are certain phenomena which eludes a satisfactory explanation in the SM. The SM is not capable to explain at least gravity, neutrino mass and oscillations, matter-antimatter asymmetry in the universe, existence of dark matter and dark energy, mass difference among quarks of same generation, among others. To solve these problems several models have been postulated but so far, although experimental evidence claiming that the SM is incomplete is accepted, there is no experimental evidence of which of the postulated models will become the next SM.
SM extensions can be categorized in several groups: extension of the gauge sector, extension of the scalar sector, extension of the fermion content, additional global symmetries and others. The literature in each of these topics is copious and represents the work of the theoretical physics since SM was postulated in the late 60's. At LHC NP searches are done in two ways: Direct NP searches in ATLAS and CMS, where NP is expected to be produced as real particles, and indirect NP searches as performed by LHCb. NP is searched as off-shell particles which appear in loop (quantum corrections) diagrams of process involving b-hadrons, and its presence could modify observables such as decay rates, cross section, angular dependance ond others. For this, it is important to perform high precision predictions of observables in the SM framework. The theory of strong interactions, quantum chromodynamics (QCD), stablish that no free quarks can be found in the nature and they are always confined within hadrons and freedom can only be reached asymptotically as energy increases [11-13]. This behaviour can be explained from the point of view of the strong running coupling constant as(Q) which is function of the energy scale Q. At the few GeV-scale, the realm of most hadrons, the magnitude of αs is large and prevents to perform a perturbative expansion of the Hamiltonian operator. Thus, several non-perturbative techniques have been developed, for instance Refs. [14-18], but the chosen technique depends widely on the process to be computed. This uncertainty is often the largest in the SM prediction of observables involving heavy hadrons transitions.
NP searches at LHCb
There are several B(u>d>s) meson decays suited too look for NP effects. These decays are commonly rare but the superb LHCb detector performance and largest heavy hadron sample in the world, of about 1011 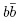 pairs inside the LHCb acceptance, allows for the study of largely suppressed transitions. Rare transitions, for instance b → s transitions like
pairs inside the LHCb acceptance, allows for the study of largely suppressed transitions. Rare transitions, for instance b → s transitions like 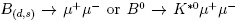 processes, are important since they are forbidden at first order in the SM and only possible via quantum corrections. In these cases NP signatures can be characterized as large decay rates or variation of angular distribution from SM expectations. Leptonic and semileptonic final states bring the possiblilty to study several observables which theoretically are not straightforward to compute, but dependance on the hadronic form factors can be reduced or isolated. Additionally, there are processes at first order in the SM, involving b → c transitions, which allows to probe fundamental consequences of the SM structure such as lepton universality. In the following we discuss many of these studies.
processes, are important since they are forbidden at first order in the SM and only possible via quantum corrections. In these cases NP signatures can be characterized as large decay rates or variation of angular distribution from SM expectations. Leptonic and semileptonic final states bring the possiblilty to study several observables which theoretically are not straightforward to compute, but dependance on the hadronic form factors can be reduced or isolated. Additionally, there are processes at first order in the SM, involving b → c transitions, which allows to probe fundamental consequences of the SM structure such as lepton universality. In the following we discuss many of these studies.
Rarity of B(d,s) →µ+µ- decays
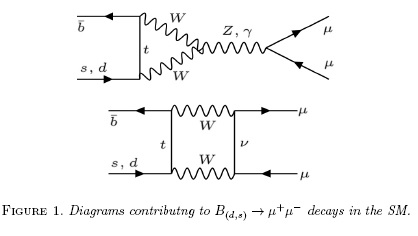
The B(d,s) →µ+µ- decays have been matter of search for the last 30 years. Several experiments have attempted to search these decays since they are forbidden in the SM model at tree level. At one loop, the main contributing diagrams to these decays are shown in Fig. 1. The observation of this decay with a large branching fraction could represent and unambiguous sign of NP. Prediction of these amplitudes in the SM have been computed in Ref. [19], to be 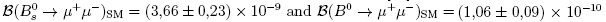 , implying that only few decays over billions of B-mesons are in these modes, which make them rare. Much has been discuss on the possible contribution of supersymmetric (SUSY) particles on these decays [20, 21]. The observation of these decay modes, is expected to reduce the parameters space and dictate which of these SUSY models could be the appropriate one. NP particles can appear as unknown particles replacing the vector bosons in Fig. 1, for instance charged Higgs bosons.
, implying that only few decays over billions of B-mesons are in these modes, which make them rare. Much has been discuss on the possible contribution of supersymmetric (SUSY) particles on these decays [20, 21]. The observation of these decay modes, is expected to reduce the parameters space and dictate which of these SUSY models could be the appropriate one. NP particles can appear as unknown particles replacing the vector bosons in Fig. 1, for instance charged Higgs bosons.
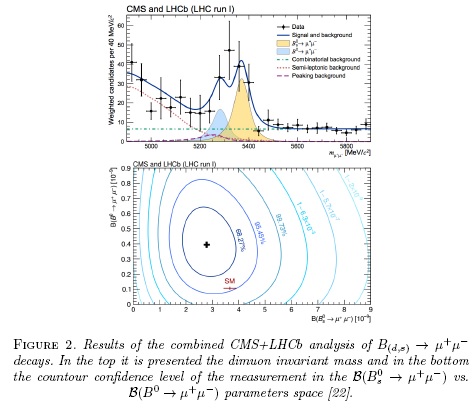
The CMS and LHCb collaborations in a joint effort, and merged their data samples and measured with precision both branching fractions [22]. This analysis was carefully done, accounting for the possible detector effects in both experiments. Peaking background from double misidentified pions from B0 → π+ π- which is the main component under the signal peaks and partially reconstructed semileptonic B decays is the largest background source for low values of the dimuon invariant mass. Combinatorial background, due to random combination of muons, has been reduced using multivariate analysis, and results have been cross-checked for different selection criteria based in the cut on the boosted trees [23]. The invarant dimuon mass fit can be observed in Fig. 2(top), where is evidenced the presence of both, B(d,s) →µ+µ-, signals.
The measured branching fraction is 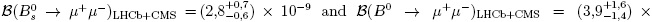 10 10 , where the quoted error includes statistical and systematic uncertainties. This measurement, which accounts for correlations among both observables, is consistent with the SM prediction within 2 standard deviations as observed in Fig. 2(bottom), and the observation of both decay modes can be claimed above 3 standard deviations. This result has largerly constrained NP phase space as discussed in Ref. [24], in particular for several SUSY extensions of the SM, where
10 10 , where the quoted error includes statistical and systematic uncertainties. This measurement, which accounts for correlations among both observables, is consistent with the SM prediction within 2 standard deviations as observed in Fig. 2(bottom), and the observation of both decay modes can be claimed above 3 standard deviations. This result has largerly constrained NP phase space as discussed in Ref. [24], in particular for several SUSY extensions of the SM, where 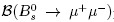 was expected to be larger.
was expected to be larger.
Angular analysis of b → sl+l- transitions
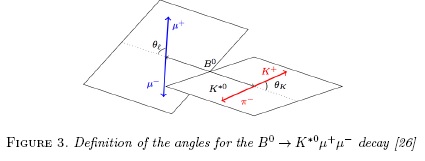
Continuing with suppressed b → sl+l- processes, we have decays such as 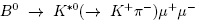 for instance. This decay is a flavor changing neutral current process and in addition has a vector meson, which angular distribution brings information on the spin content of the intermediate particles. The Feynman diagram contributing to this process in the SM, is similar to that shown in Fig. 1. An angular analysis allows to write the differential decay rate in terms of the squared transferred momentum to the dimuon system q2, the angle between θê, θl, which are defined in Fig. 3, and φ the angle between the dimuon and the K*0 decay plane. These variables are enough to perform an expansion of the amplitude in the helicity basis, where the coefficients of this expansion are extracted from the data and are related with the Wilson coefficients [14].
for instance. This decay is a flavor changing neutral current process and in addition has a vector meson, which angular distribution brings information on the spin content of the intermediate particles. The Feynman diagram contributing to this process in the SM, is similar to that shown in Fig. 1. An angular analysis allows to write the differential decay rate in terms of the squared transferred momentum to the dimuon system q2, the angle between θê, θl, which are defined in Fig. 3, and φ the angle between the dimuon and the K*0 decay plane. These variables are enough to perform an expansion of the amplitude in the helicity basis, where the coefficients of this expansion are extracted from the data and are related with the Wilson coefficients [14].
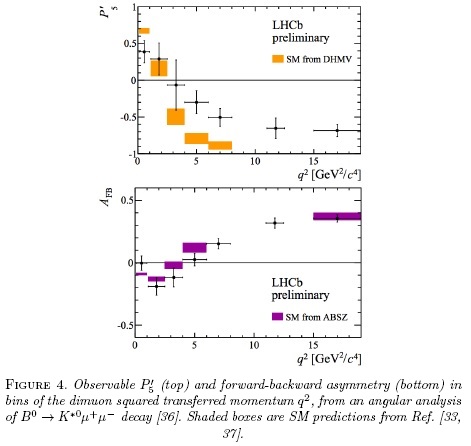
Several of these angular parameters have been measured in agreement with SM predictions [25-28]. However, the first LHCb analysis of this decay mode [29], using only 1/3 of the full data sample recorded during the LHC-Run1, showed a discrepancies between SM prediction and the LHCb measurement of 3.7 standard deviations, for an angular parameter known as P'5, in a specific q2 bin. This observable is important since its theoretical uncertainty is small and can be computed almost without form factor pollution. This anomaly triggered several theoretical papers argueing for NPs [30-35]. Within the models postulated there are leptoquarks, models including charged Higgs bosons and also additional gauge bosons like Z', among other.
A second LHCb measurement, Ref. [36], using the full LHCb data samples available was necessary to confirm or rule out this anomaly. Here, the analysis consisted on an angular analysis of CP-averaged observables for the first time, extracting them simultaneously to account for possible correlations among them and allowing for a correct statistical treatment. To improve previous measurement and profiting for larger statistics the binning in q2 was taken smaller. In the region of 4 < q2 < 8 GeV2/c4, right below the J/Ψ region, the discrepancy between LHCb data and SM prediction is evident and reaches statistical sensitivity of 3.7 standard deviations, the same as in the previous analysis, as shown in Fig. 4(top). Additionally the measured forward-backward asymmetry, AFB, is systematically below the SM prediction about 1 standard deviation, Fig. 4(bottom). Although the deviation from the theoretical prediction is established, it is not conclusive which NP model is the one that describe best the dat or if SM uncertainties, mainly hadronic, are fully understood.
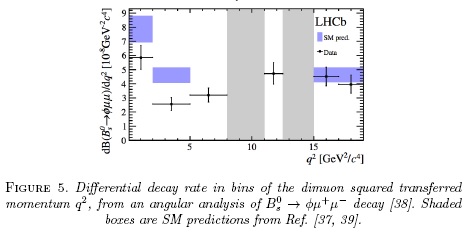
In order to collect more information about this anomaly it is mandatory to investigate more observables in this type of decays, for instance 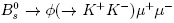 [38;]. The differential decay rate can be also expanded in the helicity basis using similar angles as the
[38;]. The differential decay rate can be also expanded in the helicity basis using similar angles as the 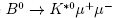 decay. The angular observables are compatible with the SM predictions but an anomaly was observed in the q2 dependant decay rate, Fig. 5. SM predictions for the decay rate of
decay. The angular observables are compatible with the SM predictions but an anomaly was observed in the q2 dependant decay rate, Fig. 5. SM predictions for the decay rate of 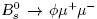 are computed in Refs. [37, 39]. This measurement, which uses full LHCb-Run1 data, reports a difference of more than 3 standard deviations between the experimental data and the SM prediction for low-q2 values.
are computed in Refs. [37, 39]. This measurement, which uses full LHCb-Run1 data, reports a difference of more than 3 standard deviations between the experimental data and the SM prediction for low-q2 values.
Lepton universality
Within the SM the effects of the weak force in the three lepton generations is expected to be the identical. In this sense, Z boson mediated decays such as 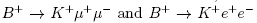 are expected to be the same up to quantum corrections. In order to cancel several hadronic effects in theoretical computations, it is convenient to define the ratio
are expected to be the same up to quantum corrections. In order to cancel several hadronic effects in theoretical computations, it is convenient to define the ratio 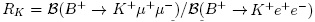 , which in the SM is know to be 1 + 40]
, which in the SM is know to be 1 + 40] 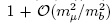 . The BaBar experiment observed a q2 dependent asymmetry in the measurement of RK [41], making this measurement interesting to be performed in LHCb.
. The BaBar experiment observed a q2 dependent asymmetry in the measurement of RK [41], making this measurement interesting to be performed in LHCb.
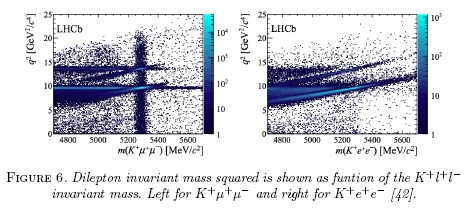
The LHCb experiment studied this ratio using all the available data samples [42]. The analysis is done in the low-q2 region since this is the range where calorimeter and Cherenkov detectors performance is better on electron tracks reconstruction. A careful treatment of efficencies, mainly those related to hardware trigger, is necessary since electron reconstruction in LHCb, behaves differently than muon detection. Main background sources come from partially reconstructed b-hadron decays and random combinations, however background level under the signal peaks is below 20 % for different trigger selection criteria. The data collected by LHCb can be observed in Fig. 6, where the dilepton invariant mass squared is shown as funtion of the K+l+l- invariant mass. Here clear peaks for the charmonia J/ψ and Ψ(25) states and also their radiative tails is observed, and to avoid possible hadronic effects from these states resonant contributions are vetoed in the nominal fit. The final LHCb measurement is 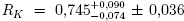 , where the first error accounts for statistical and the second for systematic uncertainties, in the range of 1 < q2 < 6 GeV2/c4. This result is compatible with SM prediction at 2.6 standard deviations. Although not too far away from the SM, it is compatible with the asymmetry measured by BaBar, and feeds the idea of having NP taking place in those decays with non universal lepton couplings of weak neutral currents.
, where the first error accounts for statistical and the second for systematic uncertainties, in the range of 1 < q2 < 6 GeV2/c4. This result is compatible with SM prediction at 2.6 standard deviations. Although not too far away from the SM, it is compatible with the asymmetry measured by BaBar, and feeds the idea of having NP taking place in those decays with non universal lepton couplings of weak neutral currents.
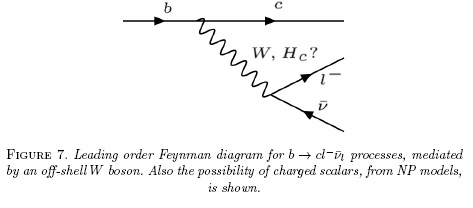
Lepton universality in the SM is not only matter of neutral weak currents but also the charged ones, W±. This means that the W/v coupling is identical for all leptons. A good scenario to test this idea is 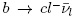 transitions. Unlike those processes we have studied so far, this process is allowed at first order in the SM as shown in Fig. 7. It means that the decay rates of the processes
transitions. Unlike those processes we have studied so far, this process is allowed at first order in the SM as shown in Fig. 7. It means that the decay rates of the processes 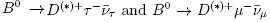 , differ only on the dependance of the lepton mass. The ratio between these two processes, R(D(*)), was largerly studied in the B-factories [43-45], where a discrepancy from the SM prediction [46] R(D*)SM = 0,252±0,003, was observed. This anomaly, although did not exceed the 3 standard deviations, was observed in both BaBar and Belle experiments. This has been studied in NP models with off-shell charged scalars, for instance models with two Higgs doublets, where the charged Higgs boson coupling to
, differ only on the dependance of the lepton mass. The ratio between these two processes, R(D(*)), was largerly studied in the B-factories [43-45], where a discrepancy from the SM prediction [46] R(D*)SM = 0,252±0,003, was observed. This anomaly, although did not exceed the 3 standard deviations, was observed in both BaBar and Belle experiments. This has been studied in NP models with off-shell charged scalars, for instance models with two Higgs doublets, where the charged Higgs boson coupling to 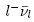 might not be the same for all leptons.
might not be the same for all leptons.
LHCb experiment measured as well the R(D*) quantity [47] using the complete LHC-Run1 dataset. Despite difficulties on the neutrino missing energy reconstruction, from the prompt neutrino and from those comming in the 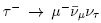 decay, LHCb has measured the branching fraction ratio with a relative 10 % total uncertainty. As usual in LHCb, large background contributions arise from partially reconstructed heavy hadrons, but in this case also from excited high mass D** states have been taken into account with dedicated Monte Carlo simulations. The largest uncertainty is driven by the size of the Monte Carlo simulated events in order to understand the missing energy spectrum. The LHCb measurement is R(D*)LHCb = 0,336 ± 0,027 ± 0,030 where the first error quoted corresponds to statistical uncertainties and the second one is given by systematic effects. This measurement is in full agreement with B-factories measurement and differs from SM prediction by 2.1 standard deviations. In conclusion, LHCb experiment observes as well a tension with the SM prediction. This deviation is not too large but already three different experiments have observed it.
decay, LHCb has measured the branching fraction ratio with a relative 10 % total uncertainty. As usual in LHCb, large background contributions arise from partially reconstructed heavy hadrons, but in this case also from excited high mass D** states have been taken into account with dedicated Monte Carlo simulations. The largest uncertainty is driven by the size of the Monte Carlo simulated events in order to understand the missing energy spectrum. The LHCb measurement is R(D*)LHCb = 0,336 ± 0,027 ± 0,030 where the first error quoted corresponds to statistical uncertainties and the second one is given by systematic effects. This measurement is in full agreement with B-factories measurement and differs from SM prediction by 2.1 standard deviations. In conclusion, LHCb experiment observes as well a tension with the SM prediction. This deviation is not too large but already three different experiments have observed it.
Conclusions
In this document we have described some of the discrepancies between the SM theory and the LHCb data trough indirect searches of NP using heavy hadron transitions. At present none of the mentioned tensions exceeds the 5 standard deviations and they do not favor or exclude any of the available NP models. The analyses discussed here, show the capability and large potential of the LHCb experiment to look inside the quantum corrections in order to search for NP. More statistic, which will be collected during LHC-Run2, and the measurement of more form factor independent observables, will provide experimental probes to identify the next benchmark model of the universe.
As a final remark, we want to state that before claiming for NP using hadron decays, we must understand the complexity of current physics and provide reliable methods to compute the large hadronic contributions present in almost all LHCb measurements.
Acknowledgements
We express our gratitude to our colleagues in the LHCb collaboration for the excellent performance of the machine and the opportunity they provide to perform high precision measurements in the heavy hadron sector.
References
[1] A. A. Alves, Jr. et al. (LHCb), JINST 3, S08005 (2008).
[2] M. Kobayashi and T. Maskawa, Prog. Theor. Phys. 49, 652 (1973).
[3] A. Salam and J. C. Ward, Phys. Lett. 13, 168 (1964).
[4] S. Weinberg, Phys. Rev. Lett. 19, 1264 (1967).
[5] S. L. Glashow, J. Iliopoulos, and L. Maiani, Phys. Rev. D2, 1285 (1970).
[6] G. 't Hooft, Nucl. Phys. B35, 167 (1971).
[7] B. Aubert et al. (BaBar), Nucl. Instrum. Meth. A479, 1 (2002), arXiv:hep-ex/0105044 [hep-ex].
[8] A. Abashian et al., Nucl. Instrum. Meth. A479, 117 (2002).
[9] G. Aad et al. (ATLAS), Phys. Lett. B716, 1 (2013), arXiv:1207.7214 [hep-ex].
[10] S. Chatrchyan et al. (CMS), Phys. Lett. B716, 30 (2012), arXiv:1207.7235 [hep-ex].
[11] H. D. Politzer, Phys. Rept. 14, 129 (1974).
[12] D. J. Gross and F. Wilczek, Phys. Rev. D9, 980 (1974).
[13] D. J. Gross and F. Wilczek, Phys. Rev. D8, 3633 (1973).
[14] K. G. Wilson, Phys. Rev. D2, 1473 (1970).
[15] D. A. Dicus, R. Jackiw, and V. L. Teplitz, Phys. Rev. D4, 1733 (1971).
[16] G. P. Lepage and S. J. Brodsky, Phys. Lett. B87, 359 (1979).
[17] L. J. Reinders, H. R. Rubinstein, and S. Yazaki, Nucl. Phys. B186, 109 (1981).
[18] B. Sheikholeslami and R. Wohlert, Nucl. Phys. B259, 572 (1985).
[19] C. Bobeth, M. Gorbahn, T. Hermann, M. Misiak, E. Stamou, and M. Steinhauser, Phys. Rev. Lett. 112, 101801 (2014), arXiv:1311.0903 [hep-ph].
[20] C.-S. Huang, W. Liao, and Q.-S. Yan, Phys. Rev. D59, 011701 (1999), arXiv:hep-ph/9803460 [hep-ph].
[21] S. R. Choudhury and N. Gaur, Phys. Lett. B451, 86 (1999), arXiv:hep-ph/9810307 [hep-ph] .
[22] V. Khachatryan et al. (LHCb, CMS), Nature 522, 68 (2015), arXiv:1411.4413 [hep-ex].
[23] J. Therhaag, Proceedings, 35th International Conference on High energy physics (ICHEP 2010), PoS ICHEP2010, 510 (2010).
[24] J. Charles et al., Phys. Rev. D91, 073007 (2015), arXiv:1501.05013 [hep-ph] .
[25] T. Aaltonen et al. (CDF), Phys. Rev. Lett. 108, 081807 (2012), arXiv:1108.0695 [hep-ex].
[26] R. Aaij et al. (LHCb), JHEP 08, 131 (2013), arXiv:1304.6325.
[27] J. T. Wei et al. (Belle), Phys. Rev. Lett. 103, 171801 (2009), arXiv:0904.0770 [hep-ex].
[28] B. Aubert et al. (BaBar), Phys. Rev. D73, 092001 (2006), arXiv:hep-ex/0604007 [hep-ex].
[29] R. Aaij et al. (LHCb), Phys. Rev. Lett. 111, 191801 (2013), arXiv:1308.1707 [hep-ex].
[30] W. Altmannshofer and D. M. Straub, Eur. Phys. J. C73, 2646 (2013), arXiv:1308.1501 [hep-ph].
[31] T. Hurth and F. Mahmoudi, JHEP 04, 097 (2014), arXiv:1312.5267 [hep-ph].
[32] S. Jager and J. Martin Camalich, JHEP 05, 043 (2013), arXiv:1212.2263 [hep-ph].
[33] S. Descotes-Genon, L. Hofer, J. Matias, and J. Virto, JHEP 12, 125 (2014), arXiv:1407.8526 [hep-ph].
[34] J. Lyon and R. Zwicky, (2014), arXiv:1406.0566 [hep-ph].
[35] R. Gauld, F. Goertz, and U. Haisch, JHEP 01, 069 (2014), arXiv:1310.1082 [hep-ph].
[36] R. Aaij et al. (LHCb), LHCb-CONF-2015-02 (2015).
[37] A. Bharucha, D. M. Straub, and R. Zwicky, (2015), arXiv:1503.05534 [hep-ph].
[38] R. Aaij et al. (LHCb), JHEP 09, 179 (2015), arXiv:1506.08777 [hep-ex].
[39] W. Altmannshofer and D. M. Straub, Eur. Phys. J. C75, 382 (2015), arXiv:1411.3161 [hep-ph].
[40] G. Hiller and F. Kruger, Phys. Rev. D69, 074020 (2004), arXiv:hep-ph/0310219 [hep-ph].
[41] J. P. Lees et al. (BaBar), Phys. Rev. D86, 032012 (2012), arXiv:1204.3933 [hep-ex].
[42] R. Aaij et al. (LHCb), Phys. Rev. Lett. 113, 151601 (2014), arXiv:1406.6482 [hep-ex].
[43] A. Bozek et al. (Belle), Phys. Rev. D82, 072005 (2010), arXiv:1005.2302 [hep-ex].
[44] J. P. Lees et al. (BaBar), Phys. Rev. Lett. 109, 101802 (2012), arXiv:1205.5442 [hep-ex].
[45] J. P. Lees et al. (BaBar), Phys. Rev. D88, 072012 (2013), arXiv:1303.0571 [hep-ex].
[46] S. Fajfer, J. F. Kamenik, and I. Nisandzic, Phys. Rev. D85, 094025 (2012), arXiv:1203.2654 [hep-ph].
[47] R. Aaij et al. (LHCb), Phys. Rev. Lett. 115, 111803 (2015), [Addendum: Phys. Rev. Lett.115,no.15,159901(2015)], arXiv:1506.08614 [hep-ex].
How to Cite
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Download Citation
License
Those authors who have publications with this journal, accept the following terms:
a. The authors will retain their copyright and will guarantee the publication of the first publication of their work, which will be subject to the Attribution-SinDerivar 4.0 International Creative Commons Attribution License that permits redistribution, commercial or non-commercial, As long as the Work circulates intact and unchanged, where it indicates its author and its first publication in this magazine.
b. Authors are encouraged to disseminate their work through the Internet (eg in institutional telematic files or on their website) before and during the sending process, which can produce interesting exchanges and increase appointments of the published work.