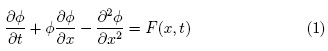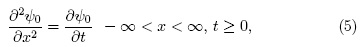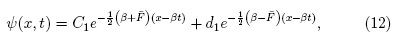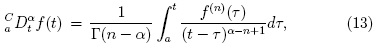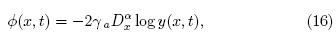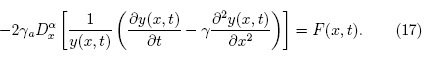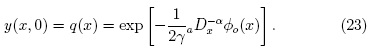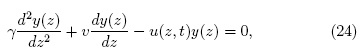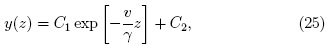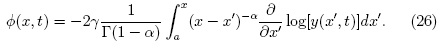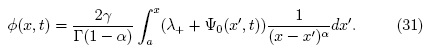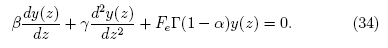ECUACIÓN FRACCIONARIA DE BURGERS NO HOMOGÉNEA
NONHOMOGENEOUS FRACTIONAL BURGERS EQUATION
DOI:
https://doi.org/10.15446/mo.n52.58889Keywords:
Ecuación de Burgers, cálculo fraccionario. (es)Burgers equation, fractional calculus. (en)
Downloads
En este artículo se estudian diferentes tipos de soluciones de la ecuación fraccionaria unidimensional no lineal de Burgers con un término no homogéneo asociado a fuerzas externas. Esta ecuación es una generalización de la ecuación de difusión no homogénea en la que se incluye una derivada fraccionaria de Caputo que describe una no linealidad no local. Por medio de la transformación de Cole-Hopf generalizada, la ecuación de Burgers fraccionaria no homogénea se convierte en una ecuación diferencial lineal en derivadas parciales, lo que permite obtener soluciones analíticas. Se exploran los efectos asociados al término no homogéneo y al orden de la derivada fraccionaria.
In this article we study solutions of the nonlinear fractional Burgers equation with a nonhomogeneous term associated with external forces. This equation is a generalization of the nonhomogeneous diffusion equation with an additional term that describes a nonlocal nonlinearity by means of a fractional order derivative of Caputo type. By using a generalized Cole-Hopf transformation, the fractional Burgers equation is mapped to a linear partial differential equation, this formalism allows to deduce analytical solutions. We explore the effects related to the nonhomogeneous term and the order of the fractional derivative.
ECUACIÓN FRACCIONARIA DE BURGERS NO HOMOGÉNEA
NONHOMOGENEOUS FRACTIONAL BURGERS EQUATION
Victor G. Buesaquillo1, Alejandro Pérez2, Alvaro Rugeles1
1 Departamento de Física. Universidad de Nariño, Pasto, Colombia.
2 Instituto de Física, Universidad Nacional Autónoma de México, México, D.F.
Alejandro Pérez: aaappprrr@gmail.com
(Recibido: Octubre/2015. Aceptado: Abril/2016)
Resumen
En este artículo se estudian diferentes tipos de soluciones de la ecuación fraccionaria unidimensional no lineal de Burgers con un termino no homogéneo asociado a fuerzas externas. Esta ecuación es una generalización de la ecuación de difusión no homogénea en la que se incluye una derivada fraccionaria de Caputo que describe una no linealidad no local. Por medio de la transformación de Cole-Hopf generalizada, la ecuación de Burgers fraccionaria no homogénea se convierte en una ecuación diferencial lineal en derivadas parciales, lo que permite obtener soluciones analíticas. Se exploran los efectos asociados al termino no homogéneo y al orden de la derivada fraccionaria.
Palabras clave: Ecuación de Burgers, cálculo fraccionario.
Abstract
In this article we study solutions of the nonlinear fractional Burgers equation with a nonhomogeneous term associated with external forces. This equation is a generalization of the nonhomogeneous diffusion equation with an additional term that describes a nonlocal nonlinearity by means of a fractional order derivative of Caputo type. By using a generalized Cole-Hopf transformation, the fractional Burgers equation is mapped to a linear partial differential equation, this formalism allows to deduce analytical solutions. We explore the effects related to the nonhomogeneous term and the order of the fractional derivative.
Keywords: Burgers equation, fractional calculus.
1. Introducción
Desde su introducción en 1939 por el científico Danés J.M. Burgers, la ecuación de Burgers, constituye el modelo no lineal más simple en el estudio de la dinámica de fluidos y ha sido estudiada con el fin de modelar gran cantidad de fenómenos en diversos sistemas físicos [1]. La ecuación de Burgers presenta diferentes tipos de soluciones matemáticas, en particular, paquetes de ondas que se propagan sin cambiar de forma debido a la compensación entre efectos no lineales y dispersivos [2]. Adicional a esto, la ecuación de Burgers puede tener términos extra asociados a fuerzas externas, lo que permite definir la ecuación de Burgers no homogénea [1].
Recientemente se ha propuesto la ecuación fraccionaria de Burgers en la que la parte no lineal se modela por medio de un término con derivadas de orden fraccionario [3]. La razón para extender el tratamiento de la ecuación de Burgers al caso fraccionario se debe a la existencia de diferentes fenómenos de carácter no local [3, 4] que se presentan cuando las propiedades de un sistema en un cierto punto de configuración o espacio de fase no solo dependen de las propiedades del sistema en este punto, sino también de las propiedades del entorno y, como consecuencia, se usa el cálculo fraccionario para describir dichos fenómenos [5, 6].
En este trabajo se estudia la ecuación fraccionaria de Burgers con un término no homogéneo. En la primera parte se analiza la ecuación de Burgers no homogénea. En la sección 2 se utiliza la transformación de Cole-Hopf para establecer una ecuación lineal por medio de la cual se obtienen en forma analítica soluciones solitónicas, también se discute el efecto del término no homogéneo en las soluciones. En la segunda parte del trabajo se analiza la ecuación fraccionaria de Burgers no homogénea. En la sección 3 se presenta brevemente el concepto de derivada fraccionaria, en particular la derivada fraccionaria de Caputo. En la sección 4 se utiliza una versión modificada de la transformación de Cole-Hopf en función de una derivada fraccionaria para usarla en la solución de la ecuación fraccionaria de Burgers no homogénea. Se analizan diversos casos con soluciones con pulsos localizados y soluciones disipativas de la ecuación fraccionaria de Burgers no homogénea.
2. Ecuación de Burgers no homogénea
En esta sección se introducen algunos resultados que son la base para el análisis de la ecuación fraccionaria de Burgers. Se parte de la ecuación de Burgers unidimensional no homogénea para Φ(x,t):
siendo -∞ <x< ∞, t ≥ Oyla condición inicial Φ(x,0) = Φ0(x). El termino F(x, t) se encuentra asociado a fuerzas externas y Φ0(x) es el perfil al tiempo t = 0 de Φ(x,t). Para el caso homogéneo F(x,t) = 0 se conocen soluciones solitónicas [7] y otro conjunto de soluciones obtenidas mediante la transformación de Cole-Hopf [8, 9]. En lo siguiente se aplica esta transformación con el fin de estudiar el caso no homogéneo.
2.1. Transformación de Cole-Hopf
En la ecuación (1) la transformación de Cole-Hopf [8, 9] describe ψ(x,t) por medio de una función φ(x,t) a través de la relación:
Cuando se introduce (2) en la ecuación (1) se obtiene la relación:
Luego se define F(x,t) en términos de un potencial V(x,t) que cumple con F(x,t) = -2. La ecuación (3) permite establecer para ψ(x, t):
con
condición inicial  donde g(x) es
obtenida aplicando (2) a la condición inicial Φ0(x). En
consecuencia, la transformación de Cole-Hopf convierte la
ecuación no homogénea de Burgers (1) en la ecuación de
difusión (4) con términos de fuente, asociados al potencial V(x,t),
de la forma V(x, t)ψ(x, t). La importancia de este tipo de
transformación radica en que establece una correspondencia entre un
problema no lineal donde no es evidente un principio de superposición y
un problema lineal donde el principio de superposición permite utilizar
el método de la función de Green.
donde g(x) es
obtenida aplicando (2) a la condición inicial Φ0(x). En
consecuencia, la transformación de Cole-Hopf convierte la
ecuación no homogénea de Burgers (1) en la ecuación de
difusión (4) con términos de fuente, asociados al potencial V(x,t),
de la forma V(x, t)ψ(x, t). La importancia de este tipo de
transformación radica en que establece una correspondencia entre un
problema no lineal donde no es evidente un principio de superposición y
un problema lineal donde el principio de superposición permite utilizar
el método de la función de Green.
2.2. Soluciones de la ecuación homogénea
Cuando se considera V(x, t) = 0 en la ecuación (4) resulta el caso particular de la ecuación de Burgers homogénea resuelta usando la transformación de Cole-Hopf [8]. En este caso, por medio de la ecuación (4), ψ0(x, t) satisface:
con la condición inicial ψ0(x, 0) = g(x). A partir de ψ0(x,t) se obtienen dos tipos de resultados para φ(x,t): soluciones disipativas y soluciones solitonicas. Teniendo en cuenta que la expresión (5) es una ecuación de difusión cuya solución toma la forma:
las
soluciones disipativas de la ecuación de Burgers homogénea se
obtienen reemplazando (6) en (2). Por otra parte, con el fin de buscar
soluciones de (5) en forma de pulso que se propaga a velocidad v, se
introduce el cambio de variables z = x - vt y en consecuencia ψ(x,t) = ψ(z) satisface  . Las soluciones de esta ecuación
toman la forma ψ (z) = α1e -vz + b1 donde α1, b1 son constantes. Por lo
tanto:
. Las soluciones de esta ecuación
toman la forma ψ (z) = α1e -vz + b1 donde α1, b1 son constantes. Por lo
tanto:
Mediante (2) y (7) se obtiene la solución solitonica de la ecuación
Teniendo
en cuenta que (5) es una ecuación lineal, es posible superponer N soluciones  , donde
, donde 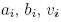 para i =
1,..., N son constantes que describen a cada uno de los solitones. De
esta manera
para i =
1,..., N son constantes que describen a cada uno de los solitones. De
esta manera 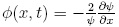 permite obtener la
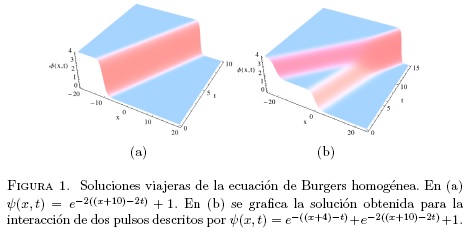
solución con N pulsos. En la Figura 1(a) se
presenta una solución solitónica y en la Figura
1(b) se presenta la interacción de dos solitones. Se nota que la velocidad
del soliton resultante después de la interacción es diferente a
la de los dos solitones iniciales. Las soluciones presentadas en esta
sección son dos grupos de soluciones que se conocen para la
ecuación de Burgers homogénea [7, 8]. En la
siguiente sección se estudia la forma en la que varían estas
soluciones al introducirse la fuerza F(x,t) en (1).
permite obtener la
solución con N pulsos. En la Figura 1(a) se
presenta una solución solitónica y en la Figura
1(b) se presenta la interacción de dos solitones. Se nota que la velocidad
del soliton resultante después de la interacción es diferente a
la de los dos solitones iniciales. Las soluciones presentadas en esta
sección son dos grupos de soluciones que se conocen para la
ecuación de Burgers homogénea [7, 8]. En la
siguiente sección se estudia la forma en la que varían estas
soluciones al introducirse la fuerza F(x,t) en (1).
2.3. Soluciones de la ecuación no homogénea
En esta
sección se analiza el efecto que tiene F(x, t) en la ecuación de
Burgers no homogénea sobre soluciones solitonicas. Cuando F(x,t) = Feδ(x
- xe) se presentan solitones. Los valores Fe, xe son, respectivamente, constantes asociadas a la magnitud de la fuerza externa y
a la posición donde es aplicada. Para este caso el potencial esta dado
por:  . La función
δ(x) denota a la delta de Kronecker y H(x) es la función de
Heaviside. Para este potencial, la ecuación (4) toma
la forma:
. La función
δ(x) denota a la delta de Kronecker y H(x) es la función de
Heaviside. Para este potencial, la ecuación (4) toma
la forma:
Tal como
se estudió en la sección anterior, la ecuación
(9) posee soluciones solitónicas en x < xe. Para la ecuación (10), existen soluciones viajeras que dan lugar
a solitones en la región x ≥ xe. Así, buscando
soluciones de la forma 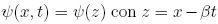 , la ecuación
(10) requiere:
, la ecuación
(10) requiere:
En la región x ≥ xe se presenta un solitón transmitido cuando Fe2 > 16β, en este caso la solución de (11) esto dada por:
donde 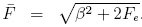 . Por medio de la
transformación de Cole-Hopf se obtiene
. Por medio de la
transformación de Cole-Hopf se obtiene![]() , que es un soliton transmitido. Las
constantes C1, d1, β se deducen a partir de las
condiciones de continuidad que establece (4) en x = xe. Cuando
β2 + 2Fe ≤ 0 se obtienen soluciones para (10)
que no son solitones transmitidos. En este caso el soliton es reflejado y en x
> xe φ(x, t) = 0, resultado que se obtiene al exigir que
ψ(x, t) sea independiente de x y de esta manera, la solución de
(10) está dada por ψ(x,t) ∞ e-Fet/2.
En la Figura 2 se ilustran estas situaciones para un caso
donde hay un soliton transmitido y otro en el que no hay transmisión.
, que es un soliton transmitido. Las
constantes C1, d1, β se deducen a partir de las
condiciones de continuidad que establece (4) en x = xe. Cuando
β2 + 2Fe ≤ 0 se obtienen soluciones para (10)
que no son solitones transmitidos. En este caso el soliton es reflejado y en x
> xe φ(x, t) = 0, resultado que se obtiene al exigir que
ψ(x, t) sea independiente de x y de esta manera, la solución de
(10) está dada por ψ(x,t) ∞ e-Fet/2.
En la Figura 2 se ilustran estas situaciones para un caso
donde hay un soliton transmitido y otro en el que no hay transmisión.
En la siguiente parte del trabajo se considera la ecuación fraccionaria de Burgers no homogénea teniendo en cuenta el formalismo planteado hasta el momento. En este sentido se utiliza la ecuación de Burgers fraccionaria propuesta en [10] y se adiciona un término F(x, t) asociado a fuerzas externas. Se utiliza una transformada de Cole-Hopf generalizada que relaciona a la ecuación de Burgers fraccionaria con una ecuación diferencial en derivadas parciales. Luego se analizan soluciones de la ecuación fraccionaria de Burgers.
3. Derivadas fraccionarias
Una
derivada es una operación que cumple con las propiedades de linealidad y
la regla de Leibniz del producto. De esta manera, en diversos contextos se
pueden definir derivadas y en el caso de funciones de una variable la derivada
tradicional de la función f (t) dada por  , se generaliza con el fin de
extender el carácter local de esta definición. Esto lleva a
establecer la derivada fraccionaria de Riemman-Liouville de orden real α
[6]:
, se generaliza con el fin de
extender el carácter local de esta definición. Esto lleva a
establecer la derivada fraccionaria de Riemman-Liouville de orden real α
[6]:  donde α y
t son valores reales que denotan los límites en los que se debe incluir
información de f (t) con el fin de evaluar la derivada, n es el
mayor entero que satisface n - 1 ≤ α < n y
Γ(z) denota a la función Gamma [6].
donde α y
t son valores reales que denotan los límites en los que se debe incluir
información de f (t) con el fin de evaluar la derivada, n es el
mayor entero que satisface n - 1 ≤ α < n y
Γ(z) denota a la función Gamma [6].
en esta definición f (n)(τ) denota la n-esíma derivada de f (τ). Es conveniente señalar que existen otros tipos de derivada fraccionaria y en general estas definiciones no son equivalentes e incluso algunas de sus propiedades difieren. Por ejemplo, la derivada de Caputo de una constante es nula, algo que no ocurre para el caso de la derivada fraccionaria de Riemman-Liouville [6]. En física, ecuaciones diferenciales con derivadas fraccionarias se han utilizado para modelar procesos en diversos sistemas [6, 11]. Una revisión del concepto de derivada fraccionaria, de las diferentes formas de definir estas derivadas y los métodos utilizados en este campo de las matemáticas, son presentados en [5, 6].
4. Ecuación fraccionaria de Burgers no homogénea
En esta sección se estudia la ecuación fraccionaria de Burgers no lineal planteada en [3, 10] con un término adicional F(x,t):
En esta
ecuación, 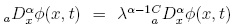 es la derivada
fraccionaria, donde
es la derivada
fraccionaria, donde  es la derivada
fraccionaria de Caputo dada por la ecuación (13) y
el factor
es la derivada
fraccionaria de Caputo dada por la ecuación (13) y
el factor 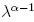 es una constante
que se introduce con el fin de que la ecuación sea correcta en sus
unidades, de esta manera λ define una longitud característica del
problema [3, 10], en la siguiente parte se toma como λ=
1. Por otra parte, F(x,t) esta asociado a fuerzas externas y γ es el
coeficiente de viscosidad. Adicional a esto, la ecuación
(14) esta sometida a la condición inicial:
es una constante
que se introduce con el fin de que la ecuación sea correcta en sus
unidades, de esta manera λ define una longitud característica del
problema [3, 10], en la siguiente parte se toma como λ=
1. Por otra parte, F(x,t) esta asociado a fuerzas externas y γ es el
coeficiente de viscosidad. Adicional a esto, la ecuación
(14) esta sometida a la condición inicial:
en donde φ(x, t) y φ0 (x) son funciones definidas en el conjunto de los números reales. El problema esto bien definido en la región α ≤ x < ∞ y 0 ≤ t, donde α es una constante real que define a las derivadas fraccionarias de la ecuación (14).
4.1. Transformación generalizada de Cole-Hopf
Para simplificar la ecuación (14) existe una transformación que es la generalización de la transformación de Cole-Hopf clásica al caso fraccionario y está definida por la expresión [3, 10]:
donde
γ es el coeficiente de viscosidad del medio. Reemplazando la ecuación (16) en (14) y teniendo en
cuenta que  conmuta con el
operador de derivación entera, se obtiene:
conmuta con el
operador de derivación entera, se obtiene:
Además, si el término de fuerza externa F(x, t) se describe mediante un potencial V(x,t) que satisface:
al reemplazar (18) en (17) resulta:
Debido a que la derivada de Caputo de una constante es cero, la ecuación (19) implica que:
donde la función C1(t) depende únicamente del tiempo ya que la derivada fraccionaria de Caputo se calcula con respecto a x. Para lo que sigue se define la función:
de tal manera que la ecuación (20) satisface:
La condición inicial se obtiene reemplazando (15) en (16) y despejando y(x, 0):
En la siguiente parte se utilizan diferentes tipos de u(x, t) para hallar la fuerza asociada a estos términos y obtener numéricamente la solución de la ecuación de Burgers. En la sección 4.2 se hace un estudio de las consecuencias de la ecuación (22) cuando y(x,t) = y(x - vt).
4.2. Ecuación fraccionaria de Burgers homogénea
Se obtienen pulsos localizados a partir de la ecuación (22) cuando y(x, t) = y(x - vt) = y(z) donde v es la velocidad del pulso. De esta manera, la ecuación (22) se expresa como:
que es una ecuación diferencial lineal homogénea. El termino u(z,t) está relacionado con la fuerza externa F(x, t) mediante la expresión (18). Con el fin de analizar el caso homogéneo de (24), se considera F(x, t) = 0, como consecuencia u(z,t)= 0. Para este caso se obtiene la solución:
donde z = x - vt. Para continuar se utiliza la ecuación (16) que está definida en términos de la derivada de Caputo, donde 0 < α < 1 implica n = 1, como consecuencia:
En la ecuación (26) aparece la expresión 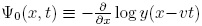 que está
dada por:
que está
dada por:
con 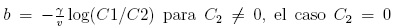 da como resultado
da como resultado 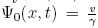 que no es una onda
viajera. La ecuación (27) es la solución de
un solitón de la ecuación de Burgers normal obtenida en la ecuación (8); se nota que el efecto de las constantes C1,
C2 es establecer el desfase b del pulso. Al incorporar el
resultado (27) en el análisis de la ecuación fraccionaria de
Burgers se obtiene:
que no es una onda
viajera. La ecuación (27) es la solución de
un solitón de la ecuación de Burgers normal obtenida en la ecuación (8); se nota que el efecto de las constantes C1,
C2 es establecer el desfase b del pulso. Al incorporar el
resultado (27) en el análisis de la ecuación fraccionaria de
Burgers se obtiene:
Teniendo
en cuenta que  , se encuentra que
en el límite α →-∞ diverge haciendo que la solución
localizada no sea posible en ese caso. Como consecuencia, tomar α finito
hace que φ(x,t) en (28) cambie su valor con una relación
proporcional al tamaño de α.
, se encuentra que
en el límite α →-∞ diverge haciendo que la solución
localizada no sea posible en ese caso. Como consecuencia, tomar α finito
hace que φ(x,t) en (28) cambie su valor con una relación
proporcional al tamaño de α.
Por otra parte, cuando u(z,t) = c es una constante diferente de cero la ecuación (24) tiene por solución:
con  . Teniendo en
cuenta
. Teniendo en
cuenta 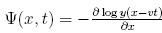 :
:
siendo 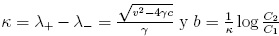 . Al buscar la
solución de la ecuación fraccionaria de Burgers se obtiene:
. Al buscar la
solución de la ecuación fraccionaria de Burgers se obtiene:
donde
Ψ0(x, t) es similar a lo encontrado en el caso u(z, t) = c = 0 con una redefinición de las constantes. En esta
expresión la integral 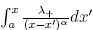 resulta en algo que aumenta de
tamaño conforme x aumenta, este no es el tipo de comportamiento
de los pulsos localizados.
resulta en algo que aumenta de
tamaño conforme x aumenta, este no es el tipo de comportamiento
de los pulsos localizados.
Por lo
tanto soluciones localizadas requieren que λ+ = 0 lo que implica que c =
0. Las soluciones obtenidas en este caso también son soluciones de la
ecuación fraccionaria, sin embargo, en estas soluciones la no linealidad
es mayor que la dispersión del pulso haciendo que el pulso aumente su
amplitud con la dinámica del sistema. Tal como en el caso ordinario,
teniendo en cuenta que (24) es una ecuación diferencial lineal, es
posible superponer soluciones de la forma  , donde i = 1,...,N determina
las constantes que describen a cada uno de los pulsos dados por yi (z). De esta manera,
, donde i = 1,...,N determina
las constantes que describen a cada uno de los pulsos dados por yi (z). De esta manera, 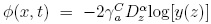 permite obtener la
solución con N pulsos para el caso fraccionario.
permite obtener la
solución con N pulsos para el caso fraccionario.
En la Figura 3(a) se presenta una solución con una onda localizada. Por otra parte, en la Figura 3(b) se presenta la interacción de dos pulsos. Dichos pulsos interaccionan de la misma manera que en el caso ordinario, sin embargo, el valor de α modifica la forma del pulso respecto al que se presenta en el caso ordinario. En la siguiente parte se busca estudiar la forma en la que varían estas soluciones al introducirse la fuerza F(x,t) en (14).
4.3. Ecuación fraccionaria no homogénea
En esta sección se busca entender lo que sucede cuando el término F(x,t) que aparece en la ecuación (14) representa una barrera de potencial. Para este caso, la ecuación (22) implica que u(x,t) = FeΓ(1 - α) H(x - xe) de tal manera que la fuerza externa es de la forma F(x,t) = - 2γFe(x - xe)-αH(x - xe), siendo Fe, xe, c constantes y el potencial V(x,t) = FeΓ(1 - α) H(x - xe) - c. Por lo tanto la ecuación (20) toma la forma:
La ecuación (32) posee soluciones localizadas en x < xe cuando la constante c es nula. Para la ecuación (33), al buscar soluciones de la forma y(x, t) = y(z) con z = x - βt, la ecuación (33) requiere:
En la región x ≥ xe la solución de (34) está dada por:
donde 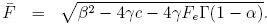 . La
solución (35) es equivalente a la que se obtuvo en la sección 4.2
si se considera
. La
solución (35) es equivalente a la que se obtuvo en la sección 4.2
si se considera  , de tal manera que
, de tal manera que 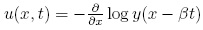 es:
es:
siendo, en
este caso,  . Por lo dicho en
la sección 4.2 para obtener soluciones que mantengan su forma es
necesario que
. Por lo dicho en
la sección 4.2 para obtener soluciones que mantengan su forma es
necesario que 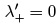 , lo cual es
equivalente a quitar la barrera de potencial y en consecuencia la ecuación
(33) no tiene soluciones solitónicas. En la Figura 3(c) se grafica la
interacción de un pulso con una barrera de fuerza donde se presenta el
pulso incidente pero en la interacción con la barrera no hay pulsos
transmitidos. No obstante, si se compara con el resultado presentado en la Figura
2(a) se observa una similitud dado que los resultados del caso fraccionario deben
coincidir con los del caso ordinario en el límite cuando el orden de la
derivada tiende a un valor entero. En la Figura 3(d) la onda es
reflejada e interacciona con la onda incidente tal como sucede en el caso
ordinario. En este caso también se puede hacer que la barrera sea
variable en el tiempo, tomando F(x, t) = f (t)(x - xe)-aH(x
- xe), donde la solución numérica es presentada en la
Figura 4 y muestra como mediante una fuerza oscilatoria con f (t) = Fe sin(ωt) el pulso incidente genera un pulso transmitido que pierde las
características de pulso localizado y es dispersado.
, lo cual es
equivalente a quitar la barrera de potencial y en consecuencia la ecuación
(33) no tiene soluciones solitónicas. En la Figura 3(c) se grafica la
interacción de un pulso con una barrera de fuerza donde se presenta el
pulso incidente pero en la interacción con la barrera no hay pulsos
transmitidos. No obstante, si se compara con el resultado presentado en la Figura
2(a) se observa una similitud dado que los resultados del caso fraccionario deben
coincidir con los del caso ordinario en el límite cuando el orden de la
derivada tiende a un valor entero. En la Figura 3(d) la onda es
reflejada e interacciona con la onda incidente tal como sucede en el caso
ordinario. En este caso también se puede hacer que la barrera sea
variable en el tiempo, tomando F(x, t) = f (t)(x - xe)-aH(x
- xe), donde la solución numérica es presentada en la
Figura 4 y muestra como mediante una fuerza oscilatoria con f (t) = Fe sin(ωt) el pulso incidente genera un pulso transmitido que pierde las
características de pulso localizado y es dispersado.

5. Conclusiones
En este trabajo se parte de los resultados conocidos para el estudio de la ecuación de Burgers no homogénea y se amplían con el fin de analizar un problema no lineal con ecuaciones diferenciales fraccionarias. Se presenta la ecuación de Burgers no homogénea y se resuelve con el uso de la transformación de Cole-Hopf. Con esto es posible obtener soluciones localizadas, analizar la interacción de pulsos y estudiar las consecuencias de la inclusión de una barrera de potencial tanto constante como una que oscila en el tiempo. A partir de ello se procede al estudio de la ecuación de Burgers fraccionaria no homogénea que se resuelve con el uso de una versión modificada de la transformación de Cole-Hopf. También se obtienen soluciones localizadas y se hace un estudio análogo al llevado a cabo con la ecuación de Burgers clásica. Los resultados de los casos clásico y fraccionario presentan similitud, sin embargo, en el caso fraccionario aparecen características que alteran las predicciones del cálculo ordinario, revelando como las fuerzas externas y la no localidad distorsionan la forma de las ondas viajeras en las soluciones.
6. Agradecimientos
Los autores de este artículo agradecemos el apoyo de la Vicerrectoría de Investigaciones y Postgrados de la Universidad de Nariño por la ayuda financiera para el desarrollo de este trabajo mediante el proyecto titulado: "Métodos variaciones y de cálculo fraccionario en teoría de solitones".
Referencias
[1] J. Bec and K. Khanin, Phys. Rep. 447, 1 (2007).
[2] P. G. Drazin and R. S. Johnson, Solitons : an introduction, Cambridge texts in applied mathematics (Cambridge University Press, Cambridge, 1989).
[3] P. Miskinis, SIGMA 9, 016 (2013).
[4] K. Deng, M. K. Kwong, and H. A. Levine, Quart. Appl. Math 50, 173 (1992).
[5] M. D. Ortigueira, Fractional Calculus for Scientists and Engineers, Lecture Notes in Electrical Engineering, Vol. 84 (Springer, 2011) pp. 1-152.
[6] S. Das, Functional Fractional Calculus, 2nd ed. (Springer Publishing Company, Incorporated, 2014).
[7] E. Hesameddini and R. Gholampour, Int. J. Contemp. Math. Sciences 5, 1541 (2010).
[8] J. D. Cole, Quart. Appl. Math 9, 225 (1951).
[9] E. Hopf, Comm. Pure Appl. Math. 3, 201 (1950).
[10] P. Miskinis, Math. Model. Anal. 7, 151 (2002).
[11] K. Diethelm, The analysis of fractional differential equations: an application-oriented exposition using differential operators of Caputo type, Vol. 2004 (Springer Verlag, New York, NY.
How to Cite
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Download Citation
License
Those authors who have publications with this journal, accept the following terms:
a. The authors will retain their copyright and will guarantee the publication of the first publication of their work, which will be subject to the Attribution-SinDerivar 4.0 International Creative Commons Attribution License that permits redistribution, commercial or non-commercial, As long as the Work circulates intact and unchanged, where it indicates its author and its first publication in this magazine.
b. Authors are encouraged to disseminate their work through the Internet (eg in institutional telematic files or on their website) before and during the sending process, which can produce interesting exchanges and increase appointments of the published work.