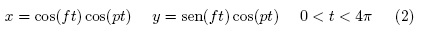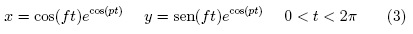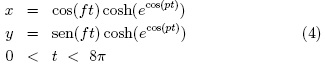MODELAMIENTO DE TRAYECTORIAS GRAVITACIONALES ALREDEDOR DE GRANDES CUERPOS MACROSCÓPICOS MEDIANTE LA UTILIZACIÓN DE FUNCIONES ANIDADAS EN LA FORMA DE ECUACIONES PARAMÉTRICAS

MODELING GRAVITATIONAL TRAJECTORIES AROUND BIG MACROSCOPIC OBJECTS BY MEANS OF NESTED FUNCTIONS IN THE FORM OF PARAMETRIC EQUATIONS

En este artículo se expondrá como obtener unas ecuaciones paramétricas que permiten el modelamiento de trayectorias orbitales de objetos alrededor de grandes cuerpos macroscópicos, en particular los agujeros negros, sin el empleo de cálculo tensorial. El modelo matemático propuesto permite caracterizar trayectorias de parejas de agujeros negros utilizando parámetros cuyo valor depende básicamente de números enteros, de un modo muy semejante a como ciertos números cuánticos determinan estados cuánticos del átomo de hidrógeno, posibilitando un simple sistema de taxonomización de las mismas.

This paper will expound how to obtain a parametric equation that make possible to model orbital trajectories of objects around large macroscopic bodies, in special black holes, without the use of tensor calculus. The mathematical model allows the characterization of trajectories of pairs of black holes using parameters whose values depend mainly on whole numbers, in a way very similar to how some quantum numbers determine quantum states of the hydrogen atom, enabling a simple taxonomic system for them.

Jose D. Avila

Ingeniería Química, Universidad Nacional de Colombia, Sede Bogotá, Colombia
Jose D. Avila: jdaa751@hotmail.com

(Recibido: Noviembre/2015. Aceptado: Mayo/2016)

---

Resumen

Palabras clave: Ecuaciones paramétricas, transformación, gravedad, órbita, precesión, frecuencia orbital, agujero negro.

---

Abstract

Keywords: Parametric equations, transformation, gravity, orbit, precession, orbital frequency, black hole.

---

Introducción

El movimiento de masas describiendo curvas cerradas o con propensión a cerrarse alrededor de un punto o un eje fijos, es condición fundamental para la conformación de sistemas físicos consistentes con la posibilidad de evolucionar en complejidad a través del tiempo (sistemas de par orbital). El más simple movimiento de este tipo es el movimiento circular [1].Existen en el universo sin embargo, desviaciones de este tipo básico de trayectoria debido a que en muchos casos los procesos naturales exhiben comportamientos no lineales derivados de la influencia de factores múltiples sobre los fenómenos físicos involucrados, que impiden en muchos casos obtener simplificaciones descriptivas de los mismos. Partiendo de la expresión matemática en la forma de ecuaciones paramétricas de un círculo, pueden efectuarse variaciones sobre la misma para conseguir descripciones de trayectorias orbitales alejadas de esta geometría base. Tales modificaciones consistirían en la aplicación de operaciones aritméticas que relacionasen las funciones seno y coseno con otras funciones trascendentes, o mediante el uso de potenciación, etc.

Como el interés en lo que a este artículo se refiere es el de las orbitas gravitacionales más extremas, el criterio para definir el tipo de transformación necesaria, debería escogerse en orden a reproducir un caso básico en el que claramente se identifica una importante desviación de las descripciones newtonianas de la gravedad. Este caso es el de la precesión de una órbita planetaria, como por ejemplo la experimentada por la trayectoria de Mercurio alrededor del sol [2].

1. Obtención de una ecuación paramétrica para el modelamiento de órbitas gravitacionales

La ecuación paramétrica que describe un círculo de radio f y centro en el origen es [3]:

Al multiplicar la ecuación anterior por la función coseno y construir la gráfica correspondiente para ƒ = 1, p = 0,9 obtenemos (Figura 1):

que es una curva semejante a la descrita por la precesión del perihelio de un planeta muy próximo a la estrella que orbita. Sin embargo es de notar que la gráfica no se corresponde con una trayectoria gravitacional, ya que no hay giros alrededor de la coordenada (0,0) ni se evidencian cambios que señalen aumento de la aceleración angular en las cercanías de este punto.

Debe encontrarse entonces una función que refleje las aproximaciones de la anterior función, pero que solvente sus deficiencias como modelo matemático para la descripción de orbitas gravitacionales.

Si se reemplaza la función coseno de las ecuaciones anteriormente citadas por la función e^cos(pt) (similar a la función coseno) y se grafica para obtener la trayectoria cerrada más simple distinta a un círculo con k = 1 y p =1 tenemos (Figura 2):

Aunque la forma de esta trayectoria coincide con una órbita alrededor de la coordenada (0, 0), no se corresponde del todo con el recorrido de un planeta alrededor de su estrella, en particular por la anómala achatadura de la curva observada en los cuadrantes contiguos a los valores negativos del eje x.

Una función de la forma _e^eCOs(pt) elimina este inconveniente. La función encontrada que consigue ajustarse mejor al modelo buscado es la siguiente: cosh(e^cos(pt)).

La función cosh(e^cos(pt)) tiene una respuesta gráfica semejante a _ecos⁽pt) para el mismo valor del parámetro p (igual número de oscilaciones/t). Sin embargo a diferencia de la función coseno (que es análoga a las anteriores) esta función no oscila entre valores negativos y positivos, obteniéndose de ella únicamente estos últimos.

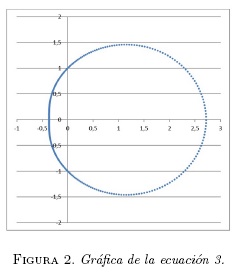
Al multiplicar la ecuación paramétrica de un circulo por la función cosh(e^cos(pt)) y construir la gráfica correspondiente para ƒ = 1, p = 0,9 obtenemos (Figura 3):

Esta nueva descripción coincide con el patrón seguido por la precesión orbital del movimiento de un planeta como Mercurio alrededor del sol [2], siendo evidente que la trayectoria de la curva indica giros entorno al punto (0, 0) y que la aceleración angular del elemento orbitaste se incrementa cada vez que hay un acercamiento a dicha coordenada.

Del análisis de la ecuación obtenida, se sigue que de ella se obtendrán una variedad de patrones complejos derivados de los valores que los parámetros ƒ y p tomen.

La forma general que se dará a la función en tres dimensiones es la siguiente:

Dónde:

ƒ: frecuencia orbital o número de revoluciones del elemento orbitante para completar un ciclo (t = 2π).
p: grado de precesión orbital. 0 < p < 1.
q: cantidad asociada a pérdida o ganancia exponencial de energía en el sistema debida a influencias externas.

t: variable angular en radianes.
k: grado de elongación orbital.

Los parámetros ƒ y p están asociados a las propiedades físicas: masa del cuerpo macroscópico alrededor del cual se realiza la órbita y momento angular del cuerpo que la describe.

Tomando como base la forma (número de "hojas"), numero de revoluciones y la frecuencia radial de orbitas de parejas de agujeros negros, estas pueden ser caracterizadas usando números racionales. Ello permite la construcción de una tabla periódica de parejas de agujeros negros [4].

2. Análisis de la ecuación paramétrica respecto a modelamiento de Orbitas

Para el análisis de esta ecuación en relación al modelamiento de trayectorias orbitales se trataran cuatro aspectos:

2.1. Forma de la Orbita

La forma de las trayectorias no sujetas a precesión recurrente (orbita cerrada multilobular) viene determinada por una relación entre números enteros (siempre que se cumpla que p/ƒ < 2) de la siguiente manera:

Círculo: p/ƒ = 0.
(Ovalo: p/ƒ = 1.
Espiral: p/ƒ< 1 y k> 1, o p/ƒ = 1/n y q< 0, donde n es un número entero a partir de 2.
Rizo simple: p/ƒ = 0,5.
Rizo doble: p/ƒ = 1/n, dónde =3,0 < t < 2πƒ.
Rizo triple: p/ƒ = 1/n, donde n = 4,0 < t < 2πƒ.
Rizo múltiple: p/ƒ = 1/n, donde n es un número entero a partir de 5,0 < t < 2πƒ.
Ojal: p/ƒ = 2/n, donde n es un número entero diferente a un múltiplo de 2. La estructura más sencilla es aquella en la que n = 3.
Trébol: p/ƒ = 3/n, donde n es un número entero diferente a un múltiplo de 3. La estructura más sencilla es aquella en la que n = 4.
4 pétalos: p/ƒ = 4/n, donde n es un número entero diferente a un múltiplo de 4. La estructura más sencilla es aquella en la que n = 3.
N pétalos: p// = N/n, donde N es un número entero diferente a un múltiplo de n.

2.2. Precesión orbital

Si el parámetro p es entero se tendrán órbitas presionadas recurrentes (trayectorias que se cierran reiterativamente). Si dicho parámetro entero se incrementa o disminuye del orden de décimas o centésimas, dichas trayectorias presentarán precesión no recurrente, es decir que la coordenada en la que la órbita se cerrará, experimentará desviaciones en las revoluciones siguientes, formando una curva abierta constituida por desfasamientos que imitarán el contorno de la correspondiente a la de la primera desviación, produciéndose finalmente un patrón similar al de un resorte.

2.3. Frecuencia orbital

En el caso de orbitas con precesión recurrente (p entero) es el número de revoluciones que experimenta el elemento orbitante antes de pasar por la misma coordenada.

En el caso de órbitas con precesión no recurrente (p entero) es el número de revoluciones que experimenta el elemento orbitante en el intervalo 0 < t < 2π.

Fijando p entero y aumentando ƒ en valores enteros, la órbita fractaliza radialmente su forma un número de veces igual al de este último parámetro antes de cerrarse por completo.

2.4. Elongación orbital

Si el parámetro k aumenta la elongación orbital es mayor. Por el contrario si este parámetro toma un valor pequeño la elongación orbital será menor. La recurrencia de líneas de trayectoria orbital al cruzarse entre sí, perfila un círculo virtual alrededor del elemento orbitado. El radio de este círculo varía de acuerdo con k. Si este parámetro aumenta el radio decrece. Por el contrario si el parámetro decrece dicho radio se incrementa.

3. Trayectorias gravitacionales obtenibles

Cuando el objeto que realiza la órbita atraviesa el radio más pequeño posible para una órbita circular (k > 1) y además p_z y k_z (parámetros en la dirección paralela al eje z en la que se produce la mayor tensión gravitacional o singularidad) son cero, se llega a la formación de un estrangulamiento espacio temporal o agujero negro. Gráficamente esto se traduce en una trayectoria como la siguiente (Figura 4):

Seguidamente se expondrán ejemplos gráficos de soluciones derivadas de la ecuación propuesta para trayectorias orbitales generadas por campos gravitacionales de cuerpos muy masivos, con precesión recurrente y no recurrente, así como también de trayectorias con diferentes grados de elongación orbital.

Las simulaciones distinguidas con un punto negro se corresponden con orbitas que se obtienen de las soluciones de Schwarzschild para las ecuaciones de la relatividad general en las que un objeto extremadamente denso ubicado en (0, 0) posee una masa concentrada dentro de su radio gravitacional (Figuras 5 y 6). El primer caso se da cuando la razón de la precesión es aproximadamente igual a la razón orbital, el segundo se da para una órbita con una energía ligeramente menor que la anterior y el tercero cuando con suficiente momento angular el objeto que realiza la orbita atraviesa el radio más pequeño posible para una órbita circular [5].

La consistencia de las geometrías obtenidas empleando el modelo matemático propuesto se cotejaron con las que se consiguen utilizando la ecuación conocida en relatividad general para la ruta geodésica a través de un espacio-tiempo curvo con simetría esférica: [5]

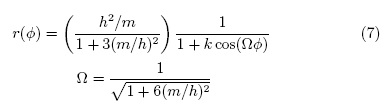
Mediante el uso de hojas de cálculo se compararon las respuestas geométricas de la ecuación anterior y la del modelo presentado en este artículo. Para m y k fijos, y aumentando gradualmente el valor de h, la evolución de las formas de las órbitas es equivalente a la del modelo propuesto en el que se hacen aumentar gradualmente los parámetros ƒ y p simultáneamente, manteniendo k fijo con un valor igual a 1.

Ejemplos de valores adoptados por los parámetros para los dos esquemas matemáticos considerando una misma solución

Existen soluciones tridimensionales para trayectorias gravitacionales que conducen a formas diversas en las que puede ser transformado geométricamente el espacio tiempo.

Para ampliar el espectro de soluciones posibles obtenibles de la ecuación paramétrica formulada se puede hacer un manejo matemático de esta, reemplazando las funciones que la componen por otras afines, haciendo la sustitución directamente o mediante combinaciones lineales de las mismas [6]. Por ejemplo, el cambio de seno por coseno dentro de la expresión de la componente correspondiente a la dirección del eje de simetría de una geometría espacio tiempo, produce un cambio en su curvatura. Para coseno la curvatura es positiva, para seno la curvatura es negativa. Si cosl (e^(sin(pt))k) y cosh(e^(-sin(^pt))^k) son soluciones ambas del esquema matemático propuesto, entonces una combinación lineal de ambas es también una solución [7]. Así también si cosh(e^(sm(pt)) ) es una solución, igualmente lo son cosh (cosh((sin(pt))^k)) y e^{(cosh(sin(pt)k))}.

Ecuaciones paramétricas para posibles geometrías en las que el espacio tiempo puede ser deformado son:

Conclusiones

Se ha demostrado en el presente trabajo la posibilidad de obtener una descripción matemática de trayectorias orbitales producidas por efecto de la gravitación -en especial el régimen de campo fuete - a partir de transformaciones matemáticas realizadas sobre las ecuaciones paramétricas de un círculo. Esto sigue la misma dirección que la de investigaciones realizadas en torno a la idea de derivar la gravedad desde entornos físicos y matemáticos alternativos al de la teoría general de la relatividad (p.e el descubrimiento de la analogía de la gravedad con la física de superconductores y la hidrodinámica, etc.).

Las taxonomías (formas clasificables) posibles para las orbitas de precesión recurrente de parejas de grandes cuerpos macroscópicos, pueden ser reproducidas utilizando el modelo propuesto empleando parámetros cuyo valor toma la forma de números enteros, pudiendo liacerse corresponder las mismas con soluciones obtenidas de la ecuación conocida en relatividad general para idéntica finalidad, aunque los valores de los parámetros difieren grandemente en este caso con respecto a los del anterior esquema matemático para la misma solución, porque representan magnitudes físicas distintas aunque relacionadas. Descripciones de orbitas con precesión no recurrente son también obtenibles a partir de sus liomologas recurrentes modificando los valores de los parámetros enteros f o p en el orden de decimas o centésimas.

El parámetro k dentro de la ecuación conocida en relatividad general para la ruta geodésica a través de un espacio-tiempo curvo, tiene la misma incidencia que el de k en la ecuación propuesta sobre la forma de las geometrías derivadas de estos esquemas matemáticos. Se abarca con todo ello la parte esencial del espectro de soluciones posibles para trayectorias gravitacionales alrededor de grandes cuerpos macroscópicos.

El modelo desarrollado presenta la ventaja de no estar sus parámetros luciendo parte de una división que pueda conducir al anularse sus valores a indeterminaciones o resultados infinitos. En este modelo, los parámetros de la ecuación se relacionan con resultantes geométricas y no con las magnitudes físicas masa, energía y tiempo como sucede en la teoría general de la relatividad. Cuando declinas magnitudes se lacen cero las ecuaciones relativistas se vienen abajo. El problema parece radicar en que estas magnitudes físicas desde el punto de vista macroscópico son emergentes y no fundamentales (la explicación radicaría en una fenomenología cuántica aun no del todo clara).

El interés por organizar todas las trayectorias gravitacionales posibles en diferentes grupos, tomando como base el camino repetitivo al que se asemejan, está en la utilidad que puede tener esto para los científicos que buscan ondas gravitacionales, porque la forma de las ondas producidas por dos agujeros negros orbitándose antes de fusionarse, depende de la configuración de sus orbitas [4].

El modelo matemático propuesto permite caracterizar trayectorias de parejas de agujeros negros utilizando parámetros cuyo valor depende básicamente de números enteros, de un modo muy semejante a como ciertos números cuánticos determinan estados cuánticos del átomo de hidrogeno.

---

Referencias

[1] A. P. Frencli, Mecánica Newtoniana - Curso de Física del M.I.T. (Reverte, S.A., 2006).

[2] C. Kittel, W. D. Kniglit, and M. A. Ruderman, Mecanica, Vol. Vol. 1 (Reverte, S.A., 1999).

[3] E. W. Swokowski, Calculus with analytic geometry (PWS Publisliers, 1988).

[4] A. Martónez, "La teoría de la relatividad - la solution de scliwarzscliild ii," (2009).

[5] J. Levin and G. Perez-Giz, arXiv.org - General Relativity and Quantum Cosmology (2008).

[6] V. A. Dobruslikin, Applied Differential Equations. The Primary Course (CRC Press, Taylor & Francis Group, 2015).

[7] P. J. Durrant and B. Durrant, Introduction to Advanced Inorganic Chemistry (Jolm Wiley inc. & sons, 1970).

[8] C. Molina, P. Martón-Moruno, and P. F. Gonzóalez-Dóaz, Plys. Rev. D 84, 104013 (2011).