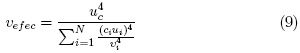ESTIMACIÓN DE INCERTIDUMBRE EN LA CALIBRACIÓN DE TACÓMETROS ÓPTICOS
UNCERTAINTY ESTIMATION IN OPTICAL TACHOMETERS CALIBRATION
DOI:
https://doi.org/10.15446/mo.n52.58894Keywords:
Incertidumbre, tacómetro, calibración, teorema del límite central, metrología. (es)Uncertainty, tachometer, calibration, central limit theorem, metrology. (en)
Downloads
Se presenta el procedimiento matemático para estimar la incertidumbre en la calibración de tacómetros ópticos. Por tratarse de un dispositivo de baja jerarquía en mediciones de tiempo y frecuencia, se utiliza el concepto estadístico de desviación estándar para considerar la componente de incertidumbre por repetibilidad en lugar de la estabilidad.
Se considera una situación relevante y frecuente en tacómetros consistente en que la componente por resolución es dominante; esto tiene una importante implicación al momento de escoger el factor de cobertura para la obtención de la incertidumbre expandida ya que no se tienen las condiciones para satisfacer de forma aproximada el teorema del límite central.
The mathematical procedure to estimate the uncertainty of the optical tachometers calibration is presented. The statistical concept of standard deviation is used to consider the repeatability component rather than stability, since this instrument is a device of low level on time and frequency measurements. A relevant and common situation is considered in which the resolution component is dominant; this has an important implication in choosing the coverage factor to obtain the expanded uncertainty because the conditions to satisfy roughly the central limit theorem are not hold.
ESTIMACIÓN DE INCERTIDUMBRE EN LA CALIBRACIÓN DE TACÓMETROS ÓPTICOS
UNCERTAINTY ESTIMATION IN OPTICAL TACHOMETERS CALIBRATION
Liz C. Hernández, Nelson Bahamon
Instituto Nacional de Metrología (INM) de Colombia, Laboratorio de Tiempo y Frecuencia, Avenida Carrera 50 No. 26 - 55 Interior 2, Bogotá, Colombia
Liz C. Hernandez: lhernandez@inm.gov.co
Nelson Bahamon: nbahamon@inm.gov.co
(Recibido: Noviembre/2015. Aceptado: Marzo/2016)
Resumen
Se presenta el procedimiento matemático para estimar la incertidumbre en la calibración de tacómetros Ópticos. Por tratarse de un dispositivo de baja jerarquía en mediciones de tiempo y frecuencia, se utiliza el concepto estadístico de desviación estándar para considerar la componente de incertidumbre por respetabilidad en lugar de la estabilidad. Se considera una situación relevante y frecuente en tacómetros consistente en que la componente por resolución es dominante; esto tiene una importante implicación al momento de escoger el factor de cobertura para la obtención de la incertidumbre expandida ya que no se tienen las condiciones para satisfacer de forma aproximada el teorema del límite central.
Palabras clave: Incertidumbre, tacómetro, calibración, teorema del límite central, metrología.
Abstract
The mathematical procedure to estimate the uncertainty of the optical tachometers calibration is presented. The statistical concept of standard deviation is used to consider the repeatability component rather than stability, since this instrument is a device of low level on time and frequency measurements. A relevant and common situation is considered in which the resolution component is dominant; this has an important implication in choosing the coverage factor to obtain the expanded uncertainty because the conditions to satisfy roughly the central limit theorem are not hold.
Keywords: Uncertainty, tachometer, calibration, central limit theorem, metrology.
1. Introducción
En Colombia hace falta una gran difusión y maduración del tema de la metrologia, como importante herramienta para el desarrollo científico y tecnico. En particular en las magnitudes de Tiempo y Frecuencia no hay documentos legales ni guías de calibration u otros relacionados, que permitan establecer lineamientos y parámetros a seguir por quienes trabajan en laboratorios de metrología de la red secundaria o en empresas que de alguna manera estían interesadas en el tema de Tiempo y Frecuencia.
Este documento hace un estudio acerca de la obtenciíon de la incertidumbre en la calibration de tacometros. Dada la alta repetibilidad que estos dispositivos tienen en su lectura, sucede con frecuencia que esta componente de incertidumbre se hace cero y la componente por resoluciíon resulta dominante.
El tema de la dominancia de una componente de incertidumbre es importante por su relacioín con la distribuciíon de probabilidad de salida asociada a la incertidumbre combinada. Se trata de un tema que se obvia con frecuencia, asumiendo de entrada que se cumplen aproximadamente las condiciones para satisfacer, el teorema del límite central, lo cual no siempre es cierto. En la seccion 3 se incluye un breve comentario sobre el tema.
Teniendo en cuenta estos elementos, este artículo tiene tambiíen el propíosito de convertirse, al menos desde el punto de vista matemaítico, en una guía para la calibraciíon de tacíometros.
Se presenta en primer lugar el aspecto del monta je experimental y de la toma de medidas (seccion 2); luego el modelo matematico en la estimación de incertidumbre (secciones 3 y 4), que es, la parte fundamental de este documento; se presentan los resultados obtenidos (seccion 5), para cuatro casos que tienen comportamientos diferentes desde el punto de vista estadístico lo cual permite hacer un aníalisis claro y general (secciíon 6). Finalmente se presentan las conclusiones (seccioín 7).
2. Aspecto Experimental
Un tacómetro es un instrumento que mide frecuencia de rotation. Puede captar la senal del objeto que rota mediante acoples mecanicos y/o mediante un fotosensor. Los tacometros de lectura íoptica, o foto tacíometros, tienen una base de tiempo interna. La frecuencia generada con el oscilador interno alimenta un transductor óptico; el transductor optico emite una senal lumínica, la cual incide sobre el objeto que rota y es reflejada; la senal reflejada se recibe en el tacometro mediante otro transductor optico (fotodiodo) y pasa a un sistema de conteo. La lectura es presentada en una pantalla digital, por lo general, en unidades de revoluciones por minuto (RPM).
2.1. Método de calibración
El míetodo de calibraciíon corresponde a mediciones directas de frecuencia [1].
La senal generada por un sintetizador de frecuencias es acoplada a un transductor íoptico; esta frecuencia es leída por el sistema íoptico del tacoímetro objeto de calibraciíon y a la vez es monitoreada en la salida del sintetizador con la ayuda de un contador de frecuencia de alta resolucioín. El sintetizador y el contador de frecuencia estían disciplinados al patríon primario del laboratorio (reloj atoímico de Cesio), el cual es trazable al sistema internacional de unidades (SI) [2, 3]. La desviaciíon fraccional de frecuencia se calcula teniendo en cuenta las dos lecturas.
2.2. Adquisicion de datos
- Se selecciona el valor patron de salida en unidades de Hertz (Hz) en el sintetizador de frecuencias.
- El diodo emisor de luz (light-emitting diode - LED), que corresponde al moídulo transductor íoptico, se enfoca hacia la ventana de recepciíon del tacoímetro bajo calibraciíon, hasta que se produzca la lectura en el mismo, en revoluciones por minuto (RPM).
- La relaciíon entre la frecuencia patríon (Hz) y la frecuencia bajo calibration (RPM) es [4]: 1 Hz = 1 revolution por segundo = 60 RPM
- Una senal de monitoreo de que el tacímetro esta leyendo corresponde a la activacion de la senal de disparo dentro de su indicador digital.
- Se registran la cantidad de lecturas para cada valor de frecuencia, apagando y prendiendo el tacíometro entre una y otra medicioín. Normalmente son diez (10) lecturas.
2.3. Alcance de medicion
- Los datos usados como referencia corresponden a datos de calibraciones de tacíometros con sistema de lectura íoptico.
- Las mediciones fueron efectuadas para el intervalo de medicioín comprendido desde 6 RPM a 99 999 RPM.
3. Acerca del teorema del límite central en el campo de la metrología
La importancia del teorema del límite central en metrología, radica en la suposicioín frecuente de que sus condiciones se cumplen de forma aproximada y de que por lo tanto la distribuciíon de probabilidad de la variable de salida es aproximadamente normal. Esto reduce el procedimiento a suponer que el factor de cobertura para la obtencioín de la incertidumbre expandida es igual a 2. La palabra "aproximadamente" es muy importante en este contexto; una distribuciíon de probabilidad completamente normal solo se tiene si el numero de variables de entrada es infinito. Una discusion mas detallada de esto, puede encontrarse en el anexo G de la referencia [5].
En sí, este documento se centra en analizar los casos en que la distribucioín de salida es aproximadamente rectangular y aproximadamente normal. Se presentan los resultados (ver secciíon 5) con 4 juegos de datos experimentales; en ninguno de estos casos el factor de cobertura es exactamente 2.
4. Estimacion de la incertidumbre
En primer lugar, se muestra la obtencioín de la incertidumbre combinada y luego el anaílisis de componente dominante de incertidumbre (fundamental en este trabajo). De este aníalisis se desprenden dos posibilidades: que la distribuciíon de salida sea aproximadamente normal o que sea aproximadamente rectangular; se muestra en cada caso la manera de obtener el factor de cobertura, para llegar a la incertidumbre expandida.
La figura 2 ilustra el proceso de estimación de incertidumbre en su totalidad.
4.1. Incertidumbre combinada
El modelo matemaítico corresponde a la desviacioín fraccional de frecuencia. Se tiene:
Donde:
fm = Frecuencia medida. Es el valor de frecuencia medido por el tacómetro.
fn = Frecuencia nominal. Es el valor de frecuencia generado por el patron.
Entonces se tienen los siguientes coeficientes de sensibilidad:
Las componentes de incertidumbre son, repetibilidad, resolution del instrumento bajo prueba y la componente del certificado del patron.
Componente de repetibilidad:
Donde:
s = Desviacion estandar muestral de los datos medidos.
n = Número de datos (normalmente 10).
Componente de resolution del instrumento:
Donde:
resol = Resolution del tacometro (por ejemplo 0.1 RPM).
Componente del certificado del patron:
Donde:
Upatrón = Incertidumbre expandida reportada por el certificado del instrumento patrúon.
kpatrón = Factor de cobertura reportado por el certificado del instrumento patroún. Incertidumbre expandida.
Dadas las expresiones 1 a 6, se tiene la siguiente expresion para la incertidumbre combinada:
Notese que las componentes de repetibilidad y resoluciún, estan asociadas al instrumento bajo prueba (tacúometro) y por esto les corresponde el coeficiente cm, mientras que a la componente del certificado le corresponde el coeficiente cn.
4.2. Análisis de dominancia
El propúosito de esta secciúon es estudiar y comprender como es la distribucioún de salida en la estimacioún de incertidumbre o en otras palabras, la distribuciúon de probabilidad asociada a la incertidumbre combinada. Este anúalisis es importante porque de ello depende la determination del factor k de cobertura que permitirúa obtener la incertidumbre expandida.
Como se comentú en la seccion 3 se podría decir que la distribution de salida es aproximadamente normal. Sin embargo es importante establecer algún control de tipo numerico que determine un límite respecto de cuanto se va a aceptar dicha presuncion y cuando no.
Lo primero que se tendrúía que tener en cuenta es el conocimiento de cúomo son las distribuciones de probabilidad de entrada. La componente de repetibilidad es de tipo normal; esto es evidente dado que la componente da razon de la dispersiún de los datos y por ello utiliza la desviaciún estandar (ver ecuacion 4) . La componente de resolucioún se asume habitualmente como rectangular por suponer simplemente que los datos se dispersan con igual probabilidad en el intervalo determinado por la resoluciúon del instrumento; se puede decir que esta componente de incertidumbre, es debida al indicador del instrumento; el valor  (ver ecuacion 5) estúa asociado a la distribuciúon rectangular. Finalmente, la componente de incertidumbre asociada al patroún, puede resultar un poco ambigua. Si en el certificado de calibration aparece el valor k = 2 como factor de cobertura, se puede presuponer que la distribuciúon es normal. Por otra parte se acostumbra con frecuencia suponer que la distribuciúon asociada a una incertidumbre tomada de alguún documento es rectangular, especialmente cuando no hay mayor conocimiento de la misma. Dadas las caracterúísticas del patrúon utilizado en el desarrollo de este trabajo (ver secciúon 2), el factor de cobertura es por lo general 2. Se supone entonces que la distribuciúon es normal. De cualquier manera, es de esperarse que la componente de incertidumbre del patron, sea pequena con respecto a las demúas y aporte poco a la incertidumbre combinada. Entonces su distribuciúon asociada no resulta tan relevante.
(ver ecuacion 5) estúa asociado a la distribuciúon rectangular. Finalmente, la componente de incertidumbre asociada al patroún, puede resultar un poco ambigua. Si en el certificado de calibration aparece el valor k = 2 como factor de cobertura, se puede presuponer que la distribuciúon es normal. Por otra parte se acostumbra con frecuencia suponer que la distribuciúon asociada a una incertidumbre tomada de alguún documento es rectangular, especialmente cuando no hay mayor conocimiento de la misma. Dadas las caracterúísticas del patrúon utilizado en el desarrollo de este trabajo (ver secciúon 2), el factor de cobertura es por lo general 2. Se supone entonces que la distribuciúon es normal. De cualquier manera, es de esperarse que la componente de incertidumbre del patron, sea pequena con respecto a las demúas y aporte poco a la incertidumbre combinada. Entonces su distribuciúon asociada no resulta tan relevante.
Una vez se tienen definidas las distribuciones de probabilidad de entrada, lo siguiente es comprender el concepto de dominancia. Es claro que de las tres componentes de incertidumbre, una harúa un mayor aporte (mayor producto ciui) a la incertidumbre combinada. Esto no significa sin embargo que dicha componente sea dominante, la dominancia significa que la componente aporta a la incertidumbre combinada en una medida tal, que incluso impone su propia distribuciún de probabilidad. Para fines de este trabajo, se propone el siguiente criterio matemúatico para determinar si una componente de incertidumbre es dominante:
Este criterio es tomado de la referencia [6]. Una vez determinada la componente de incertidumbre que hace un mayor aporte, se puede decir que es la "candidata a dominante" y que esto se va a determinar mediante la ecuaciúon 8. En esta expresiúon se coloca el mayor producto cu en el denominador y la demúas componentes, dentro de la sumatoria del radical en el numerador. Si se cumple la desigualdad, entonces la componente "candidata" es dominante.
De todas formas, dadas las expresiones 2 y 3 noútese que si fn y fm son similares, tambien lo son los coeficientes de sensibilidad. Entonces en la calibraciúon de tacúometros la componente de incertidumbre candidata a dominante, se puede determinar directamente por el valor de ui ; esta situacioún es frecuente en la magnitud de tiempo y frecuencia.
Respecto de la dominancia pueden presentarse 3 posibles situaciones:
a) Que no exista ninguna componente dominante de incertidumbre.
b) Que la distribution dominante sea normal.
c) Que la distribuciún dominante sea rectangular.
Teniendo en cuenta el teorema del límite central, se puede decir que en las situaciones a) y b) la distribuciúon de salida es normal mientras que en la situacioún c) la distribuciúon de salida es rectangular; este es el caso excepcional pero se da con cierta frecuencia en la calibraciúon de tacúometros cuando la componente por resolucioún es dominante.
4.3. Obtención de k, si la distribución de salida es aproximadamente normal
Esta situaciúon se modela matemúaticamente mediante el uso de la distribution de probabilidad t de Student. Esta distribuciún es una aproximaciúon de la normal, para el caso en que se tienen pocos datos; en la medida en que se tienen muchos datos, la distribuciúon t de Student tiende a la normal, siendo igual cuando el nuúmero de datos tiende a infinito. Desde el punto de vista matematico, esto se modela mediante el número de grados de libertad asociado a la distribución t.
Una vez obtenida la incertidumbre combinada (ecuación 7) se procede a calcular el numero de grados efectivos de libertad según la ecuación de Welch-Satterwaite [5]:
Donde:
vi = Grados de libertad de la componente i de incertidumbre.
Para el caso de la componente de repetibilidad el número de grados de libertad es n - 1.
Para el caso de la componente por resolución se tiene una distribution rectangular. En ocasiones se toman infinitos grados de libertad para estas distribuciones, ya que este seria el valor si la distribution es perfecta y todos los posibles valores de la variable caen dentro del intervalo dado por la misma. Sin embargo, la GUM [5] sugiere un criterio móas realista para estimar este valor, pues tomar infinito, es una idealization un poco extrema. El criterio esta dado por la siguiente expresion:
El Δu es el intervalo de variación de la incertidumbre. Se puede decir que es como la "incertidumbre de la incertidumbre". Entonces la expresióon dentro del paróentesis estaó dada en forma relativa. Se puede decir que se trata del nivel de duda respecto del valor de la incertidumbre y su distribution. Así por ejemplo si el nivel de seguridad sobre esta información es del 95%, el nivel de duda sera del 5% = 0.05; al reemplazar este valor en la expresión 11 se obtiene 200. Este es el criterio que se toma en este trabajo.
Por otra parte para la componente del patron, el valor k = 2 sugiere infinitos grados de libertad. Sin embargo, se trata de información que no es clara. Cuando se toman datos de incertidumbre de un documento que no especifica el nómero de grados de libertad, es vóalido tambióen seguir el criterio dado por la expresióon 11.
Se tiene: 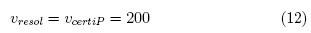
Nota: En general se sugiere no tomar infinitos grados de libertad, pero es totalmente vaólido tomar un nuómero mayor para la componente del patron. Notese por ejemplo que un nivel de duda del 1 % en la expresióon 11, da un resultado de 5000 grados de libertad.
Una vez obtenidos los grados efectivos de libertad mediante la expresióon 9, se utiliza una tabla o un paquete de software para invertir la funcióon t de Student y obtener el valor del factor k de cobertura. Finalmente se obtiene el valor de la incertidumbre expandida mediante la expresióon:
4.4. Obtención de k, si la distribución de salida es aproximadamente rectangular
Como ya se explicóo, este caso se da cuando la componente por resolucióon es dominante. Esto sucede frecuentemente cuando la componente por repetibilidad es cero. En este caso el factor de cobertura es simplemente el asociado a la distribucióon rectangular dominante. Para una probabilidad de cobertura del 95 % estóa dado por [5]:
Luego se reemplaza en la expresion 13.
5. Resultados
Se tomaron 4 puntos diferentes para 3 tacóometros como se muestra en la tabla 1 y se obtuvieron las medidas para dichos puntos, ver tabla 2.
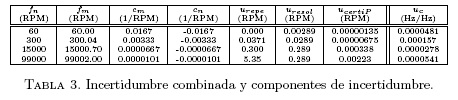
Se obtuvieron los siguientes resultados para la incertidumbre combinada (Tabla 3):
Nóotese que la incertidumbre combinada es realmente adimensional. Se acostumbra sin embargo, utilizar la expresion Hz/Hz.
Al hacer el anóalisis de dominancia se obtienen los valores mostrados en la tabla 4.
Como ya se ha mencionado, generalmente la componente por resolucióon es dominante cuando la componente por repetibilidad es cero; noótese que este es el caso del primer resultado de la tabla anterior. El siguiente paso es obtener el valor de k (Tabla 5).
Se ha dejado indicado el valor que se obtendróa para el punto de 60 RPM si se presupusiera una distribution de salida aproximadamente normal. Sin embargo (ver seccioón 3.4) el factor correcto es 1.65. Como resultado final de la calibration se tienen los valores mostrados en la tabla 6.
Es importante hacer una aclaracioón con respecto al tema de la diferencia de unidades en las tablas 3 y 6. Como puede verse en el desarrollo de la seccion 4 los resultados finales, es decir la desviacióon fraccional de frecuencia y su respectiva incertidumbre expandida (ecuaciones 1 y 13) son adimensionales (estóan en Hz/Hz). Son estos los resultados que se presentan cuando se trata de instrumentos de alta jerarquóa. En este caso por tratarse de tacóometros, es mejor pasar los resultados a unidades de RPM. Para ello se multiplica la desviacióon fraccional de frecuencia por la frecuencia nominal y la incertidumbre expandida por la frecuencia medida.
Por otra parte, tambióen es bueno aclarar, que los resultados de la tabla 6, se presentan siguiendo el criterio de la GUM [5] de utilizar maximo 2 cifras significativas en la expresion de la incertidumbre.
6. Análisis de resultados
Se ha explicado el paso a paso en la estimacioón de la incertidumbre para la calibracióon de tacóometros óopticos.
Los ejemplos desarrollados muestran con claridad como el factor de cobertura en la obtencioón de la incertidumbre expandida no siempre es 2. Si bien el Teorema del Lómite Central es de gran importancia en estadóstica y en sus aplicaciones en metrologóa, no se debe asumir siempre que la distribucioón de salida es aproximadamente normal. En el caso de tacóometros (como ya se ha dicho en este documento) es comuón que la componente de incertidumbre por repetibilidad sea cero y que la resolucióon resulte dominante. Esta situacióon se presenta con alguna frecuencia en otros dispositivos de medicioón de tipo digital y debe ser tenida en cuenta.
Por otra parte, noótese la importancia del concepto de grados de libertad en el anóalisis, ya que algunos valores del factor k de cobertura pueden ser significativamente mayores a 2.
7. Conclusiones
La compresioón del Teorema del Lómite Central y el estudio de la forma de la distribucioón de probabilidad de la funcióon de salida, resulta fundamental para una correcta estimacióon de la incertidumbre.
Agradecimientos
Agradecemos a nuestro companero, el físico Mayckol Morales Castro por su atento entusiasmo en la elaboracioón del presente artóculo.
Agradecemos a nuestro companero, el físico Alexander Martónez por su instruccioón y transmisióon de conocimientos en el tema de estimacióon de incertidumbre.
Referencias
[1] CENAM and EMA, Guía técnica sobre trazabilidad e incertidumbre en la metrología de tiempo y frecuencia., México, Revisión 01. Abril de 2008.
[2] M. A. Lombardi et al., J. Res. Natl. Inst. Stand. Technol. 116, 557 (2011).
[3] J. M. Lopez et al., in Proc. XXXth Gen. Assem. URSI (2011) p. 4.
[4] H. Diaz and L. Palma, in IEEE Conference on Precision Electromagnetic Measurements (CPEM 2014) (2014) p. 2.
[5] J. C. G. M. Evaluation of measurement data - Guide to the expression of uncertainty in measurement, Working Group 1 of the Joint Committe for Guides in Metrology, 1st ed. (2008).
[6] EA-4/02 M: 1999, Expression of the Uncertainty of Measurement in Calibration, European cooperation for Accreditation (2013).
How to Cite
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Download Citation
CrossRef Cited-by
1. Nelson Bahamon Cortes, Alexander Gutierrez Guevara, Claudia Fernanda Rodriguez Rodriguez, Liz Catherine Hernandez Forero. (2020). Analysis of dominant uncertainty in the calibration of optical tachometers. 2020 Conference on Precision Electromagnetic Measurements (CPEM). , p.1. https://doi.org/10.1109/CPEM49742.2020.9191738.
Dimensions
PlumX
Article abstract page views
Downloads
License
Those authors who have publications with this journal, accept the following terms:
a. The authors will retain their copyright and will guarantee the publication of the first publication of their work, which will be subject to the Attribution-SinDerivar 4.0 International Creative Commons Attribution License that permits redistribution, commercial or non-commercial, As long as the Work circulates intact and unchanged, where it indicates its author and its first publication in this magazine.
b. Authors are encouraged to disseminate their work through the Internet (eg in institutional telematic files or on their website) before and during the sending process, which can produce interesting exchanges and increase appointments of the published work.