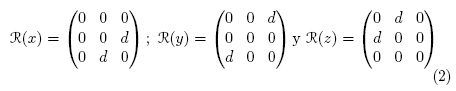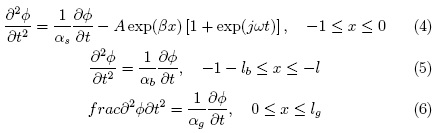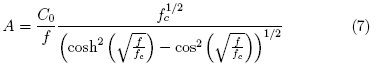DIFUSIVIDAD TÉRMICA DE MONO-CRISTALES DE GaSb Y Si(100)
THERMAL DIFFUSIVITY OF Si (100) AND GaSb SINGLE CRYSTALS
DOI:
https://doi.org/10.15446/mo.n51.56188Palabras clave:
Fotoacústica, Semiconductores, recombinación no radiativa. (es)Photoacoustic, Semiconductors, non-radiative recombination. (en)
DIFUSIVIDAD TÉRMICA DE MONO-CRISTALES DE GaSb Y Si(100)
THERMAL DIFFUSIVITY OF Si (100) AND GaSb SINGLE CRYSTALS
Álvaro Pulzara-Mora1, Roberto Bernal-Correa2, Álvaro Acevedo-Rivas1, Andrés Rosales-Rivera3
1 Laboratorio de Nanoestructuras Semiconductoras. Grupo de Magnetismo y Materiales Avanzados, Facultad de Ciencias Exactas y Naturales, Universidad Nacional de Colombia, sede Manizales. A.A. 127 Colombia.
2 Grupo DEMA, Departamento de Ciencias Básicas, Facultad de Ciencias e Ingeniería, Universidad del Sinú, Montería-Colombia.
3 Laboratorio de Magnetismo y Materiales Avanzados, Facultad de Ciencias exactas y Naturales, Universidad Nacional de Colombia, sede Manizales. A.A. 127 Colombia.
Álvaro Pulzara-Mora: aopulzaram@unal.edu.co
(Recibido: Agosto/2015. Aceptado: Noviembre/2015)
Resumen
En este trabajo, reportamos la caracterización de monocristales de Si(100) y GaSb(111) utilizando espectroscopia Raman y fotoacóstica (principal interés) en configuración abierta y cerrada, para compuestos semiconductores III-V con estructura tipo zinc blenda. Los espectros Raman generalmente muestran dos picos, un pico a baja frecuencia correspondiente a modos fononicos TO y un pico en alta frecuencia correspondiente a modos fononicos LO. Un fuerte pico es mostrado en la position 226 cm-1 y uno un poco más débil en 237 cm-1, que son los modos TO y LO respectivamente, debido a la orientación cristalina del material. Con el fin de determinar la difusividad térmica de los materiales se utilizaron láseres con longitudes de onda de 650 nm y 535 nm. Los resultados de la difusividad térmica de los monocristales de Si y GaSb, obtenidos a partir del modelo de Rosencwaig y Gersho (RG) se analizaron en función de la orientación cristalográfica. Discutimos la recombinación no-radiactiva que se origina en la superficie y en el volumen del cristal, que contribuye a la señal fotoacústica, en términos del tipo de celda y de la línea de excitación.
Palabras clave: Fotoacústica, Semiconductores, recombinación no radiactiva.
Abstract
In this work, we report the characterization of Si (100) and GaSb (111) single crystals by using Raman spectroscopy and a photoacoustic cell in open and closed configuration. For III-V compound semiconductors of the zinc-blende crystal structure, Raman spectra generally show two peaks. The lower-frequency peak corresponds to TO phonons, and the higher frequency peak corresponds to LO phonons. A strong peak was found at 226 cm-1 and a weak peak at 237 cm-1, which are the TO and LO modes, respectively. Raman spectrum of GaSb (111) show that the integrate intensity of TO mode is greater than LO mode due to disoriented of the single crystal. In order to obtain the thermal diffuivity, the crystals were exciting by means of solid-state lasers of wavelengths of 650 nm and 535 nm, respectively. The results of the thermal diffusivity of single crystals, obtained from the Rosencwaig and Gersho (RG) model were analyzed according to the crystallographic orientation. We have also discussed the contribution of the non-radiative recombination to the photoacustic signal from surface and bulk depending on the type of cell and excitation of the laser line.
Keywords: Photoacoustic, Semiconductors, non-radiative recombination.
Introducción
En los últimos años la técnica fotoacústica ha tomado gran interés debido a su alto potencial en él estudio dé los materiales, principalmente en la determinación de propiedades térmicas como: difúsividad térmica, efusividad térmica y coeficiente de difusión térmica [1-5]. Este fenómeno fue observado por primera vez por Alexander Graham Bell en el año 1880 con la aparición del fotófono en el que fotones absorbidos eran convertidos en energía cinética de las moléculas dando lugar a fluctuaciones en una celda. Posteriormente fue explicado por Rosencwaig y Gersho (RG) en los años 70's [6] quienes desarrollaron un modelo teórico que permitió explicar el comportamiento de materiales con régimen térmicamente grueso (RTG) y delgado (RTD), es decir, como es el comportamiento cuando la longitud de difusión térmica μs es mucho mayor o menor que el espesor de la muestra. En los años 80's Fujii, et. al. (FMN) y Morita et. al [7, 8] introdujeron modelos para sistemas de multicapas ópticas con el fin de aplicarlo a sistemas substrato película delgada. Los modelos RG y FMN son tema de actualidad para calcular propiedades térmicas en diferentes tipos de materiales, dentro de los que se encuentran los semiconductores con aplicaciones a celdas solares, ya que parámetros físicos como la difusividad térmica son importantes para el modelado y diseño de dispositivos basados en estos materiales [9].
En este trabajo, reportamos los resultados de medidas realizadas mediante la técnica fotoacústica (FA) en celda cerrada y abierta de cristales de Si(100) y GaSb(111),como función de la frecuencia de modulación para correlacionarlos con la orientación cristalográfica y modos fononicos obtenidos a partir de espectros Raman. Discutimos la recombinación no-radiactiva superficial y de volumen que contribuye a la señal fotoacústica, en términos del tipo de celda y de la línea de excitación.
Aspectos teóricos
La técnica fotoacústica permite medir diferentes tipos de materiales (películas delgadas, bulto, líquidos, y gases) [10-13]. Para ello es necesario considerar algunos aspectos teóricos y experimentales. En nuestro caso particular, es de interés tener en cuenta la orientación cristalográfica de Si(100) y GaSb (111) (fuertemente relacionada con los modos vibracionales), y modelos que nos permitan calcular parámetros de interés.
Los semiconductores GaSb (ZB) y Si (diamante) obedecen a los grupos espaciales F43m y Fd3m respectivamente, este es un factor importante cuando se realizan experimentos ópticos en cristales, especialmente en Raman ya que las intensidades pueden ser calculadas a partir del tensor Raman que depende de dicha simetría del cristal y está dada por
Donde ℜ es el tensor Raman
y 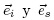 son los vectores
del haz incidente y dispersado respectivamente. De acuerdo a las reglas de
selección en el caso de los semiconductores III-V tipo zinc-blenda (ZB) en el
centro de la zona de Brillouin ZB Γ4 existe una representación triplemente
degenerada, donde para un fonon óptico polarizado a lo largo de la dirección X,
Y o Z tenemos tres tensores Raman, donde d es la componente linealmente
independiente del tensor de tercer rango.
son los vectores
del haz incidente y dispersado respectivamente. De acuerdo a las reglas de
selección en el caso de los semiconductores III-V tipo zinc-blenda (ZB) en el
centro de la zona de Brillouin ZB Γ4 existe una representación triplemente
degenerada, donde para un fonon óptico polarizado a lo largo de la dirección X,
Y o Z tenemos tres tensores Raman, donde d es la componente linealmente
independiente del tensor de tercer rango.
Estos permiten determinar los modos vibracionales en cada dirección cristalina, siendo el modo TO permitido en los planos (110) y (111) y el modo LO en los planos (100) y (111). La Tabla 1 muestra los modos permitidos en el plano (111) para una estructura ZB según las reglas de selección [14, 15]. De manera análoga se pueden determinar los modos en una estructura tipo diamante a la cual obedece el Si (100).
La difusividad térmica (α) es un parámetro importante para el estudio de los materiales y el diseño de dispositivos, y se define como:
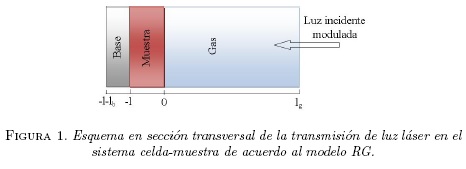
donde k es la conductividad térmica, Cp el calor especifico y ρ la densidad del material. Con el fin de determinar la difusividad térmica, haremos uso del modelo unidimensional de flujo de calor propuesto por Rosencwaig y Gersho (RG) (Figura 1), en el cual la difusión térmica en el sólido (-1 ≤ x ≤ 0) está influenciada por la fuente de calor debido a la densidad de calor producida en cada punto x por la luz absorbida en el sólido, donde se supone que la celda (-1 - lb ≤ x ≤ -l) y el gas (0 ≤ x ≤ lg) no absorben radiación, y a partir del cual se obtienen las siguientes ecuaciones necesarias para describir teóricamente cada una de las regiones del sistema, a una cierta temperatura φ.
Considerando las ecuaciones anteriores, y las condiciones de continuidad de flujo se demuestra que la amplitud A es,
Donde es la frecuencia de modulación en el sistema, fc la frecuencia de corte y o una constante [16]. Si el espesor de la muestra es mucho mayor que la longitud de difusión ( 1 >> µs) de la ecuacion (7) se puede demostrar que,
A partir de la cual se puede determinar fc (de datos experimentales), y que está relacionada con la difusividad térmica por la expresión (9)
Experimental
Implementación de la técnica fotoacústica.
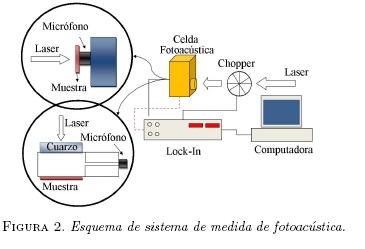
El sistema experimental implementado en el laboratorio para realizar medidas de fotoacústica se muestra en la Figura 2. Este sistema consiste principalmente de una fuente de excitación (láseres de estado sólido de 650 nm y 535 nm - óptica Flex BWTEK), el cual es modulado en frecuencia por un obturador mecánico (chopper) SR-430 Stanford Research Systems, antes de excitar a la muestra. La señal fotoacústica de la muestra es detectada por un transductor, y amplificada por un amplificador lock-in digital de doble canal, modelo SR-830 Stanford Research Systems, sensible a fase y frecuencia, conectado a una PC a través de un puerto USB, donde se registra la fase y la amplitud fotoacústica, utilizando un código desarrollado en el laboratorio mediante software NI Labview.
Configuración de celda fotoacústica
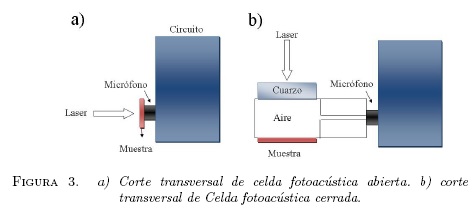
El diagrama básico de la celda fotoacuóstica abierta y cerrada se muestra en la Figura 3 a) y b). En la configuración de celda abierta (Fig. 3a), el micrófono funciona como celda fotoacústica, ya que la muestra sella el sistema al ponerse en contacto sobre el micrófono con grasa de vacío. La celda cerrada implementada en al laboratorio (Fig. 3b), está construida en acrílico, la cual esta comunicada con un micrófono electrete a través de un conducto muy estrecho para evitar fugas indebidas de la señal FA de la muestra. La luz del haz laser que excita la muestra pasa a través de una ventana de cuarzo que sella herméticamente la celda.
Las medidas de fotoacústica (señal FA) fueron realizadas sobre obleas comerciales de Si (100) tipo-p, de 350 mum de espesor, pulido espejo por la cara A y rugosa por la cara B, y GaSb (111) tipo-p de 250 /m, pulido espejo por las caras A y B.
Resultados
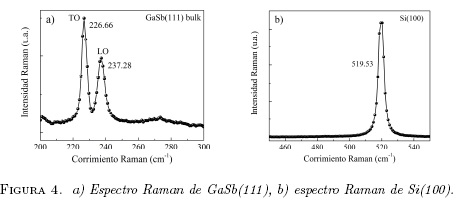
En la Figura 4 a) y b) se muestran los espectros Raman típicos para GaSb(111) y Si(100) obtenidos en configuración de retro-dispersión (resultados medidos en monocristales [16]). En esta configuración solo el modo TO de la zona centro, ΤΟ(Γ), está permitido para una estructura de zinc-blenda perfecta. La aparición del modo LO(r) en la misma zona, puede aparecer debido a de la perdida de la simetría del cristal. En figura 4 a) se observan los modos vibracionales ΤΟ(Γ) y LO(r) de GaSb(111), localizados en 226 cm-1 y 237 cm-1, respectivamente. Debido a la orientación del cristal, la intensidad integrada del modo TO es mayor respecto a la del modo LO típico de enlaces polares, y en buen acuerdo con las reglas de selección que se muestran en la Tabla 1. En el caso del Si(100) monocristalino y en ausencia de esfuerzos (internos y externos), las tres ramas ópticas del Si están degenerados, resultando en un modo vibracional óptico de primer orden en ∼ 520 cm-1, denotado como LTO(r) en la Figura 4b), como consecuencia de la discontinuidad en la densidad de estados fononicos cerca de un punto crítico.
Una manera complementaria de estudiar las diferencias fononicas en cristales con diferente orientación cristalográfica es mediante la técnica fotoacústica, a partir de la cual se pueden obtener parámetros físicos como los discutidos en este trabajo, que dependen directamente del comportamiento fononico relacionado con la dirección y calidad cristalina del material. Es decir que la magnitud de las medidas realizadas para cada uno de los experimentos está relacionada con los modos fononicos determinados a partir de espectroscopia Raman, los cuales tienen intensidades características en cada orientación cristalográfica de acuerdo a las reglas de selección para las diferentes estructuras.
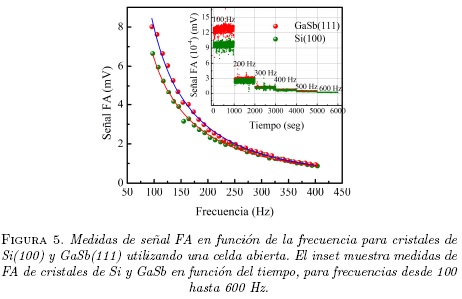
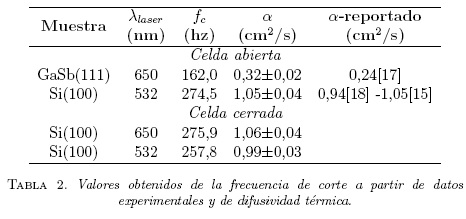
El inset de la Figura 5, muestra las medidas de la señal fotoacústica en celda abierta proveniente de los cristales de Si(100) y GaSb(111) dopado p, para frecuencias de modulación del obturador electro-Óptico de 100, 200, 300, 400, 500 y 600 Hz, registrada durante un intervalo de tiempo (At) de 1000 s, con el fin de determinar la estabilidad del sistema. De acuerdo a estos resultados, consideramos que la señal FA es estable y se procedió a realizar mediciones de señal FA en función de la frecuencia de modulación utilizando la misma configuración, como se muestra en la Fig. 5, donde los puntos verdes y rojos corresponden a los datos experimentales, Si (100) y GaSb (111), respectivamente. La línea continua representa el mejor ajuste empleando la ecuación (8) de los datos experimentales, utilizando el método de mínimos cuadrados, de los cuales se obtuvieron valores de fc. Esto permitió calcular la difusividad (a),a partir de la Ec. (9) datos que son mostrados en la Tabla 2.
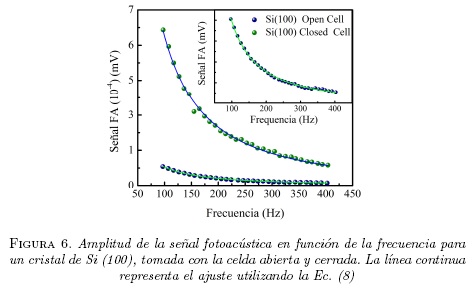
Con el fin de realizar una comparación entre las celdas fotoacústica abierta y cerrada, se realizó medidas de FA en función de la frecuencia de modulación a una oblea de Si(100), como se muestra en la Figura 6. Aunque la forma de la curva es idéntica para las dos celdas, hay una gran diferencia en los valores de la amplitud de la señal FA, debido posiblemente a la diferencia en el volumen de las celdas, y al recorrido que deben realizar las ondas sonoras antes de ser detectadas por el micrófono. Por comparación, en el recuadro se muestra la curva de señal FA de la celda abierta, lo cual verifica la similitud de las curvas de las dos celdas. El valor calculado de la frecuencia de corte (fc), fue de 274.5 Hz para la celda abierta y de 275.9 Hz para la celda cerrada, lo cual muestra que no hay gran diferencia en los valores obtenidos en las dos configuraciones.
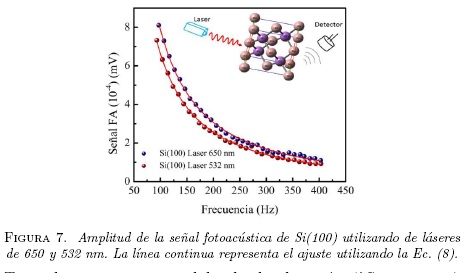
De igual manera, se realizaron medidas de señal FA sobre el cristal de Si(100) en configuración de celda cerrada con diferentes láseres, obteniendo valores de fc de 275.9 Hz para la línea del láser de 650 nm (pot. = 60 mW) y 257.8 Hz para la línea de 532 nm (pot. = 80 mW ) (Figura 7). La diferencia en el valor de fc y la amplitud de la señal FA, se debe a las características propias del láser: potencia, longitud de onda, y longitud de penetración, y de la muestra como: la orientación cristalográfica, la morfología superficial (rugosa o plana), y de sus propiedades térmicas alterando de esta manera las diferentes contribuciones de la señal FA en el cristal semiconductor, como la termalización no radiactiva intrabanda, recombinación no radiactiva en bulto, recombinación superficial no radiactiva, y su comportamiento termo-elástico [18].
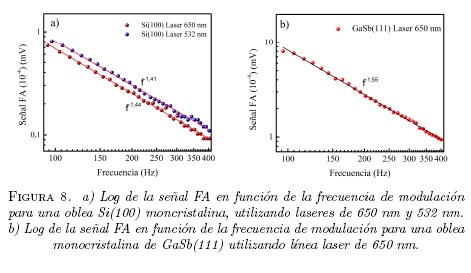
Teniendo en cuenta que el borde de absorción (ASi=1127 nm) del Si(100) se encuentra por encima de las longitudes de onda utilizadas para excitar la muestra, es posible que la absorción se deba a la interacción de ondas electromagnéticas y fonones, reflejándose en la señal fotoacústica. Con el fin de analizar los procesos de recombinación no-radiactiva graficamos log (señal FA) vs log (f), como se muestra en la Figura 8a). El ajuste con los datos experimentales determinó una dependencia de la señal FA con la frecuencia de la forma f -1.41 para el láser de 650nm, y f -1.44 para el láser de 532 nm para el rango de frecuencias entre 100 hasta 400 Hz. Los resultados obtenidos son consistentes con los reportados en la literatura ∼ f -1.5 [17], proveniente de la recombinación no-radiactiva en el bulto del exceso de pares electrón-hueco después de la difusión una distancia (Dτ)1/2, donde τ es el tiempo de vida y D, el coeficiente de difusión. Asó, podemos descartar recombinación superficial no radiactiva en la muestra para los valores de frecuencia de modulación indicados, aunque la disminución en el exponente desde -1.41 a -1.44 puede estar asociada a otros fenómenos de recombinación debido a la influencia de la longitud del láser utilizado en la excitación del Si cristalino. De igual manera, se obtuvo una dependencia de la señal FA con la frecuencia de f -1.55 (Figura 8b), para GaSb(111). Este valor está en buen acuerdo con lo reportado para semiconductores III-V, en donde esta dependencia en este rango de frecuencia es atribuida a recombinación no radiactiva en bulto [19].
Aunque para los mono-cristales de Si(100) y GaSb(111) el comportamiento es similar en la región de frecuencias (100 ≤ f ≤ 400 Hz), la diferencia en la dependencia de la señal FA con la frecuencia (∼ f -1.44 y ∼ f -1.56), y en los valores de amplitud, se atribuye a fenómenos de recombinación no-radiactiva tópicos de semiconductores, y probablemente debido a la orientación cristalográfica de Si(100) y GaSb(111), asó como también a su composición química, la estructura en la que cristalizan, (Si: diamante y GaSb zincblenda). Además, en la diferencia en los radios atómicos de Ga y Sb de Si, variando el factor de empaquetamiento, y ocasionando una mayor contribución fononica (discutida en la sección Raman). La luz incidente del láser modulada crea un exceso de concentración de portadores en el semiconductor, la cual se difunde a través de la muestra transfiriendo energía a los fonones de la red por medio de colisiones. Este exceso de energía (E-Eg) se convierte en energía térmica a través de procesos no-radiactivos, en tiempos relativamente cortos ∼ 10-12 s, que puedes suponerse instantáneos en el rango de frecuencias de modulación utilizadas FA.
Conclusiones
Se determinaron los valores de difusividad térmica para Si(100) y GaSb(111) monocristalinos, por medio de fotoacústica en configuración de celda abierta y cerrada, obteniéndose valores similares a los reportados en la literatura. Diferencias en la difusividad térmica, y en la dependencia de la señal fotoacústica con la frecuencia se atribuyen a fenomenos de recombinación no-radiactiva superficial y volumétrica. Finalmente se sugiere esta técnica como método para determinar parámetros como difusividad térmica en materiales semiconductores IV y III-V.
Acknowledgments
Este trabajo fue financiado por la dirección de Investigaciones de la Universidad Nacional de Colombia sede Manizales, Proyectos códigos 17075 - 23196. R. Bernal-Correa, agradece a COLCIENCIAS por la beca doctoral otorgada dentro del programa "Francisco José de Caldas 2011".
Referencias
[1] R. Maia, M. Siqueira, R. Araujo, K. Machado, and S. Stolf, J. Non-Cryst. Solids 426, 43 (2015).
[2] A. Bedoya, E. Marón, A. Mansanares, M. Zambrano-Arjona, I. Riech, and A. Calderon, Thermochim. Acta 614, 52 (2015).
[3] H. Abosheiasha and S. Saafan, Int. J. Thermophys. 36, 1661 (2015).
[4] Z. El-Qahtani, A. Badawi, K. Easawi, N. Al-Hosiny, and S. Abdallah, Mat. Sci. Semicon. Proc. 20, 68 (2014).
[5] C. Poffo, J. de Lima, S. Souza, D. Triches, T. Nogueira, Z. Borges, and L. Manzato, J. Mol. Struct. 1076, 737 (2014).
[6] A. Rosencwaig and A. Gersho, J. Appl. Phys. 47, 64 (1976).
[7] Y. Fujii, A. Moritani, and J. Nakai, Jpn. J. Appl. Phys. 20, 361 (1981).
[8] M. Morita, Jpn. J. Appl. Phys. 20, 835 (1981).
[9] F. Satour and A. Zegadi, J. Lumin. 132, 1688 (2012).
[10] J. Rojas-Trigos, A. Calderóon, and E. Marón, J. Mater. Sci. 46, 7799 (2011).
[11] D. G. Espinosa-Arbelóaez, R. Velóazquez-Hernaóndez, J. Petricioli-Carranco, R. Quintero-Torres, and M. E. Rodríguez-Garda, Phys. Status Solidi C 8, 1856 (2011).
[12] K. Ersching, C. Campos, J. de Lima, T. Grandi, S. Souza, and P. Pizani, Mater. Chem. Phys. 122, 528 (2010).
[13] C. Poffo, J. de Lima, S. Souza, D. Triches, T. Grandi, and R. de Biasi, Physica B 413, 47 (2013).
[14] C. Hamaguchi, Basic Semiconductor Physics, Segunda ed. (Springer Berlin Heidelberg, 2010) Chap. 5.
[15] P. Puech, G. Landa, R. Carles, and C. Fontaine, J. Appl. Phys. 82, 4493 (1997).
[16] A. Pulzara-Mora, M. Melóendez-Lira, S. Jimóenez-Sandoval, and M. Lopez-Lopez, Vacuum 80, 468 (2006).
[17] O. Pessoa, C. L. Cesar, N. A. Patel, H. Vargas, C. C. Ghizoni, and L. C. M. Miranda, J. Appl. Phys. 59, 1316 (1986).
[18] G. Penña-Rodriguez, A. Calderon, and R. A. Munñoz Hernadez, Rev. Col. de Fósica 38, 806 (2006).
[19] J.-T. Lim, J.-G. Choi, Y. H. Bak, S.-H. Park, and U. Kim., J. Korean Phys. Soc. 31, 608 (1997).
Cómo citar
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Descargar cita
Licencia
Aquellos autores/as que tengan publicaciones con esta revista, aceptan los términos siguientes:- Los autores/as conservarán sus derechos de autor y garantizarán a la revista el derecho de primera publicación de su obra, el cuál estará simultáneamente sujeto a la Licencia de reconocimiento de Creative Commons Atribución-SinDerivar 4.0 International que permite la redistribución, comercial o no comercial, siempre y cuando la obra circule íntegra y sin cambios, donde indique su autor y su primera publicación en esta revista.
- Se permite y recomienda a los autores/as difundir su obra a través de Internet (p. ej.: en archivos telemáticos institucionales o en su página web) antes y durante el proceso de envío, lo cual puede producir intercambios interesantes y aumentar las citas de la obra publicada.