Optimización del torneado multipasada para producciones sostenibles utilizando algoritmos genéticos y enjambre de partículas
Multi-passes turning optimization for sustainable productions by using genetic algorithm and particle swarm heuristics
DOI:
https://doi.org/10.15446/dyna.v85n204.68623Palabras clave:
cilindrado multipasada, optimización multiobjetivo, parámetros de corte (es)multi-pass cylindrical turning, multiobjective optimization, cutting parameters (en)
Recibido: 31 de octubre de 2017; Revisión recibida: 21 de febrero de 2018; Aceptado: 23 de febrero de 2018
Resumen
La selección de parámetros óptimos de corte es un aspecto esencial en la planificación de cualquier proceso de maquinado, principalmente cuando la sostenibilidad es un objetivo primordial. En este trabajo se presenta una optimización multiobjetivo dirigida a producciones sostenibles, con el fin de seleccionar los parámetros de corte óptimos (velocidad, avance y la profundidad de corte) en operaciones de cilindrado multipasada. Como funciones objetivos del proceso fueron considerados: el aspecto económico y el medioambiental, los cuales son pilares representativos de la sostenibilidad. Requerimientos técnicos, tales como: la potencia de corte, las fuerzas y la rugosidad superficial fueron considerados como restricciones. La optimización se llevó a cabo mediante un enfoque a posteriori; donde se obtuvo un conjunto de soluciones no dominadas (también conocidas como frontera de Pareto) que permitió la selección de la combinación más viable de objetivos para las condiciones específicas del taller. Para la optimización se emplearon dos técnicas de gradiente libre: algoritmo genético sin ordenamiento y enjambre de partículas. Se desarrolló un estudio de caso para evaluar el ajuste y la eficiencia de las técnicas propuestas. Los resultados obtenidos mostraron un mejor rendimiento del algoritmo genético usado, en cuanto a: costo computacional y calidad de la frontera de Pareto obtenida. El método propuesto demostró ser muy conveniente para la optimización sostenible del proceso de torneado, a través de una evaluación simultánea de aspectos económicos y ambientales.
Palabras clave:
cilindrado multipasada, optimización multiobjetivo, parámetros de corte.Abstract
Selecting optimal cutting parameters is a very important task in any machining process planning, especially when sustainability is in the sight. This paper presents a multi-objective optimization focused on sustainable productions, for selecting optimal cutting parameters (cutting speed, feed, and depth of cut) in multi-pass cylindrical turning operations. Both, the economic and environmental pillars of sustainability are considered as optimization targets. Technical requirements, such as cutting power, forces and surface roughness, are also taken into account as constraints. Optimization was carried out through a posteriori approach, where a set of non-dominated solutions, also known as Pareto front, were obtained and, then, the most suitable combination of targets is selected for the specific workshop conditions. Two gradient-free optimization techniques were used for carrying out the optimization: the non-sorting genetic algorithm II and the multi-objective particle swarm optimization. A study case was carried out not only for evaluating the fitness of the proposed approach but also for comparing the performance of the considered techniques. The outcomes showed a better performance by the genetic algorithms, in both the computational efficiency and the quality of the obtained Pareto front. The proposed approach demonstrated its convenience for sustainability optimization of machining processes, giving a simpler way for analyzing simultaneously the economic and environmental aspects of sustainability.
Keywords:
multi-pass cylindrical turning, multiobjective optimization, cutting parameters.1. Introducción
La determinación de los parámetros de corte óptimos, como: el número de pasadas, la profundidad corte en cada pasada, el avance y la velocidad, son una tarea primordial para cualquier proceso de maquinado. En la práctica real del taller estos parámetros de corte son seleccionados a partir de bases de datos o manuales especializados; sin embargo, los rangos que se ofrecen en esas fuentes son solo valores iniciales y no los valores óptimos [1].
La optimización de los parámetros de corte es una tarea difícil [2], donde se requieren conocimientos sobre: ecuaciones empíricas que relacionen la vida útil de la herramienta, la fuerza de corte, la potencia, la rugosidad superficial, que permitan desarrollar restricciones realísticas; especificaciones de la máquina herramienta; criterios de optimización empleados, así como la fundamentación matemática de los mismos [3].
En cualquier procedimiento de optimización, la identificación de las funciones de salida (conocidas como funciones objetivos), es un aspecto crucial. En el caso específico del proceso de torneado el criterio más usado es el de los costos específicos [4-10].
Otros criterios empleados son: los tiempos de maquinado [9-11], el consumo de energía [12, 13], la velocidad de remoción de material [13-15] y el desgaste de la herramienta [15], en estas investigaciones (más contemporáneas) se encuentran combinados varios de los criterios antes mencionados, debido a que esto permite una mejor caracterización y comprensión del proceso en estudio, no siendo así cuando se tratan como problemas enfocados en un solo objetivo, los cuales limitan la decisión que se puede tomar sobre determinada operación [16].
El enfoque a posteriori para la toma de decisiones es un recurso ventajoso en las tareas de optimización, debido a que las soluciones se muestran como un conjunto de valores no dominados, permitiendo la selección de cualquiera de esas soluciones a partir de los intereses y condiciones específicas de la producción. Estas soluciones se consideran óptimas ya que en el espacio de búsqueda no existe una solución mejor que ellas cuando son considerados todos los objetivos simultáneamente [17] y son conocidas también como soluciones óptimas de Pareto, las cuales se representan gráficamente en la frontera de Pareto.
En aplicaciones reales, la obtención del conjunto de Pareto puede resultar computacionalmente más costosa. Por esta razón se han desarrollado numerosas estrategias de búsqueda, las cuales no garantizan la obtención de soluciones óptimas pero si tratan de hallar buenas aproximaciones (near optimal solutions). Dentro de esas estrategias se destaca por su aplicación a los procesos de manufactura los algoritmos genéticos, [1, 6, 10, 11, 14, 18-20] capaces de encontrar soluciones óptimas a un costo computacional razonable. Otra heurística ampliamente aplicada a los procesos de maquinado es la de enjambre de partículas (particle swarm optimization, PSO). Hrelja y colaboradores [21] aplican esta técnica al proceso de torneado con el objetivo de mejorar la rugosidad superficial y la vida útil de la herramienta; por otra parte en el trabajo propuesto por [22] se consideran como criterios de optimización la presión específica de corte, las fuerzas y la potencia de corte en el torneado de PEEK CF30 (Poly Ether Ether Ketone) aplicando PSO. Este método fue empleado también por [23] para estudiar el efecto de la lubricación sobre las fuerzas de corte, la temperatura, el desgaste y la rugosidad superficial sobre el torneado de aleaciones de titanio.
Considerando lo planteado en el estado del arte, en este trabajo se propone la optimización multiobjetivo del cilindrado de varias pasadas con un enfoque sostenible, teniendo en cuenta como funciones objetivos, los costos de operación y el impacto ambiental (evaluado en el consumo de energía y el gasto de herramienta). Para llevar a cabo esta tarea fueron aplicadas y comparadas las heurísticas de: algoritmos genéticos (específicamente el algoritmo evolutivo no dominado, NSGA-II propuesto por [24]) y enjambre de partículas [25].
2. Definición del problema de optimización
2.1. Variables de decisión
Como variables de decisión, para la optimización del proceso de maquinado, se tomaron los parámetros del régimen de corte: velocidad, avance y profundidad de corte. En el caso considerado, correspondiente a un torneado cilíndrico de pasadas múltiples, hay que tener en cuenta que la última pasada es de acabado y las previas, de desbaste. En ese caso, asumiendo que todas las pasadas de desbaste se llevarán a cabo con el mismo régimen, se tienen seis variables de decisión: la profundidad de corte de acabado, a F; el número total de pasadas, N; el avance para el desbaste, f R, y el acabado, f F; y la velocidad de corte para el desbaste, v R, y el acabado, v F.
Nótese que la profundidad de corte para el desbaste, a R, puede calcularse mediante la expresión:
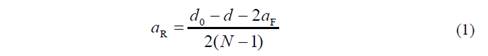
donde d 0 y d son los diámetros inicial y final, respectivamente, del escalón elaborado.
Teniendo en cuenta lo anterior, para cada una de las N pasadas, los parámetros de corte serán:

2.2. Funciones objetivos
Como funciones objetivo se toman los dos aspectos considerados de la sostenibilidad del proceso: económico y ambiental. Para el primero, se consideró el costo total de la operación, z TOT:

donde z L es el costo horario por mano de obra; z O, el total de costos horarios indirectos; z T, el costo unitario de herramienta; z E, el costo unitario de energía consumida; τ, el tiempo de producción; ξ, la vida útil consumida de la herramienta; y E, el consumo de energía. Por su parte, el tiempo de producción se calcula como:
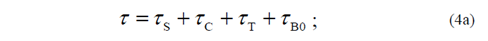
donde, τS es el tiempo de instalación y desinstalación; τC, el tiempo total de corte; τT, el tiempo de cambio de herramienta; y τB, el tiempo de retroceso de la herramienta. La ecuación 4 puede ser, entonces, rescrita de la siguiente forma:
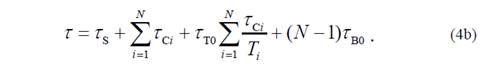
donde, ( C i es el tiempo de corte para la i-ésima pasada:
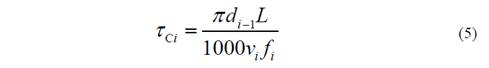
El consumo de herramienta por cada pasada se determina mediante la relación:

y la vida útil de la herramienta para cada pasada, Ti , puede ser calculada usando la ley de Taylor extendida:
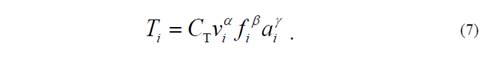
donde C T, α, β y γ son coeficientes determinados empíricamente.
El segundo objetivo es el impacto ambiental. EI, que tiene en cuenta el consumo de energía y el gasto herramental; ambos parámetros fueron normalizados, mediante una interpolación lineal, para poder establecer una relación entre ellos:
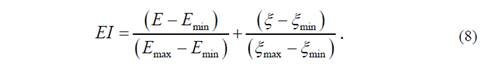
En la ecuación anterior, E, es la energía total consumida en el proceso:

siendo Ei la energía consumida; y Pi , la potencia de corte en la i-ésima pasada:
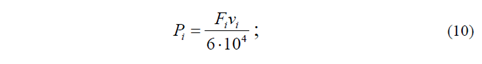
que depende de la velocidad de corte, vi , y de la fuerza, Fi , que a su vez se puede calcular por la ecuación:
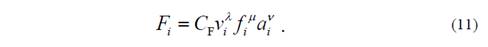
donde C F, λ, μ y ν son coeficientes determinados empíricamente.
2.3. Restricciones
Para el proceso de corte es necesario que se cumplan determinadas restricciones. Primero que todo, los parámetros de corte se deben seleccionar en el rango permitido para la herramienta seleccionada:

Además, la fuerza de corte para cada pasada, Fi , no debe sobrepasar un valor máximo, F max, el cual está dado por la resistencia y rigidez del sistema máquina-herramienta-pieza:
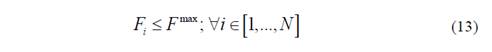
También, la potencia de corte para cada pasada, Pi , no debe ser mayor que la potencia del motor de la máquina herramienta, P mot, afectada por la eficiencia de la trasmisión, η:

Estas dos últimas restricciones deben ser especialmente analizadas en las pasadas de desbaste.
Finalmente, en la pasada de acabado la rugosidad superficial obtenida, Ri , debe ser menor o igual al valor especificado en los requerimientos tecnológicos de la superficie a elaborar, R max:

donde, r E es el radio de la punta de la herramienta.
2.4. Algoritmos empleados
La implementación de los algoritmos de optimización se realizó en el software MatLab R2013a.
Los parámetros empleados para el NSGA-II (non-dominated sorting genetic algorithm), son: tamaño de población de 1000 muestras, y un número máximo de iteraciones igual a 200. La población inicial fue creada siguiendo una distribución aleatoria y uniforme. El cruzamiento fue hecho mediante la técnica de punto simple. Para la mutación se aplicó una probabilidad de 0,01.
El algoritmo de Enjambre de Partículas se ejecutó con un tamaño de partículas de 1000 e igual número para el repositorio de la población, un factor de inercia de 0,5 y un coeficiente global de aprendizaje de 2 (estos valores se establecen a prueba y error).
Para comparar la eficiencia de ambos algoritmos (fueron ejecutadas 50 réplicas de los mismos) se seleccionó el tiempo de cómputo y el hiperárea [26], esta última evalúa la calidad de la frontera de Pareto obtenida.
3. Análisis de los resultados
3.1. Caso de studio
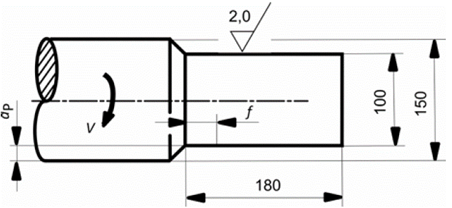
Con el objetivo de ilustrar el método de optimización propuesto, se llevará a cabo el siguiente estudio de caso. Se debe elaborar una sección de un árbol de AISI 1045, con longitud 180 mm, desde un diámetro inicial de 150 mm hasta un diámetro de 100 mm (ver Fig. 1). De acuerdo con los requisitos tecnológicos, la superficie obtenida debe tener una rugosidad no mayor de 2.0 μm (Ra).
Figura 1: Croquis de la sección considerada en el caso de estudio.
El proceso de torneado se ejecutará en un torno CNC, el cual tiene un motor de 10 kW y una eficiencia en la transmisión del 75%. La fuerza máxima permisible por la máquina herramienta es de 5000 N. El radio de la punta tanto para la herramienta de desbaste como para la de acabado es de 2 mm. Los rangos permisibles de los parámetros de corte para la herramienta seleccionada se muestran a continuación. Cabe destacar que como la herramienta para el desbaste y el acabado es la misma, el avance y la velocidad se mantienen igual para ambas operaciones.

Para la combinación pieza-herramienta empleada, se obtuvieron los siguientes modelos empíricos, para la vida útil de la herramienta y la fuerza de corte:
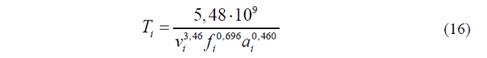
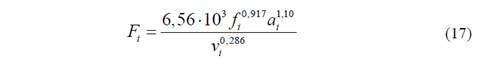
Estos modelos solo son válidos en los intervalos antes mencionados, los cuales son suministrados por el fabricante de las herramientas usadas.
El tiempo de instalación, el tiempo de cambio y el tiempo de retroceso para una herramienta, se han asumido como: 1,5; 1,0 y 0,1 min, respectivamente. Por otra parte el costo específico por mano de obra, el costo por gastos indirectos, el costo por herramienta y el costo por energía consumida son de: 0,44 $; 0,18 $; 14,17 $ y 0,20 $ respectivamente.
3.2. Discusión
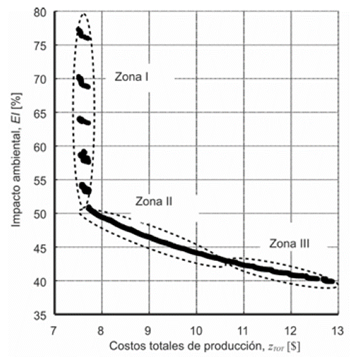
Después de ejecutar los algoritmos de optimización, los puntos no dominados o soluciones óptimas son representados gráficamente en la frontera de Pareto (ver Fig. 2 y 3), con el objetivo de facilitar el proceso de toma de decisión.
Figura 2: Resultados de la optimización con NSGA-II.
Figura 3: Resultados de la optimización con PSO.
En un análisis preliminar, entre ambas fronteras, se puede observar que la dispersión de los resultados de las diferentes réplicas es mayor en los resultados de PSO. Esto hace que los mismos sean cualitativamente inferiores a los obtenidos por NSGA-II.
Lo anterior se corrobora a través del cálculo del hiperárea, como métrica de la calidad de las fronteras de Pareto obtenidas. Como se puede observar (Tabla 1), la hiperárea de las fronteras obtenidas por NSGA-II no sólo es mayor, sino que presenta una menor dispersión.
Fuente: Elaborada por los autores.Tabla 1: Comparación entre ambos métodos.

Por otro lado, el tiempo de cómputo del NSGA-II es marcadamente inferior al del PSO. Se puede concluir que el NSGA-II es superior al PSO no sólo por la calidad de la frontera obtenida, sino también por la eficiencia computacional.
La toma de decisiones se lleva a cabo, entonces, a partir de la frontera generada por el NSGA-II (Fig. 2). Como se puede apreciar en la misma, las soluciones pueden ser dividas en tres zonas:
-
Zona I: En esta zona los costos alcanzan sus valores más bajos, y consecuentemente el impacto ambiental posee los mayores porcientos. Estas soluciones son las más convenientes cuando en el taller se presentan dificultades con los indicadores económicos.
-
Zona II: Aquí se puede notar un equilibrio aceptable entre los costos y el impacto ambiental. Esta zona es la recomendada cuando se quieren estabilizar los indicadores de sostenibilidad analizados (funciones objetivos de la optimización).
-
Zona III: En esta zona se sacrifican los costos de la operación en función de disminuir el consumo de corriente y de herramienta. Esta solución es la aconsejada cuando existan problemas con el suministro de energía o de herramental.
Evidentemente, la solución seleccionada finalmente dependerá de las condiciones específicas de la producción en cuestión.
4. Conclusiones
Como resultado del estudio realizado se formalizó una metodología para la optimización multiobjetivo del proceso de torneado enfocada a la sostenibilidad. La misma incluyó no sólo los objetivos enfocados a reflejar los aspectos económicos y ambientales del proceso, sino también las restricciones tecnológicas de éste.
Las dos técnicas de optimización libre de gradiente utilizadas (algoritmos genéticos y enjambre de partículas), mostraron ser efectivas en la solución del problema, aunque los resultados del algoritmo genéticos fueron superiores tanto en la calidad de la frontera de Pareto obtenida como en la eficiencia computacional de la optimización.
El enfoque a posteriori demostró ser una opción viable en la selección de los parámetros más convenientes en el proceso de cilindrado multipasada. Éste ofrece la ventaja de no tener que recurrir a evaluaciones subjetivas de la importancia relativa de los objetivos considerados, sino que, a través de la obtención de un grupo de soluciones no dominadas, permite la selección de la variante más conveniente en dependencia de las condiciones específicas del proceso en cuestión.
Como extensión futura del presente trabajo, se considerará la aplicación de la metodología propuesta a otros procesos de maquinado, tales como el fresado o el taladrado. También será conveniente, analizar la efectividad de otras técnicas de optimización libres de gradiente como son el recocido simulado y el método de entropía cruzada.
Referencias
Referencias
Dereli, T., Filiz, I.H., and Baykasoglu, A., Optimizing cutting parameters in process planning of prismatic parts by using genetic algorithms. International Journal of Production Research, 39(15), pp. 3303-3328, 2001. DOI: 10.1080/00207540110057891.
Sreekumar, M., Zoppi, M., Nithiarasu, P., et al., International Conference on Design and Manufacturing (IConDM2013) Optimization of Machining Parameters for end Milling of Inconel 718 Super Alloy Using Taguchi based Grey Relational Analysis. Procedia Engineering, 64, pp. 1276-1282, 2013. DOI: 10.1016/j.proeng.2013.09.208.
Quiza, R., Beruvides, G., and Davim, J.P., Modeling and optimization of mechanical systems and processes, in: Modern mechanical engineering, Davim, J.P., Ed. Springer Berlin Heidelberg, 2014, pp. 169-198.
Taylor, F.W., On the art of cutting metals. Transactions of the ASME, 28, pp. 310-350, 1907.
Saravanan, R., Asokan, P. and Vijayakumar, K., Machining parameters optimisation for turning cylindrical stock into a continuous finished profile using genetic algorithm (GA) and simulated annealing (SA). International Journal of Advanced Manufacturing Technology, 21(1), pp. 1-9, 2003. DOI: 10.1007/s001700300000.
Cus, F. and Balic, J., Optimization of cutting process by GA approach. Robotics and Computer Integrated Manufacturing, 19(1-2), pp. 113-121, 2003. DOI: 10.1016/s0736-5845(02)00068-6.
Cus, F. and Zuperl, U., Approach to optimization of cutting conditions by using artificial neural networks. Journal of Materials Processing Technology, 173(3), pp. 281-290, 2006. DOI: 10.1016/j.jmatprotec.2005.04.123.
Amiolemhen, E. and Ibhadode, A.O.A., Application of genetic algorithms-determination of the optimal machining parameters in the conversion of a cylindrical bar stock into a continuous finished profile. International Journal of Machine Tools and Manufacture, 44(12-13), pp. 1403-1412, 2004. DOI: 10.1016/j.ijmachtools.2004.02.001.
Quiza, R., Albelo, J.E. and Davim, J.P., Multi-objective optimisation of multipass turning by using a genetic algorithm. International Journal of Materials and Product Technology, 35(1-2), pp. 134-144, 2009. DOI: 10.1504/ijmpt.2009.025223.
Ganesan, H. and Mohankumar, G., Optimization of machining techniques in CNC turning centre using genetic algorithm. Arabian Journal for Science and Engineering, 38(6), pp. 1529-1538, 2013. DOI: 10.1007/s13369-013-0539-8.
D’Addona, D.M. and Teti, R., Genetic algorithm-based optimization of cutting parameters in turning processes. Procedia CIRP, 7, pp. 323-328, 2013. DOI: 10.1016/j.procir.2013.05.055.
Guo, Y., Loenders, J., Duflou, J., et al., Optimization of energy consumption and surface quality in finish turning. Procedia CIRP, 1, pp. 512-517, 2012. DOI: 10.1016/j.procir.2012.04.091.
Kumar, R., Bilga, P.S., and Singh, S., Multi objective optimization using different methods of assigning weights to energy consumption responses, surface roughness and material removal rate during rough turning operation. Journal of Cleaner Production, 164(Supplement C), pp. 45-57, 2017. DOI: 10.1016/j.jclepro.2017.06.077.
Umer, U., Qudeiri, J.A., Hussein, H.A.M., et al., Multi-objective optimization of oblique turning operations using finite element model and genetic algorithm. The International Journal of Advanced Manufacturing Technology, 71(1-4), pp. 593-603, 2014. DOI: 10.1007/s00170-013-5503-y.
Yang, S.H. and Natarajan, U., Multi-objective optimization of cutting parameters in turning process using differential evolution and non-dominated sorting genetic algorithm-II approaches. The International Journal of Advanced Manufacturing Technology, 49(5-8), pp. 773-784, 2010. DOI: 10.1007/s00170-009-2404-1.
Li, H. and Zhang, Q., Multiobjective optimization problems with complicated Pareto sets, MOEA/D and NSGA-II. IEEE Transactions on Evolutionary Computation, 13(2), pp. 284-302, 2009. DOI: 10.1109/TEVC.2008.925798.
Abbass, H.A., Sarker, R. and Newton, C. PDE: A Pareto–frontier differential evolution approach for multi objective optimization problems. in Congress on Evolutionary Computation. 2001. Piscataway, NJ (U.S.A.).
Batish, A., Bhattacharya, A., Kaur, M. et al., Hard turning: Parametric optimization using genetic algorithm for rough/finish machining and study of surface morphology. Journal of Mechanical Science and Technology, 28(5), pp. 1629-1640, 2014. DOI: 10.1007/s12206-014-0308-y.
Durairaj, M. and Gowri, S., Parametric optimization for improved tool life and surface finish in micro turning using genetic algorithm. Procedia Engineering, 64, pp. 878-887, 2013. DOI: 10.1016/j.proeng.2013.09.164.
Quiza, R., Rivas, M., and Alfonso, E., Genetic algorithm-based multi-objective optimization of cutting parameters in turning processes. Engineering Applications of Artificial Intelligence, 19(2), pp. 127-133, 2006. DOI: 10.1016/j.engappai.2005.06.007.
Hrelja, M., Klancnik, S., Irgolic, T., et al., Turning parameters optimization using particle swarm optimization. Procedia Engineering, 69(Supplement C), pp. 670-677, 2014. DOI: 10.1016/j.proeng.2014.03.041.
Hanafi, I., Cabrera, F.M., Dimane, F., et al., Application of particle swarm optimization for optimizing the process parameters in turning of PEEK CF30 Composites. Procedia Technology, 22(Supplement C), pp. 195-202, 2016. DOI: 10.1016/j.protcy.2016.01.044.
Gupta, M.K., Sood, P.K. and Sharma, V.S., Optimization of machining parameters and cutting fluids during nano-fluid based minimum quantity lubrication turning of titanium alloy by using evolutionary techniques. Journal of Cleaner Production, 135(Supplement C), pp. 1276-1288, 2016. DOI: 10.1016/j.jclepro.2016.06.184.
Deb, K., Pratap, A., Agarwal, A. et al., A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Transections on Evolutionary Computation, 6(2), pp. 182-197, 2002. DOI: 10.1109/4235.996017.
Coello, C.A., Pulido, G.T. and Lechuga, M.S., Handling multiple objectives with particle swarm optimization. IEEE Transactions on Evolutionary Computation, 8(3), pp. 256-279, 2004. DOI: 10.1109/TEVC.2004.826067.
Jiang, S., Ong, Y.S., Zhang, J. et al., Consistencies and contradictions of performance metrics in multiobjective optimization. IEEE Transactions on Cybernetics, 44(12), pp. 2391-2404 2014. DOI: 10.1109/TCYB.2014.2307319.
Cómo citar
IEEE
ACM
ACS
APA
ABNT
Chicago
Harvard
MLA
Turabian
Vancouver
Descargar cita
CrossRef Cited-by
1. Lourdes Martinez Molina, Roberto Teti, Eva Maria Rubio Alvir. (2023). Quality, efficiency and sustainability improvement in machining processes using Artificial Intelligence. Procedia CIRP, 118, p.501. https://doi.org/10.1016/j.procir.2023.06.086.
Dimensions
PlumX
Visitas a la página del resumen del artículo
Descargas
Licencia
Derechos de autor 2018 DYNA

Esta obra está bajo una licencia internacional Creative Commons Atribución-NoComercial-SinDerivadas 4.0.
El autor o autores de un artículo aceptado para publicación en cualquiera de las revistas editadas por la facultad de Minas cederán la totalidad de los derechos patrimoniales a la Universidad Nacional de Colombia de manera gratuita, dentro de los cuáles se incluyen: el derecho a editar, publicar, reproducir y distribuir tanto en medios impresos como digitales, además de incluir en artículo en índices internacionales y/o bases de datos, de igual manera, se faculta a la editorial para utilizar las imágenes, tablas y/o cualquier material gráfico presentado en el artículo para el diseño de carátulas o posters de la misma revista.