Equilibrio parcial y general: dos problemas inquietantes
Palabras clave:
Equilibrio parcial, Equilibrio general, Teoría de juegos, Piero Sraffa, Teoremas de Sonnenchein-Mantel-Debreu. (es)A pesar de los múltiples avances y modificaciones que ha sufrido la teoría microeconómica
neoclásica, sus dos modelos canónicos continúan siendo el de equilibrio parcial y el de equilibrio
general. Contrario a lo que habitualmente se expone, existe abundante literatura que torna
insatisfactorios a ambos instrumentos analíticos. El presente ensayo intenta exponer algunos
problemas de la teoría microeconómica dominante recuperando los trabajos que nos parecen
contienen los componentes más esenciales de las críticas desarrolladas hacia ambos paradigmas:
los elementos aportados por Piero Sraffa; los Teoremas de Sonnenchein-Mantel-Debreu; y
la imposibilidad de la teoría del equilibrio general tanto de poder ofrecer una explicación de la
formación de precios como de modelar economías monetarias. Finalmente, la parte final del ensayo
aborda brevemente si la teoría de juegos puede ser considerada como una salida satisfactoria a los
defectos de la teoría microeconómica convencional.
Equilibrio parcial y general: dos problemas inquietantes
"En semejante mundo en el que todo se cuenta, el arma más fácilmente accesible y a la vez más mortal es la divulgación." Milan Kundera, La lentitud
Tania Contreras Herrada*
Ivan Mendieta Muñoz**
Rogelio Huerta Quintanilla***
* Los autores agradecen a Abu Turab Rizvi (Departamento de Economía, Universidad de Vermont), Carlo Panico (Departamento de Economía, Federico II de Nápoles) y John Peirson (Escuela de Economía, Universidad de Kent) por su amabilidad en el envío de materiales y por sus comentarios al presente ensayo. Agradecemos también de sobremanera a dos dictaminadores anónimos de la revista Ensayos de Economía por sus útiles sugerencias y por la revisión del manuscrito. Sobra decir que la responsabilidad por los errores y omisiones que persistan en este trabajo recae exclusivamente sobre los autores. Tania Contreras Herrada: Facultad de Economía, UNAM.
Correo electrónico: tunich48@hotmail.com
** Ivan Mendieta Muñoz: Escuela de Economía, Universidad de Kent. Correo electrónico: ivan45_650_2@hotmail.com
*** Rogelio Huerta Quintanilla: Facultad de Economía, UNAM. Correo electrónico: rhuerta@ servidor.unam.mx
Recibido: 12-02- 2012 Aceptado: 19-06-2012 Recibido versión final: 04-07-2012.
Resumen
A pesar de los múltiples avances y modificaciones que ha sufrido la teoría microeconómica neoclásica, sus dos modelos canónicos continúan siendo el de equilibrio parcial y el de equilibrio general. Contrario a lo que habitualmente se expone, existe abundante literatura que torna insatisfactorios a ambos instrumentos analíticos. El presente ensayo intenta exponer algunos problemas de la teoría microeconómica dominante recuperando los trabajos que nos parecen contienen los componentes más esenciales de las críticas desarrolladas hacia ambos paradigmas: los elementos aportados por Piero Sraffa; los Teoremas de Sonnenchein-Mantel-Debreu; y la imposibilidad de la teoría del equilibrio general tanto de poder ofrecer una explicación de la formación de precios como de modelar economías monetarias. Finalmente, la parte final del ensayo aborda brevemente si la teoría de juegos puede ser considerada como una salida satisfactoria a los defectos de la teoría microeconómica convencional.
Palabras clave: Equilibrio parcial, equilibrio general, teoría de juegos, Piero Sraffa, teoremas de Sonnenchein-Mantel-Debreu
Abstract
Nevertheless the multiple advances and modifications that neoclassical microeconomic theory has suffered, its two canonical models continue to be partial and general equilibrium. As opposed to what is commonly presented, there exists abundant literature that turns unsatisfactory both analytical instruments. The current essay aims to put forward some problems of the dominant microeconomic theory retrieving the works that, in our view, contain the most essential components of the criticisms developed towards both paradigms: the elements provided by Piero Sraffa; the Sonnenchein-Mantel-Debreu Theorems; and the impossibility of general equilibrium theory to offer an explanation of price formation and to model monetary economies. Finally, the last part of the essay briefly tackles if game theory can be considered a satisfactory way out of the flaws of conventional microeconomic theory.
Key Words: Partialequilibrium, general equilibrium, gametheory, Piero Sraffa, theorems-Mantel-DebreuSonnenchein
JEL classification: B13, B20, B21, B50
Résumé
Malgré les nombreuses avancées et les modifications subies par la théorie microéconomique néoclassique, ses deux modèles canoniques restent l'équilibre partiel et l'équilibre général. Contrairement à ce qui est généralement exposé, il y a une abondante littérature qui fait que ces deux instruments analytiques deviennent peu satisfaisants. Cet essai vise à apporter une contribution à l'histoire de la pensée économique dans le but d'exposer l'état actuel de la microéconomie par la récupération des œuvres que, à notre avis, peuvent fournir les composants essentiels des larges expositions critiques orientées vers les deux paradigmes : les éléments proposés par Piero Sraffa ; les théorèmes de Sonnenchein-Mantel-Debreu ; et l'impossibilité de la théorie d'équilibre général pour expliquer tant la formation des prix, que la modélisation des économies monétaires. Enfin, la dernière partie de l'essai met brièvement en question si la théorie des jeux peut être considérée comme un débouché satisfaisant face aux défauts de la microéconomie traditionnelle.
Mots clés : équilibre général, équilibre partiel, théorie des jeux, Piero Sraffa, théorème de Sonnenchein-Mantel-Debreu
I. Introducción
A pesar de los múltiples avances y modificaciones que ha sufrido la teoría microeconómica convencional, sus dos modelos canónicos continúan siendo el de equilibrio parcial y el de equilibrio general. Contrario a lo que habitualmente se expone, existe abundante literatura que torna insatisfactorios ambos instrumentos analíticos. El presente ensayo intenta exponer algunos problemas de la teoría microeconómica dominante recuperando los trabajos que nos parecen contienen los componentes más esenciales de las críticas desarrolladas hacia ambos paradigmas. En este sentido, consideramos que presentar las principales debilidades y limitantes de la teoría microeconómica neoclásica utilizando los elementos desarrollados a lo largo de la historia del pensamiento económico es de importancia fundamental para el progreso no sólo de la microeconomía sino también de la ciencia económica en general.
Además de la presente introducción, el resto del ensayo se encuentra compuesto de la siguiente manera: en la sección II se aborda el equilibrio parcial concentrándose principalmente en la crítica realizada por Piero Sraffa; en la sección III se trata el equilibrio general haciendo énfasis en los resultados negativos derivados a partir de los Teoremas de Sonnenschein-Mantel-Debreu y en el escaso contenido de esta teoría al no poder ofrecer una explicación de la formación de precios ni la posibilidad de modelar economías monetarias sin entrar en dificultades; la sección IV expone brevemente si la teoría de juegos puede ser considerada una salida satisfactoria para los problemas de la teoría microeconómica convencional; y finalmente la sección V presenta las principales conclusiones.
II. Equilibrio parcial: eppur si muove
En el análisis microeconómico convencional de equilibrio parcial, las dos causas de valor (Marshall, 1890) en un mercado (industria) en particular son la oferta y la demanda, las cuales se construyen sobre el mismo principio de balance de motivaciones individuales y se consideran independientes una de la otra (Keen et al., 2001; Rosselli, 2005). Dicho en otras palabras, la oferta y la demanda son elementos simétricos (Rosselli, 2005), donde por simetría se entiende que ambas desempeñan el mismo papel en la determinación del precio y la cantidad de equilibrio en un mercado particular.
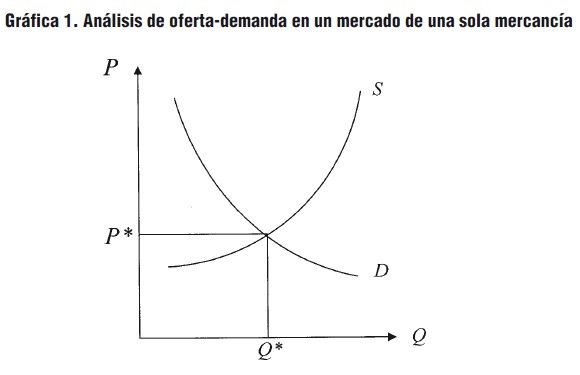
De esta forma, el modelo canónico de representación de un mercado de una sola mercancía en cuya producción interviene la existencia de un factor de producción fijo es el siguiente:
En la Gráfica 1, P denota precio y Q cantidad, S es la curva de oferta y D es la curva de demanda de mercado, mientras que P* y Q* representan, respectivamente, el precio y la cantidad de equilibrio (esto es, el precio y la cantidad que igualan la oferta y demanda del bien en el mercado).
En el esquema convencional representado en la Gráfica 1, la curva de demanda de mercado se construye a partir de la suma horizontal de las curvas de demanda de los consumidores individuales, mientras que la curva de oferta de mercado (ya sea en el corto o en el largo plazo) se deriva a partir de la suma horizontal de las curvas de oferta de las empresas individuales. La curva de oferta de una empresa individual es creciente debido a que las empresas se enfrentan a costos marginales crecientes pues en el corto plazo imperan los rendimientos decrecientes del factor de producción variable y, en el largo plazo, imperan los rendimientos decrecientes a escala.
Dejando de lado los problemas con la existencia de curvas de demanda y oferta en un mercado1 y con la teoría de la producción neoclásica (véase por ejemplo Keen, 2001; Lee y Keen, 2004; Keen y Standish, 2006), el defecto cardinal del análisis de precios y cantidades en un marco de equilibrio parcial es que éste es inadecuado para abordar el caso de industrias sujetas a costos variables (Maneschi, 1986); esto es, es inadecuado para abordar el caso de industrias cuyos costos varían con la cantidad producida. Esta fue la esencia de la crítica desarrollada por Sraffa (1925; 1926; 1930), la cual, pese haber generado un intenso debate en su momento junto con la "controversia de los costos"2, ha sido, en detrimento del avance de la ciencia económica, prácticamente olvidada (Keen et al., 2001). Así, el argumento toral de la crítica de Sraffa (1925; 1926) se refiere a que el supuesto de caeteris paribus (es decir, que la situación en el resto del sistema permanece constante) necesariamente se ve violado cuando los costos en las industrias son variables (Maneschi, 1986), y, por tanto, hace referencia a la imposibilidad del análisis parcial para poder lidiar adecuadamente con la interdependencia entre los costos de producción de los diferentes sectores (Panico, 1991; Panico y Salvadori, 1994).
Sraffa (1925) comienza por distinguir que los rendimientos crecientes y decrecientes se originan por causas distintas. Mientras que los rendimientos decrecientes (los cuales originan costos crecientes y, por tanto, curvas de oferta ascendentes) se deben principalmente a los cambios en las proporciones en que los insumos productivos se combinan en una industria determinada (es decir, cambios en los coeficientes técnicos de producción), los rendimientos crecientes (los cuales originan costos decrecientes y, por tanto, curvas de oferta descendentes) se asocian a cambios en la escala de actividad (esto es, cambios en el tamaño de la industria en cuestión) que permiten a los productores aprovechar nuevos métodos superiores de producción (Maneschi, 1986; Mongiovi, 1996). Una vez que se entiende esto, la derivación de las curvas de costos deja de ser una cuestión trivial o directa (Sraffa, 1925; Mongiovi, 1996). Por ejemplo, en una industria sujeta a rendimientos decrecientes, un incremento en la cantidad producida generará un incremento en los precios de los factores de producción utilizados (pues al aumentar la producción, aumenta también la demanda de éstos). Por tanto, para ser consistente con el supuesto de rendimientos decrecientes, el análisis de equilibrio parcial requiere postular que las condiciones de oferta y demanda de una mercancía deben ser consideradas independientes tanto entre sí como entre la oferta y la demanda de todos los otros bienes producidos en las otras industrias (Sraffa, 1926). En otras palabras, el análisis de equilibrio parcial requiere que los movimientos a lo largo de las curvas de oferta y demanda no ocasionen cambios o desplazamientos en sus posiciones (Mongiovi, 1996). Sraffa (1926) señaló que lo anterior resulta ser un supuesto ilegítimo ya que una variación en la cantidad producida por la industria analizada pone en movimiento una fuerza que actúa directamente no sólo sobre sus propios costos sino también sobre los costos de otras industrias, por lo que las condiciones requeridas para un análisis de precios-cantidades dentro de un marco de equilibrio parcial neoclásico necesariamente se ven perturbadas.
En lo que atañe a los rendimientos decrecientes (costos crecientes y, por tanto, curvas de oferta ascendentes), si una industria que produce una mercancía en particular incrementa su producción y si en la producción de la mercancía en cuestión se utiliza una parte sustancial de un factor de producción que es también utilizado en otras industrias y cuya oferta total se considera fija, entonces todas las demás industrias deberán explotarlo más intensamente. De esta forma, el costo de producción se incrementará no solamente en la industria que incrementó su producción sino también en todas las demás industrias que utilizan ese factor de producción para la producción de sus respectivas mercancías3. Además, dado que las mercancías producidas por las industrias que utilizan un mismo factor de producción son frecuentemente bienes sustitutos y complementarios y puesto que la demanda de cualquier mercancía depende del precio de todos los demás factores, entonces la modificación en el precio de la industria analizada generará un efecto sobre su respectiva demanda que no puede ser simplemente pasado por alto (Sraffa, 1926; Keen et al., 2001). Dicho en otras palabras, cualquier movimiento a lo largo de la curva de oferta de la industria estará asociado con cambios en los precios que causan que la curva de demanda de la misma industria cambie de pendiente en formas que no son obvias (Aslanbeigui y Naples, 1997). Debido a lo anterior, la curva de oferta en una industria no es independiente de su curva de demanda ni de las curvas de oferta y demanda de las demás industrias. Por tanto, para el caso de rendimientos decrecientes, el análisis de equilibrio parcial no podría ser utilizado más que en aquella clase ínfima de mercancías en cuya producción se emplea toda la cantidad existente de un factor de producción (Sraffa, 1926). Si, por el contrario, se supone que la industria en cuestión utiliza solamente una pequeña cantidad del factor de producción que es utilizado también por las demás industrias, entonces un ligero incremento en la producción por parte de la industria no generará un impacto perceptible en la intensidad del uso del factor de producción. Los costos de producción permanecerán sin cambios en todas las industrias en donde se utiliza el factor de producción, incluyendo la industria que incrementó su producción. Así, aunque las condiciones para la aplicación de un análisis de equilibrio parcial se sostienen para este último caso, lo anterior significa que las industrias operan con costos constantes y la demanda es irrelevante en la determinación del precio, contribuyendo únicamente en la determinación de la cantidad producida. Lo anterior conduce a concluir que los precios se determinan exclusivamente por el lado de la oferta, cuestión que había sido ya previamente enfatizada por los economistas clásicos y que puede representarse gráficamente como sigue:
Por tanto, la demoledora crítica presentada por Sraffa (1925; 1926; 1930) coloca al análisis basado en el equilibrio parcial con curvas de oferta ascendentes (rendimientos decrecientes) en un impasse: o éste es irrelevante (solamente útil para estudiar aquella clase de industrias donde se emplea la totalidad de la cantidad existente de un factor de producción) o es necesariamente contradictorio (porque la oferta y la demanda en una industria no son independientes entre sí ni entre la oferta y demanda de las demás industrias)4.
El argumento es similar en lo que concierne a los rendimientos crecientes (costos decrecientes y, por tanto, curvas de oferta descendentes). Para poder sostener la coherencia lógica del equilibrio parcial en este caso resulta necesario prescindir de las economías o deseconomías a escala internas a las empresas y de las economías o deseconomías a escala externas a la industria en cuestión (Sraffa, 1926)5. Dicho en otras palabras, el análisis de equilibrio parcial requiere de economías o deseconomías a escala que sean externas a las empresas pero internas a la industria, es decir, aquellas originadas por un cambio en la producción de la industria en cuestión pero que afectan únicamente a la función de costos de la empresa6 (Panico y Salvadori, 1994). Sin embargo, las economías que son externas desde el punto de vista de la empresa individual e internas para la industria en su conjunto constituyen una clase de economías a escala bastante infrecuente, tal y como el mismo Alfred Marshall se encargó de enfatizar (Sraffa, 1926). Por tanto, las curvas de oferta decrecientes son curvas de oferta cuya existencia es bastante improbable (Aslanbeigui y Naples, 1997) y, por tanto, el modelo general consistente con el equilibrio parcial debe partir del uso de curvas de oferta horizontales (Sraffa, 1926).
Resumiendo, se puede decir entonces que una variación en la cantidad producida en una industria sujeta a rendimientos crecientes o decrecientes provoca efectos colaterales similares en otras industrias relacionadas (Opocher, 2003), violando el caeteris paribus de la metodología del equilibrio parcial y, consecuentemente, las funciones de demanda de los factores de producción necesarias para la construcción de las curvas de costos marginales, las cuales a su vez construyen las curvas de oferta en los diferentes mercados (Lee y Keen, 2004). Por tanto, la interdependencia mutua entre las industrias es la principal fuente del problema del análisis parcial (Panico, 1991) puesto que es incorrecto enfatizar los efectos de las leyes de los rendimientos sobre una industria en particular mientras se ignoran los efectos de igual importancia sobre su propia curva de demanda y sobre el grupo de industrias relacionadas (Opocher, 2003).
III. Equilibrio general: la vacuidad como teorema de la teoría
Tanto la "controversia de los costos" iniciada en la década de 1920 como los escritos de Sraffa (1925; 1926; 1930) contribuyeron al abandono de las líneas de investigación basadas en el marco del equilibrio parcial. A partir de entonces la discusión se movió en tres principales direcciones (Blankenburg y Harcourt, 2007): la exploración del potencial de la teoría del equilibrio general (TEG en adelante); la alternativa de Sraffa (1960) sobre la teoría de los precios, la distribución y la reproducción del sistema capitalista; y las teorías endógenas de la innovación, crecimiento y desarrollo económico basadas en el principio de causalidad acumulativa (Nicholas Kaldor, Gunnar Myrdal y Joseph Schumpeter, entre otros). A pesar de no haber recibido demasiada atención en la década de 1930 y 1940, la microeconomía neoclásica se decidió por explorar intensamente la primera vía a partir de 1950.7 Los resultados obtenidos a partir de esta extensa investigación son considerados por muchos como el súmmum de la síntesis neoclásica y, para la teoría convencional, aparecen como la respuesta más desarrollada a las preguntas sobre el proceso y las condiciones de la coordinación mercantil de individuos descentralizados, fungiendo como el núcleo de un paradigma que, hasta la fecha, se utiliza como plataforma para pensar cualquier problema viejo o nuevo y como un marco para eventualmente absorber y discutir cualquier otra teoría (Ackerman, 2002; Cataño, 2004).
A) Los Teoremas de Sonnenshein-Mantel-Debreu y la naturaleza arbitraria de las funciones agregadas de exceso de demanda
A pesar de haber sufrido virajes y transformaciones, la TEG ha mantenido un paradigma invariante constituido en intentar demostrar tres resultados fundamentales (Ingrao e Israel, 1990): que existe un estado de compatibilidad de las acciones de los agentes económicos en un mercado competitivo, esto es, la existencia del equilibrio; que solo un estado de este tipo es posible, esto es, la unicidad del equilibrio; y que las "fuerzas del mercado" conducen inevitablemente hacia este estado de compatibilidad, esto es, la estabilidad del equilibrio.
La primera demostración rigurosa de los conceptos fundamentales de la TEG formulada por León Walras llegó con los trabajos de Arrow y Debreu (1954) y McKenzie (1954)8. Junto con estos trabajos, los elaborados por Debreu (1959) y el libro de Arrow y Hahn (1971) pueden ser considerados como las piedras angulares de la TEG. Utilizando los supuestos estándares sobre las dotaciones, las posibilidades de producción, las preferencias de los agentes económicos, y recurriendo al uso del teorema de punto fijo de Kakutani9, fue posible demostrar la existencia de un equilibrio general en una economía competitiva y que en él se cumplían los dos Teoremas Fundamentales de la Teoría del Bienestar: 1) todo equilibrio competitivo es un óptimo de Pareto (esto es, un estado en que ningún individuo puede mejorar su bienestar a menos que se empeore el bienestar de otro); y 2) todo óptimo de Pareto es un equilibrio de mercado para algún conjunto de condiciones iniciales.
Posteriormente a la demostración de existencia, la TEG parecía poseer un futuro prometedor para la resolución de los problemas por los que había sido convocada. Los siguientes pasos se dieron para intentar demostrar las dos propiedades faltantes: la unicidad, requerida para poder afirmar que a un conjunto de parámetros (técnicas, gustos y dotaciones) le correspondería uno y sólo un equilibrio (Cataño, 2004); y la estabilidad, necesaria puesto que, al ser un equilibrio estático, el equilibrio en una economía del tipo Arrow-Debreu-McKenzie sólo tiene sentido como punto de llegada de un proceso dinámico (Benetti, 1996). Los trabajos de Arrow y Hurwicz (1958), Arrow et al. (1959) y Arrow y Hahn (1971) abordaron conspicuamente el estudio de ambas propiedades. Siguiendo el segundo método de Lyapunov y utilizando restricciones bastantes fuertes destinadas específicamente a generar funciones agregadas de exceso de demanda con pendiente negativa tales como la sustituibilidad bruta (esto es, que a nivel agregado no existen mercancías complementarias y, por tanto, que el incremento en el precio de una mercancía no genera la disminución de la demanda de alguna otra), el cumplimiento del axioma débil de las preferencias reveladas (lo que implicaría que todos los agentes poseen las mismas preferencias) y la dominancia diagonal (véase Arrow y Hahn, 1971), fue posible demostrar la unicidad y la estabilidad global del ajuste de precios mediante el tanteo Walrasiano10.
A pesar de ser plenamente conscientes de que las restricciones para la demostración de unicidad y estabilidad eran bastantes restrictivas, se tenía la confianza de que posteriores trabajos podrían traer resultados más satisfactorios. Sin embargo, los resultados negativos no tardaron en aparecer. Aunque Scarf (1960) ya había presentado un contraejemplo de una economía de intercambio (sin comportamientos patológicos de los consumidores) en la que el sistema no era estable, los resultados totalmente negativos arribaron con los trabajos de Sonnenshein (1972; 1973) y las generalizaciones de Mantel (1974) y Debreu (1974). Los resultados derivados a partir de estos trabajos se conocen como los Teoremas de Sonnenshein-Mantel-Debreu (TSMD en adelante) y su esencia puede ser sintetizada de la siguiente manera (Ingrao e Israel, 1990; Rizvi, 1994b; 2003; 2006; Ackerman, 2002; Cataño, 2004; Hands, 2008): las únicas restricciones que la disponibilidad de axiomas bien comportados a nivel individual imponen a las funciones agregadas de exceso de demanda derivadas a partir de los modelos formalistas Walrasianos de equilibrio general son las propiedades de continuidad; homogeneidad de grado cero en precios (lo cual se traduce en que los únicos precios relevantes son los precios relativos); la Ley de Walras (es decir, para la economía en su conjunto se satisface la restricción presupuestaria)11; y la condición límite de la demanda (la cual garantiza que a medida que los precios se aproximan a cero la cantidad demanda se incrementa). Lo anterior es un resultado profundamente negativo pues el corolario es que casi cualquier función continua valuada en números reales puede ser una función de exceso de demanda, lo que torna extremadamente sencillo, en primer lugar, generar economías Walrasianas con equilibrios múltiples o no únicos12 (Rizvi, 2006; Cataño, 2004; Hands, 2008), y, en segundo lugar, que casi cualquier patrón de variación de precios pueda aparecer (por ejemplo, ciclos de cualquier duración, caos, etc.), lo que indica que el equilibrio general no solamente falla en ser estable sino que su dinámica puede ser tan mala como se desee (Ackerman, 2002; Cataño, 2004).
Dicho en otras palabras, los TSMD demuestran que las funciones agregadas de exceso de demanda de los mercados derivadas a partir de la agregación de las funciones de demanda de los agentes individuales poseen propiedades útiles y directas con las cuales es posible demostrar la existencia de un equilibrio (continuidad, homogeneidad de grado cero en precios, Ley de Walras, y la condición límite); sin embargo, las funciones agregadas de exceso de demanda no poseen propiedades adicionales que garanticen que éstas posean pendiente negativa (esto es, que sean bien comportadas) y, por tanto, la conclusión directa es que su naturaleza es esencialmente arbitraria. Ergo, no existe posibilidad alguna de demostrar ni unicidad (lo que implicaría que uno de los puntos de equilibrio posibles podría ser socialmente más deseable que otro y que el proceso de ajuste de mercado podría con-verger hacia el equivocado) ni estabilidad del equilibrio (lo que implicaría que algún punto de equilibrio podría nunca alcanzarse, o bien que, aún si fuese alcanzado, la economía no se mantendría en él cuando fuera sacudida por pequeños eventos) dentro de un marco de equilibrio general a menos que se recurra al uso de supuestos bastante restrictivos (por ejemplo, la sustituibilidad bruta para la demostración de la unicidad del equilibrio; o bien, que se suponga directamente que a nivel agregado se satisface el axioma débil de las preferencias reveladas para garantizar la estabilidad) que actúan directamente para generar funciones agregadas de exceso de demanda bien comportadas (es decir, con pendiente negativa) y que, por tanto, limitan seriamente su alcance como teoría general13.
Con lo anterior se pone no solo en tela de juicio la posibilidad de realizar análisis de estática comparativa ya que nada garantizaría que una desviación con relación al equilibrio irá seguida de una convergencia hacia un nuevo punto de equilibrio (Ackerman, 2002; Cataño, 2004), sino también que la era de los microfundamentos estrictos de fenómenos agregados ha llegado a su fin ya que la hipótesis de racionalidad individual y los otros supuestos realizados a nivel micro no ofrecen guía alguna al fenómeno macro, lo que significa que el supuesto de racionalidad o de la maximización de utilidades no es suficiente para hablar de regularidades sociales agregadas (véase Rizvi, 1994b; 1998; 2003).
Por tanto, los TSMD demostraron que la formalización del equilibrio general había arribado a un callejón sin salida: además de la existencia de equilibrio general, no era posible la obtención de algún otro resultado general14. Lo anterior representa probablemente el resultado negativo más importante dentro de la economía convencional desde las controversias del capital y el teorema de la imposibilidad de Arrow (Rizvi, 1994b).
B) Formación de precios y economías monetarias: dos problemas adicionales en la Teoría del Equilibrio General
Adicionalmente a los TSMD, la TEG posee dos dificultades adicionales:
No ofrece una teoría de la formación de precios (Benetti, 1990; 1998; Benetti, et al., 2004; Cataño, 2004). En la TEG las fuerzas de la oferta y de la demanda son impotentes de formar precios de manera endógena pues necesariamente se debe recurrir a la decisión arbitraria de una voluntad externa al mercado, esto es, la presencia del subastador. Aun suponiendo que se logre demostrar la estabilidad y la unicidad del equilibrio (como hemos visto, bajo condiciones bastante restrictivas), la trayectoria que conduciría a éste sería arbitraria en el sentido de que no sería generada por el mercado sino por la voluntad del subastador, es decir, la voluntad de un ente externo. Recientemente, Benetti et al. (2004) han afirmado que las transformaciones utilizadas en los modelos de equilibrio general para demostrar la existencia de un equilibrio son matemáticamente convenientes pero carentes de significado económico ya que no corresponden a un proceso de variación de precios plausible pues no expresan la ley de la oferta y la demanda. En consecuencia, la demostración de la existencia del equilibrio general no dice algo sobre el sistema socio-económico al que pertenece y, por tanto, resultaría abusivo designarlo como el equilibrio competitivo de una sociedad comercial pura de individuos que actúan descentralizadamente (Benetti, 1990; 1998; Cataño, 2004)15.
La TEG no aborda la existencia de economías monetarias (Benetti, 1990; 1996; 1998; Benetti y Cartelier, 1998; Itoh y Lapavitsas, 1999). Dado el vector de precios de equilibrio, las asignaciones óptimas de consumo (es decir, un vector de planes de consumo) y de recursos (es decir, un vector de planes de producción) se deben realizar por medio de transacciones entre agentes, de tal manera que se hagan efectivos los gastos de los presupuestos de hogares y empresas y la adquisición de las asignaciones óptimas utilizando el intercambio mercantil (Cataño, 2004). Esto se puede realizar mediante dos formas:
a) Como lo hace Debreu (1959) al incluir una Caja de Compensación de Pagos para garantizar la ausencia de costos de transacción y, por tanto, no ofreciendo teoría del dinero alguna y suponiendo que la economía funciona sin la ayuda de un bien que sea utilizado como medio de cambio.
b) Se integra el dinero en el modelo central como un bien adicional que los agentes adoptan voluntariamente como medio de cambio común; es decir, el dinero se piensa a partir de la teoría de la elección y no como una regla social impuesta a los individuos comerciantes (Hahn, 1982). Así, el dinero se introduce mediante una función de utilidad, es decir, atribuyendo a la moneda una utilidad intrínseca al igual que los demás bienes (Benetti, 1996).
Si se quiere obtener una teoría monetaria es claro que el único método posible es el expuesto en b). Sin embargo, el problema monetario en este modelo consiste en ofrecer una explicación del valor del dinero (es decir, el dinero debe poseer alguna propiedad especial relativa a todos los otros bienes) ya que, en un modelo con horizonte finito (tal y como las economías del tipo Arrow-Debreu-McKenzie), el dinero nunca puede ser elegido como reserva de valor (Benetti, 1990; 1996; Benetti y Cartelier, 1998)16. Hahn (1982) propuso una salida al afirmar que el dinero reduce los costos de transacción del intercambio: el dinero compra bienes más barato que lo que los bienes compran bienes, es decir, combinando el intercambio secuencial con la minimización de los costos (Kiyotaki y Wright, 1989). Sin embargo, tal y como Hahn (1982) posteriormente admite, la teoría del equilibrio general no posee una forma fundamental para explicar cómo las transacciones son generadas dentro del proceso de cambio por sí mismo, y por tanto, no existe una forma analíticamente satisfactoria de mostrar porque existe la aceptabilidad general del dinero. Lo más que se puede demostrar es que, si todo mundo acepta el dinero, los agentes que utilizan dinero pueden adquirir bienes más barato que los agentes que intercambian bienes por bienes. Lo anterior resulta ser un razonamiento circular: ¿Por qué el dinero es especial? Simplemente porque es dinero (Itoh y Lapavitsas, 1999).
Como la presente sección ha intentado mostrar, mientras que los TSMD socavan gravemente las bases de la TEG al exponer la naturaleza arbitraria de las funciones agregadas de exceso de demanda de los mercados, tanto la ausencia de una teoría de la formación de precios como la imposibilidad de modelar una economía monetaria reducen profundamente la capacidad explicativa de la TEG al no poder describir un sistema que funciona a través del mecanismo de precios y mediante un bien que sea utilizado como medio de cambio, es decir, la descripción de lo que es el propio sistema capitalista. Así, el aforismo de Christopher Bliss no parece ser una conclusión disparatada: "La cercana vacuidad de la teoría del equilibrio general es un teorema de la teoría" (citado por Rizvi, 2003: 385; traducción nuestra).
IV. La teoría de juegos: ¿una salida satisfactoria?
Después del callejón sin salida al que las teorías del equilibrio parcial y general arribaron, la teoría de juegos se ha convertido en la herramienta predilecta de los desarrollos teóricos en microeconomía. Casi setenta años después de la aparición del seminal libro de John von Neumann y Oskar Morgenstern (Theory of Games and Economic Behavior), el tipo de juegos no cooperativos (esto es, equilibrios de Nash, juegos racionales, estrategias mixtas y juegos repetidos) es el que más ha proliferado en las aplicaciones económicas (Rizvi, 1994a).
Posiblemente uno de los principales alicientes del auge de la teoría de juegos es que, de esta manera, la teoría microeconómica convencional actual ha dejado de preocuparse por encontrar explicaciones para los temas de la formación de precios, la producción de bienes, la distribución del ingreso, etc.; es decir, ha dejado de preocuparse por la búsqueda de teorías generales que incluyan las actividades que son el objeto de investigación de la ciencia económica. En este sentido, las aplicaciones contemporáneas de la teoría de juegos sirven únicamente como ejemplos muy particulares y no pueden ser caracterizadas como un enfoque general a los problemas económicos (Fisher, 1989; Rizvi, 1994a). Por tanto, en primer lugar, se tiene que las aplicaciones de la teoría de juegos son incapaces de proveer el enfoque unificado que caracteriza a las teorías exitosas (Rizvi, 1994a).
En segundo lugar, parece ser que la teoría de juegos se interesa casi exclusivamente en la dificultad de caracterizar al comportamiento racional humano, lo cual es útil para admirar la gran habilidad formal y complejidad matemática que impregna los modelos pero es de escasa utilidad en la resolución de problemas económicos concretos (Guerrien, 2004). Como el propio Rubinstein (2001) ha expresado, la teoría de juegos es un tema fascinante y abstracto, que se encuentra más cerca de la filosofía que de las páginas económicas de los periódicos.
Finalmente, ignorando algunos problemas fundamentales derivados de los juegos no cooperativos (Rizvi, 1994a; Guerrien, 2004; Guerrien, 2007) y aun suponiendo que es posible alcanzar algún resultado preciso en un modelo construido dentro de este marco, el resultado obtenido dependerá de una gran cantidad de detalles aparentemente irrelevantes: "[a]sí, si un modelo se propone demostrar x, aún cuando puede esperarse que esta conclusión sea única, otro modelo puede ser construido que demuestre algo diferente de x simplemente haciendo lo que deberían ser considerados cambios inconsecuentes: cambiando el orden del juego, el concepto preciso de solución, el número de jugadores, el valor de la tasa de descuento, etc." (Rizvi, 1994a: 24; traducción nuestra). La explicación más inmediata de la arbitrariedad de los resultados obtenidos a partir de la teoría de juegos es que el análisis no puede moverse más allá de este pantano pues la teoría de juegos no constituye una teoría general y, por tanto, se limita más bien a ser una abstracción estéril para el estudio de la realidad económica.
Ergo, la teoría de juegos no se encuentra exenta de problemas fundamentales en su interior (Rizvi, 1994a; Guerrien, 2004; Guerrien, 2007), parece poseer escaso interés en la resolución de problemas económicos concretos (Guerrien, 2004) y parece poseer problemas de arbitrariedad en sus resultados (Rizvi, 1994a) pues no constituye un marco unificador necesario para poder ser considerada una teoría general exitosa. Puesto que la construcción de modelos no conoce límites (Rizvi, 1994a), hoy en día los economistas han tendido a ignorar los fundamentos conceptuales y se han concentrado en buscar aplicaciones, lo cual es muy útil para publicar modelos en top journals, pero de escasa utilidad para elaborar teorías generales que logren explicar los hechos estilizados, visibles y cuantificables de las economías capitalistas.
IV. Conclusiones
El estado actual de la teoría microeconómica convencional es una mezcla de pluralismo con una buena cantidad de confusión (Rizvi, 2003) que se torna todavía más manifiesto en el contenido de los libros de texto actuales y en el auge de la teoría de juegos. Muy pocas de sus partes inquietantes han podido ser rigurosamente eliminadas, sobre todo si consideramos que estas partes inquietantes son sus dos elementos centrales: el equilibrio parcial y el equilibrio general. Mientras que el panorama para el equilibrio parcial parece ser bastante lúgubre a la luz de los elementos aportados por Piero Sraffa, el viraje sufrido hacia el equilibrio general no parece haber sido exitoso debido a que los Teoremas de Sonnenshein-Mantel-Debreu y la imposibilidad de poder ofrecer una explicación de la formación de precios y de modelar economías monetarias dentro de este enfoque sin entrar en problemas otorgan un valor casi anecdótico a tal teoría. El nuevo cambio encaminado hacia la teoría de juegos tampoco puede ser considerado como una vía alterna satisfactoria debido principalmente a los problemas de arbitrariedad en sus resultados, a que no se encuentra exenta de problemas en su interior, y a que parece poseer escaso interés en la resolución de problemas económicos concretos.
El presente ensayo ha intentado mostrar que es un error tajante considerar que los paradigmas microeconómicos convencionales gozan de un estado de buena salud. En este sentido, siguiendo a Lee y Keen (2004) se puede decir que la teoría microeconómica convencional no debe ser desestimada porque sus herramientas y modelos carecen de realismo o por el uso de lenguaje matemático abstruso. Respecto a lo primero podemos decir que lo relevante no es una cuestión del grado de realismo existente, sino una cuestión de si tales proposiciones son o no consistentes internamente; respecto a lo segundo podemos decir que el lenguaje matemático permanece neutral en lo que concierne a las herramientas teóricas y modelos. De esta manera, la explicación de los resultados insatisfactorios por parte de la teoría microeconómica convencional no reside en su excesiva abstracción o formalización matemática, sus defectos cardinales se encuentran en las propias bases sobre los que han sido construidos que desembocan irremediablemente en las profundas inconsistencias e incoherencias internas que se han intentado mostrar.
La teoría microeconómica neoclásica no parece ser el único ni el mejor método que se tiene para modelar la realidad económica, en su estado actual no puede ser acogida como la mejor descripción de la forma del funcionamiento de los mercados y, por tanto, no puede ser considerada como una teoría satisfactoria que aporte elementos útiles para pronosticar la evolución de las economías. En este lúgubre panorama resulta necesaria la seria reconsideración de teorías heterodoxas que posiblemente sean más apropiadas para elaborar descripciones menos limitadas de los fenómenos económicos observables.
1. Un tratamiento de las condiciones que garantizan la existencia de curvas de demanda y oferta en los mercados individuales excede los propósitos del presente ensayo. Sin embargo, es posible afirmar que no existe razón alguna para presuponer la existencia per se de curvas de oferta y demanda puesto que para su existencia se requieren condiciones muy específicas de agregación individual que no pueden ser simplemente soslayadas (véase Keen, 2001 y Lee y Keen, 2004, además de la amplia bibliografía que allí se refiere).
2. La así llamada "controversia de los costos" se inicia con Clapham (1922), quien señala que las leyes de los rendimientos representan un aparato lógico/teórico desprovisto de cualquier contenido empírico, precisión o claridad (Aslanbeigui y Naples, 1997; Huerta Quintanilla, 2001). Para una buena síntesis de este importante debate del que hoy en día poco se habla véanse los trabajos de Aslanbeigui y Naples (1997) y Blackenburg y Harcourt (2007).
3. El grado de variación en los costos de cualquier industria dependerá de que tan intensamente la industria en cuestión utilice el factor de producción que es compartido.
4. Las críticas de Sraffa (1925; 1926) provocaron dos reacciones diferentes. Por una parte, Pigou (1927, 1928) argumentó que las curvas de costos de largo plazo de las empresas y de las industrias eran en forma de L: los costos declinaban hasta que alcanzaban el rango horizontal. Nuevamente, este camino sugería un regreso a la visión clásica de que el precio era determinado por el lado de la oferta de la economía y adicionalmente dejaba indeterminado el tamaño de la empresa debido a que curvas de costos constantes conducen a competencia monopolística u oligopólica (Aslanbeigui y Naples, 1997). Por otra parte, la síntesis de Stigler (1942) sobre el debate encontraba que el producto creciente de la industria en cuestión incrementaba los precios de los factores de producción y por tanto conducía a la existencia de curvas de oferta crecientes en las industrias. Este argumento deja entonces intacta la crítica de Sraffa (1925; 1926): la demanda y la oferta de una mercancía en una industria son interdependientes (Aslanbeigui y Naples, 1997).
5. En su Industry and Trade, Alfred Marshall explica que las economías a escala internas son aquellas determinadas por la producción de amplia escala, que, a su vez, es consecuencia del incremento en el tamaño de las empresas. La producción de amplia escala hace posible la aplicación de nuevos métodos y la introducción de nueva maquinaria. Por su parte, las economías a escala externas son aquellas resultantes de la concentración de industrias especializadas en localidades particulares. Estas economías no dependen necesariamente del tamaño de las empresas individuales sino que son un caso especial resultante del desarrollo de la economía en su conjunto (Sylos-Labini, 1990).
6. Si las economías (deseconomías) a escala fuesen internas a la empresa, ésta última se vería alentada a expandir (contraer) su nivel de actividad, transformándose eventualmente en un monopolio u oligopolio. Si, por otro lado, las economías o deseconomías fuesen externas a la industria, nuevamente se violarían las condiciones de caeteris paribus ya que, como el mismo Marshall expresó, éstas se encuentran ligadas (correlacionadas) a (con) amplios grupos de industrias, por lo que su introducción requeriría de un cambio considerable en la producción de la mercancía, lo cual nuevamente violaría las condiciones del equilibrio parcial (Maneschi, 1986).
7. Como es bien sabido, el marco del equilibrio general ya había sido abordado desde 1874 por León Walras en sus Éléments d'économie politique pure y por los teóricos del Coloquio de Viena alrededor de 1930. De hecho, las matemáticas utilizadas por los teóricos del equilibrio general (Kenneth Arrow, Gérard Debreu, Tjalling Koopmans, Lionel McKenzie, etc.) fundamentadas en la topología (esto es, en el estudio abstracto de los conceptos de vecindad y continuidad) y en los teoremas de punto fijo se asemejan más a las técnicas de los economistas del Coloquio de Viena que a los métodos del cálculo infinitesimal propuestos por John Hicks y Paul Samuelson (Rizvi, 2003).
8. El trabajo de McKenzie (1954) presenta un teorema de la existencia de un equilibrio general competitivo para el modelo de comercio internacional de Graham. A pesar de las similitudes que guarda con el trabajo de Arrow y Debreu (1954), el contexto y algunas otras características hacen que las comparaciones entre ambos trabajos no sean del todo precisas (Ingrao e Israel, 1990).
9. De forma un tanto imprecisa, un teorema de punto fijo establece la hipótesis bajo la cual una transformación f de un conjunto X en sí mismo (esto es, f:X→X) posee al menos un "punto fijo"; es decir, la hipótesis bajo la cual existe un punto x que pertenece al conjunto X (esto es, x: x∈X) tal que f(x)=x. Así, la demostración del equilibrio general se consiguió transformando el problema de la búsqueda de soluciones en un sistema de ecuaciones en el problema de la búsqueda de un punto fijo (Ingrao e Israel, 1990). El primer teorema desarrollado en la topología fue el de Brouwer, el cual fue posteriormente fue generalizado por Kakutani (véase Nikaido, 1989 e Ingrao e Israel, 1990 para una exposición más extensa del tema).
10. El tâtonnement Walrasiano es un mecanismo de ajuste de precios en el que la tasa de variación del precio de cualquier mercancía es proporcional al exceso de demanda de ésta; véase al respecto Ingrao e Israel (1990) y Fisher (1996).
11. La Ley de Walras es una expresión de la interdependencia de las ecuaciones de exceso de demanda derivadas de las restricciones presupuestarias de los agentes económicos y cuya utilidad directa estriba en que si n mercados se encuentran en equilibrio y el n-ésimo mercado restante posee un precio positivo, entonces éste último se encontrará también en equilibrio. Para una exposición más completa véase Patinkin (1983).
12. Posiblemente el mayor avance que se puede encontrar respecto a la unicidad del sistema es el inaugurado con el trabajo de Debreu (1976), en donde se cambia el concepto de economías con equilibrio único por el de "economías regulares". Éstas últimas son caracterizadas principalmente por la posesión de un conjunto discreto de equilibrio, es decir, un número de equilibrios virtualmente finito. Por tanto, lo más que se puede decir respecto al problema de unicidad es que el número de equilibrios es finito (Ingrao e Israel, 1990; Ackerman, 2002).
13. Los TSMD se han visto todavía más reforzados en fechas recientes. En lo que concierne a la unicidad, los trabajos de Mas-Colell (1977) y Kehoe (1985) muestran, respectivamente, que para cualquier economía bien comportada la arbitrariedad de las funciones agregadas de exceso de demanda implica la arbitrariedad de los precios de equilibrio, y que las condiciones que implican la unicidad del equilibrio son demasiado restrictivas para ser económicamente interpretables. Por otra parte, respecto a la estabilidad, Kirman y Koch (1986) demuestran que, mientras que el número de niveles de ingreso sea al menos tan grande como el número de mercancías, virtualmente cualquier dinámica continua de precios puede ocurrir aunque los individuos posean preferencias idénticas y una distribución del ingreso sea escogida arbitrariamente. Finalmente, el "Teorema de la Imposibilidad de Saari" (Saari, 1996; Cataño, 2004) muestra que aún si existiera un sistema estable de n mercancías, al aumentar a n+1 el número de mercancías nada garantiza que esa estabilidad se conserve, por lo que los resultados dinámicos probados para modelos pequeños de equilibrio general no se aplican para otros más grandes.
14. Es posible construir ejemplos especiales que conducen a la unicidad y estabilidad sobre la existencia de preferencias que generan tales propiedades. Sin embargo, esto implicaría reducir el modelo a un ejemplo particular (Kirman, 1989), es decir, referirse a casos particulares más pequeños (ejemplos) de una teoría más general existente (Rizvi, 1994b).
15. Nótese que el señalamiento de Cataño (2004) resulta ser muy pertinente: si lo único que queda es la demostración de la existencia de un equilibrio, nada impide, en principio, que ese equilibrio también pueda ser asociado a una economía del tipo planificada o socialista.
16. En efecto, la modelación de una economía monetaria requiere que exista intercambio a diario (Itoh y Lapavitsas, 1999) y el modelo debería ser entonces uno del tipo de una secuencia y no del tipo de una economía Walrasiana en el que las transacciones se completan en un punto en el tiempo una vez que se ha alcanzado el equilibrio.
Referencias Bibliográficas
Ackerman, F. (2002), "Still dead after all these years: interpreting the failure of general equilibrium theory", Journal of Economic Methodology, 9 (2): 119-139.
Arrow, K. y Debreu, G. (1954), "Existence of an equilibrium for a competitive economy", Econometrica, 22 (3): 265-290.
Arrow, K. y Hahn, F. (1971), General Competitive Analysis, San Francisco, Holden-Day.
Arrow, K. y Hurwicz, L. (1958), "On the stability of the competitive equilibrium, I", Econometrica, 26 (4): 522-552.
Arrow, K., Block, H. y Hurwicz, L. (1959), "On the stability of the competitive equilibrium, II", Econometrica, 27 (1): 82-109.
Aslanbeigui, N. y Naples, M. (1997), "Scissors or horizon: neoclassical debates about returns to scale, costs and long-run supply", Southern Economic Journal, 64 (2): 517-530.
Benetti, C. (1990), Moneda y Teoría del Valor, México, UAM-Fondo de Cultura Económica.
_________ (1996), "La teoría del desequilibrio: una crítica y una propuesta", en Ortiz, E. (ed.), Teoría de los Precios, México, UAM: 263-290.
_________ (1998), "El método normativo de la teoría económica positiva", Cuadernos de Economía, XVII (26): 53-70.
Benetti, C. y Cartelier, J. (1998), "Dinero, forma y determinación del valor", Cuadernos de Economía, XVII (28): 53-70.
Benetti, C., Nadal, A. y Salas, C. (2004), "The Law of Supply and Demand in the Proof of Existence of General Competitive Equilibrium", en Ackerman, F., Nadal, A. y Gallagher, K., The Flawed Foundations of General Equilibrium: Critical Essays in Economic Theory, Londres, Routledge: 79-99.
Blankenburg, S. y Harcourt, G. (2007), "The debates on the representative firm and increasing returns: then and now", en Arestis, P., Baddeley, M. y McCombie, J. (eds.), Economic Growth: New Directions in Theory and Policy, Cheltenham, Edward Elgar: 44-64.
Cataño, J. (2004), "La teoría neoclásica del equilibrio general: apuntes críticos", Cuadernos de Economía, XXIII (40): 175-204.
Clapham, J. (1922), "Of Empty Economic Boxes", The Economic Journal, 32 (127): 305-314.
Debreu, G. (1959), Theory of Value, New Haven, Cowles Foundation.
_________ (1974), "Excess demand functions", Journal of Mathematical Economics, 1 (1), Elsevier: 15-21
_________ (1976), "Regular Differentiable Economies", The American Economic Review, 66 (2): 280-287.
Fisher, F. (1989), "Games economists play: a noncooperative view", The RAND Journal of Economics, 20 (1): 113-124.
_________ (1996), "La formación de las magnitudes económicas: desequilibrio e inestabilidad", en Ortiz, E. (ed.), Teoría de los Precios, México, Unidad Xochimilco-UAM: 187-225.
Guerrien, B. (2004), "Can We Expect Anything from Game Theory?", en Fullbrook, E. (ed.), A Guide to What's Wrong with Economics, Londres, Anthem Press, 2004b, 198-208.
__________ (2007), "El talón de Aquiles de la teoría de juegos", Economía Informa, 345: 238-245.
Hahn, F. (1982), Money and Inflation, Oxford, Blackwell.
Hands, W. (2008), "What a Difference a Sum Makes: Agony and Ecstasy in the Rationalization of Demand", Social Science Research Network, Working Paper Series.
Huerta Quintanilla, R. (2001), "De nuevo los rendimientos decrecientes", Aportes, 18: 73-90.
Ingrao, B. e Israel, G. (1990), The Invisible Hand. Economic Equilibrium in the History of Science, Palatino, MIT Press.
Itoh, M. y Lapavitsas, C. (1999), Political Economy of Money and Finance, Londres, Macmillan Press.
Keen, S. (2001), Debunking Economics: The Naked Emperor of the Social Sciences, Nueva York, St. Martin´s Press.
Keen, S., Legge, J. y Fishburn, G. (2001), "A 75th Anniversary Present for Sraffa", mimeo.
Keen, S. y Standish, R. (2006), "Profit maximation, industry structure and competition: A critique of neoclassical theory", Physica A, 370 (1): 81-85.
Kehoe, T. (1985), "Multiplicity of Equilibria and Comparative Statics", The Quarterly Journal of Economics, 100 (1): 119-147.
Kirman, A. y Koch, K. (1986), "Market excess demand in exchange economies with identical preferences and collinear endowments", The Review of Economic Studies, 53 (3): 457-463.
Kirman, A. (1989), "The intrinsic limits of modern economic theory: the emperor has no clothes", The Economic Journal, 99 (395): 126-139.
Kiyotaki, N. y Wright, R. (1989), "On Money as a Medium of Exchange", The Journal of Political Economy, 97 (4): 927-954.
Lee, F. y Keen, S. (2004), "The Incoherent Emperor: A Heterodox Critique of Neoclassical Microeconomic Theory", Review of Social Economy, LXII (2): 169-199.
Maneschi, A. (1986), "A comparative evaluation of Sraffa´s `The laws of returns under competitive conditions´ and its Italian precursor", Cambridge Journal of Economics, 10 (1): 1-12.
Mantel, R. (1974), "On the characterization of aggregate excess demand", Journal of Economic Theory, 7 (3): 348-353.
Marshall, A. (1890) [1966], Principles of Economics, Londres, Macmillan Press.
Mas-Colell, A. (1977), "On the equilibrium price set of a pure exchange economy", Journal of Mathematical Economics, 4 (2): 117-126.
McKenzie, J. (1954), "On Equilibrium in Graham´s Model of World Trade and Other Competitive Systems", Econometrica, 22 (2): 54-71.
Mongiovi, G. (1996), "Sraffa´s critique of Marshall: a reassessment", Cambridge Journal of Economics, 20 (2): 207-224.
Nikaido, H. (1989), "Fixed point theorems", en Eatwell, J., Milgate, M. y Newman, P. (eds.), The New Palgrave: General Equilibrium, Londres, Macmillan Press: 139-144.
Opocher, A. (2003), "`Interrelated prices´ and Sraffa´s critique of partial equilibrium", The European Journal of the History of Economic Thought, 10 (3): 479-496.
Panico, C. (1991), "Some notes on Marshallian supply functions", The Economic Journal, 101 (46): 557-569.
Panico, C. y Salvadori, N. (1994), "Sraffa, Marshall and the problem of returns", The European Journal of the History of Economic Thought, 1 (2): 323-343.
Patinkin, D. (1983) [1989], "Walras´s Law", en Eatwell, J., Milgate, M. y Newman, P. (ed.), The New Palgrave: General Equilibrium, Londres, Macmillan Press: 328-339.
Pigou, A. (1927), "The laws of diminishing and increasing cost", The Economic Journal, 37 (146): 188-197.
________ (1928), "An analysis of supply", The Economic Journal, 38 (150): 238-257.
Rizvi, A. (1994a), "Game theory to the rescue?", Contributions to Political Economy, 13(1): 1-28.
_______ (1994b), "The microfoundations project in general equilibrium theory", Cambridge Journal of Economics, 18 (4): 357-377.
_______ (1998), "Responses to Arbitrariness in Contemporary Economics", en Davis, J. (ed.), New Economics and its History, Durham, Duke University Press: 273-288.
_______ (2003), "Postwar Neoclassical Microeconomics", en Samuels, W., Biddle, J. y Davis, J. (eds.), A Companion to the History of Economic Thought, Cornwall, Blackwell: 377-394.
_______ (2006), "The Sonnenschein-Mantel-Debreu Results after Thirty Years", History of Political Economy, 38 (1): 228-245.
Rosselli, A. (2005), "Sraffa and the Marshallian Tradition", The European Journal of the History of Economic Thought, 12 (3): 403-423.
Rubinstein, A. (2001), "A theorist's view of experiments", European Economic Review, 45 (4-6): 615-628.
Saari, D. (1996), "The ease of generating chaotic behavior in economics", Chaos, Solutions and Fractals, 7 (12): 2267-2278.
Scarf, H. (1960), "Some Examples of Global Instability of the Competitive Equilibrium", International Economic Review, 1 (3): 157-172.
Sonnenschein, H. (1972), "Market excess demand functions", Econometrica, 40 (2): 549-563.
________________ (1973), "Do Walras identity and continuity characterize the class of community excess demand functions?", Journal of Economic Theory, 6 (4): 345-354.
Sraffa, P. (1925) [1928], "On the Relations Between Cost and Quantity Produced", en Pasinetti, L. (ed.), Italian Economic Papers, vol. 3, Oxford, Oxford University Press: 323-363.
________ (1926), "The Laws of Return under Competitive Conditions", The Economic Journal, 36 (144): 535-550.
________ (1930), "Symposium on `Increasing returns and the representative firm`. A criticism and reply", The Economic Journal, 40 (157): 89-93.
________ (1960), Production of Commodities by Means of Commodities, Cambridge, Cambridge University Press.
Stigler, G. (1942), The Theory of Competitive Price, Nueva York, Macmillan.
Sylos-Labini, P. (1990), "Sraffa´s Critique of the Marshallian Theory of Prices", en Bharadwaj, K. y Schefold, B. (eds.), Essays on Piero Sraffa: Critical Perspectives on the Revival of Classical Theory, Londres, Unwin Hyman: 3-19.
Cómo citar
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Descargar cita
Visitas a la página del resumen del artículo
Descargas
Licencia
Derechos de autor 2012 Ensayos de Economía

Esta obra está bajo una licencia internacional Creative Commons Atribución-NoComercial-SinDerivadas 4.0.
Se autoriza la reproducción sin ánimo de lucro de los materiales, citando la fuente.