Published
Prediction of financial crises by means of rough sets and decision trees
Keywords:
crisis financieras, inteligencia artificial, rough sets, árboles de decisión, C4.5. (es)Downloads
influyen en la aparición de crisis financieras. Utilizando una
amplia muestra de datos de países entre 1981 y 1999, se aplican
dos metodologías del campo de la Inteligencia Artificial (la
teoría Rough Set y el algoritmo C4.5) para analizar el papel de
un conjunto de variables macroeconómicas y financieras (tanto
de tipo cualitativo como de tipo cuantitativo) en la explicación
de las crisis bancarias. Estos métodos no requieren que las variables
o los datos utilizados satisfagan ningún tipo de hipótesis,
al contrario que las técnicas estadísticas empleadas tradicionalmente,
que presentan el inconveniente de que parten de hipótesis
acerca de las propiedades distribucionales de las variables
explicativas que no se suelen cumplir, lo que dificulta el análisis.
Se han obtenido muy buenos resultados en términos de acierto
en la clasificación (80% de clasificaciones correctas sobre una
muestra independiente), lo que demuestra la precisión de ambos
métodos.
Zuleyka Díaz-Martínez*, Alicia Sánchez-Arellano** & Maria Jesús Segovia-Vargas***
* Department of Financial Economics and Accounting I, Universidad Complutense de Madrid, Spain. Correo electrónico: zuleyka@ccee.ucm.es
** Banco de España. Madrid, Spain. Correo electrónico: asanchis@bde.es
*** Department of Financial Economics and Accounting I, Universidad Complutense de Madrid, Spain. Correo electrónico: mjsegovia@ccee.ucm.es
Recibido: octubre de 2009 Aprobado: septiembre de 2010
Abstract:
This paper tries to further investigate the factors behind a financial crisis. By using a large sample of countries in the period 1981 to 1999, it intends to apply two methods coming from the Artificial Intelligence (Rough Sets theory and C4.5 algorithm) and analyze the role of a set of macroeconomic and financial variables in explaining banking crises. These variables are both quantitative and qualitative. These methods do not require variables or data used to satisfy any assumptions. Statistical methods traditionally employed call for the explicative variables to satisfy statistical assumptions which is quite difficult to happen. This fact complicates the analysis. We obtained good results based on the classification accuracies (80% of correctly classified countries from an independent sample), which proves the suitability of both methods.
Keywords:
financial crises, artificial intelligence, rough sets, decision trees, C4.5.
Resumen:
Este trabajo intenta profundizar en los factores que influyen en la aparición de crisis financieras. Utilizando una amplia muestra de datos de países entre 1981 y 1999, se aplican dos metodologías del campo de la Inteligencia Artificial (la teoría Rough Set y el algoritmo C4.5) para analizar el papel de un conjunto de variables macroeconómicas y financieras (tanto de tipo cualitativo como de tipo cuantitativo) en la explicación de las crisis bancarias. Estos métodos no requieren que las variables o los datos utilizados satisfagan ningún tipo de hipótesis, al contrario que las técnicas estadísticas empleadas tradicionalmente, que presentan el inconveniente de que parten de hipótesis acerca de las propiedades distribucionales de las variables explicativas que no se suelen cumplir, lo que dificulta el análisis. Se han obtenido muy buenos resultados en términos de acierto en la clasificación (80% de clasificaciones correctas sobre una muestra independiente), lo que demuestra la precisión de ambos métodos.
Palabras clave:
crisis financieras, inteligencia artificial, rough sets, árboles de decisión, C4.5.
Résumé:
Ce travail a pour objectif de réaliser une étude approfondie des facteurs produisant l'apparition de crises financières. A partir d'un échantillon important de données de pays entre 1981 et 1999, deux méthodologies sont appliquées dans le domaine de l'Intelligence Artificielle (la théorie Rough Set et l'algorithme C4.5) pour analyser le rôle d'un ensemble de variables macroéconomiques et financières (autant qualitatives que quantitatives) dans l'explication des crises bancaires. Suivant ces méthodes, les variables ou les données utilisées ne doivent pas correspondre à un type d'hypothèse, à l'inverse des techniques statistiques utilisées traditionnellement qui présentent l'inconvénient de partir d'une hypothèse concernant les propriétés de distribution des variables explicatives qui ne sont pas respectées, ce qui rend l'analyse difficile. De très bons résultats ont été obtenus en ce qui concerne la classification (80% de classifications correctes pour un échantillon indépendant), démontrant la précision des deux méthodes.
Mots-clefs:
crise financière, intelligence artificielle, rough sets, arbres de décision, C4.5.
Resumo:
Este trabalho tenta aprofundar sobre os fatores que influem na aparição de crises financeiras. Utilizando uma ampla mostra de dados de países entre 1981 e 1999, aplicam-se duas metodologias do campo da Inteligência Artificial (a teoria Rough Set e o algoritmo C4.5) para analisar o papel de um conjunto de variáveis macroeconômicas e financeiras (tanto de tipo qualitativo como de tipo quantitativo) na explicação das crises bancárias. Estes métodos não requerem que as variáveis ou os dados utilizados satisfaçam nenhum tipo de hipóteses, ao contrario das técnicas estatísticas empregadas tradicionalmente, que apresentam o inconveniente de que partem de hipóteses acerca das propriedades distribucionais das variáveis explicativas que geralmente não se cumprem, o que dificulta a análise. Obteve-se resultados muito bons em termos de acerto na classificação (80% de classificações corretas sobre uma mostra independente), o que demonstra a precisão de ambos os métodos.
Palavras chave:
crises financeiras, inteligência artificial, rough sets, árvores de decisão, C4.5.
Introduction[1]
As the current crisis has painfully proved, the financial system plays a crucial role in economic development as it is responsible for the allocation of resources over time and among different alternatives of investment. Sound macroeconomic policies together with a sound financial system reinforce each other, guaranteeing financial stability and sustainable growth. Although the current crisis is being of an exceptional magnitude, financial crises are recurrent phenomena in the modern financial system. Apart from the current crisis in the last twenty years at least ten countries have experienced the simultaneous onset of a banking and currency crisis, with contractions in Gross Domestic Product of between 5% and 12% in the first year of the crisis, and negative or only slightly positive growth for several years thereafter (Stiglitz and Furman, 1998; Hanson, 2005). It is too early to quantify the final cost for the ongoing crisis but up to now, the major economies have spent large amounts in rescue plans for hit banks, guarantees for depositors, and measures to stimulate the damaged economies.[2] Therefore, preserving financial stability has been one of the main goals for policy makers since the beginning of the monetary systems and is clearer now than ever.
The unique role that banks play in the financial system and their specific function as money issuers, explains why the banking sector has played a leading role of a great number of financial crises. Such proliferation of large scale banking sector problems raised widespread concern, as banking crises disrupt the flow of credit to households and enterprises, reducing investment and consumption and possibly forcing viable firms into bankruptcy. Banking crises may also jeopardize the functioning of the payments system and, by undermining confidence in domestic financial institutions, they may cause a decline in domestic savings and/ or a large scale capital outflow. Finally, a systemic crisis may force sound banks to go bankrupt.
In most countries policy-makers have attempted to shore up the consequences of banking crises through various types of intervention (see footnote [2]). However, even when they are carefully designed the rescue operations have several drawbacks. They are often very costly, may allow inefficient banks to remain in business, they are likely to create the expectation of future bail-outs, reducing incentives for adequate risk management by banks and other markets participants (moral hazard). In addition, managerial incentives are also weakened when -as it is often the case- rescue operations force healthy banks to bear the losses of ailing institutions. Finally, loose monetary policy to shore up banking sector losses can be inflationary and, in countries with an exchange rate commitment, it may trigger a speculative attack against the currency.
Therefore, preventing the occurrence of systemic banking problems must be a chief objective for policy-makers. Understanding the mechanisms that are behind the surge in banking crises in the last fifteen years is a first step in this direction. A number of studies have analyzed various episodes of banking sector distress in an effort to draw useful policy lessons. Most of this work consists of case studies and econometric analyses are few. González-Hermosillo (1996) use an econometric model to predict bank failures using Mexican data for 1991-95. Using a sample of 20 countries, Kaminsky and Reinhart (1999) examined the behaviour of a number of macroeconomic variables in the months before and after a banking crisis; using a methodology developed for predicting the turning points of business cycles, they attempt to identify variables that act as "early warning signals" for crises.[3] They found that a loss of foreign exchange reserves, high real interest rate, low output growth, and a decline in stock prices tend to signal an incoming crisis.[4]
In this research we try to identify the features of the economic environment that tend to breed banking sector fragility and, ultimately, lead to systemic banking crises, focusing in particular in the role of monetary policy. Our panel includes all market economies for which data were available in the period 1981-1999. Although the sample could seem out-of-date, we chose it mainly for three reasons. First, there is a reliable database, on which there are consensus on the definition of the crisis period. Second, the aim of the paper is to analyze whether it is worth to add the new tools we present on it to the current arsenal to expand the range of available tools to prevent financial crises. Using this sample we can compare the performance of the tools we present with others already used. Finally, we think that there are still lessons to learn from the past crisis episodes.
The explanatory variables capture many of the factors suggested by the theory and highlighted by empirical studies, including not only macroeconomic variables and structural characteristics of the financial sector. Almost all of the crises in the 1990s and post-2000s were not just external crises, they often began in the domestic banking sectors, and banking sector problems complicated policymaking in all cases. In the typical case, runs on banks quickly turned into runs on currencies, forcing central banks to abandon attempts to peg the exchange rate and deal with bank failures (Caprio et al., 2005).
In this paper, we specially focus in the role played by the monetary policy. There is no clear consensus on how monetary policy and financial stability are related. In particular, it is not clear whether there are any trade-offs or synergies between them. The design of monetary policy should be particularly important since the central bank has a natural role in ensuring financial stability, as argued by Padoa-Schioppa (2002)[5] and Schinasi (2003), and has virtually always been involved in financial stability, directly or indirectly. [6] This issue is therefore very relevant, since it could help devise arrangements and policy responses to promote both monetary and financial stability.
In the past a large number of methods have been proposed to deal with these matters. Most approaches applied are classical statistical techniques such as discriminant, logit or probit analysis. However, although the obtained results have been satisfactory, all these techniques present the drawback that they make some assumptions about the model or the data distribution that are not usually satisfied, and, given the complexity of these techniques, a nonexpert user can find it difficult to extract conclusions from their results. To avoid these inconveniences of statistical methods, techniques coming from the Artificial Intelligence field that are non-parametric, have recently been suggested in the economic field. The techniques framed in the Machine Learning-the Artificial Intelligence area that develops algorithms which are able "to learn" a model from a set of examples-are very useful tools to tackle our problem.
These methods have mainly five positive features. First, they are useful to analyze information systems representing knowledge gained by experience; second, we can use qualitative and quantitative variables and it is not necessary that the variables employed satisfy any assumption; third, through this analysis the elimination of the redundant variables is got, so we can focus on minimal subsets of variables to evaluate insolvency or instability and, therefore, the cost of the decision making process and time employed by the decision maker are reduced; fourth, the analysis process results in a model consisted of a set of easily understandable decision rules so usually it is not necessary the interpretation of an expert and finally; fifth, these rules are based on the experience and they are well supported by a set of real examples so this allows the argumentation of the decisions we make.
The goal of this paper is to show, by means of an empirical study, the efficiency of two Machine Learning techniques, Rough Set theory and C4.5 decision tree learner, to detect possible financial crises. We understand this problem as a classification one with two predefined classes, crisis or financial stability. We use as attributes a set of financial and macroeconomic variables. The prior research for prediction of bank failure by means of decision trees and rough set approach is focused on financial ratios and individual crises (Bonsón Ponte et al., 1996; Dimitras et al., 1999; Martín-Zamora, 1999; Mckee, 2000, Slowinski and Zopounidis, 1995; Tam and Kiang, 1992).
The rest of the paper is structured as follows: Section II introduces the theoretical models underlying the selection of explanatory variables for financial crisis. In Section III , we explain the two methodologies. Section IV describes the empirical models and the main results obtained are presented. Finally, Section V highlights the main conclusions.
The determinants of banking crises. Data and variable selection
Houben et al. (2004) define financial stability in terms of its ability to help the economic system allocate resources, manage risks, and absorb shocks. Moreover, financial stability is considered a continuum, changeable over time and consistent with multiple combinations of its constituent elements. In the same paper we find an appendix that provides an overview of definitions or descriptions of financial stability by a selected group of officials, central banks and academics.
Another strand of the literature focuses on extreme realizations of financial instability. According to Mishkin (1996) a financial crisis is a disruption to financial markets in which adverse selection and moral hazard become much worse, so that financial markets are unable to efficiently channel funds to those who have the most productive investment opportunities.
We are particularly interested in banking crises, as a financial stability outcome, because the design of the central bank is more directly related to the functioning of the banking system than to the rest of the financial system.
The literature offers several definitions of banking crises. From the early definitions of Friedman and Schwartz (1963) and Bordo (1986), who concentrate on bank panics, more general definitions have followed. Such definitions are description of a banking crisis. A more complex matter is how to summarize such a description in one single quantitative indicator, or a set of them. Existing indicators, such as those mentioned by Lindgren et al. (1996) are not readily available for a large number of countries, or else there is a lack of comparable cross-country data to construct such an indicator. This is why the empirical literature has opted for identifying banking crises as events, expressed through a binary variable, constructed with the help of cross-country surveys (Caprio and Klingebiel, 2003; Lindgreen et al., 1996). This will be our approach as well.
Regarding the determinants of a banking crisis, the literature suggests a variety of mechanisms that can bring about banking sector problems.
Banks are financial intermediaries whose liabilities are mainly short-term deposits and whose assets are usually short and long-term loans to businesses and consumers. When the value of their assets falls short of the value of their liabilities, banks become insolvent. Moreover, the nature of their business results in banks as heavily leveraged institutions. The value of a bank's assets may drop because borrowers become unable or unwilling to service their debt (credit risk). However, we cannot eliminate default risk without severely curtailing the role of banks as financial intermediaries.[7] If loan losses exceed a bank's compulsory and voluntary reserves as well as its equity cushion, then the bank becomes insolvent. When a significant portion of the banking system experiences loan losses in excess of their capital, a systemic crisis occurs.
Thus, the theory predicts that shocks that adversely affect the economic performance of bank borrowers and that cannot be diversified should be positively correlated with systemic banking crises. Furthermore, for given shocks banking systems that are less capitalized should be more vulnerable. The empirical literature has highlighted a number of economic shocks associated with episodes of banking sector problems: Cyclical output downturns, terms of trade deteriorations, declines in asset prices such as equity and real estate (Caprio and Klingebiel, 1997; Gorton, 1988; Kaminsky and Reinhart, 1999; Lindgren et al., 1996).
Even in the absence of an increase in non-performing loans, bank balance sheets can deteriorate if the rate of return on bank assets falls short of the rate that must be paid on liabilities. Perhaps the most common example of this type of problem is an increase in short term interest rates that forces banks to increase the interest rate paid to depositors.[8] Because the asset side of bank balance sheets usually consists of loans of longer maturity at fixed interest rates, the rate of return on assets cannot be adjusted quickly enough, and banks must bear losses. All banks within a country are likely to be exposed to some degree of interest rate risk because maturity transformation is one of the typical functions of the banking system; thus, a large increase in short-term interest rates is likely to be a major source of systemic banking sector problems. In turn, several factors determine the increase in short-term interest rates, such as an increase in the rate of inflation, a shift towards more restrictive monetary policy that raises real rates, an increase in international interest rates, the removal of interest rate controls due to financial liberalization (Pill and Pradhan, 1995), or the need to defend the exchange rate against a speculative attack (Kaminsky and Reinhart, 1999).[9]
Another case of rate of return mismatch occurs when banks borrow in foreign currency and lend in domestic currency. In this case, an unexpected depreciation of the domestic currency threatens bank profitability. Many countries have regulations limiting banks' open foreign currency positions, but sometimes such regulations can be circumvented. In addition, banks that raise funds abroad may choose to issue domestic loans denominated in foreign currency, thus eliminating the open position. In this case, foreign exchange risk is shifted onto the borrowers, and an unexpected devaluation would still affect bank profitability negatively through an increase in non-performing loans. Foreign currency debt was a source of banking problems in Mexico in 1995, in the Nordic Countries in the early 1990s, and in Turkey in 1994 (Mishkin, 1996).
When bank deposits are not insured, deterioration in the quality of a bank's asset portfolio may trigger a run, as depositors rush to withdraw their funds before the bank declares bankruptcy. Because bank assets are typically illiquid, runs on deposits accelerate the onset of insolvency. In fact, bank runs may be self-fulfilling, i.e. they may take place simply because depositors believe that other depositors are withdrawing their funds even in the absence of an initial deterioration of the bank's balance sheet. The possibility of self-fulfilling runs makes banks especially vulnerable financial institutions. A run on an individual bank should not threaten the banking system as a whole unless partially informed depositors take it as a signal that other banks are also at risk (contagion).[10] In these circumstances, bank runs turn into a banking panic.
A sudden withdrawal of bank deposits with effects similar to those of a bank run may also take place after a period of large inflows of foreign short-term capital, as indicated by the experience of a number of Latin American, Asian, and Eastern European countries in the early 1990's. Such inflows, often driven by the combined effect of capital account liberalization and high domestic interest rates due to inflation stabilization policies, result in an expansion of domestic credit. When domestic interest rates fall, or when confidence in the economy wavers, foreign investors quickly withdraw their funds, and the domestic banking system may become illiquid. In countries with a fixed exchange rate, a speculative attack against the currency may also triggers banking problems: if devaluation is expected to occur soon, depositors (both domestic and foreign) rush to withdraw their bank deposits to convert them into foreign currency deposits abroad leaving domestic banks illiquid.[11]
In what follows, we attempt to use our data set to identify which of these mechanisms played a major role in the crises of the 1980's and early 1990's.
In this paper, we focus on the design of monetary policy. The existing literature on monetary policy design has concentrated on issues different than financial stability (mainly price stability but also output stabilization). In particular, literature has well documented that a high degree of central bank independence and an explicit mandate to restrain inflation are important institutional devices to ensure price stability (Berger et al., 2001). The role of the monetary policy strategy chosen is less clear even for price stability and output stabilization although inflation targeting has received more support in the recent literature.[12]
The impact of the monetary policy design on financial stability is related to the very much debated question of the relation between price stability and financial stability. The economic literature is divided as to whether there are synergies or a trade-off between them. If synergies existed between the two objectives it would seem safe to argue that the same monetary policy design which helps achieve price stability (namely, narrow central bank objectives and central bank independence) also fosters financial stability. However, if there were a trade-off, it would be much harder to establish an apriori on the impact of price stability on financial stability. It may also be possible that the relationship between the monetary policy variables and financial stability is not linear and that trade off or synergies can appear depending on the circumstances (e.g., the level of growth, the institutional framework, etc.).
In addition, it can happen that an apparent short term trade-off is a synergy when taking a long term view.
Among the arguments for a trade-off, Mishkin (1996) argues that high level of interest rates, necessary to control inflation, negatively affect banks' balance sheets and firms' net financial worth, especially if they attract capital inflows. This is because capital inflows contribute to over-borrowing and increase credit risk, and may lead to currency mismatches if foreign capital flows are converted into domestic-currency denominated loans. Cukierman et al. (1992) state that the inflation control may require fast and substantial increases in interest rates, which banks cannot pass as quickly to their assets as to their liabilities. This increases interest rate mismatches and, thus, market risk. Another type of trade-off stems from too low inflation or deflation, which reduces banks' profit margins and, by damaging borrowers (and not lenders as inflation) increases the amount of nonperforming loans in banks' balance sheets (Fisher, 1933).
Among the arguments for synergies between price and financial stability, Schwartz (1995) states that credibly maintained prices provide the economy with an environment of predictable interest rates, leading to a lower risk of interest rate mismatches, minimizing the inflation risk premium in long-term interest rates and, thus, contributing to financial soundness. From this strong view of synergies, where price stability is practically considered a sufficient condition for financial stability, some more cautious supporters of the "synergies" view argue that price stability is a necessary condition for financial stability but not a sufficient one (Issing, 2003; Padoa-Schioppa, 2002).
Regarding the choice of the monetary policy strategy, there is a wealth of literature on the advantages and disadvantages of each strategy for achieving price stability but no clear consensus on which one is preferred, at least in a long enough time span. Furthermore, no evidence exists on how it may affect financial stability. While the choice of the monetary strategy will mainly depend on its relation with the central bank's main objective (the inflation outcome or sometimes the macroeconomic performance) -on the basis that one instrument should serve one objective- it is still interesting to know whether there are spillovers from the choice of the strategy towards financial stability.
As an additional aspect of the monetary policy design, we introduce central bank independence. The rationale behind it is that the government may interfere in the pursuit of the central bank's objectives if the central bank is not independent. The a priori for the impact of central bank independence on financial stability should, therefore, follow the same reasoning as for the central bank objectives. If synergies exist, a high degree of central bank independence, which has been proved to foster price stability, should also contribute to financial stability.
The current crisis has made evident the need to rethink the role of the monetary policy and other financial stability tools in the prevention/management of financial crises. One line of thought supports the idea that the monetary policy should broaden its objective so as to include not only consumption good prices but investment asset prices (property prices, financial asset prices). On this way the link between low interest rates and low financial assets prices that in turn are the seeds of financial price bubbles would be properly taken into account. A more broad monetary policy objective that also covers the stabilization of investment prices is seen as the appropriate way forward to content financial crises in the future. Others see the central bank active management of the eligible collateral haircuts as a new tool that central banks can use to prevent asset price bubbles on a more tailored way. Finally, liquidity ratios based on the value of the eligible collateral is seen for others as the most promising way to create a more direct link between the prudential regulatory framework and the macroeconomic policy.
Besides, we have mentioned that the employed approaches in this paper are especially well suited to classification problems. One of these problems is a multi-attribute classification problem which consists of the assignment of each object, described by values of attributes, to a predefined class or category. In financial instability prediction, we try to assign countries described by a set of macroeconomic and financial variables to a category (crisis or financial stability).
As for the data employed, we have used a sample of 79 countries in the period 1981-1999 (annual data). The dependent variable can be defined in this way: Systemic and non-systemic banking crises dummy equals one during episodes identified as in Caprio and Klingebiel (2003). The independent variables included are dictated by the theory on the determinants of banking crisis. We provide a detailed list of variables and sources in the Appendix. We included two types of variables in our estimations: macroeconomic variables and financial variables. Among the macroeconomic variables we include: the real growth of GDP, the level of real GDP per capita, the inflation rate and the real interest rate to capture the external conditions that countries face. Among the financial variables we include Domestic credit growth, Bank Cash to total assets, and Bank foreign liabilities to foreign assets. We have employed qualitative and quantitative variables. The possibility of using both kinds of variables is one of the advantages of these methodologies. Therefore, we selected the variables taking into account the several factors usually highlighted by the literature.
The methodologies
C4.5 algorithm: main concepts
As we have mentioned, Machine Learning algorithms are a set of techniques that automatically build models, describing the structure at the heart of a set of data, that is, they induce a model or output from a given set of observations or input. Such models have two important applications. First, if they accurately represent the structure underlying the data, they can be used to predict properties of future data points. Second, if they summarize the essential information in human-readable form, people can use them to analyze the domain from which the data originates (Frank, 2000).
These two applications are not mutually exclusive. To be useful for analysis, a model must be an accurate representation of the domain, and that makes it useful for prediction as well. However, the reverse is not necessarily true: some models are designed exclusively for prediction and do not lend themselves naturally to analysis, as it happens in the case of the popular Artificial Neural Networks or the more recent Support Vector Machines. In many applications this "black box" approach is a serious drawback because users cannot determine how a prediction is derived and match this information with their knowledge of the domain. This makes it impossible to use these models in critical applications in which a domain expert must be able to verify the decision process that leads to a prediction -for example, in medical applications.
Decision trees are one of the most fruitful and widely used approaches in Machine Learning because they are potentially powerful predictors that embody an explicit representation of all the knowledge that has been induced from the dataset. Moreover, compared to other sophisticated models, they can be generated very quickly. Given a decision tree or a set of rules, a user can determine manually how a particular prediction is derived, and which attributes are relevant in the derivation. This makes it an extremely useful tool for many applications where both predictive accuracy and the ability to analyze the model are important, that is, where both prediction and explanation are important.
In this paper we will use in fact one of these techniques, the well-known algorithm of induction of decision trees C4.5.
Decision trees are a way of representing the underlying regularity in the data like a set of exhaustive and mutually exclusive conditions which are organized in an arborescent hierarchical structure which is composed by internal and external nodes connected by branches. An internal node contains a test that evaluates a decision function to determine which node will be visited next. In contrast, an external node, which is frequently called leaf or terminal node, doesn't have any son and it is associated with a label or a value which characterizes to the data that are propagated to it.
In general, a decision tree is used in the following way: to derive a prediction, an instance is filtered down the tree, starting from the root node, until it reaches a leaf -in this paper, an instance will be a country described by a set of macroeconomic and financial variables-. At each node one of the instance's attributes is tested, and the instance is propagated to the branch that corresponds to the outcome of the test. The prediction is the class label that is attached to the leaf.
As for the way of generating a tree, standard learning algorithms for decision trees generate a tree structure by splitting the training data into smaller and smaller subsets in a recursive top-down fashion. Starting with all the training data at the root node, at each node they choose a split and divide the training data into subsets accordingly. They proceed recursively by partitioning each of the subsets further. Splitting continues until all subsets are "pure", or until their purity cannot be increased any further. A subset is pure if it contains instances of only one class. The aim is to achieve this using as few splits as possible so that the resulting decision tree is small and the number of instances supporting each subset is large. To this end, various split selection criteria have been designed, and at each node, the learning algorithm selects the split that corresponds to the best value for the splitting criterion.
Some of the most outstanding split selection criteria are the Gini index, which is employed in the CART system Classification and Regression Trees (Breiman et al., 1984), and the "information gain" or the "gain ratio", which are used by C4.5. They all provide ways of measuring the purity of a split. C4.5 is the most popular and widely used to date decision tree program. It was developed by J. Ross Quinlan in the eighties and early nineties (Quinlan, 1993) as a descendant from his first classifier program, which was named ID 3 (Quinlan, 1979, 1983, 1986). To carry out the partitions, C4.5 is based on the entropy of a random variable (which is a measure of the randomness or uncertainty of the variable) and the mutual information between different variables (which indicates the reduction in the uncertainty of one of the variables that is produced when the value of the other one or the other ones is known). C4.5 works with both continuous and discrete attributes and incorporates several additional features that turn it into a very powerful and flexible technique, such as, for example, its method for handling with missing values. Very briefly, such a method is the following one: once a splitting attribute has been chosen, training cases with unknown values of this attribute cannot be associated with a particular outcome of the test, so a weighting scheme is used to allow recursive application of the decision tree formation procedure on each of the daughter nodes. Instances for which the relevant attribute value is missing are notionally split into pieces, one piece for each branch, in the same proportion as the known instances go down the various branches, so the number of cases that are propagated to the nodes and leaves of the tree could be a fractional value. A similar approach is taken when the decision tree is used to classify a new case. If a decision node is encountered at which the relevant attribute value is unknown, so that the outcome of the test cannot be determined, the system explores all possible outcomes and combines the resulting classifications arithmetically. Since there can now be multiple paths from the root of a tree or subtree to the leaves, a "classification" is a class distribution rather than a single class. When the total class distribution for the case has been established in this way, the class with the highest probability is assigned as the predicted class.
A common problem for most of machine learning techniques is that models they generate can be adapted to the training dataset, so the classification obtained will be nearly perfect. Consequently, the model developed will be very specific and if we want to classify new objects, the model will not provide good results, especially if the training set has noise. In this last case, the model would be influenced by errors (noise) which would lead to a lack of generalization. This problem is known as overfitting.
The most frequent way of limiting this problem in the context of decision trees consists in deleting some conditions of the tree branches, to achieve more general models. This procedure can be considered as a pruning process. This way we will increase the misclassifications in the training set, but at the same time, we probably decrease the misclassifications in a new dataset that has not been used to develop the decision tree.
C4.5 incorporates a post-pruning method for an original fitted tree. This method consists of simplifying the tree by discarding one subtree (or more) and replacing it with a leaf or with its most frequently used branch, provided this replacement lead to a lower predicted error rate. It is clear that the probability of error in a node of the tree cannot be exactly determined, and the error rate on the training set from which the tree was built does not provide a suitable estimate. To estimate the error rate, C4.5 works in the following way: assume that there is a leaf that covers N objects and misclassifies E of them. This could be considered as a binomial distribution in which the experiment is repeated N times obtaining E errors. From this issue, the probability of error pe is estimated, and it will be taken as the aforementioned predicted error rate. Therefore, to estimate a confidence interval for the error probability of the binomial distribution is necessary. The upper limit of this interval will be pe (note that this is a pessimistic estimate).
Then, in the case of a leaf that covers N objects, the number of predicted errors will be N x pe. Similarly, the number of predicted errors associated with a subtree will be just the sum of the predicted errors of its branches, and the number of predicted errors associated with a branch will be the sum of the predicted errors of its leaves. Therefore, a subtree will be replaced by a leaf or a branch, that is, the subtree will be pruned when the number of predicted errors for the last ones is lower than that for the subtree.
Furthermore, the C4.5 algorithm includes additional functions such as a method to change the obtained tree into a set of classification rules that are generally easier to understand than the tree. Even though the pruned trees are more compact than the originals, when the problem is very complex, the tree is very large and consequently difficult to understand since each node has a specific context established by the outcomes of tests at antecedent nodes. For a more detailed description of the features and workings of C4.5 algorithm see Quinlan (1993).
Rough Set (RS) theory: main concepts
RS Theory was firstly developed by Pawlak (1991) in the 1980s as a mathematical tool to deal with the uncertainty or vagueness inherent in a decision making process. Though nowadays this theory has been extended (Greco et al., 1998, 2001), we refer to classical approach that does not order attribute domains as it assumes that different values of the same attribute are equally preferable and that only the predictive value of the attribute, as revealed by the data, will be factored into the model. The extended approach handle dominance relations, in addition to indescernibility relations, incorporating data about the ordering properties of the attributes analyzed, if these exit and are known. The resultant model is potentially more compact since some rules conflicts for certain cases are eliminated. Therefore, it uses additional information to generate a simpler final model, but the classical approach makes a less restrictive data assumption than does the extended approach (McKee, 2000, p. 162).
This section presents some concepts of RS Theory following Pawlak's reference and some remarks by Slowinski (1993) and Dimitras et al. (1999).
The philosophy of this approach is based on the assumption that with every object of the universe we are considering we can associate knowledge, data. Objects described by the same data or knowledge are indiscernible in view of such knowledge. The indiscernibility relation leads to mathematical basis for the RS Theory. Vague information causes indiscernibility of objects by means of data available and, as a result, this prevents their precise assignment to a set. Intuitively, a rough set is a set or a subset of objects that cannot be expressed exactly by employing available knowledge. If this information or knowledge consists of a set of objects described by another set of attributes, we consider a rough set as a collection of objects that, in general, cannot be precisely characterized in terms of the values of the set of attributes.
RS Theory represents knowledge about the objects as a data table, that is, an information table in which rows are labelled by objects (states, processes, firms, patients, candidates...) and columns are labelled by attributes. Entries of the table are attribute values. Therefore, for each pair object-attribute, x-q, there is known a value called descriptor, f(x, q). The indiscernibility relation would occur if for two objects, x and y, all their descriptors in the table have the same values, that is if, and only if, f(x, q) = f(y, q).
Indiscernible objects by means of attributes prevent their precise assignment to a class. Therefore, some categories (subsets of objects) cannot be expressed exactly by employing available knowledge and, consequently, the idea of approximation of a set by other sets is reached. A rough set is a pair of a lower and an upper approximation of a set in terms of the classes of indiscernible objects. That is, it is a collection of objects that, in general, cannot be precisely characterized in terms of the values of the set of attributes, while a lower and an upper approximation of the collection can be. Therefore, each rough set has boundary-line cases, that is, objects that cannot be classified certainly as members of the set or of its complement and can be represented by a pair of crisp sets, called the lower and the upper approximation. The lower approximation consists of all objects that are certain to belong to the set and can be classified with certainty as elements of that set, employing the set of attributes in the table (the knowledge we are considering). The upper approximation contains objects that possibly belong to the set and can be possibly classified as elements of that set using the set of attributes in the table. The boundary or doubtful region is the difference between the lower and the upper approximation and is the set of elements that cannot be classified with certainty to a set using the set of attributes. Therefore, the borderline region is the undecidable area of the universe, that is, none of the objects belonging to the boundary can be classified with certainty into a set or its complement as far as knowledge is concerned.
Because we are interested in classifications, the quality of classification is defined as the quotient between the addition of the cardinalities of all the lower approximations of the classes in which the objects set is classified, and the cardinality of the objects set. It expresses the percentage of objects which can be correctly classified to classes employing the knowledge available.
A fundamental problem in the rough set approach is discovering dependencies between attributes in an information table because it enables to reduce the set of attributes removing those that are not essential (unnecessary) to characterize knowledge. This problem will be referred to as knowledge reduction or, in general terms, as a feature selection problem. The main concepts related to this question are core and reduct. A reduct is the minimal subset of attributes which provides the same quality of classification as the set of all attributes. If the information table has more than one reduct, the intersection of all of them is called the core and is the collection of the most relevant attributes in the table.
An information table which contains condition and decision attributes is referred as a decision table. A decision table specifies what decisions (actions) should be undertaken when some conditions are satisfied. Thus, a reduced information table may provide decision rules of the form "if conditions then decisions".
These rules can be deterministic when the rules describe the decisions to be made when some conditions are satisfied and non-deterministic when the decisions are not uniquely determined by the conditions so they can lead to several possible decisions if their conditions are satisfied. The number of objects that satisfy the condition part of the rule is called the strength of the rule and is a useful concept to assign objects to the strongest decision class when rules are non-deterministic.
The rules derived from a decision table do not usually need to be interpreted by an expert as they are easily understandable by the user or decision maker. The most important result in this approach is the generation of decision rules because they can be used to assign new objects to a decision class by matching the condition part of one of the decision rule to the description of the object. Therefore rules can be used for decision support.
Empirical model and results
If we developed a model and we test it with the same sample, the results obtained could be conditioned. To avoid it, we formed a training set and a holdout sample to validate the obtained decision rules, i.e., the test set. Both sets were randomly selected. The training information table consisted of 421 data from 79 countries in the period 1981-1997 (annual data) described by the variables explained in Section The determinants of banking crises. Data and variable selection, and assigned to a decision class: next year crisis -1 or next year not crisis -0. Thus, it has to be noted that the forecasting horizon is one year. We have 293 objects for class 0 and 128 objects for class 1. The test information table consisted of 100 data described by the same variables in the period 1997-1999 (36 objects for class 1, and 64 objects for class 0). This way we can test the predictive accuracy of both models.
C4.5 model and results
The algorithm was performed using the data-mining package WEKA from the University of Waikato (Witten and Frank, 2005). The Weka's implementation of the C4.5 decision tree learner -described in Section The determinants of banking crises. Data and variable selection- is called J4.8 algorithm (J4.8 actually implements a later and slightly improved version called C4.5 Revision 8, which was the last public version of this algorithm before C5.0, the commercial implementation, was released. We have not used the more recent commercial version because some aspects of its functioning have not been described in the open literature). Next, the output is shown:
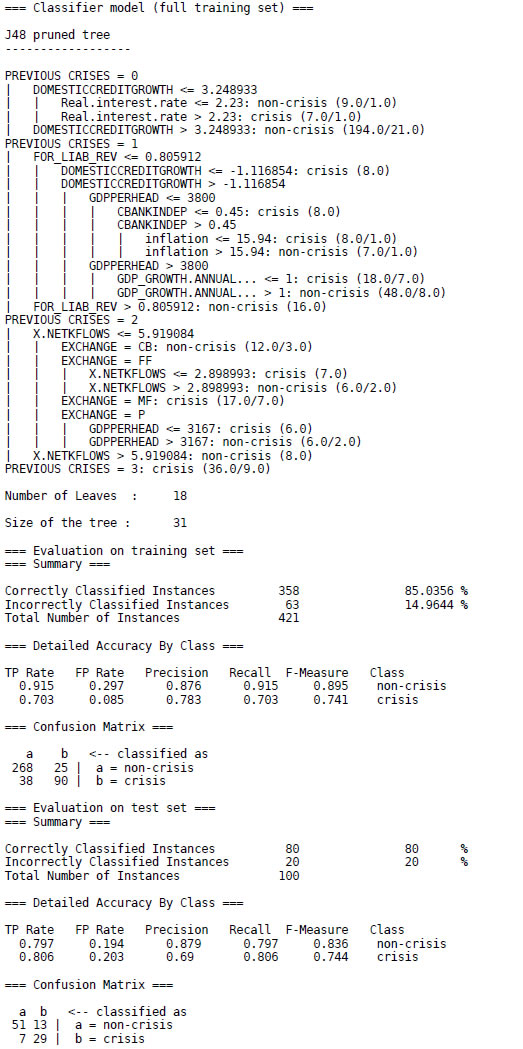
At the beginning, there is a pruned decision tree in textual form, which would be read in the following way:
- If previous crises = 0 and domestic credit growth is less than or equal to 3.25 and real interest rate is less than or equal to 2.23, then non-crisis.
- If previous crises = 0 and domestic credit growth is less than or equal to 3.25 and real interest rate is greater than 2.23, then crisis.
- If previous crises = 0 and domestic credit growth is greater than 3.25, then non-crisis.
- If... and so on.
Every leaf of the tree is followed by a number n or n/m. The value of n is the number of cases in the sample that are mapped to this leaf, and m (if it appears) is the number of them that are classified incorrectly by the leaf, expressed as a decimal number because of the way the algorithm uses fractional instances to handle missing values. Beneath the tree structure the number of leaves is printed; then the total number of nodes (Size of the tree).
The next part of the output shows the results obtained from the training data. This evaluation is not likely to be a good indicator of future performance. Because the classifier has been obtained from the very same training data, any estimate of performance based on that data will be optimistic. Although it is not a reliable predictor of the true error rate on new data, it may still be useful because it generally represents an upper bound to the model's performance on fresh data. In this case, 358 of 421 training instances (or 85%) are classified correctly. As well as the classification error, the evaluation module also outputs some statistics for each class. TP, FP, TN , and FN are the number of true positives, false positives, true negatives, and false negatives, respectively, and
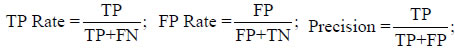
Recall is the same as TP Rate (different terms are used in different domains), and finally, F-Measure is a weighted average between Precision and Recall:
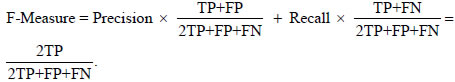
From the confusion matrix at the end, we can see that 25 instances of class "non-crisis" have been assigned to class "crisis" and 38 of class "crisis" are assigned to class "non-crisis".
Of course, what we are interested in is the likely future performance on new data, not the past performance on old data. To predict the performance of the tree on new data, we need to assess its error rate on a dataset that played no part in the formation of the tree. So the last part of the output gives estimates of the tree's predictive performance that are obtained using the test set of 100 instances. As we can see, 80% of the cases are classified correctly, a quite satisfactory result.
As in any other classification methodology we cannot see the exact cut offs in each variable as determinant. In case of borderline values we should try to look at more carefully and maintain open various alternative outcomes. However, in general we can be quite confident about the results.
Regarding the economical interpretation of the tree, looking at the variables that have a role in the classification we see that the most important, given that it is implied in the classification of all units is the variable "previous crisis". The variables that influence a country finally suffer a crisis or not in a given year are different if the country is not yet in a crisis (previous crisis = 0), the country is at the beginning of a crisis (previous crisis = 1), it is in a more mature stage of a crisis (previous crisis = 2) or is in a persistent one (previous crisis = 3). Therefore it is important to know what variables are the important ones in each case to extract policy lessons. The appropriate policy mix may be not the same if we just want to maintain a stable situation, especially if we want to overcome a crisis just at the start or if we want to overcome a long lasting crisis. Confidence is a crucial factor to maintain financial stability and when a crisis emerges there is a general loss of confidence that is more difficult to re-establish when the crisis is more persistent. The lack of confidence in turn implies more sacrifice in real terms to come back to a stability scenario.
In fact our tree predicts that countries with a crisis longer than 3 years will be in crisis in the next period. This result of course cannot be read as deterministic but the small number of cases we have in our sample for this situation do not give enough information to the system to be more precise. However, it is an indication of the difficulties that entail to overcome a long lasting crisis.
It is interesting to notice that the most important variable is the domestic credit growth which explains why a country enters a crisis. There are arguments that an excessive domestic credit could pose some risks in terms on overheating the economies, but it seems that in general, rates of growth above 3% are associated with countries that will not enter a crisis. In general, a stable credit growth is associated with growing countries with a developed internal financial market that is a good feature to contain a financial crisis (Caprio et al., 2005).
Therefore, for the countries with ratios of domestic credit growth lower than 3% and with an undeveloped financial system, the variable that makes the difference is the real interest rate. Real interest rates higher than 2.25% are associated with a crisis, while lower than 2.25% are compatible with a non crisis situation.
The explanation became more complex for countries that have just entered a crisis. Here, the second most important variable in explaining a crisis is the foreign liabilities ratio that is defined as total foreign liabilities divided by the sum of total foreign liabilities to total foreign assets. When this ratio is higher than 0.8 it means that foreign liabilities are four times foreign assets and the tree then predicts that the country will leave the crisis. Although this type of disequilibrium implies a currency risk in case of a depreciation of the national currency, given the lower value of the national assets compared with the value of the liabilities, in the short term the possibility to hold foreign deposits within the banking system can help banks, at least temporarily, in their efforts to maintain their deposit base (see García-Herrero, 1997), therefore contributing to maintain financial stability.
In the countries with the ratio of foreign liabilities lower than 80% the domestic credit growth is again the important variable. For ratios of domestic credit growth significantly negative, and therefore a significant contraction in the banking business, the country will continue in crisis. If the domestic credit growth is not higher than this threshold then it comes on stage the wealthiest of the country. Richer countries (with GDP per capita above 3800$) with growth ratios above 1% will leave the crisis while same countries growing below this threshold (1%) will continue in crisis. The situation in poorer countries depends on the independence of the central bank. Price stability, and therefore currency stability, is vital in maintaining a climate of confidence and stability. The monetary policy regime is an important factor to maintain price stability. But once a situation of uncontrolled inflation has emerged then the credibility on the monetary policy authorities is an important factor, making easier to recover stability. With a more dependent central bank or a more independent central bank, but in a context of inflation below 15%, the country will continue in crisis. On the other hand, with an independent central bank in a context of inflation above 15%, the country will go out of the crisis. However, in times of a crisis, a dependent central bank does not have the credibility to control inflation and therefore to maintain the currency value at a reasonable cost. So the most probable outcome is that deterioration continues. But independence only changes things when inflation is higher than 15%, therefore when the real benefits of price stability are enough to compensate the sacrifice in terms of real income that a restrictive policy implies.
For countries with a more mature crisis, the first variable in explaining if a country can go out or not of a crisis is capital net flows. If capital net flows are above 6%, they can go out to the crisis. This means that if there is enough external capital, based on the confidence of the external investors on this economy, it plays an important role for overcome the situation. If external factors are not enough (below 6%) then it is important the exchange regime. The currency regime could be use to recover the confidence in the economy through stabilizing the level of prices. The success of this strategy will depend on the credibility in maintaining the commitments that each regime implies. A currency board regime permits to go out of the crisis, while managed floating does not. The first is the regime that constrains internal monetary policy the most, which will be completely determined by the monetary policy of the benchmark country (usually US). The second regime is the one that is in the worst position to contribute to the recovery of the confidence. It neither implies a commitment in terms of monetary policy nor responds to the market discipline. Then, this regime introduces more uncertainty in the policy decisions, which are discretionary, and therefore in the economy. A free floating regime combined with a volume of capital net flows above 3% can lead the economy to overcome the crisis, if the capital net flows are below 3% then crisis will continue. In addition, a free floating regime implies that the currency exchange is fixed by the markets and this tool cannot be used to maintain competitiveness. For the pegged regime it depends on the GDP per capita, poorer countries (below 3200$) cannot support the restriction that this type of commitment implies so this policy is not credible and therefore cannot attract investment and cannot contribute to the end of the crisis. This commitment is not as restrictive for the internal monetary policy as the currency board but also implies a sacrifice. Given that the commitment is not so well defined this regime finds it more difficult to remain credible, and this credibility difficulty is more important the higher the sacrifice it implies in real terms (the case of poorer countries). In this instance a combination of a strong commitment with credibility seems to be the solution.
To sum up, some interesting conclusions emerge from the results in terms of economic policy. The first conclusion is that there are real variables (real interest rates) that determine the probability to enter in a crisis. The second conclusion is that once the crisis is in place then the recovery of the confidence in the system is crucial to overcome the situation. In the beginning of a crisis internal policies can be enough to recover the confidence, but when the crisis is more persistent then the government should "borrow" this confidence from a reference country by using the exchange rate regime to anchor their monetary policy and therefore the expectations. The quality of the commitment in terms of monetary policy and the credibility of this commitment are two key factors in determining the success of a policy in going out of a crisis.
Rough Set model and results
This section presents the model and some results following the Sanchis et al. (2007) reference. The algorithm has been performed using the ROSE software provided by The Institute of Computing Science of Poznan University of Technology (www-idss.cs.put.poznan.pl/rose, Predki et al., 1998; Predki and Wilk, 1999).
The training information table was entered into an input file in ROSE . We have recoded the continuous variables into qualitative terms (low, medium, high and very high) with corresponding numeric values such us 1, 2, 3 and 4. The four subintervals are based on the quartiles for the actual variable values (year 1) for the whole sample because percentiles are frequently used in scientific researches to divide a domain into subintervals (Laitinen, 1992; McKee, 2000). This recoding was made dividing the original domain into subintervals. The RS theory does not impose this recoding, but it is very useful to draw general conclusions from the ratios in terms of dependencies, reducts and decision rules (Dimitras et al., 1999).
The analysis of the coded table shows that the core consists of four attributes: Inflation, Domestic Credit Growth, Real GDP per capita, and Bank Foreign Liabilities to Foreign Assets, which represent the most relevant attributes in the table. We obtained 19 reducts from the table which contains 9-10 attributes. We selected the reduct consisting of Central Bank Independence, Inflation, Domestic Credit Growth, Real GDP growth, Bank Foreign Liabilities to Foreign Assets, Real GDP per capita, World Growth, Real Interest Rate and Previous Crisis. The model was selected because of its better performance in terms of correctly classified firms as well as in terms of economic interpretation. Thus, we obtained a reduced table to get the decision rules. We have obtained 116 deterministic rules (63 for class 0 and the other ones for class 1). To interpret the rules, we only selected the strongest (3.12%) rules (40 rules, Table 2) for each decision class. Through this, we covered 85.5% objects in the table.
The 116 rules were tested on data from the testing test, i.e., on the 100 firms that were not used to estimate the algorithm. The classification accuracy as a percentage of correctly classified firms is 80%, which coincides with the one reached by C4.5 (see previous subsection C4.5 model and results). This result is satisfactory comparing with previous analysis. Demirgüç-Kant and Detragiache (1997) obtained similar results and in general the corrected R-square is well below this percentage (Domaç and Martinez Peria, 2000; Eichengreen and Arteta, 2000).
These results show the importance of the four variables in the core to forecast financial instability in a country. Moreover, they are well in line with previous research. Demirgüç-Kant and Detragiache (1997) found that crisis tend to erupt when growth is low and inflation is high. Eichengreen and Arteta (2000) discover among the robust causes of emerging banking crisis a rapid domestic credit growth and large bank liabilities relative to reserves.
An interesting result to observe in the role of the design of monetary policy in determining financial stability is the fact that in 18 of the 19 reducts, at least one of the three variables related with the design of the monetary policy (Exchang, Independence and Monetarypol) appears. Given the co-linearity between them it is not strange that generally only one of them was chosen in each model. This result confirms the idea that the design of the monetary policy is a relevant variable to explain financial stability, as the paper of García-Herrero and del Río (2003) suggests.
Moreover, between the four variables that belong to the core, there are two directly related to monetary policy: the level of inflation and the domestic credit growth.
From the analysis of the 116 rules, we can see that the Central Bank Independence variable enters in 52 of the 116 rules. This represents the 45% percent of the total rules. However in terms of objects covered by the rules (strength) represents the 58%. The percentage in terms of classified units in the rules for no crisis is 66% and in the crisis group 46%. So, results suggest that this variable play an important role in determining financial crisis.
However, the rules show that a higher degree of independence is not always associated with financial stability. Seventy four units with a degree of independency belonging to the lowest quartile showed financial stability, while 55 units in the highest quartile also showed stability. In these two extremes in the distribution we can see that only a reduced number of crisis are associated, indicating that a clear independence or a clear dependency is almost always associated with financial stability.
On the contrary, the crises are clearly associated with levels of independence in the second and third quartile of the distribution highlighting that no clear definition of the monetary policy objectives is a factor that contributes to the financial crisis.
In other words, it is more important for financial stability that financial agents know the reaction function on monetary policy rather than the function itself. This result is independent on the level of inflation since there is a control variable accounting for this. A way to see that central bank independence is not picking up the effect of the inflation variable is by looking at the correlation between both variables. The coefficient of correlation, calculated with the original continuous variables is very low, 0.05. This coefficient could be influenced by outliers that play a different role when we use discrete variables. Thus, we calculate a measure using the discretized variables and, although the result is not so strong (0.55% of cases show a distance lower than two in absolute terms) we can conclude that there is no clear correlation between central bank independence and inflation in our sample.
This result differs from the results obtained in previous researches by García-Herrero and del Río (2003) who found a negative relationship between the degree of central bank independence and the emergence of financial crisis. A multivariate linear probit and logit models are used respectively. [13] Linear models do not have the flexibility to capture non monotonic relationships as we have found, so it is reasonable that results differ as we have a much more flexible methodological approach.
Conclusions
In this paper, we analyze the role of a set of variables in explaining banking crises and specifically the role of monetary policy. We applied two data analysis methodologies from the field of Machine Learning, C4.5 algorithm and Rough Set theory, to a sample of countries in the period 1981 to 1999 to assess to what extent it is worthwhile including these tools among the arsenal to prevent financial crisis.
We found that these tools are competitive alternatives to existing prediction models for this problem and have great potential capacities that undoubtedly make them attractive for application to the field of business classification. The results we obtained in terms of classification are quite good for both models with an 80% of correct classifications using the test. This result is quite satisfactory compared with previous analyses based on traditional statistical techniques. For example, Demirgüç-Kant and Detragiache (1997) obtained worse results in terms of insample classification accuracy using a multivariate logit model to study the factors associated with the emergence of systemic banking crises, and in general the corrected Rsquare are well below this percentage (Domaç and Martinez Peria, 2000; Eichengreen and Arteta, 2000). Besides, in line with previous researches (Demirgüç-Kant and Detragiache, 1997; Eichengreen and Arteta, 2000) our work has also shown the significance of some variables such as Inflation, Domestic Credit Growth, Real GDP per capita, and Bank Foreign Liabilities to Foreign Assets.
Besides that, our empirical results show that these techniques offer a great predictive accuracy as they are non-parametric methods. Thus, they do not require the pre-specification of a functional form, or the adoption of restrictive assumptions about the characteristics of statistical distributions of the variables and errors of the model. The decision models provided by both methods are easily understandable. This representation of the results makes it easier for economic interpretation than other non-parametric techniques like Neural Networks or Support Vector Machines. Moreover, the flexibility of the decision rules with changes of the models over the time allows us to adapt them gradually to the appearance of new cases representing changes in the situation.
In practical terms, the decision rules generated can be used to preselect countries to examine more thoroughly, quickly and inexpensively, thereby, managing the financial user's time efficiently. They can also be used to check and monitor countries as a "warning system" for investors, management, financial analysts, banks, auditors, policy holders and consumers. Of course, for this approach to be useful in real life, to count with timing and reliable databases -what could be not always the case- is essential. The current crisis has made evident important gaps of information in this respect to the assessment of financial stability and an intense work is in progress by the IMF and the FSB (Financial Stability Board) to fill in most of these gaps.[14] Moreover, to overcome the problem of lack of timing information a useful extension of this work could be to build a model with data lagged more than 1 year that allows us to predict a crisis with less timely data.
In spite of these problems, our focus is to show the suitability of these machine-learning techniques as support decision methods, without replacing the expert's opinion. To finish, we can extract some tentative conclusions in terms of economic policy. First we can highlight the crucial role played by real interest rates in the emergence of a crisis. Both models support the idea that high real interest rates contribute to financial instability. Second, the importance of the monetary policy to recover the confidence once it is lost. Third, the models support the idea that the effectiveness of the policies based on monetary commitments in recovering confidence does not follow linear rules regarding these variables but depends on the credibility of the commitments that these policies imply.
For example, higher central bank independence does not always guarantees a higher level of stability. It depends on the quality of the design of the commitment. A clearly specified commitment, consistent with the specific real and political situation, determines its credibility and, therefore, its effectiveness.
Footnotes
[1] This work has been partially supported by Banco Santander Central Hispano & Universidad Complutense de Madrid of Spain through project ref. Santander-UCM PR34/07-15788.
[2] See for example: "Communication from the Commission to the European Council. A European Economic Recovery Plan". European Commission. 26.11.2008; "State aid: Overview of national rescue measures and guarantee schemes". European Commission. 18.11.2008; US bail out plan: "http://clipsandcomment.com/wpcontent/uploads/2008/10/senate_bailout.pdf"
[3] Though this approach provides numerous interesting insights, a questionable aspect of the work is that the criteria used to judge which variables are useful signals is somewhat arbitrary.
[4] The study also examines balance-of-payments crises using the same methodology.
[5] In his words, "the issue of financial stability was part of the central banks' genetic code".
[6] For a description of the role of central banks in financial stability across regimes see Borio and Lowe (2002).
[7] The amount of risk that bank managers choose to take on, however, is likely to exceed what is socially optimal because of limited liability. Hence the need for bank regulators to impose minimum capital requirements and other restrictions. When bank deposits are insured, incentives to take on excessive risk are even stronger.
[8] According to Mishkin (1996), most banking panics in the U. S. were preceded by an increase in short term interest rates.
[9] Higher real interest rates are likely to hurt bank balance sheets even if they can be passed on to borrowers, as higher lending rates result in a larger fraction of non-performing loans.
[10] For an in-depth discussion of the theory of bank runs, see Bhattacharya and Thakor (1994).
[11] This mechanism seems to have been at work in Argentina in 1995: following the Mexican devaluation in December 1994, confidence in the Argentinean peso plunged, and the banking system lost 16 percent of its deposits in the first quarter of 1995 (IM F, 1996).
[12] In terms of macroeconomic performance, however, it is hard to argue that inflation targeting is clearly superior.
[13] Non-linear probit/logit models can be developed by performing a non-monotonic transformation of the variables or a transformation into nominal categorical variables.
[14] The financial crisis and information gaps progress report. Action plans and timetables prepared by the IM F staff and the FSB Secretariat. May 2010.
Appendix
Financial crisis database
Dependent variable
Systemic and non-systemic banking crises dummy: Equals one during episodes identified as in Caprio and Klingebiel (2003). They present information on 117 systemic banking crises (defined as much or all of bank capital being exhausted) that have occurred since the late 1970s in 93 countries and 51 smaller non-systemic banking crises in 45 countries during that period. The information on crises is cross-checked with that of Domaç and Martinez-Peria (2000) and with IM F staff reports and financial news.
The objective variables:
- Monetary policy strategies: These variables (Exchange rate target, Monetary policy target) are dummies. The exchange rate target takes four values depending on the exchange rate regime: free floating, managed floating, pegged currencies and currency board. The Monetary policy target equals one during periods in which targets were based on monetary aggregates, two when the objective was inflation, three when the two variables are into the objective function and zero in other cases, according to the chronology of the Bank of England survey of monetary frameworks, in Mahadeva and Sterne (2000). Since it provides a chronology for the 1990s, we have complemented it with information from other sources for the previous years. Regarding exchange rate arrangements, we use classifications of exchange rate strategies in Reinhart and Rogoff (2002), Kuttner and Posen (2001), and Berg et al., (2002) for Latin America countries. Data for monetary and inflation targets were complemented with the information taken from Kuttner and Posen (2001) and Carare and Stone (2003). It should be noted that some judgement has gone into the classification of regimes.
- Central Bank Independence measures to what extent the central banks are legally independent according to their charters, following the approach of Cukierman et al. (1992). This variable goes from 0 (least independent) to 1 (most independent) and is taken from Cukierman et al. (1992), for the 1970s and 1980s). For the 1990s, Mahadeva and Sterne (2000) and Cukierman et al., (2002). The index of independence is assumed to be constant through every year of each decade.
Control Variables:
- Macroeconomic variables
- Inflation: Percentage change in the GDP deflator. Source: International Monetary Fund, International Financial Statistics, line 99bir.
- Real Interest Rate: Nominal interest rate minus inflation in the same period, calculated as the percentage change in the GDP deflator. Source: International Monetary Fund, International Financial Statistics. Where available, money market rate (line 60B); otherwise, the commercial bank deposit interest rate (line 60l); otherwise, a rate charged by the Central Bank to domestic banks such as the discount rate (line 60).
- Net Capital Flows to GDP: Capital Account + Financial Account + Net Errors and Omissions. Source: International Monetary Fund, International Financial Statistics, lines (78bcd + 78bjd +78cad).
- Real GDP per capita in 1995 US dollars: This variable is expressed in US dollars instead of PPP for reasons of data availability. GDP per capita in PPP was available only for two points in time. Source: The World Bank, World Tables; and EBRD, Transition Report, for some transition countries.
- Real GDP growth: Percentage change in GDP Volume (1995=100). Source: International Monetary Fund, International Financial Statistics (line 99bvp) where available; otherwise, The World Bank, World Tables; and EBRD, Transition Report, for some transition countries.
- World Real GDP growth: Percentage change in GDP Volume (1995=100). Source: International Monetary Fund, International Financial Statistics (line 99bvp) where available; otherwise, The World Bank, World Tables; and EBRD, Transition Report, for some transition countries.
- Financial variables
- Domestic credit growth: Percentage change in domestic credit, claims on private sector. Source: International Monetary Fund, International Financial Statistics, line 32d.
- Bank cash to total assets: Reserves of Deposit Money Banks divided by total assets of Deposit Money Banks. Source: International Monetary Fund, International Financial Statistics, line 20 divided by lines (22a + 22b + 22c +22d +22f).
- Bank foreign liabilities to foreign assets: Deposit money banks foreign liabilities to foreign assets. Source: International Monetary Fund, International Financial Statistics, lines (26c+26cl) divided by line 21.
- Previous crisis: This variable equals zero if the country has not previous crisis; one, if the country has suffered one previous crisis; two, in case of two or three previous crisis, and, three, otherwise.
References
Berg, A., Borensztein, E., & Mauro, P. (2002). An evaluation of monetary regime options for Latin America. IMF WP 211.
Berger, H., Haan, J. & Eijffinger, S. (2001). Central bank independence: an update of theory and evidence. Journal of Economic Surveys, 15(1), 33-40.
Bhattacharya S. & Thakor, A. (1994). Contemporary banking theory. Journal of Financial Intermediation, 3(1), 95-133.
Bonsón-Ponte, E., Escobar-Rodríguez, T. & Martín-Zamora, M.P. (1996). Sistemas de inducción de árboles de decisión: utilidad en el análisis de crisis bancarias. Zaragoza: Biblioteca Electrónica CiberConta, http://ciberconta.unizar.es.
Bordo, M. (1986). Financial crises, banking crises, stock market crashes, and the money supply: some international evidence, 1870-1933. In Capie, F. & Wood, G. (eds.), Financial crises and the world banking system. New York: St. Martin's.
Borio, C. & Lowe, P. (2002). Asset prices, financial and monetary stability: Exploring the nexus, BIS Working Papers 114.
Breiman, L., Friedman, J. H., Olshen, R. A. & Stone, C. J. (1984). Classification and regression trees. Belmont, California: Wadsworth International Group.
Caprio, G., Hanson, J. & Litan, R. (2005). Financial crisis. Lessons from the past. Preparation for the future. Washington D.C.: Brookings Institution Press.
Caprio, G. & Klingebiel, D. (1997). Bank Insolvencies: Cross-Country Experience, Policy Research. The World Bank WP 1620.
Caprio, G. & Klingebiel, D. (2003). Episodes of systemic and borderline financial crises. Dataset mimeo, The World Bank.
Carare, A. & Stone, M. (2003). Inflation targeting regimes, IMF WP 9.
Cukierman, A., Webb, S. B. & Neyapti, B. (1992). Measuring the independence of central banks and its effect on policy outcomes. The World Bank Economic Review, 6, 353-398.
Cukierman, A., Miller, G. P. & Neyapti, B. (2002). Central bank reform, liberalization and inflation in transition economies an international perspective. Journal of Monetary Economics, 49, 237-264.
Demirgüç-Kant, A. & Detragiache, E. (1997). The determinants of banking crisis: Evidence from developing and developed countries. IMF WP, 106.
Dimitras, A., Slowinski, R., Susmaga, R. & Zopounidis, C. (1999). Business failure prediction using Rough Sets. European Journal of Operational Research, 114, 263-280.
Domaç, I. & Martínez-Peria, M. S. (2000). Banking crises and exchange rate regimes: Is there a link? The World Bank WP, 2489.
Eichengreen, B. & Arteta, C. (2000). Banking crisis in emerging markets: Presumptions and evidence. Center for International and Development Economics research (University of California, Berkeley).
Fisher, I. (1933). The debt-deflation theory of great depressions. Econometrica, 1(4), 337-357.
Frank, E. (2000). Pruning decision trees and lists. New Zealand: University of Waikato, Ph. D. Dissertation.
Friedman, M. & Schwartz, A. J. (1963). A monetary History of the United States, 1867-1960. Princeton, NJ: Princeton University Press.
García-Herrero, A. (1997). Monetary impact of a banking crisis and the conduct of monetary policy. IMF WP, 124.
García-Herrero, A. & Del Rio, P. (2003). Financial Stability and the design of monetary policy. Documento de trabajo Banco de España, 15.
Goldstein, M. (2005). The next emerging-market financial crisis. In Caprio, G., Hanson, J. A., Litan, R. E. (eds.), Financial crisis. Washington D. C: Brooklings Instituition, pp. 121-209.
González-Hermosillo, B. (1996). Banking sector fragility and systemic sources of fragility, IM F WP 12.
Gorton, G. (1998). Banking panics and business cycles. Oxford Economic Papers, 40, 751-781.
Greco, S., Matarazzo, B., & Slowinski, R. (1998). A new rough set approach to evaluation of bankruptcy risk, In Zopounidis, C. (ed.), New operational tools in the management of financial risks. Dordrecht: Kluwer Academic Publishers, 121-136.
Greco, S., Matarazzo, B., & Slowinski, R. (2001). Rough sets theory for multicriteria decision analysis. European Journal of Operational Research, 129(1), 1-47.
Gupta, P. (1996). Currency crises, banking crises and twin crises: A comprehensive review of the literature. International Monetary Fund. Mimeo.
Hanson, J. A. (2005). Postcrisis challenges and risks in East Asia and Latin America. In Caprio, G., HANSON , J. A. & LITAN , R. E. (eds.), Financial crisis. Washington D.C: Brooklings Instituition, pp. 15-61
Houben, A., Kakes, J. & Schinasi, G. (2004). Toward a framework for safeguarding financial stability. IMF WP 101.
Issing, O. (2003). Monetary and financial stability: Is there a tradeoff? Conference on Monetary stability, financial stability and the business cycle, March 28-29, Bank for International Settlements, Basle.
Kaminsky, G. & Reinhart, C. (1999). The twin crises: the causes of banking and balance-of-payments problems. American Economic Review, 89(3), 473-500.
Kuttner, K. N. & Posen, A. S. (2001). Beyond bipolar: A three-Dimensional Assessment of Monetary frameworks. Oesterreichische Nationalbank WP, 52.
Laitinen, E. K. (1992). Prediction of failure of a newly founded firm. Journal of Business Venturing, 7(4), 323-340.
Lindgren, C. J., García, G. & Saal, M. I. (eds.). (1996). Bank soundness and macroeconomic policy, International Monetary Fund. New York: imf Press.
Mahadeva, L. & Sterne, G. (eds.). (2000). Monetary policy frameworks in a global context. London: Routledge.
Martín-Zamora, M. P. (1999). La solvencia en las cajas rurales provinciales andaluzas (1978-1985). Huelva: Servicio de Publicaciones, Universidad de Huelva.
McKee, T. (2000). Developing a bankruptcy prediction model via rough sets theory. International Journal of Intelligent Systems in Accounting, Finance and Management, 9, 159-173.
Mishkin, F. S. (1996). Understanding financial crises: A developing country's perspective. Cambridge, Mass: National Bureau of Economic Research WP, 5600.
Padoa-Schioppa, T. (2002). Central banks and financial stability: Exploring a land in between. Paper presented at the Second ECB Central Banking Conference The transformation of the European financial system, Frankfurt am Main, October.
Pawlak, Z. (1991). Rough sets. Theoretical aspects of reasoning about data. Dordrecht/ Boston/London: Kluwer Academic Publishers.
Pill, H. & Pradhan, M. (1995). Financial indicators and financial change in Africa and Asia. IMF WP, 23.
Predki, B., Slowinski, R., Stefanowski, J., Susmaga, R. & Wilk, S. (1998). ROSE -Software Implementation of the Rough Set Theory. In L. Polkowski, A. Skowron (eds.), Rough sets and current trends in computing, lecture notes in artificial intelligence (pp. 605-608), vol. 1424. Berlin: Springer-Verlag.
Predki, B. & Wilk, S. (1999). Rough Set based data exploration using ROSE System. In Z. W. Ras, A. Skowron (eds.), Foundations of intelligent systems, lecture notes in artificial intelligence (pp. 172-180), vol. 1609. Berlin: Springer-Verlag.
Quinlan, J. R. (1979). Discovering rules by induction from large collections of examples. In D. Michie (ed.), Expert systems in the micro electronic age (pp. 168-201). Edinburgh, UK: Edinburgh University Press.
Quinlan, J. R. (1983). Learning efficient classification procedures and their application to chess endgames. In R. S. Michalski, J. G. Carbonell y T. M. Mitchell (eds.), Machine learning: An artificial intelligence approach (pp. 463-482). Palo Alto, California: Tioga Publishing Company.
Quinlan, J. R. (1986). Induction of decision trees. Machine Learning, 1(1), 81-106.
Quinlan, J. R. (1993). C4.5: Programs for machine learning. San Mateo, California: Morgan Kaufmann.
Reinhart, C. M. & Rogoff, K. S. (2002). The modern history of exchange rate arrangements: A reinterpretation, NBER WP, 8963, Cambridge: National Bureau of Economic Research.
Sanchis, A., Segovia, M. J., Gil, J. A., Heras, A. & Vilar, J. L. (2007). Rough sets and the role of the monetary policy in financial stability (macroeconomic problem) and the prediction of insolvency in insurance sector (microeconomic problem). European Journal of Operational Research, 181(3), 1554-1573.
Schinasi, G. J. (2003). Responsibility of central banks for stability in financial markets. IMF WP 121.
Schwartz, A. (1995). Systemic risk and the macroeconomy. In G. Kaufman (ed.), Banking financial markets and systemic risk. Research in financial services, Private and public policy, 7, JAI . Hampton Press Inc.
Slowinski, R. (1993). Rough set learning of preferential attitude in multicriteria decision making. In J. Komorowski & Z. W. Ras (eds.), Methodologies for Intelligent Systems. Lecture Notes in Artificial Intelligence (pp. 642-651), vol. 689. Berlin: Springer-Verlag.
Slowinski, R. & Zopounidis, C. (1995). Application of the rough set approach to evaluation of bankruptcy risk. International Journal of Intelligent Systems in Accounting, Finance and Management, 4(1), 27-41.
Stiglitz, J. & Furman, J. (1998). Evidence and insights from East Asia. Brookings papers on economic activity, 2, 1-135.
Tam, K. Y. & Kiang, M. Y. (1992). Managerial applications of neural networks: The case of bank failure predictions. Management Science, 38(7), 926-947.
Witten, I. H. & Frank, E. (2005). Data mining: Practical machine learning tools and techniques (2nd Edition). San Francisco: Morgan Kaufmann.
How to Cite
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Download Citation
Article abstract page views
Downloads
License
Copyright (c) 2011 Innovar

This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License.
All contents published by Innovar are open access and licensed under the Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International copyright license (cc by-nc-nd 4.0).
Once the articles for a specific issue have been selected, and before starting editorial production, authors must sign a transfer of economic rights. Innovar adheres to Colombian regulations on copyright.
Material from this journal may be reproduced or quoted for scholarly purposes, citing the source.
This work is licensed under a Creative Commons License:




















