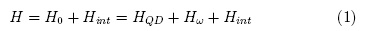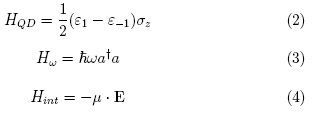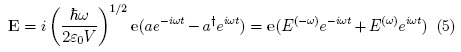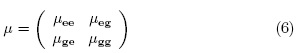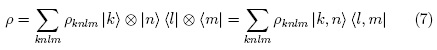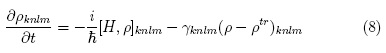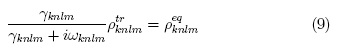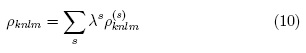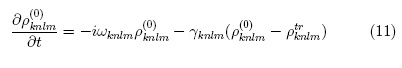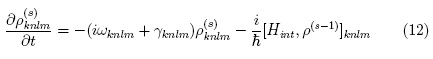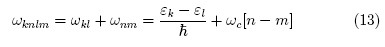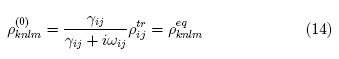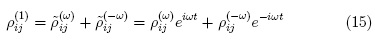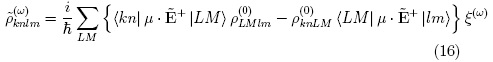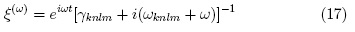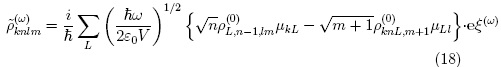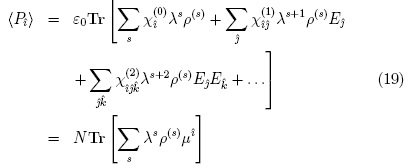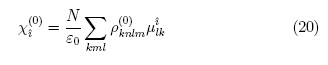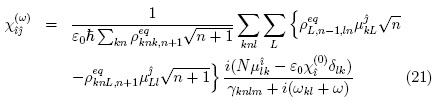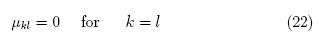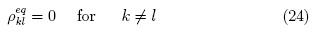TEORÍA COMPLETAMENTE CUÁNTICA DE LA SUSCEPTIBILIDAD ELÉCTRICA LINEAL
ALL QUANTUM THEORY OF LINEAR ELECTRICAL SUSCEPTIBILITY
DOI:
https://doi.org/10.15446/mo.n52.58893Keywords:
Susceptibilidad lineal, susceptibilidad espontánea, índice de refracción dependiente del número de fotones, puntos cuánticos asimétricos. (es)Linear susceptibility, spontaneous susceptibility, photon number dependent refraction index, asymmetric quantum dots. (en)
Downloads
En este trabajo derivamos una expresión completamente cuántica para la susceptibilidad eléctrica lineal usando un formalismo de matriz densidad donde el campo electromagnético también está cuantizado. Del tratamiento se deduce de manera natural una susceptibilidad de orden cero. Mediante el estudio de la dependencia de la susceptibilidad con la asimetría de la materia y el estado cuántico de la luz, predecimos fenómenos nuevos e intrigantes como el índice de refracción dependiente del número de fotones.
Here we derive a completely quantum mechanical expression for linear susceptibility using a density matrix formalism where the electromagnetic field is also quantized. A zeroth order susceptibility emerges naturally from the treatment.
By studying the dependence of susceptibility on material asymmetry and on the quantum state of light, we predict new and intriguing phenomena such as photon number dependent refraction index.
ALL QUANTUM THEORY OF LINEAR ELECTRICAL SUSCEPTIBILITY
TEORÍA COMPLETAMENTE CUÁNTICA DE LA SUSCEPTIBILIDAD ELÉCTRICA LINEAL
Jairo D. García1, Herbert Vinck-Posada2, Boris A. Rodríguez1
1 Instituto de Física, Facultad de Ciencias Exactas y Naturales, Universidad de Antioquia UdeA; Calle 70 No. 52-21, Medellín-Colombia.
2 Departamento de Física, Facultad de Ciencias, Universidad Nacional de Colombia, Sede Bogotá, Carrera 30 Calle 45-03, CP111321, Bogotá, Colombia.
Herbert Vinck-Posada: hvinckp@unal.edu.co
(Recibido: Agosto/2015. Aceptado: Enero/2016)
Abstract
Here we derive a completely quantum mechanical expression for linear susceptibility using a density matrix formalism where the electromagnetic field is also quantized. A zeroth order susceptibility emerges naturally from the treatment. By studying the dependence of susceptibility on material asymmetry and on the quantum state of light, we predict new and intriguing phenomena such as photon number dependent refraction index.
Keywords: Linear susceptibility, spontaneous susceptibility, photon number dependent refraction index, asymmetric quantum dots.
Resumen
En este trabajo derivamos una expresión completamente cuántica para la susceptibilidad eléctrica lineal usando un formalismo de matriz densidad donde el campo electromagnético también esta cuantizado. Del tratamiento se deduce de manera natural una susceptibilidad de orden cero. Mediante el estudio de la dependencia de la susceptibilidad con la asimetría de la materia y el estado cuántico de la luz, predecimos fenómenos nuevos e intrigantes como el índice de refracción dependiente del número de fotones.
Palabras clave: Susceptibilidad lineal, susceptibilidad espontánea, índice de refracción dependiente del número de fotones, puntos cuánticos asimétricos.
Introduction
The analytical expressions of electrical susceptibilities of different orders are well known in the semiclassical approximation [1]. They have been extensively used to understand the susceptibility dependence on material symmetry properties, dipole moments, and energy levels. Semiclassical expressions have also been proved to be useful both to obtain reliable numerical predictions of susceptibility values [2], as to envision strategies to enhance nonlinear responses [3-5]. Nonetheless, a fully quantum mechanical theory of susceptibility is desirable not only because it should be more accurate, but because it would allow to understand the effect of the quantum state of light on the susceptibility, if there is any. This is especially important as nonclassical states of light, microcavities and nanostructures are nowadays so frequently used in laboratories [6, 7].
Model
The theory can be applied to many kinds of matter but, for definiteness, we shall think of a quantum dot (QD) with two active levels whose excited |1) and ground |-1) states have energies |ε1) and |ε-1), respectively. This QD interacts with a single mode |ωc) of the electromagnetic field in a cavity of volume V. In the dipolar approximation the system Hamiltonian reads [7]:
where:
α† and a are the creation and annihilation operators of the field mode and E is the electric field operator which has polarization vector e. Using standard second quantization such mode can be written as:
Due to the fact that QDs usually have peculiar shapes that break inversion symmetry [8] or may be subject to asymmetric external forces [9], the dipole moment ì can be represented as a non-diagonal matrix [10]:
where µee and µgg are different from zero.
On the other hand, we will describe the state of the system by a density matrix:
Where |k) and |l) represent QD states, while |n) and |m) represent Fock states of the field.
Analytical Solution
Using a phenomenological master equation, time evolution of the state of the system is given by:
Where, as is customary, we have added a phenomenological term 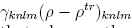 to take into account non Hamiltonian processes that change the state of the system. Such processes can be collision decays and/or pumping that push the system towards the equilibrium state peq at a rate γknlm through a transition state ptr :
to take into account non Hamiltonian processes that change the state of the system. Such processes can be collision decays and/or pumping that push the system towards the equilibrium state peq at a rate γknlm through a transition state ptr :
We will seek a perturbative solution of 8 in powers of a parameter λ varying between zero and one that characterizes the perturbation intensity:
For the density matrix 7 to be a solution of equation 8, the following relations should be satisfied:
Where ωknlm is the system transition frequency:
Finding contributions to density matrix at different orders is possible thanks to these recurrence relations. Zeroth order contribution is given by the steady state solution of eq. 11:
This solution plays an important role: given the iterative approach it will appear in higher order terms. In the semiclassical theory this zeroth order density matrix is assumed to be diagonal [1]. Such statement can no longer be accepted in a fully quantum mechanical treatment because matrix elements associated with the electric field are not diagonal in the Fock basis [7].
Once known the zeroth order density matrix we can integrate eq. 12 with s = 1 to find the first order contribution (p(ij1)):
The integration procedure is described with detail in standard text books [1] and leads to the expression:
Where L runs over QD states, M runs over Fock states and:
Further algebraic manipulations allow us to obtain:
A similar expression is found for 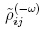 .
.
Having the contributions to density matrix up to first order we can find and compare the expectation values of the Cartesian components of polarization along direction î by two ways: using an expansion on the electric field and using the dipole moment:
Where N is the number of atoms per unit volume. A very important difference between the semiclassical and the all quantum mechanical theories of susceptibility is that the last one requires to take the trace over the Fock states of the electric field. As a result, additional time dependent factors appear in every expectation value. Finding the susceptibilities of different order is made possible only by appropriated matching of the combinations of factors in the left hand side of eq 19 with those of the right hand side. It is to make easier such task that factor λ7- was introduced.
Results
Replacing in the values of corresponding orders of the density matrix in we get the following expressions for zeroth and first order susceptibilities:
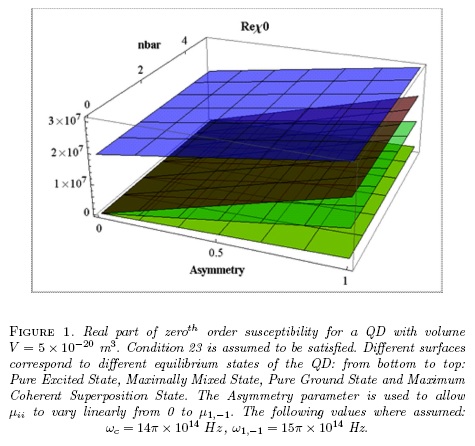
Eq. 20 predicts a polarization even when the field has zero amplitude. Such a spontaneous polarization is evident in polar materials which are all non centrosymmetric. Fig. 1 shows the real part of zeroth order susceptibility for different equilibrium states of a QD with some parameters taken from [11]. The imaginary part is null for every equilibrium state and every value of asymmetry. For a spontaneous polarization to be seen in symmetric materials, a Coherent Superposition Equilibrium State is required -blue surface in Fig. 1.
Note that zeroth order susceptibility is null when the following conditions are satisfied:
i) The QD is fully symmetric:
ii) The QD reduced density matrix is diagonal:
iii) The QD is fully symmetric:
Conditions 22 to 24 are all implicit in the usual semiclassical treatment [1].
It is enlightening to see that, when condition 23 is satisfied, zeroth order susceptibility reduces to:
Eq. 21 expresses the all quantum linear susceptibility with the corrections due to spontaneous polarization. Note that, if condition 22 is satisfied, those contributions are null. Even then, spontaneous polarization might have effects on the second order susceptibility; that has to be figured out yet.
Expression 21 predicts a dependence of linear susceptibility on the average photon number for some equilibrium states of light; this is a completely new phenomenon that has no semiclassical counterpart. It may be compared to the Intensity Dependent Refraction Index phenomenon, but they are of a very different nature. The first one is linear and is more relevant for low intensity fields while the last one is nonlinear and typically requires high intensities fields.
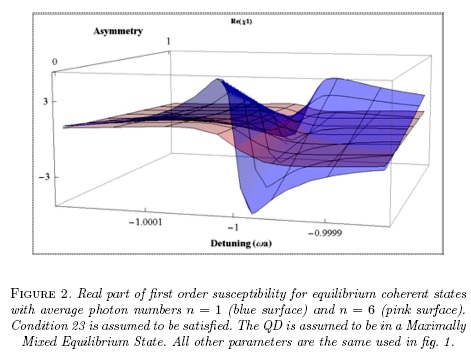
As an example fig. 2 shows the real part of the linear susceptibility of a QD in a Maximally Mixed Equilibrium State interacting with Coherent States of the field with different average photon numbers. The imaginary part of susceptibility -not shown- is also photon number dependent.
So, measuring the dispersion or the absorption of a QD using different low intensity Coherent States would help to test the validity of this if predictions. This should sound not so weird to the reader as it has been proved that the capture of a single photon into a cavity containing a QD affects the probability of admittance of a second photon [12].
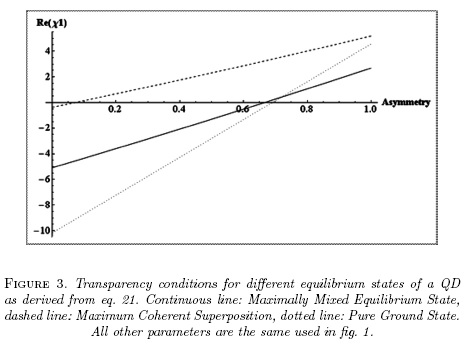
Fig. 2 reveals how important are for the linear susceptibility diagonal terms of dipole moment. In fact, such figure suggests not only that susceptibility size and sign depend on asymmetry, but that transparency can be induced on the QD. That may happen if asymmetries are such that factor 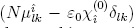 in eq. 21 becomes zero. This condition is hard to achieve as it depends on the material and the equilibrium states. Notwithstanding, it may eventually be achieved by controlled application of external asymmetric constrains that force diagonal dipole moments to take appropriated values (see fig. 3). Inducing such a transparency would be a proof of the physical reality of zeroth order susceptibility.
in eq. 21 becomes zero. This condition is hard to achieve as it depends on the material and the equilibrium states. Notwithstanding, it may eventually be achieved by controlled application of external asymmetric constrains that force diagonal dipole moments to take appropriated values (see fig. 3). Inducing such a transparency would be a proof of the physical reality of zeroth order susceptibility.
Finally we would like to mention that, as the reader might expect, eq. 21 for linear susceptibility reduces to semiclassical the expression if conditions 23, 26 and 27 are fulfilled:
Conclusions
This is, to the best of our knowledge the first time a completely quantum mechanical expression for linear susceptibility has been derived. Other authors have claimed to achieving complete quantum-mechanical expressions for nonlinear susceptibilities but, at some point, they use the semiclassical approximation [13], [14]. Our expression predicts intriguing phenomena such as photon number dependent refraction index and contains the semiclassical expression as a particular case. Determining the influence of the equilibrium state of light on the susceptibility is also allowed by this expression. A zeroth order susceptibility that can be used to take into account the effects of spontaneous polarization on susceptibility is also predicted and an experiment.
References
[1] R. W. Boyd, Nonlinear Optics (Academic Press, 1992).
[2] Y. R. Shen, The Principles of Nonlinear Optics (Wiley, 1984).
[3] E. Rosencher and P. Bois, Phys. Rev. B 44, 11315 (1991).
[4] F. Capasso, C. Sirtori, and A. Y. Cho, IEEE Journal of Quantum Electronics 30, 1313 (1994).
[5] M. Sugawara, H. Ebe, N. Hatori, M. Ishida, Y. Arakawa, K. O. T. Akiyama, and Y. Nakata, Phys. Rev. B 69, 235-332 (2004).
[6] K. J. Vahala, Nature 424, 839 (2003).
[7] C. Gerry and P. Knight, Introductory Quantum Optics (CAMBRIDGE UNIVERSITY PRESS, 2005).
[8] L. Jacak, Eur. J. Phys. 21, 487 (2000).
[9] O. V. Kibis, G. Y. Slepyan, S. A. Maksimenko, and A. Hoffmann, Phys. Rev. Lett. 102, 023601 (2009).
[10] I. G. Savenko, O. V. Kibis, and I. A. Shelykh, Phys. Rev. A 85, 053818 (2012).
[11] A. Majumdar, M. Bajcsy, and J. Vuckovic, Phys. Rev. A 85, 041801(R) (2012).
[12] A. Faraon, I. Fushman, D. Englund, N. Stoltz, P. Petroff, and J. Vuckovic, Nature Physics 4, 859 (2008).
[13] R. Andrews, E. R. Pike, S. Sarkar, and C. Adlard, Pure Appl. Opt. 7, 293 (1998).
[14] L. C. Lew-Yan-Voon and L. R. Ram-Mohan, Phys. Rev. B 50, 14421 (1994).
How to Cite
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Download Citation
CrossRef Cited-by
1. Jairo D. García, Boris A. Rodríguez. (2023). Quantum extension to the semiclassical theory of electrical susceptibility. Journal of the Optical Society of America B, 40(11), p.2999. https://doi.org/10.1364/JOSAB.502568.
Dimensions
PlumX
Article abstract page views
Downloads
License
Those authors who have publications with this journal, accept the following terms:
a. The authors will retain their copyright and will guarantee the publication of the first publication of their work, which will be subject to the Attribution-SinDerivar 4.0 International Creative Commons Attribution License that permits redistribution, commercial or non-commercial, As long as the Work circulates intact and unchanged, where it indicates its author and its first publication in this magazine.
b. Authors are encouraged to disseminate their work through the Internet (eg in institutional telematic files or on their website) before and during the sending process, which can produce interesting exchanges and increase appointments of the published work.