Abstract

UNIVERSO CON ENERGÍA OSCURA HOLOGRÁFICA

In this work we explore a Holographic Dark Energy Model in a flat Friedmann-LemaÎtre-Robertson-Walker Universe, which contains baryons, radiation, cold dark matter and dark energy within the framework of General Relativity. Furthermore, we consider three types of phenomenological interactions in the dark sector. With the proposed model we obtained the algebraic expressions for the cosmological parameters of our interest: the deceleration and coincidence parameters. Likewise, we graphically compare the proposed model with the ΛCDM model.

En este trabajo exploramos un modelo de energía oscura holográfica en un universo plano de Friedmann-Lemaître-Robertson-Walker, que contiene bariones, radiación, materia oscura fría y energía oscura en
el marco de la relatividad general. Además, consideramos tres tipos de interacciones fenomenológicas en el sector oscuro. Con el modelo propuesto obtuvimos las expresiones algebraicas para los parámetros cosmológicos de nuestro interés: los parámetros de desaceleración y coincidencia. Del mismo modo, comparamos gráficamente el modelopropuesto con el modelo ΛCDM.

(Recibido: 12/2019. Aceptado: 04/2020)

In this work we explore a Holographic Dark Energy Model in a flat Friedmann-Lematre-Robertson-Walker Universe, which contains baryons, radiation, cold dark matter and dark energy within the framework of General Relativity. Furthermore, we consider three types of phenomenological interactions in the dark sector. With the proposed model we obtained the algebraic expressions for the cosmological parameters of our interest: the deceleration and coincidence parameters. Likewise, we graphically compare the proposed model with the ΛCDM model.

Keywords: Holographic dark energy, general relativity, Friedmann- Lemaître -Robertson-Walker Universe, ΛCDM model.

Resumen

Palabras clave: Energía oscura holográfica, relatividad general, Universo Friedmann- Lemaître -Robertson-Walker, modelo ΛCDM.

Introduction

Nowadays it is well known that cosmological models must describe an accelerated expansion of the Universe at the present era [1–3]. To achieve this, sources of matter capable of generating this acceleration are considered, which are commonly dubbed dark energy [4].

A cosmological constant Λ is an important candidate for dark energy providing a good explanation for the current acceleration. But the cosmological constant faces some problems [5, 6] such as, the mismatch between the expected value of the vacuum energy density and the energy density of the cosmological constant, and the lock of an explanation of why densities of dark energy and dark matter are of same order at present while they evolve in rather different ways. So, as an alternative, dynamic dark energy models have been proposed and analyzed in the literature, highlighting the Holographic Dark Energy Models [7–12], these originate from the holographic principle in Cosmology [13]. The holographic principle asserts that the number of relevant degrees of freedom of a system dominated by gravity must vary along with the area of the surface bounding the system [14]. According to this principle, the vacuum energy density can be bounded [15] as ρ_x ≤ M_p²L⁻², where ρ_x is the dark energy density (the vacuum energy density), M_p is the reduced Planck mass, and L is the size of the region (i.e IR cutoff). This bound implies that, the total energy inside a region of size L, should not exceed the mass of a black hole of the same size. From effective quantum field theory, an effective IR cutoff can saturate the length scale, so that the dark energy density can be written as                            [16], where c is a dimensionless parameter, and the factor 3 is for mathematical convenience. In the Holographic Ricci Dark Energy Model, L is given by the average radius of the Ricci scalar curvature |R|^−1/2, so in this case the density of the Holographic Dark Energy (hereafter, abbreviated as HDE) is ρ_x ∝ R.

In a spatially flat Friedmann- Lemaître -Robertson-Walker (FLRW) universe, the Ricci scalar of the spacetime is given by R = 6(H˙ + 2H²), where H(t) = a˙(t)/a(t) is the Hubble expansion rate of the universe in terms of the scale factor a, where the dot denotes the derivative with respect to the cosmic time t. In this sense, the authors of reference [7] introduced the following generalization:

                                                         ρ_x = 3(αH² + βH^˙ )                                     (1)

where α and β are constants to be determined. This model works fairly well in fitting the observational data, and it is a good candidate to alleviate the cosmic coincidence problem [8–11, 17].

Basic Equations

In the framework of General Relativity we consider a homogeneous, isotropic and flat universe scenario through the FLRW metric [18] ds² = dt² − a²(t)[dr² + r²(dθ² + sin² θdφ²)] (2)

where (t,r,θ,φ) are comoving coordinates. Friedmann’s equations in this context are written as

                                                                     3H²         =    ρ                                       (3)

                                                       2H^˙ + 3H²              = −p                                     (4)

where ρ is the total energy density, p is the total pressure and 8πG = c = 1 is assumed. Also, the conservation of the total energy-momentum tensor is given by [18]

                                                        ρ˙ + 3H(ρ + p) = 0                                     (5)

Holographic Dark Energy Model

We studied a scenario that contains baryons, radiation, cold dark matter and HDE, i.e. ρ = ρ_b + ρ_r + ρ_c + ρ_x and p = p_b + p_r + p_c + p_x. In addition, we consider a barotropic equation of state for the fluids, p_i = ω_i ρ_i with ω_b = 0, ω_r = 1/3, ω_c = 0 and ω_x = ω. By including a phenomenological interaction in the dark sector, we split the conservation equation (5) in the following equations.

where prime denotes a derivative with respect to lna³ and Γ represents the interaction function between cold dark matter and the HDE. From Eqs. (1) and (3) we obtain

Given that radiation and baryons are separately conserved, we have ρ_r ∝ a⁻⁴ and ρ_b ∝ a⁻³.

From here it is easy to realize that

On the other hand, in the study of HDE scenarios usually it is only considered the dark sector, since these predominate in the current universe. Also, it is possible to analyze a HDE scenario with two different approaches, the first one considers a variable state parameter for the HDE or assuming a parameterization as shown in [11], while the second approach considers an interaction term between the dark components [8, 12, 19]. We work in the last approach.

For convenience, we denote the energy density of the dark sector as ρ_d := ρ_c + ρ_x. Then, by combining equations (6) - (7) we obtain

where the submipt 0 denotes a current value. Notice that the Eq. (8) can be easily solve when                                 . In the literature (see [20, 21] and its references) scenarios have been studied where only the dark components of the Universe are considered and a phenomenological interaction between them is included. It is usual to choose scenarios of interaction with a linear term, or linear combinations of the dark components [22]. For example, terms of interaction of the form were studied:

 

among others [20, 21]. Scenarios with linear interaction of type Γ ∝ ρ_c and Γ ∝ ρ_x, are particular cases studied in [22–24]. In the reference [23], the authors studied the interaction between dark matter and holographic dark energy, with an interaction term of the form Γ ∝ ρ, con ρ = ρ_x, ρ = ρ_c and ρ = ρ_x+ρ_c, and obtained a second order differential equation for H. While that in [24], the authors studied the interaction of dark matter and holographic dark energy with ω = ω(r), where r = ρ_c/ρ_x. Then, they obtained the interaction term Γ = Γ(ρ,ρ^’), and finally, ρ_i = ρ_i(a) and ω = ω(a). It is so that in this work we consider the following types of linear interactions [20–22]:

 

 

The energy density of the dark sector

We can convenient rewrite Eq. (8) as

including the three interaction types of our interest where the values of the constants b₁, b₂, b₃ and b₄ are shown in Table 1. The general solution of Eq. (9) is:

                                    ρd(a) = Aa−3 + B a−4 + C1 a3λ1 + C2 a3λ2                                        (10)

where the integration constants C₁ and C₂ are given by

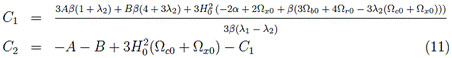
where H₀, Ω_c0, and Ω_x0 are the current values of the Hubble parameter, the density parameters for dark matter and HDE (i.e.)                                                                                  respectively. The coefficients in eq. (10) are                                                                          

 as well as

 

 

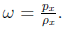The state parameter of the HDE

The state parameter of the HDE corresponds to the ratio

Using the expression (7) in Eq. (6), and the linear interactions Γ_i, we find

                                                                                                                                    

where A^˜ = (2α − 3β)(A + ρ_b0), B^˜ = 2(α − 2β)(B + ρ_r0), C^˜_1,2 = C_1,2(3βλ_1,2 + 2α) and the constant coefficients D_i are shown in table 2.

In the limit to the future, a → ∞, the expression (12) remains as                                for λ₁ > λ₂ > 0, while for λ₂ > λ₁ > 0,

we have                                

The coincidence and deceleration parameters

To examine the problem of cosmological coincidence, we define r ≡ ρ_c/ρ_x. Then, using ρ_c = ρ_d − ρ_x, together with the expression (7), we find

       

Then,           for          all          our         interactions          we          get                                                           a constant that depends on the

interaction parameters, where λ_i = max{λ₁,λ₂} for λ_i > 0.

On the other hand, the deceleration parameter q is a dimensionless measure of the cosmic acceleration in the evolution of the universe.

It is defined by                                                         [18]. Using (10), we obtain

Given the expressions (12)-(14), hereinafter we use the following values for the parameters [3]: Ω_b0 = 0,0484, Ω_r0 = 1,25 × 10⁻³,

Ω_c0 = 0,258, Ω_x0 = 0,692, H₀ = 67,8 km s⁻¹ Mpc⁻¹, and ω_ΛCDM = −1. In addition, (α₁,β₁) = (−0,0076,0) and (α₂,β₂) = (0,0074,0) [20, 21] are considered. It is very important to emphasize that the interaction models between dark energy and dark matter [20, 21, 25] are based on the premise that no known symmetry in Nature prevents or suppresses a non-minimal coupling between these components, therefore, this possibility should be investigated in the light of observational data (see, for example [26]). In some classes of these interaction models, the coincidence problem can be greatly alleviated when compared to ΛCDM. Thus, several interaction models have been proposed with both analytical and numerical solutions [20, 21, 25–27].

Note that in equation (6), Γ > 0 indicates a transfer of dark matter to dark energy and Γ < 0 indicates otherwise. It is so, that in the Fig. 1, we analyze the behavior of the interaction terms for each model. It is shown that model 1 and 2 undergo a sign change in that function, while model 3 does not. The change of sign in the interaction term highlights the domain of one of the different types of matter in each epoch of evolution of the universe (fundamentally late universe). Thus, models 1 and 2 are useful for our study of the evolution of the universe.

Figura 1. Evolution of interaction term without dimensions for holographic interaction models. The orange, green and brown lines represent Models 1, 2 and 3, respectively.

In Fig. 2 we show the evolution of the coincidence and deceleration parameters in term of the redshift z, where a(z) = (1 + z)⁻¹. The blue line represents ΛCDM, the orange line the model Γ₁ with (α,β) = (0,86,0,46) and the green line the model Γ₂ with (α,β) = (1,01,0,45). In the cases shown for the HDE models with interaction Γ₁ and Γ₂, the problem of cosmological coincidence is alleviated, given that the coincidence parameter r tend asymptotically to a positive constant. Besides, we note that the HDE models resemble the ΛCDM model, in the evolution of both parameters, noting only differences in quickness of falling of deceleration parameter value. However contrasting this with figure 1, i.e., taking into account the characteristics of interaction model, model 2 is the one that best describes the evolution of the late universe, the last two stages being dominated by dark components. It goes from a time dominated by matter (Γ < 0) to a dominated by dark energy (Γ > 0), in our case this dark energy is of holographic type.

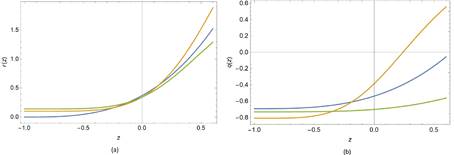
Figura 2. (a) Evolution of coincidence parameter r as a function of redshift z. (b) Evolution of deceleration parameter q as a function of redshift z. In the figures, z =0 represents current time.

Final Remarks

A theoretical model was developed according to the current components of the Universe, such as baryons, radiation, cold dark dark and HDE, with interaction in the dark sector, obtaining for the HDE, the functions ω(z), r(z) and q(z). The proposed model was compared graphically with ΛCDM, using referential values for the HDE parameters and the given interactions.

In the near future we expect to contrast the present scenarios with the observational data (SNe Ia, CC, BAO, CMB), using Bayesian statistics.

Acknowledgments

This research was supported by Universidad del Bío-Bío through “Beca de Postgrado”, and research projects DIUBB 181907 4/R (MC) and GI 172309/C (MC).

Referencias

[1]      A. Riess et al., Astron. J. 116, 1009 (1998).

[2]      S. Perlmutter et al., Astrophys. J. 517, 565 (1999).

[3]      P. Ade et al., Astron. Astrophys. 594, 63 (2016).

[4]      J. Weller and A. Lewis, Mon. Not. Roy. Astron. Soc. 346, 987

(2003).

[5]      B. Copeland et al., Int. J. Mod. Phys. D 15, 1753 (2006).

[6]      A. Riess et al., Astrophys. J. 826, 56 (2016).

[7]      L. Granda and A. Oliveros, Phys. Lett. B 669, 275 (2008).

[8]      C. Gao et al., Phys. Rev. D 79, 043511 (2009).

[9]      S. Del Campo et al., Phys. Rev. D 83, 123006 (2011).

[10]  S. Lepe and F. Pen˜a, Eur. Phys. J. C 69, 575 (2010).

[11]  F. Arevalo et al., Astrophys. Space Sci. 352, 899 (2014).

[12]  L. Chimento et al., AIP Conf. Proc. 1471, 39 (2012).

[13]  J. Maldacena, Int. J. Theor. Phys. 38, 1113 (1999).

[14]  G. ’t Hooft, Conf. Proc. C930308, 284 (1993).

[15]  A. Cohen et al., Phys. Rev. Lett. 82, 4971 (1999).

[16]  M. Li, Phys. Lett. B 603, 1 (2004).

[17]  T. Mathew et al., Int. J. Mod. Phys. D 22, 1350056 (2013).

[18]  B. Ryden, Introduction to Cosmology (Ohio State University Press, 2006).

[19]  S. Chattopadhyay and A. Pasqua, Indian J. Phys. 87, 1053

(2013).

[20]  F. Arevalo et al., Eur. Phys. J. C 77, 565 (2017).

[21]  A. Cid et al., JCAP 1903, 030 (2019).

[22]  M. Cataldo et al., JCAP 1002, 024 (2010).

[23]  T.-F. Fu et al., Eur. Phys. J. C72, 1932 (2012).

[24]  L. Chimento et al., AIP Conf. Proc. 1471, 39 (2012).

[25]  W. Zimdahl and D. Pavon, Phys. Lett. B521, 133 (2001).

[26]  B. Wang et al., Rept. Prog. Phys. 79, 096901 (2016).

[27]  F. Arevalo et al., Class. Quant. Grav. 29, 235001 (2012).