Parametric linear programming for a materials requirement planning problem solution with uncertainty

Uso de la programación lineal paramétrica en la solución de un problema de planeación de requerimiento de materiales bajo condiciones de incertidumbre

Using fuzzy set theory as a methodology for modelling and analysing decision systems is particularly interesting for researchers in industrial engineering because it allows qualitative and quantitative analysis of problems involving uncertainty and imprecision. Thus, in an effort to gain a better understanding of the use of fuzzy logic in industrial engineering, more specifically in the field of production planning, this article was aimed at providing a materials requirement planning (MRP) problem with uncertainty in the automotive industry; this was solved using fuzzy parametric linear programming.

El uso de la teoría de los conjuntos difusos como una metodología para el modelado y análisis de sistemas de decisión es de particular interés para investigadores en ingeniería industrial debido a la capacidad para permitir un análisis cualitativo y cuantitativo de los problemas que implican vaguedad e imprecisión. Es así como, en un esfuerzo por obtener una mejor comprensión sobre el uso de la lógica difusa en la ingeniería industrial y más específicamente en el campo de la planificación de la producción, se proporciona en el presente artículo un problema de planeación de requerimiento de materiales (MRP) bajo condiciones de incertidumbre aplicado a la industria automotriz, el cual es solucionado a través de programación lineal paramétrica difusa.

• HTML (es)
• HTML (en)

Uso de la programación lineal paramétrica en la solución de un problema de planeación de requerimiento de materiales bajo condiciones de incertidumbre Parametric linear programming for a materials requirement planning problem solution with uncertainty

Martin Darío Arango Serna¹ , Conrado Augusto Serna² y Giovanni Pérez Ortega³

¹ Ingeniero Industrial, Unaula. Especialista en finanzas, formulación y evaluación de proyectos, Universidad de Antioquia, Medellín, Colombia. Especialista en docencia universitaria, Universidad Politécnica de Valencia, España. M.Sc., en ingeniería de sistemas, Universidad Nacional de Colombia. Ph.D., en Ingeniería Industrial, Politécnica de Valencia, España. Escuela Ingeniería de la Organización, Facultad de minas, Universidad Nacional de Colombia, Medellín, Colombia. mdarango@unal.edu.co

² Ingeniero Industrial, Universidad Nacional de Colombia. M.Sc., en Ingeniería administrativa, Universidad Nacional de Colombia, Medellín, Colombia. Instituto Tecnológico Metropolitano. casernau@unal.edu.co

³ Ingeniero administrativo, Universidad Nacional de Colombia.  Especialista en Docencia universitaria, Universidad Industrial de Santander, Santander, Colombia. M.Sc., en Desarrollo, Universidad Pontificia Bolivariana. Escuela Ingeniería de la Organización, Facultad de minas, Universidad Nacional de Colombia, Medellín, Colombia. gperezo@unal.edu.co

---

RESUMEN

Palabras claves: programación matemática difusa, programación lineal paramétrica, plan de requerimiento de materiales (MRP), análisis de decisiones.

---

ABSTRACT

Keywords: Fuzzy mathematical programming, parametric linear programming, materials requirement planning (MRP), decision analysis.

---

Recibido: agosto 3 de 2009
Aceptado: noviembre 15 de 2010

Introducción

La toma de decisiones es posiblemente uno de los aspectos más importantes de aplicación de la matemática en diversas esferas de la actividad humana; esto si consideramos que el primer paso para intentar resolver un problema de toma de decisiones consiste en formular un modelo matemático de un sistema o una situación a analizar. Sin embargo, en condiciones reales la toma de decisiones es imprecisa debido, al menos en parte, a la incertidumbre que rodea a tales situaciones. Es así como, si tenemos la intención de hacer modelos matemáticos razonablemente adecuados al mundo real, se debe ser capaz de introducir la incertidumbre en dichos modelos y sugerir medios para el procesamiento de la información imprecisa (Pandian et al., 2002). En la industria, por ejemplo, la imprecisión y la incertidumbre están presentes en la información referida a los tiempos de flujo, la mano de obra, el rendimiento de los materiales, los tiempos de suministro, y así sucesivamente; estos datos, fáciles de definir e involucrar en un modelo como medidas absolutas, son siempre imprecisos debido en parte a información incompleta y a la incertidumbre que pueden generar factores internos y externos. Por lo tanto, se hace atractivo resolver este tipo de problemas mediante la aplicación de la teoría de conjuntos difusos. A continuación se hace un RESUMEN de algunos de los trabajos que usan los modelos difusos para la solución de problemas en el campo industrial:

En 1981 Dan B. Rinks empleó reglas lingüísticas del tipo if- then en modelos de planificación agregada; esta técnica fue complementada y mejorada con los trabajos de I. Burhan Turksen (Mula, 2004). Reynoso et al. (2002) presentaron un primer enfoque sobre un MRP II basado en la lógica difusa y la teoría de la posibilidad para el tratamiento de la incertidumbre y la imprecisión de la demanda. Ben-Arieh et al. (2004) exhibieron un modelo de redes Petri que combina las capacidades de modelación, planeación y evaluación de desempeño para las operaciones de ensamble. Esta herramienta de modelamiento puede representar los aspectos relacionados con el grado de dificultad asociado a la secuencia de ensambles. Hop (2006) abordó un modelo de balanceo de línea con tiempo de procesamiento difuso y formuló un método de programación lineal binaria difusa para su solución. Mula (2006) proporcionó un nuevo modelo de programación lineal, denominado MRPDet, para la planificación de la producción a mediano plazo en un entorno de fabricación MRP con restricciones de capacidad, multiproducto, multinivel y multiperíodo. Niu y Dartnall (2008) analizaron el modelo Fuzzy-MRP-II, el cual reúne toda la información que permite considerar el conjunto de posibilidades que pueden tener lugar en la realización de los pedidos. Lan et al. (2008) consideraron una nueva clase de problema de planeación de la producción multiperíodo con niveles de servicio, donde un fabricante tiene un número de plantas y subcontratistas para satisfacer la demanda de sus productos de acuerdo al nivel de servicio exigido por sus clientes. Arango et al. (2009) reunieron seis modelos de programación matemática difusa aplicados a la planificación de la producción con limitaciones de capacidad; en estos modelos la incertidumbre se considera tanto en la función objetivo como en los parámetros de las restricciones.

Programación lineal difusa

En los problemas de programación lineal en escenarios deterministas el objetivo es minimizar o maximizar una función objetivo lineal considerando restricciones lineales. Sin embargo, en la práctica el tomador de decisiones puede no estar en posición para especificar el objetivo o las funciones de restricción con precisión, pero sí puede definirlas en términos imprecisos. En tales situaciones es preferible usar programación lineal difusa para obtener mejores resultados de los modelos a través de la flexibilización de la toma de decisiones (Pandian et al., 2002).

En la Tabla 1 se muestra un problema de programación lineal típico y su equivalente difuso.

En el modelo (2), A‾_ij, B‾_i, C‾_j son números difusos, X_i son variables difusas, y las operaciones de suma y multiplicación son operaciones aritméticas difusas; además el símbolo <= denota una desigualdad difusa. Este modelo supone que tanto la función objetivo como las restricciones pueden incluir números y variables difusas.

Un modelo de toma de decisiones difuso se caracteriza por tener un conjunto X de posibles alternativas y un conjunto de metas Z_i (i = 1, 2, …., p), junto con un conjunto de restricciones B_j (j = 1, 2,…, n), cada uno de los cuales es expresado por un conjunto difuso en X. Para este tipo de modelos de tomas de decisión, Zadeh (1975) en sus trabajos pioneros propone que una decisión difusa es determinada por un adecuado complemento entre los conjuntos difusos B_j (j = 1, 2,…, n) y Z_i (i = 1, 2, …., p). Por lo tanto, un conjunto difuso D podría ser definido como sigue: D = (Z₁ ∩ Z₂ ∩ . . . ∩ Z_p) ∩ (B₁ ∩ B₂ ∩ . . . ∩ B_n), o lo que es igual, µ_D : X → [0, 1], donde µ_D(x) = mín. µ_Zi (x), µ_Bj (x), lo que en la teoría de conjuntos difusos se conoce como operador mín. Una vez la decisión difusa D es conocida, se puede definir x^* Є X para ser una solución óptima si µ_D(x^*) = máx. µ_D(x).

Una de las consideraciones que puede hacerse es tomar un modelo con objetivo difuso donde la función de pertenencia sea la siguiente :

donde Z₀ es el nivel de aspiración para el valor de la función objetivo y p₀ es la máxima violación aceptable del nivel Z₀. De manera similar, las funciones de pertenencia para las restricciones pueden ser definidas como sigue:

   

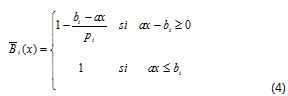
donde p_i es el máximo valor de violación a la restricción i.

Chanas (1983) argumenta que dado el poco grado de conocimiento sobre la región factible difusa, no es fácil establecer el nivel de aspiración Z₀ y su tolerancia p₀; de modo que sugiere resolver primero el modelo anterior sin considerar la función objetivo como difusa. Con esta aproximación el problema es transformado en uno de programación lineal paramétrica definido por:

   

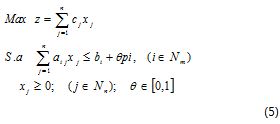
donde θ (0<=θ<=1) es un parámetro que se interpreta como el grado de violación de la restricción, y p_i (p₁, p₂,…, p_m) es el vector de tolerancia para cada una de las m restricciones, el cual puede ser definido por el tomador de decisiones. Α = 1- θ es el nivel de satisfacción del decisor. Para todo valor de θ es posible obtener una solución óptima x*(θ) con el respectivo valor óptimo Z*(θ), donde la condición B‾_i(x*(θ))≥ 1-θ = α es válida. Además, para todas las soluciones no nulas existe al menos un i tal que B‾_i(x*(θ))= 1-θ . Por lo tanto, el grado común de satisfacción para las restricciones es el mínimo de B‾_i(x*(θ)), definido como B‾_c(x*(θ))=miniB‾_i(x*(θ))= 1-θ.

Al resolver el modelo (5) por técnicas de programación paramétrica (Hillier, 2002) se obtiene el conjunto de soluciones que maximizan la función objetivo dependiendo del parámetro θ (Safi et al., 2007). Esto es, para todo valor de θ se obtiene una solución óptima x*(θ) con el respectivo valor óptimo Z*(θ) que satisfaga conjuntamente las restricciones en el grado 1- θ. Esta solución óptima es presentada al tomador de decisiones, quien elige Z₀ y el correspondiente valor de p₀. Con esta información es posible construir la función de pertenencia para la función objetivo:

  

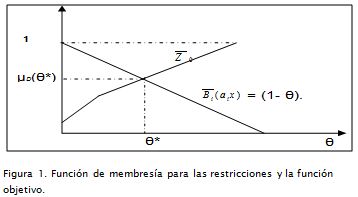
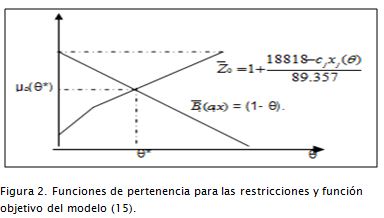
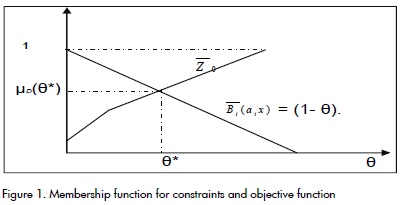
Por lo tanto, la solución óptima, siguiendo esta metodología, se obtiene tomando x^*(θ*) con el valor óptimo z^*(θ*), donde θ* es elegido tal que μ_D(θ*) = máx. _θ μ_D(θ) = máx. _θ (mín. (Z₀(θ), B_c(θ), el cual es el operador mín. (Figura 1).

Para este fin Jiménez et al. (2007) usan la t-norma del producto algebraico entre Z₀(θ) y B_c(θ) para hallar el valor de θ*. En el siguiente ejemplo práctico se describe más en detalle este proceso.

Formulación del modelo MRP con incertidumbre

El principal objetivo del plan de producción es satisfacer la demanda al menor costo posible. Sin embargo, las previsiones de la demanda no son siempre precisas, lo que en definitiva afecta el funcionamiento de todo el sistema de producción. Así por ejemplo, al subestimarse la demanda pueden generarse roturas de stock que conllevan pérdidas de ventas, retrasos y, en definitiva, un mal servicio; por otro lado, sobreestimar la demanda puede llevar a tener una gran cantidad de materias primas o productos terminados en inventario. Es así como se acude a los stocks de seguridad y ajustes de previsiones de la demanda de manera interdisciplinaria; sin embargo, los métodos usados para este fin son en muchas ocasiones subjetivos, por lo que es pertinente usar modelos difusos para la planificación de la producción (Arango et al., 2008).

El modelo de programación lineal paramétrica que se propone a continuación tiene como objetivo minimizar los costos totales de un plan de requerimiento de materiales (MRP) con restricciones de capacidad, multinivel y multiperíodo. Los costos a ser considerados en el modelo son los de tardanza, almacenamiento, pedido y capacidad adicionada; es necesario aclarar que, para este modelo, sólo se hará uso de los costos marginales, es decir, sólo se incluirán aquellos que pueden cambiar como resultado de las decisiones tomadas; el costo de las materias primas, por ejemplo, no se incluirá, dado que los gastos en este aspecto se hacen con independencia del plan elegido. Igualmente, en la mayoría de las situaciones pueden excluirse los costos del tiempo regular de trabajo. Además, al menos en el corto plazo, la planificación de la mano de obra, en cuanto a contrataciones y despidos, tiene poca incidencia en los costos del plan, por lo que puede ser separada del modelo.

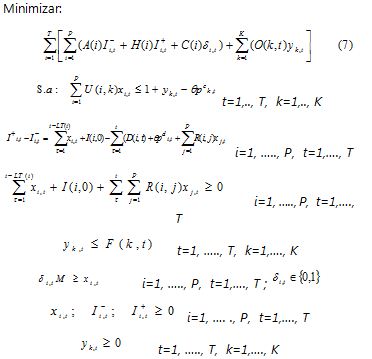
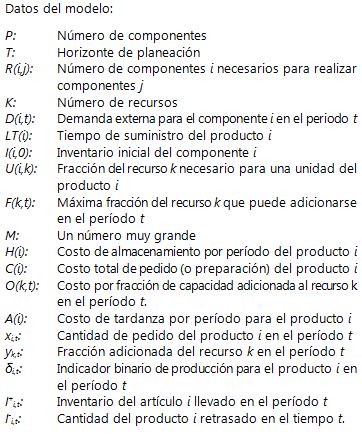
La incertidumbre en este caso está referida a las restricciones de balance de inventario y la capacidad disponible, por lo que θ (0≤θ≤1) representa el nivel con que se violan las restricciones de inventario y de capacidad. Adicional a esta nueva variable, se ha tenido en cuenta cierto nivel de tolerancia p, definido por p^d y p^c, los cuales representan, respectivamente, el nivel máximo que puede alcanzar la demanda y la mayor proporción en el que el recurso k puede estar no disponible. Uno de los conjuntos de restricciones más importantes en el modelo es el grupo de restricciones de los requerimientos de materiales, las cuales están definidas de la siguiente manera:

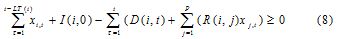
Tal conjunto de restricciones requiere que la suma del inventario inicial y la producción para cada período debe ser mayor o igual al total de la demanda externa y la demanda para los subensambles usados en los artículos. La demanda requiere ser satisfecha con lo producido en períodos iguales o anteriores a t - LT(i) para cada período, dado que el trabajo ha de iniciarse LT períodos antes de que pueda ser usado para satisfacer la demanda. El producto R(i, j)*x_j,_t anticipa la demanda para el artículo i que resulta cuando es componente de un artículo j; este producto es cero en la mayoría de los casos. Para permitir pedidos retrasados la restricción anterior también puede tomar valores negativos. Para este fin se define a I_i,t, como el inventario (negativo o positivo) del producto i en el período t, el cual está determinado por

Partiendo de esta definición, el conjunto de restricciones de balance de los requerimientos de materiales y demanda es reevaluado para permitir que existan retrasos en los pedidos. Por lo tanto, en vez de usar la expresión

      

se emplea la restricción

 

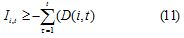
la cual permite una posición negativa del inventario. Al reemplazar I_i,t, por la expresión que lo define, la restricción requerimiento de materiales y demanda se reduce a:

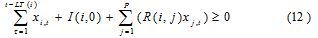
Si adicional a esto se ha definido a I⁺_i,t como la cantidad de producto i en inventario y I^-_i,t la cantidad de producto i retrasado en el periodo t, la siguiente restricción debe ser cumplida:

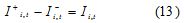
El siguiente grupo de restricciones en importancia, son las de capacidad:

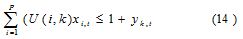
De acuerdo al lado derecho de la ecuación, la capacidad del recurso k puede ser excedida, con el costo que esto conlleva, y de acuerdo a las limitaciones que se tengan la fracción extra del recurso k en el período t es representada como y_k,t.

Para analizar la solución de este modelo a través de técnicas de programación lineal difusa a continuación se describe un proceso industrial con la información necesaria para resolver el modelo MRP propuesto.

Descripción del proceso industrial seleccionado

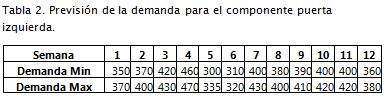
El proceso de ensamble de vehículos consiste generalmente en tres procesos: armado, pintura y montaje, los cuales se subdividen en varios subprocesos y actividades. Dentro de estos subprocesos destacamos el proceso de montaje de puertas, que si bien no es el más complejo de todos sí puede llegar a ser representativo dada su importancia en el ensamble final del vehículo. En la Tabla 2 se muestran las demandas mínima y máxima que se espera obtener en el transcurso de doce semanas del componente de la puerta izquierda.

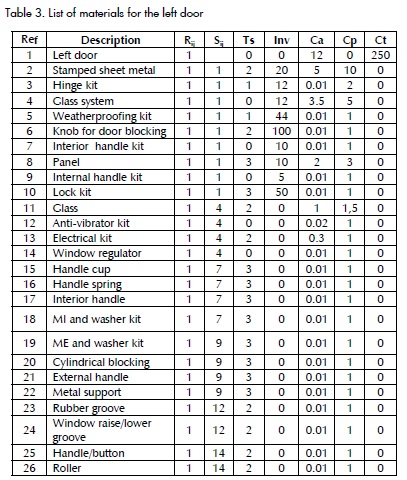
La explosión de producto y el análisis posterior se realiza sólo para la puerta izquierda, considerando que la puerta derecha posee componentes similares. En la Tabla 3 se da la lista de materiales correspondiente, donde S_ij especifica el padre i, del cual hace parte el componente j (S_4,11 entonces vidrios -referencia 11-, es componente de sistema de vidrios -referencia 4-), y R_ij representa la cantidad del producto hijo i necesario para hacer el producto padre j; también se especifican los plazos de entrega (ts) en semanas, el inventario inicial (Inv), costos de almacenamiento (Ca) del componente i por semana, costo de pedidos (Cp) y costo por tardanza del componente i (Ct).

Las restricciones de capacidad sólo estarán referidas a la línea de ensamble a la cual pertenece el vehículo seleccionado. Para el proceso de montaje de puertas esta capacidad se estima en el 15% del total de la capacidad de la línea. Es así como, si la empresa cuenta con un turno laboral de ocho horas, cinco días a la semana, se tiene un total de 40 horas semanales en la línea de producción, de las cuales 6 estarán destinadas al montaje de las puertas. Si se considera además que la capacidad promedio de producción de la línea es de 9 vehículos/ hora, el tiempo de ensamble de una puerta es de 1 minuto, o 0.01666 horas/puerta.

La empresa puede usar horas extras para incrementar la capacidad disponible. El costo de adicionar una hora extra es de $3.800. Para efectos prácticos, la capacidad de la línea sólo puede ser aumentada un 10% a través de las horas extras. Por otra parte, definirá a p^c como el porcentaje en el que la sección de montaje puede no estar disponible, para efectos prácticos p^c = 0,01, mientras que p^d está definido por la diferencia entre la demanda máxima y la demanda mínima (Tabla 2).

Solución del modelo

Este modelo se resuelve en dos pasos:

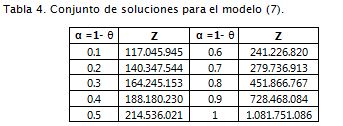
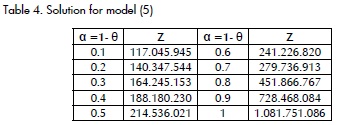
Primer paso: se soluciona el modelo (5) a través de programación lineal paramétrica y se fijan los valores de Z₀ y P₀. Para esto el tomador de decisiones puede estar interesado en tener un nivel de satisfacción en el conjunto de restricciones superior a α= 0.4, por lo que se define a Z₀ = 18818.023 y p₀ = 89.357 (Tabla 4).

Segundo paso: una vez fijados Z₀ y p₀ se elabora la función membresía para la función objetivo, de donde se obtiene que:

   

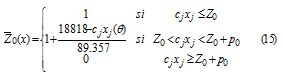
La representación gráfica de este modelo se enseña en la Figura 2.

Para encontrar una solución óptima, con un nivel de aspiración que satisfaga tanto las funciones de membresía de las restricciones como la de la función objetivo, se debe calcular el índice de compatibilidad de cada solución con los niveles de aspiración del decisor (Jiménez et al., 2007).

   

Para encontrar la solución óptima correspondiente debe elegirse θ* tal que μ_D(θ*) = máx. _θ μ_D(θ) = máx. _θ (mín. (Z₀(θ), B_c(θ)). Para este fin Jiménez et al. (2007) usan la t-norma del producto algebraico entre Z₀(θ) y B_c(θ) para hallar el valor de θ*, de la siguiente manera:

   

De acuerdo a estos resultados, se observa que con θ*= 0.7 se obtiene el mayor nivel de satisfacción (0.6272) con respecto a la función objetivo:

Z = 28098.990; Nivel de satisfacción = 0.6272

Análisis de resultados

Si bien el costo en el que se incurre en la solución obtenida con esta metodología es alto en relación con la meta trazada para el plan, al considerar la capacidad y la demanda como valores inciertos los costos pueden ser aún mucho mayores, por lo que el costo del plan Z = 28098.990 es una solución intermedia que equilibra los criterios pesimistas y optimistas del tomador de decisiones, además de significar un nivel de satisfacción cercano al 63% con respecto al menor costo que se podría obtener en condiciones ideales y deterministas.

En la Figura 3 se enseña el conjunto de soluciones para μ_D(θ) y se muestra el nivel máximo de satisfacción al que podría aspirarse con una solución difusa.

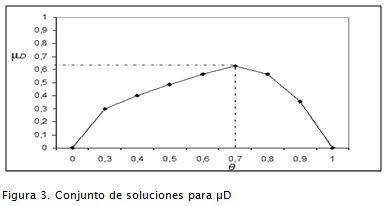
Debe anotarse que, en la medida en que la información con la cual cuenta el decisor sea más precisa, su nivel de satisfacción será mayor. Por lo tanto, la utilidad de las metodologías aquí mostradas redunda en la admisión de niveles de incertidumbre asociados en la formulación de los coeficientes y metas implicados en las funciones objetivo, así como en las restricciones y recursos del problema.

Conclusiones

Un nivel de satisfacción de 0.62 puede no ser muy atractivo en la planificación industrial; sin embargo, al considerar los factores de incertidumbre inherentes al proceso productivo esta cifra cobra un mayor significado, debido en parte a la simplicidad de su cálculo y a su fácil interpretación.

La metodología aquí presentada es sólo un ejemplo de las diferentes aplicaciones que pueden tener los conjuntos difusos y la lógica difusa para facilitar la toma de decisiones en los procesos de producción. El paso a seguir es el de llevar estas técnicas a la práctica y validarlas con los resultados que se pueden obtener a través de métodos convencionales con el fin de establecer la forma más apropiada de decidir en entornos inciertos.

Una de las bondades de la metodología expuesta es que la complejidad de un modelo MRP con restricciones de capacidad no se afecta al considerar la vaguedad e imprecisión de alguno de sus parámetros, por lo tanto la programación paramétrica difusa puede llegar a constituirse en una efectiva herramienta de planeación industrial.

Si bien la lógica difusa no es la respuesta a todos los problemas que surgen en los sistemas de producción, sí constituye una herramienta fácilmente entendible y manejable que puede ser usada en la mayoría de los programas de optimización. Por otro lado, al considerarse funciones de pertenencia más que funciones de probabilidad, se está más acorde con la realidad que presentan las plantas de producción, donde la imprecisión está presente en la mayoría de los procesos de toma de decisiones.

Bibliografía

Arango, D., Serna, C., Álvarez, K., Modelos Difusos Aplicados a la Planeación de la Producción., Centro de publicaciones Universidad Nacional de Colombia, Medellín, 2009.

Arango, D., Serna, C., Pérez, G., Aplicaciones de Lógica Difusa a las Cadenas de Suministro., Avance en Sistemas e Informática, Vol. 5, No. 3, Dic. 2008, pp. 17-23.

Ben-Arieh, D., Kumar R., Tiwari, M., Analysis of Assembly Operations' Difficulty Using Enhanced Expert high-level Colored Fuzzy Petri net model., Robotics and Computer-Integrated Manufacturing, Vol. 20, No. 5, 2004, pp. 385-403,

Chanas, S., The Use of Parametric Programming in Fuzzy Linear Programming., Fuzzy Sets and Systems,  Vol. 11, 1983, pp. 243-251.

Hillier, F., Lieberman, G., Introduction to Operations Research., Seventh edition, Mcgraw-Hill. New York, 2001.

Jiménez, M., Arenas, M., Bilbao, A., Rodriguez, M. Linear Programming with Fuzzy Parameters: An Interactive Method Resolution., European Journal of Operational Research, Vol. 177, 2007, pp. 1599-1609.

Hop, N. V., A Heuristic Solution for Fuzzy Mixed-Model Line Balancing Problem., European Journal of Operational Research, Vol. 168, No. 3, 2006, pp. 798-810.

 Mula, J., Aplicaciones de la Teoría de los Conjuntos Difusos en la Planificación de la Producción: Un Estudio de la Literatura., Memorias VIII Congreso de Ingeniería de Organización, Leganés, septiembre, 2004, pp. 101-110.

Mula, J., Poler, R., Garcia, J., Models for Production Planning Under Uncertainty: A review., International Journal of Production Economics, 103, 2006, pp. 271-285.

Niu, J., Dartnall, J., Application of Fuzzy-MRP-II in Fast Moving Consumer Goods Manufacturing Industry., Proceedings of the 2008 Winter Simulation Conference, 2008.

Pandian, M., Nagarajan, R., Sazali, Y., Fuzzy Linear Programming: a Modern Tool for Decision Making.,  Journal Technology, Vol. 37, 2002, pp. 31-44.

Reynoso, G., Grabot, B., Geneste, L., Verot, S., Integration of Uncertain and Imprecise Orders in MRPII. Ninth International Multi-Conference on Advanced Computer Systems., Conference on Production System Design, Supply Chain Managem, 2002.

Safi, M., Maleki, H., Zaeimazad, E., A Note On the Zimmermann Method for Solving Fuzzy Linear Programming Problems., Iranian Journal of Fuzzy Systems, Vol. 4, No. 2, 2007, pp. 31-45.

Lan, Y., Liu, Y., Sun, G., Modeling Fuzzy Multi-Period Production Planning and Sourcing Problem with Credibility Service Levels., Journal of Computational and Applied Mathematics, 2008.

Zadeh, L., Fuzzy Sets and Their Applications to Cognitive and Decision Processes., Academic Press Inc. London. 1975.

Parametric linear programming for a materials requirement planning problem solution with uncertainty

Martin Darío Arango Serna¹, Conrado Augusto Serna² y Giovanni Pérez Ortega³

¹Industrial Engineer, Unaula. Specialist in finance, development and evaluation, Universidad de Antioquia, Medellín, Colombia. University Teaching Specialist, Universidad Politécnica de Valencia, España. M.Sc., in Computer Engineering, Universidad Nacional de Colombia. Ph.D., Industrial Engineering, Politécnica de Valencia, España. Engineering School Organization, School of Mines, Universidad Nacional de Colombia, Medellín, Colombia. mdarango@unal.edu.co

² Industrial Engineer, Universidad Nacional de Colombia. M.Sc., administrative Engineering, Universidad Nacional de Colombia, Medellín, Colombia. Instituto Tecnológico Metropolitano. casernau@unal.edu.co

³ Administrative Engineer, Universidad Nacional de Colombia. Higher education specialist, Universidad Industrial de Santander, Santander, Colombia. M.Sc., in Development, Universidad Pontificia Bolivariana. Engineering School Organization, School of Mines, Universidad Nacional de Colombia, Medellín,Colombia. gperezo@unal.edu.co

---

ABSTRACT

Keywords: fuzzy mathematical programming, parametric linear programming, materials requirement planning (MRP), decision analysis.

---

Received: august 3th 2009

Accepted: november 15th 2010

Introduction

Decision-making is possibly one of the most important issues in which mathematics is applied in different levels of human activity; this is true if we consider that the first step for trying to solve a decision- making problem consists in formulating a mathematical model of the systems or the situation to be analysed. However, in real conditions, decision-making is imprecise, at least due to the uncertainty concerning such situation. If one wishes to create rational-suitable mathematical models of the real world, then they must be able to incorporate uncertainty and suggest how to process imprecise information (Pandian et al., 2002). It is thus possible to use the concepts and techniques of fuzzy set theory and manage imprecision in an quantitative way, since most conventional procedures do not treat imprecision and implicitly assume a fixed structure, when, in fact, decisionmaking needs flexible and robust models to deal with real life situations.For example, imprecision and uncertainty in industry are included in information about flux times, labour, materials performance, lead times, and so on. This data, which is easy to define and include in a model having absolute measurements, is always imprecise, partly due to the uncompleted information and the uncertainty that could exist with internal and external factors. It is thus attractive to solve this kind of problem through fuzzy set application.

Dan B Rinks used "if-then" linguistic rules in aggregated planning models in 1981. This technique was complemented and improved with the works of I. Burhan Turksen (Mula, 2004). Reynoso et al., (2002) presented a first draft of MRP II based on fuzzy logic and possibility theory for imprecision and uncertainty treatment of demand. Ben-Arieh et al., (2004) presented a Petri net model combining modelling, planning and evaluating performance capacity for assembly operations. This modelling tool can represent aspects related to the associated degree of difficulty in assembly sequences. Hop (2006) worked on a balancing model of a product line process using fuzzy processing times and fuzzy binary lineal programming formula for its solution. Mula (2006) developed a new lineal programming model, named MRPDet, for production planning in middle time in a materials requirement planning (MRP) manufacturing environment with capacity constraints, multi-product, multi-level and multi-period. Niu and Dartnall (2008) analysed a MRP-II-fuzzy model which included considering all the information allowing all possibilities which can occur in order-making processes. Lan et al., (2008) considered a new kind of multi-period planning problem having service levels, in which a producer has a defined number of plants and subcontracted workers for satisfying her/his product demand accordingto requested customer service level. Arango et al., (2009) have presented six fuzzy mathematical programming models applied to production planning with capacity constraints, in which uncertainty has been considered in both objective functions and constraint parameters.

Fuzzy lineal programming

The objective in a lineal programming problem in a deterministic scenario is to minimise or maximise a lineal objective function by considering lineal constrains. However, in practice, a decision-maker cannot be in a position for precisely specifying objectives or constraint functions, but it is possible to define them in imprecise terms. In such situation, it is preferred to use fuzzy lineal programming for obtaining better results in the models through the flexibility of the decision-making process (Pandian et al., 2002).

Table 1 shows a ty-pical lineal programming tool and its fuzzy equivalent.

In model (2), A‾_ij, B‾_i, C‾_j are fuzzy numbers, Xi are fuzzy variables and adding-subtracting operations are subjected to fuzzy arithmetic, Also, the "<=" symbol denotes a fuzzy unequal comparison. This model assumes that both the objective function and the constraints can include fuzzy numbers and fuzzy variables.

A fuzzy decision-making model is characterised by containing a set of possible alternatives "X" and a goal set Z_i (i = 1, 2, .., p), with constraint set B_j (j = 1, 2,., n); each of these is expressed by a fuzzy set "X". For this kind of decision-making model, Zadeh (1975), in his pioneer works, proposed that a fuzzy decision is determined by a right complement between fuzzy sets B_j (j = 1, 2,., n) and Z_i (i = 1, 2, .., p). So, fuzzy set D can be defined as: D = (Z₁ ∩ Z₂ ∩ . . . ∩ Z_p) ∩ (B₁ ∩ B₂ ∩ . . . ∩ B_n), being equal to µ_D : X → [0, 1] where µ_D(x) = mín. µ_Zi (x), µ_Bj (x), known in fuzzy set theory as a min (minimum) operator. Once fuzzy decision D is known,x^* Є X could be defined to be an optimum solution if µ_D(x^*) = máx. µ_D(x).

One consideration is to take a model with a fuzzy objective where the membership function is as follows:

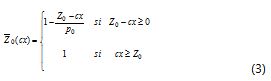
Where Z₀ is the desire level for the objective function value, and p₀ is the maximum acceptable violation of level Z₀. Likewise, constraint membership functions can be defined as:

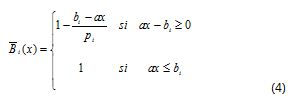
Where pi is maximum violation value of constraint i.

Chanas (1983) has argued that due to less knowledge about the fuzzy feasible region, it is not easy to establish desired level Z₀ and its tolerance to p₀; it is thus suggested first solving the model without considering the objective function to be a fuzzy one. With this approximation, the problem becomes a parametric lineal programming problem, defined as:

   

Where θ (0<=θ<=1) is a parameter interpreted as being the violation degree of the constraint, and p_i (p₁, p₂,., p_m) is the tolerance vector for each m constraint and can be defined by the decision-maker. α = 1- θ, is decision-maker satisfaction level. For each value of θ it is possible to obtain an optimum solution x*(θ) with the respective optimum value Z*(θ) where condition B‾_i(x*(θ))≥ 1-θ = α  is valid. Furthermore, for all non-null solutions, there is at least an i , so that B‾_i(x*(θ))= 1-θ . Thus, the common degree of satisfaction for the constraints is the minimum ofB‾_i(x*(θ)) , defined as B‾_c(x*(θ))=miniB‾_i(x*(θ))= 1-θ.

When solving the parametrical programming model (5) (see Hillier, 2002), a set of solutions is obtained maximising the objective function, depending on parameter θ (Safi et al., 2007). This is, for every θ, an optimal solution x*(θ) is obtained with respective Z*(θ) value that jointly satisfies constraints in degree 1- θ. This optimum solution is presented to the decision-maker who chooses Z₀ and the corresponding p₀ value. With this information it is possible to build the membership function for the objective function:

  

The optimal solution for this methodology is obtained by taking x*(θ*) with optimum value z*(θ*) where θ* is chosen so that μD(θ*) = maxθ μD(θ) = max θ (min (Z0(θ), Bc(θ) which is the min operator (see (Figure 1)).

For this purpose, Jiménez et al., (2007) have used the T-rule of the algebraic product between Z0(θ) and Bc(θ) for finding the θ* value. This procedure is described in more detail in the following practical example.

MRP with uncertainty model formulation

The main objective of the production plan is to satisfy demand at lower cost. However, demand forecasting is not always accurate, thereby affecting the behaviour of the whole production system. For example, when demand is underestimated, it could generate stockouts which can lead to loss of sales, delays and definitely a bad service; on the other hand, overestimating demand can lead to having a large amount of stocks and raw materials in inventory. Companies thus use safety stocks and provide for adjustments in demand. However, the methods used for such purpose are very subjective in many cases, thus making it really important to use fuzzy models in production planning (Arango et al., 2008).

The parametric lineal programming model proposed below was aimed at minimising total costs for an MRP involving multilevel and multi-period capacity constraints. The costs considered in the models were those for delay, warehousing, ordering and capacity auditioning; it should be clarified that only marginal costs were used for this model, e.g. only costs were included that could change as a result of a particular decision made. Raw material costs were not included due to expenditure on such materials being independent of the chosen plan. Likewise, costs associated with regular work time were excluded in most situations. Moreover (at least in the short term), labour planning in terms of hiring and dismissing has little incidence on planned costs which is why such costs could be separated from the model.

In this case, uncertainty referred to constraints on inventory balance and available capacity, so that, θ (0 ≤ θ ≤ 1), represented the level at which inventory constraints and capacity were violated. Additionally to this new variable, a certain tolerance level p has been taken into account defined by p^d and p^c, representing, respectively, maximum demand and the higher percentage by which resource k would not be available. One of the model´s most important set of constraints was the group of material requirement constraints, defined as follows:

Such constrains set required that the sum of the initial inventory and production for every period was greater than or equal to the total of the sum of external demand and the demand of the sub-assemblies used in the products. Demand needed to be satisfied by the amount produced in recent or previous periods to t- LT(i) for each period, since work had to be started LT periods before it could be used to satisfy demand. Product R(i, j)*x_j,_t anticipated the demand for product i that resulted when it was a component of product j; this produc was null in almost all cases. The past constraint could also be negative for allowing delayed orders.I_i,t was thus defined as the inventory (negative or positive) of product i in period t, which was determined by:

From this definition, the constraint set of the requirement balance of material and demand was re-evaluated to allow the existence of delays in orders. Instead of using equation 10, the constraint in equation 11 had to be used.

        

This allowed a negative inventory value. Replacing I_i,t for the expressio defining it, the constraint of material requirement and demand was reduced to:

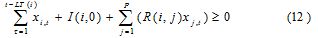
if I⁺_i,t is defined as the amount of product i in inventory and I^-_i,t the amount of product i delayed in period t, the following constrain had to be accomplished.

The next group in importance were the capacity constrains:

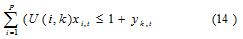
According to the right side of the equation, the capacity of resource k could be exceeded, with an associated cost and with some limitations; the extra fraction of resource k in period t was represented asy_k,t.

The next section describes an industrial process with the required information for solving the proposed MRP model to analyse the model solution through fuzzy lineal programming techniques.

Description of a selected industrial process

Vehicle assembly consists of three steps: piecing together, painting and assembly, which are sub-divided into several sub-processes and activities. Door mounting can be highlighted here as, although it is not the most complex process, it can be very representative due to its importance in final assembly. Table 2 shows the expected minimum and maximums in the 12 week study

The product explanation and subsequent analysis is only for the left door (as the right door has the same components). Table 3 shows a list of corresponding materials where S_ij represents the parent i from which part j is a component (S_4,11 then glasses - reference 11-, is a component of the glass system - reference 4) and R_ij represents the amount of products i necessary for making parent product j; delivery times (ts) are specified in weeks, initial inventory (Inv), warehousing costs (Ca) of component i by week, order costs (Cp), costs for delaying component i (Ct).

Capacity constraints only refer to the assembly line to which the selected vehicle belongs. There is 15% estimated door-mounting capacity regarding total assembly line capacity. If the company has a single labour 8 hours/week shift, there is a 40-hour weekly assembly line in which 6 hours are destined to door-mounting. The past is the actual description of company shifts. If average assembly line production capacity is 9 vehicles per hour , then door assembly time is one minute or 0.0166 hours per door.

The company can use extra labour hours for increasing available capacity. The costs involved in using every extra hour are $3,800. For practical purposes, line capacity can only be increased by 10% through extra hours. Also, pc is defined as the percentage representting assembly line non-availability. For practical purposes pc=0.01. pd is defined by the difference between maximum and minimum demand (see Table 2).

Model solution

This model can be solved in two steps.

First step: model (5) is solved through parametric lineal programming and values Z₀ and P₀ are fixed. Decision-makers are thus interested in having a constraint satisfaction level set above α= 0.4, which is why Z₀=18818.023 and p₀=89.357 are defined (see Table 4).

Second step: once Z₀ and p₀ have been fixed, a membership function for the objective function is set, obtaining:

   

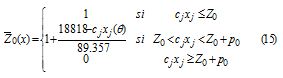
This model´s graphical representation is depicted in Figure 2.

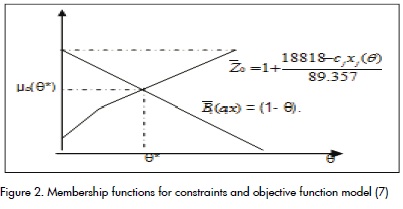
The compatibility index for each solution having the desired decision- making levels must be calculated to find an optimal solution, having a desired level satisfying both constraints and objective function membership (Jiménez et al., 2007).

   

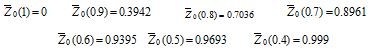
θ* must be chosen to find the correspondent optimal solution so that μ_D(θ*) = max_θ μ_D(θ) = max _θ (min (Z₀(θ), B_c(θ)). Jiménez et al., (2007) used the T-rule for the algebraic product between Z₀(θ) and B_c(θ) to find the value of θ*, as follows:

   

According to these results, it can be observed that θ*= 0.7 can lead to obtaining a higher satisfaction level (0.6272) regarding objective function.

Z= 28098.990; Satisfaction level = 0.6272

Result analysis

Even if the cost incurred in the solution obtained with this methodology is high regarding the desired goal, when considering capacity and demand as uncertainty values, then costs could be much higher. Plan cost Z=28098.990 is an intermediate solution balancing decision-making pessimistic and optimistic criteria, besides having a satisfaction level near to 63% regarding the lower cost that can be obtained in ideal and deterministic conditions.

Figure 3 shows the solution for μ_D(θ) and the maximum satisfaction level that can be obtained with a fuzzy solution.

It should be noticed that if a decision-maker has more accurate information, then satisfaction level will be higher. So, the usefulness of the methodology shown here is the admission of associated uncertainty levels in coefficient formulation, the goals involved in the objective function and the constraints and in the problem´s resources.

Conclusions

A 0.62 satisfaction level cannot be very attractive in industrial planning; however, if considering the uncertainty factors inherent in production, this number takes on great meaning, patly due to the simplicity of its calculation and easy interpretation

The methodology presented here is just one example of the different applications for fuzzy sets and fuzzy logic for facilitating decision-making analysis related to production. These techniques should lead to practice and be validated by results obtained through conventional methods aimed at establishing the most appropriate way of making decisions in environments involving uncertainty.

A good aspect of the methodology presented here is that the complexity of an MRP model with capacity constraints is not affected by considering the uncertainty and imprecision of some of its parameters; fuzzy parametric programming can thus be an effective tool for Industrial planning.

Even if fuzzy logic is not the answer to all production system problems, this constitutes an easy-to-understand and easy-to-manage tool that can be used in most optimisation programmes. When considering membership instead of probabilistic functions, it is also more realistic regarding real production plants where uncertainty and imprecision are presented in almost all decision-making.

References

Arango, D., Serna, C., Álvarez, K., Modelos Difusos Aplicados a la Planeación de la Producción., Centro de publicaciones Universidad Nacional de Colombia, Medellín, 2009.

Arango, D., Serna, C., Pérez, G., Aplicaciones de Lógica Difusa a las Cadenas de Suministro., Avance en Sistemas e Informática, Vol. 5, No. 3, Dic. 2008, pp. 17-23.

Ben-Arieh, D., Kumar R., Tiwari, M., Analysis of Assembly Operations’ Difficulty Using Enhanced Expert high-level Colored Fuzzy Petri net model., Robotics and Computer-Integrated Manufacturing, Vol. 20, No. 5, 2004, pp. 385-403,

Chanas, S., The Use of Parametric Programming in Fuzzy Linear Programming., Fuzzy Sets and Systems,  Vol. 11, 1983, pp. 243-251.

Hillier, F., Lieberman, G., Introduction to Operations Research., Seventh edition, Mcgraw-Hill. New York, 2001.

Jiménez, M., Arenas, M., Bilbao, A., Rodriguez, M. Linear Programming with Fuzzy Parameters: An Interactive Method Resolution., European Journal of Operational Research, Vol. 177, 2007, pp. 1599-1609.

Hop, N. V., A Heuristic Solution for Fuzzy Mixed-Model Line Balancing Problem., European Journal of Operational Research, Vol. 168, No. 3, 2006, pp. 798-810.

 Mula, J., Aplicaciones de la Teoría de los Conjuntos Difusos en la Planificación de la Producción: Un Estudio de la Literatura., Memorias VIII Congreso de Ingeniería de Organización, Leganés, septiembre, 2004, pp. 101-110.

Mula, J., Poler, R., Garcia, J., Models for Production Planning Under Uncertainty: A review., International Journal of Production Economics, 103, 2006, pp. 271-285.

Niu, J., Dartnall, J., Application of Fuzzy-MRP-II in Fast Moving Consumer Goods Manufacturing Industry., Proceedings of the 2008 Winter Simulation Conference, 2008.

Pandian, M., Nagarajan, R., Sazali, Y., Fuzzy Linear Programming: a Modern Tool for Decision Making.,  Journal Technology, Vol. 37, 2002, pp. 31-44.

Reynoso, G., Grabot, B., Geneste, L., Verot, S., Integration of Uncertain and Imprecise Orders in MRPII. Ninth International Multi-Conference on Advanced Computer Systems., Conference on Production System Design, Supply Chain Managem, 2002.

Safi, M., Maleki, H., Zaeimazad, E., A Note On the Zimmermann Method for Solving Fuzzy Linear Programming Problems., Iranian Journal of Fuzzy Systems, Vol. 4, No. 2, 2007, pp. 31-45.

Lan, Y., Liu, Y., Sun, G., Modeling Fuzzy Multi-Period Production Planning and Sourcing Problem with Credibility Service Levels., Journal of Computational and Applied Mathematics, 2008.

Zadeh, L., Fuzzy Sets and Their Applications to Cognitive and Decision Processes., Academic Press Inc. London. 1975.