Implementing FEM-DtN for an incompressible material on an unbounded domain

Implementación MEF-DtN para un material incompresible en un dominio no acotadoaImplementación MEF-DtN para un material incompresible en un dominio no acotado

This paper presents the implementation of the finite element method combined with Dirichlet-to-Neumann (DtN) mapping (derived in terms of an infinite Fourier series) for studying the solvability of an exterior problem arising in linear incomepressible 2D-elasticity. A reliable numerical experiment is also presented showing the accuracy of DtN mapping; only a few Fourier series terms were needed to get a good approximation to the solution. The stable Taylor-Hood element was used for finite element discretisation.

En este trabajo presentamos la implementación de un método de elementos finitos combinado con la aplicación Dirichlet-to-Neumann (DtN), obtenida en términos de series de Fourier, para estudiar la existencia de soluciones de un problema exterior que proviene de la teoría de elasticidad lineal incompresible bidimensional. Finalmente, se presenta un método numérico que demuestra la precisión de nuestra aplicación DtN, puesto que sólo se necesitan unos cuantos términos de la serie de Fourier para obtener una buena aproximación de la solución. Para la discretización del problema se emplea el elemento estable Taylor-Hood.

• HTML (es)
• HTML (en)

Implementación MEF-DtN para un material incompresible en un dominio no acotado

Liliana Camargo ¹ y Jairo Duque ²

¹ Matemática, Universidad del Valle, Cali, Colombia. Universidad del Valle. lilicaz85@gmail.com.

² Dr. rer. nat., Universidad del Valle, Cali, Colombia. jjduque@univalle.edu.co

---

RESUMEN

En este trabajo presentamos la implementación de un método de elementos finitos combinado con la aplicación Dirichlet-to-Neumann (D†N), obtenida en términos de series de Fourier, para estudiar la existencia de soluciones de un problema exterior que proviene de la teoría de elasticidad lineal incompresible bidimensional. Finalmente, se presenta un método numérico que demuestra la precisión de nuestra aplicación D†N, puesto que sólo se necesitan unos cuantos términos de la serie de Fourier para obtener una buena aproximación de la solución. Para la discretización del problema se emplea el elemento estable Taylor-Hood.

Palabras clave: método de elementos finitos mixto, elemento Taylor-Hood, técnica D†N, elasticidad lineal, condición infsup.

---

Recibido: septiembre 4 de 2009

Aceptado: noviembre 15 de 2010

Introducción

En este trabajo se explica un procedimiento para estudiar la aproximación de Galerkin de un material incompresible en un dominio exterior no acotado Ω. El procedimiento emplea la aplicación Dirichlet-to-Neumann (D†N) (Han y Bao, 1997; Gatica, Gatica y Stephan, 2003; Kako y Touda, 2004), que consiste en introducir una frontera artificial dibujando en Ω un círculo Γ_R en R² de radio R. Entonces Ω se divide en la parte acotada Ω_i y la no acotada Ω_R. Para resolver el problema en el dominio acotado Ω_i se dan condiciones de frontera exactas y aproximadas sobre la frontera artificial Γ_R (Figura 1).

Figura 1. Dominio Ω = Ω_i; ∪ Ω_R y frontera artificial Γ_R.

Sea Ω С R² un dominio no acotado y simplemente conexo con frontera Lipschitz continua Γ. Teniendo en cuenta las condiciones de frontera tipo Dirichlet dadas sobre Γ se define el espacio . Así, el problema de elasticidad lineal por resolver consiste en encontrar (u,p) ∈ tal que:

Aquí u: Ω → R representa el desplazamiento y p es la presión del material en cada punto x:= (x₁,x₂ )^T ∈ Ω por el efecto de la fuerza externa ƒ, µ > 0 es la constante de Lamé y ε(u) representa el tensor de esfuerzos de componentes para i, j =1,2. De este material suponemos válida la relación tensiónesfuerzo para pequeñas deformaciones, tal como se discute en Necas (1986); véanse también Necas (1981) y Zeidler (1988). En este trabajo suponemos que la fuerza ƒ tiene soporte compacto y que está contenida en la región Ω_i.

Sean espacios dotados con las normas de L² (Ω) y H¹(Ω) respectivamente. Entonces, siguiendo el procedimiento estándar de integración por partes, se llega a la siguiente formulación variacional del problema (1):

Nótese que este problema está definido en el dominio no acotado Ω y Ω_i es el dominio computacional para nuestro método de elementos finitos, que se obtiene al introducir la frontera artificial Γ_R. Entonces es necesario deducir la formulación variacional del problema (1) en Ω_i; nuevamente mediante integración por partes, y teniendo en cuenta que para el tensor distorsión σ (u, p):= 2 με(u) - pI , donde I es la matriz identidad de orden 2, se tiene que – div (σ(u, p) = 2μ div ε (u ) + grad p, y a partir de esto se obtiene la formulación débil:

El análisis se concentra ahora en la integral de frontera, Nuestro objetivo es obtener una expresión para el tensor σ (u, p) a lo largo de la frontera artificial Γ_R. Consideremos entonces la siguiente descomposición del desplazamiento u, en el dominio no acotado Ω_R =

siendo G₁ , G₂ y W funciones armónicas que determinaremos más adelante. En particular, las funciones G_j satisfacen el siguiente problema de valores de frontera:

Nótese que los valores de G_j y u_j coinciden a lo largo de Γ_R. Usando el método de separación de variables obtenemos las siguientes representaciones de G_j en términos de los coeficientes de Fourier:

donde los coeficientes a_n,b_n y d_n están dados por:

Usando la condición div (u)= 0 y la representación (3) se obtiene , y de aquí

Análogamente, usando la ecuación de balance en Ω_R, grad p = 2μ div ε(u), obtenemos grad y de aquí se deduce que . Ahora estamos en condiciones de calcular a lo largo de Γ_R. Recordando que los valores de u_j y G_j coinciden sobre Γ_R, y que la presión p se conoce en términos de W se obtiene:

donde

que sólo depende de la variación de u a lo largo de Γ_R. El operador T(u) se conoce como aplicación Dirichlet to Neumann. Obsérvese que el problema variacional (2) es la formulación débil del problema:

Existencia y unicidad de soluciones

Consideremos las formas bilineales y el funcional lineal F: X→ R definidos mediante:

y respectivamente. Entonces el problema variacional (2) consiste en encontrar (u,p) ∈ X x M tal que

La demostración de existencia y unicidad de este problema se basa en el teorema de Brezzi, puesto que la forma A(u,v) + A₀ (u,v) es continua y coerciva, y el operador B satisface la condición inf-sup (Han y Bao, 1997; Camargo, 2008).

Método de elementos finitos

El método de elementos finitos que presentamos en este trabajo no aproxima la solución del problema (4), sino la solución del problema que se obtiene truncando la serie de Fourier, en términos de la cual está definido el operador T(u). Al reemplazar por para un valor entero de N, obtenemos el problema aproximado: encontrar ( u_N , p_N ) ∈ X x M tal que

con j = 1, 2. El estudio de existencia y unicidad del problema (5) es análogo al del problema exacto (Han y Bao, 1997; Camargo, 2008). Además, se tiene el siguiente estimativo para el error de la aproximación ( u_N , p_N ).

Teorema 1. Sean las soluciones de los problemas variacionales (4) y (5), respectivamente. Además, suponga con m ∈ Z. Entonces el siguiente estimativo del error se cumple:

donde C es una constante independiente de N y m.

Ahora, sean X_h С X y M_h С M los espacios de elementos finitos correspondientes al elemento Taylor-Hood, (Brezzi, 1991), y denotemos por T_h la partición regular del dominio Ω_i, en elementos triangulares curvilíneos T de diámetro h_t , donde . Entonces,el método de elementos finitos para aproximar el problema (5)con-siste en encontrar tal que

Nótese que el elemento Taylor-Hood satisface la condición inf-sup (Brezzi, 1991) y nuevamente por el teorema de Brezzi es inmediata la existencia de una única solución para (6).

Teorema 2. Suponga que es la solución del problema (4) y es la solución del problema (6(, así que el siguiente estimativo de error se cumple:

donde C es una constante independiente de h y N.

Demostración. Sea la solución del problema (5)para cualquier entero N ≥0 y consideremos los errores y empleando la técnica estándar del método de elementos finitos mixto se sigue que existe independiente de N y el diámetro h de la triangulación de Ω_i tal que:

Además,

y empleando (7) se sigue que

lo que concluye la demostración del teorema.

Implementación de la técnica D†N

Sea Ω el dominio no acotado la circunferencia de radio R = 2 y

donde y . Entonces, es la única solución del siguiente problema de valores de frontera:

Dado n ∈ N, una partición uniforme de la parametrización del círculo definida poy y (t)= R(cos (t), sen(t))^T. Entonces denotamos con Ω_h la región anular acotada por (cos(t),sen (t)) Γ= y la línea poligonal cerrada Γ_h con vértices y sea T_h una triangulación regular de Ω_h con triángulos T de diámetro h_T tal que .

Ahora consideramos el triángulo canónico con vértices como un triángulo de referencia , e introducimos la familia de transformaciones afines biyectivas tal que para todo T ∈ T_h. Es bien conocido que 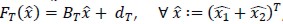, donde y depende de los vértices del triángulo T. Además, dado un entero l > 0 y un subconjunto S of R², denotamos con P_i( S) el espacio de polinomios en dos variables definidos en S de grado total a lo más l.

Con el fin de especificar X_h y M_h tomamos

Entonces discretizamos X usando

      Figura 2. Secuencia T_o,h, … T_3,h de mallas usadas en la implementación.

y M con

Los espacios X_h y M_h constituyen los subespacios de elementos finitos Hood y Taylor más sencillos que satisfacen la condición inf-sup. En nuestra implementación usamos varias triangulaciones. Nosotros arrancamos la experimentación numérica con la malla inicial T_o,h con 26 elementos. Cada malla refinada uniformemente T_1,h ,…,T_3,h se generó dividiendo cada triángulo en cuatro más pequeños. El resultado se puede observar en la figura 2.

Tabla 1. Grados de libertad (Gdl) y norma L²; de los errores cuando N = 7.

La tabla 1 muestra la norma L² de los errores u - u_h,N¸ p - p_{h, N} cuando N = 7 para las mallas T_o,h,…,T_3,h

Tabla 2. Norma L² de los errores para T_3,h cuando N = 0, 1, 3, 5, 7.

La tabla 2 muestra la norma L² de los errores u - u_h,N¸ p - p_{h, N}; para la malla T_3,h

cuando N = 0, 1, 3, 5, 7.

La figura 3 muestra los valores de y p_h para todas las mallas y N = 7. Como muestra la figura, N = 7 produce buena aproximaci&loacute;n y pocos términos se necesitan en la forma bilineal A₀ para obtener resultados precisos.

Figura 3. y p para las mallas T_o,h,…,T_1,h y T_3,h cuando N = 7.

Conclusiones

En este artículo se usa una aplicación D†N para aproximar la solución de un problema exterior no acotado. Con este fin se introduce una frontera artificial en el dominio computacional acotado, en el que se aproxima la solución usando el método de elementos finitos.

Específicamente, se implementa el elemento Taylor-Hood, el cual se define en términos de una serie de Fourier sobre la frontera artificial. Los cálculos numéricos muestran que truncando la serie en siete términos se logra una buena convergencia. Sin embargo, en nuestra aproximación el operador de frontera tiene asociada una matriz de rigidez densa y se usaron precondicionadores especiales para obtener buena convergencia.

Bibliografía

Brezzi F., Fortin M., Mixed and hybrid finite element methods.,Springer-Verlag, 1991.

Camargo, L., Aplicación D†N-FEM a un problema elástico lineal.,BSc Mathematics thesis, Universidad del Valle, 2008.

Gatica G. N., Gatica L. F., Stephan E. P., A FEM–D†N formulation for a non-linear exterior problem in incompressible elasticity., Mathematical Methods in the Applied sciences, 26, 2003, pp. 151–170.

Han H., Bao W., The artificial boundary conditions for incompressible materials on an unbounded domain.,Numerische Mathematik, 1997.

Kako T., Touda K., Numerical simulation of voice generation based on finite element method in unbounded region.,Department of computer science, Japan, 2004.

Necas, J. Introduction to the theory of nonlinear elliptic equations., John Wiley & Sons, 1986.

Necas, J., Hlavacek, I., Mathematical theory of elastic and elastoplastic bodies: an introduction., Elsevier scientific publishing company, 1981.

Zeidler, E., Nonlinear functional analysis and its applications IV., Springer-Verlag, New York, 1988.

---

Liliana Camargo¹ and Jairo Duque²

¹ Mathematics, Universidad del Valle, Cali, Colombia. Universidad del Valle. lilicaz85@gmail.com.

² Dr. rer. nat., Universidad del Valle, Cali, Colombia. jjduque@univalle.edu.co.

---

ABSTRACT

This paper presents the implementation of the finite element method combined with Dirichlet-to-Neumann (D†N) mapping (derived in terms of an infinite Fourier series) for studying the solvability of an exterior problem arising in linear incomepressible 2D-elasticity. A reliable numerical experiment is also presented showing the accuracy of D†N mapping; only a few Fourier series terms were needed to get a good approximation to the solution. The stable Taylor-Hood element was used for finite element discretisation.

Keywords: mixed finite element method, Taylor-Hood element, D†N technique, linear elasticity, inf-sup condition.

---

Received: september 4th 2009

Accepted: november 15th 2010

Introduction

This article presents a procedure for studying the Galerkin approximation to an incompressible material on unbounded exterior domain Ω. This procedure used Dirichlet-to-Neumann mapping (D†N), (Han and Bao, 1997; Gatica, Gatica and Stephan, 2003; Kako and Touda, 2004), consisting of introducing an artificial boundary by drawing circumference Γ_R in R² with radius R in domain Ω; Ω was then divided in bounded part Ω_i and unbounded part Ω_R. Exact and approximate boundary conditions were given on artificial boundary Γ_R to solve the problem on bounded domain (Figure 1).

Figure 1. Domain Ω = Ω_i Ω_R and artificial boundary γ_R

Ω С R² was an unbounded and simply connected domain with Lipschitz continuous boundary Γ. Because of Dirichlet boundary conditions on space was defined. Hence, the problem of linear elasticity consisted in finding (u,p) ∈ so that:

Here u: Ω → R was the displacement and p was the pressure of a material subjected to some external force ƒ, µ > 0 was the Lamé constant and ε(u) the strain tensor given by for i, j =1,2. It was assumed for this material that the stress-strain ratio was valid for small deformations, as discussed in Necas (Necas 1986; Necas, 1981; Zeidler, 1988). It was supposed that force ƒ had compact support in this work and was defined inside region Ω_i.

Next, notation was adopted with norms L² (Ω) and H¹(Ω), respectively. Standard integration by parts led to the following variational formulation of the problem (1)

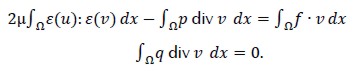
Notice that problem (1?) defined on unbounded domain Ω and Ω_i was the computational domain for the finite element method used here which was obtained by introducing artificial boundary Γ_R. The variational formulation of problem (1) in Ω_i had to be deduced next. Integration by parts was used, by virtue of stress tensor σ (u, p):= 2 με(u) - pI, where I was the identity matrix of R^2x2, this gave – div (σ(u, p) = 2μ div ε (u ) + grad p, leading to weak formulation.

Boundary integral was then analyzed. The next goal was to obtain one expression representing tensor σ (u, p) on artificial boundary Γ_R. The following decomposition of displacement u on unbounded domain Ω_R =

was then considered, where G₁ , G₂ and W were the harmonic functions to be determined. In particular, function G_j satisfied the following boundary-value problem

G_j is bounded, when r → + ∞.

Notice that values for G_j and u_jcoincided along Γ_R. Using the separation of variables method the following representations of G_j were obtained using Fourier series development

where coefficients a_n, b_n c_n and d_n were given by:

Using condition div (u)= 0 and representation (3) the following equation was obtained , and so .

Similarly, using the balanced equation in Ω_R, grad p = 2μ div ε(u) grad p = grad was obtained and hence Next could be estimated along Γ_R. To this end, it was first recalled that the values of u_j and G_j coincided on Γ_R, and pressure p was known in terms of W, leading to

Where

just depending on the variation of u along Γ_R. Operator T(u) represented Dirichlet to Neumann mapping. It was stated that variational formulation (2) was the weak formulation of the problem

Existence and uniqueness of solutions

Bilinear forms and linear functional F: X→ R defined by

and , respectively, were considered. Variational formulation of (2) would then read: Find (u,p) ∈ X x M so that

The proof of existence and uniqueness was based on Brezzi's theorem, since the form A(u,v) + A₀ (u,v) was continuous andcoercive, and operator B satisfied the inf-sup condition (Han and Bao, 1997; Camargo, 2008).

Finite element method

The finite element method presented in this article did not approximate the solution of the problem (4), but provided the solution to the problem obtained by truncating operator T(u) in the corresponding Fourier series. If were replaced by for integer value N, the variational formulation of the approximate problem would read: Find ( u_N , p_N ) ∈ X x M so that

with j = 1, 2. The study of existence and uniqueness of the problem (5) was similar to the exact problem (Han and Bao, 1997; Camargo, 2008). Furthermore, the following error estimate of the approximation ( u_N , p_N ) held.

Theorem 1. were the solutions to variational problems (4) and (5), respectively. In addition, it was supposed that with ∈ Z. Then the following abstract error estimate would hold

where C was a constant independent of N and M.

Next, X_h С X and M_h С M were the spaces of finite element corresponding to Taylor-Hood element (Brezzi, 1991). The regular partition of domain Ω_i was denoted by T_h using curved triangular elements T having diameter h_T , where . Then, the finite element method of (5) would read: Find o that

Notice that the Taylor-Hood element satisfied the inf-sup condition (Brezzi, 1991) and again, by Brezzi’s theorem, the unique solvability of the variational formulation (6) was obtained.

Theorem 2. was the solution to problem (4) and was the solution to problem (6), then the following error estimate would hold

where C was a constant independent of h and N.

Proof. Let be the solution of problem (5) for any integer N ≥ 0 and consider errors and then according to the standard technique of mixed finite element method, would exist independently of N and diameter h of triangulation Ω_i so that

Therefore,

and (7) would yield

concluding the theorem proof.

Implementing the DD†N technique

Let Ω be unbounded domain the circumference with radius R = 2 and.

Where and then, would be the unique solution for the following boundary value problem

Given n ∈ N, let a partition uniform of be the parametrisation of a circle defined by y(t)= R(cos (t), sen(t))^T. The annular region bounded by was then denoted by Ω_h and closed polygonal line Γ_h with vertices and T_h was regular triangulation of Ω_h with triangles T of diameter h_T so that .

.

Reference triangle with vertices was then considered and the family of similar bijective transformations introduced so that for all T ∈ T_h. It is well-known that whe-re and depend on the vertices of triangle T. Therefore, given integer l > 0 and subset S of R² P_i( S) denoted the space of polynomials defined in S having two variables and great degrees of freedom at most L.

Next,

was defined to specify X_h and M_h and discretised X and M using

Figure 2. Sequence T_o,h, … T_3,h of meshes used in the implementation

and

Spaces X_h and M_h were Hood and Taylor finite element subspaces satisfying inf-sup condition. Several triangulations were used in our numerical experiment. Numerical experimentation was started with initial mesh T_o,h which had 26 elements. Each uniformly refined mesh T_1,h ,…,T_3,h was generated by dividing each triangle into four smaller triagles.The result can be seean in figure 2.

Table 1. Degrees of freedom and norm L² of errors when N = 7

Table 1 . show norm L² of errors u - u_h,N¸ p - p_{h, N} when N =7 for meshes T_o,h,…,T_3,h

Table 2. Norm L² of errors for T_3,h when N = 0, 1, 3, 5, 7

Table 2 shows norm L² of errors u - u_h,N¸ p - p_{h, N}5 for mesh T_3,h when N = 0, 1, 3, 5, 7.

Figure 3 shows values of and p_h for meshes T_{0, h,} T_{1, h,}, T_{3, h,} and ?N = 7. As Figure 3 shows, N = 7 produced a good approximation and only a few terms were needed in bilinear form A₀ to obtain good results.

Conclusions

D†N mapping was used this paper to approximate the solution of an unbounded exterior problem. An artificial boundary was introduced into the domain to approximate the solution on a bounded computational domain by using a finite element method

.The Taylor-Hood element defined in terms of a Fourier series on the artificial domain was implemented in this work as finite element method. The numerical calculations showed that good convergence had been obtained just by truncating the Fourier series to seven terms. However, our discretisation produced a dense stiffness matrix, corresponding to the boundary operator; special preconditioners have to be used to obtain good convergence by very refined meshes.

Figure 3. and p_h for the meshes T_o,h,…,T_1,h and T_3,h when N = 7.

---

References

Brezzi F., Fortin M., Mixed and hybrid finite element methods.,Springer-Verlag, 1991.

Camargo, L., Aplicación D†N-FEM a un problema elástico lineal.,BSc Mathematics thesis, Universidad del Valle, 2008.

Gatica G. N., Gatica L. F., Stephan E. P., A FEM–D†N formulation for a non-linear exterior problem in incompressible elasticity., Mathematical Methods in the Applied sciences, 26, 2003, pp. 151–170.

Han H., Bao W., The artificial boundary conditions for incompressible materials on an unbounded domain.,Numerische Mathematik, 1997.

Kako T., Touda K., Numerical simulation of voice generation based on finite element method in unbounded region.,Department of computer science, Japan, 2004.

Necas, J. Introduction to the theory of nonlinear elliptic equations., John Wiley & Sons, 1986.

Necas, J., Hlavacek, I., Mathematical theory of elastic and elastoplastic bodies: an introduction., Elsevier scientific publishing company, 1981.

Zeidler, E., Nonlinear functional analysis and its applications IV., Springer-Verlag, New York, 1988.