Numerical flow solutions on a backward-facing step using the lattice Boltzmann equation method

Solución numérica del flujo sobre un escalón utilizando el método de la ecuación reticular de Boltzmann

Numerical solutions of 2-D laminar flow over a backward-facing step using the lattice Boltzmann equation method (LBEM) are presented in this article. Unlike conventional numerical schemes based on macroscopic continuum equation (mass conservation and Navier-Stokes) discretisation, the LBEM is based on microscopic models and mesoscopic kinetic equations. The simulations were validated for a wide range of Reynolds numbers (100 ≤ Re ≤ 1,000), comparing them to previous studies. Several flow features, such as primary and secondary vortex location at the bottom and top of the wall, respectively, were investigated regarding Reynolds number. Two typical classes of boundary condition were implemented in the LBEM model: the Drichlet condition at the inlet flow (parabolic speed profile) and the Newman condition at the outlet flow (zero gradient speed). The results showed that the LBEM gave accurate results over a wide range of Reynolds number; these were compared with other numerical methods and experimental data.

Se presenta una solución numérica del flujo sobre un escalón en dos dimensiones utilizando el método de la ecuación reticular de Boltzmann (LBEM). A diferencia de los métodos numéricos tradicionales basados en la discretización de las ecuaciones macroscópicas del continuo (conservación de la masa y Navier-Stokes), los LBEM se fundamentan en modelos microscópicos y mesoscópicos de las ecuaciones cinéticas. Se muestran los resultados obtenidos para este flujo en el estado estacionario y para un amplio rango de números de Reynolds (100 ≤ Re ≤ 1000), y se han comparado con estudios previos. Se ha investigado la aparición y localización de los principales vórtices en el flujo, tanto en la pared inferior como en la superior, y su comportamiento en función del número de Re. Se han implementado al modelo LBEM dos tipos comunes de condiciones de frontera: condición de Drichlet a la entrada (perfil de velocidad parabólico) y condición de Newman a la salida (derivada nula de la velocidad). Los resultados obtenidos muestran gran exactitud del método utilizado para un amplio rango de números de Reynolds, al ser comparados con resultados experimentales y numéricos de otros autores.

• HTML (es)
• HTML (en)

Elkin Florez¹, Yamid Carranza², Yesid Ortiz³

¹ Ingeniero Mecánico, Universidad Francisco de Paula Santander, Colombia. Magíster en Ingeniería Mecánica, Universidad de los Andes, Colombia. Magíster en Ingeniería Química y de Procesos, Universidad de Rovira i Virgili, España. Doctor en Ingeniería Mecánica, Aeronáutica y de Fluidos. Universidad Politécnica de Cataluña, España. Profesor asociado, Universidad de Pamplona. eflorez@unipamplona.edu.co

² Ingeniero Mecánico, Universidad Tecnológica de Pereira, Colombia. Magister en Ingeniería Mecánica , Universidad de los Andes, Colombia. Estudiante de doctorado, Politécnico de Monterrey, México. Profesor Asistente, Universidad Tecnológica de Pereira, Colombia. yamidc@utp.edu.co

³ Ingeniero Mecánico, Universidad Francisco de Paula Santander, Colombia. Magíster en Ingeniería Mecánica, Universidad de los Andes, Colombia. Profesor Asistente, Universidad Tecnológica de Pereira, Colombia. yosanchez@utp.edu.co

---

RESUMEN

Palabras clave: flujo de fluidos, método de la ecuación reticular de Boltzmann, simulación numérica

ABSTRACT

Keywords: fluid flow, lattice Boltzmann equation method, numerical simulation.

---

Recibido: febrero 16 de 2010

Aceptado: mayo 25 de 2011

Introducción

Los flujos por canales donde existe separación y recirculación de la capa límite se encuentran con frecuencia en muchos problemas de flujos en ingeniería. Ejemplos típicos son los flujos en un intercambiador de calor y en ductos. Entre estos tipos de problemas, el flujo sobre un escalón puede ser considerado como la más sencilla geometría con un rico contenido físico que se pone de manifiesto en los vórtices que se presentan y sus respectivas recirculaciones, todas éstas dependiendo del número de Reynolds (Re) y del parámetro que relaciona la altura del escalón con la altura del canal.

En la literatura es posible encontrar muchos estudios numéricos de un flujo 2D incompresible y estable para el flujo alrededor de un escalón en un canal (BFS). En estos estudios se puede determinar una controversia sobre si es posible o no obtener una solución estable para un Re ≥ 800. Este hecho ha sido discutido en detalle (Gresho et al.,1993), donde se concluyó que el flujo sobre un escalón es estable y computable a Re = 800. Otros autores (Keskar y Lyn, 1999; Barton, 1997; Sheu y Tsai, 1999; Biagioli, 1998; Erturk, 2008) han presentado soluciones del flujo BFS por encima de Re = 800, utilizando diversos métodos de discretización de las tradicionales ecuaciones de Navier-Stokes.

No es necesario mencionar que los LBEM están en desarrollo a un alto ritmo y se han convertido en un poderoso método para la simulación de flujos de fluido (Moahamad y Kuzmin, 2010). Sin embargo, hay aún muchas temáticas que necesitan más investigaciones y evaluaciones críticas. Además, el método no es muy utilizado por algunos autores debido a las limitaciones y restricciones que generan los parámetros inherentes en los LBEM. Algunos de éstos son: el tratamiento adecuado de las condiciones de frontera, condiciones iníciales, y el tiempo de relajación, que son los temas estudiados en este trabajo.

Los LBEM están definidos como un esquema en diferencias finitas y tiempo explícito de la ecuación de Boltzmann continua en el espacio de fase y tiempo (He y Luo, 1997). Los LBEM cuentan con una retícula cartesiana en el espacio, a consecuencia de la simetría del conjunto de la velocidad discreta y el hecho de que el espaciado reticular Dx está relacionado con el paso de tiempo Δt por Δx Δt = c, donde c es la unidad base de la velocidad discreta. Esto hace de los LBEM un esquema muy simple que consiste en dos pasos esenciales: la colisión y la advección. Los modelos de colisión hacen referencia a las diversas interacciones entre las partículas del fluido y la advección simplemente traslada las partículas desde una celda de la red a otra vecina de acuerdo con sus velocidades. La simplicidad y la naturaleza cinética de los LBEM son unas de las características que los hacen atractivos.

El método de la ecuación reticular de Boltzmann se basa en la idea original de los autómatas celulares de gases en redes (Frisch, 1986). Para simular el movimiento del fluido dentro de la retícula se utiliza un esquema mesoscópico, donde el paso del tiempo es unitario y existe una fase-espacio discreta. En el dominio reticular cada celda representa un elemento volumen del fluido, y este elemento de volumen consiste de un grupo de partículas para las cuales su movimiento está especificado por una función de distribución de partículas (fdp). En el modelo clásico la fdp es la distribución de Maxwell-Boltzmann. En cada paso de tiempo las partículas se mueven, de acuerdo al modelo seleccionado, hacia las celdas adyacentes (paso de propagación) y colisionan con otras partículas que vienen o viajan hacia la misma celda en diferentes direcciones (paso de colisión). Las variables macroscópicas como la densidad y la velocidad son calculadas a partir de las fdp (Maxwell, 1997; Dieter, 2000).

Con el fin de conocer la eficacia del LBEM, en el presente trabajo se ha resuelto numéricamente el flujo sobre un escalón para números de Reynolds de 100 ≤ Re ≤ 1000, y se ha determinado la exactitud del método, comparando y haciendo una breve discusión con los datos, tanto numéricos como experimentales, obtenidos por otros autores.

Metodología

El principio que guía los LBEM es la construcción de un sistema dinámico en una retícula simple y simétrica (en su mayoría cuadrados en 2D y en 3D cúbicos) el cual involucra una serie de cantidades que pueden ser interpretadas como la pdf de partículas ficticias sobre los vínculos de la retícula. Estas cantidades luego evolucionan en un tiempo discreto según ciertas reglas que se seleccionan para lograr un comportamiento macroscópico deseable que surge con relación a las grandes escalas con el espaciado reticular (Lalleman y Luo, 2000). La ecuación reticular de Boltzmann está dada por (He y Luo, 1997; Dieter, 2000; Succi, 2001):

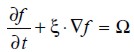[1]

donde Ω es la función de colisión, término que puede simplificarse bastante utilizando la aproximación de Bhatnagar-Gross-Krook (BGK), con un solo tiempo de relajación τ (SRT), el método más sencillo utilizado para resolver la ecuación (1 ). éste consiste en reemplazar el término de colisión por un término que relaciona la diferencia entre la función f y la función de equilibrio de Maxwell-Boltzmann, y un tiempo de relajación.

El argumento básico para el uso de estos tipos de métodos cinéticos simplificados en la simulación de flujos de fluidos macroscópicos es el de que la dinámica macroscópica de un fluido es el resultado de la conducta colectiva de muchas partículas microscópicas en el sistema y que la dinámica macroscópica no es sensible a los detalles subyacentes en la física microscópica. Mediante el desarrollo de una versión simplificada de las ecuaciones cinéticas complejas, como lo es la ecuación de Boltzmann, es posible evitar que sigue a cada partícula como en simulaciones de dinámica molecular (Chen y Doolen, 1998). El LBEM se puede escribir como

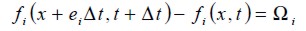[2]

Donde f_i(x,∪,t), son las funciones de distribución de las partículas, con x y ∪ como la posición y la velocidad de la partícula, respectivamente, sobre el espacio fase (x, ∪) y tiempo t. Aquí las cantidades macroscópicas, como la velocidad y la densidad, se pueden obtener a partir de los momentos de f (x,∪,t). El operador de colisión Ω del lado derecho de la ecuación (2) utilizando la aproximación BGK puede ser reemplazado por (Dieter, 2000):

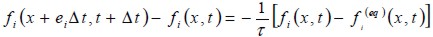[3]

donde fi^(eq)(x,t) es la función de distribución de equilibrio, ei son los vectores de velocidades discretas y Τ; es el tiempo de relajación, el cual está relacionado con la viscosidad cinética del fluido mediante (He y Luo, 1997):

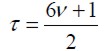[4]

La figura 1 muestra el modelo estándar D2Q9 (bidimensional y nueva velocidades discretas) de la celda utilizada en el presente trabajo, donde la función de distribución de equilibrio para flujos isotérmicos y estables está definida por (Quian, 1992):

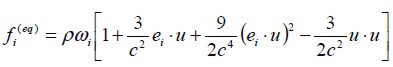[5]

donde ρ y u son la velocidad macroscópica y la densidad, respectivamente, y ω_i son los factores de peso constantes, que para el modelo D2Q9 están dados por:

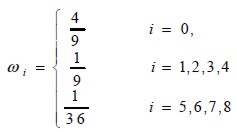[6]

Las velocidades discretas, ei, para el modelo D2Q9 (figura 1) están definidas como sigue:

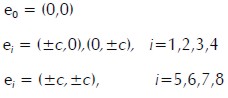donde c=Δx/Δt=Δy/Δt, Δx y Δt son el espacio de la celda y el paso de tiempo, respectivamente, que son un unitarios. Las cantidades hidrodinámicas básicas se obtienen mediante la sumatoria de los momentos en el espacio-velocidad.

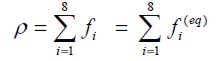[7]

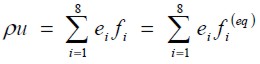[8]

La viscosidad macroscópica se obtiene a partir de:

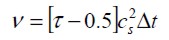[9]

donde c_s el la velocidad del sonido e igual a c/Ö3 (Mohamad et al., 2010).

La evolución del sistema para el modelo BGK está determinada por dos pasos principales: propagación (movimiento hacia las celdas vecinas) y colisión (redistribución de las f’^s de cada celda), calculados mediante:

Collision step:

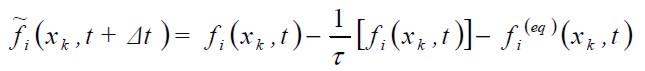[10]

Streaming step:

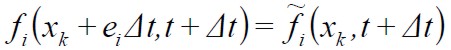donde ƒⁱ, representa el paso de poscolisión. Este paso es totalmente local, y el de propagación no exige grandes prestaciones computacionales (Quian, 1992; Maxwell, 1997).

Modelo del flujo por medio de un escalón

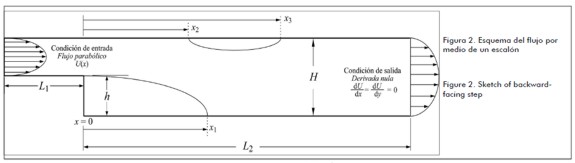
En la figura 2 se muestra el esquema del flujo considerado. En este estudio la entrada del flujo está ubicada aguas arriba del escalón y se localiza a una distancia L₁ = 4h detrás del escalón y la salida ubicada a una distancia L₂ = 35h El número de nodos en la dirección horizontal es N_x = (L₁ + L₂). La longitud del canal a la salida se seleccionó teniendo en cuenta que los puntos de recirculación del flujo no sean afectados por la misma condición de salida del flujo. La altura del canal utilizada es de H = 2h.= N_y-2, donde N_y es el número de nodos en la dirección vertical del canal. La malla utilizada o retícula es totalmente uniforme en todo el dominio. La distancia x1 determina el punto donde se presenta la recirculación del flujo en la pared inferior y las distancias x₂ y x₃ definen los puntos de recirculación en la pared superior. Todas las distancias son referenciadas al escalón, en x=0 según la figura (2).

Condiciones a la entrada del flujo

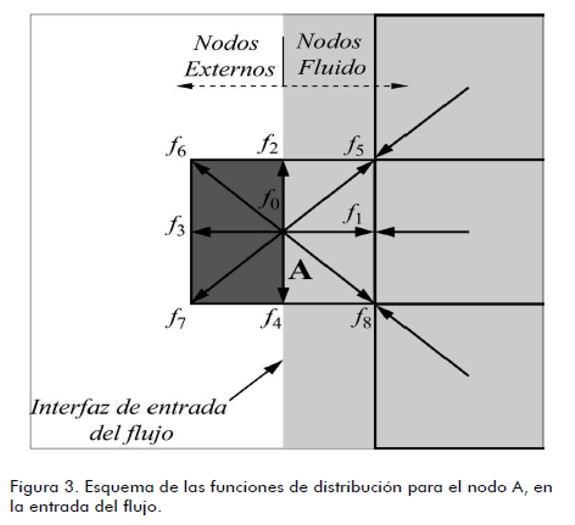
Barton (1997) estudió el efecto de la longitud del canal antes del escalón (entrada del flujo) y demostró que las soluciones que se obtienen del flujo sólo son afectadas para bajos números de Reynolds. En esta investigación la longitud de la entrada del canal, antes del escalón, fue seleccionada igual a; L₁ = 4h. La condición impuesta es la de un flujo totalmente desarrollado tal como un flujo de Poiseuille entre dos placas planas, que equivale a la imposición de un perfil parabólico para la velocidad (U = u_x, u_y = 0). Las funciones de distribución ( f_i ) desconocidas en los nodos de la entrada son calculadas utilizando las f’s que arriban a éstos desde el interior del dominio y el valor correspondiente de la velocidad en cada nodo. Para el modelo D2Q9, y tomando como ejemplo el nodo x_A que muestra la figura 3, después del paso de propagación la f₀ f₂, f₃, f₄, f₆, y la f₇ son conocidas, debido a que arriban de los nodos siguientes a x_A, y las funciones f₁, f₅, y f₈ se calculan utilizando las ecuaciones (7) y (8) y la condición de igualdad para la función de distribución de no equilibrio en la dirección normal a la entrada del flujo. éstas se determinan de la siguiente forma:

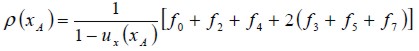[11]

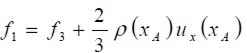[12]

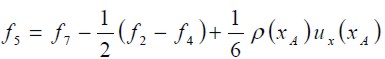[13]

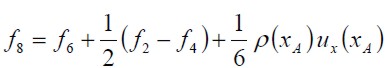[14]

Un paso de colisión es necesario a los fines de obtener 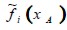para i = 1,5 y 8. Tanto en la esquina superior como en la inferior el cálculo de las f ’s desconocidas requiere un tratamiento especial para evitar la pérdida de partículas.

Condiciones a la salida del flujo

Aquí se comprobaron dos tipos de condiciones. Primero se implementó la misma condición que a la entrada (condición de Drichlet) imponiendo un perfil parabólico de velocidad, con la diferencia de que a la salida, las f ’s a calcular son f₃, f₆ y f₇. También, se implementó la condición de derivada nula para la velocidad (condición de Newman), donde el valor de la velocidad en el nodo perteneciente a la salida tiene el mismo valor que el nodo inmediatamente anterior en la dirección x. Estas condiciones han demostrado no afectar considerablemente el flujo (Zou y He, 1997; Bouzide et al., 2001; Latt, 2008).

Condiciones de pared fija

Para tratar el paso de propagación en presencia de fronteras de pared fija se utiliza la aproximación lineal propuesta por Bouzidi (2001), conocida como Bounce-back, en la que se ubica la pared en la mitad del camino entre el nodo sólido y el nodo fluido. Suponiendo que rl es un nodo fluido tal que r_l + e_i es un nodo sólido, y llamando a e_{i ’} la velocidad invertida o de dirección inversa de e_i (e_{i ’} = -e_i), se tiene que

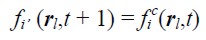[15]

En el lado derecho de la ecuación (15), la f c es tomada después de la colisión y antes de la propagación. La f ( ·¸ t + 1) del lado izquierdo de la ecuación se usaría en valores después de la colisión y de la propagación, la cual corresponde a un paso de tiempo LBM completo. Lo anterior indica que la dinámica de los nodos sólidos y los nodos fluido, vecinos de la pared, difieren únicamente en el paso de propagación (Flórez, 2008).

Resultados y discussion

El diagrama de flujo utilizado para el desarrollo del código computacional con el cual se obtuvieron los resultados es el propuesto por Flórez (2008). El lenguaje de programación utilizado es Fortran 90. Los valores definidos en unidades reticulares según Latt (2008), fueron seleccionados teniendo en cuenta la teoría existente y las restricciones del método, éstos son: tiempo de relajación τ = 0,54, velocidad máxima a la entrada del canal U_max = 0,057, el número de Reynolds, Re = 2h·U_max/3v, donde v es obtenida de la ecuación (3), el número de nodos utilizados N_x y N_y son función del Re a simular. Los respectivos valores son: Re = 100 N_x = 850, N_y = 52, Re = 200 N_x = 1.700, N_y = 102, Re = 300 N_x = 2.550, N_y = 152, Re = 400 N_x = 2.550, N_y = 152 y, para Re > 500 N_x = 4.250, N_y = 252.

Como se muestra en la ecuación (16), donde r define la coordenada del nodo y t el paso del tiempo, la velocidad promedio calculada mediante todo el dominio fue el criterio de convergencia utilizado en todas las simulaciones. Buscando una gran exactitud en los resultados la tolerancia utilizada estuvo definida por tol = 10 ^-7.

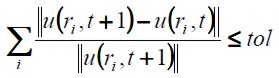[16]

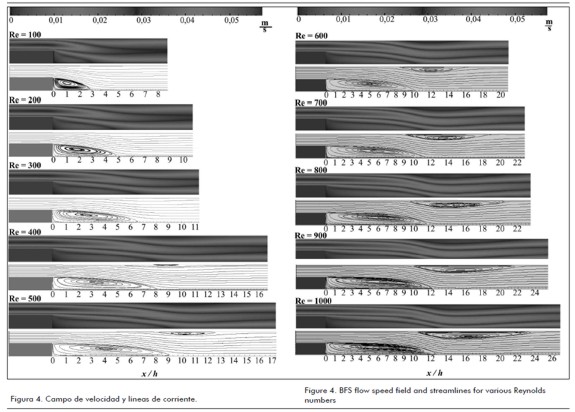
La figura 4 muestra los campos de velocidad y las respectivas líneas de corriente del flujo por medio de un escalón para 100 ≤ Re ≤ 1.000. En los campos de velocidad se puede ver cómo se distribuye la magnitud de la velocidad dentro del canal a medida que el número de Re se incrementa. Las líneas de corriente exhiben la formación de las regiones de recirculación. Es de notar que en esta figura la escala en la dirección x e y se ha manipulado para poder observar con claridad la diferencia en los detalles para todo el rango de números de Re. Y es importante mencionar que las líneas de corriente permiten observar de forma clara la aparición de la recirculación en la pared superior para Re ≥ 400. En todo el rango de números de Re, 100 ≤ Re ≤ 1.000 los resultados han sido comparados con los obtenidos numérica y experimentalmente por otros autores. En la mayoría de los casos este flujo ha sido investigado hasta un Re de 800.

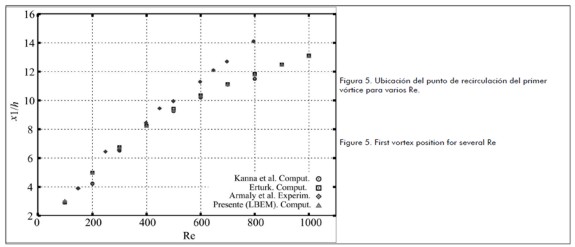
La figura 5 muestra el punto de recirculación del primer vórtice sobre la pared inferior del canal comparado con los resultados computacionales obtenidos por (Kanna et al., 2006) y (Erturk, 2008) y los resultados experimentales obtenidos por (Armaly et al., 1983).

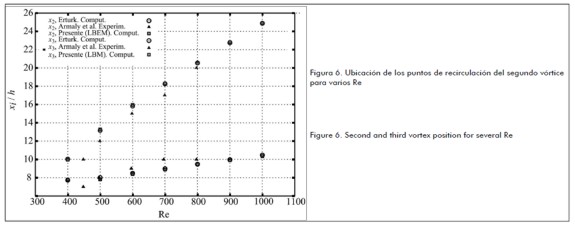
En la figura 6 se muestran los puntos de recirculación del vórtice que se genera en la pared superior del canal y es comparada, al igual que en la figura 5, con los resultados numéricos y experimentales de otros autores.

En la tabla 1 se presentan los resultados numéricos obtenidos de las coordenadas de los puntos de recirculación, logrados en la simulación del flujo mediante el uso de los LBM.

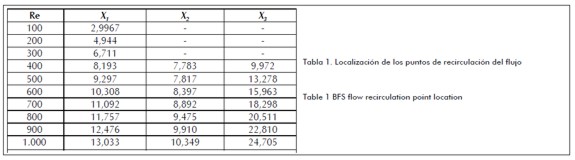
El cálculo de la coordenada de los puntos de recirculación se realizó en toda la dirección x. Se utilizó la velocidad del nodo fluido inmediatamente después de la pared inferior (y = 2), para determinar la coordenada x₁ de la primera recirculación, y del nodo fluido inmediatamente anterior de la pared superior (y = N_y -1) para determinar las coordenadas x₂ y x₃ de la segunda recirculación.

Conclusiones

Se ha presentado una solución numérica del flujo bidimensional por medio de un escalón y en estado estable utilizando el método de la ecuación reticular de Boltzmann. En la simulación se utilizó un perfil de velocidad parabólico a la entrada del flujo y la condición de derivada nula a la salida. La salida se ubicó a una distancia, aguas abajo, del escalón, lo suficientemente alejada de él para que los vórtices que se generan en el flujo no se viesen afectados por la condición de salida. Se utilizaron varios tamaños de malla, desde 850 x 52 para Re = 100, hasta 4.250 x 252 para Re = 1.000. El método de la ecuación reticular de Boltzmann ha demostrado dar resultados numéricos bastante exactos para la simulación de flujos laminares estables con presencia de vórtices.

Se ha revelado un punto importante en la recirculación que genera el flujo en la pared superior. Esta recirculación reflejó un comportamiento de un solo vórtice para todos los números de Re, a diferencia de la simulación para el Re = 800, donde se revelaron tres vórtices en la misma recirculación (ver figura 4.). Los autores creen que dicho comportamiento es debido a que el número de Re = 800 es un punto de transición del flujo y que a partir de este Re el flujo no es totalmente estable.

---

Referencias

Armaly, B. F., Durst, F., Pereira, J. C. F., Schonung, B., Experimental and theoretical investigation of backward-facing step flow., Journal of Fluid Mechanics, 127, 1983, pp. 473-96.

Barton, I. E., The entrance effect of laminar flow over a backward -facing step geometry., Int J. Numer. Methods Fluids, 25, 1997, pp. 633-44.

Biagioli, F., Calculation of laminar flows with second-order schemes and collocated variable arrangement., Int J. Numer. Methods Fluids, 26, 1998, pp. 887-905.

Bouzidi, M., d´Humieres, D., Lallemand, P., Luo, L., Lattice Boltzmann Equation on a Two-Dimensional Rectangular Grid., Journal of Computational Physics, 172, 2001, pp. 704-717.

Dieter, A. Wolf-Gladrow., Lattice-Gas Cellular Automata and Lattice Boltzmann Models, Springer (ed.), 2000, pp. 40-65

Erturk, E., Numerical solution of 2D steady imcompressible flow over a backward-facing step, Part I: High Reynolds number solutions., Computer & fluids, 37, 2008, pp. 633-55.

Florez, S. E., Cuesta, I., Salueña, C., Flujo de Poiseuille y la cavidad con pared movil calculado usando el método de la ecuación de lattice Boltzmann., Ingeniería & Desarrollo, 24, 2008, pp. 117-32.

Frisch, U., Hasslacher, B., Pomeau, Y., Lattice-gas automata for the Navier-Stokes equation., Phys. Rev. Lett, 56, 1986, pp.1505-1515.

Gresho, P.M., Gartling, D.K., Torczynski, J.R., Cliffe, K.A., Winters K.H., Garratt T.J., Is the steady viscous incompressible two-dimensional flor over a backward-facing step at Re =800 stable?., Int J. Numer., Methods Fluids, 17, 1993, pp. 501-41.

He, X., Luo, L-S., Theory of the lattice Boltzmann method: From the Boltzmann equation to the lattice Boltzmann equation., Phys. Rev. E, 56 (6), 1997, pp. 6811-17.

Kanna, P. R., Das, M. K., A short note on the reattachment length for BFS problem., Int J. Numer. Methods Fluids, 50, 2006, pp. 683-692.

Keskar, J., Lyn, D.A., Computation of laminar backward-facing step flow at Re = 800 with spectral domain decomposition method., Int. J. Numer, Methods Fluids, 29, 1999, pp. 411- 427.

Latt, J., Choice of units in lattice Boltzamnn Simulation., Lattice Boltzmann Howtos: http://www.lbmethod.org/howtos:main. 2008.

Maxwell, B. J., Lattice Boltzmann methods in Interfacial Wave Modelling., Ph. D. Tesis. Edinburgh´s University, 1997.

Quian, Y., d´Humieres, D., Lallemand, P., Lattice BGK models for Navier-Stokes Equation., Europhys. Lett., 17, 1992, pp.479-84.

Sheu, T., Tsai, S., Consistent Petrov Galerkin finite element simulation of channel flows., Int J. Numer. Methods Fluids: 31,1999, pp. 1297-310.

Succi, S., The lattice Boltzmann Equation for Fluid Dynamics and Beyond. Oxford (ed.), 2001, pp. 64- 93.

Zou, Q., He, X., On pressure and velocity boundary conditions for the lattice Boltzmann BGK model. Phys Fluids: 9, 1997, pp. 1591-1598.

---

Elkin Florez¹, Yamid Carranza², Yesid Ortiz³

¹Mechanical Engineer, Universidad Francisco de Paula Santander, Colombia. Master of Mechanical Engineering, Universidad de los Andes, Colombia. Master in Chemical and Process Engineering, Universidad de Rovira i Virgili, Spain. Doctor in Mechanical Engineering, Aeronautics and Fluid, Universidad Politécnica de Cataluña, Spain. Associate Professor, Universidad de Pamplona. eflorez@unipamplona.edu.co

² Mechanical Engineer, Universidad Tecnológica de Pereira, Colombia. Master of Mechanical Engineering, Universidad de los Andes, Colombia. PhD Student, Politécnico de Monterrey, México. Assistant Professor, Universidad Tecnológica de Pereira, Colombia. yamidc@utp.edu.co

³ Mechanical Engineer, Universidad Francisco de Paula Santander, Colombia. Master of Mechanical Engineering, Universidad de los Andes, Colombia. Assistant Professor, Universidad Tecnológica de Pereira, Colombia. yosanchez@utp.edu.co

---

ABSTRACT

Keywords: fluid flow, lattice Boltzmann equation method, numerical simulation.

---

Received: February 16th 2010

Accepted: May 25th 2011

Introduction

Flows through channels where there is separation and recirculation of the boundary layer is often found in many flow problems in engineering. Typical examples would be flows in a heat exchanger and pipelines. A backward-facing step (BFS) flow can be considered to be the simplest geometry having great physical content shown by the vortices that are presented and their recirculation, all of these depending on the Reynolds number (Re) and the aspect ratio parameter.

In the literature one can find many numerical studies of a twodimensional, incompressible and stable BFS flow. Controversy can be identified in these studies regarding whether a stable solution for Re > 800 can be obtained. This has been discussed in detail by Gresho (Gresho et al., 1993) who concluded that the BFSF is stable and computable at Re = 800. Other authors (Keskar and Lyn, 1999; Barton, 1997; Sheu and Tsai, 1999; Biagioli, 1998; Erturk, 2008) have presented BFS flow solutions above Re = 800, using different methods for the discretisation of traditional Navier-Stokes equations.

LBEM has been the object of high paced development and has become a powerful method for simulating fluid flows (Moahamad and Kuzmin, 2010). However, many issues need more investigation and critical evaluation. The method has also been used by some authors paying less attention to LBEM parameter limitations and constrains. Some of these issues concern the treatment of boundary conditions, initial conditions and relaxation time, these being the topics being studied in the present paper.

The LBEM is an explicit time finite difference scheme for continuous Boltzmann equation in phase space and time (He and Luo, 1997). The LBEM has a underlying Cartesian lattice grid in space as a consequence of discrete speed set symmetry and the fact that lattice spacing Dx is related to time step size Dt by Dx = cDt, where c is the basic discrete speed set unit. This makes the LBEM a very simple scheme as it consists of two essential steps: collision and advection. Collision models various interactions amongst fluid particles and advection simply moves particles from one grid point to another, according to their speed. LBEM simplicity and kinetic nature are among its appealing features.

LBEM are based on the original idea of lattice gas cellular automaton (Frisch, 1986). A mesoscopic scheme is used to simulate fluid motion within the lattice, where time step is unitary and there is discrete phase-space. Each cell represents an element of fluid volume in the domain grid; the volume element consists of a group of particles whose motion is specified by a particle distribution function (pdf). In the classical model, the pdf is the Maxwell-Bolztamnn distribution. The particles move to adjacent cells, according to the model selected at each time step (propagation step) and collide with other particles coming from or traveling to the same cell in different directions (step collision). Macroscopic variables such as density and speed are calculated from the pdf (Maxwell, 1997) (Dieter, 2000).

The backward facing step flow has been numerically solved for a wide range of Reynolds numbers 100 ≤ Re ≤ 1,000 in this work to determine LBEM effectiveness and the method' s accuracy has been determined, comparing and making a brief discussion of data regarding both numerical and experimental results obtained by other authors.

Solution method

The LBEM' s guiding principle is to construct a dynamic system on a simple high-symmetry lattice (mostly square in 2D and cubic in 3D) involving a number of quantities which can be interpreted as the pdf of fictitious particles on the lattice links. These quantities then evolve in discrete time according to certain rules chosen to attain some desirable macroscopic behavior emerging on large scales relative to lattice spacing (Lalleman and Luo, 2000). The lattice Boltzmann equation has been defined (He and Luo, 1997; Dieter, 2000; Succi, 2001) as:

[1]

where Ω is the collision operator. This term can be simplified significantly using the Bhatnagar-Gross-Krook approximation (BGK), using a single relaxation time t (SRT) which is the simplest method used for solving the equation (1). This involves replacing the collision term by a term that relates the difference between function f and the Maxwell-Boltzmann equilibrium function with determined relaxation time.

The basic premise for using these types of simplified kinetic methods for macroscopic fluid flows is that the macroscopic dynamics of a fluid result from the collective behaviour of many microscopic particles in the system and that macroscopic dynamics are not sensitive to underlying details in microscopic physics. By developing a simplified version of complicated kinetic equations, such as the full Boltzmann equation one does not have to follow each particle, as in molecular dynamics simulations (Chen and Doolen, 1998). The LBEM can be written as:

[2]

where f_i(x,∪,t), are the particle distribution function, x and υ being position and particle speed, respectively, in phase space (x, υ) and time t. Here macroscopic quantities such as speed and density can be obtained through the first moments of f (x,υ,t). Collision operator Ω, on the right-hand side of equation (2) using the BGK approximation, will be replaced by (Dieter, 2000):

where fi^(eq)(x,t) is the equilibrium distribution function, e_i are discrete speed vectors and τ is relaxation time related to fluid kinetic viscosity (He and Luo, 1997):

[3]

[4]

Figure 1 shows the standard D2Q9 lattice model (two-dimensional and nine discrete speeds) used in this work where equilibrium distribution function is defined by isothermal and incompressible flows as (Quian, 1992):

[5]

where ρ and u are macroscopic speed and density, respectively, and ω_i constant weight factor, for D2Q9 given as:

[6]

Discrete speeds, e_i, for D2Q9 (Figure figura 1) are defined as follows:

where c=Δx/Δt=Δ and /Δt, Δx y Δt are lattice space and lattice time step size, respectively, being set to unity. The basic hydrodynamic quantities are obtained through moment summations in the speed space

[7]

[8]

Macroscopic viscosity is determined by

[9]

where c_s is the speed of sound and equal to c/Ö–3 (Mohamad et al., 2010).

The evolution of the medium, for the BGK model, consists of two steps: streaming (motion towards relevant neighbours) and collision (redistribution of the f' s at each node). These are calculated by means of:

Collision step:

[10]

Streaming step:

whereƒⁱ, represents the post-collision step. The post-collision step is totally local and the streaming step does not require large computational effort (Quian, 1992) (Maxwell, 1997).

Backward-facing step model

Figure 2 shows the scheme for the flow considered in the current study. Here, flow entry was located up-stream from the step and was placed at L₁ = 4h behind the step and the exit was located L₂ = 35h down-stream of the step. The number of horizontal nodes was N_x = (L₁ + L₂). Channel length to the exit was selected bearing in mind that flow recirculation points were not affected by the same exit condition. Channel height was defined as H = 2h.= N_y-2, where Ny was the number of nodes in the channel' s vertical direction. The lattice was completely uniform in the whole domain. Distance x₁ determined the point where flow recirculation appeared near the bottom of the channel' s low and distances x₂ and x₃ defined recirculation points at the top of the wall. All distances were indexed to the step, in x = 0, according to t Figure 2.

Inlet flow condition

Barton (1997) studied the effect of channel length on flow upstream of the step (inlet flow) and demonstrated that the numerical flow solutions so obtained were only affected for low Reynolds numbers. In this research, this length was selected as being equal to L₁ = 4h. The assumption was that flow was completely developed (like Poiseuille flow) between two flat plates, equivalent to imposing a parabolic profile for speed (U = u_x, u_y = 0). Unknown distribution functions for nodes at the inlet were calculated using the f ^{' s} derived from those within the domain and their corresponding speed value. For the D2Q9 model, and taking node xA as an example (shown in Figure 3), f₀, f₂, f₃, f₄, f₆, and f₇ became known after the propagation step because they were derived from nodes neighbouring x_A, and functions f₁, f₅, and f₈ were calculated using equations (7) and (8), as was equality for the non-equilibrium distribution function in a normal direction at the inlet flow. These were determined as follows:

[11]

[12]

[13]

[14]

Taking equation 10 into account in the collision step, then had to be obtained for i = 1, 5 and 8. Calculating the unknown f ^{' s} needed special treatment to avoid the loss of particles in both the top and low corners.

Outlet flow condition

Here, two types of conditions were verified. A fixed speed flow (i.e. Drichlet condition) was first implemented at inlet and outlet flow imposing a parabolic speed profile, the difference being that the f^{' s} to be calculated at the outlet were f₃, f₆, and f₇. The null derivative condition for outlet flow speed was also studied (Newman condition) where the value of speed in the exit node had the same value as the immediately previous node in direction x. These conditions have been seen to not greatly affect flow (Zou y He, 1997; Bouzide, et al., 2001; Latt, 2008).

Fixed boundary condition

The linear approach, proposed by Bouzidi (2001), known as bounce-back, was used to treat the propagation step in the presence of a fixed wall where the wall was located halfway between the solid and fluid nodes. Supposing that rl described fluid node position f, then r_l + e_i would be solid node position and assuming e_i' were inverted speed or inverse direction for e_i, namely (e_{i '} = -e_i), then:

[15]

On the right-hand side of the equation ((15)), f ^c was taken after collision and before propagation. f ( ,t + 1) would then be used for values after collision and propagation, corresponding to a completed LBM time step. The previous factor indicated that solid and fluid node dynamics, wall neighbours, only differed regarding the propagation step (Flórez, 2008).

Results and Discussion

The computational code for developing the flow diagram was proposed by Flórez (2008); Fortran 90 programming language was used. Latt (2008) was used for defining/selecting LBM unit values, bearing existing theory in mind and the method' s limitations, these being t = 0.54 relaxation time, U_max = 0.057 maximum speed at inlet channel, Re = 2h-·_max/3n Reynolds number where n was obtained from equation 9, N_x the number of nodes used and N_y a function of Re to be simulated. The respective values were: Re = 100 N_x = 850, N_y = 52, Re = 200 N_x = 1.700, N_y = 102, Re = 300 N_x = 2.550, N_y = 152, Re = 400 N_x = 2.550, N_y = 152 y, para Re > 500 N_x = 4.250, N_y = 252.

Equation (16) shows where r defined a node' s coordinates and t the time. The speed calculated throughout the whole domain was the criterion of convergence used in all simulations. Looking for high accuracy in the results, tolerance was defined by, tol = 10^-7.

[16]

Figure 4 shows speed fields and their respective flow streamlines for 100 ≤ Re ≤ 1,000. The speed fields show how speed magnitude became distributed inside the channel as the number of Re increased. The streamlines allowed observing vortex formation. It can be noticed that in this Figure the scale in x and y direction have been manipulated to clearly identify difference regarding the different details present in the flow for the whole rank of Re numbers. Moreover, it should be stressed that the streamlines allow clearer observation of the appearance of recirculation at the top of the wall for Re ³ 400. The results for the whole range of numbers for Re100 ≤ Re ≤ 1,000 have been compared to numerically and experimentally ones obtained by other authors; in most cases this flow has been investigated up to Re = 800.

Figure 5 shows the position of the first recirculation point or vortex present at the channel' s low wall compared to computational results obtained by Kanna et al., (2006) and Erturk (2008) and experimental results obtained by Armaly et al. (1983).

Figure 6 shows recirculation points or vortex generated at the channel' s top wall. This was compared (Figure 5) to other authors' numerical and experimental results.

Table 1 shows the numerical results obtained for recirculation point coordinates using the LBEM.

Recirculation point coordinates were calculated for the whole of the x direction. Fluid node speed was taken immediately after the low wall (y = 2) to determine coordinate x1 for the first recirculation and immediately prior to vertical fluid node at the top of the wall (y = Ny-1) to determine second recirculation coordinates x₂ and x₃.

Conclusions

The steady state backward-facing step stable state problem has been numerically resolved using the lattice Boltzmann equation method. A parabolic speed profile was used at inlet flow and the null derivative condition at the outlet in such simulation. The outlet flow was located downstream from the step sufficiently away from it so that the vortex generated in the flow was not affected by the outlet. Different mesh sizes were used, from 850 x 52 for Re = 100, up to 4250 x 252 for Re = 1,000. The lattice Boltzman method has been seen to give highly accurate numerical results for simulating laminar flows in the presence of a vortex An important point was revealed in the recirculation generated by the flow at the top of the wall. This recirculation reflected a single-vortex pattern for all Re numbers, unlike the simulation for Re = 800 where three vortexes were revealed in the same recirculation (See Figure 4). The authors believe that the pattern mentioned above was due to Re = 800 being a flow transition point and that flow was not completely stable from this Re onwards.

---

References

Armaly, B. F., Durst, F., Pereira, J. C. F., Schonung, B., Experimental and theoretical investigation of backward-facing step flow., Journal of Fluid Mechanics, 127, 1983, pp. 473-96.

Barton, I. E., The entrance effect of laminar flow over a backward -facing step geometry., Int J. Numer. Methods Fluids, 25, 1997, pp. 633-44.

Biagioli, F., Calculation of laminar flows with second-order schemes and collocated variable arrangement., Int J. Numer. Methods Fluids, 26, 1998, pp. 887-905.

Bouzidi, M., dÂ' Humieres, D., Lallemand, P., Luo, L., Lattice Boltzmann Equation on a Two-Dimensional Rectangular Grid., Journal of Computational Physics, 172, 2001, pp. 704-717.

Dieter, A. Wolf-Gladrow., Lattice-Gas Cellular Automata and Lattice Boltzmann Models, Springer (ed.), 2000, pp. 40-65

Erturk, E., Numerical solution of 2D steady imcompressible flow over a backward-facing step, Part I: High Reynolds number solutions., Computer & fluids, 37, 2008, pp. 633-55.

Florez, S. E., Cuesta, I., Salueña, C., Flujo de Poiseuille y la cavidad con pared movil calculado usando el método de la ecuación de lattice Boltzmann., Ingeniería & Desarrollo, 24, 2008, pp. 117-32.

Frisch, U., Hasslacher, B., Pomeau, Y., Lattice-gas automata for the Navier-Stokes equation., Phys. Rev. Lett, 56, 1986, pp.1505-1515.

Gresho, P.M., Gartling, D.K., Torczynski, J.R., Cliffe, K.A., Winters K.H., Garratt T.J., Is the steady viscous incompressible two-dimensional flor over a backward-facing step at Re =800 stable?., Int J. Numer., Methods Fluids, 17, 1993, pp. 501-41.

He, X., Luo, L-S., Theory of the lattice Boltzmann method: From the Boltzmann equation to the lattice Boltzmann equation., Phys. Rev. E, 56 (6), 1997, pp. 6811-17.

Kanna, P. R., Das, M. K., A short note on the reattachment length for BFS problem., Int J. Numer. Methods Fluids, 50, 2006, pp. 683-692.

Keskar, J., Lyn, D.A., Computation of laminar backward-facing step flow at Re = 800 with spectral domain decomposition method., Int. J. Numer, Methods Fluids, 29, 1999, pp. 411- 427.

Latt, J., Choice of units in lattice Boltzamnn Simulation., Lattice Boltzmann Howtos: http://www.lbmethod.org/howtos:main. 2008.

Maxwell, B. J., Lattice Boltzmann methods in Interfacial Wave Modelling., Ph. D. Tesis. Edinburgh' s University, 1997.

Quian, Y., d' Humieres, D., Lallemand, P., Lattice BGK models for Navier-Stokes Equation., Europhys. Lett., 17, 1992, pp.479-84.

Sheu, T., Tsai, S., Consistent Petrov Galerkin finite element simulation of channel flows., Int J. Numer. Methods Fluids: 31,1999, pp. 1297-310.

Succi, S., The lattice Boltzmann Equation for Fluid Dynamics and Beyond. Oxford (ed.), 2001, pp. 64- 93.

Zou, Q., He, X., On pressure and velocity boundary conditions for the lattice Boltzmann BGK model. Phys Fluids: 9, 1997, pp. 1591-1598.

---