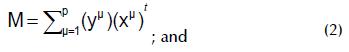Using hybrid associative classifier with translation (HACT) for studying imbalanced data sets
Estudio de conjuntos de datos desbalanceados usando un modelo asociativo con traslación de ejes
DOI:
https://doi.org/10.15446/ing.investig.v32n1.28522Keywords:
data set, associative model, under sampling, class imbalance, pre-processing (en)Modelo asociativo, bajo-muestreo, clase des-balanceada, pre-procesamiento (es)
Class imbalance may reduce the classifier performance in several recognition pattern problems. Such negative effect is more notable with least represented class (minority class) Patterns. A strategy for handling this problem consisted of treating the classes included in this problem separately (majority and minority classes) to balance the data sets (DS). This paper has studied high sensitivity to class imbalance shown by an associative model of classification: hybrid associative classifier with translation (HACT); imbalanced DS impact on associative model performance was studied. The convenience of using sub-sampling methods for decreasing imbalanced negative effects on associative memories was analysed. This proposal's feasibility was based on experimental results obtained from eleven real-world datasets.
En diversos problemas de reconocimiento de patrones, se ha observado que el desequilibrio de clases puede disminuir el desempeño del clasificador, principalmente en los patrones de las clases minoritarias. Una estrategia para resolver el problema del desbalance, consiste en tratar por separado las clases incluidas en el problema (clase minoritaria o mayoritaria), a fin de equilibrar los conjuntos de datos. En este sentido, la motivación del presente artículo estriba en el hecho de que el modelo asociativo visto como Clasificador Híbrido Asociativo con Traslación (CHAT), es muy sensible al desbalance de las clases. Por ello, se analiza el impacto que los conjuntos de datos desbalanceados pueden tener sobre el rendimiento del CHAT. Adicionalmente, se analiza la conveniencia de utilizar métodos de bajo-muestreo para disminuir los efectos negativos que el modelo asociativo pueda sufrir. La viabilidad de este estudio se sustenta con los resultados experimentales obtenidos de once conjuntos de datos reales. Finalmente, el presente trabajo se considera como una investigación analítica-sintética.
Using hybrid associative classifier with translation (HACT) for studying imbalanced data sets
Estudio de conjuntos de datos desbalanceados usando un modelo asociativo con traslación de ejes
Laura Cleofas Sánchez1, M. Guzmán Escobedo2, Rosa María Valdovinos Rosas3, Cornelio Yáñez Márquez4, Oscar Camacho Nieto5
1 PhD Candidate in Computer Sciences, Centro de Investigación en Computación, Mexico. Instituto Politécnico Nacional, MSc in Computer Sciences, Instituto Tecnológico de Toluca, Mexico. Centro de Investigación en Computación, Juan de Dios Bátiz s/n esq. Miguel Othón de Mendizábal, Unidad Profesional Adolfo López Mateos, Del. Gustavo A. Madero, Mexico. E-mail:laura18cs77@gmail.com.
2 Computational Systems Engineer, Instituto Técnico Superior de Hidalgo, Mexico. E-mail: janyne20@hotmail.com.
3 PhD in Computational Sciences, Universitat Jaume I, Spain. Universidad Autónoma del Estado de México, Centro Universitario Valle de Chalco, Mexico. E-mail: li_rmvr@hotmail.com.
4 PhD in Computational Sciences, Instituto Politécnico Nacional, Mexico. Instituto Politécnico Nacional, Centro de Investigación en Computación, Mexico. E-mail: cyanez@cic.ipn.mx.
5 PhD in Computational Sciences, Instituto Politécnico Nacional, Mexico. Instituto Politécnico Nacional, Centro de Innovación y Desarrollo Tecnológico en Cómputo, Mexico. Corresponding author E-mail: ocamacho@ipm.mx.
Received: August 19th 2011; Accepted: January 26th 2012
RESUMEN
En diversos problemas de reconocimiento de patrones, se ha observado que el desequilibrio de clases puede disminuir el desempeño del clasificador, principalmente en los patrones de las clases minoritarias. Una estrategia para resolver el problema del desbalance, consiste en tratar por separado las clases incluidas en el problema (clase minoritaria o mayoritaria), a fin de equilibrar los conjuntos de datos. En este sentido, la motivación del presente artículo estriba en el hecho de que el modelo asociativo visto como Clasificador Híbrido Asociativo con Traslación (CHAT), es muy sensible al desbalance de las clases. Por ello, se analiza el impacto que los conjuntos de datos desbalanceados pueden tener sobre el rendimiento del CHAT. Adicionalmente, se analiza la conveniencia de utilizar métodos de bajo-muestreo para disminuir los efectos negativos que el modelo asociativo pueda sufrir. La viabilidad de este estudio se sustenta con los resultados experimentales obtenidos de once conjuntos de datos reales. Finalmente, el presente trabajo se considera como una investigación analítica-sintética.
Palabras clave: Modelo asociativo, bajo-muestreo, clase desbalanceada, pre-procesamiento.
ABSTRACT
Class imbalance may reduce the classifier performance in several recognition pattern problems. Such negative effect is more notable with least represented class (minority class) Patterns. A strategy for handling this problem consisted of treating the classes included in this problem separately (majority and minority classes) to balance the data sets (DS). This paper has studied high sensitivity to class imbalance shown by an associative model of classification: hybrid associative classifier with translation (HACT); imbalanced DS impact on associative model performance was studied. The convenience of using sub-sampling methods for decreasing imbalanced negative effects on associative memories was analysed. This proposal's feasibility was based on experimental results obtained from eleven real-world datasets.
Keywords: data set, associative model, under sampling, class imbalance, pre-processing.
Introduction
Karl Steinbuch introduced the first associative model, called Lern-matrix, in 1961 (Santiago, 2003); it can be used as a binary pattern classifier. Various associative models have been developed since, for example the HACT, morphological and alpha beta models (Santiago, 2003).
Classifier performance is strongly related to two aspects in pattern recognition, regardless of application (Japkowicz, 2002; Huang et al., 2006): a learning model used by the classifier and the quality of the data set (DS) used for training. Some inherent DS problems are imbalanced DS, redundant patterns, atypical and high dimension (Barandela et al., 2005). This paper is focused on the imbalance problem.
Imbalance occurs when one class (minority) is heavily under-represented compared to other classes (majority) (Weiss, 2004). Real cases (text categorisation, credit analysis) typically have few minority class samples (Tan, 2005; Huang et al., 2006). Low minority class representation complicates classifier learning (Weiss, 2004) and there is currently no universal solution for addressing such problem. Proposed solution strategies have included sampling (over sampling or under sampling) or adjusting the training algorithm (Barandela et al., 2005; Chawla et al., 2002).
This study analyses an associative model's (HACT) performance in imbalance involving two aspects: how model training is affected when using unbalanced DS and the desirability of using low DS sampling.
The imbalance problem
The negative effect of imbalance on classifier performance is basically due to the false assumption of balanced distribution of classes (Japkowicz, 2002; Huang et al., 2006). Research in this area can be categorised into three large groups: addressing data (Japko-wicz, 2002) or algorithm imbalance (Ezawa et al., 1996), measuring classifier performance in unbalanced domains (Ranawana et al., 2006), (Daskalaki, 2006) and analysing the relationship between class imbalance and data complexity (Prati et al., (a) 2004; Prati et al., (b) 2004).
Data pre-processing
Typical sub-sampling proposals for solving class imbalance would include majority class under-sampling or minority class over-sampling; under sampling is aimed at striking a balance between classes by eliminating negative patterns and thus reducing majority class cardinality by using strategies such as random algorithms, cleaning, condensate and genetic algorithms (Barandela et al., 2005; Kuncheva et al., 1999), using unsupervised hierarchical algorithms (Cohen et al., 2006; Batista et al., 2000).
Wilson editing (WE) is the most popular data cleaning algorithm (Wilson, 1972). The idea is to identify and remove noisy or atypical patterns, especially those in the overlap area between two or more classes. It involves applying the rule of k nearest neighbour rule (typically with k = 3) to estimate the class label corresponding to each pattern in the training set (TS) and eliminate patterns whose class label does not match the class for most of its k nearest neighbours. The WE method is expressed as follows:
Input: TS original, xi = training set patterns
Output: S = edited DS.
Begin
1. S = TS
2. For each xi in TS do
3. If xi is misclassified do //applying the nearest neighbour rule
4. Discard xi from S
5. End If
6. End for
End
Condensate algorithms consider building a small TS representative group. The algorithm uses a type of pruning to remove patterns considered unnecessary (Hart, 1968). The resulting subset is called selective subset (SSM) and contains patterns nearest to a boundary decision considered prototypes of an original DS (Barandela et al., 2001). The method for a twoclass problem can be described as follows:
Input: T // original training set
Output: SSM selective subset of T
Begin 1. S = T, C = T
2. Di = mind (xi, xj), class(xi) ≠ class(xj), ∀ xi xj∈T
3. yi = argmind (xi, yj), class(xi) ≠ class(yj) ∀ yj ∈T
4. vii = xj∈T |class(xi) = class(xj), d(xi, xj) < d(xi, yi)
5. While C ≠ 0 do xk = argmin Di C = C − xk Sk = xi ∈ S|xk∈vi
6. IF Sk ∩S≠ 0 then SSM = SSM Uxk S = S − Sk
7. End if
8. End while
End
Associative memories
An associative memory is constructed from a finite set of associations called a fundamental set, denoted as:
where p is fundamental set cardinality.
Associative models involve two phases (Aldape, 2007): learning and recalling. Associative memory is constructed during the learning phase making associations between input and output patterns while patterns learned during the learning phase are recalled during the recalling phase.
Hybrid associative classifier (HAC)
HAC is a classifier combining linear associator (learning phase) (Santiago, 2003) and Lernmatrix (recalling phase), eliminating each one's disadvantages. Input patterns must be binary (0 and 1) in the Lernmatrix model the input patterns are orthonormal in the linear associator model. HAC accepts real values in each input pattern component to solve this situation, as described in the following steps (Santiago, 2003):
1. Fundamental set input patterns are real values; they are integrated by n components and separated into C classes;
2. Output patterns are considered ''one hot'' vectors: n − th out-put pattern component values are zeros, except in the component representing the class having a value of one;
3. The learning phase concerns the associative model linear associator, the sum of each fundamental set association's external products being found to obtain the memory:
4. Input pattern class is determined during the operation (Lernma-trix) phase.
HAC performance is affected when input patterns are grouped in the same quadrant, input pattern magnitudes greatly differ and the HAC tends to classify lesser magnitude patterns into pattern classes having greater magnitude. This situation leads to misclassification.
Hybrid associative classifier with translation (HACT)
HACT is an improved model of HAC associative memory in which translation axes solve some HAC difficulties (Santiago, 2003). Figure 1 (a) shows that input patterns are grouped in the same quadrant and new pattern sets become placed in different quadrants following translation (Fig. 1b); such aspect strengthens HAC associative classification.
HACT considers the following steps for axis translation (Santiago, 2003):
1) A mean vector is obtained from input patterns:
2) Mean vector is taken as the new coordinate axis centre,; input and test patterns are thus translated:
3) The linear associator's learning phase is carried out and
4) The Lernmatrix's recalling phase is performed.
Methodology
This section explains the tools, methods and scenarios used in this study.
Data sets
The experimental results came from experiments involving 11 DSs with deferent classes (Cl) and features (Fe) obtained from www.ics.uci.edu/˜mlearn (Table 1). A 5-fold cross-validation was used for each DS.
Several DS (having more than two classes) were transformed as a two-class problem for increasing imbalance level, as follows:
- DS Glass: class 6 was the minority class (24 patterns) and remaining classes the majority class (150 patterns);
- DS Vehic: class 1 was the minority class (170 patterns), remaining classes the majority class (508 patterns); and
- DS Satim: class 4 was the minority class (500 patterns), remaining classes the majority class (4647 patterns).
Classifier performance evaluation
Overall accuracy is usually used (eq. 5) for evaluating classifier performance regarding imbalance, assuming that the cost of error associated with each class is equal. This has been challenged as being unrealistic because a DS having severe imbalance usually has no uniform error cost. For example, in a hypothetical case involving only 0.2% positive pattern labelling, identifying all negative patterns may be 99.8% accurate overall but with the inconvenience that any positive pattern will also be identified.
where ne is the number of misclassified examples and nt is the total number of examples tested.
The geometric mean is commonly used as a criterion for determining classifier imbalance context performance (Álvarez, 1994):
where  is minority class accuracy and
is minority class accuracy and  is majority class accuracy.
is majority class accuracy.
Study scenarios
This study was aimed at analysing HACT associative model behaviour when working with imbalanced data. The study scenarios involved:
1) E1 DS without pre-processing;
2) E2 DS edited (with WE, k = 3);
3) E3 DS condensate (with modified selective (SS); and
4) E4 DS edited and condensate (WE+SS, k = 3).
Results
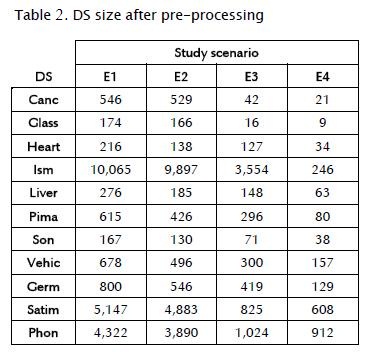
Table 2 shows resulting DS sizes after applying pre-processing algorithms.
Table 2 shows a considerable reduction in DS; for example, the condensate method of (E3) DS reduction was higher compared to the editing method (E2); however, DS reduction became much greater by combining both pre-processing methods (E4),
Classification was made after the reduction step. Table 3 shows the results (rounded up) as geometric mean, the original DS (E1) and associative memory trained with pre-processed DS. Values in brackets indicate standard deviation and values in bold indicate the best result for each DS.
Table 3 shows that HACT had better results (presented in E2) for all DS regarding low sampling strategies than non-pre-processed DS (E1), except for Glass and Satim DS.
Since HACT involves the spread of information DS, study stage performance may indicate that training HACT was highly susceptible to imbalanced DS or that HACT required the decision boundary to be well defined for proper performance, plus maintaining excessive pattern removal. The best performance obtained with HACT involved using the Wilson editing method (E2) as a low sampling strategy.
Conclusions
When DS are imbalanced HACT classifier performance becomes affected by not adequately recognising the patterns of the lesser classes represented. This study examined using two well-known algorithms for under sampling DS using associative models, intending to maintain or increase accuracy rates using eleven DS.
The results showed that using the WE algorithm tended to improve accuracy rates and reduced DS size as added value, resulting in computational cost reduction, for example, the Heart database (216 patterns) was reduced to 34 patterns.
It was proved that Wilson editing was the most conductive method for HACT performance, establishing an interesting situation. This clearly defined decision boundary and class density needed for good pattern conditions; an open study line was thus focused on using known over sampling algorithms for low density DS.
Further study with other filtering algorithms and incorporating cost-based functions to address imbalance represented an alternative for future study of imbalance without affecting class density (a priori) or probability.
Acknowledgements
This work was financed by UAEM project 3072/2011, Conacyt 239450, ICyTDF, PIFI 2010055, SIP (20100538, 20100554 and 20101709) and Instituto Politécnico Nacional COFAA.
References
Aldape-Pérez, M., Implementación de los modelos ALFA-BETA con lógica reconfigurable., MSc Computer Engineering thesis (digital systems), Centro de Investigación en Computación, IPN, 2007. pp. 6-16.
Álvarez, M., Estadística., ISBN 84-7485-327-3, Universidad de Deusto, Bilbao, 1994, pp.51-63.
Barandela, R., Cortés, N., Palacios, A., The nearest neighbour rule and the reduction of the training sample size., In Proceedings of the 9th Spanish Symposium on Pattern Recognition and Image Analysis, Universitat Jaume I, Benicasim, Spain, 2001, pp. 103-108.
Barandela, R., Hernández, J.K., Sánchez, J.S., Ferri, F.J., Imbalanced training set reduction and feature selection through genetic optimization., Proceeding of the 2005 conference on Artificial Intelligence Research and Development, ACM DL, Amsterdam, The Netherlands, 2005, pp. 215-222.
Batista, G. E. A. P.A., Carvalho, A. C. P. L. F., Monard, M. C., Applying one-sided selection to unbalanced datasets., Lecture Notes in Artificial Intelligence, Vol. 1793, 2000, pp. 315-325.
Cohen, G., Hilario, M., Hugonnet, S., Geissbuhler, A., Learning from Imbalanced data in surveillance of nosocomial infection. Artificial Intelligence in Medicine, ElSEVIER, Vol. 37, 2006, pp. 7-18.
Chawla, V. N., Bowyer, K. W., Hall, L. O., Kegelmeyer, W. P., SMOTE: Synthetic minority over-sampling technique., Journal of Artificial Intelligence Research, Vol. 16, 2002, pp. 321-357.
Daskalaki, S., Kopanas, I., Avouris, N., Evaluation of classifiers for an uneven class distribution problem., Applied Artificial Intelligence, Vol. 20, 2006, pp. 1-37.
Ezawa, K. J., Singh, M., Norton, S. W., Learning goal oriented Bayesian networks for telecommunications risk management., Machine Learning, Proceedings of the 13th International Conference, Ed. Morgan Kaufmann, Bari, Italy,1996, pp. 139-147.
Hart, P. E., The condensed nearest neighbour rule., IEEE Transactions on Information Theory, Vol. 14, 1968, pp. 515-516.
Huang, Y. M., Hung, C. M., Jiau, H. C., Evaluation of neural networks and data mining methods on a credit assessment task for class imbalance problem, Nonlinear Analysis: Real World Applications., Vol. 7, 2006, pp. 720-757.
Japkowicz, N., Stephen, S., The class imbalance problem: A systematic study, Intelligent Data Analysis., Vol. 6, 2002, pp. 429-449.
Kuncheva, L. O., Jain, L. C., Nearest neighbour classifier: simultaneous editing and feature selection., Pattern Recognition Letters, Vol. 20, 1999, pp. 1149-1156.
Prati, R. C., Batista, G. E. A. P. A., Monard, M. C., Class imbalance versus class overlapping: An analysis of a learning system behaviour., Lecture Notes in Computer Science, Vol. 2972, 2004a, pp. 312-321.
Prati, R. C., Batista, G. E. A. P. A., Monard, M. C., Learning with class skews and small disjoints. Proceedings of the 17th Brazilian Symposium on Artificial Intelligence, Ed. Springer, São Luís, Maranhão - Brazil, 2004b, pp. 1119-1139.
Ranawana, R., Palade, V., A new measure for classifier performance evaluation., Proceedings of IEEE Congress on Evolutionary Computation, IEEE, Vancouver, BC, 2006, pp. 2254-2261.
Santiago, R., Clasificador híbrido de patrones basado en la Lern-matrix de Steinbuch y el linear associator de Anderson Kohonen., MSc Computer Science thesis Centro de Investigación en Computación, IPN, 2003.
Tan, S., Neighbour-weighted Knearest neighbour for unbalanced text corpus, Expert Systems Applications., Vol. 28, 2005, pp. 667-671.
Weiss, G. M., Mining with rarity: a unifying framework., ACM SIGKDD Explorations Newsletter, Vol. 6, 2004, pp. 7-19.
Wilson, L., Asymptotic properties of nearest neighbour rules using edited data., IEEE Transactions on Systems, Man and Cybernetics, Vol. 2,1972, pp. 408-421.
Nomenclature
DS Data set
E1 DS without pre-processing
E2 DS edited (with Wilson (WE))
E3 DS condensate (with modified selective (SS))
E4 DS edited and condensate (WE+SS).
HAC Hybrid associative classifier
HACT Hybrid associative classifier with translation
SS Selective subset EPA, Title 40 Subchapter I-Solid waste, 258 criteria for municipal solid waste landfills, Environmental Protection Agency, USA, 2000.
References
Aldape-Pérez, M., Implementación de los modelos ALFA-BETA con lógica reconfigurable., MSc Computer Engineering thesis (digital systems), Centro de Investigación en Computación, IPN, 2007. pp. 6-16.
Álvarez, M., Estadística., ISBN 84-7485-327-3, Universidad de Deusto, Bilbao, 1994, pp.51-63.
Barandela, R., Cortés, N., Palacios, A., The nearest neighbour rule and the reduction of the training sample size., In Proceedings of the 9th Spanish Symposium on Pattern Recognition and Image Analysis, Universitat Jaume I, Benicasim, Spain, 2001, pp. 103-108.
Barandela, R., Hernández, J.K., Sánchez, J.S., Ferri, F.J., Imbalanced training set reduction and feature selection through genetic optimization., Proceeding of the 2005 conference on Artificial Intelligence Research and Development, ACM DL, Amsterdam, The Netherlands, 2005, pp. 215-222.
Batista, G. E. A. P.A., Carvalho, A. C. P. L. F., Monard, M. C., Applying one-sided selection to unbalanced datasets., Lecture Notes in Artificial Intelligence, Vol. 1793, 2000, pp. 315-325. DOI: https://doi.org/10.1007/10720076_29
Cohen, G., Hilario, M., Hugonnet, S., Geissbuhler, A., Learning from Imbalanced data in surveillance of nosocomial infection. Artificial Intelligence in Medicine, ElSEVIER, Vol. 37, 2006, pp. 7-18. DOI: https://doi.org/10.1016/j.artmed.2005.03.002
Chawla, V. N., Bowyer, K. W., Hall, L. O., Kegelmeyer, W. P., SMOTE: Synthetic minority over-sampling technique., Journal of Artificial Intelligence Research, Vol. 16, 2002, pp. 321-357. DOI: https://doi.org/10.1613/jair.953
Daskalaki, S., Kopanas, I., Avouris, N., Evaluation of classifiers for an uneven class distribution problem., Applied Artificial Intelligence, Vol. 20, 2006, pp. 1-37. DOI: https://doi.org/10.1080/08839510500313653
Ezawa, K. J., Singh, M., Norton, S. W., Learning goal oriented Bayesian networks for telecommunications risk management., Machine Learning, Proceedings of the 13th International Conference, Ed. Morgan Kaufmann, Bari, Italy,1996, pp. 139-147.
Hart, P. E., The condensed nearest neighbour rule., IEEE Transactions on Information Theory, Vol. 14, 1968, pp. 515-516. DOI: https://doi.org/10.1109/TIT.1968.1054155
Huang, Y. M., Hung, C. M., Jiau, H. C., Evaluation of neural networks and data mining methods on a credit assessment task for class imbalance problem, Nonlinear Analysis: Real World Applications., Vol. 7, 2006, pp. 720-757. DOI: https://doi.org/10.1016/j.nonrwa.2005.04.006
Japkowicz, N., Stephen, S., The class imbalance problem: A systematic study, Intelligent Data Analysis., Vol. 6, 2002, pp. 429-449. DOI: https://doi.org/10.3233/IDA-2002-6504
Kuncheva, L. O., Jain, L. C., Nearest neighbour classifier: simultaneous editing and feature selection., Pattern Recognition Letters, Vol. 20, 1999, pp. 1149-1156. DOI: https://doi.org/10.1016/S0167-8655(99)00082-3
Prati, R. C., Batista, G. E. A. P. A., Monard, M. C., Class imbalance versus class overlapping: An analysis of a learning system behaviour., Lecture Notes in Computer Science, Vol. 2972, 2004a, pp. 312-321. DOI: https://doi.org/10.1007/978-3-540-24694-7_32
Prati, R. C., Batista, G. E. A. P. A., Monard, M. C., Learning with class skews and small disjoints. Proceedings of the 17th Brazilian Symposium on Artificial Intelligence, Ed. Springer, São Luís, Maranhão - Brazil, 2004b, pp. 1119-1139.
Ranawana, R., Palade, V., A new measure for classifier performance evaluation., Proceedings of IEEE Congress on Evolutionary Computation, IEEE, Vancouver, BC, 2006, pp. 2254-2261.
Santiago, R., Clasificador híbrido de patrones basado en la Lern-matrix de Steinbuch y el linear associator de Anderson Kohonen., MSc Computer Science thesis Centro de Investigación en Computación, IPN, 2003.
Tan, S., Neighbour-weighted Knearest neighbour for unbalanced text corpus, Expert Systems Applications., Vol. 28, 2005, pp. 667-671. DOI: https://doi.org/10.1016/j.eswa.2004.12.023
Weiss, G. M., Mining with rarity: a unifying framework., ACM SIGKDD Explorations Newsletter, Vol. 6, 2004, pp. 7-19. DOI: https://doi.org/10.1145/1007730.1007734
Wilson, L., Asymptotic properties of nearest neighbour rules using edited data., IEEE Transactions on Systems, Man and Cybernetics, Vol. 2,1972, pp. 408-421. DOI: https://doi.org/10.1109/TSMC.1972.4309137
How to Cite
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Download Citation
CrossRef Cited-by
1. Batuhan Emre Tosun, Erdem Yorulmaz, Furkan Enes Ergul, Busra Buyuktanir, Gozde Karatas Baydogmus, Kazim Yildiz. (2025). Comparative Analysis of Relational Classification Algorithms on Benchmark Datasets. 2025 10th International Conference on Computer Science and Engineering (UBMK). , p.790. https://doi.org/10.1109/UBMK67458.2025.11206974.
2. Oleksandr Matviichuk, Oksana Biloshytska, Olena Horodetska, Vladimir Pavlov, Mykola Linnik, Ievgen Nastenko. (2022). Positional Approach to the Voting Function Formation of Random Forest Trees as an Example of Solving the Differentiating Tuberculosis Forms Problem. 2022 IEEE 17th International Conference on Computer Sciences and Information Technologies (CSIT). , p.555. https://doi.org/10.1109/CSIT56902.2022.10000450.
Dimensions
PlumX
Article abstract page views
Downloads
License
Copyright (c) 2012 Laura Cleofas Sánchez, Magali Guzmán Escobedo, Rosa María Valdovinos Rosas, Cornelio Yáñez Márquez, Oscar Camacho Nieto

This work is licensed under a Creative Commons Attribution 4.0 International License.
The authors or holders of the copyright for each article hereby confer exclusive, limited and free authorization on the Universidad Nacional de Colombia's journal Ingeniería e Investigación concerning the aforementioned article which, once it has been evaluated and approved, will be submitted for publication, in line with the following items:
1. The version which has been corrected according to the evaluators' suggestions will be remitted and it will be made clear whether the aforementioned article is an unedited document regarding which the rights to be authorized are held and total responsibility will be assumed by the authors for the content of the work being submitted to Ingeniería e Investigación, the Universidad Nacional de Colombia and third-parties;
2. The authorization conferred on the journal will come into force from the date on which it is included in the respective volume and issue of Ingeniería e Investigación in the Open Journal Systems and on the journal's main page (https://revistas.unal.edu.co/index.php/ingeinv), as well as in different databases and indices in which the publication is indexed;
3. The authors authorize the Universidad Nacional de Colombia's journal Ingeniería e Investigación to publish the document in whatever required format (printed, digital, electronic or whatsoever known or yet to be discovered form) and authorize Ingeniería e Investigación to include the work in any indices and/or search engines deemed necessary for promoting its diffusion;
4. The authors accept that such authorization is given free of charge and they, therefore, waive any right to receive remuneration from the publication, distribution, public communication and any use whatsoever referred to in the terms of this authorization.