Sucker rod string design of the pumping systems
Diseño de sarta de varillas para sistemas de bombeo mecánico.
DOI:
https://doi.org/10.15446/ing.investig.v35n2.48667Keywords:
Sucker rod string, fatigue endurance, tapered rod string, equal equivalent stress, rod taper percentage. (en)Sarta de varillas de bombeo, resistencia a la fatiga, sarta de varillas cónica, estrés equivalente igual, porcentaje de la varilla cónica (es)
El actual diseño de sarta de varillas de succión parte del principio que asume que una sarta de varillas es expuesta a una carga simple de tensión, cuyo objetivo es mantener el mismo estrés modificado en la parte superior de cada cono. La mejora que hasta ahora se había propuesto en el diseño de la varilla consistía en conseguir el mismo grado de seguridad en cada sección, utilizando una distribución dinámica de la fuerza proporcional a lo largo de toda la sarta. Sin embargo, los procedimientos disponibles no proporcionan la precisión deseada para un análisis pertinente y los operadores no pudieron identificar los fenómenos específicos que se producen en los pozos de CBM. En el presente trabajo se desarrollan modelos matemáticos de las cargas las varillas y en la sarta de varillas basados en la naturaleza periódica de carga en la sarta de varillas; el método de resistencia a la fatiga es utilizado para diseñar una única sarta de varillas; y la sarta de varilla cónica está diseñada para obtener la misma tensión en cada una de las partes superiores de cada sección. Sus características de aplicación se demuestran con el ejemplo de los pozos de CBM en la Cuenca de Ordos. Las interpretaciones de los resultados muestran que el diseño anterior daba a las varillas individuales un mayor diámetro y a las varillas en la sarta un mayor porcentaje que el del método propuesto. El cálculo debería enfocarse en la inercia, la vibración y las fuerzas de fricción para ilustrar la propagación de los esfuerzos elásticos en el material de la varilla con la velocidad del sonido. La sarta única debe ser diseñada usando medidores de resistencia de fatiga debido a la tensión pulsante asimétrica de la carga de varilla; y la sarta cónica debe tener un diseño equilibrado que permita fijar una igual resistencia a la fatiga en cada sección. Una longitud de carrera más corta da un mayor porcentaje de la varilla cónica y un aumento de los resultados de la capacidad de carga a un diámetro de varilla mejorado. El diámetro de la varilla aumenta con el tamaño de la bomba y la capacidad de carga de la sarta única; y el porcentaje de la varilla cónica en las cuerdas de varillas superiores aumenta con el diámetro del émbolo para la sarta cónica. La presente investigación busca mejorar la eficiencia del sistema de bombeo, asegurar buenas condiciones de funcionamiento, y reducir los costos totales de producción.
DOI: https://doi.org/10.15446/ing.investig.v35n2.48667
Sucker rod string design of the pumping systems
Diseño de sarta de varillas para sistemas de bombeo mecánico
C. Hua. L1
1 Chun Hua Liu: Associate Professor. Affiliation: China University of Petroleum (East China), Qingdao, Shandong, People's Republic of China. E-mail: xfliu82@126.com
How to cite: Hua, C. L. (2015). Sucker rod string design of the pumping systems. Ingeniería e Investigación, 35(2), 6-14.
DOI: https://doi.org/10.15446/ing.investig.v35n2.48667
ABSTRACT
The existing design of sucker rod string mainly focuses on the simplifying assumptions that rod string was exposed to simple tension loading. And its goal was to have equal modified stress at the top of each taper. The improved rod design was to have the same degree of safety at each section, and it used a dynamic force distribution that was proportional along the whole string. Moreover, the available procedures did not provide the desired accuracy of its pertinent analysis, and the operators could not identify the specific phenomena that occur in CBM wells. In this paper, the mathematical models of rod loads and string length were developed based on the cyclic nature of rod string loading. And the fatigue endurance method is utilized to design the single rod string, and the tapered rod string is designed to have an equal equivalent stress at the top of each section. Its application characteristics are demonstrated by the example of CBM wells in Ordos Basin. The interpretations of results show that the previous design gave the single rods a larger diameter and the top rods in the string a greater percent than the proposed method would dictate. The calculation should concern about inertial, vibration and friction forces to illustrate the elastic force waves travelling in the rod material with the speed of sound. The single string should be designed using fatigue endurance ratings due to asymmetric pulsating tension of rod loading. And the tapered string involves a balanced design by setting the fatigue endurance at each section equal. A shorter stroke length gives a greater rod taper percentage and an increased load capacity results to an enhanced rod diameter. The rod diameter increases with the pump size and load capacity for the single string, and the rod taper percentage of the top rod strings increases with plunger diameter for the tapered string. The proposed research improves efficiency of the pumping system, assures good operating conditions, and reduces total production costs.
Keywords: Sucker rod string, fatigue endurance, tapered rod string, equal equivalent stress, rod taper percentage.
RESUMEN
El actual diseño de sarta de varillas de succión parte del principio que asume que una sarta de varillas es expuesta a una carga simple de tensión, cuyo objetivo es mantener el mismo estrés modificado en la parte superior de cada cono. La mejora que hasta ahora se había propuesto en el diseño de la varilla consistía en conseguir el mismo grado de seguridad en cada sección, utilizando una distribución dinámica de la fuerza proporcional a lo largo de toda la sarta. Sin embargo, los procedimientos disponibles no proporcionan la precisión deseada para un análisis pertinente y los operadores no pudieron identificar los fenómenos específicos que se producen en los pozos de CBM. En el presente trabajo se desarrollan modelos matemáticos de las cargas las varillas y en la sarta de varillas basados en la naturaleza periódica de carga en la sarta de varillas; el método de resistencia a la fatiga es utilizado para diseñar una única sarta de varillas; y la sarta de varilla cónica está diseñada para obtener la misma tensión en cada una de las partes superiores de cada sección. Sus características de aplicación se demuestran con el ejemplo de los pozos de CBM en la Cuenca de Ordos. Las interpretaciones de los resultados muestran que el diseño anterior daba a las varillas individuales un mayor diámetro y a las varillas en la sarta un mayor porcentaje que el del método propuesto. El cálculo debería enfocarse en la inercia, la vibración y las fuerzas de fricción para ilustrar la propagación de los esfuerzos elásticos en el material de la varilla con la velocidad del sonido. La sarta única debe ser diseñada usando medidores de resistencia de fatiga debido a la tensión pulsante asimétrica de la carga de varilla; y la sarta cónica debe tener un diseño equilibrado que permita fijar una igual resistencia a la fatiga en cada sección. Una longitud de carrera más corta da un mayor porcentaje de la varilla cónica y un aumento de los resultados de la capacidad de carga a un diámetro de varilla mejorado. El diámetro de la varilla aumenta con el tamaño de la bomba y la capacidad de carga de la sarta única; y el porcentaje de la varilla cónica en las cuerdas de varillas superiores aumenta con el diámetro del émbolo para la sarta cónica. La presente investigación busca mejorar la eficiencia del sistema de bombeo, asegurar buenas condiciones de funcionamiento, y reducir los costos totales de producción.
Palabras clave: Sarta de varillas de bombeo, resistencia a la fatiga, sarta de varillas cónica, estrés equivalente igual, porcentaje de la varilla cónica.
Received: January 28th 2015
Accepted: June 3rd 2015
Introduction
Sucker rod string provides the link between the surface pumping unit and the subsurface pump in CBM wells (Hojjati and Lukasiewicz, 2005; Vicki and Paul, 2002). And it is a vital part of the pumping system, since proper design of sucker rod string has a great impact on the system efficiency. Sucker rod failures always involve servicing costs and lost production. The early rod string design (Hardy, 1964) all utilized the simplifying assumption that the rod string was exposed to simple tension loading. And their goal was to keep the maximum rod string stress at a value based on a percentage of the tensile strength of the rod material. However, their methods generally resulted in the overloading of the lower rod sections. West (1973) corrected the inherent error of previous procedures and developed a rod taper design that gave the same amount of safety for every taper section. His goal was to have the same ratio of maximum stress to allowable stress in each taper. But the utility was limited by the calculation accuracy and the manual iteration required for optimum taper lengths. Neely (1976) introduced the design concept for equal “modified stress” at the top of each taper. “Modified stress” was the stress level that would give equivalent loading if the minimum stress during the pumping cycle were zero. Several simplifying assumptions were made in his calculation, such as the empirical formula calculated with his correlation coefficient, equal rod stresses on the upstroke and downstroke, linear dynamic forces and the use of the modified stress. But these assumptions did not include rod friction and resulted in the taper designs which were not optimum. Gault (1990) proposed the improved rod design that was to have the same degree of safety at the top of every taper section. The actual service factors will all be the same. The use of the taper lengths saved the time for a detailed rod string design, but this method used a dynamic force distribution that was proportional along the whole string and included rod friction proportional to the rod masses. The need for carrying out actual designs is further amplified by some non-apparent limitations. Therefore, these methods generally modified the simplified assumptions and applied analytic approach of conventional oil & gas fields to design the rod string. These modeling procedures, if applied to the CBM wells, do not give satisfactory results mainly because CBM well production is so different from that of typical oil/gas formations (Han et al., 2009; Liu, 2013; Tang et al., 2004). Moreover, the special design of sucker rod strings for CBM wells has not further studied and the available procedures do not provide the desired accuracy of the system designing and its pertinent analysis. Consequently, the operators could not identify the specific phenomena that occur in the CBM wells.
To assure good operating conditions, and to reduce total production costs and increase income, the rod string design is developed for the sucker rod pumping systems in CBM wells. In the design procedure, the rod loads are variable as a function of time during one pumping cycle. The improvement is the way the distribution of inertial forces along the rod string, vibration force waves travelling in the rod material with the speed of the sound and friction forces caused by the interaction forces among the rod, tubing, fluid and pump. Then the rod string length is calculated due to the loads considered. The other improvement is that an accurate rod design is obtained with fatigue endurance ratings for the single string and the same degree of intensity at the top of every taper section. Then the actual equivalent stress will all be the same. And a rod string diagram is proposed for carrying out actual rod designs based on the actual pumping speed, stroke length, rod string length and plunger size.
Determination of Rod String Length
Computation of rod loads
In the long string, the property is its elastic behavior and the time required for transmission of force is responsible for the complexity of modeling its operation. The rod loads that excite the string at its two ends, at the surface through the polished rod and at the end by the pump, produce elastic force waves which travel through the rod material with the speed of the sound. During one pumping cycle, the rod load can be calculated as a function of time, variable which can reach the maximum and minimum values. The analysis is based on the four phases (Firu et al., 2003) of a complete pumping cycle including the deformation period of the rod string and tubing, upstroke period, deformation period of rod string and tubing, downstroke period.
Static loads are caused by weights given by the rod string and column of liquids and the pressures on piston imposed by liquid columns while the pumping system is stopping (Liu et al., 2013). Therefore, the static loads for the upstroke (FSU) and for the downstroke (FSD) can be calculated as the sum of the mentioned loads.
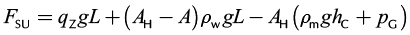 (1a)
(1a)
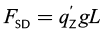 (1b)
(1b)
Where A is the rod cross-sectional area, AH is the plunger cross-sectional area, hC is the submergence depth, ρG is the pressure on dynamic fluid level, qZ is the rod weight of unit length, q’Z is the rod weight of unit length in well liquid, ρ is the rod material density, ρm is the annular liquid density, and ρw is the well liquid density.
Dynamic loads are the loads which the rod suffers while the pumping system is working. The loads, including inertial and vibration loads, are the results of changes in the polished-rod acceleration during the pumping production (Hirschfeldt and Ruiz, 2009), and of the moving weights given by the pumping rod string and column of liquids in the wellbore. The inertial forces can be calculated as the product of the moving weights of rod string and column of liquids and the rod acceleration. Therefore, the inertial forces for the upstroke (FIU) and for the downstroke (FID) can be calculated as follows:
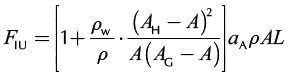 (2a)
(2a)
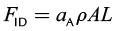 (2b)
(2b)
During one pumping cycle, the magnitude and direction of the inertial loads are variable as a function of the polished-rod acceleration. Consequently, the maximum inertial loads (FImax) can be determined, as follows:
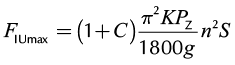 (3a)
(3a)
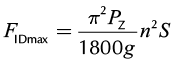 (3b)
(3b)
where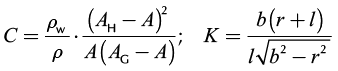 ;
;
The behavior of sucker rod string is complex. And the rod string, belonging to elastomer, can be regarded as a long spring. The wave equation is ideal for the purpose because the problem at hand involves the propagation of waves in a continuous medium. And it is a linear hyperbolic differential equation that describes the longitudinal vibrations of a long, slender rod (Everitt and Jennings, 1992; Yang et al., 2005). Based on the solution of the wave equation with viscous damping, we can approximate the motion of the sucker rod string and determine the vibration load (FV), as follows:
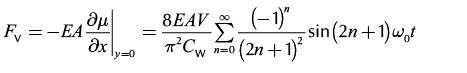 (4)
(4)
where AG is the tubing cross-sectional area, b is distance between saddle bearing and equalizer bearing, Cw is the propagation velocity of elastic longitudinal wave, E is rod material elastic modulus, l is pitman length, n is pumping speed, r is length of crank, V is the relative velocity for lower end of rod string, and ω0 is circular frequency.
The friction forces in pumping system are of two kinds: fluid friction and mechanical friction. Fluid is moving with the rod string during the upstroke and against them during the downstroke. Mechanical friction is opposite in direction to the movement of rod string. Interaction forces between the rod string and tubing, F1, are not more than 1.5 % of the rod weights based on the statistic data for the vertical CBM wells in Ordos Basin. The semi-dry friction forces between piston and pump barrel, F2, can be approximately calculated by Chen’s formulae (Chen et al., 2004). And the forces, F3, are caused by the friction between the rod string and well liquid during the downstroke period and the maximum value (Wan and Luo, 2008) can be determined in terms of stroke length, S, and well liquid viscosity, μw. Interaction forces between tubing and well fluid, F4, are caused by their relative movements on the upstroke. The forces caused by pressure drops across the pump valves, F5, are the main reasons for generating flexural deformation at the lower parts of rod strings and can be determined as follows:
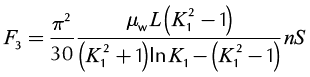 (5)
(5)
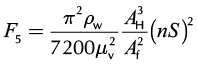 (6)
(6)
Therefore, the maximum friction forces on the upstroke, FFU, increase the rod loads and can be determined as the sum of the loads, F1, F2, and F4, while the loads during the downstroke, FFD, decrease rod loads and are the sum of the loads, F1, F2, F3, and F5, as follows:
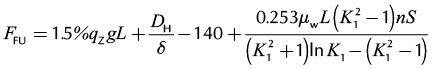 (7a)
(7a)
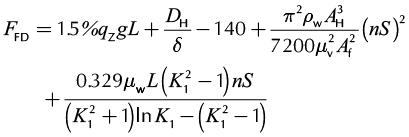 (7b)
(7b)
where 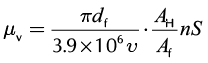
Where Af is the valve ball area, DH is the plunger diameter, df is valve ball diameter, K1 is the diameter ratio of tubing to rod, δ is the single-sided interstice, and υ is the kinematical viscosity.
A sum of above mentioned loads gives the total rod loads that reflect the sum of forces acting at the top of the rod string. During one pumping cycle, the rod load is a function of time, variable which can reach peak values (Fmax) due to the static loads, dynamic loads and friction forces, and minimum values (Fmin) which consists of only the buoyant weight of rods minus dynamic loads and friction forces. Therefore, the extreme values can be found by the formulae given below:
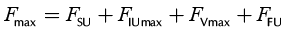 (8a)
(8a)
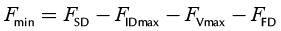 (8b)
(8b)
Computation of rod string length
Based on the analysis of vertical flow effects and conditions along the tubing stretching over a wider range, two assumptions to CBM wells are proposed, as follows:
1. The lift height of well liquid equals to pump setting depth (the hole is vertical).
2. No pressure drop is raised on or by the gas from dynamic fluid level to well head.
Taking into account these two assumptions, the sucker rod string length (Lmax), equal to pump setting depth, can be calculated by substituting Equations (1a), (3a), (4), and (7a) into Equation (8a).
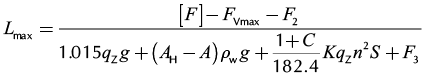 (9)
(9)
where [F] is pump unit load capacity. Equation (9) is a function of the total rod loads, allowable polished rod load, stroke length and pumping speed. This rod string length can be calculated accurately while it incorporates the vertical flow effects and well behaviors.
Design of Sucker Rod String
Single rod string design
For single rod string design, the solid steel string can be regarded as a perfect “slender bar”, since its weight is distributed along its length and any section has to carry at least the rod weight below it (Tuan and Duan, 1994). An examination of the loads of polished rod during one complete pumping cycle shows that the rod string is exposed to cyclic loading (Lukasiewicz, 1991; Xu and Hu, 1993). In practice, the upper rods are always in tension, and the tension level increases due to the polished rod loads on the upstroke while it decreases due to the loads on the downstroke. Therefore, the loading of the rod string is asymmetric pulsating tension, and some form of fatigue endurance is utilized in the
implementation of the proposed design method. With this method, most rod body breaks are fatigue failures which are occurring at rod stresses below the ultimate tensile strength or even the yield strength of the solid steel, so the rod design must include the cyclic nature of rod string loading. The maximum and minimum tension stresses at any cross section i of the rod string can be determined as follows:
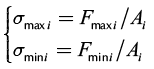 (10)
(10)
Then the mean stress, σm, and the range of tension stress, σF, at any cross section i are given by:
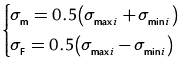 (11)
(11)
where Ai is the rod cross-sectional area at any cross section i, Fmaxi is the maximum load at any cross section i, Fmini is the minimum load at any cross section i, σmaxi is the maximum tension stress at any cross section i, and σmini is the minimum tension stress at any cross section i.
Since the string loading is pulsating tension, the rod string should be designed using fatigue endurance parameters. For the modeling procedure, the design should consider not only the maximum tension stress allowed, σmax, being within the tensile strength as the rod loading above plastic deformation changes material properties but also the range of stress, σF, between maximum and minimum stress at any cross section. In order to do this, the equivalent stress, σE, is introduced to illustrate the variation of cyclic loading and defined as follows:
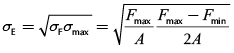 (12)
(12)
Taking into account the fatigue endurance limit of the material and service factor to account for the corrosiveness of the environment, the fatigue strength of rods can be calculated as follows:
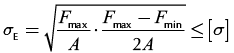 (13)
(13)
where [σ] is the allowable stress of the rod material, and the quotient of fatigue endurance limit for rod steels under cyclic tension-compression and pulsating tension loads and service factor. It is obtained based on tests of a polished laboratory specimen of the steel rod with different material and thermal treatment. The rod diameter can be calculated by substituting Equations. (8a) and (8b) into Equation (13).
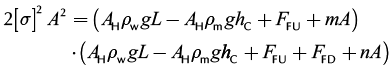 (14)
(14)
where 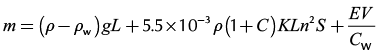 ;
;
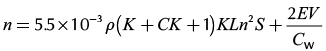 .
.
Equation (14) is a function of the rod string length, plunger size, stroke length and pumping speed. The single rod cross-sectional area can be calculated accurately using these production parameters.
Tapered rod string design
Since the slender bar results in stretch and a continuous taper from top to bottom is impractical, tapered strings with sections of decreasing diameters are used in design practice (Lea et al., 1995). For tapered rod string design, it involved a balanced design, based on the total rod loads, by setting the fatigue endurance at the top of each section equal, and then selecting the diameter and length of rods that could safely handle this stress. The rod string taper uses two-stage rod taper and the design procedure gives reasonable rod life for the depths of CBM wells within 1500 m in China. In order for each rod taper to have the equal endurance, the rod string taper is designed to have an equal equivalent stress, σE, at the top section of each taper.
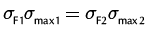 (15)
(15)
The maximum and minimum rod stresses and range value, σF1, at the top section of first rod taper near the plunger are calculated by the following relations.
 (16)
(16)
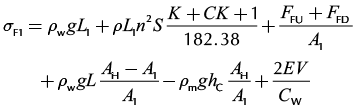 (17)
(17)
The maximum rod stress and range value, σF2, at the top section of second rod taper near the polished rod are calculated by the formulae given below:
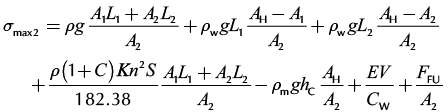 (18)
(18)
 (19)
(19)
Where Ai is i-th rod taper cross-sectional area and Li is i-th rod taper length. The friction force can be neglected while designing rod taper in the CBM wells with relatively low pump setting depth, wellhead pressure, stroke length and pumping speed. After combining above mentioned relations, the length of first rod taper (L1) can be calculated by the following equation:
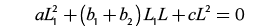 (20)
(20)
where, 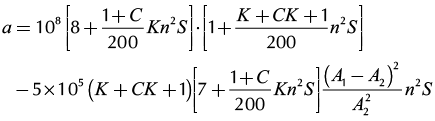 ;
;
 ;
;
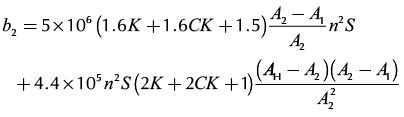 ;
;
 .
.
The length of second rod taper can be determined as the difference of the total string length and first rod taper. When the length of i-th rod taper is determined, it is accumulated to the total designed rod string length.
Application and Interpretation
Field application
The application characteristics of the rod string design are demonstrated by the example of SJ9-V1, SJP01-2 and WL2-10 wells in Sanjiao coalfield of Ordos Basin. These wells make continuous production after their completion and fracturing and accumulate plenty of data. As is known, the operational parameters and independent variables that might influence rod loads in the CBM wells were furnished for the proposed design method. The following operational parameters and their assigned values were selected for the wells studied and presented in Table 1.
Table 1: Operational parameters in the CBM wells studied.
|
Parameter |
CBM well No. |
||
|
SJ9-V1 |
SJP01-2 |
WL2-10 |
|
|
Total string length, L /m |
582 |
643 |
746 |
|
Tubing diameter, D /mm |
73.02 |
73.02 |
73.02 |
|
Wall thickness of tubing, DW /mm |
7.82 |
7.82 |
7.82 |
|
Plunger diameter, DH /mm |
56 |
44 |
51 |
|
Rod diameter, d /mm |
22 |
19 |
22 |
|
Rod cross-sectional area, A/cm2 |
3.80 |
2.84 |
3.80 |
|
Parameter |
CBM well No. |
||
|
SJ9-V1 |
SJP01-2 |
WL2-10 |
|
|
Rod weight in air, qZ /(kg·m-1) |
3.14 |
2.35 |
3.14 |
|
Rod weight in liquid, q’Z /(kg·m-1) |
2.75 |
2.06 |
2.75 |
|
Well liquid density, ρw /(kg·m-3) |
1 012 |
1 010 |
1 012 |
|
Dynamic fluid level, H /m |
473 |
457 |
512 |
|
Bottomhole pressure, pwf /MPa |
2.89 |
2.63 |
2.33 |
|
Annular liquid density, ρm /(kg·m-3) |
856 |
968 |
8.96 |
|
Pumping speed, n /(r·min-1) |
8.5 |
9.0 |
7.5 |
|
Stroke length, S /m |
2.1 |
1.8 |
2.5 |
To find the rod loads by applying this calculation model developed is possible using measured well data from the field. The dynamometer cards (Elcxmeier, 1967; Keating et al., 1989) presented in Figure 1 are the plot of the total rod loads at the various positions over one complete stroke and used for determining pumping unit loading and downhole pump operation. The extreme rod loads based on West’s method, as shown in Figure 1a, were calculated to be 27.9 kN and 13.5 kN, respectively. The rod loads included weight of rods and well liquid, but they did not include the pressures on piston, dynamic loads and rod friction forces. These calculated values cannot illustrate the dynamic property of the elastic behavior. The extreme rod loads calculated by Neely’s method, as shown in Figure 1b, were 29.9 kN and 12.5 kN, respectively. The rod loads included weight of rods and well liquid and linear dynamic forces, but they neglect rod friction. And the use of the modified stress resulted in the non-minimum taper designs. The extreme rod loads determined by Gault’s method, as shown in Figure 1c, were 31.2 kN and 10.9 kN, respectively. The rod loads included the distribution of dynamic forces along the rod string and rod friction proportional to the rod masses linear dynamic forces, but they neglect the vibration forces and disproportional rod friction. And the same degree of safety cannot demonstrate the cyclic nature of rod string loading. The maximum and minimum rod loads predicted by the proposed method, as shown in Figure 1d, were 27.5 kN and 9.2 kN, respectively. The possible rod loads at any depth in the string can be classified into static, inertial, vibration and friction forces. The calculated loads, due to the distribution of dynamic and friction forces, can illustrate the elastic force waves that travel in the string. The waves are of different magnitude and phase and affect the actual rod forces in any section. However, the previous rod design disregards these rod loads arising from such effects due to the complexity of describing these force waves. It is believed that this approach gives more realistic rod loads than previous approximations.

(a) The loadings calculated by West’s method.
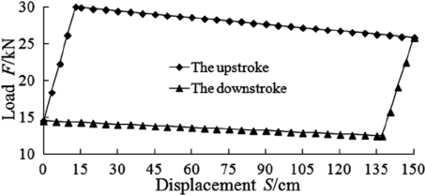
(b) The loadings calculated by Neely’s method.
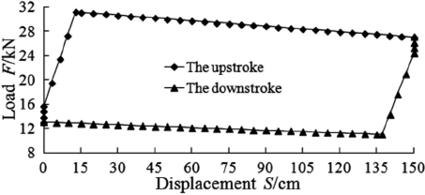
(c) The loadings calculated by Gault’s method.
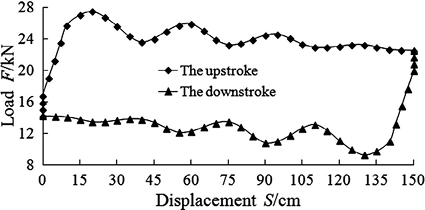
(d) The loadings calculated by the proposed method.
Figure 1. The loadings of the rod string at the various positions during one complete pumping cycle.
Figure 1d is also given to illustrate the components of rod load with its combined action of static, dynamic and friction forces. The static load plays a major role and the static to total load ratio is approximately 80 %. The ratios of inertial and vibration to total load are calculated to be more than 8 % and 7 %, respectively. Consequently, the dynamic load effect on rod loading cannot be neglected for CBM wells. The friction load ratio is approximately 5 % and it also should be included.
The rod size, rod taper length, plunger size and stroke length are determined using the principle of rod string taper proposed. And the results are shown in Table 2. The previous design methods generally modified the simplified assumptions and applied analytic approach to design the rod string for the oil & gas wells. These modeling procedures, if applied to the CBM wells, do not give satisfactory results of the system designing due to the different well conditions. WL2-10 well shows the tapered rod designs using the equal equivalent stress method for the same pumping conditions as were used in the comparison of Neely vs. Gault method. These are: 19 mm × 16 mm and 22 mm × 19 mm rod strings with 38 mm and 51 mm pumps at 37 % × 63 % (780 m rod string length), 42 % × 58 % and 40 % × 60 % (746 m rod string length) taper percentage with polished rod stroke lengths of 2.1 m and 2.5 m during the pumping cycle. SJ9-V1 well shows the single 0rod designs using the fatigue endurance method for the same pumping conditions as were used in the comparison of Neely vs. Gault design method. These are: 16 mm, 22 mm and 19 mm rod strings with 44 mm, 63 mm and 56 mm pumps at 610 m and 582 m rod string lengths with polished rod stroke lengths of 1.5 m and 2.1 m.
Table 2. The results of rod string design in the CBM wells studied.
(a) The results of rod string design used Needly’s method.
|
Design parameter |
Needly’s method |
||
|
SJ9-V1 |
SJP01-2 |
WL2-10 |
|
|
Rod string length, L /m |
582 |
643 |
746 |
|
Rod string diameter, d /mm |
22 |
19 × 16 |
22 × 19 |
|
Rod cross-sectional area, A/cm2 |
3.80 |
2.84 × 2.0 |
3.8 × 2.84 |
|
Rod taper percentage, η/% |
— |
48 %×52 % |
42 %×58 % |
|
Tubing diameter, D /mm |
73.02 |
73.02 |
73.02 |
|
Wall thickness of tubing, DW /mm |
7.82 |
7.82 |
7.82 |
|
Plunger diameter, DH /mm |
63 |
44 |
51 |
|
Pumping speed, n /(r·min-1) |
1.9~9.0 |
2.1~9.5 |
2.1~9.6 |
|
Stroke length, S /m |
2.1 |
1.8 |
2.5 |
(b) The results of rod string design used Gault’s method.
|
Design parameter |
Gault’s method |
||
|
SJ9-V1 |
SJP01-2 |
WL2-10 |
|
|
Rod string length, L /m |
582 |
643 |
746 |
|
Rod string diameter, d /mm |
19 |
19 × 16 |
19 × 16 |
|
Rod cross-sectional area, A/cm2 |
2.84 |
2.84 × 2.0 |
2.84 × 2.0 |
|
Rod taper percentage, η/% |
— |
42 %×58 % |
40 %×60 % |
|
Tubing diameter, D /mm |
73.02 |
73.02 |
73.02 |
|
Wall thickness of tubing, DW /mm |
7.82 |
7.82 |
7.82 |
|
Plunger diameter, DH /mm |
56 |
44 |
51 |
|
Pumping speed, n /(r·min-1) |
1.9~9.1 |
2.0~9.2 |
2.0~9.2 |
|
Stroke length, S /m |
2.1 |
1.8 |
2.5 |
(c) The results of rod string design used the proposed method.
|
Design parameter |
The proposed method |
||
|
SJ9-V1 |
SJP01-2 |
WL2-10 |
|
|
Rod string length, L /m |
610 |
680 |
780 |
|
Rod string diameter, d /mm |
16 |
16 |
19 × 16 |
|
Rod cross-sectional area, A/cm2 |
2.0 |
2.0 |
2.84 × 2.0 |
|
Rod taper percentage, η/% |
— |
— |
37 %×63 % |
|
Tubing diameter, D /mm |
60.32 |
60.32 |
73.02 |
|
Wall thickness of tubing, DW /mm |
6.45 |
6.45 |
7.82 |
|
Plunger diameter, DH /mm |
44 |
38 |
38 |
|
Pumping speed, n /(r·min-1) |
1.8~9.0 |
1.9~9.5 |
1.7~8.5 |
|
Stroke length, S /m |
1.5 |
1.5 |
2.1 |
Table 2a to Table 2c also illustrate that specific calculations for each pumping condition are most desirable. If we compare the operational parameters of the CBM wells studied in Table 1 with the design results in Table 2, we may draw the conclusion that the present design of sucker rod string for CBM wells mainly applies the previous design methods; and the available procedures do not provide the desired accuracy of the string designing and its pertinent analysis. Needly and Gault methods give the rod strings a larger diameter and a shorter total string length, and the top rods in the string a greater percent than the proposed design method would dictate for the pumping conditions examined. This results in poorer fatigue endurance and makes the rods the most likely to fail. Moreover, a larger diameter of single rods and a greater percent of top rods in the string adversely affect the maximum rod load and enhance the energy requirements of pumping systems. For tapered rod string, failures in the top rod may cause damage to the lower sections of the rod string in CBM wells. In addition, a shorter rod string length leads to a higher submergence depth above the upper part of coal bed. This makes producing pressure drop decrease, which is unfavorable to CBM desorption and production.
Rod diagram and its interpretation
The rod string diagrams of beam pumping unit in CBM wells can be determined by applying the method proposed and are presented in Table 3. The basis of these diagrams is that well liquid density is 1 010 kg·m-3, the lift height of well liquid and pump setting depth are equal, and rod material elastic modulus is 200 GPa. The rod diagrams include three tables of the short stroke (Table 3a), middle stroke (Table 3b), and long stroke (Table 3c). And these tables illustrate the rod size and rod taper length for different sizes of pumping units and pumps.
Table 3: The rod string diagrams for the CBM wells.
(a) The rod diagram of the short stroke. mm
|
Pump |
Designation (CSJ) |
||||
|
2-0.6-2.8 |
3-1.2-6.5 |
4-1.5-9 |
5-1.8-13 |
8-2.1-18 |
|
|
28 |
13 |
13 |
16 × 13 4 %×57 % |
19 × 16 31 %×69 % |
22 × 19 24 %×76 % |
|
32 |
13 |
13 |
16 × 13 48 %×52 % |
19 × 16 34 %×66 % |
22 × 19 26 %×74 % |
|
38 |
16 |
16 |
19 × 16 41 %×59 % |
19 × 16 40 %×60 % |
22 × 19 30 %×70 % |
|
44 |
16 |
19 |
19 × 16 47 %×52 % |
19 × 16 45 %×55 % |
22 × 19 33 %×66 % |
|
51 |
16 |
19 |
19 |
22 × 19 39 %×64 % |
22 × 19 37 %×63 % |
|
56 |
19 |
19 |
19 |
22 × 19 42 %×58 % |
22 × 19 40 %×60 % |
|
63 |
19 |
19 |
19 |
22 × 19 45 %×55 % |
22 × 19 43 %×57 % |
|
70 |
22 |
22 |
22 |
22 |
22 × 19 48 %×52 % |
(b) The rod diagram of the middle stroke. mm
|
Pump |
Designation (CSJ) |
||||
|
3-1.5-6.5 |
4-2.5-13 |
5-2.1-13 |
6-2.5-26 |
8-2.5-26 |
|
|
28 |
13 |
16 × 13 39 %×61 % |
19 × 16 30 %×70 % |
19 × 16 30 %×70 % |
22 × 19 24 %×76 % |
|
32 |
13 |
16 × 13 43 %×57 % |
19 × 16 33 %×67 % |
19 × 16 33 %×67 % |
22 × 19 26 %×74 % |
|
38 |
16 |
19 × 16 37 %×63 % |
19 × 16 38 %×62 % |
19 × 16 37 %×63 % |
22 × 19 29 %×71 % |
|
44 |
19 |
19 × 16 42 %×58 % |
19 × 16 44 %×56% |
22 × 19 32 %×68 % |
22 × 19 32 %×68 % |
|
51 |
19 |
19 × 16 46 %×54 % |
22 × 19 38 %×62 % |
22 × 19 36 %×64 % |
22 × 19 36 %×64 % |
|
56 |
19 |
19 |
22 × 19 41 %×59 % |
22 × 19 39 %×61 % |
22 × 19 39 %×61 % |
|
63 |
19 |
19 |
22 × 19 43 %×57 % |
22 × 19 40 %×60 % |
22 × 19 41 %×59 % |
|
70 |
22 |
22 |
22 |
22 × 19 45 %×55 % |
22 × 19 46 %×54 % |
(c) The rod diagram of the long stroke. mm
|
Pump |
Designation (CSJ) |
||||
|
3-2.1-13 |
4-3.0-18 |
5-2.5-18 |
5-3.0-26 |
8-3.0-37 |
|
|
28 |
13 |
16 × 13 37 %×63 % |
19 × 16 30 %×70 % |
19 × 16 29 %×71 % |
22 × 19 24 %×76 % |
|
32 |
13 |
16 × 13 41 %×59 % |
19 × 16 32 %×68 % |
19 × 16 31 %×69 % |
22 × 19 26 %×74 % |
|
38 |
16 |
19 × 16 36 %×64 % |
19 × 16 37 %×63 % |
19 × 16 36 %×64 % |
22 × 19 28 %×72 % |
|
44 |
19 |
19 × 16 40 %×60 % |
19 × 16 42 %×58 % |
19 × 16 40 %×60 % |
22 × 19 31 %×69 % |
|
51 |
19 |
19 × 16 44 %×56 % |
22 × 19 36 %×64 % |
22 × 19 34 %×66 % |
22 × 19 34 %×66 % |
|
56 |
19 |
19 |
22 × 19 39 %×61 % |
22 × 19 37 %×63 % |
22 × 19 37 %×63 % |
|
63 |
19 |
19 |
22 × 19 41 %×59 % |
22 × 19 39 %×61 % |
22 × 19 39 %×61 % |
|
70 |
22 |
22 |
22 × 19 46 %×54 % |
22 × 19 43 %×57 % |
22 × 19 43 %×57 % |
It can be seen from these tables that the main rod diameters are 16 mm and 19 mm for sucker rod pumping systems of the CBM wells in Ordos Basin. 13 mm rod strings can be selected for 20 kN and 30 kN load capacity with low water production and 22 mm rod strings are typically for 50 kN, 60 kN and 80 kN load capacity with high water production.
Figure 2a describes the variation of rod diameter versus plunger diameter about 20 kN pump unit load capacity. It is apparent from the figure that an increased pump size result to an enhanced rod diameter for the single rod string. For this size of pumping unit, rod diameter increases from 13 mm up to 16 mm and then to 22 mm, while plunger diameter enhances from 28 mm to 56 mm and then to 95 mm. Figure 2b shows the relationship between the two design variables with 30 kN unit load capacity for the single rod string. It can be seen from this figure that rod diameter increases with the pump size and load capacity. If we assume that only load capacity changes for the same well conditions, rod diameter will increase resulting from increases in load capacity. Rod diameter increases from 16 mm up to 19 mm while load capacity enhances from 20 kN to 30 kN with 44 mm and 51 mm pumps. Moreover, the rod diameter does not alter with the stroke length for the same sizes of pumps and units.
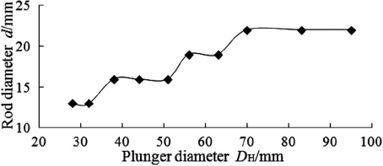
(a) The variation for 20 kN pump unit load capacity.
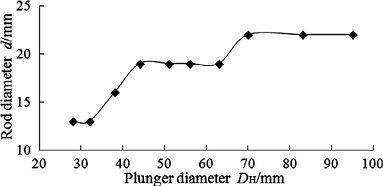
(b) The variation for 30 kN pump unit load capacity.
Figure 2. The rod diameter of single string vs. different pump sizes.
Figure 3a shows the effects of pump size on the rod taper percentage of the top rods in the string for different stroke length about 50 kN pump unit load capacity. The rod diameter increases with pump size for the identical size of pumping unit and stroke length, starting from 19 mm × 16 mm to 22 mm × 19 mm rod strings with the plunger diameter from 44 mm to 51 mm. And the rod taper percentage of the top rods in the string enhances due to decreases in stroke length for the same sizes of pumping units. Figure 3b is given to illustrate the relationships between rod taper percentage and various pump sizes with different stroke length for 80 kN unit load capacity in CBM wells. The rod taper percentage of the top rods in the string increases approximately linearly with plunger diameter, starting from the minimum value of 24.7 % up to the maximum value of 48.7 % with the plunger diameter from 28 mm to 70 mm with the short stroke length.
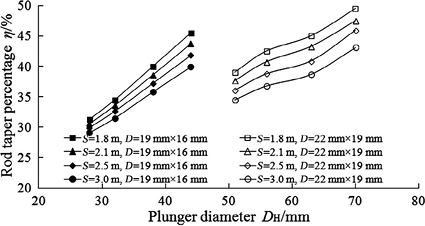
(a) The effects of pump size on the rod taper percentage for different stroke length about 50 kN pump unit load capacity.
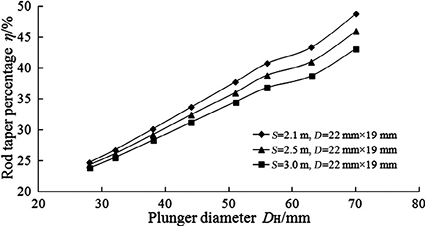
(b) The effects of pump size on the rod taper percentage for different stroke length about 80 kN pump unit load capacity.
Figure 3. The rod taper percentage of the top rods in the string.
It can be seen from these two figures that a shorter stroke length, for the same sizes of pumping units, gives a greater rod taper percentage. For 56 mm pumps, the rod taper percentage increases from 36.8 % up to 38.8 % and then to 40.7 % while stroke length diminishes from 3.0 m to 2.5 m and to 2.1 m. Moreover, an increased load capacity, for the same stroke length, results to an enhanced size of rod string. 19 mm × 16 mm and 22 mm × 19 mm rod strings, for the same well conditions, are calculated to match with 50 kN and 80 kN load capacity, respectively.
Conclusions
(1) The previous design methods generally modified simplified assumptions and applied analytic approach to design the rod strings for oil & gas wells. These methods give the single rod strings a larger diameter and a shorter total string length, and the top rods in the string a greater percent than the proposed design method would dictate for the well conditions examined. And this results in poorer fatigue endurance and enhances the energy requirements.
(2) Compared with the oil/gas fields, the dynamic and friction to rod load ratios are relatively high. Consequently, the calculation developed should involve the distribution of inertial forces along the rod string, vibration force waves travelling in the rod material with the speed of the sound and friction loads.
(3) During one complete pumping cycle, the loading of the rod string is asymmetric pulsating tension, and the fatigue endurance method is utilized for the single rod string. The design should consider the maximum tension stress allowed and the range of extreme stress at any cross section. The tapered rod string is designed to have a same equivalent stress by setting the fatigue endurance at the top of each section equal.
(4) A rod string diagram is proposed for carrying out actual rod designs. The main rod diameters are 16 mm and 19 mm for the pumping systems in CBM wells. A shorter stroke length, for the same unit sizes, gives a greater rod taper percentage. For the single string, rod diameter increases with the pump size and load capacity and does not alter with stroke length. For the tapered string, the rod taper percentage of the top rods increases linearly with plunger diameter and decreases with stroke length.
Acknowledgements
These research results are part of a key project carried out in 2011–2015 and financially supported by the Special and Significant Project of National Science and Technology “Development of Large Oil/Gas Fields and Coalbed Methane” (Grant No. 2011ZX05038). The authors gratefully acknowledge the China National Petroleum Corporation (CNPC) and China National Offshore Oil Corporation (CNOOC) technicians for their support, contributions and useful discussions.
References
Chen, X.K., Ye, L.P., & Gu, Y.B. (2004). Oil recovery technique for pumping units[M]. Beijing: Publishing House of Oil Industry.
Elcxmeier, J.R. (1967). Diagnostic Analysis of Dynamometer Cards[J]. Journal of Petroleum Technology, 13(1): 97-106.
Everitt, T.A., & Jenings, J.W. (1992). An improved finite-difference calculation of downhole dynamometer cards for sucker-rod pumps[C]. SPE Annual Technical Conference and Exhibition, Houston, Texas, USA, October 2-5, 121-127. DOI: 10.2118/18189-pa.
Firu, L.S., Chelu, & T., Petre, C.M. (2003). A modern approach to the optimum design of sucker-rod pumping system[C]. SPE Annual Technical Conference and Exhibition, Denver, Colorado, USA, October 5-8, 1-9.
DOI: 10.2118/84139-ms.
Gault, R.H., & Takacs, G. (1990). Improved rod string taper design[C]. SPE Annual Technical Conference and Exhibition, New Orleans, LA, USA, September 23-26, 605-614. DOI: 10.2118/20676-MS.
Keating, J.F., Laine R.E., & Jennings, J. W. (1989). Pattern Recognition Applied to Dynamometer Cards[C]. SPE 64th Annual Technical Conference and Exhibition, San Antonio, Texas, USA, October 8-11, 1-3.
Han, J.Z., Sang, S.X., Chen, Z.Z., et al. (2009). Exploitation technology of pressure relief coalbed methane in vertical surface wells in the Huainan coal mining area [J]. Mining Science and Technology, 19(1): 25-30.
DOI: 10.1016/s1674-5264(09)60005-3.
Hardy, A.A. (1964). Sucker-rod string design and the Goodman diagram[C]. Petroleum Mechanical Conference of the ASME, Los Angeles, California, USA, September 20-23, 1-15.
Hirschfeldt, C.M., & Ruiz, R. (2009). Selection criteria for artificial lift system based on the mechanical limits: case study of Golfo San Jorge Basin[C]. SPE Annual Technical Conference and Exhibition, New Orleans, Louisiana, USA, October 4-7, 1-14.
DOI: 10.2118/124737-ms.
Hojjati, M.H., & Lukasiewicz, S.A. (2005). Modeling of sucker rod string. Journal of Canadian Petroleum Technology, 44(12): 55-58. DOI: 10.2118/05-12-02.
Lea, J.F., Pattillo, P.D., & Studenmund, W.R. (1995). Interpretation of calculated forces on sucker rods[J]. SPE Production & Facilities, 41(2): 41-45.
Liu, X.F. (2013). Prediction of flowing bottomhole pressures for two-phase coalbed methane wells[J]. Acta Geologica Sinica, 87(5): 1412-1420. DOI: 10.1111/1755-6724.12138.
Liu, X.F., Qi, Y.G., Li, Y.X., et al. (2010). Design calculation of sucker rod pumps in coalbed methane wells[J]. Journal of China Coal Society, 35(10): 1685-1691.
Lukasievicz, S.A. (1991). Dynamic behavior of the sucker rod string in the inclined well[J]. SPE Production & Facilities, 37(4): 313-321.
Needly, A.B. (1976). Sucker rod string design[J]. Petroleum Engineer, 22(3): 58-66.
Tang, S.H., Sun, S.L., & Hao, D.H. (2004). Coalbed methane-bearing characteristics and reservoir physical properties of principal target areas in north China[J]. Acta Geologica Sinica, 78(5): 724-728.
Tuan, X.Z., Duan, Y.Y. (1994). The analysis of sucker rod string in directional wells[J]. SPE Journal, 40(5): 1-12.
Vicki, A.H, & Paul, S.S. (2002). A guide to coalbed methane operations. Alabama, Birmingham: Gas Research Institute.
Wan, R.F., Luo, & Y.J. (2008). A handbook of oil recovery technique (Revised Edition)[M]. Beijing: Publishing House of Oil Industry.
West, P.A. (1973). Improved method of sucker rod string design[J]. Petroleum Engineer, 19(5): 157-163.
West, P.A. (1973). Improving sucker rod string design[J]. Petroleum Engineer, 19(7): 68-77.
Xu, J., & Hu, Y.R. (1993). A method for designing and predicting the sucker rod string in deviated pumping wells[J]. SPE Production & Facilities, 39(11): 383-392.
Yang, H.B., Di, Q.F., & Wang, W.C. (2005). Prediction of serious abrasion position and mechanism of uneven abrasion between sucker rod string and tubing[J]. Acta Petrolei Sinica, 26(2): 100-103.
How to Cite
APA
ACM
ACS
ABNT
Chicago
Harvard
IEEE
MLA
Turabian
Vancouver
Download Citation
CrossRef Cited-by
1. Xinfu Liu, Chunhua Liu, Yong Yang. (2017). Dynamic Behavior of the Polished Rod for the Coalbed Methane Pumping Installations. Oil & Gas Science and Technology – Revue d’IFP Energies nouvelles, 72(3), p.16. https://doi.org/10.2516/ogst/2017011.
2. Qin Li, Bo Chen, Zhiqiang Huang, Haipin Tang, Gang Li, Lei He, Andrés Sáez. (2019). Study on Equivalent Viscous Damping Coefficient of Sucker Rod Based on the Principle of Equal Friction Loss. Mathematical Problems in Engineering, 2019(1) https://doi.org/10.1155/2019/9272751.
3. Jianxun Jiang, Xinli Wan, Kaijun Li, Jingguo Du, Yinhua Liu, Jiajun Jing, Jiansong Li. (2024). Research progress of sucker rod fracture detection and prediction model. Engineering Failure Analysis, 159, p.108119. https://doi.org/10.1016/j.engfailanal.2024.108119.
Dimensions
PlumX
Article abstract page views
Downloads
License
Copyright (c) 2015 Chun Hua Liu

This work is licensed under a Creative Commons Attribution 4.0 International License.
The authors or holders of the copyright for each article hereby confer exclusive, limited and free authorization on the Universidad Nacional de Colombia's journal Ingeniería e Investigación concerning the aforementioned article which, once it has been evaluated and approved, will be submitted for publication, in line with the following items:
1. The version which has been corrected according to the evaluators' suggestions will be remitted and it will be made clear whether the aforementioned article is an unedited document regarding which the rights to be authorized are held and total responsibility will be assumed by the authors for the content of the work being submitted to Ingeniería e Investigación, the Universidad Nacional de Colombia and third-parties;
2. The authorization conferred on the journal will come into force from the date on which it is included in the respective volume and issue of Ingeniería e Investigación in the Open Journal Systems and on the journal's main page (https://revistas.unal.edu.co/index.php/ingeinv), as well as in different databases and indices in which the publication is indexed;
3. The authors authorize the Universidad Nacional de Colombia's journal Ingeniería e Investigación to publish the document in whatever required format (printed, digital, electronic or whatsoever known or yet to be discovered form) and authorize Ingeniería e Investigación to include the work in any indices and/or search engines deemed necessary for promoting its diffusion;
4. The authors accept that such authorization is given free of charge and they, therefore, waive any right to receive remuneration from the publication, distribution, public communication and any use whatsoever referred to in the terms of this authorization.



























