Queries about the largest empty rectangle in large 2-dimensional datasets stored in secondary memory

Consultas sobre el rectángulo vacío de mayor área en grandes conjuntos de datos de dos dimensiones, almacenados en memoria secundaria

Let  be a set of points located in a rectangle  and  is a point that is not in . This article describes the design, implementation, and experimentation of different algorithms to solve the following two problems: (i) Maximum Empty Rectangle (MER), which consists in finding an empty rectangle with a maximum area contained in R and does not contain any point from   and (ii) Query Maximum Empty Rectangle (QMER), which consists in finding the rectangle with the same restrictions given for the MER problem but must also contain . It is assumed that both problems have insufficient main memory to store all the objects in set . According to the literature, both problems are very practical in fields such as data mining and Geographic Information Systems (GIS). Specifically, the present study proposes two algorithms that assume that  is stored in secondary memory (mainly disk) and that it is impossible to store it completely in main memory. The first algorithm solves the QMER problem and consists of decreasing the size of S by using dominance areas and then processing the points that are not eliminated using an algorithm proposed by Orlowski (1990). The second algorithm solves the MER problem and consists of dividing R into four subrectangles that generate four subsets of similar size; these are processed using an algorithm proposed in Edmons  et al. (2003), and finally the partial solutions are combined to obtain a global solution. For the purpose of verifying algorithm efficiency, results are shown for a series of experiments that consider synthetic and real data. 

Sea S un conjunto de puntos ubicado en un rectángulo R, y q un punto que no está en S.- Este artículo describe el diseño, la implementación y experimentación de diferentes algoritmos para resolver los siguientes problemas: (i) MER, que consiste en encontrar un rectángulo vacío de máxima área contenido en R y que no contiene un punto de S, y (ii) QMER, que consiste en encontrar un rectángulo con las mismas restricciones dadas para el problema MER y que, además, debe contener a q. En ambos problemas se asume que no existe suficiente memoria para almacenar todos los objetos del conjunto S. De acuerdo con la literatura, ambos problemas son de mucha utilidad práctica, en ámbitos como la minería de datos, sistemas de información geográfica, por nombrar algunos. Concretamente, en este trabajo se proponen dos algoritmos que asumen que S se encuentra almacenado en memoria secundaria y que no es posible almacenarlo completamente en memoria. El primero resuelve el problema QMER y consiste en disminuir el tamaño de mediante la utilización de zonas de dominancia y luego, mediante un algoritmo propuesto por Orlowski (1990), se procesan los puntos no descartados. El segundo, a su vez, resuelve el problema MER y consiste en dividir R en cuatro subrectángulos generando cuatro subconjuntos de similar tamaño los que se procesan mediante un algoritmo propuesto en Edmonds et al. (2003), combinando finalmente las soluciones parciales para obtener la solución global. Con el objeto de verificar la eficiencia de los algoritmos, se muestran los resultados de una serie de experimentos considerando datos sintéticos y reales.

Felipe Lara ¹, Gilberto Gutiérrez ² , María Antonieta Soto ³, and Antonio Corral ⁴

---

¹Universidad del Bío-Bío, Chile. E-mail: fellara@alumnos.ubiobio.cl.

²Department of Computing and IT, Universidad del Bío-Bío, Chile. E-mail: ggutierr@ubiobio.cl.

³Department of Computing and IT, Universidad del Bío-Bío, Chile. E-mail: msoto@ubiobio.cl.

⁴Universidad de Almería, Spain. E-mail: acorral@ualmeria.es.

---

How to cite: Lara, F., Gutiérrez, G., Soto, M.A., Corral, A. (2017). Queries about the largest empty rectangle in large 2-dimensional datasets stored in secondary memory. Ingeniería e Investigación, 37(3), 133-140.

DOI: 10.15446/ing.investig.v37n3.60339.

---

ABSTRACT

-Let S be a set of points located in a rectangle R and q is a point that is not in S.- This article describes the design, implementation, and experimentation of different algorithms to solve the following two problems: (i) Maximum Empty Rectangle (MER), which consists in finding an empty rectangle with a maximum area contained in R and does not contain any point from S and (ii) Query Maximum Empty Rectangle (QMER), which consists in finding the rectangle with the same restrictions given for the MER problem but must also contain q. It is assumed that both problems have insufficient main memory to store all the objects in set S. According to literature, both problems are very practical in fields such as data mining and Geographic Information Systems (GIS). Specifically, the present study proposes two algorithms that assume that S is stored in secondary memory (mainly disk) and that it is impossible to store it completely in main memory. The first algorithm solves the QMER problem and consists of decreasing the size of S by using dominance areas and then processing the points that are not eliminated using an algorithm proposed by Orlowski (1990). The second algorithm solves the MER problem and consists of dividing R into four subrectangles that generate four subsets of similar size; these are processed using an algorithm proposed in Edmonds et al. (2003), and finally, the partial solutions are combined to obtain a global solution. For the purpose of verifying algorithm efficiency, results are shown for a series of experiments that consider synthetic and real data.

---

Keywords: Geometric algorithms, spatial databases, geometric problems.

---

RESUMEN

.Sea S un conjunto de puntos ubicado en un rectángulo R, y q un punto que no está en S.- Este artículo describe el diseño, la implementación y experimentación de diferentes algoritmos para resolver los siguientes problemas: (i) MER, que consiste en encontrar un rectángulo vacío de máxima área contenido en R y que no contiene un punto de S, y (ii) QMER, que consiste en encontrar un rectángulo con las mismas restricciones dadas para el problema MER y que, además, debe contener a q. En ambos problemas se asume que no existe suficiente memoria para almacenar todos los objetos del conjunto S. De acuerdo con la literatura, ambos problemas son de mucha utilidad práctica, en ámbitos como la minería de datos, sistemas de información geográfica, por nombrar algunos. Concretamente, en este trabajo se proponen dos algoritmos que asumen que S se encuentra almacenado en memoria secundaria y que no es posible almacenarlo completamente en memoria. El primero resuelve el problema QMER y consiste en disminuir el tamaño de mediante la utilización de zonas de dominancia y luego, mediante un algoritmo propuesto por Orlowski (1990), se procesan los puntos no descartados. El segundo, a su vez, resuelve el problema MER y consiste en dividir R en cuatro subrectángulos generando cuatro subconjuntos de similar tamaño los que se procesan mediante un algoritmo propuesto en Edmonds et al. (2003), combinando finalmente las soluciones parciales para obtener la solución global. Con el objeto de verificar la eficiencia de los algoritmos, se muestran los resultados de una serie de experimentos considerando datos sintéticos y reales.

---

Palabras clave: Algoritmos geométricos, bases de datos espaciales, problemas geométricos.

---

Received: September 28th 2016

Accepted: August 8th 2017

---

Introduction

Computational geometry is an area of mathematics that studies and proposes algorithmic solutions to geometric problems. It is a relatively new area and the first results date back to the 80s. Let S1 and S2 be two point sets located in regions (typically d = 2) and , respectively. Some of the problems studied with computational geometry are (i) finding the convex hull of S1, (ii) given a point q not belonging to S1 and a parameter k > 0, finding the k-points of S1 nearest to q, (iii) given a parameter k > 0, finding the k pairs of points (one from S1 and the other from S2) whose distances (Euclidean distance) are the shortest among all possible pairs that can be formed, and (iv) given a point q not belonging to S1, finding the empty rectangle with the largest area included in R1. The usefulness of algorithmic solutions for these problems is well established in the literature. The solutions to geometric problems from the perspective of computational geometry suppose that it is possible to store all the objects in the main memory of a computer. However, with the incidence of large spatial datasets, it has become necessary to extend or create solutions that assume data are found in multidimensional data structures residing in secondary memory (mainly disk). In this context, the operations that predominate or determine the efficiency of an algorithm are related to input/output operations or access to disk blocks, whose runtime is very expensive. Currently, solutions exist for some of the above-mentioned problems. Böhm and Kriegel (2001) propose an algorithm that solves problem (i); Roussopoulos, Kelley and Vincent (1995) describe an algorithm for problem (ii); Corral, Manolopoulos, Theodoridis, and Vassilakopoulos (2004, 2006) propose several algorithms to solve problem (iii), and Gutiérrez and Paramá (2012) provide solutions for a variant of problem (iv). This article proposes two algorithms to solve problem (iv), which will be referred to as QMER and an algorithm to solve a variant of problem (iv) proposed by Edmonds et al. (2003), which will be referred to as MER.

Figure 1. MER and QMER problems.

Source: Gutiérrez et al. (2014)

The MER and QMER problems are formally defined below. Let S be a finite point set of size n located in a rectangle(typically d = 2) whose sides are parallel to the plane axes, and let q be a point such that According to Naamad, Lee, and Hsu (1984), a rectangle M is said to be a restricted rectangle if it satisfies the following three conditions. (1) M is completely contained in R, (2) M does not contain points from S in its interior, and (3) each arc of M contains a point S or coincides with the arc of R. The MER problem (Figure 1a) consists of finding the rectangle M with the largest area. On the other hand, rectangle M must also contain point q in the QMER problem (Figure 1b). Thus, the QMER problem consists of finding the rectangle M with the largest area and contains q.

Applications: The MER problem could be applied as follows. Let us suppose that a steel sheet with small regions has imperfections or flaws and we are interested in obtaining flawless regions on the sheet. Other applications can be found in the context of geographic information systems (GIS); for example, you want to build a park in a region and have the georeferenced landmarks (buildings, houses, streetlights, etc.). It can be interesting to solve efficiently the queries as to (1) identifying the largest area of the empty area in which to build the park or (2) finding the largest free space (rectangular-shaped) around a point where you wish to build the park. It should be noted that problem (1) can be modeled as a MER problem and problem (2) as QMER.

The rest of this article is organized as follows: Section 2 includes a literature review (related work) describing the principal algorithms available for both problems from the computational geometry point of view, as well as from the spatial databases (large volumes of data). Sections 3 and 4 show the detailed design and implementation of the qMER and MER algorithms, respectively, along with their complexity analyses and experimental results. Finally, the conclusions and future work are described in Section 5.

Related work

This section reviews the main algorithms proposed in the literature for MER and QMER problems. Firstly, we analyze the proposed solutions for each problem from the standpoint of computational geometry; that is, we assume that the point set can be fitted in main memory. We then discuss proposals where points are stored in secondary memory and do not fit in main memory.

The MER problem was initially established from computational geometry by supposing that all points fit in the main memory. Under this scenario, the MER problem has been extensively studied. The first known study was by Naamad, Lee, and Hsu (1984), who described two algorithms that consider points as being randomly located within space. The first algorithm needs points to be ordered and compared one with the other. It run in O(n2) time and it needs O(n) storage. The second one has an expected-time complexity O ( n ( log2 n ) ) and O (n) storage; it reads the unordered points and stores them in a semi-dynamic heap. (From this point on, logn is considered as log2 n). Chazelle, Drysdale, and Lee (1986) propose a divide and conquer style algorithm with time O (nlog3 n) using O (nlog n) storage. Aggarwal and Suri (1987), who used O (nlog3 n) time and O (n) storage, discussed an algorithm with similar complexity. Orlowski (1990) demonstrates an algorithm that uses time O(slog n) where s is the number of maximum empty rectangles. His algorithm creates rectangles using two points as vertices and extends them toward the sides until an MER is formed. The time complexity of this algorithm is O (nlog n + s). In a more recent study, De and Nandy (2011) propose an algorithm with O(n log2 n + s) time and O (log n) storage using a priority search tree. Other studies also focus on solving the MER problem in three dimensions. In this case, the algorithm computes maximum empty cubes; Nandy and Bhattacharya (1998) and De and Nandy (2011) proposed algorithms to solve this problem.

Augustine et al. (2010a, 2010b) suggest an algorithm to solve the qMER problem. This algorithm pre-processes the points where space is divided into a set of cells so that all the points falling into the same cell produce the same maximum empty rectangle that contains query point q. These cells are stored in main memory and organized in a two-dimensional data structure called range tree. The pre-processing stage uses O (n log2 n) storage and O (n2) time. Additional O (log n) time is needed to extract the response. Kaplan, Mozes, Nussbaum, and Sharir (2012) suggest another approach that significantly improves the pre-processing time as compared to Augustine (2010a, 2010b). More specifically, O(nα (n) log3n) storage space is required by this algorithm to maintain the data structure being used (segment tree) and O(nα (n) log4n) time to construct it, where a is the inverse of Ackermann’s function.

All the previously discussed algorithms consider that the objects can be stored in main memory. More recently, Gutiérrez et al. (2012) and Gutiérrez et al. (2014) propose algorithms to solve the QMER problem; these consider the limitations of main memory and assume that the objects reside in secondary memory in a multidimensional R-tree data structure. These algorithms increase R-tree abilities. It is clear that they are inadequate when objects are not stored in an R-tree because the construction process of this structure is time-consuming. However, under many scenarios the considered objects do not fit in main memory and are stored in a raw file. Edmonds et al. (2003) propose an algorithm to obtain maximum empty rectangles (MER problem) in an area made up of large datasets; this algorithm requires O (|X| × |Y|) time and O (|X|) storage with |X| being the number of different values in the X-axis and |Y| all the different values found in the Y-axis.

qMER algorithm

Our first algorithm, called qMER, solves the QMER problem. The qMER algorithm takes the advantage of the dominance relationship of the points in S compared to the query point q (see Figure 2).

Figure 2. Dominance areas.

Source: Authors

Figure 2 shows that point q divides rectangle R into four quadrants: Upper Left (UL), Upper Right (UR), Bottom Left (BL), and Bottom Right (BR). The dominance area of a given point p compared to a given point q is defined as the area formed by the rectangle defined by p and the point in the corner of R opposite p within the quadrant. For example, viewing the UR quadrant in Figure 2, the dominance area of p1 (hatched area) is given by the rectangle defined by point p1 and the extreme upper right point of R. The dominance areas for the other quadrants are defined in a similar manner.

Algorithm 1: qMER algorithm to solve the QMER problem

Source: Authors

Our algorithm uses these dominance areas as elimination areas to obtain set whose size is smaller than S (we assume that is sufficiently small to be located in the main memory), and solve the qMER problem by a computational geometry algorithm with set as input. The idea behind our algorithm (see Algorithm 1) is to obtain dominance areas in stage 1, which cover an area as near as possible to area R to reduce the size of S in stage 2. To accomplish this, the k-neighbors nearest to q in accordance with the Euclidean distance (Algorithm 1, line 5) are obtained for each quadrant; these nearest points define the dominance areas for each quadrant (line 6) (see Figure 3). Each point is verified to see if it intersects some dominance area of its corresponding quadrant. If such is the case, the point is eliminated; otherwise, it is added to set . Finally (stage 3), in line 14 of Algorithm 1, set is processed using an adaptation of Orlowski’s algorithm (Orlowski, 1990), which is, according to the literature, one of the most efficient algorithms to solve the MER problem.

The main contribution of qMER consists in reducing the size of S, (stages 1 and 2). The size can be influenced by adjusting the value of k. In spite of this, and according to the distribution of S, it could occur that qMER does not discard points, for example, if all points are dominant. In such scenarios, the QMER problem can be solved using an algorithm for secondary memory, such as qAREMAV, which is an adaptation of the algorithm proposed by Edmonds et al. (2003).

Time complexity: It was previously demonstrated that the qMER algorithm can be separated into three phases: (i) finding the k points nearest to q for each quadrant, (ii) examining the points once again and eliminating all points dominated by the nearest k-neighbors in each quadrant, and (iii) solving the qMER problem with Orlowski’s algorithm with an input set consisting of all the points that have not been dominated. The complexity of phase (i) is O (nlog k) = O (n) because k is a constant, phase (ii) is O (nk) = O (n), and phase (iii) is O (nlog n + s), where sis the number of maximum empty rectangles. Therefore, the complexity of qMER is O (n) + O (n) + O (nlog n + s) = O (nlog n + s).

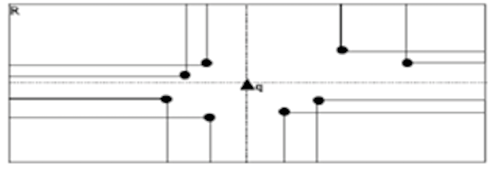
Figure 3. “k-neighbors” algorithm with k = 2.

Source: Authors

Experiments: We evaluate the performance of qMER through a series of experiments and compare it with a base algorithm called qAREMAV, which is a direct adaptation of the algorithm proposed by Edmonds et al. (2003) to solve the QMER problem. The qAREMAV and qMER algorithms were implemented with the Java programming language. Synthetic point sets between 10,000 and 50,000,000 points with uniform spatial distribution [0, 1] × [0, 1] were considered. Different values for parameter k (1, 5, 10, 15, 20, 50, and 100) were studied. Algorithm runtime (elapsed time) in the experiments was measured and, in the case of qMER, the filtering percentage, which is related to the percentage of points that were not eliminated, was also measured. The experiments were conducted in a machine with a 4-core processor with 3.092 MHz and 8GB RAM.

In the first experiment, we studied the effect of k on the size of set and the filtering time in qMER. Different values for k were studied by examining 10 million points. Results showed that as k increases, runtime tends to remain relatively stable, and this occurs from k = 10 at approximately 22 seconds. This k value was used for the rest of the experiments. When the qMER performance ratio (stages 1 and 2), in terms of k, increases, the time spent calculating the k-neighbors is an inconvenient compared to the benefit obtained, that is, by reducing the size of . Letting k be constant always helps to achieve a significant reduction of the original set without increasing runtime.

Figure 4. Runtime comparison of algorithms.

Source: Authors

Having already defined an adequate k for qMER, it can be compared with the qAREMAV algorithm. Results are displayed in Figure 4, where it can be seen that qMER outperforms qAREMAV by several orders the magnitude. This favorable difference for qMER is achieved by reducing the size of the original set in stages 1 and 2, which can be performed in O (n) by allowing an important reduction in the value of n and therefore in the value of s in the global time complexity O (nlong n + s) of the qMER algorithm.

MER algorithm

In this section, we explain our second algorithm, called MER, which solves the MER problem. Our algorithm is based on the AREMAV algorithm presented by Edmonds et al. (2003). The latter algorithm showed low performance when point set S has low density.

Edmonds et al. (2003) define density as where |T| is the number of points, |X| and |Y| are the number of values that differ from the X and Y coordinates of the point set, respectively.

For example, if we take into account the 17 points in Figure 5, we obtain assuming that no points exist that share a coordinate. A property of this metric is that to the extent that the value of D decreases, the number of points sharing a coordinate also decreases.

The MER algorithm attempts to complement the AREMAV algorithm by improving runtime in lower density point sets, which are more frequent in a wide range of real-world applications. The decision as to which algorithm to use can be established based on point set density, which can be obtained in linear time because the set is ordered. The idea behind the MER algorithm is to divide the original point set into point subsets of approximately the same size. Each one of these subsets is then solved with AREMAV and solutions are combined to obtain the final result.

The MER algorithm (Algorithm 2) is characterized by dividing the original R space into four subsets (UL, UR, BL, and BR as previously observed in the qMER algorithm) (see Figure 5) (Algorithm 2, line 2). This separation is undertaken to decrease the number of points to be analyzed. There is also an attempt to include a similar number of points in each subset because this will make the algorithm faster.

The point set division was performed with a data structure suggested by Blott and Weber (1997), called VA-file (Vector approximation file). The idea behind the VA-file is to divide the space (usually d-dimensional, 2-dimensional for this algorithm) into 2b cells. Given that four subsets are being used, b = 2 (Figure 5).

When obtaining the R divisions, it will be necessary to read all the points in the original set and determine which division they intersect (Algorithm 2, line 3). The four point subsets will thus be created (Figure 5). Once the points belonging to each subset are defined, the AREMAV algorithm is used for each subset (Algorithm 2, lines 5 and 6). The rectangles generated by AREMAV (Figure 6a) can be of different types grouped as follows: rectangles that are generated within the subset: Rectangles that cannot continue growing (Figure 6a, MER1), rectangles that are generated on the bottom edge: Rectangles that could continue growing downward (see Figure 6a, MER2), and rectangles that are generated on the right edge: Rectangles that could grow toward the right (see Figure 6a, MER3).

t is useful to know which type of rectangle is generated when analyzing the neighbor subset. For example, in the case of analyzing the UL subset, rectangles that have an edge on the right side will be brought to subset UR and the rectangles that have their bottom edge in subset UL will be brought to subset BL (Algorithm 2, line 9). If subset UR is being analyzed, only the rectangles that are generated on the bottom edge of the UR subset will be taken and brought to subset BR (Algorithm 2, line 13). In the case of subset BL, only the rectangles that are generated on the right edge will be taken and be brought to subset BR (Algorithm 2, line 16).

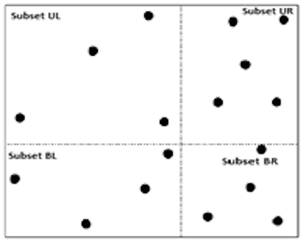
Figure 5. Division of original set of four subsets using VA-files with d =2 and b =2.

Source: Authors

Algorithm 2: MER algorithm

Source: Authors

Analyzing subset BR will generate the maximum empty rectangles typical of the subset together with the last maximum empty rectangles that could not be “closed” in the previous subsets; all the rectangles obtained are therefore compared with the largest previous maximum empty rectangle. The rectangle with the largest area will be the solution. For the set in Figure 5, the solution is obtained from the BL subset (Figure 6b).

Figure 6. a) Possible MER of SI subset. b) MER of initial set.

Source: Authors

Time complexity: The execution of the MER algorithm includes four different steps, (i) taking a sample of size k ≤ n of S, (ii) dividing R in four subregions, (iii) dividing S into four subsets with a similar number of points and (iv) using AREMAV in all the subsets to obtain the solution. The time complexity of phase (i) is O (n), phase (ii) is O (klog k), phase (iii) is O (n), and phase (iv) is . Therefore, the time complexity of MER is

O (n) + O (klog k) + O (n) +

Experiments :This section displays a series of experiments that compare the MER and AREMAV algorithms. Algorithm runtime (elapsed time) in the experiments was measured. The machine used for these experiments was the same one as for the qMER algorithm experiments. The MER and AREMAV algorithms are sensitive to point set density. Experiments were conducted with real and synthetic point sets. Within the synthetic point sets, the following distributions were used: Uniform Distribution: set size ranges from 500,000 to 10,000,000 points and density varies between 10% and 20%. These point sets were constructed according to Edmonds et al. (2003) where point sets are |X| = 1000; Zipf Distribution: sets have 125,000 and 250,000 tuples and 5% density; and Cluster Distribution: sets have 125,000 and 250,000 tuples and 1 % density.

The real data correspond to points in North America3. The density of these sets is approximately zero.

The experiments measure how different types of distributions and densities influence runtime of the AREMAV and MER algorithms.

Density in different algorithms. This first experiment was conducted to show the effect of density in the two algorithms using a set of 200,000 points with uniform distribution and density of ≈ 0 %, 1 %, 5 %, 10 %, 15 %, and 20 %. It can therefore be experimentally demonstrated that it is better to use the MER algorithm for low-density sets and the AREMAV algorithm for higher-density sets. Results are displayed in Figure 7.

Figure 7. Runtime of MER and AREMAV algorithms with different densities and uniform distribution.

Source: Authors

Figure 7 indicates that the MER algorithm is more efficient than the AREMAV algorithm for runtime when density is less than 3%.

Real point set. This experiment shows the behavior of both algorithms for real point sets. Results are illustrated in Figure 8. For real data, this experiment shows that the MER algorithm is more efficient than the AREMAV algorithm for runtime. The MER algorithm outperforms AREMAV algorithm because on average it requires 28% of the time needed by AREMAV (Figure 8). This higher performance is because the MER algorithm significantly reduces the size of |X| and |Y| when separating the point sets in subsets.

Cluster distribution. The cluster distribution with 5 % density was used for this experiment because for this type of distribution the points are grouped in different clusters in the plane where there is higher density in the center of the clusters and lower density as they move away from the center. Results are illustrated in Figure 9. It can be observed that the MER algorithm has better runtime than the AREMAV algorithm. On the other hand, the performance of the AREMAV algorithm has improved quite a bit compared to the previous case.

Zipf distribution. Density decreased in this experiment and the type of distribution was Zipf with 5 % density where points are grouped close to the origin and dispersed as they move away. Figure 10 shows that the MER algorithm is somewhat better than the AREMAV algorithm, but the latter reaches runtimes very similar to those of the MER algorithm because of high density.

Figure 8. Runtime (seconds) of MER and AREMAV algorithms on real datasets.

Source: Authors

Figure 9. Runtime of MER and AREMAV algorithms on sets with cluster distribution and 5 % density.

Source: Authors

Uniform distribution. The last experiment compares both algorithms under the scenario where the AREMAV algorithm is at an advantage as explained by Edmonds et al. (2003) and demonstrated by Lara (2014) because performance is better when density is higher between points. Data are plotted in Figure 11. Both algorithms have similar behaviors, but the MER algorithm is not more efficient than the AREMAV algorithm for runtime. Although the MER algorithm uses the AREMAV algorithm to obtain the maximum empty rectangles, it also uses many disk accesses, thus increasing runtime. Therefore, in accordance with the experimental results obtained under the different scenarios, it can be stated that the MER algorithm is a complement to the AREMAV algorithm because it allows solving problems under very unfavorable scenarios for the AREMAV algorithm (low-density sets). As a general conclusion is that the use of a heuristic based on set density can therefore be designed to decide which one of the two algorithms to be used.

Figure 10. Runtime of MER and AREMAV algorithms on sets with Zipf distribution and 1 % density.

Source: Authors

Figure 11. Runtime (seconds) of MER and AREMAV algorithms on sets with uniform distribution and 20 % density.

Source: Authors

Conclusions

Two algorithms are presented in this article, one to solve the QMER (qMER) problem and another for the MER (MER) problem.

In accordance with experimental results, qMER outperforms qAREMAV algorithm in several orders of magnitude. This difference is explained by reducing the size of the original set, which is achieved in stages 1 and 2, it was reduced on average by 0.02 %. When comparing our algorithm with the qAREMAV algorithm, it can be concluded that qMER is highly advantageous for both memory requirements and runtime. This allows qMER to solve problems that consider large point sets that are impossible to store in main memory.

As for MER, the experimental results show the influence of different point set densities. It can be observed that when the set density is low (less than 3 %), our algorithm requires approximately, on average, 43 % runtime of the AREMAV algorithm. On the contrary, it can be observed that when density is higher, the AREMAV algorithm is approximately, on average, 50 % faster than the MER algorithm. These behaviors demonstrate that the MER and AREMAV algorithms are complementary. There are currently many applications requiring real low-density point sets; using the MER algorithm is therefore a better alternative under this scenario.

Future work will be focused on optimizing the manner in which the MER algorithm finds the maximum empty rectangle. This could be done by recursively creating more quadrants until the contained points can be stored in main memory and, in this way, use an algorithm in these subsets that works in main memory and later join the solutions. In addition, we plan to design algorithms that solve the QMER and MER problems by considering rectangles with arbitrary orientation and taking into account main memory limitations.

Acknowledgements: This study was partly financed by the Universidad del Bío-Bío research groups: “Bases de Datos” and “Algoritmos y Bases de Datos”. In addition, we received support from the Universidad del Bío-Bío research projects DIUBB 142719 3/R and DIUBB 171319 4/R. We are also grateful to the Asociación Universitaria Iberoamericana de Postgrado (AUIP), who sponsored the transportation scholarship to Spain.

References

Aggarwal, A., & Suri, S. (1987, October). Fast algorithms for computing the largest empty rectangle. In Proceedings of the third annual symposium on Computational geometry (pp. 278-290). ACM.

Augustine, J., Das, S., Maheshwari, A., Nandy, S. C., Roy, S., & Sarvattomananda, S. (2010). Recognizing the largest empty circle and axis-parallel rectangle in a desired location. arXiv preprint arXiv:1004.0558.

Augustine, J., Das, S., Maheshwari, A., Nandy, S., Roy, S., & Sarvattomananda, S. (2010). Querying for the largest empty geometric object in a desired location. arXiv preprint arXiv:1004.0558.

Blott S, Weber R (1997) A simple vector-approximation file for similarity search in high-dimensional vector spaces. Technical report, Institute of Information Systems, ETH Zentrum, Zurich, Switzerland

Böhm, C., & Kriegel, H. P. (2001, September). Determining the convex hull in large multidimensional databases. In International Conference on Data Warehousing and Knowledge Discovery (294-306). Springer Berlin Heidelberg.

Chazelle, B., Drysdale, R. L., & Lee, D. T. (1986). Computing the largest empty rectangle. SIAM Journal on Computing, 15(1), 300-315.

Corral, A., Manolopoulos, Y., Theodoridis, Y., & Vassilakopoulos, M. (2004). Algorithms for processing K-closest-pair queries in spatial databases. Data & Knowledge Engineering, 49(1), 67-104.

Corral, A., Manolopoulos, Y., Theodoridis, Y., & Vassilakopoulos, M. (2006). Cost models for distance joins queries using R-trees. Data & Knowledge Engineering, 57(1), 1-36.

De, M., & Nandy, S. C. (2011). Inplace algorithm for priority search tree and its use in computing largest empty axis-parallel rectangle. arXiv preprint arXiv:1104.3076.

De, M., & Nandy, S. C. (2011). Space-efficient Algorithms for Empty Space Recognition among a Point Set in 2D and 3D. In CCCG.

Edmonds, J., Gryz, J., Liang, D., & Miller, R. J. (2003). Mining for empty spaces in large data sets. Theoretical Computer Science, 296(3), 435-452.

Gutiérrez, G., & Paramá, J. R. (2012, June). Finding the largest empty rectangle containing only a query point in large multidimensional databases. In International Conference on Scientific and Statistical Database Management
(pp. 316-333). Springer Berlin Heidelberg.

Gutiérrez, G., Paramá, J. R., Brisaboa, N., & Corral, A. (2014). The largest empty rectangle containing only a query object in Spatial Databases. GeoInformatica, 18(2), 193-228.

Guttman, A. (1984). R-trees: a dynamic index structure for spatial searching, 14(2), 47-57. ACM.

Kaplan, H., Mozes, S., Nussbaum, Y., & Sharir, M. (2012, January). Submatrix maximum queries in Monge matrices and Monge partial matrices, and their applications. In Proceedings of the twenty-third annual ACM-SIAM symposium on Discrete Algorithms (pp. 338-355). SIAM.

Lara, F. (2014) Implementación en Java de algoritmos geométricos sobre grandes conjuntos de datos. In: Memoria de Titulo, Ingeniería Civil en Informática, Universidad del Bío-Bío.

Naamad, A., Lee, D. T., & Hsu, W. L. (1984). On the maximum empty rectangle problem. Discrete Applied Mathematics, 8(3), 267-277.

Nandy, S. C., & Bhattacharya, B. B. (1998). Maximal empty cuboids among points and blocks. Computers & Mathematics with Applications, 36(3), 11-20.

Orlowski, M. (1990). A new algorithm for the largest empty rectangle problem. Algorithmica, 5(1-4), 65-73.

Roussopoulos, N., Kelley, S., & Vincent, F. (1995, June). Nearest neighbor queries. In ACM sigmod record, 24(2), 71-79. ACM.

Attribution 4.0 International (CC BY 4.0) Share - Adapt