Research on supply chain partner selection and task allocation based on fuzzy theory under an uncertain environment

Investigación sobre la selección de socios de la cadena de suministro y asignación de tareas basada en la teoría difusa en un entorno incierto

Nowadays the enterprises pay the closer attention to the relationship among suppliers, manufacturers and distributors due to the global competitive market economy. And they manage the supply chain through establishing strategic cooperative partnership, which can greatly enhance the competitive advantage and obtain greater overall profits. In this paper, the fuzzy theory is applied to study the supply chain partner selection and the task coarse allocation problem in under multi-attribute fuzzy comprehensive decision-making and fuzzy constraints. Finally, the fuzzy comprehensive decision of supply chain network structure was verified through the case of Shaoxing textile.

Hoy en día las empresas prestan más atención a la relación entre proveedores, fabricantes y distribuidores debido a la competitiva economía de mercado global. Y manejan la cadena de suministro a través del establecimiento de una asociación estratégica de cooperación, que puede mejorar en gran medida la ventaja competitiva y obtener mayores beneficios en general. En este artículo, la teoría difusa se aplica para estudiar la selección de socios de la cadena de suministro y el problema de asignación de tareas gruesas en la toma de decisiones globales difusas de múltiples atributo y las restricciones difusas. Por último, la decisión global difusa de la estructura de la red de la cadena de suministro se verificó a través del caso de Shaoxing textil.

Xinyi Fu ¹,and Tinggui Chen ²

---

¹ Master of E-Business, Zhejiang Gongshang University, China. Affiliation: Master Candidate, School of Management and E-Business, Zhejiang Gongshang University, China. E-mail: fxi718@163.com

² Master of Systems Engineering, Faculty of Mechanical Science and Engineering, Huazhong University of Science and Technology, China. Affiliation: Associate Professor, PHD, School of Management and E-Business, Zhejiang Gongshang University, China. E-mail: ctgsimon@mail.zjgsu.edu.cn (corresponding author)

---

How to cite: Fu, X., and Chen, T. (2018). Research on supply chain partner selection and task allocation based on fuzzy theory under an uncertain environment. Ingeniería e Investigación, 38(1), 83-95.

DOI: 10.15446/ing.investig.v38n1.64675

---

ABSTRACT

Nowadays enterprises pay closer attention to the relationship between suppliers, manufacturers and distributors due to the global competitive market economy. They manage the supply chain by establishing a strategic cooperative partnership, which can greatly enhance the competitive advantage and obtain greater overall profits. In this paper, the fuzzy theory is applied to study the supply chain partner selection and the task coarse allocation problem, under multi-attribute fuzzy comprehensive decision-making and fuzzy constraints. Finally, the fuzzy comprehensive decision of the supply chain network structure was verified through the case of Shaoxing textile.

---

Keywords: Fuzzy theory, supply chain partner selection, task allocation, ordered weighted averaging (OWA), analytic hierarchy process (AHP).

---

RESUMEN

Hoy en día las empresas prestan más atención a la relación entre proveedores, fabricantes y distribuidores debido a la competitiva economía de mercado global. Y manejan la cadena de suministro a través del establecimiento de una asociación estratégica de cooperación, que puede mejorar en gran medida la ventaja competitiva y obtener mayores beneficios en general. En este artículo, la teoría difusa se aplica para estudiar la selección de socios de la cadena de suministro y el problema de asignación de tareas gruesas en la toma de decisiones globales difusas de múltiples atributo y las restricciones difusas. Por último, la decisión global difusa de la estructura de la red de la cadena de suministro se verificó a través del caso de Shaoxing textil.

---

Palabras clave: Teoría difusa, selección de socios de la cadena de suministro, asignación de tareas, promedio ponderado ordenado, proceso de jerarquía analítica.

---

Received: May 7th 2017

Accepted: October 13th 2017

---

Introduction

In the process of supply chain coordination and optimization, a challenging problem is dealing with the existing uncertain factors (Ju & Chen, 2017; He et al., 2016a). The uncertainty theory was established in the operational research field by introducing probability theory and fuzzy theory, which enables researchers to do the dynamic study of complexity and uncertainty in the supply chain through various methods (Chen & Jiang, 2015). To choose the appropriate upstream and downstream partners is an important task in supply chain network optimization. Enterprise partner selection is a multi-attribute problem. It includes not only qualitative indicators but also quantitative indicators. Qualitative indicators are characterized by a lot of fuzziness, and quantitative indicators are subject to errors and incompleteness because of information asymmetry and dynamic operation.

In the process of supply chain partner selection, most researchers focused on how to choose the suppliers. Kumar et al. (2004, 2006) solved the problem with fuzzy integer programming method. Similar work was conducted by Rezaei et al. (2015) and Wu et al. (2014). In addition, there were methods like the fuzzy multi-objective programming method in distributors selection (Yeh & Chuang, 2011) and fuzzy multi-objective integer programming in multi-product supplier selection (Zhou & Mou, 2007).

Another method named fuzzy multi-attribute decision-making can be applied to solve the supply chain partner selection problem. Ashayeri et al. (2012) introduced an intuitionistic fuzzy Choquet integral operator based approach to partners and configuration selection. In order to bring structure in the evaluation process, the supply chain operations reference (SCOR) model developed by Supply Research Council was employed. The paper discussed the development of the value chain concept from partners selection perspective, outlined general similarities and differences of the value chain and the SCOR, and used a simple V-form supply chain example to establish the proposed approach. Wang and Che (2007) developed an integrated model of supplier selection based on the fuzzy theory under the condition of manufacturers structure change. Chou and Chang (2008) built a decision support system for supplier selection by fuzzy multi-attribute sorting in the strategic alliance. Mikhailov (2002) applied the fuzzy analytic hierarchy process (FAHP) to partner selection in the process of forming virtual enterprises. Wang and Chen (2007) improved the method put forward by Mikhailov giving full consideration to the consistency of fuzzy preference relation in the fuzzy hierarchy analysis. Wu and Barnes (2016) presented a model for green partner selection and supply chain construction by combining analytic network process (ANP) and multi-objective programming (MOP) methodologies. The model offered a new way of solving the green partner selection and supply chain construction problem both effectively and efficiently, as it enabled decision-makers to simultaneously minimize the negative environmental impact of the supply chain whilst maximizing its business performance. Chang et al. (2006) introduced the fuzzy semantic operators into the supply chain partner selection, and also gave full consideration to the characteristics of different stages in the product life cycle. Others include virtual enterprise partner selection based on fuzzy group decision (Li et al., 2004), supplier selection based on fuzzy semantic distance (Li & Xu, 2004), fuzzy evaluation of virtual enterprise (Huang et al., 2008), large-scale alliance partner selection based on genetic algorithm and fuzzy decision (Jiang et al., 2007), supplier selection fuzzy decision method (Keshavarz et al., 2016), supplier selection based on multi-objective fuzzy optimization model (Wu et al., 2010), supplier partner selection based on AHP (Chen et al., 2010; He et al., 2016b), green supplier selection fuzzy decision (Zhang & Mei, 2015), etc.

At present, most research discuss the fuzzy uncertainty of supply chain and fuzzy optimization of single node enterprise. However, fuzzy uncertainty analysis and fuzzy optimization in supply chain network system are still in its infancy and there is few relatively complete systemic research papers. Based on the fuzzy theory and with the supply chain network under uncertain environment as the object, this paper focuses on studying the dynamic allocation problem in the supply chain partner selection under multi-attribute fuzzy comprehensive decision-making and fuzzy constraints. Meanwhile, it depends on different targets and value orientation of the dominant enterprises in the supply chain to choose different types of partners dynamically, after fully considering the added value of candidate partners in the supply chain and its competitive strength. All in all, the dynamic decision model of supply chain partner selection and task allocation based on fuzzy theory is shown in Figure 1.

The rest is organized as follows: in section 2, the fuzzy multiple attribute decision-making method in supply chain partner selection is introduced. Subsequently, production task allocation technology oriented to supply chain network optimization is also presented in section 3. Section 4 uses a case of Shaoxing textile to verify the proposed method. Section 5 presents the conclusions and future work of the paper.

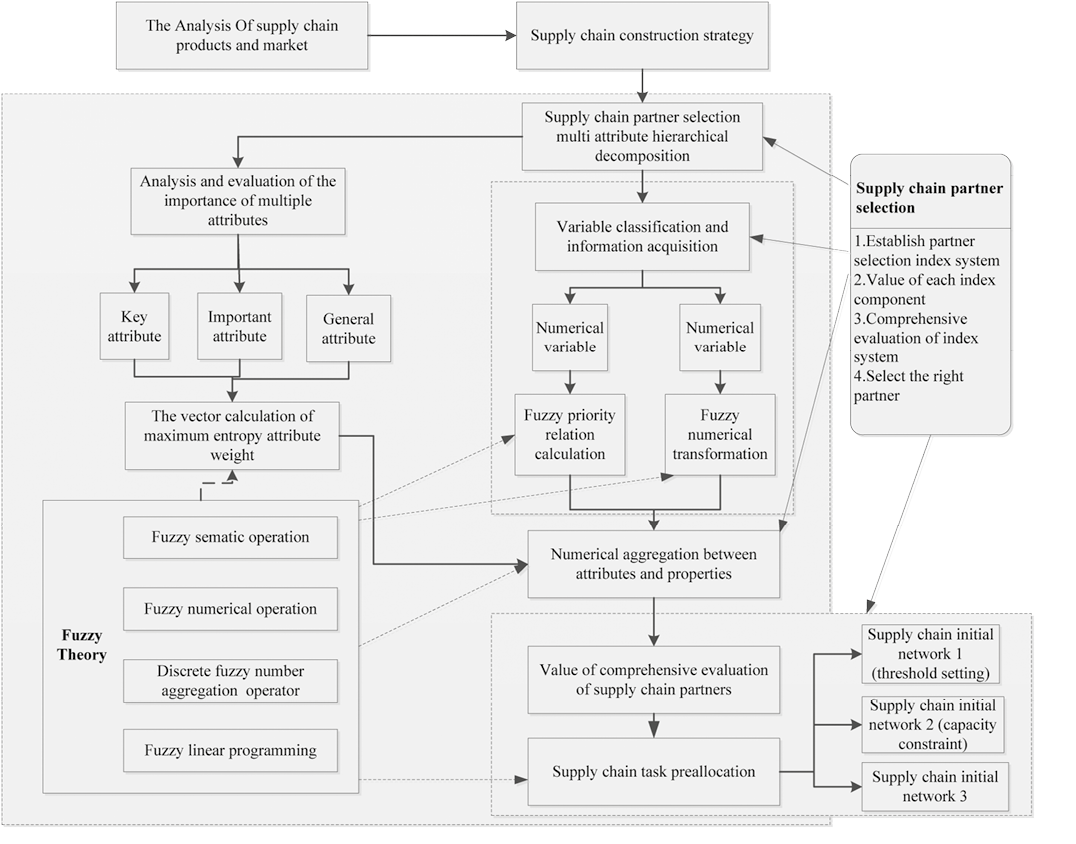
Figure 1. Dynamic supply chain partner selection and task allocation model based on fuzzy theory.

Source: Authors

Fuzzy multiple attribute decision-making in supply chain partner selection

Rules of discrete information fuzzy semantic comprehensive decision-making and the confirmation of weight vector

OWA (Ordered weighted averaging) operator is a kind of operator between maximum and minimum. If then .

If then .

Generally, the amount of information is decided by the attribute importance of information and fuzzy semantic. For example, the vast information is accepted if properties are important, and if properties are general then the information is accepted as much as possible. The fuzzy semantics such as ‘vast’ and ‘as much as possible’ essentially reflect the weight vector of fuzzy semantic decision, which are determined by the following formula.

Due to the monotonicity of fuzzy semantic operator,

(1)

(2)

Where the function Q satisfies:

(3)

Weight vector is determined by the function Q(r), which presents the membership degree of r belongs to Q, that is the degree that r is in accordance with Q. The value of Q(r) is determined by different fuzzy semantic operator and the common fuzzy semantic operators are including the vast majority, at least half and as much as possible.

In order to evaluate the decision condition of decision-makers under fuzzy semantic, the measures of the orness and entropy of the corresponding weight vector are as follows:

(4)

(5)

The former indicates the optimistic or pessimistic degree of the decision maker, and the latter calculates the weight sequence information. The weight vector of property aggregation guided by fuzzy semantic is between the range ‘and’ and ‘or’. However, the real weight is a random variable under unknown circumstances and is uncertain. It only constrains to . To determine the weight vector of each attribute in multiple attribute decision-making, one important objective is to minimize as much as possible the uncertainty of each attribute weight coefficient. With known value of orness, Filev and Yager (1995) put forward a method to calculate the weight vector of OWA operator when entropy value is maximal, by solving the maximum entropy constrained nonlinear programming problem. Its solving steps can be summarized simply as: obtain the weight vector by Equations (1) and (2), calculate orness(ω) by Equation (4), get the value of h by Equation (6), and finally calculate the value of ω* by Equation (7).

(6)

(7)

Multi-attributes classification and OWA operator fuzzy semantic matching under supply chain strategy

Supply chain partner selection is a multi-indicator and multi-attribute decision making process, and due to the different emphasis on selection, the importance of multi-attribute that comes up by the decision-making group which is appointed by the superior enterprises is different. That is, some attributes are dominant, while some are less important. The decision-making process can be roughly divided into three categories according to its importance: important attributes, secondary attributes and general properties.

In the actual decision-making process, the decision maker determines the amount of factors or attributes when selecting through the various fuzzy semantics of OWA operator. It will be found that it is impossible to meet the requirements of all factors or properties. The more the factors considered, the more pessimistic the result, the lower the satisfaction degree. Thus, trade-offs between the importance of information and the breadth of making full use of information should be made, so as to ensure an effective choice. According to three fuzzy semantic in this paper, at least half, the vast majority, as much as possible, it can be seen that with the enlargement of the consideration, the value decreases in turn. According to the classification of attribute importance and from the point of improving choice satisfaction degree, we match important attributes with at least half, secondary attributes with the vast majority, and general properties with as much as possible. Figure 2 shows the fuzzy multiple attribute decision-making.

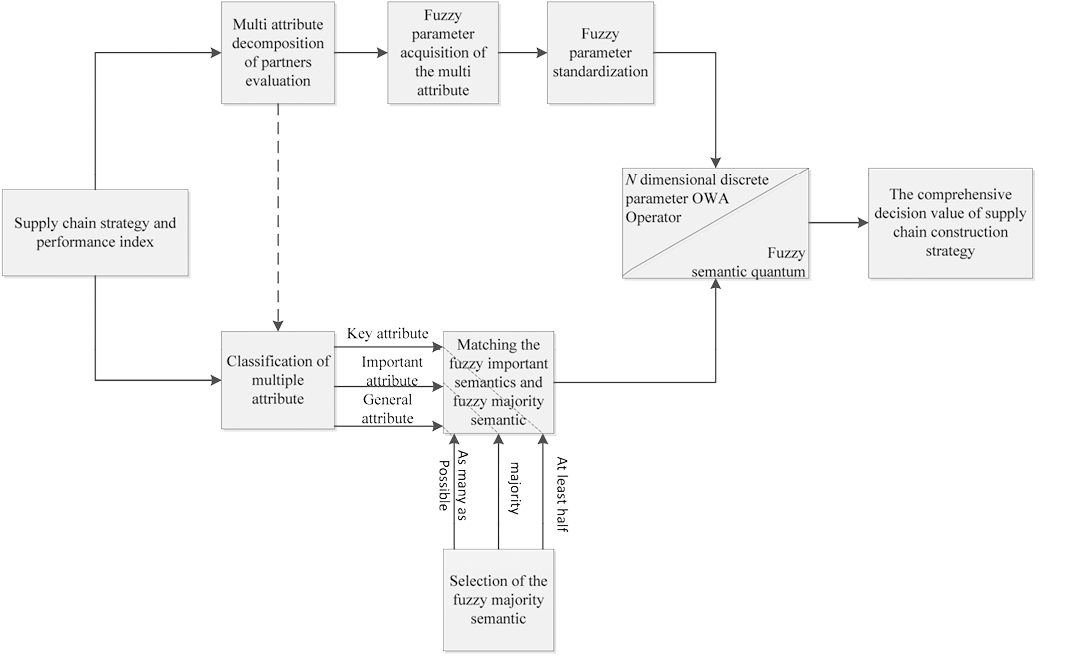
Figure 2. Chart of partner selection fuzzy multi- attributes under supply chain strategy.

Source: Authors

Calculation of supply chain partner correlation

The enterprises should have cooperation intention and mutual trust with each other at the beginning of building a partner. Now, the partner correlation is introduced in the paper, that is, after putting forward partner selection multi-attribute by expert group, by discussing with upstream and downstream enterprises, and doing the respective evaluation according to the multi-attribute. Then the expert group calculated the collected data by fuzzy OWA operator, and formed optimal evaluation of the required enterprise to make a decision. Finally, they integrated the optimal evaluation by multiplying as the basis of building partnership.

Let i(i=1,2,…,I) and j(j=1,2,…,J) be respectively enterprises in supply chain upstream and downstream adjacent levels of n and n+1. Then, i is supplier and j is manufacturer. Obviously, manufacturers choosing i is a supply behavior selection, and suppliers selecting j is a demand behavior selection. Each of them makes a fuzzy comprehensive decision of object choice based on the multi-attribute rule. presents the optimal degree for i relative to j, presents the optimal degree for j relative to i. Building partnership is a process of mutual recognition between enterprises, so the definition of partner correlation is as follows:

(8)

Take upstream node enterprises as a benchmark to do normalization processing to the value in Equation (8) so as to carry out the compared selection.

(9)

Steps of supply chain partner selection

All in all, the process of decision-making in partner selection is as follows:

Step 1: According to the product type, production tasks and supply chain strategy, the decision-making expert group, which is entrusted or specified by dominant enterprises comes up with properties for the selection and evaluation of enterprise partner. Large properties can be divided into smaller ones that can be implemented specifically. Construct a comprehensive and detailed evaluation attribute system in accordance with the AHP model.

Step 2: Using interactive way and based on the evaluation index system, the decision maker can fully consult candidates, and acquire, respectively, the attribute assessment information for the selection of their upstream or downstream enterprises. Then based on the collected information, the AHP evaluation multi-attribute system can be revised and consummated further.

Step 3: Adjust and standardize the quantum and qualitative information of attribute. Before adjusting the qualitative attribute information, it should be transferred into corresponding fuzzy numbers according to fuzzy semantics.

Step 4: According to the number of vector of attribute in multiple attribute system, calculate the weight of each vector in the condition of maximum entropy to three kinds of fuzzy semantics: at least half, the vast majority, as much as possible.

Step 5: Depending on the type of products, production stage and supply chain strategy, classify the properties according to their importance in AHP. That is to say, make sure which are the key attributes, which are the important attributes, and which are the general attributes. Then match key attributes with at least half, important attributes with vast majority, general attributes with as much as possible. Gather the information of child attributes and get the value information of each attribute. Next, gather the information according to the semantic-most experts agree, get optimal partnership selection.

Step 6: Integrate the optimal partnership by multiplying to the candidates of adjacent level, and then get the partnership correlation of each two candidates. Next, normalize the partnership correlation of adjacent level. Finally, the numerical value presents the selection priority of partnership.

The steps are shown in figure 3.

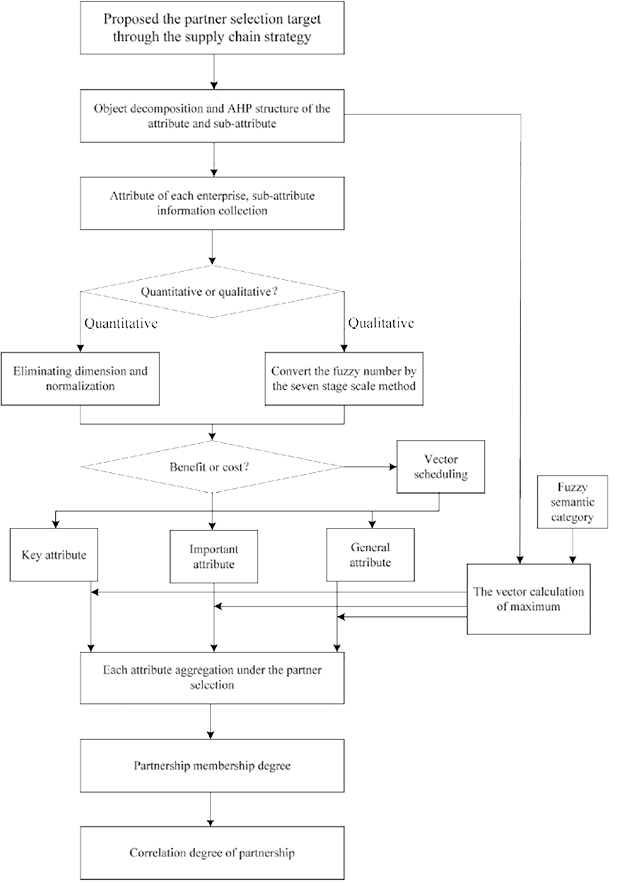
Figure 3. Evaluation selection process of supply chain partner

Source: Authors

Production task allocation oriented to supply chain network optimization

Partnership correlation reflects the willingness of two connected enterprise. The greater the correlation value is, the closer strategic cooperation between the relevant enterprises. When allocating the pre-allocated tasks in supply chain, fully considering partnership correlation concentrates the strategic partnership built in supply chain network and important enterprises. According to the nature of production task and the total amount, superior enterprises can consider pre-allocated task of supply chain network from three kinds of situation. Assume that the total amount of the product market demand during a certain period is Q, the material transformation relations in supply chain between the layers is 1.

1) If the value of Q is very large, the corresponding task capacity of node enterprise in each level of supply chain will also be very big. At this time, each enterprise’s production capacity constraints must be considered. If these constraint parameters are fuzzy, we can use the integer programming equations with fuzzy constraint, and take the partnership correlation as the weight of task allocation.

(10)

s.t (11)

(12)

(13)

(14)

Where Equation (11) is the capacity constraint. Equation (12) is the logistic constraint. Equation (13) is a demand constraint. Equation (14) is a nonnegative constraint.

2) If the value of Q is not very large, generally, the corresponding task capacity of node enterprise in each level of supply chain will not be very big. At this time, the enterprise’s capacity constraints are not necessary to be considered. Similarly, in accordance with the rules of strategic partnership and important enterprises, and being simple, the partnership correlation can be used as weight to allocate task.

(15)

3) When the value of Q is not very large, but the task is very important, such as “should be done on time”, “should not make any mistake” and so on, then the absolutely reliable node enterprise must be considered. Therefore, before allocating tasks, the superior enterprises can set a limit value W to partnership correlation. If the value is larger than W then we can assign the task to node enterprises, else not. Obviously, the supply chain network based on the task allocation doesn’t include those enterprises that are not considered. When allocating the following tasks, we still take partnership correlation as the weight of task allocation. But some node enterprises are deleted, so the original partnership correlation should be normalized.

(16)

Where the value of α is met that then the tasks are allocated by the following formula:

(17)

Case study

Take sports apparel production and processing as an example, its complete industrial chain involved polyester, chemical fiber, weaving, dyeing and finishing, garment design processing, and sales. Assume the supply chain network topology is five layers, then {N1−N2−N3−N4−N5} respectively presents one fiber factory in the first layer, (E1,1), three manufactures in the second layer, (E2,1, E2,2, E2,3), three dyeing and finishing plants in the third layer, (E3,1, E3,2, E3,3), four garment design processing plants in the forth layer, (E4,1, E4,2, E4,3, E4,4), and three sales companies in the fifth layer, (E5,1, E5,2, E5,3). The supply chain strategies select green production, which means low pollution and low noise, as well as cost control.

For any node enterprises in supply chain network topology, the indicators of the selection of upstream and downstream enterprises are different. According to the step one, mentioned above, combined with AHP hierarchy decomposition, the indicators are given in table 1 and 2. Based on this, each enterprise can respectively evaluate their upstream and downstream partners. Table 3 and 4 show the evaluation information for node enterprise E3,1 regarding its upstream partners E2,1, E2,2, E2,3 and downstream partners E4,1, E4,2, E4,3, E4,4. s0-s6 are fuzzy semantic codes. According to the supply chain strategy, determine the importance of the evaluation criteria, as shown in table 5. We gathered the number of individual principles and whole principles by OWA operator through maximum entropy weight vector, and the results are summarized in table 5.

Table 1. Selection evaluation criteria of upstream enterprises

Criterion	Sub criterion	Instruction
Green technology U1	Safety of machining process U1,1	Impact of processing on human health and product contamination
	Pollution control level U1,2	Enterprises in the production process of various pollution control
	Energy consumption of production process U1,3	Energy consumption of unit product in production
Cost U2	Basic order cost U2,1	Unit product price at normal order
	Quantity discount U2,2	Reduce the amount of discount on the basis of a basic order
	Emergency shipping cost U2,3	Increase in delivery time
Product quality U3	Product technical content U3,1	Leading products in the industry
	Product qualification rate U3,2	Average qualified rate of delivered goods within one order unit
	Product quality stability U3,3	A change in delivery product quality within an order unit
Agility ability U4	Normal contract delivery U4,1	Normal delivery time
	Emergency order delivery U4,2	The shortest delivery time
	Product variety satisfaction rate U4,3	Product customer processing ability
	Product change delivery U4,4	Lead time of product quantity specification change
Service capability U5	Delivery accuracy U5,1	Agreed delivery rate
	Quantitative accuracy U5,2	Contract number of anastomosis
	After sales service quality U5,3	Service response attitude

Source: Authors

Table 2. Selection evaluation criteria of downstream enterprises

Criterion	Sub criterion	Instruction
Purchasing capability V1	Purchase price of raw materials V1,1	Enterprises attach importance to the quality products of raw materials, and the ability to offer quality
	Payment timeliness V1,2	To be able to make the payment in time within the specified time
	Procurement performance status V1,3	Changes in the purchase contract
	Purchasing personnel quality V1,4	Professional level of purchasing personnel
Product performance V2	Product technical content V2,1	Leading products in the industry
	Product quality V2,2	The overall quality of the product
	Product update degree V2,3	New product R & D capability
Processing level V3	Production capacity V3,1	Maximum processing capacity of the product
	Customer processing capacity V3,2	Ability to respond to customer requirements
	Staff technical ability V3,3	Technical proficiency of employees
	Production process management level V3,4	Coordination and monitoring level in the process of production and processing
	Production equipment level V3,5	Advanced level of production and processing line
Performance V4	Product marketing ability V4,1	Marketing network, marketing plan, etc.
	Enterprises in peer reputation V4,2	Overall identity in peers
	Enterprise historical performance V4,3	Production and sales in the past
	Product after sales service V4,4	Service network, service attitude, product shelf life, etc.

Source: Authors

Table 3. Basic information of the upstream node enterprises when evaluating

Criterion	Sub- criterion	Enterprise E2,1		Enterprise E2,2		Enterprise E2,3
		Collected information	Transferred value	Collected information	Transferred value	Collected information	Transferred value
Green technology U1	U1,1	S0	1,00	S1	0,84	S1	0,84
	U1,2	S4	0,67	S3	0,84	S4	0,67
	U1,3	S3	0,50	S4	0,33	S2	0,67
Cost U٢	U٢,١	٢٢ Yuan/m	٠,٧٥	٢٥ Yuan/m	٠,٠٠	٢١ Yuan/m	١,٠٠
	U٢,٢	٧٪	٠,٠٠	٥٪	٠,٥٠	٧٪	٠,٠٠
	U٢,٣	١٢٪	٠,٦٠	١٥٪	٠,٠٠	١٠٪	١,٠٠
Product quality U٣	U٣,١	S٥	٠,٨٤	S٣	٠,٥٠	S٤	٠,٦٧
	U٣,٢	٩٩٪	١,٠٠	٩٨٪	٠,٦٧	٩٦٪	٠,٠٠
	U٣,٣	S٦	١,٠٠	S٤	٠,٦٧	S٤	٠,٦٧
Agility Ability U٤	U٤,١	١٠ days	١,٠٠	١٥ days	٠,٠٠	١٢ days	٠,٦٠
	U٤,٢	٥ days	١,٠٠	٥ days	١,٠٠	٧ days	٠,٠٠
	U٤,٣	S٣	٠,٨٤	S٣	٠,٥٠	S٣	٠,٨٤
	U٤,٥	٣ days	١,٠٠	٤ days	٠,٠٠	٤ days	٠,٠٠
Service capability U٥	U٥,١	٩٩٪	١,٠٠	٩٥٪	٠,٠٠	٩٩٪	١,٠٠
	U٥,٢	٩٨٪	٠,٦٧	٩٩٪	١,٠٠	٩٦٪	٠,٠٠
	U٥,٣	S٣	٠,٨٤	S٦	١,٠٠	S٤	٠,٦٧

Source: Authors

Table 4. Basic information of the downstream node enterprises when evaluating

Criterion	Sub- criterion	Enterprise E٤,١		Enterprise E٤,٢		Enterprise E٤,٣		Enterprise E٤,٤
		Collected information	Transferred value	Collected information	Transferred value	Collected information	Transferred value	Collected information	Transferred value
Purchasing capability V1	V١,١	S٥	٠,٨٤	S٣	٠,٥٠	S٤	٠,٦٧	S٣	٠,٥٠
	V١,٢	S٣	٠,٥٠	S٤	٠,٦٧	S٣	٠,٥٠	S١	٠,١٦
	V١,٣	S٤	٠,٦٧	S٣	٠,٥٠	S٤	٠,٦٧	S٤	٠,٦٧
	V١,٤	S٤	٠,٦٧	S١	٠,١٦	S٥	٠,٨٤	S٣	٠,٥٠
Product performance V2	V٢,١	S٤	٠,٦٧	S٢	٠,٣٣	S٣	٠,٥٠	S٥	٠,٥٠
	V٢,٢	S٦	١,٠٠	S٤	٠,٦٧	S٥	٠,٨٤	S٢	٠,٣٣
	V٢,٣	S٤	٠,٣٣	S٣	٠,٥٠	S٢	٠,٦٧	S١	٠,١٦
Processing level V3	V٣,١	S٥	٠,٨٤	S٤	٠,٦٧	S٤	٠,٦٧	S٣	٠,٥٠
	V٣,٢	S٤	٠,٦٧	S٤	٠,٦٧	S٤	٠,٦٧	S٢	٠,٣٣
	V٣,٣	S٤	٠,٦٧	S٣	٠,٥٠	S٥	٠,٨٤	S١	٠,١٦
	V٣,٤	S٥	٠,٨٤	S٣	٠,٥٠	S٤	٠,٦٧	S٣	٠,٥٠
	V٣,٥	S٤	٠,٦٧	S١	٠,١٦	S٣	٠,٥٠	S٢	٠,٣٣
Performance V4	V٤,١	S٤	٠,٦٧	S٤	٠,٦٧	S٣	٠,٥٠	S١	٠,١٦
	V٤,٢	S٤	٠,٦٧	S٢	٠,٣٣	S٣	٠,٥٠	S٣	٠,٥٠
	V٤,٣	S٤	٠,٦٧	S٣	٠,٥٠	S٥	٠,٨٤	S٢	٠,٣٣
	V٤,٤	S٥	٠,٨٤	S١	٠,١٦	S٤	٠,٦٧	S٢	٠,٣٣

Source: Authors

Table 5. Criteria adaptation strategy and corresponding data aggregation results

Adaptation strategy	Basic criterion	Key criterion	Important criterion	Important criterion	Important criterion	The “vast majority” of the guidelines
Fuzzy semantics	as many as possible	At least half	Mostly	Mostly	Mostly
Evaluation criteria-upstream	Green technology	Cost	Product quality	Agility ability	Service capability
Enterprise E2,1	0,5665	0,6725	0,9233	0,9499	0,7915	0,7609
Enterprise E2,2	0,4688	0,3639	0,5885	0,3067	0,5205	0,4353
Enterprise E2,3	0,6804	0,9388	0,3487	0,2984	0,4167	0,5050
valuation criteria-downstream		Processing level	Purchasing ability	Product performance	Performance
Enterprise E4,1		0,8039	0,6496	0,5750	0,7028	0,6681
Enterprise E4,2		0,6133	0,4263	0,4757	0,3810	0,4594
Enterprise E4,3		0,4589	0,4263	0,2835	0,3096	0,3567
Enterprise E4,4		0,7452	0,6496	0,5885	0,6496	0,6489

Source: Authors

The last column numbers in table 5, 0,7609, 0,4353 and 0,5050, indicate the priority values when the node enterprise E3,1 select an upstream partner among E2,1, E2,2, E2,3. And 0,6681, 0,4594, 0,3567, 0,6489 indicate the priority values when the node enterprise E3,1 selects a downstream partner among E4,1, E4,2, E4,3, E4,4. Traversing all the nodes enterprises, we can get the priority values of any node enterprises choosing upstream and downstream partners and partnership correlation between adjacent levels in supply chain, as shown in table 6.

Table 6. Partnership relationship

Evaluation of upstream node enterprises		Evaluation of downstream node enterprises		Relational degree of partnership
Node relationship	Weight	Node relationship	Weight
E1,1E2,1	1,0000	E1,1E2,1	0,6457	0,6457	0,4391
E1,1E2,2	1,0000	E1,1E2,2	0,2183	0,2183	0,1485
E1,1E2,3	1,0000	E1,1E2,3	0,6065	0,6065	0,4124
E2,1E3,1	0,7609	E2,1E3,1	0,6543	0,4979	0,5977
E2,1E3,2	0,4463	E2,1E3,2	0,4319	0,1928	0,2315
E2,1E3,3	0,6276	E2,1E3,3	0,2267	0,1423	0,1708
E2,2E3,1	0,4353	E2,2E3,1	0,5835	0,2815	0,4887
E2,2E3,2	0,5312	E2,2E3,2	0,3123	0,1659	0,2880
E2,2E3,3	0,6645	E2,2E3,3	0,1936	0,1286	0,2233
E2,3E3,1	0,5050	E2,3E3,1	0,7477	0,4073	0,4685
E2,3E3,2	0,3452	E2,3E3,2	0,3109	0,1073	0,1234
E2,3E3,3	0,6182	E2,3E3,3	0,5739	0,3548	0,4081
E3,1E4,1	0,6923	E3,1E4,1	0,6681	0,4764	0,3307
E3,1E4,2	0,6742	E3,1E4,2	0,4595	0,3098	0,2151
E3,1E4,3	0,7015	E3,1E4,3	0,3567	0,2503	0,1738
E3,1E4,4	0,6535	E3,1E4,4	0,6182	0,4040	0,2805
E3,2E4,1	0,4537	E3,2E4,1	0,6552	0,2973	0,2846
E3,2E4,2	0,4963	E3,2E4,2	0,6234	0,3077	0,2945
E3,2E4,3	0,5534	E3,2E4,3	0,5625	0,3113	0,2980
Evaluation of upstream node enterprises		Evaluation of downstream node enterprises		Relational degree of partnership
Node relationship	Weight	Node relationship	Weight
E3,3E4,1	0,3581	E3,3E4,1	0,5186	0,1857	0,1873
E3,3E4,2	0,4692	E3,3E4,2	0,2853	0,1339	0,1351
E3,3E4,3	0,4283	E3,3E4,3	0,6054	0,2593	0,2615
E3,3E4,4	0,6826	E3,3E4,4	0,6043	0,4125	0,4161
E4,1E5,1	0,6258	E4,1E5,1	0,5438	0,3403	0,7827
E4,1E5,2	0,5782	E4,1E5,2	0,1637	0,0945	0,2173
E4,2E5,1	0,6149	E4,2E5,1	0,6085	0,3742	0,5242
E4,2E5,2	0,5936	E4,2E5,2	0,5722	0,3397	0,4758
E4,3E5,1	0,6427	E4,3E5,1	0,5487	0,3526	0,7670
E4,3E5,2	0,4162	E4,3E5,2	0,2573	0,1071	0,2330
E4,4E5,1	0,6018	E4,4E5,1	0,2175	0,1716	0,3496
E4,4E5,2	0,5727	E4,4E5,2	0,5576	0,3193	0,6504

Source: Authors

Through a series of two-way interactive evaluations, node enterprises form a correlation partnership. The value indicates the cooperation willingness of two adjacent upstream and downstream partners. In general, the greater the correlation partnership value is the greater the cooperation intention. This can be used as a credential to build partnership in supply chain’s credentials.

According to what is presented in this paper, we can build or optimize the corresponding supply chain network from the actual three different situations. First, ignore the overall production requirements of the supply chain. The production capacity of each node enterprise is very large which is no constraint. In order to control the size of the supply chain alliance, dominant enterprises can set up a threshold value of partnership correlation, such as 0,25, and then get the supply chain network as shown in Figure 4.

Secondly, consider the overall production requirements of the supply chain. For example, the customer requirements are 7 million sets of dresses. The production capacity of each node enterprise is very large that is no constraint. Assume that each set consumes 1,5 meters of fabric, and the average weight of chemical fiber fabric is 9 kg/100 m. Ignore the middle material loss, thus processing and distribution of all the dresses will consume10,5 million meters of fabric and 945 tons of chemical fiber filament. The production task of each node enterprise can be distributed by proportion according to the partnership correlation. The specific data is shown in Figure 4, and the mark beside arrow.

Thirdly, consider the overall production requirements of the supply chain, the same as above. There is constraint to the production capacity of each node enterprise, and the specific data are marked below the node enterprise. This time, to fully consider the partnership correlation, the supply chain network can be built by solving the Equation (11) and Equation (18) through Lingo 8.0 software. The result is shown in Figure 5.

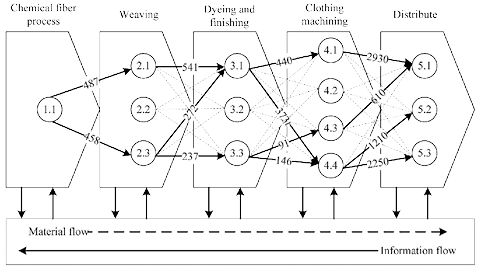
Figure 4. Supply chain network without capacity constraints.

Source: Authors

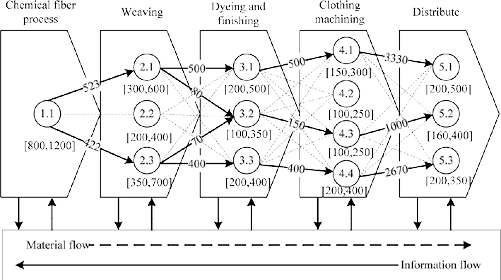
Figure 5. Supply chain network under constraints of production demands and capacity.

Source: Authors

Conclusions

This paper analyzed the dynamic partner selection and task allocation based on fuzzy theory under an uncertain environment and presented a corresponding decision model based on fuzzy theory. Due to the multiple attribute evaluation and decision-making in supply chain partners, fuzzy sets were used to describe the fuzzy uncertainty of qualitative and quantitative parameters in multi-attribute. Different dimension parameters were standardized. Based on this, this paper focused on studying fuzzy multiple attribute numerical rally and fuzzy comprehensive decision with supply chain strategy oriented, introduced and expanded by ordered weighted average OWA fuzzy operator which integrated the discrete data information, matched supply chain strategy, attributed importance classification and fuzzy semantic reasoning decision to determine the weight of OWA operator. By gathering the discrete numerical rally with OWA operator, the result could reflect the wishes and preferences of decision-makers. Based on this, the mutual dynamic evaluation in the process of supply chain partner selection was carried out, and then it was seen as the partner correlation. In addition, the dynamic optimal method of supply chain network with task allocation oriented was also discussed. Finally, the effectiveness of the method proposed in this paper was verified through a given simulation example.

Acknowledgements

This research is supported by the National Natural Science Fund Project of China (Grant No. 71401156), Zhejiang Provincial Natural Science Foundation of China (No. LY18G010001), achievements of Hangzhou philosophy and social science planning project (Grant No. Z18JC044), Key Laboratory of Electronic Business and Logistics Information Technology of Zhejiang Province (2011E10005) as well as Contemporary Business and Trade Research Center and Center for Collaborative Innovation Studies of Modern Business of Zhejiang Gongshang University of China (Grant No. 14SMXY05YB).

References

Ashayeri J., Tuzkaya G., Tuzkaya. R. R. (2012). Supply chain partners and configuration selection: An intuitionistic fuzzy Choquet integral operator based approach, Expert Systems with Applications, 39(3): 3642-3649. DOI: 10.1016/j.eswa.2011.09.055.

Chang S. L., Wang R. C., Wang S. Y. (2006) Applying fuzzy linguistic quantifier to select supply chain partners at different phases of product life cycle, International Journal of Production Economics, 100(3): 348-359. doi: 10.1016/j.ijpe.2005.01.002.

Chen T. G., Jiang Y. H. (2015) Research on operating mechanism for creative products supply chain based on game theory, Discrete and Continuous Dynamical Systems-Series S, 8(6): 1103-1112, DOI: 10.3934/dcdss.2015.8.1103.

Chen S. H., Wang P. W., Chen C. M., Lee H. T. (2010) An analytic hierarchy process approach with linguistic variables for selection of an R&D strategic alliance partner, Computers & Industrial Engineering, 58(2): 278-28. DOI: 10.1016/j.cie.2009.10.006.

Chou S. Y., Chang Y. H. (2008) A decision support system for supplier selection based on a strategy-aligned fuzzy SMART approach, Expert Systems with Applications, 32(1): 2241-2253, DOI: 10.1016/j.eswa.2007.03.001.

Filev D., Yager R R. (1995) A nalyticproperties of maximum entropy OWA operators, Information Sciences, 85(1-3): 11-27, DOI: 10.1016/0020-0255(94)00109-0.

He X. F., Ai X. Z., Jing Y W., Liu Y. Y. (2016a) Partner selection of agricultural products supply chain based on data mining, Concurrency and Computation-Practice & Experience, 28(4): 1246-1256, DOI: 10.1002/cpe.3625.

He Y. D., Wang X., Lin Y., Zhou F. L. (2016b) Optimal partner combination for joint distribution alliance using integrated fuzzy EW-AHP and TOPSIS for online shopping, Sustainability, 8(4), Article ID: 341.DOI: 10.3390/su8040341.

Huang M., Ip W. H., Yang H. M., Wang X. W., Lau H. C. W., Henry C. W. (2008) A fuzzy synthetic evaluation embedded tabu search for risk programming of virtual enterprises, International Journal of Production Economics, 116(1): 104-114, DOI: 10.1016/j.ijpe.2008.06.008.

Jiang K., Cao W. G., Yu Z. H. (2007) Study of Partner Selection Algorithm based on GAS and Fussy Decision-Making, Systems Engineering-Theory & Practice, 28(1):169-174. (in Chinese)

Ju C. H., Zhou G. L., Chen T. G. (2017) Disruption management for vehicle routing problem with time-window changes, International Journal of Shipping and Transport Logistics, 9(1): 4-28, DOI: 10.1504/IJSTL.2017.10000921.

Keshavarz G. M., Zavadskas E. K., Amiri M., Turskis Z. (2016) Extended EDAS method for fuzzy multi-criteria decision-making: An application to supplier selection, International Journal of Computers Communications & Control, 11(3): 358-371, DOI: 10.15837/ijccc.2016.3.2557.

Kumar M., Vrat P., Shankar R. (2004) A fuzzy goal programming approach for vendor selection problem in a supply chain, Computers & Industrial Engineering, 46(1): 69-85, DOI:10.1016/j.cie.2003.09.010.

Kumar M., Vrat P., Shankar R. (2006) A Fuzzy programming approach for vendor selection problem in a supply chain, International Journal of Production Economics, 101(2): 273-285, DOI: 10.1016/j.ijpe.2005.01.005.

Li S., Guo Y. J., Yi P. T. (2004) Partner Selection Based on Fuzzy Group Decision-Making for Virtual Enterprise Formation, Journal of Northeastern University, 25(1): 295-298. (in Chinese)

Li Q., Xu G. F. (2004) Application of the fuzzy semantic distance to supplier selection problem, Journal of Harbin Institute of Technology, 36(2): 1672-1675. (in Chinese)

Mikhailov L. (2002) Fuzzy analytical approach to partnership selection in formation of virtual enterprises, Omega, 30(5): 393-401, DOI: 10.1016/S0305-0483(02)00052-X.

Rezaei J. (2015) A two-way approach to supply chain partner selection, International Journal of Production Research, 53(16): 4888-4902. DOI: 10.1080/00207543.2014.1003663.

Wang H. S., Che Z. H. (2007) An integrated model for supplier selection decisions in configuration changes, Expert Systems with Applications, 32(6): 1132-1140. DOI: 10.1016/j.eswa.2006.02.015.

Wang T. C., Chen Y. H. (2007) Applying consistent fuzzy preference relations to partnership selection, Omega, 35(1): 384-388, DOI: 10.1016/j.omega.2005.07.007.

Wu C., Barnes D. (2014) Partner selection in agile supply chains: a fuzzy intelligent approach, Production Planning & Control, 25(10): 821-839, DOI: 10.1080/09537287.2013.766037.

Wu C., Barnes D. (2016) An integrated model for green partner selection and supply chain construction, Journal of Cleaner Production, 112(3): 2114-2132. DOI: 10.1016/j.jclepro.2015.02.023.

Wu D. D., Zhang Y. D., Wu D. X., OIson D. L. (2010) Fuzzy multi-objective programming for supplier selection and risk modeling: A possibility approach, European Journal of Operational Research, 200(3): 774-787, doi: 10.1016/j.ejor.2009.01.026.

Yeh W. C., Chuang M. C. (2011) Using multi-objective genetic algorithm for partner selection in green supply chain problems, Expert Systems with Applications, 38(4): 4244-4253, DOI: 10.1016/j.eswa.2010.09.091.

Zhang M., Mei G. B. (2015) Research on Selection of Suppliers in SCM Based on FAHP, Logistics Technology, 33(9): 116-118. (in Chinese)

Zhou J., Mou X. L. (2007) Model of fuzzy multi-objective integer programming for vendor selection under multi-product purchases, Industrial Engineering Journal, 10(4): 128-132. (in Chinese)

Attribution 4.0 International (CC BY 4.0) Share - Adapt